② 南方海洋科学与工程广东省实验室(广州),广东广州 511458;
③ 深圳市深远海油气勘探技术重点实验室(南方科技大学),广东深圳 518055;
④ 南方科技大学地球与空间科学系,广东深圳 518055
② Southern Marine Science and Engineering Guangdong Laboratory (Guangzhou), Shenzhen, Guangdong 511458, China;
③ Shenzhen Key Laboratory of Deep Offshore Oil and Gas Exploration Technology, Southern University of Science and Technology, Shenzhen, Guangdong 518055, China;
④ Department of Earth and Space Sciences, Southern University of Science and Technology, Shenzhen, Guangdong 518055, China
随着非常规油气资源逐步成为中国能源领域勘探开发的主战场之一,储层压裂改造在现有经济和技术条件下显现出巨大的应用潜力[1-2]。但目前中国非常规油气储层高效开发面临埋藏深、有效动用难度大、地质与开发条件复杂、成本高等挑战,对储层压裂改造效果评价技术提出了更高的要求[3]。作为提高采收率的主要技术手段之一,地球物理储层压裂监测广泛应用于非常规油气资源勘探开发领域。其中,通过监测压裂改造过程产生的微地震活动,获取储层时空展布特征,可提供评价压裂效果的关键信息[4-5]。然而,储层压裂过程中压裂区围岩或储层破碎严重,若储层介质较软,微地震信号会很微弱;若储层介质较硬,则导致大量微震噪声产生,资料解释困难[6]。基于导电流体和裂缝中的压裂剂在导电性方面的敏感性,电磁法正逐步应用于储层压裂改造评价领域[7],其中高效、高精度的压裂监测技术是关键。
地面观测系统是当前地球物理电磁储层压裂监测领域应用较广泛的数据采集方式之一,其通过在地面设置电性源或磁性源激发一次场、在地面采用接地电极或感应器观测电磁信号,进行储层压裂监测[8-9]。这种间接式的供电及观测系统不可避免地受到围岩介质的信号衰减作用及地表环境干扰的影响,并非最佳观测方式。井筒电磁法将供电或接收端置于地下井孔内,由于观测系统靠近压裂监测目标体,会抑制信号的衰减作用,在一定程度上弥补了上述地面观测系统应用于储层压裂监测领域的缺陷[10-11]。基于将供电或观测系统靠近压裂监测目标体,进而提高观测信号幅值、提高压裂监测精度的理念[12],本文开展了接触式电法储层压裂监测的研究。
对地球物理勘探目标体而言,存在天然的或者人工揭露的良导体露头、地下水出露点等可接入电流的一类目标体。传统充电法正是利用直接供电的优势,通过两个测量电极观测充电电场的分布及变化规律,推测、监测良导体的物性及空间分布[13-14]。由于充电介质的范围、形状与观测电位异常分布特征较相似,通常可以根据观测电位或电位梯度异常推断实际充电介质范围,可广泛应用于金属勘探、水文地质、工程地质、注液驱油及压裂驱油、环境监测及农业地球物理等勘探领域。但地面观测的电位或电位梯度异常通常较微弱,抗干扰能力也弱,储层压裂监测精度不能满足复杂油气储层地质目标监测的需求[15]。因而,联合电阻率和极化率参数,开展接触式直流激发极化法复杂地质目标体地球物理压裂监测具有重要的现实意义。
传统充电法以稳定电流场中理想导体(电阻率为零)的等位体为前提,如金属矿体或高矿化度地下水,相对于围岩电阻率很低,可近似看成理想导体。通常也将非理想导体(不等位体或有损耗介质)近似为理想导体。但实际应用中,充电介质的电阻率通常不为零,即有损耗介质目标体,而目前尚缺乏一种有效针对有损耗介质接触式激发极化法的高效数值模拟方法。目前,积分方程类[16-17]和微分方程类[18]数值模拟方法广泛应用于三维直流电数值模拟。但积分方程法仅局限于规则目标体模拟;微分方程有限差分法对复杂结构体的模拟精度低;微分方程有限元法可高效、高精度地模拟复杂结构体,但所需的计算内存较前两种方法大。总体上,由于计算机硬件、计算能力的提高和数值计算方法的进步,有限元法已得到广泛应用[19]。
本文基于三维交错四面体网格有限元法实现了接触式直流激发极化法的数值模拟。首先介绍有限元算法的实现步骤和关键技术,包括接触式场源离散、有损耗介质电流定义方法和接触式激电极化率及电阻率的计算方法;然后通过数值算例和土槽试验算例验证算法的可行性及有效性,并与传统中间梯度激发极化法对相同模型的模拟结果进行对比;最后,将此方法应用于沁水盆地南部某煤气层压裂监测区的三维模型,通过与地面传统中间梯度法三维直流电阻率及极化率模拟结果进行对比,验证了方法的有效性。
1 方法理论 1.1 接触式激发极化法原理接触式激发极化法的具体观测方式为:电极一端置于目标体内部供电,另一端置于无穷远,这种方式对场地的环境要求较低,易于实施。在目标体内部直接供电,电流主要聚集在具有流动性和连续性的目标体范围,形成最高强度的一次场激励[12]。接触式供电的一次场电场与点电流源场相近,其对目标体分布不存在契合度问题(传统激电需要的均匀场),理论上目标体分布范围与供电电流聚集范围是一致的,可对任意形状的目标体进行有效的最佳一次场激励。接触式供电装备可直接利用现有传统激发极化法大功率激电供电系统,因而其实施过程是现实的、可行的。地下任何赋存液体的地方均可发生上述微观的物理、化学和电化学活动,能否用于勘探取决于液体包含的微观双相介质层是否足以形成可观的电位异常。
以上因素可能是传统激发极化法间接供电和间接观测在规模小、赋存深度大及观测环境复杂的油气储层压裂监测领域效果不佳的主要原因。在本文提出的接触式供电或观测条件下,这种化学的、电化学的活动将更强烈,这些规模小、赋存深度大及观测环境复杂的液态储存体周围有无数微观双电层发生叠加,足以形成可观的激发极化电位异常。
1.2 基于有限单元法的接触式电法模拟假设充电点S的坐标为(xs, ys, zs),供电电流强度为Itotal,对任意形状三维有损耗介质区域采用交错四面体网格剖分(图 1),其电阻率可随剖分单元网格位置的变化而变化,记为ρq,这里q表示网格编号, 围岩介质电阻率为ρb。将剖分单位网格视为点电源所在位置,网格q内的电流强度记为Iq。地面观测点坐标为(xa, ya, za)。剖分单位网格节点接触式供电电源条件下引起的总电位为u。
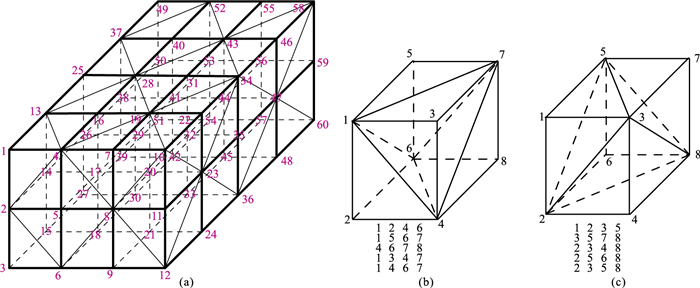
|
图 1 交错四面体网格剖分示意图 (a)2×3×4规则六面体剖分;(b)、(c)两种四面体网格剖分方式图中数字表示节点编号,图b、图c下方数字组合表示四面体组合节点 |
以电流强度Itotal进行充电时,任意形状三维有损耗介质区域的第q个剖分单元网格的点电源电流强度系数为
| $ I_{q}=\left(I_{\mathrm{total}} \times \frac{1}{r_{\mathrm{s}, q}} \times \frac{\rho_{\mathrm{b}}}{\rho_{q}}\right)^{-1} $ | (1) |
式中rs,q为充电点S到第q个剖分单元网格点电源中心点的距离。接触式充电下的总电位u满足边值问题
| $ \left\{\begin{array}{l} \nabla \cdot\left(\frac{1}{\rho} \nabla u\right)=\sum\limits_{q=1}^{N}\left[-\frac{4 {\rm{ \mathsf{ π} }}}{\omega_{q}} I_{q} \delta(q)\right] \in \boldsymbol{\varOmega} \\ \frac{\partial u}{\partial \boldsymbol{n}}=0 \quad \in \boldsymbol{\varGamma}_{\mathrm{s}} \\ \frac{\partial u}{\partial \boldsymbol{n}}+\frac{u}{r_{2}-r_{1}}\left[\frac{r_{2}}{r_{1}} \cos \left(\boldsymbol{r}_{1}, \boldsymbol{n}\right)-\frac{r_{1}}{r_{2}} \cos \left(\boldsymbol{r}_{2}, \boldsymbol{n}\right)\right]=0 \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \in \boldsymbol{\varGamma}_{\infty} \end{array}\right. $ | (2) |
式中:ρ表示剖分网格电阻率;N为网格剖分总数;ωq为区域Ω对电流源点Iq所张的立体角;Гs和Г∞分别为区域Ω的地面边界和地下无穷远边界;n为边界的法向向量方向;δ为狄拉克函数;r1和r2分别为计算点至供电点A、B的空间距离矢量,且r1=|r1|, r2=|r2|;cos(·, ·)为方向余弦函数。
通过采用有限单元法的线性插值、单元积分、边界积分,最终总体合成、再扩展成由全体节点组成的矩阵,并对全部单元相加,得
| $ \begin{aligned} F(u) &=\sum F_{\mathrm{e}}(u) \\ &=\sum \frac{1}{2 \rho} \boldsymbol{u}_{\mathrm{e}}^{\mathrm{T}}\left(\boldsymbol{K}_{1 \mathrm{e}}+\boldsymbol{K}_{2 \mathrm{e}}\right) \boldsymbol{u}_{\mathrm{e}}-\sum\limits_{q=1}^{N} I_{q} u_{q} \\ &=\sum \frac{1}{2} \boldsymbol{u}_{\mathrm{e}}^{\mathrm{T}} \boldsymbol{K}_{\mathrm{e}} \boldsymbol{u}_{\mathrm{e}}-\sum\limits_{q=1}^{N} I_{q} u_{q} \\ &=\sum \frac{1}{2} \boldsymbol{u}^{\mathrm{T}} \overline{\boldsymbol{K}_{\mathrm{e}}} \boldsymbol{u}^{\mathrm{T}} \boldsymbol{p} \\ &=\frac{1}{2} \boldsymbol{u}^{\mathrm{T}} \sum \overline{\boldsymbol{K}_{\mathrm{e}}} \boldsymbol{u}-\boldsymbol{u}^{\mathrm{T}} \boldsymbol{p} \\ &=\frac{1}{2} \boldsymbol{u}^{\mathrm{T}} \boldsymbol{K} \boldsymbol{u}-\boldsymbol{u}^{\mathrm{T}} \boldsymbol{p} \end{aligned} $ | (3) |
式中:u是全部节点u组成的列向量;Ke=(K1e+K2e)/ρ,其中e、1e、2e分别表示总单元积分、单元积分及边界积分;K=∑Ke,其中Ke是Ke的扩展矩阵;p=(0,I1,I2,…,Iq,0)T,其中非零元素为充电点源所在节点的电流值,其余节点均为零。
令式(3)的变分为0,得到线性方程组
| $ \boldsymbol{K u}=\boldsymbol{p} $ | (4) |
采用预条件共轭梯度超松弛迭求解式(4)方程组,得到u。再通过等效电阻率公式求解考虑激电效应下的u,根据极限极化率公式可计算得到地面观测的极化率值。
1.3 视电阻率的计算作为充电有损耗介质的电性参数之一,地面观测的充电有损耗介质视电阻率异常的计算一直是一个具有挑战性的课题。由于充电有损耗介质源的存在,传统的视电阻率计算方法不能直接应用于接触式激发极化法视电阻率的计算。使用其他的观测装置(如Wenner装置)的电阻率层析成像方法,并将其与传统充电法观测结果结合、相辅相成进行综合解释是比较常用的野外勘探方案[20-21]。目前尚缺乏一种有效的针对有损耗介质充电情况下地面观测视电阻率的计算方法。为此,本文提出了一种计算在有耗介质内注入电流下接触式激发极化法视电阻率的近似计算方法。这种方法的思路是假定测量的电势等于充电介质和周围背景介质的电势积分综合响应。接触式激发极化法的视电阻率计算公式为
| $ \rho_{\mathrm{s}}^{\prime}=\frac{U_{\mathrm{s}}}{U_{\mathrm{b}}} \times \rho_{\mathrm{b}} $ | (10) |
式中:Us表示地面观测的包含充电介质和围岩的综合响应的电势;Ub是围岩介质空间引起的电势响应。通常,油气监测领域考虑近似均匀或近似层状围岩介质,其模型及参数可从油气藏监测前期的地质及钻孔资料等信息获得,从而可用数值模拟或模拟实验获得围岩介质的纯电势异常响应,而ρb的空间分布亦可以通过岩心物性测试等手段获得。因此,式(5)可应用于实际油气勘探监测领域。
2 数值算例 2.1 电位差理论上,采用接触式供电场源可提高目标体响应的幅值,而地面供电场源、充电法场源等传统电源的响应较弱。为此,开展不同场源激励的电位差模拟,并进行对比研究。
图 2为三种场源(传统充电法、中间梯度激电法及本文接触式激电法)观测系统示意图。其中,椭球体模型三方向(x、y、z)轴长分别为20、20、4m,其中心点位于坐标原点(0,0,0),电阻率和极化率分别为25Ω·m和3.2%。均匀半空间(围岩)介质的电阻率和极化率分别为100Ω·m和1.0%。传统充电法及本文接触式激电法的接入电流点坐标为x=-10m,y=12m,中间梯度激电法的地面供电电极坐标为x=38m,y=-38m,用单位电流(1A)进行供电。
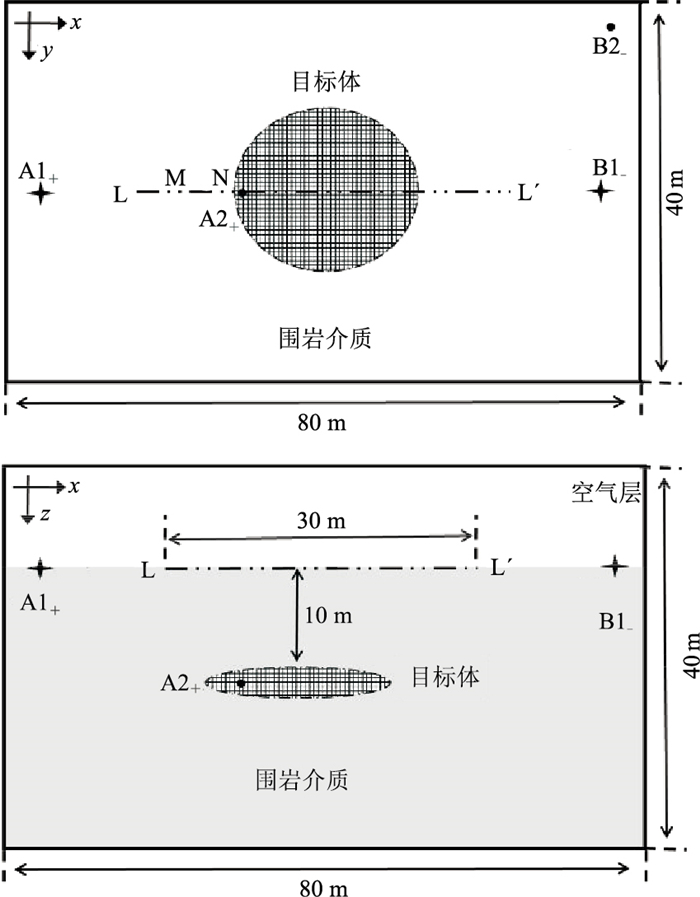
|
图 2 不同场源观测系统示意图 上为平面图,下为剖面图。A1+和B1-分别是传统充电法供电系统的正极和负极,一般布置于测线两端;M、N是中间梯度法测量电极对;A2+和B2-是接触式激电电极对,前者接触目标体,后者置于无穷远。LL′表示测线。图 4同。 |
图 3为上述三种类型场源下,在考虑激电效应与未考虑激电效应两种条件下模拟计算的总电位差△u曲线对比。由图可见,本文接触式场源下的总电位差比其他两种传统方法的极大值高数百倍,且传统方法总电位差的极值点位置对应供电点,而本文方法的高幅值范围对应目标体的水平范围(-10~10m)。根据极限极化率计算公式,总电位差幅值越大,抗干扰能力越强,极化率的计算精度就越高。由此,验证了本文接触式激电方法的可行性及有效性。
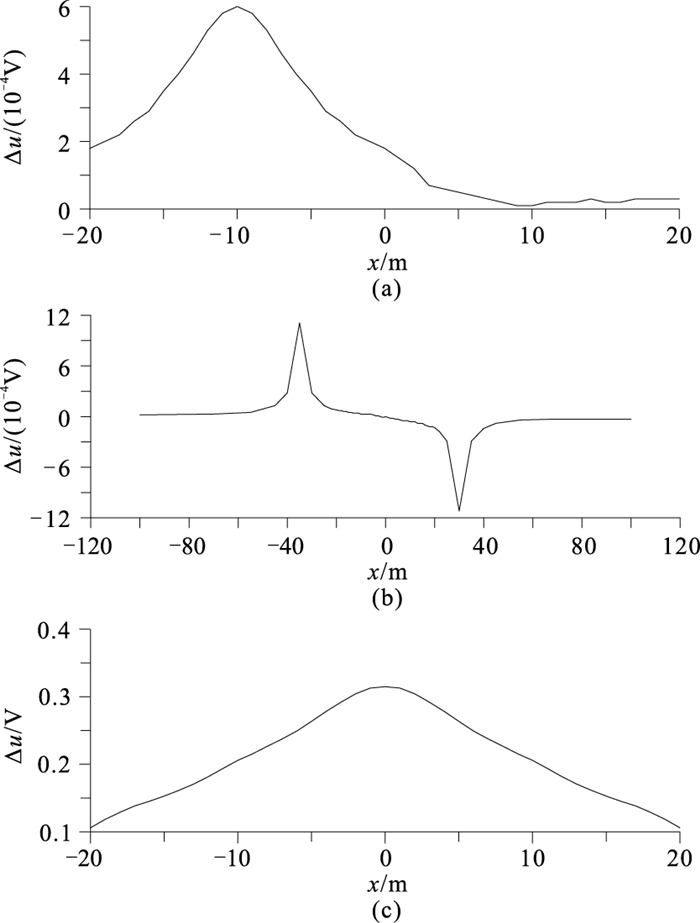
|
图 3 不同场源下考虑激电效应与不考虑激电效应的总电位差曲线 (a)传统充电法(点源);(b)中间梯度激发极化法(双点源);(c)接触式损耗介质源 |
由于目前鲜见针对充电有损耗介质极化率计算解析解的研究,本文采用土槽物理模拟实验验证数值模拟算法的正确性。图 4为土槽模拟实验模型及观测系统示意图。其中极化目标体为实地采集样品填入,经物性测试,其电阻率和极化率分别为10Ω·m和3.2%;围岩介质电阻率为40Ω·m,极化率为1.0%。极化率观测系统正负交替供电脉冲宽度为8s,断电延迟为200ms,供电电流为2A。

|
图 4 土槽物理模拟模型及观测系统示意图 (a)平面图;(b)剖面图 |
图 5是采用接触式激发极化法的视电阻率和视极化率物理模拟结果及数值模拟结果,可见物理模拟结果与数值模拟结果吻合较好,视电阻率和视极化率曲线的拟合误差均低于5%。另外,模型边界处两者差异较大,这是因为数值模拟无法仿真现实中的边界渗漏区域的双电层效应。与传统中间梯度方法物理模拟结果对比可见,接触式激发极化法可获得更高幅值、更准确的视电阻率及视极化率异常。
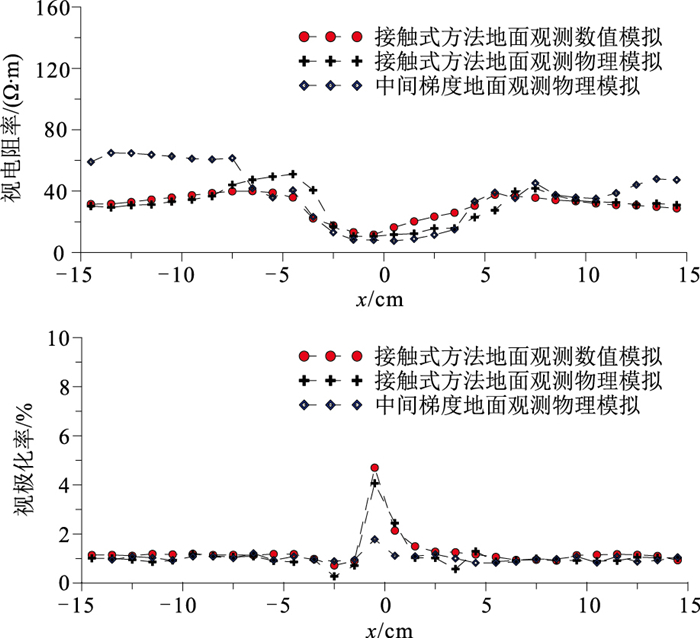
|
图 5 本文数值模拟与土槽物理模拟不同观测方法视电阻率(上)和视极化率(下)曲线 |
基于已有的沁水盆地南部某煤层气压裂监测三维电性模型[18],本文采用上述三维有限单元法数值模拟,进一步验证接触式激发极化法对复杂储层模型的压裂监测效果,并分析本文方法的有效性。
复杂储层电性模型来源于于沁水盆地南部开采区域,该区域地质条件复杂,煤层的渗透率较高且含气量高,煤层埋藏较浅、厚度较大[22-23]。压裂后,压裂剂赋存空间相对于上覆和下伏地层而言为富水层,呈现低阻特征[24],而煤层气区域通常为高阻特征,因而具备较好的开展物探方法监测的前提[25-26]。常规地面直流电类方法正是基于上述电阻率异常特征开展煤层气压裂监测研究,但无法有效揭示复杂储层压裂进程的细微特征[18]。煤层气藏本身的极化率较低,当前基于激发极化效应开展煤层气探测的主要思路是通过探测煤层气渗漏或扩散外围次生矿物的激电效应,探测原生煤层气的空间分布[27]。不同地质条件作用下,煤层气渗漏形成的激电效应模型复杂多变,传统激电方法监测具有一定的局限性[28]。煤层气藏属于连续型储层,煤层压裂改造可通过压裂剂将井孔与煤层天然裂隙有效连通,因而具备本文提出的接触式激发极化法的基本观测条件,即通过井孔将直流电流导入压裂剂区域,电流会在低阻压裂剂内流动并形成高极化异常,这种流动性和连续性形成的激电异常就是本文方法研究的主要对象。
沁水盆地南部煤层气模型的计算范围为2km×2km×1km,煤层气空间分布范围为x=-76~92m,y=-50~50m,z=124~190m。图 6是模型示意图,可见煤层气模型整体呈双峰—单谷形态,在x轴负方向的埋藏较浅,坡度较缓,隆起区域(x=-30~-20m)煤层气厚度较小,坐标原点为煤层气模型低谷的中心;在x轴正方向埋藏较深,坡度较大,在隆起区域(x=4~20m)煤层气厚度较大。设模型围岩电阻率为100Ω·m,极化率为1.0%;煤层气藏电阻率为5000Ω·m,极化率为1.0%;压裂剂电阻率为1Ω·m,极化率为6.0%[18, 22]。接触式激发极化法探测的供电点坐标为(-74m, 0, 150m),供电电流强度为20A,地面观测测线沿x方向。x方向测点布设范围为-88~124m,点距为4m;y方向观测范围为-80~80m,测线间隔为5m。
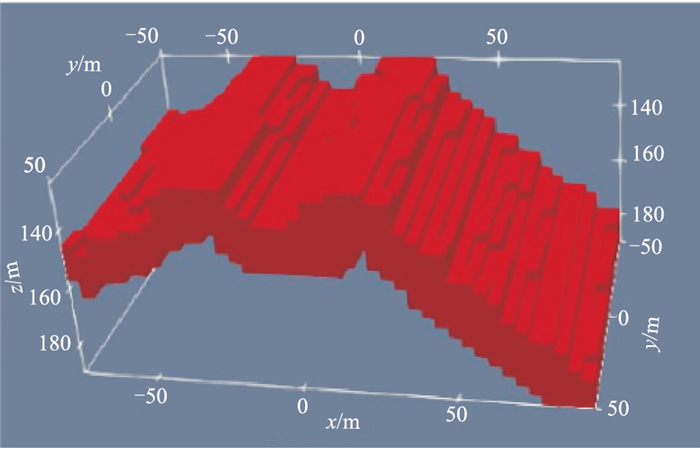
|
图 6 沁水盆地南部煤层气模型示意图[18] |
图 7为模型压裂完成、充满压裂剂状态时接触式激发极化法的计算视电阻率及视极化率平面图。由图 7a可见,视电阻率在x方向上呈现分段特征,即-70~20m区域内呈由中高阻向低阻变化的特征,20m附近出现视电阻率极大值,20~100m区域内出现次低阻异常。上述特征与接触式激化法的电流密度在起伏模型中的分布特征较吻合,即上倾斜方向顶部区域电流密度低,视电阻率较小;下倾斜方向底部区域电流密度高,视电阻率出现极大值。另外,y方向25~50m范围高电阻率值异常范围较大,这是因为此处模型厚度较大。总体上,相比传统直流电方法[18]而言,本文接触式激发极化法计算得到的视电阻率异常提供了更详细的煤层气空间信息。然而,仅依据视电阻率异常无法对该煤层气模型的双峰—单谷特征进行细节描述。图 7b是接触式激发极化法下的视极化率异常,可见视极化率异常分段特征在x方向上更明显,而且模型两端的中高视极化率区域较明显。因此,模拟结果中的两端高极化率、中间低极化率异常与模型中部的双峰—单谷构造特征吻合;而x方向两端不同坡度的起伏特征在图 7b中则对应不同异常幅度的变化。因此,接触式激发极化法模拟结果可有效描述复杂储层的精细空间特征。
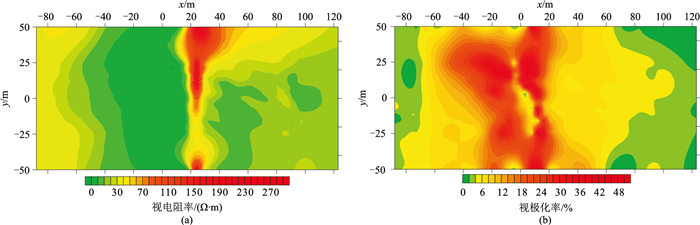
|
图 7 压裂完成(煤层气模型完全充满压裂剂)状态下地面接触式激发极化法计算视电阻率(a)及视极化率(b)平面图 |
为进一步验证本文方法对复杂储层压裂进程监测的数值模拟效果,建立了与沁水盆地南部煤层气压裂三个阶段相对应的模型(图 8上):压裂初始阶段,即压裂剂充满模型左侧倾斜区域;压裂中期阶段,即仅模型右端下倾斜区域密闭储层空间充满煤层气;完成阶段,即整个储层充满压裂剂。本算例接触式激发极化法观测系统采用与图 7所示算例相同参数,并与传统中间梯度激电地面观测结果进行对比分析。中间梯度激电系统的供电极距为800m,观测网度与接触式激发极化法一致。为便于对比分析,模拟结果仅展示y=16m剖面(图 8)。从图 8a可见,在压裂初始阶段,接触式激发极化法观测的视电阻率曲线在压裂剂充满区域呈现低阻、高极化异常特征;在压裂剂与煤层气接触面附近出现视电阻率和视极化率极值突变特征;在充满煤层气区域出现中高阻、低极化率异常特征。随着压裂进程的持续开展,压裂中期阶段对比结果见图 8b,可见接触式激发极化法的低阻、高极化异常区域及极值突变区域与压裂剂空间分布较一致。此阶段,接触式视电阻率极值异常主要为右端倾斜煤层气顶端所致,视极化率异常与模型中部的双峰—单谷形状较吻合。图 8c所示为压裂完成阶段的模拟结果,由图可见,接触式激发极化法模拟的视电阻率和极化率异常与煤层气模型的空间分布较吻合。总体上,对比接触式激发极化法与传统中间梯度激电法的视电阻率、视极化率模拟结果可见,传统中间梯度激电结果异常幅值较小,无法反映压裂进程状态的变化;接触式激发极化法可有效指示压裂不同阶段模型的细节变化。因此,本文提出的方法在煤层气压裂监测领域具有重要的实用价值。
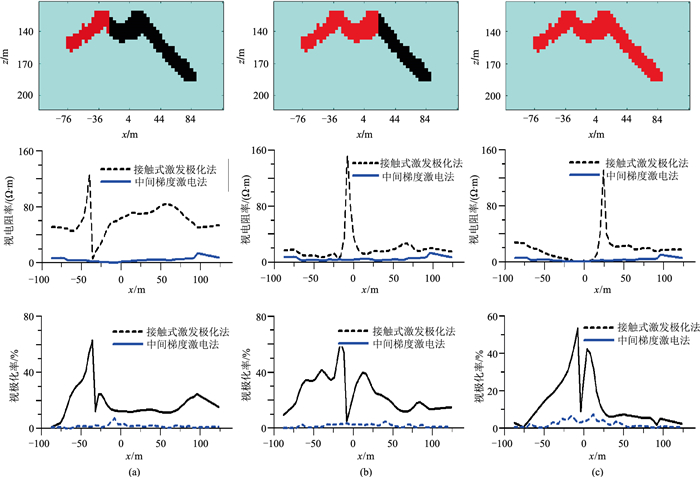
|
图 8 煤层气模型压裂进程不同阶段(上)的模拟视电阻率(中)及视极化率(下)曲线 (a)初始阶段;(b)中期阶段;(c)完成阶段上图中红色代表压裂剂,黑色代表煤层气,蓝色代表背景介质。 |
基于高效、高精度油气储层压裂监测需求的现实问题,本文开展了接触式激发极化法油气储层监测有限元数值模拟研究。从理论上系统阐述了接触式激发极化法应用于油气储层压裂监测领域的可能性及预期有效性,指出在压裂剂中接触式注入电流可形成有效高幅值的激电效应,压裂监测具有较好的物性基础。通过理论模型计算交错四面体离散网格单位电流分布,实现了接触式场源的有限元法数值模拟算法。定义了接触式激发极化法视电阻率计算公式,通过不同方法场源总电位差算例、土槽模拟实验算例及煤层气压裂监测算例分析,验证了接触式激发极化法作为储层压裂监测技术的可行性和实用性。
| [1] |
贾承造. 中国石油工业上游科技进展与未来攻关方向[J]. 石油科技论坛, 2021, 40(3): 1-10. JIA Chengzao. China's petroleum industrial upstream technological development and its future research areas[J]. Petroleum Science and Technology Forum, 2021, 40(3): 1-10. |
| [2] |
邹才能, 赵群, 王红岩, 等. 非常规油气勘探开发理论技术助力我国油气增储上产[J]. 石油科技论坛, 2021, 40(3): 72-79. ZOU Caineng, ZHAO Qun, WANG Hongyan, et al. Theory and technology of unconventional oil and gas exploration and development helps China increase oil and gas reserves and production[J]. Petroleum Science and Technology Forum, 2021, 40(3): 72-79. DOI:10.3969/j.issn.1002-302x.2021.03.007 |
| [3] |
刘国强. 非常规油气时代测井评价技术的挑战与对策[J/OL]. 石油勘探与开发, 2021(5): 1-12(2021-07-28)[2022-04-08]. http://kns.cnki.net/kcms/detail/11.2360.TE.20210728.0857.002.html LIU Guoqiang. Challenges to log evaluation in unconventional petroleum era and countermeasures[J]. Petroleum Exploration and Development, 2021(5): 1-12(2021-07-28)[2022-04-08]. http://kns.cnki.net/kcms/detail/11.2360.TE.20210728.0857.002.html |
| [4] |
赵超峰, 张伟, 田建涛, 等. 基于微地震监测技术的油田开发方案调整及效果——以辽河探区J2块为例[J]. 地球物理学进展, 2022, 37(1): 320-327. ZHAO Chaofeng, ZHANG Wei, TIAN Jiantao, et al. Adjustment and effect of oilfield development based on microseismic monitoring technology: a case study from the block J2 in Liaohe exploration area[J]. Progress in Geophysics, 2022, 37(1): 320-327. |
| [5] |
陈海潮, 唐有彩, 钮凤林, 等. 利用微地震参数评估水力压裂改造效果研究进展[J]. 石油科学通报, 2016, 1(2): 198-208. CHEN Haichao, TANG Youcai, NIU Fenglin, et al. Recent advances in microseismic monitoring and implications for hydraulic fracturing mapping[J]. Petroleum Science Bulletin, 2016, 1(2): 198-208. |
| [6] |
TAFTI T A, SAHIMI M, AMINZADEH F, et al. Use of microseismicity for determining the structure of the fracture network of large-scale porous media[J]. Physical Review E, 2013, 87(3): 032152. DOI:10.1103/PhysRevE.87.032152 |
| [7] |
BESKARDES G D, WEISS C J. Modelling responses of 3-D complex fracture networks[J]. Geophysical Journal International, 2018, 214(3): 1901-1912. DOI:10.1093/gji/ggy234 |
| [8] |
张龙, 张继锋, 黄日华, 等. 基于双二次插值的CSAMT2.5维有限元数值模拟及在煤层气勘探可行性研究[J]. 地球物理学进展, 2017, 32(5): 2140-2147. ZHANG Long, ZHANG Jifeng, HUANG Rihua, et al. Finite element forward modeling of 2.5-D CSAMT based on biquadratic interpolation and research on feasibility of CBM exploration[J]. Progress in Geophysics, 2017, 32(5): 2140-2147. |
| [9] |
张林, 刘旭宁, 郑健, 等. 激发电磁法在水力压裂监测中的应用[C]. SPG/SEG南京2020年国际地球物理会议论文集, 2020, 1407-1410. ZHANG Lin, LIU Xuning, ZHENG Jian, et al. Application of excited electromagnetic method in hydraulic fracturing monitoring[C]. Proceedings of SPG/SEG Nanjing 2020 International Geophysical Conference, 2020, 1407-1410. |
| [10] |
李静和. 用于油气藏勘探的井筒电磁法反演算法研究[D]. 湖北武汉: 中国地质大学, 2015.
|
| [11] |
李静和, 何展翔, 孟淑君, 等. 三维地形频率域井筒电磁场区域积分方程法模拟[J]. 物理学报, 2019, 68(14): 247-256. LI Jinghe, HE Zhanxiang, MENG Shujun, et al. Domain decomposition based integral equation modeling of 3-dimensional topography in frequency domain for well electromagnetic field[J]. Acta Physica Sinica, 2019, 68(14): 247-256. |
| [12] |
李静和, 何展翔, 杨俊, 等. 针对渗漏型目标的新型接触式激电法及应用[J]. 石油地球物理勘探, 2021, 56(3): 659-669. LI Jinghe, HE Zhanxiang, YANG Jun, et al. Contact-type induced polarization and its application for detecting leakage[J]. Oil Geophysical Prospecting, 2021, 56(3): 659-669. |
| [13] |
何展翔, 江汶波. 井中充电多参数网络监测方法及正反演研究[J]. 石油地球物理勘探, 2004, 39(增刊1): 135-138. HE Zhanxiang, JIANG Wenbo. Research on multi-parameter network monitoring method and forward and inverse modeling of well charging[J]. Oil Geophysical Prospecting, 2004, 39(S1): 135-138. |
| [14] |
张炯, 李雪松. 井—地充电法地表电位分布正演数值模拟研究[J]. 物探化探计算技术, 2010, 32(3): 284-291. ZHANG Jiong, LI Xuesong. Forward numerical mo-deling of surface electrical potential distribution by the borehole-to-surface mise-à-la-masse method[J]. Computing Techniques for Geophysical and Geoche-mical Exploration, 2010, 32(3): 284-291. DOI:10.3969/j.issn.1001-1749.2010.03.011 |
| [15] |
曹辉, 王绪本, 何展翔, 等. 水平层状介质条件下的井地电磁场响应计算[J]. 石油地球物理勘探, 2012, 47(2): 338-343. CAO Hui, WANG Xuben, HE Zhanxiang, et al. Calculation of borehole-to-surface electromagnetic responses on horizontal stratified earth medium[J]. Oil Geophysical Prospecting, 2012, 47(2): 338-343. |
| [16] |
LI J H, HE Z X, XU Y X. Three-dimensional numerical modeling of surface-to-borehole electromagnetic method for monitoring reservoir[J]. Applied Geophysics, 2017, 14(4): 559-569. |
| [17] |
李静和, 何展翔. 地井垂直电磁Walkaway剖面法油藏开发三维模型电场响应特征[J]. 石油地球物理勘探, 2012, 47(4): 653-664. LI Jinghe, HE Zhanxiang. 3D electrical response characteristics modeling for surface-to-borehole vertical electromagnetic Walkaway profile[J]. Oil Geophysical Prospecting, 2012, 47(4): 653-664. |
| [18] |
赵宁, 黄明卫, 申亚行, 等. 高阶自适应有限元三维直流电阻率正演方法及其在沁水盆地煤气层压裂监测中的应用[J]. 石油地球物理勘探, 2021, 56(1): 209-216. ZHAO Ning, HUANG Mingwei, SHEN Yahang, et al. Forward modeling of 3D DC resistivity based on high-order adaptive finite element and its application in Qinshui basin[J]. Oil Geophysical Prospecting, 2021, 56(1): 209-216. |
| [19] |
司兆伟, 邓少贵, 林发武, 等. 泥浆侵入各向异性地层阵列侧向测井响应数值模拟[J]. 石油地球物理勘探, 2020, 55(1): 187-196. SI Zhaowei, DENG Shaogui, LIN Fawu, et al. Nume-rical simulation of array laterolog responses in anisotropic formation with mud invasion[J]. Oil Geophysical Prospecting, 2020, 55(1): 187-196. |
| [20] |
CARLO L D, PERRI M T, CAPUTO M C, et al. Characterization of a dismissed landfill via electrical resistivity tomography and mise-à-la-masse method[J]. Journal of Applied Geophysics, 2013, 98: 1-10. DOI:10.1016/j.jappgeo.2013.07.010 |
| [21] |
LING C, REVIL A, ABDULSAMAD F, et al. Leaka-ge detection of water reservoirs using a mise-à-la-masse approach[J]. Journal of Hydrology, 2019, 572: 51-65. DOI:10.1016/j.jhydrol.2019.02.046 |
| [22] |
李琼, 何建军, 曹均. 沁水盆地和顺地区煤层气储层物性特征[J]. 石油地球物理勘探, 2013, 48(5): 734-739. LI Qiong, HE Jianjun, CAO Jun. Physical characte-ristics of coalbed methane reservoir in Heshun area of Qinshui basin[J]. Oil Geophysical Prospecting, 2013, 48(5): 734-739. |
| [23] |
闫文华, 陈宗翠, 马喜梅, 等. 煤层气地震解释技术应用及效果——以沁水盆地郑庄区块三维为例[J]. 石油地球物理勘探, 2012, 47(增刊1): 66-71. YAN Wenhua, CHEN Zongcui, MA Ximei, et al. 3D seismic interpretation of coalbed methane in Zhengzhuang block, Qinshui basin[J]. Oil Geophysical Prospecting, 2012, 47(S1): 66-71. |
| [24] |
赵睿, 范涛, 李宇腾, 等. 钻孔瞬变电磁探测在水力压裂效果检测中的应用[J]. 煤田地质与勘探, 2020, 48(4): 41-45. ZHAO Rui, FAN Tao, LI Yuteng, et al. Application of borehole transient electromagnetic detection in the test of hydraulic fracturing effect[J]. Coal Geology & Exploration, 2020, 48(4): 41-45. DOI:10.3969/j.issn.1001-1986.2020.04.006 |
| [25] |
陈理, 秦其明, 王楠, 等. 低频电磁探测技术在煤层气富集区的应用[J]. 石油地球物理勘探, 2018, 53(5): 1095-1102. CHEN Li, QIN Qiming, WANG Nan, et al. Application of low-frequency magnetotelluric detection in coalbed methane enrichment areas[J]. Oil Geophysical Prospecting, 2018, 53(5): 1095-1102. |
| [26] |
王楠, 赵姗姗, 惠健, 等. 沁水盆地南部煤层气藏三维音频大地电磁探测[J]. 地球物理学进展, 2016, 31(6): 2664-2676. WANG Nan, ZHAO Shanshan, HUI Jian, et al. Three-dimensional audio magnetotelluric sounding of coal-bed methane reservoirs in southern Qinshui basin[J]. Progress in Geophysics, 2016, 31(6): 2664-2676. |
| [27] |
王妙月, 王谦身, 石昆法, 等. 天然气直接探测技术机理基础研究[J]. 天然气地球科学, 1996, 7(6): 1-65. WANG Miaoyue, WANG Qianshen, SHI Kunfa, et al. Basic research on mechanism of natural gas direct detection technology[J]. Natural Gas Geoscience, 1996, 7(6): 1-65. |
| [28] |
陈进超. 煤层气富集区非地震综合物探技术及试验研究[D]. 四川成都: 成都理工大学, 2012.
|



 李静和,广西壮族自治区桂林市雁山区建干路12号桂林理工大学地球科学学院,541004。Email:
李静和,广西壮族自治区桂林市雁山区建干路12号桂林理工大学地球科学学院,541004。Email: 