黏土束缚水是黏土矿物颗粒表面吸附的极性水分子在黏土表面形成的一层薄水膜,它被静电引力吸附于黏土颗粒表面,通常情况下不易流动。黏土表面的水膜虽然很薄,但因黏土颗粒极细,故具有较大的比表面积,能吸附大量的极性水分子,对岩石导电性[1]具有较大影响,导致电阻率、核磁共振、中子、密度等测井响应特征产生较大差异。因此,黏土束缚水评价对于储层岩性、电性[2]、物性及含油气性[3]关系研究具有重要意义。
20世纪50年代Hill等[4]开展了黏土矿物的电导率、阳离子交换量及电化学电位的早期测量。Grismer等[5]通过实验测量研究了黏土表面吸附水的复杂物理—化学过程;Fukue等[6]进一步研究总结出黏土束缚水主要受弱结合水控制的结论。袁建滨[7]针对黏土矿物表面结合水进行了定量实验测量,分析了黏土表面结合水的类型,厘清了不同黏土矿物吸附结合水的差异。Waxman等[8]将黏土束缚水引起的附加导电引入泥质砂岩导电模型,校正黏土附加导电影响,用于饱和度计算。Clavier等[9]针对黏土束缚水产生的阳离子交换量不易计算的难题,提出双水模型,通过扩散双电层理论厘定阳离子交换量与黏土束缚水之间的关系;贾景超等[10]进一步开展了不同黏土类型下这两者之间相关性研究。崔云江等[11]通过常规测井计算黏土束缚水孔隙度(ϕcw),进而计算扩散双电层中低矿化度地层水条件下的阳离子交换量。
针对常规测井黏土束缚水计算难题,因核磁共振测井能测量不同尺寸孔隙中的含水体积,在黏土束缚水评价中具有较大潜力。目前核磁共振测井主要应用于孔隙度[12]、孔隙结构[13]评价,近年来通过可变T2截止值[14]的研究进一步提高测井评价精度,但对黏土束缚水的研究相对较少。张冲等[15]通过岩心实验研究了核磁共振黏土束缚水与阳离子交换量之间的关系;罗兴平等[16]将该关系应用于核磁共振测井,计算黏土束缚水。上述研究均采用固定3ms截止值,导致黏土束缚水计算精度有限。王伟等[17]通过不同黏土类型测定黏土束缚水弛豫时间,认为黏土束缚水T2截止值为1.7ms,传统3ms截止值的选取使得黏土束缚水的计算结果存在一定误差。
本文通过阳离子交换能力与核磁共振实验,确定黏土束缚水T2截止值与ϕcw之间的关系,建立了变黏土束缚水T2截止值计算模型;通过核磁共振测井精细计算ϕcw,使其计算精度进一步提高。
1 核磁共振测井ϕcw计算方法 1.1 理论公式推导Clavier等[9]认为泥质砂岩储层孔隙中除自由水以外,包含一定量黏土束缚水,分布在黏土颗粒表面,同时聚集了大量可交换的阳离子Na+,具有阳离子交换导电作用,且与黏土类型无关。阳离子交换量[18]由下式计算
| $Q_{\mathrm{v}}=\frac{1}{\alpha V_{Q}} \frac{\phi_{\mathrm{cw}}}{\phi_{\mathrm{t}}} $ | (1) |
式中:Qv为泥质砂岩的阳离子交换量(mmol/cm3);ϕcw为黏土束缚水孔隙度;ϕt为总孔隙度;α为Na+离子扩散层的扩散因子(无量纲);VQ为Qv= 1mmol/cm3时黏土水占据的孔隙体积。
VQ、α的计算公式为
| $ \begin{cases}V_{Q}=\frac{1}{2.853+0.019 T} & \\ \alpha= \begin{cases}1 & P_{\mathrm{w}}>P_{\mathrm{wo}} \\ \sqrt{P_{\mathrm{wo}} / P_{\mathrm{w}}} & P_{\mathrm{w}} \leqslant P_{\mathrm{wo}}\end{cases} \end{cases} $ | (2) |
式中:T为地层温度;Pw为地层水矿化度(mmol/cm3);Pwo为Na+离子扩散层厚度在赫尔库兹厚度时的地层水矿化度,通常为0.35mmol/cm3。
由于实验室条件下Qv难以直接测量,通常测量阳离子交换能力(CCEC)[18]表征岩石的阳离子交换作用大小。CCEC代表每单位质量干岩样含有的可交换阳离子量(mmol/100g),该值与Qv关系为
| $Q_{\mathrm{v}}=\frac{C_{\mathrm{CEC}}\left(1-\phi_{\mathrm{t}}\right) \rho_{\mathrm{g}}}{\phi_{\mathrm{t}}} $ | (3) |
式中ρg为岩石的平均颗粒密度。
根据式(1)~式(3)可得到实验室条件下的ϕcw计算公式
| $ \phi_{\mathrm{cw}}= \begin{cases}\frac{C_{\mathrm{CEC}}\left(1-\phi_{\mathrm{t}}\right) \rho_{\mathrm{g}}}{2.853+0.019 T} & P_{\mathrm{w}}>P_{\mathrm{wo}} \\ \sqrt{\frac{P_{\mathrm{wo}}}{P_{\mathrm{w}}} }\frac{C_{\mathrm{CEC}}\left(1-\phi_{\mathrm{t}}\right) \rho_{\mathrm{g}}}{2.853+0.019 T} & P_{\mathrm{w}} \leqslant P_{\mathrm{wo}}\end{cases} $ | (4) |
由式(4)可知,阳离子交换能力与黏土束缚水孔隙度总体上呈现正相关关系,即随着阳离子交换能力的不断增强,ϕcw逐渐增大,黏土导电能力逐渐增强,因此产生的黏土附加导电作用降低了油层电阻率,即形成低阻油层。
1.2 变黏土束缚水T2截止值确定方法核磁共振测井主要测量地层中的氢核数,相比常规中子、密度等孔隙度测井方法,核磁共振测井能有效区分储层中不同孔隙尺寸条件下的氢核数,可将孔隙大致划分为三部分,即黏土束缚水、毛管束缚水、可动流体占据的孔隙体积(图 1)。因此,核磁共振测井在黏土束缚水评价中具有不可替代的优势。
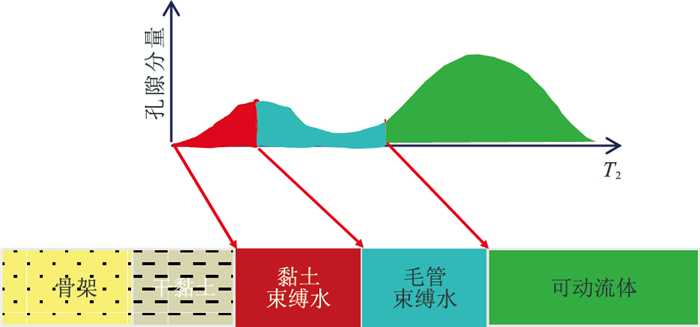
|
图 1 核磁共振孔隙结构划分示意图 |
核磁共振T2谱计算ϕcw,需给定黏土束缚水弛豫时间截止值。传统观点认为,核磁共振3ms弛豫时间为黏土束缚水截止值时间,该值被广泛应用于核磁共振测井ϕcw计算中,其公式为
| $ \phi_{\mathrm{cw}}=\sum\limits_{t_{i}=T_{\min }}^{3} \phi_{t_{i}} $ | (5) |
式中:ti为弛豫时间;ϕti为ti弛豫时间对应的孔隙度分量;Tmin为最小弛豫时间。
邓克俊等[19]统计了实验条件下不同类型黏土T2弛豫时间分布,发现不同类型黏土T2弛豫时间分布范围较广(表 1)。从表 1可见,蒙脱石与伊利石弛豫时间较短,而高岭石弛豫时间较长,传统3ms弛豫时间截止值划分ϕcw误差较大。
|
|
表 1 不同类型黏土T2弛豫时间分布统计 |
采用式(4)对渤海QHD油田新近系馆陶组岩心阳离子交换能力测量结果进行计算得到ϕcw。根据岩心核磁共振实验结果,依据ϕcw值得到对应核磁共振T2谱黏土束缚水T2截止值(T2cc),如表 2所示。可见不同岩心对应的T2cc分布范围是0.54~3.92ms,与3ms差异较大。由于该区馆陶组黏土成分以蒙脱石、伊蒙混层为主,黏土束缚水T2弛豫时间相对较低,与表 1相关实验结果有较好的对应关系,也进一步表明式(4)计算的ϕcw数据较可靠。
|
|
表 2 不同方法确定的ϕcw值及相关参数统计 |
表 2同时给出采用式(5)传统3ms弛豫时间对核磁共振实验(即核磁法)计算得到的ϕcw结果。可见传统核磁法计算结果与Qv法差异较大,其绝对误差分布范围是0.03%~11.10%。因此,采用传统固定3ms截止值计算的黏土束缚水存在较大误差。
通过表 2可看出,传统3ms核磁法确定的ϕcw与Qv法计算结果差异较大。选取表 2中相对误差较大的第1、第4号岩心和相对误差较小的第13、第15号岩心核磁共振实验T2谱做对比(图 2)。核磁共振实验采用6s等待时间,回波间隔为0.6ms,回波个数选取18000,扫描次数为32。从图 2可看出,第1、第4号岩心小孔隙发育,束缚水含量高,而第13、第15号岩心大孔隙发育,束缚水含量低,因此随着储层孔隙结构变差,束缚水含量增高,传统核磁法ϕcw计算误差不断增大。

|
图 2 不同孔隙结构样品T2谱分布 |
由相同岩心核磁共振与阳离子交换实验可知,核磁共振T2谱对应的T2cc已不再为定值,它受黏土类型及含量、孔隙结构等影响较大。现今,核磁共振测井是确定ϕcw的首选测井项目,为此根据核磁共振测井资料确定合理的T2cc值,将成为ϕcw计算准确与否的关键。
由表 2还可看出,ϕcw与T2cc并无较好的对应关系,直接通过T2cc计算ϕcw较困难。通过表 2进一步发现,T2cc与ϕ3cw(3ms截止值对应的黏土束缚水孔隙度)具有一定的对应关系:在通常情况下(ϕcw较小),当T2cc较低时,ϕ3cw较高;当T2cc较高时,ϕ3cw较低。由于核磁共振测井能较好地获取不同弛豫时间对应的孔隙度,因此通过建立T2cc与不同弛豫时间对应的孔隙度关系,即可得到可变的黏土束缚水T2截止值。为了确定不同弛豫时间对应的孔隙度与T2cc之间的相关性,分别统计弛豫时间为0.5、1.0、2.0、3.0、4.0、5.0ms时,对应的黏土束缚水体积与T2cc之间的相关性(图 3),可见当弛豫时间为3.0ms时两者相关性最高,进而选取ϕ3cw做回归计算,建立ϕ3cw与T2cc的经验模型用于计算T2cc,此时T2cc不再为定值,计算的ϕcw更为准确。
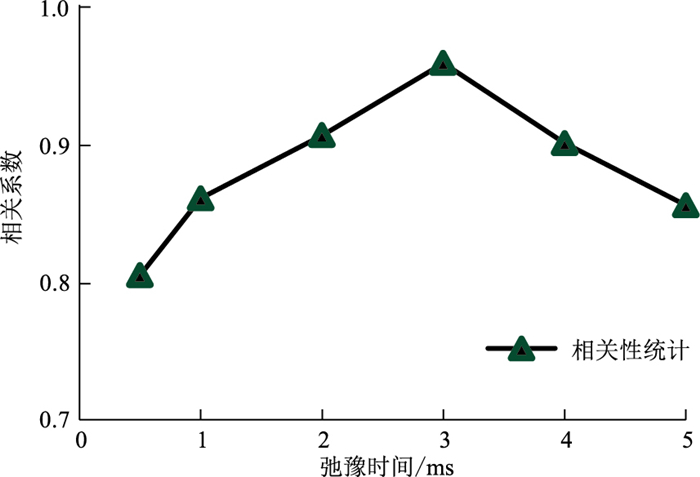
|
图 3 T2cc与不同弛豫时间对应的孔隙度相关性统计 |
由QHD油田馆陶组阳离子交换能力与核磁共振实验可知,ϕ3cw与T2cc相关性达到最高。图 4为ϕ3cw与T2cc交会图,可看出该油田两者存在较好的幂函数关系,相关系数达到0.9579,由此建立可变的T2cc计算公式
| $ T_{2 \mathrm{cc}}=13.143 \phi_{3 \mathrm{cw}}^{-1.198} $ | (6) |
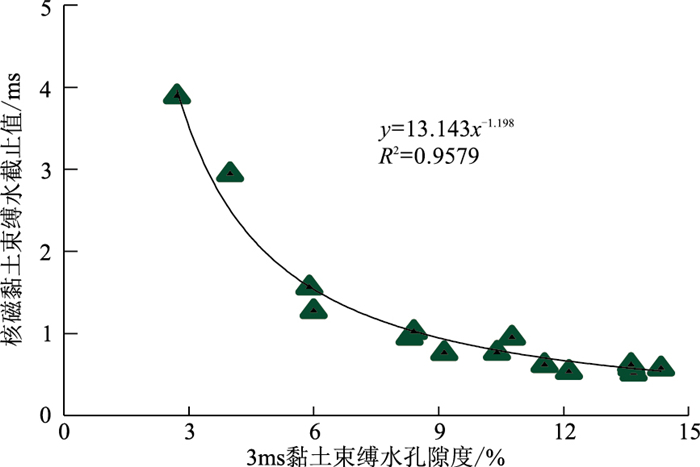
|
图 4 QHD油田馆陶组变黏土束缚水T2截止值确定方法 |
通过测定、分析渤海新近系地层阳离子交换与核磁共振实验数据,建立一种可变黏土束缚水T2截止值的计算方法,在此基础上通过核磁共振测井资料实现储层ϕcw精细评价。具体方法如下:
(1) 开展岩心核磁共振与阳离子交换联测实验,根据阳离子交换能力计算ϕcw值;
(2) 根据ϕcw计算核磁共振T2谱黏土束缚水弛豫时间截止值(T2cc);
(3) 建立T2cc与核磁共振不同弛豫时间对应的ϕcw交会图,回归分析并选取相关性最好的弛豫时间(Tbest)对应的ϕcw,进而得到Tbest与T2cc计算公式;
(4) 通过核磁共振T2谱计算Tbest截止值对应的ϕcw,再依据步骤(3)确定的可变黏土束缚水截止值回归公式求取T2cc,利用该值计算最终ϕcw,具体计算公式为
| $ \phi_{\mathrm{cw}}=\sum\limits_{t_{i}=T_{\min }}^{T_{2 \mathrm{cc}}} \phi_{t_{i}} $ | (7) |
采用核磁共振测井资料根据上述步骤(1)~步骤(4)可准确地计算地层ϕcw。在此基础上根据式(1)可计算阳离子交换量(Qv),确定黏土附加导电影响,深入分析油层导电机理。
2 应用效果分析CFD油田位于渤海西部海域,主要含油层系为新近系馆陶组,以辫状河沉积为主,馆陶组岩性以细砂岩为主,砂岩厚度较大,储层以正韵律沉积特征为主,部分储层黏土含量较高,地层水矿化度较低,黏土附加导电明显,低阻油层广泛分布。
图 5为CFD油田9井ϕcw及阳离子交换量计算效果图。该井实施了随钻伽马、电阻率、核磁共振测井。通过自然伽马(第1列黑线)、电阻率(第3列红线)曲线特征,共解释油、水层6小层并经钻采证实结论可靠。其中①、②、③、⑤小层为油层,④小层为差油层,⑥小层为水层。由电阻率曲线可看出:①小层(1523~1527m)、②小层(1530~1540m)电阻率较低(约3Ω·m),核磁T2谱显示可动孔隙度较小(第4道),黏土束缚水较高,为典型低阻油层;③小层(1547~1552m)电阻率较高(18Ω·m),核磁T2谱显示可动孔隙度较大,为正常油层;⑥小层(1565~1580m)电阻率较低,核磁可动孔隙较高,为水层。

|
图 5 CFD油田9井测井解释结果对比图 |
对该井岩心开展了阳离子交换能力实验测量,根据式(4)计算岩心ϕcw值,采用本文提供的实验方法,通过建立T2cc的相关函数计算可变ϕcw截止值,进而通过该井核磁共振测井计算得到ϕcw值(第5列红线),可看出计算的ϕcw值与岩心计算结果较吻合,而通过传统3ms黏土束缚水截止值计算得到的ϕcw(第5列蓝线)与岩心计算结果差异较大,尤其在ϕcw值较大的储层,两者相差更明显(表 3)。
|
|
表 3 ϕcw计算精度对比表 |
通过ϕcw与阳离子交换量计算效果可看出,导致①、②小层低阻油层的主要原因为黏土束缚水含量高,附加导电明显,导致油层电阻率值降低明显,而③、⑥小层ϕcw值较低,为正常油层和水层。
3 结束语(1) 以扩散双电层理论推导建立了阳离子交换能力与ϕcw之间的理论公式,通过阳离子交换实验可较为准确地确定ϕcw。
(2) 依据核磁共振—阳离子交换能力联测实验明确了传统3ms固定黏土束缚水T2截止值计算ϕcw存在的弊端,且随着孔隙结构逐渐变差,ϕcw值计算误差逐渐加大。根据联测实验建立可变的黏土束缚水T2截止值计算模型,在此基础上根据核磁共振测井资料可更准确地获取ϕcw数据。
| [1] |
冯渊, 秦康, 李二党, 等. 基于黏土矿物分析的低电阻率油层识别[J]. 新疆石油地质, 2020, 41(2): 237-242. FENG Yuan, QIN Kang, LI Erdang, et al. Identification of low-resistivity oil layers based on clay mineral analysis[J]. Xinjiang Petroleum Geology, 2020, 41(2): 237-242. |
| [2] |
张丽华, 潘保芝, 王云梅, 等. 砂岩中绿泥石包膜与岩石润湿性及岩电参数的关系研究[J]. 石油物探, 2020, 59(4): 647-654. ZHANG Lihua, PAN Baozhi, WANG Yunmei, et al. Relationship between pore-lining chlorite and wettability of rocks, and rock electrical parameters of sandstone[J]. Geophysical Prospecting for Petroleum, 2020, 59(4): 647-654. DOI:10.3969/j.issn.1000-1441.2020.04.015 |
| [3] |
郑观有, 韩晓程, 杨可, 等. 黏土矿物对储层饱和度实验结果的影响及解决方法探讨[J]. 石化技术, 2021, 28(2): 134-136. ZHENG Guanyou, HAN Xiaocheng, YANG Ke, et al. The influence and solution of clay minerals on the experimental results of reservoir saturation[J]. Petrochemical Industry Technology, 2021, 28(2): 134-136. DOI:10.3969/j.issn.1006-0235.2021.02.061 |
| [4] |
HILL H J, MILBURN J D. Effect of clay and water salinity on electrochemical behavior of reservoir rocks[J]. Transactions of the AIME, 1956, 207(1): 65-72. DOI:10.2118/532-G |
| [5] |
GRISMER M E. Water vapor adsorption kinetics and isothermal infiltration[J]. Soil Science, 1988, 146(5): 297-302. DOI:10.1097/00010694-198811000-00001 |
| [6] |
FUKUE M, MINATO T, CHIDA T. Thickness of adsorbed water layer for clay particles[J]. Clay Science for Engineering, 2001, 423-427. |
| [7] |
袁建滨. 黏土中结合水特性及其测试方法研究[D]. 广东广州: 华南理工大学, 2012. YUAN Jianbin. The Study for Properties of Bound Water on Clayey Soils and Their Quantitative Me-thods[D]. South China University of Technology, Guangzhou, Guangdong, China, 2012. |
| [8] |
WAXMAN M H, SMITS L J M. Electrical conductivities in oil-bearing shaly sands[J]. Society of Petroleum Engineers Journal, 1968, 8(2): 107-122. DOI:10.2118/1863-A |
| [9] |
CLAVIER C, COATES G, DUMANOIR J. Theoretical and experimental bases for the dual water model for interpretation of shaly sands[J]. Society of Petroleum Engineers Journal, 1984, 24(2): 153-168. DOI:10.2118/6859-PA |
| [10] |
贾景超, 杨庆. Gouy-Chapman双电层模型在蒙脱石长程膨胀中应用[J]. 大连理工大学学报, 2010, 50(2): 239-244. JIA Jingchao, YANG Qing. Application of Gouy-Chapman double layer model to long-range swelling of montmorillonite[J]. Journal of Dalian University of Technology, 2010, 50(2): 239-244. |
| [11] |
崔云江, 王培春, 李瑞娟, 等. 基于扩散双电层理论的低对比度油层判别新方法[J]. 测井技术, 2018, 42(3): 294-299. CUI Yunjing, WANG Peichun, LI Ruijuan, et al. New method for discrimination of low contrast reservoir based on diffusion double layer theory[J]. Well Logging Technology, 2018, 42(3): 294-299. |
| [12] |
毛志强, 张冲, 肖亮. 一种基于核磁共振测井计算低孔低渗气层孔隙度的新方法[J]. 石油地球物理勘探, 2010, 45(1): 105-109. MAO Zhiqiang, ZHANG Chong, XIAO Liang. A NMR-based porosity calculation method for low porosity and low permeability gas reservoir[J]. Oil Geo-physical Prospecting, 2010, 45(1): 105-109. |
| [13] |
刘卫, 肖忠祥, 杨思玉, 等. 利用核磁共振(NMR)测井资料评价储层孔隙结构方法的对比研究[J]. 石油地球物理勘探, 2009, 44(6): 773-778. LIU Wei, XIAO Zhongxiang, YANG Siyu, et al. Comparative studies on methods of evaluation of re-servoir pore structure by using NMR (nuclear magnetic resonance) well logging data[J]. Oil Geophysical Prospecting, 2009, 44(6): 773-778. DOI:10.3321/j.issn:1000-7210.2009.06.022 |
| [14] |
朱明, 贾春明, 穆玉庆, 等. 基于正态分布拟合的致密砂砾岩储层核磁共振测井可变T2截止值计算方法[J]. 石油地球物理勘探, 2021, 56(3): 612-621. ZHU Ming, JIA Chunming, MU Yuqing, et al. A method of predicting T2 cutoffs from NMR logging data of tight glutenite reservoirs based on normal distribution simulation[J]. Oil Geophysical Prospecting, 2021, 56(3): 612-621. |
| [15] |
张冲, 张占松, 宋秋强. 基于岩心核磁共振实验数据确定阳离子交换容量[J]. 测井技术, 2013, 37(2): 128-131. ZHANG Chong, ZHANG Zhansong, SONG Qiu-qiang. Qv determination based on NMR testing data[J]. Well Logging Technology, 2013, 37(2): 128-131. |
| [16] |
罗兴平, 苏东旭, 王振林, 等. 核磁共振测井在低阻油层评价中的应用——以准格尔盆地阜东斜坡头屯河组为例[J]. 新疆石油地质, 2017, 38(4): 470-476. LUO Xingping, SU Dongxu, WANG Zhenlin, et al. Application of NMR logging in low-resistivity reservoir evaluation: a case study of Toutunhe formation on the eastern Fukang slope, Junggar basin[J]. Xinjiang Petroleum Geology, 2017, 38(4): 470-476. |
| [17] |
王伟, 赵延伟, 毛锐, 等. 页岩油储层核磁有效孔隙度起算时间的确定——以吉木萨尔凹陷二叠系芦草沟组页岩油储层为例[J]. 石油与天然气地质, 2019, 40(3): 550-557. WANG Wei, ZHAO Yanwei, MAO Rui, et al. Determination of the starting time for measurement of NMR effective porosity in shale oil reservoir: a case study of the Permian Lucaogou shale oil reservoir, Jimusaer sag[J]. Oil & Gas Geology, 2019, 40(3): 550-557. |
| [18] |
雍世和, 张超谟. 测井数据处理与综合解释[M]. 山东东营: 石油大学出版社, 2002: 188-192. YONG Shihe, ZHANG Chaomo. Logging Data Processing and Comprehensive Interpretation[M]. Dongying, Shandong: University of Petroleum Press, 2002: 188-192. |
| [19] |
邓克俊, 谢然红. 核磁共振测井理论及应用[M]. 山东东营: 中国石油大学出版社, 2010: 52-55. DENG Kejun, XIE Ranhong. Theory and Application of Nuclear Magnetic Resonance Logging[M]. Dongying, Shandong: China University of Petroleum Press, 2010: 52-55. |



 陆云龙,天津市滨海新区海川路2121号海洋石油大厦B座,300459。Email:
陆云龙,天津市滨海新区海川路2121号海洋石油大厦B座,300459。Email: