② 长江大学地球物理与石油资源学院,湖北武汉 430100
② College of Geophysics and Petroleum Resources, Yangtze University, Wuhan, Hubei 430100, China
近年来,碳酸盐岩油气藏勘探不断取得重大突破,展示出良好的勘探前景[1]。然而,碳酸盐岩储层普遍发育多种孔隙,储层具有较强的各向异性特征,对利用测井资料评价储层有效性及流体识别带来了一系列技术难题。另外,碳酸盐岩储层各向异性对大斜度井及水平井的测井结果影响更明显,进一步增加了储层测井评价的难度。因此,基于测井数据的碳酸盐岩储层各向异性校正方法仍然亟待研究[2]。
双侧向测井是目前开展碳酸盐岩储层含油性评价的重要测井方法之一[3]。由于屏蔽电极的聚焦作用,双侧向测井主电极发射的电流可以垂直于井眼方向进入地层,从而实现较深的径向探测深度。在垂直井中,双侧向测井主电极发射电流方向与地层层理面平行,主要受地层水平电阻率的影响。而在大斜度井中,双侧向测井主电极发射电流方向与地层层理面之间存在夹角,因而受到地层水平电阻率和地层垂直电阻率的共同影响[4]。大量双侧向测井结果表明,受碳酸盐岩储层各向异性的影响,大斜度井中储层电阻率值明显高于邻近直井[5-6],若直接利用未经各向异性校正的大斜度井储层电阻率值,将给储层含油饱和度评价带来较大误差。因此,利用双侧向测井数据准确评价大斜度井碳酸盐岩储层含油性的核心是对储层电阻率各向异性校正方法进行研究[7-8]。
数值模拟是研究双侧向测井响应特性的常用方法,主要有解析法、有限差分法、有限元法等。其中三维有限元法是针对考虑电阻率各向异性的碳酸盐岩储层大斜度井最有效的方法[9-10]。基于有限元方法,国内外部分学者对碳酸盐岩储层双侧向测井各向异性校正方法进行了深入研究。Pezard等[11]将具有等间距平行平板状裂缝组的地层等效为宏观均匀各向异性介质, 利用二维电导率张量矩阵计算了任意裂缝角度的双侧向测井响应;李善军等[12]将灰岩裂缝储层等效为宏观各向异性介质,通过双侧向测井三维有限元模型反演得到了储层裂缝参数;史謌等[13]基于三维有限元方法分析了双侧向测井与裂缝参数的关系,并提出储层裂缝计算公式和裂缝倾角划分模型;高杰等[14]基于大斜度井双侧向测井三维有限元模型分析了井斜角对仪器响应的影响,并提出一种校正电阻率曲线的快速反褶积方法;王磊等[15]基于洞穴型碳酸盐岩储层三维有限元模型分析了双侧向不同探测模式对井旁洞穴的敏感性和差异性;袁超等[16]利用各向异性地层阵列侧向测井三维有限元模型分析了地层倾角和电各向异性的影响,并利用物理模拟结果验证了数值模拟结果。
上述模拟研究成果总结并加深了业界对于碳酸盐储层电各向异性成因的认识,但在双侧向测井电各向异性校正方法方面还有待系统地深入研究。目前,碳酸盐储层双侧向测井电各向异性的研究主要依赖于经验公式,但部分公式的物理意义尚不明确,在实际应用中存在许多局限性[17-18]。因此,对于碳酸盐岩储层电各向异性校正的研究还需要进行系统的数值模拟和岩石物理实验。
本文建立了一套大斜度井碳酸盐岩储层双侧向测井三维有限元模型,制作了适用于实际双侧向测井仪器的电各向异性校正图板。基于四川盆地灯影组储层对水平方向和垂直方向岩心进行了高温、高压岩电实验,提出了一套储层电各向异性系数温压校正方法。基于数值模拟和岩电实验结果,总结出一套适用于大斜度井碳酸盐岩储层电各向异性校正的方法,并用实际测井资料进行了验证。
1 各向异性储层双侧向测井响应 1.1 各向异性储层双侧向测井有限元模拟对于电各向同性地层,地层导电性可以用一个电导率标量来描述,而对于电各向异性地层,则需要利用电导率张量表示。如图 1所示,令平行于地层沉积层理方向的水平电导率为σh,垂直于地层沉积层理方向的垂直电导率为σv。
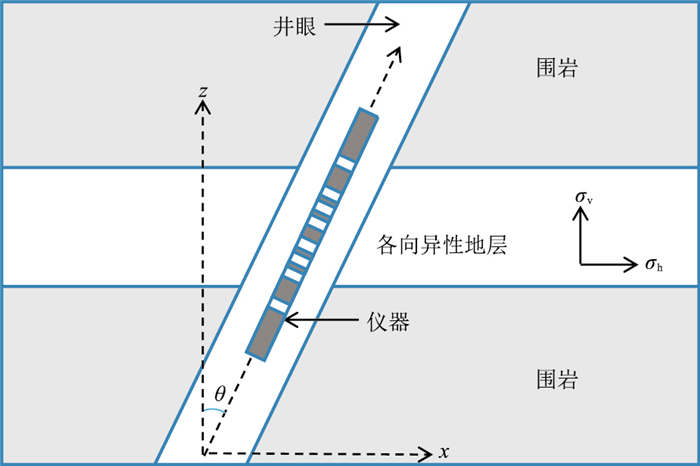
|
图 1 大斜度井各向异性地层双侧向测井示意图 |
通常定义电导率各向异性系数λ描述地层电导率各向异性程度[19]
| $ \lambda=\sqrt{\frac{\sigma_{\mathrm{v}}}{\sigma_{\mathrm{h}}}} $ | (1) |
当井眼倾斜时,双侧向测井的测量结果是式(1)中σh和σv综合作用的结果。当井轴与垂直地层层理面的z轴之井斜夹角为θ时,假设σh不随方位角发生变化,则大斜度井中地层电导率张量为[20]
| $ \boldsymbol{\sigma}=\left[\begin{array}{ccc} \sigma_{\mathrm{h}} \cos ^{2} \theta+\sigma_{\mathrm{v}} \sin ^{2} \theta & 0 & \left(\sigma_{\mathrm{h}}-\sigma_{\mathrm{v}}\right) \sin \theta \cos \theta \\ 0 & \sigma_{\mathrm{h}} & 0 \\ \left(\sigma_{\mathrm{h}}-\sigma_{\mathrm{v}}\right) \sin \theta \cos \theta & 0 & \sigma_{\mathrm{h}} \sin ^{2} \theta+\sigma_{\mathrm{v}} \cos ^{2} \theta \end{array}\right] $ | (2) |
对于双侧向测井仪器,视电阻率表达式为
| $ \rho_{\mathrm{a}}=K \frac{U_{\mathrm{M}}}{I_{0}} $ | (3) |
式中:主电极发射电流I0和仪器系数K为已知常数;UM为监督电极平均电位,与地层电导率成正比。
对双侧向测井响应进行数值模拟的核心是求取求解域中电位U的分布,U在求解域内(包括不同介质交界面)满足Laplace方程[21]
| $ \nabla^{2} \boldsymbol{U}=\frac{\partial^{2} \boldsymbol{U}}{\partial x^{2}}+\frac{\partial^{2} \boldsymbol{U}}{\partial y^{2}}+\frac{\partial^{2} \boldsymbol{U}}{\partial z^{2}}=0 $ | (4) |
在恒流电极A表面,电位U满足第二类边界条件[22],即
| $\int_{D} \boldsymbol{\sigma} \cdot \boldsymbol{E} \mathrm{d} s=I_{\mathrm{A}} $ | (5) |
式中:IA为恒流电极A所供电流;D为电极A表面区域;E表示电极表面的电场强度。
对于大斜度井电各向异性地层模型,上述电位U方程只有数值解。根据有限元法变分原理,将上述方程求解化简为求解泛函的极值问题[23]
| $ \begin{gathered} F(\boldsymbol{U})=\frac{1}{2} \iiint_{\varOmega} \boldsymbol{\sigma}\left(\frac{\partial^{2} \boldsymbol{U}}{\partial x^{2}}+\frac{\partial^{2} \boldsymbol{U}}{\partial y^{2}}+\frac{\partial^{2} \boldsymbol{U}}{\partial z^{2}}\right) \mathrm{d} x \mathrm{~d} y \mathrm{~d} z- \\ I_{\mathrm{A}} U_{\mathrm{A}}=0 \end{gathered} $ | (6) |
式中:UA为电极A的供电电位;Ω为电极系外的三维求解域。
根据实际仪器和地层尺寸,本次研究建立了高30m、直径30m的圆柱形三维有限元模型(图 2),其剖分四面体单元总数约为700000个。在求解稀疏矩阵时,基于Intel(R) i7-10750H的12核心笔记本电脑,采用GMRES迭代算法提高计算效率,该模型单点计算时间为5min,完全满足研究需要。

|
图 2 大斜度井双侧向测井三维有限元模型 |
在大多数校正双侧向测井各向异性的研究中,均采用经验公式描述仪器视电阻率ρa与井斜角θ和水平电阻率ρh的关系[24]
| $ \rho_{\mathrm{a}}=\frac{\lambda \rho_{\mathrm{h}}}{\sqrt{1+\left(\lambda^{2}-1\right) \cos ^{2} \theta}} $ | (7) |
根据式(7)可绘制双侧向测井电各向异性校正图板。随着λ和θ增大,ρa受垂直电导率σv影响逐渐增大,仪器视电阻率校正系数ρa/ρh也逐渐增大。在实际资料处理中,斜井地层电阻率可作为视电阻率ρa,在获得地层电各向异性系数λ后计算出校正后的ρh。
式(7)虽然被广泛用于地层电各向异性校正,但其背后的物理含义尚不明确,受地层电各向异性的影响,仪器视电阻率与真实仪器响应之间存在一定误差。为此,本文基于双侧向测井真实仪器参数和各向异性地层参数,建立了各向异性储层双侧向测井三维有限元模型,正演模拟双侧向测井在不同井斜角地层中受电各向异性的影响情况。
该模型设置ρh=10 Ω·m,未考虑井眼、侵入带、围岩等地层环境因素的影响,共计算了6组不同λ、10种不同θ条件下双侧向测井仪器的响应。按照仪器不同探测模式的响应特性,分别计算并制作了深、浅探测模式的各向异性校正图板(图 3)。由图可见,当ρv>ρh时,双侧向测井仪器响应同时受到ρh、ρv的影响,并且随着仪器倾斜角度增大,ρv的影响逐渐增大,从而导致视电阻率值增大。另外由于ρv>ρh, 仪器发射的电流会被迫沿着水平方向流动,因而深探测模式电流更加聚焦,受ρv的影响更小。深(图 3c)、浅(图 3b)探测模式校正图板比传统按照同一公式(图 3a)进行校正的方法更合理,更加适用于实际各向异性地层中双侧向测井仪器响应校正。
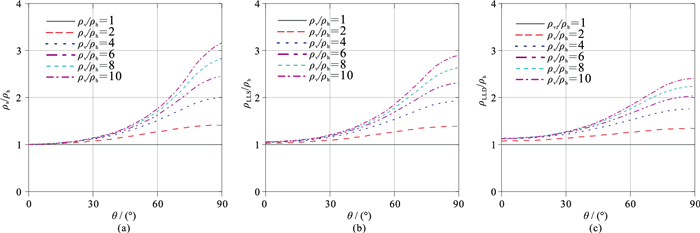
|
图 3 大斜度井电各向异性校正图板 (a)传统经验公式校正;(b)浅探测电阻率(ρLLS)模式;(c)深探测电阻率(ρLLD)模式 |
利用式(7)校正地层电各向异性影响的关键是准确求取λ值。在没有岩心数据时,常将斜井电阻率和对应直井电阻率分别当作ρa和ρh代入式(7)计算得到λ的最小二乘解。但是,由于井眼、侵入带及围岩等环境因素的影响,直井中双侧向测井值并不严格等于地层水平电阻率值。此外,同一套储层在不同井中所处深度位置也有差异,因此不同深度地层温度、压力的影响也不能忽略,直接将斜井电阻率和对应直井电阻率引入式(7)计算得到的λ值往往存在较大误差。
2.1 高温、高压条件下岩石电阻率实验测量对研究区块的白云岩储层取心,如图 4所示,为了测量岩心水平、垂直电阻率,对所取全直径岩心进行水平方向和垂直方向重新取样,岩心观察结果显示,该储层段孔隙、缝洞发育明显,具有较强的各向异性。根据实际地层水矿化度配备了80000mg/L的NaCl溶液对岩心进行饱和,并根据储层实际温压条件进行高温、高压岩电实验。

|
图 4 大斜度井碳酸盐岩储层水平样及垂直样取心 |
实验设备采用高温、高压复电阻率频谱实验系统,最大围压值为70MPa,最大实验温度为150℃,可采集20Hz至10MHz频段岩心复电阻率频谱。由于实验岩心缝洞发育明显,高温、高压条件下极易导致夹持器中绝缘胶套破裂,从而影响实验安全,因此实验最终确定的最高温度、围压分别为100℃和60MPa。对高温、高压岩心复电阻率频谱实验数据进行拟合分析,利用拟合得到的零频实部电阻率制作电阻率各向异性温压校正图板。
2.2 岩石电阻率各向异性温压校正方法通过实验得到垂直方向和水平方向岩样电阻率温压校正图板(图 5)。如图所示,随着围压在10MPa至60MPa范围内逐渐增大,饱和NaCl溶液的岩样导电通道变窄,ρh和ρv呈线性增大;随着温度在20℃至100℃范围内逐渐升高,岩心孔隙中的Na+和Cl-离子迁移速率增大,导致岩心导电性增强,因而ρh和ρv呈对数函数降低。对研究区储层而言,温度是岩心电阻率变化的主控因素,围压对其影响相对较小。上述实验结果与前期研究及其他大部分相关文献的研究结论一致。
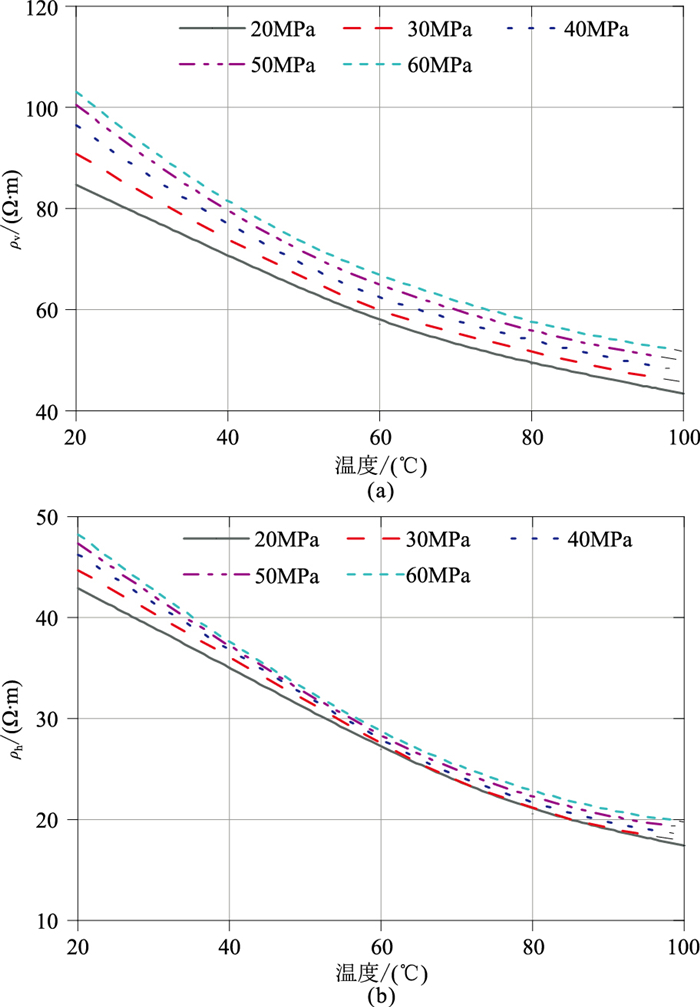
|
图 5 岩心电阻率温压校正图板 (a)垂直电阻率;(b)水平电阻率 |
当温度和压力一定时,储层的ρv明显大于ρh,表明该储层具有明显电各向异性。同时,ρh和ρv随温度、围压变化趋势一致,但是变化程度各不相同,表明计算得到的岩心电阻率各向异性系数λ并非随温度、围压呈简单线性变化。因此,在进行储层电阻率各向异性校正时,用λ与温度、压力直接拟合将存在较大误差。本文针对岩心ρh、ρv随温度和围压的变化特点,提出先对ρh、ρv分别进行温压校正,然后再计算储层温度条件下各向异性系数的校正方法。
3 实测数据各向异性校正选用四川盆地A区块内2口邻近的直井和大斜度井的实测数据。如图 6所示,两口井目的层段为灯影组碳酸盐岩储层,垂直深度范围为5040~5047m,图中红色实线表示直井测井曲线,蓝色实线表示大斜度井测井曲线,黑色虚线表示进行了电各向异性校正后的电阻率曲线。由图可见,大斜度井与直井中测井曲线存在明显差异,大斜度井中双侧向测井探测电阻率曲线受储层电各向异性影响大,其值明显大于直井中对应段电阻率值。
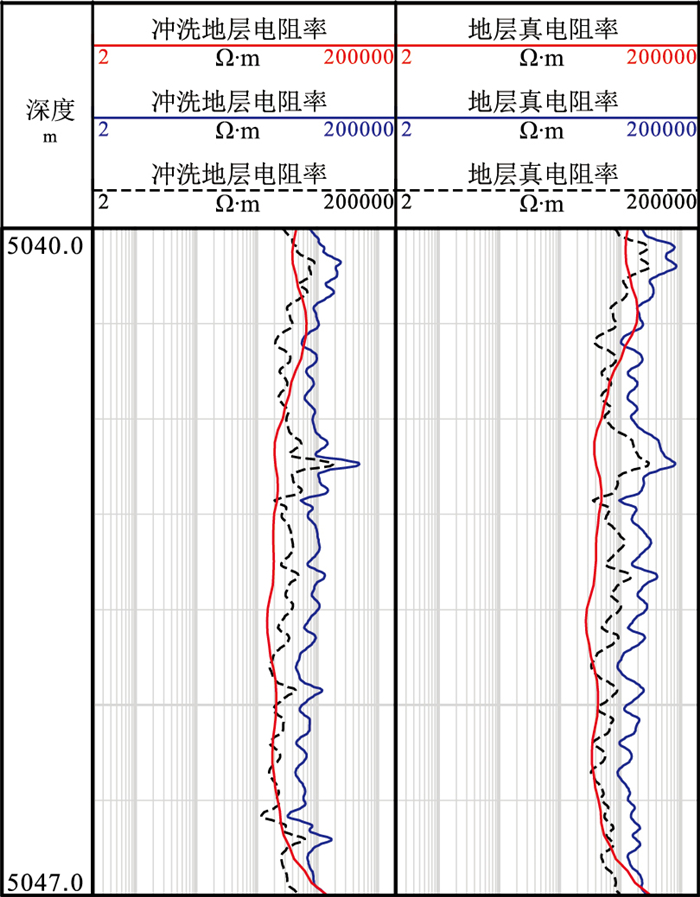
|
图 6 大斜度井碳酸盐岩储层电阻率各向异性校正结果 |
通过测、录井等相关资料的整理分析,得知该井段地层水矿化度为80000mg/L,储层所在深度的温度、压力分别为140℃、60MPa。基于图 5电阻率温压校正图板分别提取了60MPa条件下ρh、ρv与温度的关系曲线。由于储层温度超过了最高实验温度,因此对图 5实验数据进行了拟合分析,得到60MPa条件下储层ρh、ρv与温度的关系表达式
| $ \begin{cases}\rho_{\mathrm{h}}=-18.21 \ln T+103.40, & R^{2}=0.9948 \\ \rho_{\mathrm{v}}=-32.37 \ln T+200.07, & R^{2}=0.9986\end{cases} $ | (8) |
式中:T为储层温度;R为拟合数据的相关系数。
利用式(8)拟合出储层温度条件下ρh、ρv分别为13.41 Ω·m、40.11 Ω·m,进而代入式(1)得到储层电各向异性系数λ值为1.73。根据井斜曲线求得该储层平均井斜角为84.3°,结合所求λ值和双侧向测井电阻率各向异性校正图板计算出大斜度井储层段双侧向测井深、浅探测电阻率各向异性校正系数分别为1.2和1.3。如图 6所示,大斜度井校正后的深、浅探测电阻率曲线(黑色虚线)均明显小于未校正前的测量值,与邻近直井中对应段曲线测量值更接近。
为了定量分析大斜度井电各向异性图板校正效果,对上述储层段直井及大斜度井校正前、后双侧向测井值进行离散采样并制作交会图,采样间隔为0.5m,共15个采样点。如图 7所示,校正前大斜度井中双侧向测井电阻率值明显大于直井中对应电阻率值,利用本文方法校正电各向异性影响后,两口井的深、浅探测模式电阻率数据均具有较好一的致性。
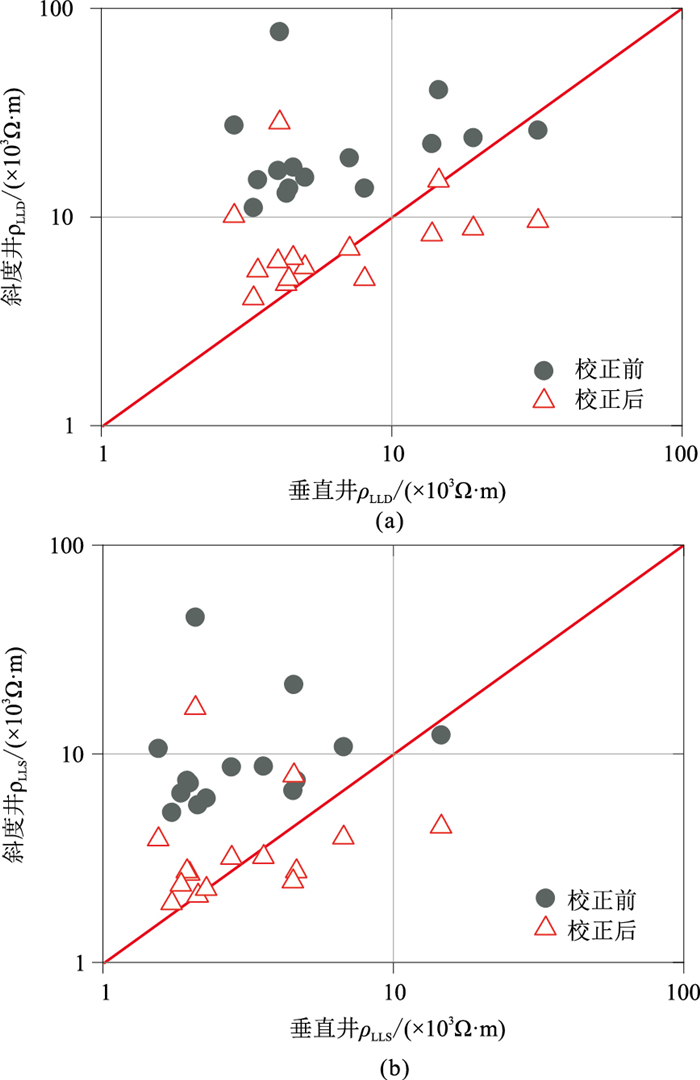
|
图 7 双侧向测井电阻率电各向异性校正前、后交会图 (a)深探测模式;(b)浅探测模式 |
为了进一步验证校正效果,对图 7中同一储层段含水饱和度进行了计算,并与校正前数据做交会对比(图 8)。结果显示,在对大斜度井储层进行电阻率各向异性校正后,其储层含水饱和度与对应直井储层段含水饱和度一致性明显变好,较好地消除了大斜度井储层电阻率各向异性对含水饱和度评价的影响。
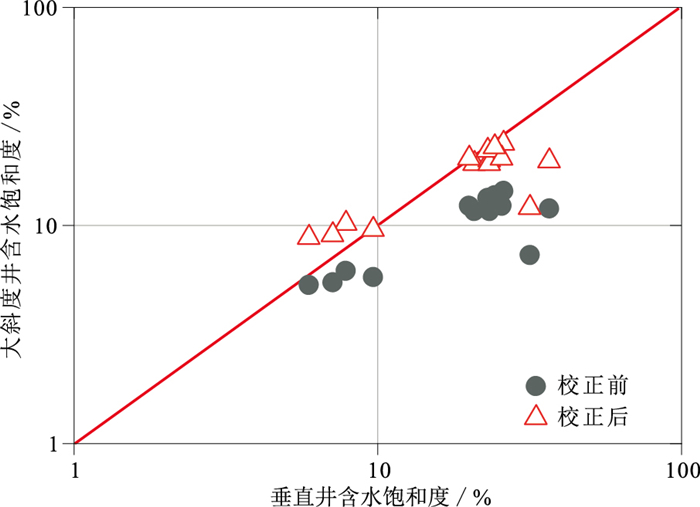
|
图 8 直井与大斜度井含水饱和度校正前、后交会图 |
(1) 本文基于三维有限元法建立了考虑双侧向测井实际仪器结构及地层各向异性的正演模型,分别制作了大斜度井双侧向测井深、浅探测电阻率各向异性校正图板。相较于传统的电各向异性校正公式,该校正图板考虑了双侧向测井过程中实际仪器电场分布特性,具有更明确的物理意义。
(2) 选取四川盆地灯影组碳酸盐岩储层,沿平行和垂直储层层理方向进行组合取心,并开展高温、高压条件下岩电实验。基于岩电实验数据,为准确求取储层电各向异性系数λ提供了温压校正图板和方案。相比传统电各向异性公式反演得到的λ能更加准确地描述碳酸盐岩储层电各向异性特征。
(3) 结合电各向异性校正图板对大斜度井双侧向测井实测数据进行了校正。校正后大斜度井的电阻率值明显减小,与邻近直井中对应双侧向测井电阻率数据相关性更好,验证了方法的有效性。
本文方法具有较好的应用前景,但仅考虑了各向异性对双侧向测井的影响,要获得准确的储层电阻率,还需在环境影响校正方面做进一步研究。
| [1] |
贾承造, 郑民, 张永峰. 中国非常规油气资源与勘探开发前景[J]. 石油勘探与开发, 2012, 39(2): 129-136. JIA Chengzao, ZHENG Min, ZHANG Yongfeng. Unconventional hydrocarbon resources in China and the prospect of exploration and development[J]. Petroleum Exploration and Development, 2012, 39(2): 129-136. |
| [2] |
李宁. 中国海相碳酸盐岩测井解释概论[M]. 北京: 科学出版社, 2013. LI Ning. Introduction to Logging Interpretation of Marine Carbonate Rocks in China[M]. Beijing: Science Press, 2013. |
| [3] |
周灿灿, 王昌学. 水平井测井解释技术综述[J]. 地球物理学进展, 2006, 21(1): 152-160. ZHOU Cancan, WANG Changxue. Technology review on the log interpretation of horizontal well[J]. Progress in Geophysics, 2006, 21(1): 152-160. DOI:10.3969/j.issn.1004-2903.2006.01.022 |
| [4] |
范宜仁, 王磊, 葛新民, 等. 洞穴型地层双侧向测井响应模拟与特征分析[J]. 石油勘探与开发, 2016, 43(2): 237-243. FAN Yiren, WANG Lei, GE Xinmin, et al. Response simulation and corresponding analysis of dual latero-log in cavernous reservoirs[J]. Petroleum Exploration and Development, 2016, 43(2): 237-243. |
| [5] |
谢关宝, 李永杰, 吴海燕, 等. 近井眼洞穴型地层双侧向测井敏感因素分析[J]. 石油钻探技术, 2020, 48(1): 120-126. XIE Guanbao, LI Yongjie, WU Haiyan, et al. Analysis of sensitive factors in dual laterologs for caver-nous/Karst formations near the borehole[J]. Petro-leum Drilling Techniques, 2020, 48(1): 120-126. |
| [6] |
葛新民, 范宜仁, 李军, 等. 井旁裂缝的双侧向测井物理模拟及特征分析[J]. 地球物理学报, 2019, 62(1): 354-360. GE Xinmin, FAN Yiren, LI Jun, et al. Experimental studies and investigations on the dual lateral log response of near borehole fractures[J]. Chinese Journal of Geophysics, 2019, 62(1): 354-360. |
| [7] |
孔繁达, 何涛, 姜洪福. 薄互层水平井测井电阻率的各向异性校正[J]. 北京大学学报(自然科学版), 2011, 47(2): 302-308. KONG Fanda, HE Tao, JIANG Hongfu. Anisotropic correction for resistivity logging of horizontal well in thin interlayer reservoir[J]. Acta Scientiarum Naturalium Universitatis Pekinensis, 2011, 47(2): 302-308. |
| [8] |
陈冬, 王彦春, 汪中浩, 等. 水平井地层电阻率各向异性研究[J]. 物探与化探, 2007, 31(3): 233-235. CHEN Dong, WANG Yanchun, WANG Zhonghao, et al. Analyze formation resistivity anisotropy in horizontal well[J]. Geophysical and Geochemical Exploration, 2007, 31(3): 233-235. DOI:10.3969/j.issn.1000-8918.2007.03.012 |
| [9] |
舒心, 柯式镇, 许巍, 等. 高分辨率阵列侧向测井井眼影响自动校正研究[J]. 断块油气田, 2016, 23(4): 470-475. SHU Xin, KE Shizhen, XU Wei, et al. Auto-correction of borehole effect for high-resolution array latero-log[J]. Fault-Block Oil and Gas Field, 2016, 23(4): 470-475. |
| [10] |
YIN C F, KE S Z, XU W, et al. 3D laterolog array sonde design and response simulation[J]. Applied Geophysics, 2014, 11(2): 223-234. DOI:10.1007/s11770-014-0439-z |
| [11] |
PEZARD P A, Anderson R N. In situ measurements of electrical resistivity, formation anisotropy, and tectonic context[C]. SPWLA 31st Annual Logging Symposium, Lafayette, Louisiana, 1990, SPWLA-1990-M.
|
| [12] |
李善军, 肖承文, 汪涵明, 等. 裂缝的双侧向测井响应的数学模型及裂缝孔隙度的定量解释[J]. 地球物理学报, 1996, 39(6): 845-852. LI Shanjun, XIAO Chengwen, WANG Hanming, et al. Mathematical model of dual laterolog response to fracture and quantitative interpretation of fracture porosity[J]. Chinese Journal of Geophysics, 1996, 39(6): 845-852. DOI:10.3321/j.issn:0001-5733.1996.06.014 |
| [13] |
史謌, 何涛, 仵岳奇, 等. 用正演数值计算方法开展双侧向测井对裂缝的响应研究[J]. 地球物理学报, 2004, 47(2): 359-363. SHI Ge, HE Tao, WU Yueji, et al. A study on the dual laterolog response to fractures using the forward numerical modeling[J]. Chinese Journal of Geophy-sics, 2004, 47(2): 359-363. DOI:10.3321/j.issn:0001-5733.2004.02.027 |
| [14] |
高杰, 谢然红. 大斜度井侧向测井三维正演数值模拟及曲线快速校正方法研究[J]. 石油勘探与开发, 2000, 27(2): 69-71. GAO Jie, XIE Ranhong. 3D numerical forward mo-deling and fast correction of dual-laterolog for high angle deviated wells[J]. Petroleum Exploration and Development, 2000, 27(2): 69-71. DOI:10.3321/j.issn:1000-0747.2000.02.019 |
| [15] |
王磊, 范宜仁, 高衍武, 等. 基于3D-FEM的洞穴型地层双侧向测井数值模拟及响应特征研究[J]. 地球物理学报, 2017, 60(5): 2011-2019. WANG Lei, FAN Yiren, GAO Yanwu, et al. Numerical simulation and characteristics analysis of dual la-terolog in cavernous reservoirs on the basis of 3D-FEM[J]. Chinese Journal of Geophysics, 2017, 60(5): 2011-2019. |
| [16] |
袁超, 李潮流, 周灿灿, 等. 各向异性地层阵列侧向电阻率响应仿真模拟及应用[J]. 石油勘探与开发, 2020, 47(1): 77-85. YUAN Chao, LI Chaoliu, ZHOU Cancan, et al. Forward simulation of array laterolog resistivity in anisotropic formation and its application[J]. Petroleum Exploration and Development, 2020, 47(1): 77-85. |
| [17] |
罗少成, 汪中浩, 唐冰娥, 等. 水平井地层电阻率各向异性校正方法研究[J]. 测井技术, 2009, 33(2): 126-129, 147. LUO Shaocheng, WANG Zhonghao, TANG Bing'e, et al. Research on anisotropy corrections of horizontal well formation resistivity[J]. Well Logging Techno-logy, 2009, 33(2): 126-129, 147. DOI:10.3969/j.issn.1004-1338.2009.02.006 |
| [18] |
蔡琳, 张承森, 刘瑞林, 等. 碳酸盐岩地层水平井电阻率各向异性校正方法研究及应用[J]. 石油天然气学报, 2014, 36(12): 122-126. CAI Lin, ZHANG Chengsen, LIU Ruilin, et al. The method and application of horizontal well resistivity anisotropy correction in carbonate formation[J]. Journal of Oil and Gas Technology, 2014, 36(12): 122-126. DOI:10.3969/j.issn.1000-9752.2014.12.030 |
| [19] |
邓少贵, 莫宣学, 卢春利, 等. 缝—洞型地层缝洞的双侧向测井响应数值模拟[J]. 石油勘探与开发, 2012, 39(6): 706-712. DENG Shaogui, MO Xuanxue, LU Chunli, et al. Numerical simulation of the dual laterolog response to fractures and caves in fractured-cavernous formation[J]. Petroleum Exploration and Development, 2012, 39(6): 706-712. |
| [20] |
李智强, 陈中权, 张克. 高分辨率双侧向测井数值分析[J]. 地球物理学进展, 2016, 31(4): 1614-1619. LI Zhiqiang, CHEN Zhongquan, ZHANG Ke. Analysis of numeric simulation of high-resolution dual la-terolog response[J]. Progress in Geophysics, 2016, 31(4): 1614-1619. |
| [21] |
王小明, 万文春, 赵建武, 等. 水平井网状裂缝储层双侧向响应特性研究[J]. 物探与化探, 2014(6): 1218-1221. WANG Xiaoming, WAN Wenchun, ZHAO Jianwu, et al. Characteristics of dual laterolog response of net-fracture reservoirs in horizontal well[J]. Geophysical and Geochemical Exploration, 2014(6): 1218-1221. |
| [22] |
赵江青, 王成龙, 叶青竹. 岩石各向异性在水平井测井解释中的应用[J]. 测井技术, 1998, 21(1): 38-43. ZHAO Jiangqing, WANG Chenglong, YE Qingzhu. Laboratory measurement of rock anisotropy and its application to horizontal well log interpretation[J]. Well Logging Technology, 1998, 21(1): 38-43. |



 赖强,四川省成都市高新区天府大道北段12号西南油气田分公司勘探开发研究院地球物理研究所,610041。Email:
赖强,四川省成都市高新区天府大道北段12号西南油气田分公司勘探开发研究院地球物理研究所,610041。Email: