② 中国石油大学(北京)油气资源与探测国家重点实验室,北京 102249
② State Key Laboratory of Petroleum Resources and Prospecting, China University of Petroleum (Beijing), Beijing 102249, China
测井资料在储集层描述和油气资源评估中具有十分重要的作用[1-3]。利用测井数据可以划分岩性及评价储集层物性、含油性、生产价值和生产情况[4-6]。但是由于钻井、测井条件差异以及仪器故障等原因,经常出现部分测井段数据缺失的情况,甚至出于勘探成本考虑而放弃获取某些特定的测井数据。为了解决这个问题,研究者试图通过经验模型和多元回归分析等方法[7-10]揭示不同测井曲线之间的非线性关系,基于已有的测井数据对缺失段进行重构。但是,基于理想假设条件的经验模型通常依赖研究者的主观经验,不具有广泛适用性。多元回归分析基于测井数据间的内在联系生成测井曲线,然而井下地质情况复杂多变,数据间的映射关系很难用确定性的函数描述,所以预测精度通常较低。
近年来,随着计算机科学的发展,机器学习方法逐渐应用于测井解释[11]、岩性判别[12-13]和储层预测[14-15]等。也有部分研究者将机器学习用于测井曲线的重构,其中大多采用人工神经网络方法[16-20]。但是人工神经网络在训练过程中存在收敛速度慢、局部最小化和泛化能力差等问题,这些缺点限制了模型的预测性能[21]。同时,神经网络这种典型的黑箱问题,相对于其他机器学习算法更不具有可解释性[22]。在梯度提升决策树(GBDT)的基础上提出的XGBoost具有更高的性能及更快的速度[23],其中决策树的结构可直接使模型可视化,并且通过全局特征重要性评估增强模型的可解释性。相对于GBDT算法,XGBoost模型中加入了正则化项并将拟合模型精细化,因此在理论上拥有更强的预测能力,在众多领域也取得了较好的预测效果[24-25]。在测井信息解释方面,闫星宇等[26]通过XGBoost建立了致密砂岩储层的孔隙度与渗透率回归预测模型。谷宇峰等[27]从优化参数角度出发,基于XGBoost建立了渗透率预测模型。但是该模型算法应用于测井曲线重构方面的研究则很少。Zhong等[28]利用钻井和测井数据,基于XGBoost对煤层气井的地层密度进行了预测,但并未将其拓展到其他测井数据重构中,而且也未与其他机器学习算法进行比较。
本文提出利用XGBoost进行多源测井曲线的重构,内容包括测井曲线补全和生成两个部分,然后将其与GBDT、随机森林(RF)、全连接神经网络(FNN)方法进行对比,最后结合地质背景分析预测效果。结果表明,无论在准确度还是稳定性方面,XGBoost模型都取得了较好的表现。
1 原理与方法 1.1 XGBoost算法Chen等[23]提出的XGBoost是一种集成的树模型,这种基于GBDT的改进Boosting算法具有训练速度快、预测精度高等优点。Boosting属于集成学习算法,由多个弱学习器按照不同的权重组合成为一个强学习器。本文的XGBoost算法选择CART回归树作为基学习器,并在损失函数中添加正则项以约束损失函数的下降和模型的整体复杂度。XGBoost模型表达式为
| $ \hat{y}_{i}=\sum\limits_{k=1}^{K} f_{k}\left(x_{i}\right) \quad f_{k} \in \boldsymbol{F} $ | (1) |
式中:xi为第i个样本;
XGBoost模型旨在通过迭代方式集成弱分类器以形成预测精度和鲁棒性更高的模型[29]。每一次迭代都是在前一步的基础上增加一棵树,而新增的树视为拟合上次预测的残差。迭代过程为
| $\left\{\begin{array}{l} \hat{y}_{i}^{(0)}=0 \\ \hat{y}_{i}^{(1)}=f_{1}\left(x_{i}\right)=\hat{y}_{i}^{(0)}+f_{1}\left(x_{i}\right) \\ \hat{y}_{i}^{(2)}=f_{1}\left(x_{i}\right)+f_{2}\left(x_{i}\right)=\hat{y}_{i}^{(1)}+f_{2}\left(x_{i}\right) \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \vdots \\ \hat{y}_{i}^{(t)}=\sum\limits_{b=1}^{t} f_{k}\left(x_{i}\right)=\hat{y}_{i}^{(t-1)}+f_{t}\left(x_{i}\right) \end{array}\right. $ | (2) |
目标函数是研究一切机器学习问题的出发点,XGBoost的目标函数由损失函数和正则项两部分组成。正则项用于控制模型的复杂度,模型的预测精度由偏差和方差共同决定。为了降低方差、防止过拟合,需要在目标函数中添加正则项
| $ \varOmega\left(f_{k}\right)=\gamma T+\lambda \frac{1}{2} \sum\limits_{j=1}^{T} \omega_{j}^{2} $ | (3) |
式中:T为叶子结点数量;ωj为叶子节点分数;γ和λ均表示系数。
综上,XGBoost的目标函数为
| $L^{(t)}=\sum\limits_{i=1}^{n} l\left(y_{i}, \hat{y}_{i}\right)+\sum\limits_{k=1}^{K} \varOmega\left(f_{k}\right) $ | (4) |
式中:yi为真实值;
XGBoost采用增量训练的方式进行迭代以最大化地降低目标函数[30]。在t轮迭代之后,目标函数更新为
| $ L^{(t)}=\sum\limits_{i=1}^{n} l\left[y_{i}, \hat{y}_{i}^{(t-1)}+f_{t}\left(x_{i}\right)\right]+\varOmega\left(f_{t}\right) $ | (5) |
为了使损失函数梯度收敛更快、更准确,XGBoost利用泰勒展开式对所有二阶可导的损失函数做近似替换,目标函数近似为
| $ \begin{aligned} \widetilde{L}^{(t)} \simeq & \sum\limits_{i=1}^{n}\left\{l\left[y_{i}, \hat{y}_{i}^{(t-1)}+f_{t}\left(x_{i}\right)\right]+\right.\\ &\left.\frac{1}{2} h_{i} f_{t}^{2}\left(x_{i}\right)\right\}+\varOmega\left(f_{t}\right) \end{aligned} $ | (6) |
将式(6)中每个数据的损失函数值相加,得
| $ \begin{aligned} \widetilde{L}^{(t)} & \simeq \sum\limits_{i=1}^{n}\left[g_{i} f_{t}\left(x_{i}\right)+\frac{1}{2} h_{i} f_{t}^{2}\left(x_{i}\right)\right]+\varOmega\left(f_{t}\right) \\ &=\varPsi\left(x_{i}\right)+\varOmega\left(f_{t}\right)+\lambda T+\lambda \frac{1}{2} \sum\limits_{j=1}^{T} \omega_{j}^{2} \\ &=\sum\limits_{j=1}^{T}\left[G_{j} w_{j}+\frac{1}{2}\left(H_{j}+\lambda\right) w_{j}^{2}\right]+\lambda T \end{aligned} $ | (7) |
| $\varPsi\left(x_{i}\right)=\sum\limits_{i=1}^{n}\left[g_{i} w_{q}\left(x_{i}\right)+\frac{1}{2} h_{i} w_{q}^{2}\left(x_{i}\right)\right] $ | (8) |
式中:
在式(7)、式(8)中,每个ωj是相互独立的,对于一元二次项
| $ \omega_{j}^{*}=-\frac{G_{j}}{H_{j}+\lambda} $ | (9) |
| $\widetilde{L}^{*(t)}=-\frac{1}{2} \sum\limits_{j=1}^{T} \frac{G_{j}}{H_{j}+\lambda}+\lambda T $ | (10) |
式中:ωj*为叶节点对应最优权重;
引入评价指标量化评估模型性能,评价指标衡量的是预测数据与真实数据之间的差异。本次研究选择的三个评价指标分别是平均绝对误差(MAE)、均方根误差(RMSE)和预测模型拟合准确程度的R方值(R2)。
| $\mathrm{MAE}=\frac{1}{m} \sum\limits_{i=1}^{m}\left|\hat{y}_{i}-y_{i}\right| $ | (11) |
| $\mathrm{RMSE}=\sqrt{\frac{1}{m} \sum\limits_{i=1}^{m}\left(\hat{y}_{i}-y_{i}\right)^{2}} $ | (12) |
| $R^{2}=1-\frac{\sum\limits_{i=1}^{m}\left(\hat{y}_{i}-y_{i}\right)^{2}}{\sum\limits_{i=1}^{m}\left(\bar{y}-y_{i}\right)^{2}} $ | (13) |
式中:m是测试数据点数量;y为平均值。
RMSE越小,说明模型稳定性越好;MAE越小,说明模型准确度越高;R2越接近于1,说明模型综合性能越好。
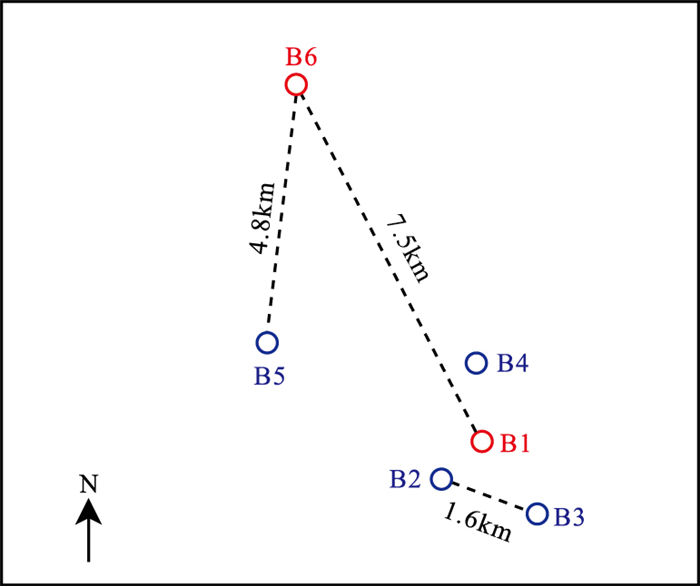
1.3 数据处理本次研究数据来自渤海湾盆地的6口定向井,井位分布如图 1所示,B2、B3、B4、B5为训练井,B1、B6为测试井,其中B1、B2、B3和B4井之间距离较近,B5和B6井与其他井距离较远。研究的测井曲线包括声波时差(DT)、井径(CAL)、中子孔隙度(CN)、自然伽马(GR)、深侧向电阻率(RD)、自然电位(SP)、补偿密度(DEN)和光电吸收截面指数(PE)。由于训练数据的质量对机器学习模型预测的准确度具有很大影响,因此需要对原始测井数据进行预处理,主要包括异常值清理和缺失值填充。
|
图 1 井位分布图 |
(1) 异常值清理。对于测井数据首尾两端用于填充空值的异常值,可以根据经验直接删除。对于测井数据内部的异常值,利用基于距离的K近邻算法对离群点进行识别清理。
(2) 缺失值填充。首先评估所有测井数据的完整性,对于缺失值较少的测井数据,先利用K近邻算法计算邻近的k(本文k取100,即10m的长度)个数据,然后填充它们的均值;对于具有部分测井数据缺失的井段,如果选择直接删除该井数据,就会使训练数据更加稀少,而机器学习对数据的数量十分敏感,这样可能导致预测模型准确度降低。因此,对于缺失部分数据的训练井,可以通过对其现有数据进行训练,然后对缺失段测井曲线进行预测补全,进而得到完整井段的测井曲线。
预处理前、后的数据量统计如表 1所示。B1~B4井的测井深度均达到4000m左右,B6井的测井深度较小。
|
|
表 1 预处理前、后数据量统计 |
为了测试XGBoost模型重构测井曲线的能力,进行了测井曲线补全实验和生成实验。主要研究内容包括:①评估XGBoost基于自身测井数据自动补全缺失井段数据的可信度;②评估XGBoost基于邻井数据生成特定测井曲线的准确度;③对比XGBoost、GBDT、RF和FNN模型的性能。
2.1 测井曲线补全实验如果一口井的部分井段测井数据缺失,可通过模型计算对缺失井段数据进行预测补全,然后将预测结果继续作为训练数据用于后续测井曲线生成实验。测井曲线补全实验可以弥补因部分数据缺失造成的数据量不足,在一定程度上也可以看作测井曲线生成实验的数据预处理过程。以表 1提供的B4井为例,验证XGBoost自动补全缺失段数据的能力。
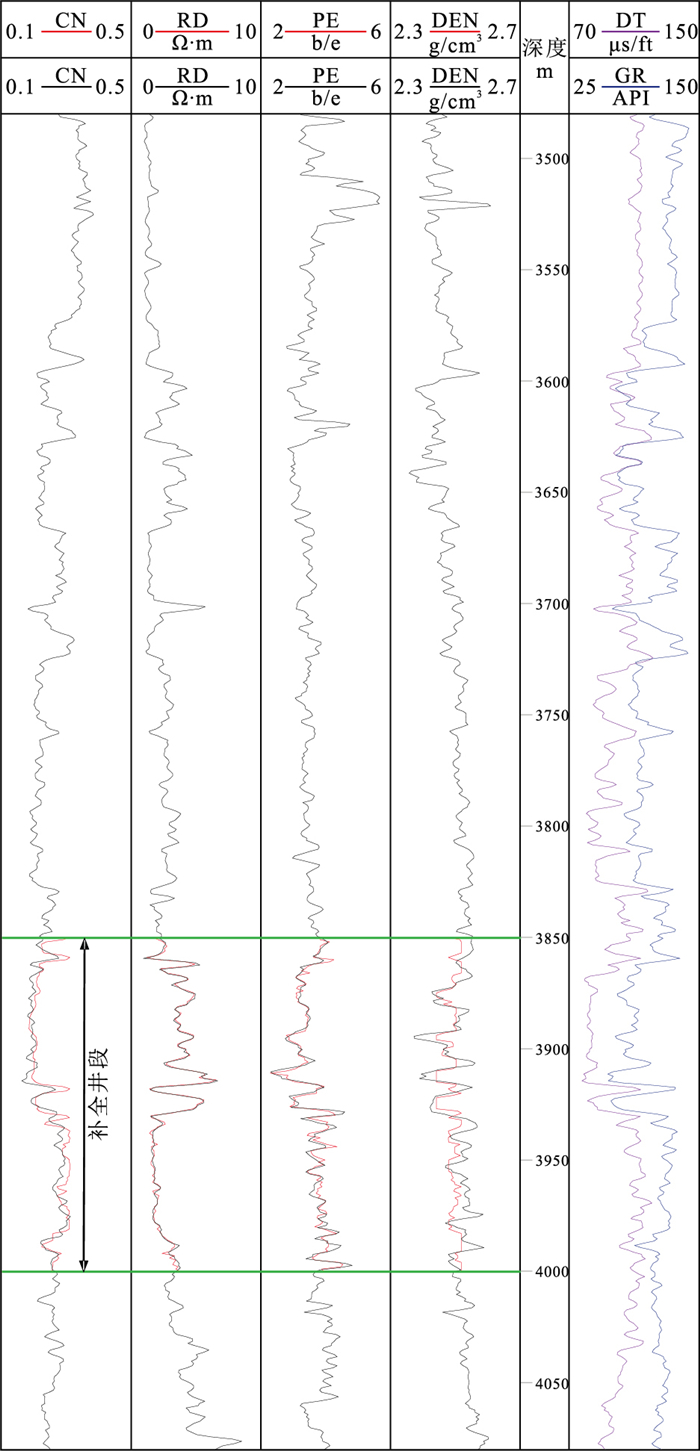
实验涉及的测井曲线共6条,井深3480~4075m,测井段总长595m(图 2)。为了验证补全数据的效果,将井深3850~4000m的CN、DEN、RD和PE测井曲线隐去,人为模拟数据缺失段,缺失段长度占总长度的22%。训练数据集由3480~3850m和4000~4075m两个完整测井段组成,采样间隔为0.1m。以DT和GR作为输入,CN、DEN、RD和PE作为输出,通过XGBoost算法进行训练。
|
图 2 测井曲线自动补全示意图 图中黑色曲线为真实的测井数据,红色曲线为XGBoost模型预测结果 |
由图可见,预测补全的RD、PE测井曲线不仅能够捕捉真实曲线的变化趋势,而且具体数值也十分接近。而补全的CN曲线虽然没有很好地捕捉到真实测井曲线的变化趋势,但是其数值与真实曲线一直维持在较小的偏差范围内。对于DEN曲线,虽然补全曲线没有很好地模拟出真实测井曲线的波动幅度,但是两条曲线的变化趋势存在相似度,也具有一定的参考价值。整体来说,XGBoost模型具有较好的自动补全缺失段数据的能力。因此对于缺失大段数据而测井数据量不足的情况,可以考虑通过XGBoost模型利用该井中完整段的测井数据对缺失段进行自动补全。
2.2 测井曲线生成实验将表 1中的B2、B3、B4、B5井作为训练井,B1、B6井作为测试井。每口井都包含相同类型的测井曲线,选取其中CAL、RD、SP作为输入数据,DT、CN、GR、DEN作为输出,分别采用XGBoost、GBDT、RF和FNN模型生成人工测井曲线。其中XGBoost、GBDT是基于决策树的Boosting集合算法,RF是基于决策树的Bagging集合算法,FNN为全连接神经网络,属于深度学习的范畴,本实验构造的是具有3个隐藏层的全连接神经网络。模型输入和输出的测井曲线之间映射关系可能非常复杂,因此在具体应用时通过K折交叉检验对模型性能进行验证,选择出使模型泛化性能最优的超参值。
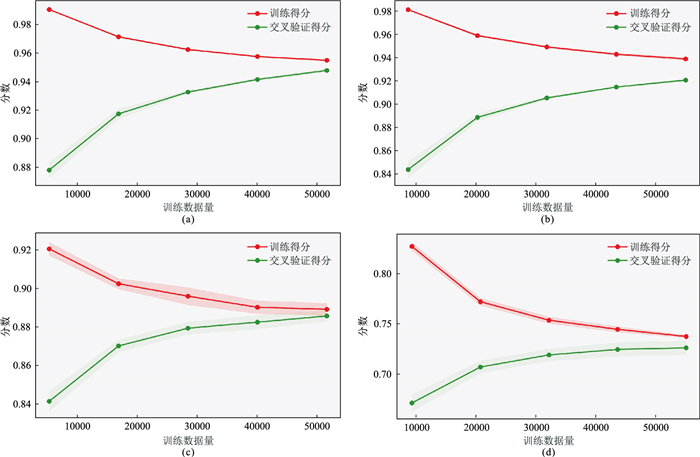
使用网格搜索对上述四种机器学习模型进行参数调优,并通过5折交叉检验验证模型性能,即将训练集随机划分为5个部分,利用其中的4个部分作为训练集,剩余的1个部分作为测试集,最后取平均测试误差作为泛化误差。使训练集的所有样本成为训练数据地同时也必然有机会成为一次测试数据,从而更好地发掘训练集数据的使用价值。图 3为4种模型的训练过程学习曲线,可见,RF、FNN模型训练曲线均有一定程度的欠拟合,FNN训练效果最差;GBDT模型在训练集表现较好,但是在交叉验证集不尽人意,表现出过拟合的倾向;XGBoost则在训练集和交叉验证集中都表现出较好的效果,这是因为XGBoost在代价函数中加入了正则项,降低了模型的方差,使训练模型更加简单,同时XGBoost借鉴了RF模型算法,采用列采样,既降低了过拟合又减少了训练次数,使训练速度大幅提高。
|
图 3 4种模型训练过程学习曲线 (a)XGBoost; (b)GBDT; (c)RF; (d)FNN |
利用各个模型完成对B2~B5训练井数据的训练后,获得了测试井B1、B6的生成曲线DT、CN、GR和DEN。
表 2记录了由4种模型得到的测试井生成曲线预测结果的评价指标数据,可以看出,FNN模型预测效果最差,此结论与交叉验证中FNN训练学习曲线欠拟合相对应。RF模型预测效果一般,XGBoost和GBDT模型的预测效果与前两者相比明显更好,并且XGBoost预测效果最好。以B1井为例,相对于GBDT、RF和FNN,其MAE分别减少了16.3%、50.0%和76.9%,RMSE分别减少了12.2%、33.5%和61.5%,R2分别增加了3.2%、9.1%和20.0%。说明XGBoost生成测井曲线的精度和稳定性都是最好。
|
|
表 2 测试井基于不同模型的预测结果 |
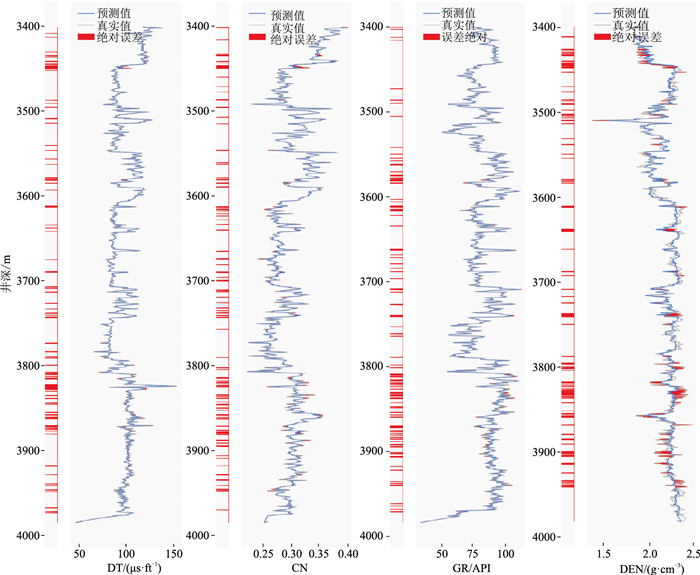
图 4展示了基于XGBoost对B1井生成测井曲线的结果。生成的测井曲线包括DT、CN、GR和DEN,为了便于和真实测井曲线对比,将两曲线上绝对误差大于平均绝对误差与标准差之和的部分标红。由图可见,DT、CN和GR曲线的预测效果非常好,大部分曲线段位于设定的误差范围内,即使是曲线波动幅度较大的井段,生成测井曲线的误差也被控制在很小的范围内。对于DEN曲线波动幅度较大的井段,生成的DEN测井曲线不能很好地捕捉其变化幅度,造成了较大偏差,但是其变化趋势与真实测井曲线类似,整体的预测效果较好。
|
图 4 基于XGBoost生成的B1井人工测井曲线 |
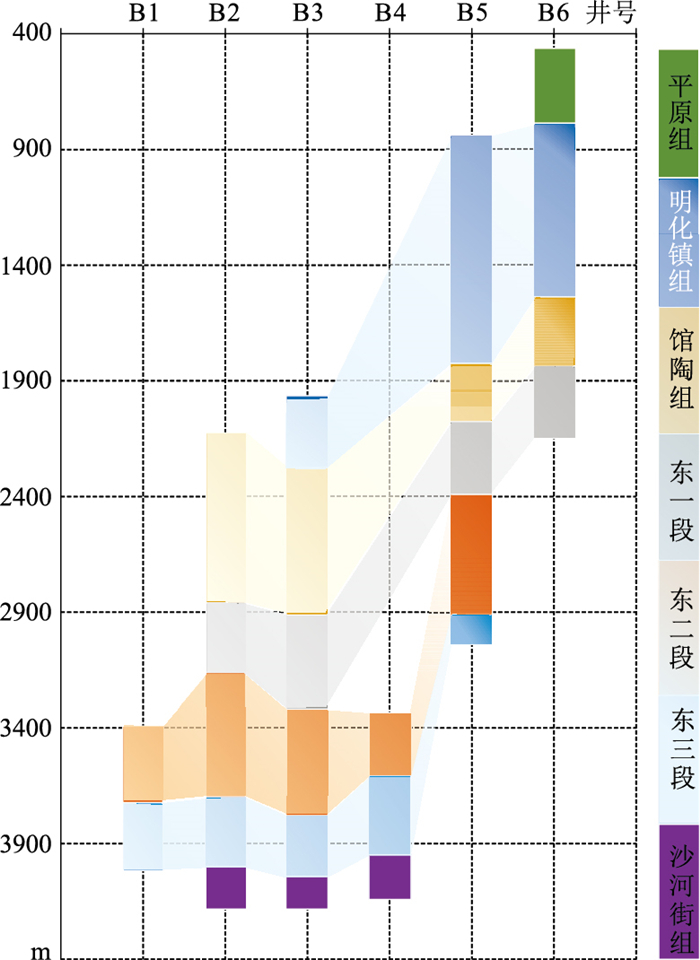
另外,由表 2可知,B6井的预测效果较B1井差,原因可能有两个方面:①B6井位于研究区北部,其余井位于研究区南部(图 1),研究区南、北地层受区域构造背景和成岩作用影响,具有不同的地层沉积特征。如图 5所示,B6井的地层与B1~B4井存在很大差异,B6井测井段中占据相当比例的明化镇组,在B3、B5井仅存上部一小段,而B6井上部平原组在其他井测井段中则完全没有。②B1、B2、B3和B4井之间距离较小,B1井处于4口井的中心位置,且其地层分布在训练井中均发育;B6井与其他井距离较大,虽然其下部地层分布在B5井也发育,但是由于训练井中对应数据量不足及B6井与训练井所在区域距离较大,导致B6井预测效果有所降低。选择该井作为训练井,可以在一定程度上检验模型的泛化能力。
|
图 5 研究区地层分布图 |
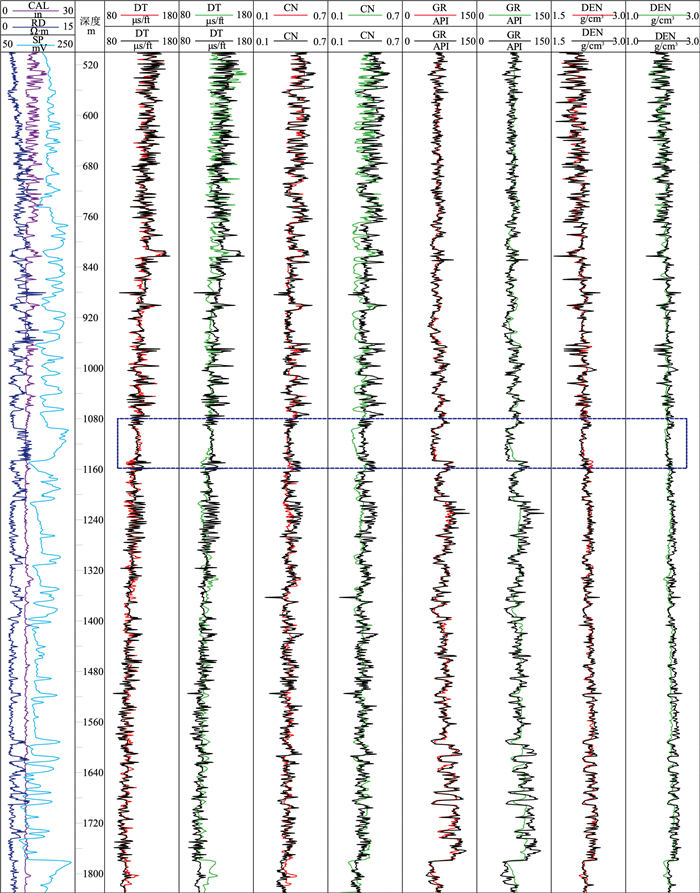
以表 2中预测结果相对不好的B6井为例,将基于XBGoost和FNN生成的测井曲线进行效果对比。如图 6所示,图中第1列为输入的3条已知测井曲线(CAL、RD和SP),第3、5、7、9列为基于XGBoost生成的人工测井曲线(红色)与作为参照的实际测井曲线(黑色)的对比,第4、6、8、10列为基于FNN的生成测井曲线(绿色)与实际测井曲线(黑色)的对比。可以发现,由于B6井上部井段测井数据在其他训练井中很少甚至没有相关映射,导致其上部井段生成的测井曲线的准确度低于下部井段,XGBoost和FNN的预测结果均出现了偏差,但是XGBoost更好地预测了测井曲线的变化趋势,生成曲线与实际曲线偏差比较小,这说明XGBoost在面对未知数据集时,具有较强的泛化能力。在井深1080~1160m处(图中蓝色虚线框内),可以发现DT、CN和GR曲线在此区间内出现一个阶跃式变化,XGBoost和FNN模型也都捕捉到了测井曲线上的这种变化,但是FNN在此区间内生成的测井曲线与真实值存在较大偏差,而XGBoost的预测准确度和稳定性均显著高于FNN。
|
图 6 基于XGBoost和FNN生成的B6井的人工测井曲线 |
(1) 为了使梯度收敛更快、更准确,XGBoost算法对损失函数进行二阶泰勒展开,并加入了正则项以权衡目标函数和模型的复杂程度,降低了模型的方差,可以很好地解决在基于神经网络的测井曲线重构方法中容易出现的过拟合问题,有效地提升了XGBoost测井曲线重构的准确性。
(2) 基于XGBoost对渤海湾盆地1口定向井的测井数据缺失段进行自动补全实验。该测试井的测井曲线中有22%的数据缺失,实验不包含其他井的测井数据,仅依靠同一口井中完整段的测井曲线对缺失段进行补全。结果显示,测井曲线补全的准确度和稳定性均达到较好效果,能在一定程度上弥补数据缺失导致的数据量不足。
(3) 基于XGBoost、GBDT、RF和FNN对渤海湾盆地2口定向井进行人工测井曲线生成实验。通过K折交叉验证检验上述模型的性能,并结合地质背景对预测效果进行对比分析。结果显示,基于XGBoost模型生成的测井曲线准确度和稳定性最高, 在面对未知的数据集时,XGBoost也表现出了较强的泛化能力。
| [1] |
王濡岳, 丁文龙, 王哲, 等. 页岩气储层地球物理测井评价研究现状[J]. 地球物理学进展, 2015, 30(1): 228-241. WANG Ruyue, DING Wenlong, WANG Zhe, et al. Progress of geophysical well logging in shale gas re-servoir evaluation[J]. Progress in Geophysics, 2015, 30(1): 228-241. |
| [2] |
HEIDARI Z, TORRES-VERDÍN C, PREEG W E. Improved estimation of mineral and fluid volumetric concentrations from well logs in thinly bedded and invaded formations[J]. Geophysics Journal of the Socie-ty of Exploration Geophysicists, 2012, 77(3): WA79. |
| [3] |
AVSETH P, SKJEI N, SKALNES A. Rock physics modelling of 4D time-shifts and time-shift derivatives using well log data: a North Sea demonstration[J]. Geophysical Prospecting, 2013, 61(2): 380-390. DOI:10.1111/j.1365-2478.2012.01134.x |
| [4] |
SINGH U K. Fuzzy inference system for identification of geological stratigraphy off Prydz Bay, East Antarctica[J]. Journal of Applied Geophysics, 2011, 75(4): 687-698. DOI:10.1016/j.jappgeo.2011.08.001 |
| [5] |
CHEN Y K, CHEN H M, XIANG K, et al. Geologi-cal structure guided well log interpolation for high-fidelity full waveform inversion[J]. Geophysical Journal International, 2016, 207(2): 1313-1331. DOI:10.1093/gji/ggw343 |
| [6] |
OWOLABI A O, OMANG B O, OYETADE O P, et al. Reservoir evaluation and volumetric analysis of Rancho field, Niger delta, using well log and 3D seismic data[J]. Open Journal of Geology, 2019, 9(13): 974-987. DOI:10.4236/ojg.2019.913100 |
| [7] |
廖茂辉. 多元回归方法校正扩径对密度曲线声波曲线的影响[J]. 物探与化探, 2014, 38(1): 174-179, 184. LIAO Maohui. The application of multiple regression method to the calibration of the influence of hole enlargementon density and acoustic logs[J]. Geophysical and Geochemical Exploration, 2014, 38(1): 174-179, 184. |
| [8] |
MOUSAVI S M A, SHADIZADEH S R, RIAHI M A, et al. NMR log prediction from seismic attributes: Using multiple linear regression and neural network methods[J]. Energy Sources Part A-Recovery Utilization and Environmental Effects, 2015, 37(7): 781-789. DOI:10.1080/15567036.2011.592914 |
| [9] |
LORENZEN R. Multivariate linear regression of so-nic logs on petrophysical logs for detailed reservoir characterization in producing fields[J]. Interpretation, 2018, 6(3): T531-T541. DOI:10.1190/INT-2018-0007.1 |
| [10] |
HILL E J, PEARCE M A, STROMBERG J M. Improving automated geological logging of drill holes by incorporating multiscale spatial methods[J]. Mathematical Geosciences, 2021, 53(1): 21-53. DOI:10.1007/s11004-020-09859-0 |
| [11] |
何旭, 李忠伟, 刘昕, 等. 应用卷积神经网络识别测井相[J]. 石油地球物理勘探, 2019, 54(5): 1159-1165. HE Xu, LI Zhongwei, LIU Xin, et al. Log facies re-cognition based on convolutional neural network[J]. Oil Geophysical Prospecting, 2019, 54(5): 1159-1165. |
| [12] |
WANG G C, CARR T R, JU Y W, et al. Identifying organic-rich Marcellus Shale lithofacies by support vector machine classifier in the Appalachian basin[J]. Computers & Geosciences, 2014, 64(3): 52-60. |
| [13] |
REN X X, HOU J G, SONG S H, et al. Lithology identification using well logs: A method by integrating artificial neural networks and sedimentary patterns[J]. Journal of Petroleum Science and Engineering, 2019, 182(5): 106336. |
| [14] |
付超, 林年添, 张栋, 等. 多波地震深度学习的油气储层分布预测案例[J]. 地球物理学报, 2018, 61(1): 293-303. FU Chao, LIN Niantian, ZHANG Dong, et al. Prediction of reservoirs using multi-component seismic data and the deep learning method[J]. Chinese Journal of Geophysics, 2018, 61(1): 293-303. |
| [15] |
张国印, 王志章, 林承焰, 等. 基于小波变换和卷积神经网络的地震储层预测方法及应用[J]. 中国石油大学学报(自然科学版), 2020, 44(4): 83-93. ZHANG Guoyin, WANG Zhizhang, LIN Chengyan, et al. Seismic reservoir prediction method based on wavelet transform and convolutional neural network and its application[J]. Journal of China University of Petroleum (Edition of Natural Science), 2020, 44(4): 83-93. DOI:10.3969/j.issn.1673-5005.2020.04.010 |
| [16] |
MA Y Z, GOMEZ E, LUNEAU B. Integration of seismic and well-log data using statistical and neural network methods[J]. The Leading Edge, 2017, 36(4): 324-329. DOI:10.1190/tle36040324.1 |
| [17] |
张东晓, 陈云天, 孟晋. 基于循环神经网络的测井曲线生成方法[J]. 石油勘探与开发, 2018, 45(4): 598-607. ZHANG Dongxiao, CHEN Yuntian, MENG Jin. Synthetic well logs generation via recurrent neural networks[J]. Petroleum Exploration and Development, 2018, 45(4): 598-607. |
| [18] |
ONALO D, ADEDIGBA S, KHAN F, et al. Data driven model for sonic well log prediction[J]. Journal of Petroleum Science & Engineering, 2018, 170: 1022-1037. |
| [19] |
HAN J, LU C H, CAO Z M, et al. Integration of deep neural networks and ensemble learning machines for missing well logs estimation[J]. Flow Measurement and Instrumentation, 2020, 73: 101748. DOI:10.1016/j.flowmeasinst.2020.101748 |
| [20] |
张宝录, 罗丹婷, 胡鹏, 等. 一种基于深度神经网络模型的测井曲线生成方法[J]. 电子测量技术, 2020, 43(11): 107-111. ZHANG Baolu, LUO Danting, HU Peng, et al. A well log curve generation method based on deep neural network[J]. Electronic Measurement Technology, 2020, 43(11): 107-111. |
| [21] |
余本国. BP神经网络局限性及其改进的研究[J]. 山西农业大学学报(自然科学版), 2009, 29(1): 89-93. YU Benguo. Discussion on the limitation and improvement of BP neural network[J]. Journal of Shanxi Agricultural University(Natural Science Edition), 2009, 29(1): 89-93. DOI:10.3969/j.issn.1671-8151.2009.01.023 |
| [22] |
FENG R H, GRANA D, BALLING N. Imputation of missing well log data by random forest and its uncertainty analysis[J]. Computers & Geosciences, 2021, 152: 104763. |
| [23] |
CHEN T Q, GUESTRIN C. XGBoost: A scalable tree boosting system[C]. Proceedings of the 22nd ACM SIGKDD International Conference on Know-ledge Discovery and Data Mining, 2016, 785-794.
|
| [24] |
FAN Z Y, ZHAN Q M, YANG C, et al. Estimating PM2.5 concentrations using spatially local XGBoost based on Full-Covered SARA AOD at the urban scale[J]. Remote Sensing, 2020, 12(20): 3368. DOI:10.3390/rs12203368 |
| [25] |
陈振宇, 刘金波, 李晨, 等. 基于LSTM与XGBoost组合模型的超短期电力负荷预测[J]. 电网技术, 2020, 44(2): 614-620. CHEN Zhenyu, LIU Jinbo, LI Chen, et al. Ultra short-term power load forecasting based on combined LSTM-XGBoost model[J]. Power System Technology, 2020, 44(2): 614-620. |
| [26] |
闫星宇, 顾汉明, 肖逸飞, 等. XGBoost算法在致密砂岩气储层测井解释中的应用[J]. 石油地球物理勘探, 2019, 54(2): 447-455. YAN Xingyu, GU Hanming, XIAO Yifei, et al. XGBoost algorithm applied in the interpretation of tight-sand gas reservoir on well logging data[J]. Oil Geophysical Prospecting, 2019, 54(2): 447-455. |
| [27] |
谷宇峰, 张道勇, 鲍志东. 测井资料PSO-XGBoost渗透率预测[J]. 石油地球物理勘探, 2021, 56(1): 26-37. GU Yufeng, ZHANG Daoyong, BAO Zhidong. Permeability prediction using PSO-XGBoost based on logging data[J]. Oil Geophysical Prospecting, 2021, 56(1): 26-37. |
| [28] |
ZHONG R Z, JOHNSON R, CHEN Z W. Generating pseudo density log from drilling and logging-while-drilling data using extreme gradient boosting (XGBoost)[J]. International Journal of Coal Geology, 2020, 220: 103416. DOI:10.1016/j.coal.2020.103416 |
| [29] |
SAGI O, ROKACH L. Approximating XGBoost with an interpretable decision tree[J]. Information Sciences, 2021, 572: 522-542. DOI:10.1016/j.ins.2021.05.055 |
| [30] |
GóMEZ-RÍOS A, LUENGO J, HERRERA F. A study on the noise label influence in boosting algorithms: AdaBoost, GBM and XGBoost[C]. International Conference on Hybrid Artificial Intelligent Systems, 2017.
|



 张家臣,北京市昌平区府学路18号中国石油大学(北京)石油工程学院,102249。Email:
张家臣,北京市昌平区府学路18号中国石油大学(北京)石油工程学院,102249。Email: