孔隙度是指示储层物性的关键参数之一,可用于精细油藏研究。岩石物理反演是定量预测孔隙度的主要手段,其思路是以岩石物理模型为基础,利用纵、横波速度等弹性参数反演孔隙度、泥质含量等物性参数[1-5]。现今的岩石物理反演方法主要以非线性岩石物理模型为基础,构建反演目标函数,并采用非线性算法求解,如蒙特卡洛法、模拟退火法等。但此类算法多解性强,且计算量巨大[6-8]。为此,近年来人们研究了线性反演方法。Grana[9]提出了对岩石物理模型线性近似的方法,并以此为基础,实现了三参数(储层孔隙度、泥质含量与饱和度)线性化反演,大幅降低了计算量与反演多解性,为在实际生产中推广应用奠定了基础。凌东明等[10]针对远离均值点模型近似结果偏差较大的问题,采用岩性约束相分段近似Xu-White模型,提高了储层物性预测精度。张佳佳等[11]以前人研究成果为基础,利用阻尼最小二乘算法直接求解线性化岩石物理反演问题,提高了三参数反演的计算效率。
现有的岩石物理线性化反演方法均为三参数反演,是将叠前弹性反演得到的纵、横波速度及密度作为已知量,求取孔隙度、泥质含量与饱和度三个未知量[9-11]。与纵、横波速度相比,密度对反射系数贡献较小,反演密度需要更大的叠前地震道集角度范围[12-13]。在储层深埋条件下,由于叠前地震道集反射角较小,导致密度反演结果不可靠;在忽略密度项的情况下,岩石物理三参数反演方程为欠定形式,无法得到唯一解,从而限制了现有岩石物理线性化反演方法对深埋储层的预测。
在前人研究基础之上,本文提出一种基于迭代算法的储层孔隙度反演方法。该方法是在岩石物理模型线性近似的基础上,推导纵、横波速度与孔隙度、泥质含量的线性关系式,然后基于贝叶斯理论构建孔隙度迭代反演目标函数,再利用二分法迭代求解。该方法不依赖于密度项,适用于储层深埋条件的孔隙度反演。
1 孔隙度迭代反演方法 1.1 线性反演的局限性分析岩石物理模型是岩石物理反演的基础,建立了储层物性参数与弹性参数之间的关系,可表示为
| $ \boldsymbol{d}=\boldsymbol{f}(\boldsymbol{m})+\boldsymbol{e} $ | (1) |
其中
| $ \left\{\begin{array}{l} \boldsymbol{d}=\left(\begin{array}{c} V_{\mathrm{P}} \\ V_{\mathrm{S}} \\ \rho \end{array}\right) \\ \boldsymbol{m}=\left(\begin{array}{c} \varphi \\ \phi \\ S_{\mathrm{W}} \end{array}\right) \end{array}\right. $ | (2) |
式中:d为由岩石纵波速度VP、横波速度VS和密度ρ组成的向量;f(m)为岩石物理模型函数,m为由孔隙度φ、泥质含量ϕ和含水饱和度SW组成的向量;e为误差向量。岩石物理反演以式(1)为基础求解模型参数m。在一般情况下,f(m)为非线性函数,需采用复杂的迭代算法求解,而此类算法多解性强,且计算量巨大,难以用于生产。为此,采用泰勒级数展开f(m),保留一阶项得到线性近似式
| $ \boldsymbol{d} \cong \boldsymbol{f}\left(\boldsymbol{m}_{0}\right)+\boldsymbol{J}_{\boldsymbol{m}_{0}} \cdot\left(\boldsymbol{m}-\boldsymbol{m}_{0}\right)+\boldsymbol{\delta} $ | (3) |
其中
| $ \boldsymbol{J}=\left(\begin{array}{lll} \frac{\partial V_{\mathrm{P}}}{\partial \varphi} & \frac{\partial V_{\mathrm{P}}}{\partial \phi} & \frac{\partial V_{\mathrm{P}}}{\partial S_{\mathrm{W}}} \\ \frac{\partial V_{\mathrm{S}}}{\partial \varphi} & \frac{\partial V_{\mathrm{S}}}{\partial \phi} & \frac{\partial V_{\mathrm{S}}}{\partial S_{\mathrm{W}}} \\ \frac{\partial \rho}{\partial \varphi} & \frac{\partial \rho}{\partial \phi} & \frac{\partial \rho}{\partial S_{\mathrm{W}}} \end{array}\right) $ | (4) |
式中:Jm0为f(m)在已知点m0处的雅可比矩阵,在反演过程中可将m0设置为常值模型;δ为e的一阶近似。在实际应用中需根据目的层特征选择合适的岩石物理模型建模,得到适合的模型参数,进而计算f(m0)与Jm0。
令b=f(m0)-Jm0·m0,对式(3)重新整理,得到储层物性参数与弹性参数之间的线性关系式
| $ \left(\begin{array}{c} V_{\mathrm{P}}-b^{(\mathrm{P})} \\ V_{\mathrm{S}}-b^{(\mathrm{S})} \\ \rho-b^{(\rho)} \end{array}\right)=\left(\begin{array}{lll} \frac{\partial V_{\mathrm{P}}}{\partial \varphi} & \frac{\partial V_{\mathrm{P}}}{\partial \phi} & \frac{\partial V_{\mathrm{P}}}{\partial S_{\mathrm{W}}} \\ \frac{\partial V_{\mathrm{S}}}{\partial \varphi} & \frac{\partial V_{\mathrm{S}}}{\partial \phi} & \frac{\partial V_{\mathrm{S}}}{\partial S_{\mathrm{W}}} \\ \frac{\partial \rho}{\partial \varphi} & \frac{\partial \rho}{\partial \phi} & \frac{\partial \rho}{\partial S_{\mathrm{W}}} \end{array}\right) \cdot\left(\begin{array}{c} \varphi \\ \phi \\ S_{\mathrm{W}} \end{array}\right)+\left(\begin{array}{l} \delta_{\mathrm{P}} \\ \delta_{\mathrm{S}} \\ \delta_{\rho} \end{array}\right) $ | (5) |
式中:b(P)、b(S)和b(ρ)分别为泰勒级数展开后纵、横波速度和密度对应的系数项;δP、δS、δρ分别为泰勒级数展开后纵、横波速度和密度对应的误差项。现有的岩石物理线性反演方法均以式(5)为基础,构建目标函数求解[9-11]。式(5)为正定方程组,将叠前弹性反演得到的纵、横波速度及密度作为已知量,可以得到唯一的孔隙度、泥质含量与含水饱和度参数。但在储层深埋条件下,叠前道集反射角较小,无法达到反演密度需要的最小角度范围。若忽略密度项,则式(5)改为
| $ \left(\begin{array}{l} V_{\mathrm{P}}-b^{(\mathrm{P})} \\ V_{\mathrm{S}}-b^{(\mathrm{S})} \end{array}\right)=\left(\begin{array}{lll} \frac{\partial V_{\mathrm{P}}}{\partial \varphi} & \frac{\partial V_{\mathrm{P}}}{\partial \phi} & \frac{\partial V_{\mathrm{P}}}{\partial S_{\mathrm{W}}} \\ \frac{\partial V_{\mathrm{S}}}{\partial \varphi} & \frac{\partial V_{\mathrm{S}}}{\partial \phi} & \frac{\partial V_{\mathrm{S}}}{\partial S_{\mathrm{W}}} \end{array}\right) \cdot\left(\begin{array}{c} \varphi \\ \phi \\ S_{\mathrm{W}} \end{array}\right)+\left(\begin{array}{c} \delta_{\mathrm{P}} \\ \delta_{\mathrm{S}} \end{array}\right) $ | (6) |
式(6)包含两个方程、三个未知量,为欠定方程组,以此为基础进行岩石物理反演无法得到唯一解。因此,在储层深埋条件下无法得到可靠密度反演结果,导致常规岩石物理线性反演方法不适用。
1.2 孔隙度反演方程推导式(6)为储层深埋条件下的纵、横波速度与孔隙度、泥质含量及饱和度的线性关系,雅可比矩阵系数项反映了不同物性参数对速度的贡献程度。在油、水两相饱和岩石中,孔隙度变化对速度影响最大,泥质含量次之,饱和度最小[14],即纵、横波速度对饱和度变化不敏感。为此,将饱和度作为扰动项,则式(6)变为
| $ \begin{aligned} &\left(\begin{array}{l} V_{\mathrm{P}}-b^{(\mathrm{P})}-\frac{\partial V_{\mathrm{P}}}{\partial S_{\mathrm{W}}} \cdot S_{\mathrm{W}} \\ V_{\mathrm{S}}-b^{(\mathrm{S})}-\frac{\partial V_{\mathrm{S}}}{\partial S_{\mathrm{W}}} \cdot S_{\mathrm{W}} \end{array}\right)= \\ &\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left(\begin{array}{cc} \frac{\partial V_{\mathrm{P}}}{\partial \varphi} & \frac{\partial V_{\mathrm{P}}}{\partial \phi} \\ \frac{\partial V_{\mathrm{S}}}{\partial \varphi} & \frac{\partial V_{\mathrm{S}}}{\partial \phi} \end{array}\right) \cdot\left(\begin{array}{l} \varphi \\ \phi \end{array}\right)+\left(\begin{array}{l} \delta_{\mathrm{P}} \\ \delta_{\mathrm{S}} \end{array}\right) \end{aligned} $ | (7) |
由此可见,当给定初始饱和度时,式(7)为正定方程组,利用纵、横波速度即可反演唯一的孔隙度与泥质含量。因此,可以式(7)为基础,基于贝叶斯理论构建反演目标函数。
为公式推导方便起见,令
| $ \boldsymbol{d}^{\prime}=\left(\begin{array}{l} V_{\mathrm{P}}-b^{(\mathrm{P})}-\frac{\partial V_{\mathrm{P}}}{\partial S_{\mathrm{W}}} \cdot S_{\mathrm{W}} \\ V_{\mathrm{S}}-b^{(\mathrm{S})}-\frac{\partial V_{\mathrm{S}}}{\partial S_{\mathrm{W}}} \cdot S_{\mathrm{W}} \end{array}\right) $ |
| $ \boldsymbol{G}=\left(\begin{array}{ll} \frac{\partial V_{\mathrm{P}}}{\partial \varphi} & \frac{\partial V_{\mathrm{P}}}{\partial \phi} \\ \frac{\partial V_{\mathrm{S}}}{\partial \varphi} & \frac{\partial V_{\mathrm{S}}}{\partial \phi} \end{array}\right) $ |
| $ \boldsymbol{m}^{\prime}=\left(\begin{array}{l} \varphi \\ \phi \end{array}\right) $ |
则式(7)简化为
| $ \boldsymbol{d}^{\prime}=\boldsymbol{G} \cdot \boldsymbol{m}^{\prime}+\boldsymbol{\delta} $ | (8) |
依据贝叶斯理论,后验概率密度分布函数正比于似然函数与先验分布的乘积[15]。假设误差项δ与先验模型参数m′均服从高斯分布,基于式(8)可构建后验概率密度分布函数近似式
| $ \begin{aligned} &P\left(\boldsymbol{m}^{\prime} \mid \boldsymbol{d}^{\prime}\right) \cong \lambda \times \\ &\exp \left[-\frac{1}{2}\left(\boldsymbol{d}^{\prime}-\boldsymbol{G} \cdot \boldsymbol{m}^{\prime}\right)^{\mathrm{T}} \cdot \boldsymbol{C}_{\boldsymbol{\delta}}^{-1} \cdot\left(\boldsymbol{d}^{\prime}-\boldsymbol{G} \cdot \boldsymbol{m}^{\prime}\right)\right] \times \\ &\exp \left[-\frac{1}{2}\left(\boldsymbol{m}^{\prime}-\boldsymbol{m}^{\prime}{}_{0}\right)^{\mathrm{T}} \cdot \boldsymbol{C}_{\boldsymbol{m}^{\prime}}^{-1} \cdot\left(\boldsymbol{m}^{\prime}-\boldsymbol{m}^{\prime}{}_{0}\right)\right] \end{aligned} $ | (9) |
式中:λ为常数;Cδ、Cm′分别为δ、m′的协方差矩阵,与常值模型m′0共同作为先验信息(均由统计测井数据得到)约束求解过程。求解式(9)概率最大值等效于求解目标函数
| $ \begin{aligned} L=&\left(\boldsymbol{d}^{\prime}-\boldsymbol{G} \cdot \boldsymbol{m}^{\prime}\right)^{\mathrm{T}} \cdot \boldsymbol{C}_{\boldsymbol{\delta}}^{-1} \cdot\left(\boldsymbol{d}^{\prime}-\boldsymbol{G} \cdot \boldsymbol{m}^{\prime}\right)+\\ &\left(\boldsymbol{m}^{\prime}-\boldsymbol{m}^{\prime}{}_{0}\right)^{\mathrm{T}} \cdot \boldsymbol{C}_{\boldsymbol{m}^{\prime}}^{-1} \cdot\left(\boldsymbol{m}^{\prime}-\boldsymbol{m}^{\prime}{}_{0}\right) \end{aligned} $ | (10) |
的最小值。为此,令∂L/∂m′=0,得到反演方程
| $ \begin{aligned} \boldsymbol{m}^{\prime}=&\left(\boldsymbol{G}^{\mathrm{T}} \cdot \boldsymbol{C}_{\boldsymbol{\delta}}^{-1} \cdot \boldsymbol{G}+\boldsymbol{C}_{\boldsymbol{m}^{\prime}}^{-1}\right)^{-1} \cdot \\ &\left(\boldsymbol{G}^{\mathrm{T}} \cdot \boldsymbol{C}_{\boldsymbol{\delta}}^{-1} \cdot \boldsymbol{d}^{\prime}+\boldsymbol{C}_{\boldsymbol{m}^{\prime}}^{-1} \cdot \boldsymbol{m}^{\prime}{}_{0}\right) \\ =& \boldsymbol{m}^{\prime}{}_{0}+\boldsymbol{C}_{\boldsymbol{m}^{\prime}} \cdot \boldsymbol{G}^{\mathrm{T}} \cdot\left(\boldsymbol{G} \cdot \boldsymbol{C}_{\boldsymbol{m}^{\prime}} \cdot \boldsymbol{G}^{\mathrm{T}}+\boldsymbol{C}_{\boldsymbol{\delta}}\right)^{-1} \cdot \\ &\left(\boldsymbol{d}^{\prime}-\boldsymbol{G} \cdot \boldsymbol{m}^{\prime}{}_{0}\right) \end{aligned} $ | (11) |
利用式(11)求解孔隙度与泥质含量时,需给定饱和度项,即反演精度与饱和度准确程度相关。为验证反演结果对饱和度的敏感性,应用理论模型进行分析。
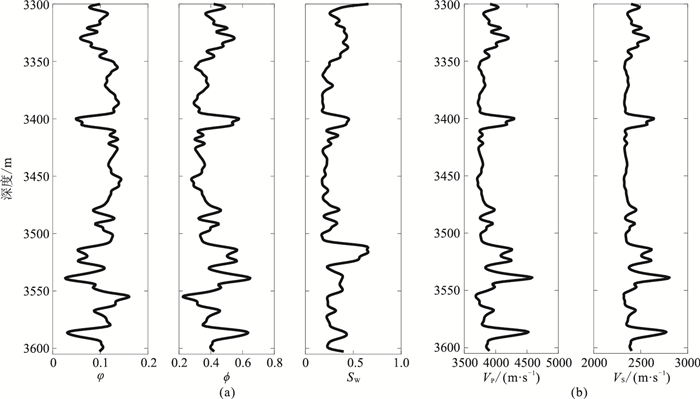
已知油、水两相流体饱和岩石孔隙度、泥质含量与含水饱和度曲线(图 1a),通过岩石物理正演得到纵波速度与横波速度(图 1b)。在正演过程中,选用适用砂、泥岩储层的Xu-White模型[16]作为岩石物理模型。为进行极限测试,给定不同常值饱和度模型,利用纵、横波速度反演孔隙度与泥质含量,进而分析饱和度对反演精度的影响。
|
图 1 油、水两相流体饱和岩石一维正演模型 (a)储层物性测井曲线;(b)正演曲线 各组分岩石物理参数为理论值[17],根据实际工区特点取砂、泥岩组分孔隙横纵比分别为0.150、0.005 |
图 2为不同饱和度模型的反演与正演结果。由图可见:当含水饱和度为1.00时,反演、正演结果均与模型曲线存在较大偏差(图 2a);当含水饱和度为0时(与饱和度均值较接近),反演、正演效果得到明显改善(图 2b);当含水饱和度为0.50时(进一步逼近饱和度均值),反演、正演效果进一步提升(图 2c);当含水饱和度为模型均值(0.29)时,反演、正演结果与模型具有较好的一致性(图 2d)。

|
图 2 不同饱和度模型的反演与正演结果 (a)饱和度为1.00;(b)饱和度为0;(c)饱和度为0.50;(d)饱和度为模型均值(0.29) 蓝色为模型曲线,红色为反演结果,绿色为利用反演的孔隙度、泥质含量与给定饱和度通过正演得到的纵、横波速度曲线 |
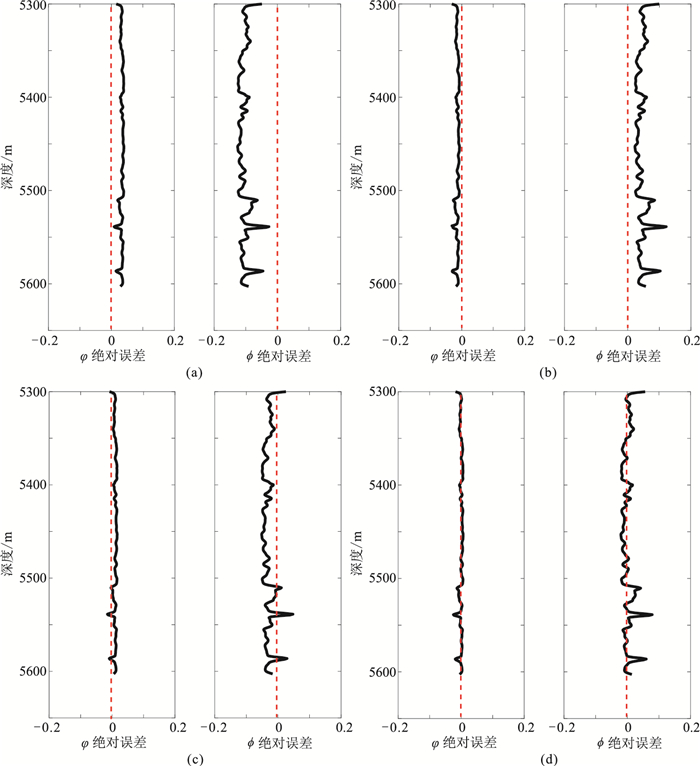
图 3为图 2对应的反演结果绝对误差。由图可见,设定饱和度越接近模型饱和度均值,绝对误差越小,具体表现为:当饱和度为1.00时,孔隙度平均绝对误差为0.034,泥质含量平均绝对误差为0.106(图 3a);当饱和度为0时,孔隙度平均绝对误差为0.013,泥质含量平均绝对误差为0.042(图 3b);当饱和度为0.50时,孔隙度平均绝对误差为0.01,泥质含量平均绝对误差为0.033(图 3c);当饱和度为模型饱和度均值(0.29)时,孔隙度平均绝对误差为0.003,泥质含量平均绝对误差为0.011(图 3d)。因此,对于油、水两相的流体饱和岩石模型,反演结果对饱和度模型的精度要求低,给定合理的常值饱和度模型,即可保证相对反演结果的可靠性,说明反演结果对饱和度不敏感。
|
图 3 图 2对应的反演结果绝对误差 (a)饱和度为1.00;(b)饱和度为0;(c)饱和度为0.50;(d)饱和度为模型饱和度均值(0.29) 黑色实线为误差曲线,红色虚线为0值线 |
由上述分析可知,反演精度取决于对真实饱和度均值的搜索,常值模型的饱和度越接近真实饱和度均值,反演精度越高。为此,本文采用二分法迭代求解式(11),思路如下:
(1) 分别设置初始模型的含水饱和度为0、1.00进行第一次反演,得到孔隙度与泥质含量,并基于岩石物理模型,结合反演结果正演纵、横波速度,并计算正演结果与实测结果的平均相关系数γ0、γ1;
(2) 按二分法,对初始饱和度模型求平均,得到第二次反演所需的饱和度常值模型,即为0.50,并计算正演相关系数γ2,对比γ0,γ1,γ2,保留两项最大相关系数及对应饱和度进入下一轮反演;
(3) 如果反演结果的精度满足要求,则终止迭代,输出最终反演结果,否则,求取平均孔隙度继续迭代,直到反演结果满足要求或达到最大迭代次数为止。
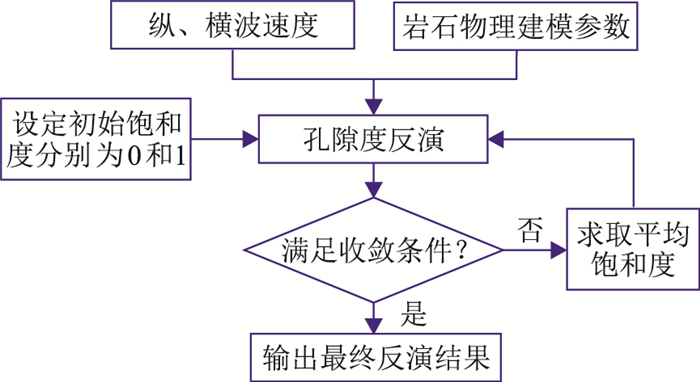
上述迭代反演方法可忽略密度项影响,仅利用纵、横波速度即可得到相对可靠的孔隙度(图 4)。
|
图 4 孔隙度迭代反演流程 |
为验证孔隙度迭代反演方法的可行性与反演结果的有效性,利用一维正演模型(图 1)进行测试。以正演过程采用的岩石物理模型为基础,利用纵、横波速度迭代反演孔隙度与泥质含量。
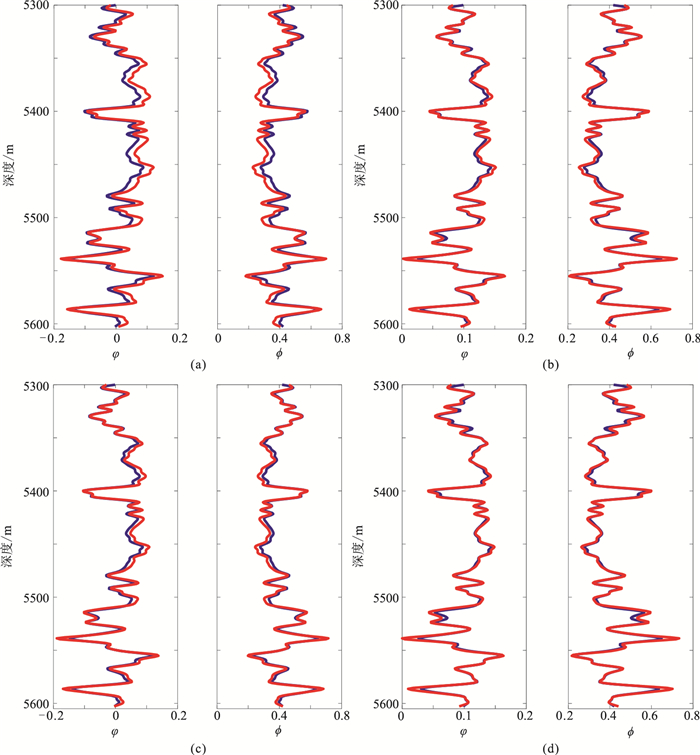
图 5为一维模型孔隙度迭代反演结果,图 6为图 5对应的反演结果绝对误差。由图可见:随着迭代次数增加,饱和度均值趋于模型饱和度均值0.29,反演结果逐渐收敛(图 5);孔隙度、泥质含量反演结果绝对误差接近0(图 6),并且收敛速度较快,2~4次迭代即可得到最优解。上述结果说明所提迭代反演方法可行、有效。
|
图 5 一维模型孔隙度迭代反演结果 (a)第一次迭代(由二分法得到的饱和度均值为0.500);(b)第二次迭代(由二分法得到的饱和度均值为0.250);(c)第三次迭代(由二分法得到的饱和度均值为0.375);(d)第四次迭代(由二分法得到的饱和度均值为0.3125) 红、蓝色线分别为反演曲线与模型曲线 |
|
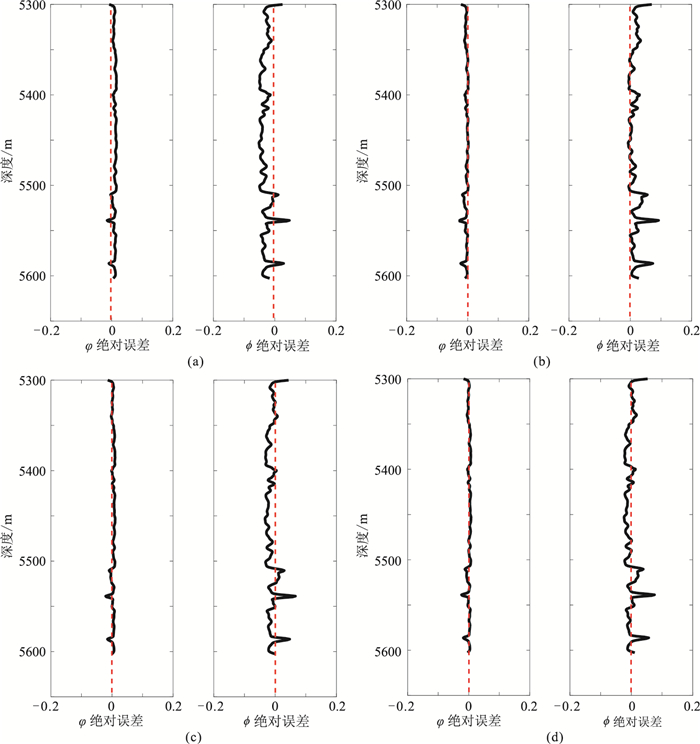
图 6 图 5对应的反演结果绝对误差 (a)第一次迭代;(b)第二次迭代;(c)第三次迭代;(d) 第四次迭代 黑色实线为误差曲线,红色虚线为0值线 |
M区位于塔里木盆地北部凹陷,研究目标为底水块状油藏,埋深大于5000m,目的层为砂岩储层,厚度约为100m,以滨岸相沉积为主。储层物性相对均匀,且地震资料品质较好,适合孔隙度迭代反演测试。该区W1井测井序列相对完整,包含纵、横波速度及密度数据,通过计算可得到孔隙度、泥质含量及饱和度。以W1井数据为基础进行岩石物理建模,选用适合砂岩储层的Xu-White模型[16]。
图 7为M区岩石物理模型正演结果,可见实测曲线与正演结果较吻合,证明所建岩石物理模型有效。通过岩石物理建模,确定M区砂、泥岩组分孔隙横纵比分别为0.190、0.008,岩石物理基本建模参数如表 1所示。

|
图 7 M区岩石物理模型正演结果 黑色线为实测曲线,红色线为正演结果 |
|
|
表 1 各组分岩石物理基本参数 |
基于岩石物理建模结果,结合叠前同步反演得到的纵、横波速度等弹性参数,并将饱和度分别为1和0的初始含水饱和度模型作为输入,进行迭代反演,求取孔隙度与泥质含量(图 8)。

|
图 8 M区孔隙度(a)与泥质含量(b)迭代反演剖面 W2井揭示,在东河砂岩下段储层物性发生变化,泥质含量增加、孔隙度降低 |
图 8为M区孔隙度与泥质含量迭代反演剖面。由反演结果可见一条高泥质含量条带(图 8b),且对应位置的反演孔隙度出现明显低值区(图 8a),稳定泥岩段上覆于巨厚块状砂体之上,与钻井成果及地质认识相吻合。因此,反演结果较好地表征了目的层段储盖组合。为了进一步验证反演效果,提取井点位置的反演曲线进行分析。
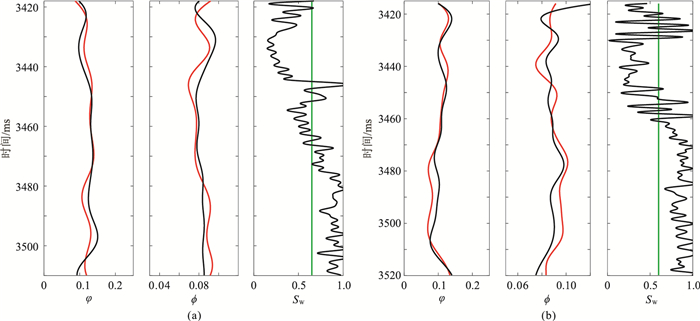
图 9为W1、W2井井位处目的层段反演结果。由图可见,孔隙度、泥质含量反演结果与实测曲线的相对变化规律基本一致,但二者的绝对值在局部存在差异,其原因是迭代得到的常值模型饱和度与实际饱和度的差异所致。因此,反演结果对目的层段储层物性具有一定指示作用,对于纯油层或纯水层,反演精度高,但当流体性质存在纵向分异时,反演精度有所下降。
|
图 9 W1(a)、W2井(b)井位处目的层段反演结果 黑色线为实测曲线,红色线为反演结果,绿色线为最终迭代产生的含水饱和度曲线。为对比方便,按地震频带范围,对孔隙度与泥质含量实测曲线进行滤波 |
本文以岩石物理线性近似模型为基础,推导了纵、横波速度与孔隙度、泥质含量的线性关系式,并基于贝叶斯理论构建反演目标函数,利用二分法求解,迭代反演了储层孔隙度、泥质含量。该方法不依赖于密度项,适用于储层深埋条件下的孔隙度预测,拓宽了岩石物理线性反演方法的适用性。理论模型与实际数据测试结果表明,所提方法具有一定可行性,且应用效果较明显。
针对油、水两相流体饱和岩石,本文方法反演结果对饱和度模型不敏感,应用迭代反演方法可以得到相对可靠的孔隙度预测结果。对于纯油层或纯水层,反演精度高,但当流体性质存在纵向分异时,反演精度有所下降。对于气层,反演结果对饱和度模型的精度要求较高,可能会降低孔隙度迭代反演方法的适用性。关于含气储层的孔隙度反演方法有待进一步研究和完善。
| [1] |
DOYEN P M. Seismic Reservoir Characterization: An Earth Modelling Perspective[M]. EAGE Publications, 2007.
|
| [2] |
吴媚, 符力耘, 李维新. 高分辨率非线性储层物性参数反演方法和应用[J]. 地球物理学报, 2008, 51(2): 546-557. WU Mei, FU Liyun, LI Weixin. A high-resolution nonlinear inversion method of reservoir parameters and its application to oil/gas exploration[J]. Chinese Journal of Geophysics, 2008, 51(2): 546-557. DOI:10.3321/j.issn:0001-5733.2008.02.027 |
| [3] |
印兴耀, 崔维, 宗兆云, 等. 基于弹性阻抗的储层物性参数预测方法[J]. 地球物理学报, 2014, 57(12): 4132-4140. YIN Xungyao, CUI Wei, ZONG Zhaoyun, et al. Petrophysical property inversion of reservoirs based on elastic impedance[J]. Chinese Journal of Geophy-sics, 2014, 57(12): 4132-4140. DOI:10.6038/cjg20141224 |
| [4] |
李志勇, 钱峰, 胡光岷, 等. 储层弹性与物性参数地震叠前同步反演的确定性优化方法[J]. 地球物理学报, 2015, 58(5): 1706-1716. LI Zhiyong, QIAN Feng, HU Guangmin, et al. Prestack seismic joint inversion of reservoir elastic and petrophysical parameters using deterministic optimization method[J]. Chinese Journal of Geophysics, 2015, 58(5): 1706-1716. |
| [5] |
杨培杰. 砂泥岩储层孔隙度和含水饱和度同步反演[J]. 地球物理学报, 2018, 61(2): 673-682. YANG Peijie. Porosity and water saturation simultaneous inversion for sand-mudstone reservoir[J]. Chinese Journal of Geophysics, 2018, 61(2): 673-682. |
| [6] |
李坤, 印兴耀. 混合概率模型驱动的叠前地震反演方法[J]. 石油地球物理勘探, 2020, 55(4): 839-853. LI Kun, YIN Xingyao. Prestack seismic inversion driven by mixture probabilistic models[J]. Oil Geophysical Prospecting, 2020, 55(4): 839-853. |
| [7] |
李祺鑫, 罗亚能, 张生, 等. 高分辨率波阻抗贝叶斯序贯随机反演[J]. 石油地球物理勘探, 2020, 55(2): 389-397. LI Qixin, LUO Yaneng, ZHANG Sheng, et al. High-resolution Bayesian sequential stochastic inversion[J]. Oil Geophysical Prospecting, 2020, 55(2): 389-397. |
| [8] |
SEN M K, STOFFA P L. Global Optimization Me-thods in Geophysical Inversion[M]. Cambridge University Press, 2013.
|
| [9] |
GRANA D. Bayesian linearized rock-physics inversion[J]. Geophysics, 2016, 81(6): D625-D641. DOI:10.1190/geo2016-0161.1 |
| [10] |
凌东明, 杜启振, 田军, 等. 基于岩相约束的Xu-White模型线性化近似与反演[J]. 石油地球物理勘探, 2019, 54(3): 577-586. LING Dongming, DU Qizhen, TIAN Jun, et al. The Xu-White model linearized approximation and inversion based on lithofacies constraint[J]. Oil Geophysical Prospecting, 2019, 54(3): 577-586. |
| [11] |
张佳佳, 印兴耀, 张广智, 等. 基于线性化岩石物理反演的物性参数预测方法[J]. 石油勘探与开发, 2020, 47(1): 57-64. ZHANG Jiajia, YIN Xingyao, ZHANG Guangzhi, et al. Prediction method of physical parameters based on linearized rock physics inversion[J]. Petroleum Exploration and Development, 2020, 47(1): 57-64. |
| [12] |
Downton J E, Laurence R L. Three term AVO waveform inversion[J]. SEG Technical Program Expanded Abstracts, 2004, 23: 215-218. |
| [13] |
田军, 吴国忱, 宗兆云. 鲁棒性AVO三参数反演方法及不确定性分析[J]. 石油地球物理勘探, 2013, 48(3): 443-449. TIAN Jun, WU Guocheng, ZONG Zhaoyun. Robust three-term AVO inversion and uncertainty analysis[J]. Oil Geophysical Prospecting, 2013, 48(3): 443-449. |
| [14] |
凌东明, 杜启振, 崔永平, 等. 塔里木盆地深层东河砂岩油藏剩余油地震预测——以东河1油藏为例[J]. 石油地球物理勘探, 2018, 53(5): 1031-1040, 1094. LING Dongming, DU Qizhen, CUI Yongping, et al. Residual oil prediction on seismic data in a deep sand reservoir, Tarim Basin: A case study of the reservoir Donghe 1[J]. Oil Geophysical Prospecting, 2018, 53(5): 1031-1040, 1094. |
| [15] |
陈建江, 印兴耀. 基于贝叶斯理论的AVO三参数波形反演[J]. 地球物理学报, 2007, 50(4): 1251-1260. CHEN Jianjiang, YIN Xingyao. Three-parameter AVO waveform inversion based on Bayesian theorem[J]. Chinese Journal of Geophysics, 2007, 50(4): 1251-1260. DOI:10.3321/j.issn:0001-5733.2007.04.035 |
| [16] |
XU S Y, WHITE R E. A new velocity model for clay-sand mixtures[J]. Geophysical Prospecting, 1995, 43(1): 91-118. DOI:10.1111/j.1365-2478.1995.tb00126.x |
| [17] |
葛瑞·马沃可. 岩石物理手册: 孔隙介质中地震分析工具[M]. 安徽合肥: 中国科学技术大学出版社, 2008.
|



 田军,新疆自治区库尔勒市机场路58号东方地球物理公司研究院库尔勒分院,841000。Email:
田军,新疆自治区库尔勒市机场路58号东方地球物理公司研究院库尔勒分院,841000。Email: 