② 中国石油大学(华东)地球科学与技术学院,山东青岛 266580
② School of Geosciences, China University of Petroleum (East China), Qingdao, Shandong 266580, China
储层物性参数(如孔隙度、泥质含量等)可为储层评价提供依据。随着油气勘探开发目标日趋复杂,对储层物性参数的反演精度的要求越来越高。
目前,常规的储层物性参数预测大多是基于贝叶斯理论框架,利用物性参数的先验分布信息,构建储层弹性参数与物性参数之间的似然函数,寻找最大后验概率解并将其作为反演结果。Mukerji等[1-2]在贝叶斯理论框架下,将统计岩石物理模型与叠前地震反演相结合,实现了岩性识别及流体预测。Eidsvik等[3]将岩石物理模型作为先验信息,将地震数据与储层参数之间的关系作为似然函数,实现了储层及流体预测。Bachrach[4]基于Gassmann方程建立岩石物理模型,实现了孔隙度与含水饱和度的联合反演。邓继新等[5]考虑孔隙度、饱和度与储层岩石弹性特征的相关性,在岩石物理模型基础上,结合贝叶斯统计反演,实现了孔隙度与含气饱和度的联合反演。Grana等[6]将统计岩石物理模型与贝叶斯反演相结合,在不同条件下对储层参数进行概率估计,提高了反演精度。印兴耀等[7]基于统计岩石物理模型、蒙特卡洛模拟及期望最大化算法,提出了基于弹性阻抗反演的储层物性参数预测方法。Gui等[8]针对不同弹性参数之间精度的差异,构建了包含权重系数的储层物性参数与弹性参数之间的加权关系,在贝叶斯框架下,结合马尔科夫链蒙特卡洛(MCMC)随机模拟技术,提高了储层物性参数的反演效率。李志勇等[9]在贝叶斯反演框架下,对目标函数的梯度用泰勒公式近似展开,并将储层弹性参数对物性参数的梯度用差分形式表示,通过共轭梯度算法实现了储层物性参数与弹性参数的同步反演。杨培杰[10]通过Simon模型建立砂泥岩物性参数与弹性参数之间的定量关系,并基于贝叶斯理论构建多信息联合约束的反演目标函数,联合蒙特卡洛模拟与遗传算法求解,实现了孔隙度与含水饱和度的同步反演。凌东明等[11]将岩相约束下线性化近似的Xu-White模型引入贝叶斯框架中,结合最小二乘优化算法实现了储层物性参数反演。张佳佳等[12]对复杂岩石物理模型进行泰勒展开,得到线性化岩石物理模型,利用阻尼最小二乘算法求解精确解析解,预测了储层物性参数。李坤等[13]提出差分进化MCMC随机模型的相约束叠前地震概率化反演方法,实现了碎屑岩储层物性参数同步预测。时磊等[14]针对致密砂岩储层建模及参数反演难度大的问题,利用岩石物理敏感性分析作为指导,通过核贝叶斯判别法反演了致密砂岩储层孔隙度、渗透率等参数。张健等[15]基于贝叶斯理论得到储层弹性参数、物性参数及岩相后验概率分布的解析表达式,由此提出一种构造约束联合概率反演方法,引入构造信息和井信息,提高了反演结果的横向连续性及分辨率。但地球物理反问题的非线性特征易导致常规算法在求解过程中陷入局部极值。因此,如何避免这种情况,是提高预测精度的关键点之一。
智能算法可避免陷入局部最优解,提高求解结果的准确性。近年来,部分学者将智能优化算法引入地球物理问题求解中。田景文等[16]针对模拟退火算法和BP算法的不足,将模拟退火算法与Powell算法有机组合并引入BP算法中,提高了算法的收敛速度和精度,实现了薄互层物性参数预测。Fattahi等[17]将智能优化方法,如粒子群算法优化的支持向量机回归(SVR-PSO)、减法聚类及自适应神经模糊推理系统(ANFIS-SCM)等,与传统贝叶斯方法预测的孔隙度、含水饱和度进行对比,验证了智能优化方法的可行性与准确性。张冰等[18]基于岩石物理模型的反演流程,引入模拟退火优化粒子群算法,解决了多参数同时反演问题。邢凯[19]联合变权系数混合高斯模型与布谷鸟算法,解决了在没有考虑地质结构及初始岩相比例时得到的结果与实际地层分布不符合的问题,针对传统随机反演方法的不确定性,引入信息熵模型,并与布谷鸟混合高斯MCMC反演方法耦合,增强了反演结果的稳定性,提高了反演的精度。王鹏飞等[20]针对传统全局寻优算法收敛速度慢、易陷入局部极值的缺点,将布谷鸟算法与单纯形法、粒子群算法相结合,提高了大地电磁数据反演的精度。王峣钧等[21]将布谷鸟算法与MCMC方法相融合,避免了在高维数据多参数同步反演时传统MCMC方法因抽样随机性而陷入局部最优的问题,实现了不同岩相条件下储层参数的精细描述。
将智能优化算法引入地球物理问题的求解时,部分智能优化算法由于较强的局部搜索能力,增强了在某一范围内的搜索精度,但同时会导致算法的全局搜索能力不够,在求解过程中易陷入局部最优问题中。
本文在前人研究的基础上,以弹性阻抗与储层物性参数关系为基础,建立储层物性参数反演所需的目标函数,针对地球物理反问题非线性特点以及部分智能优化算法全局搜索能力较弱的问题,引入一种新型元启发式算法——布谷鸟算法,对反演目标函数进行求解,从而预测储层物性参数。相比于其他智能优化算法,布谷鸟算法作为一种新的全局优化算法,其Levy飞行机制使算法有相对较高的概率生成大步长,增强了在求解过程中的全局搜索能力,较大概率避免了算法陷入局部极值,适用于解决地球物理反演非线性问题,同时也解决了部分优化算法全局搜索能力较弱的问题。通过模型试算及实际资料测试,验证了本文方法能够有效实现储层物性参数预测。
1 方法原理 1.1 岩石物理模型构建岩石物理方法是联系储层弹性参数与物性参数的桥梁,对地震正演和反演结果的定量解释有着十分重要的意义[22-23]。经典岩石物理模型(如Xu-White模型等)因其自身假设条件(如岩石矿物组分、孔隙类型不够丰富,岩石及组成成分均为各向同性、线性和弹性介质等),无法兼具不同地区参数性质的多样性,因而导致经典岩石物理模型在实际资料应用中受限。
在实际资料处理过程中,地震弹性参数与物性参数之间的关系可用曲线拟合方式刻画。在误差允许的条件下,可通过线性近似将二者的关系表示为
| $ \left\{\begin{array}{l} V_{\mathrm{P}}=a_{1} \varphi+b_{1} V_{\mathrm{sh}}+c_{1} S_{\mathrm{w}}+d_{1} \\ V_{\mathrm{S}}=a_{2} \varphi+b_{2} V_{\mathrm{sh}}+c_{2} S_{\mathrm{w}}+d_{2} \\ \rho=a_{3} \varphi+b_{3} V_{\mathrm{sh}}+c_{3} S_{\mathrm{w}}+d_{3} \end{array}\right. $ | (1) |
改写为矩阵形式
| $ \left[\begin{array}{c} V_{\mathrm{P}} \\ V_{\mathrm{S}} \\ \rho \end{array}\right]=\left[\begin{array}{lll} a_{1} & b_{1} & c_{1} \\ a_{2} & b_{2} & c_{2} \\ a_{3} & b_{3} & c_{3} \end{array}\right]\left[\begin{array}{c} \varphi \\ V_{\mathrm{sh}} \\ S_{\mathrm{w}} \end{array}\right]+\left[\begin{array}{c} d_{1} \\ d_{2} \\ d_{3} \end{array}\right] $ | (2) |
式中:VP为纵波速度;VS为横波速度;ρ为密度;φ为孔隙度;Vsh为泥质含量;Sw为含水饱和度;系数ai、bi、ci(i=1, 2, 3)和常数项di(i=1, 2, 3)可由测井资料多元回归得到。
当地震弹性参数与物性参数的关系无法近似为线性时,可通过多项式拟合的方法,将其表示为多元高阶方程的形式
| $ \left\{\begin{aligned} &V_{\mathrm{P}}= a_{1, n} \varphi^{n}+a_{1, n-1} \varphi^{n-1}+\cdots+a_{1,1} \varphi+\\ &\ \ \ \ \ \ \ \ \ \ b_{1, n} V_{\mathrm{sh}}^{n}+b_{1, n-1} V_{\mathrm{sh}}^{n-1}+\cdots+b_{1,1} V_{\mathrm{sh}}+\\ &\ \ \ \ \ \ \ \ \ \ c_{1, n} S_{\mathrm{w}}^{n}+c_{1, n-1} S_{\mathrm{w}}^{n-1}+\cdots+c_{1,1} S_{\mathrm{w}}+d_{1} \\ &V_{\mathrm{S}}= a_{2, n} \varphi^{n}+a_{2, n-1} \varphi^{n-1}+\cdots+a_{2,1} \varphi+\\ &\ \ \ \ \ \ \ \ \ b_{2, n} V_{\mathrm{sh}}^{n}+b_{2, n-1} V_{\mathrm{sh}}^{n-1}+\cdots+b_{2,1} V_{\mathrm{sh}}+\\ &\ \ \ \ \ \ \ \ \ c_{2, n} S_{\mathrm{w}}^{n}+c_{2, n-1} S_{\mathrm{w}}^{n-1}+\cdots+c_{2,1} S_{\mathrm{w}}+d_{2} \\ &\rho= a_{3, n} \varphi^{n}+a_{3, n-1} \varphi^{n-1}+\cdots+a_{3,1} \varphi+\\ &\ \ \ \ \ \ \ b_{3, n} V_{\mathrm{sh}}^{n}+b_{3, n-1} V_{\mathrm{sh}}^{n-1}+\cdots+b_{3,1} V_{\mathrm{sh}}+\\ &\ \ \ \ \ \ \ c_{3, n} S_{\mathrm{w}}^{n}+c_{3, n-1} S_{\mathrm{w}}^{n-1}+\cdots+c_{3,1} S_{\mathrm{w}}+d_{3} \end{aligned}\right. $ | (3) |
式中系数ai, j、bi, j、ci, j(i=1, 2, …, n;j=1, 2, 3,…, n)和常数项dj(j=1, 2, 3)皆通过最小二乘拟合得出。通过式(1)或式(3)可建立弹性参数与物性参数之间的联系,结合阻抗方程可进一步建立这种联系。Connolly[24]对弹性阻抗方程进行了推导,具体为
| $ \mathrm{EI}(\theta)=V_{\mathrm{P}}^{1+\tan ^{2} \theta} V_{\mathrm{S}}^{-8 K \sin ^{2} \theta} \rho^{1-4 K \sin ^{2} \theta} $ | (4) |
式中:θ为入射角度;K=(VS/VP)2,一般令其等于0.25。
Whitcombe[25]在式(4)基础上,引入归一化常数,方程变换为
| $ \mathrm{EI}(\theta)=V_{\mathrm{P}_{0}} \rho_{0}\left(\frac{V_{\mathrm{P}}}{V_{\mathrm{P}_{0}}}\right)^{1+\tan ^{2} \theta}\left(\frac{V_{\mathrm{S}}}{V_{\mathrm{S}_{0}}}\right)^{-8 K \sin ^{2} \theta}\left(\frac{\rho}{\rho_{0}}\right)^{1-4 K \sin ^{2} \theta} $ | (5) |
式中VP0、VS0、ρ0分别为测井资料中纵波速度、横波速度、密度的均值。
对式(5)两边取对数,整理得
| $ \ln \mathrm{EI}=A \ln V_{\mathrm{P}}+B \ln V_{\mathrm{S}}+C \ln \rho+D $ | (6) |
其中A=1+tan2θ, B=-8Ksin2θ, C=1-4Ksin2θ,D=-tan2θ·lnVP0+8Ksin2θ·lnVS0+4Ksin2θ·lnρ0。
为了同时反演孔隙度、泥质含量、含水饱和度三个参数,需要引入三个角度的弹性阻抗[26]。将三个角度θ1、θ2、θ3所对应的弹性阻抗分别记为EI1、EI2、EI3,则式(6)可以表示为
| $ \left[\begin{array}{l} \ln \mathrm{EI}_{1} \\ \ln \mathrm{EI}_{2} \\ \ln \mathrm{EI}_{3} \end{array}\right]=\left[\begin{array}{ccc} A_{1} & B_{1} & C_{1} \\ A_{2} & B_{2} & C_{2} \\ A_{3} & B_{3} & C_{3} \end{array}\right]\left[\begin{array}{c} \ln V_{\mathrm{P}} \\ \ln V_{\mathrm{S}} \\ \ln \rho \end{array}\right]+\left[\begin{array}{c} D_{1} \\ D_{2} \\ D_{3} \end{array}\right] $ | (7) |
将式(1)或式(3)代入式(7),可得表征弹性阻抗与储层物性参数之间关系的函数,即
| $ \left[\mathrm{EI}_{1}, \mathrm{EI}_{2}, \mathrm{EI}_{3}\right]=f_{\mathrm{RPM}}\left(\varphi, V_{\mathrm{sh}}, S_{\mathrm{w}}\right) $ | (8) |
引入随机误差项ε,则岩石物理模型可表示为
| $ \left[\mathrm{EI}_{1}, \mathrm{EI}_{2}, \mathrm{EI}_{3}\right]=f_{\mathrm{RPM}}\left(\varphi, V_{\mathrm{sh}}, S_{\mathrm{w}}\right)+\varepsilon $ | (9) |
至此,建立了弹性阻抗与物性参数之间的函数关系,为后续储层物性参数的反演奠定了基础。
1.2 布谷鸟搜索算法布谷鸟搜索算法(Cuckoo Search Algorithm)是由Yang等[27-28]受布谷鸟孵育寄生现象启发而提出的一种新型元启发式算法。相对于其他启发式算法,该算法具有参数少、全局搜索能力强的优点。布谷鸟搜索算法的主要思路是布谷鸟的巢寄生行为(育雏行为)与鸟类的Levy飞行机制两种策略的结合。根据巢寄生行为,如果宿主发现布谷鸟的卵,则放弃该巢,并利用Levy飞行机制寻找新的位置。鸟类的Levy飞行行为作为一种典型的随机游走机制,具有高度随机性,由较长时间的短步长与较短时间的长步长组成。随机游走步长满足重尾分布,偶尔的长步长能扩大搜索范围,增加种群多样性,有效避免算法陷入局部极值。
在布谷鸟搜索算法中,设定了三个理想状态:①每只布谷鸟一次只产一只蛋,并随即选择寄生鸟巢;②在一组鸟巢中,质量最好的鸟巢将被保留到下一代;③鸟巢的数量是固定的,且宿主发现外来鸟蛋的概率即发现概率Pa∈0, 1。
在这三个理想状态下,设X(0)=[x1(0), x2(0), …, xM(0)]为全部鸟巢的初始位置,由给定边界内随机产生,M为初始化生成鸟巢的个数。则t+1代由t代根据布谷鸟寻巢路径和位置更新公式为
| $ \boldsymbol{x}_{k}^{(t+1)}=\boldsymbol{x}_{k}^{(t)}+\alpha \oplus \operatorname{Levy}(\beta) \quad k=1,2, \cdots, M $ | (10) |
式中:xk(t)表示第t代的第k个解;α>0为步长控制因子,用于控制布谷鸟随机搜索的范围;⊕表示点对点乘法;β是用来控制Levy飞行生成随机路径的参数,Levy(β)表示布谷鸟随机搜索路径,由Levy分布产生
| $ \operatorname{Levy}(\beta) \sim u=t^{-\lambda} \quad 1<\lambda \leqslant 3 $ | (11) |
式中:u为随机步长;λ为幂次系数。在布谷鸟算法实现过程中,Levy飞行的随机步长由Mantegna算法计算得到
| $ \operatorname{Levy}(\beta) \sim \frac{\mu}{|\nu|^{\frac{1}{\beta}}} $ | (12) |
式中:β=3/2;μ和ν为服从正态分布的随机数,即
| $ \mu \sim N\left(0, \sigma_{\mu}^{2}\right), \nu \sim N(0,1) $ | (13) |
| $ \sigma_{\mu}=\frac{\Gamma(1+\beta) \sin \frac{{\rm{ \mathsf{ π} }} \beta}{2}}{\Gamma\left(\frac{1+\beta}{2}\right) 2^{\frac{\beta-1}{2}} \beta} $ | (14) |
式中Γ为标准Gamma函数。
布谷鸟搜索算法通过上述Levy飞行机制对鸟巢的位置更新,将更新后的新解与原来的解进行对比,选择较好的结果并保留;利用发现概率Pa对相对较差的解利用下式进一步更新
| $ \boldsymbol{x}_{k}^{(t+1)}=\boldsymbol{x}_{k}^{(t)}+\gamma H\left(P_{\mathrm{a}}-r\right)\left[\boldsymbol{x}_{i}^{(t)}-\boldsymbol{x}_{j}^{(t)}\right] $ | (15) |
式中:γ、r均为0~1之间均匀分布的随机数;H(·)为赫维赛德函数;xi(t)和xj(t)为在第t代所有鸟巢中随机选取的两个鸟巢。
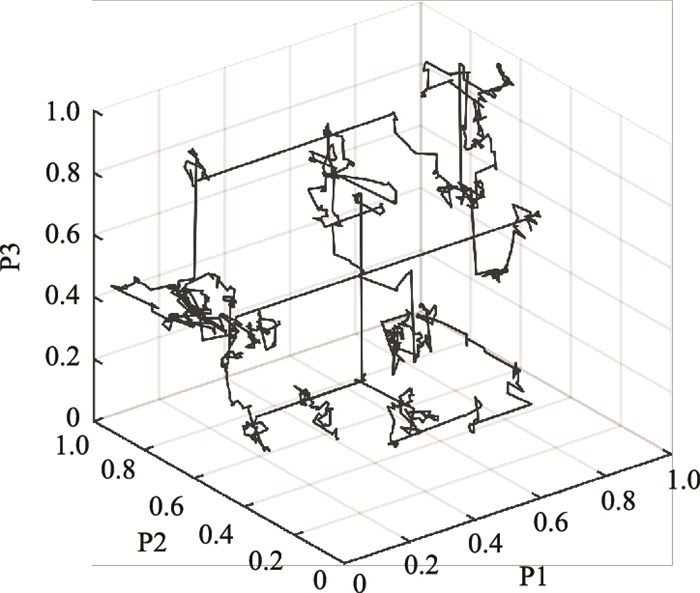
重复以上的过程,直到满足设定误差的最优解或者达到限制的最大迭代次数。图 1为三维空间Levy飞行示意图[29],展示了布谷鸟搜索算法在三维空间中随机搜索步长。
|
图 1 三维空间Levy飞行示意图 P1、P2、P3分别表示三维坐标系的坐标轴 |
通过弹性阻抗与储层物性参数之间的关系可构建反演目标函数[30],具体形式为
| $ F(\boldsymbol{m})=\min \left[\sum\limits_{i=1}^{3}\left|\mathrm{EI}_{\mathrm{cal}, i}(\boldsymbol{m})-\mathrm{EI}_{\mathrm{real}, i}(\boldsymbol{m})\right|\right] $ | (16) |
式中:参数向量m=(φ, Vsh, Sw)是待反演的储层物性参数,分别为孔隙度、泥质含量、含水饱和度;EIreal, i(m)为利用实际数据计算得到的弹性阻抗;EIcal, i(m)为利用式(9)计算得到的弹性阻抗;i=1, 2, 3表示三个不同角度。
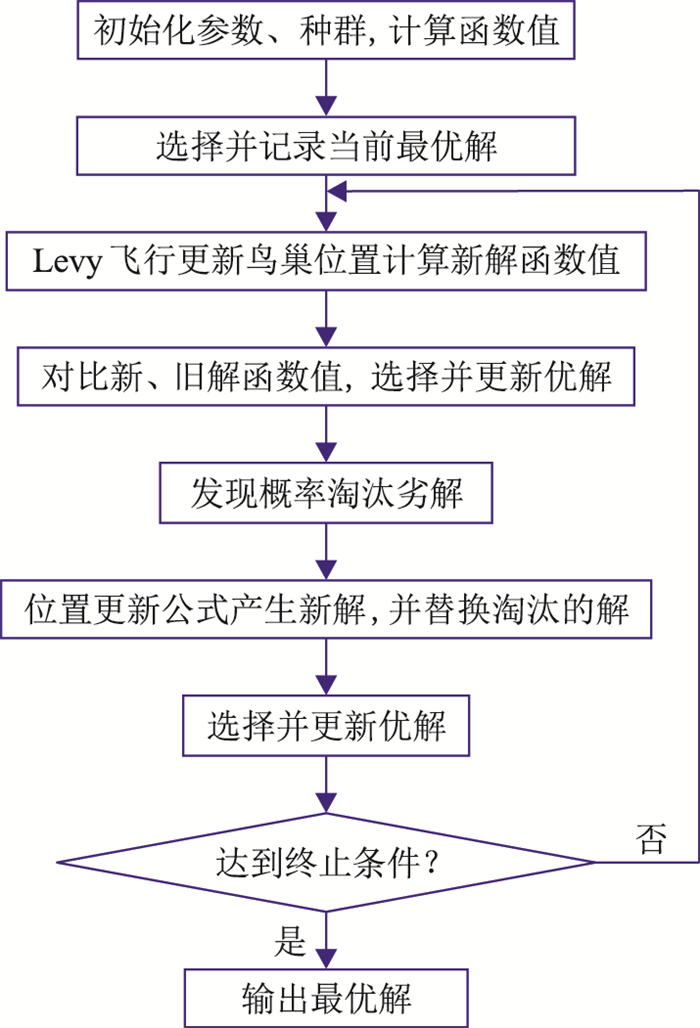
2.2 基于布谷鸟算法的储层物性参数反演引入全局寻优算法中的布谷鸟搜索算法对目标函数进行求解。首先,对测井资料中孔隙度、泥质含量、含水饱和度分别进行统计、分析,得到参数的搜索区间,最小值、最大值分别用mminwell=(φmin, Vsh-min, Sw-min)、mmaxwell=(φmax, Vsh-max, Sw-max)表示[31];其次,利用物性参数搜索区间对种群初始化,并设置布谷鸟搜索算法的相关参数(种群规模、发现概率、预计算精度、最大迭代次数等);最后,基于布谷鸟搜索算法将每一个鸟巢个体视作目标函数的一个解,最终找到在搜索区间最符合条件的鸟巢,即目标函数的最优解,实现对储层物性参数的预测。基于布谷鸟算法的储层物性参数反演具体步骤(图 2)如下。
|
图 2 基于布谷鸟算法的储层物性参数反演流程图 |
(1) 初始化算法参数。设鸟巢个数为N,最大迭代次数为Max_iter,预计算精度为Tol,发现概率Pa∈(0,1),初始化鸟巢M0=[m1(0), m2(0), …, mN(0)]并计算每个初始鸟巢mi(0)的函数值F[mi(0)]。
(2) 对比初始鸟巢函数值,并记录当前最优解Gbest、函数值F(G)。
(3) 根据当前鸟巢的位置,利用Levy飞行公式(式(10))对鸟巢位置进行更新,计算更新后的鸟巢位置mi(t+1)的函数值F[mi(t+1)],并与上一代鸟巢位置mi(t)对比,选取较优鸟巢,更新最优解Gbest、函数值F(G)。
(4) 产生一组在(0,1)均匀分布的随机数r,并与发现概率Pa比较。若r>Pa,则利用式(15)对该位置进一步更新,反之不变。计算更新后鸟巢位置的函数值,与之前对应的鸟巢位置进行对比、选择,进一步更新最优解Gbest、函数值F(G)。
(5) 判断搜索结果是否满足本文算法的预设条件(Max_iter、Tol),若没有达到预设条件,则返回步骤(3);若满足预设条件,停止迭代,输出最优解Gbest。
3 模型试算为检验本文基于布谷鸟搜索算法的储层物性参数预测方法的效果,选用一维模型数据进行试算。
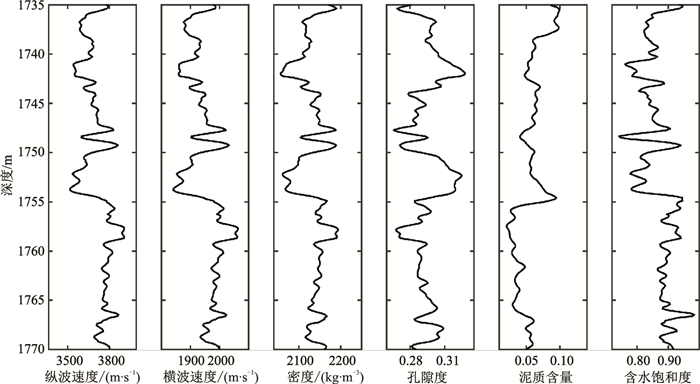
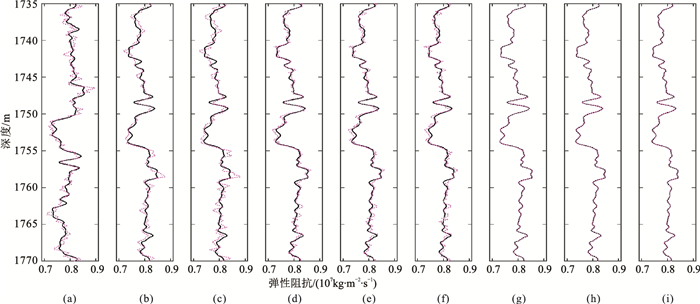
模型数据曲线如图 3所示。图 4是利用孔隙度、泥质含量、含水饱和度计算得到的三个角度(10°、20°和30°)的弹性阻抗与利用弹性参数表征的弹性阻抗方程计算得到的三个角度的真实弹性阻抗的对比。由图可以看出,非线性条件下建立的统计岩石物理模型(式(9))计算得到的弹性阻抗曲线与利用弹性阻抗公式计算(式(5))得到的结果吻合程度较高,说明本文所建立的统计岩石物理模型是准确的、合理的。
|
图 3 一维模型曲线 |
|
图 4 不同角度、不同模型真实(黑线)与计算(红虚线)弹性阻抗对比 不同角度线性关系下得到的确定性岩石物理模型:(a)10°;(b)20°;(c) 30°。不同角度线性关系下得到的统计性岩石物理模型:(d)10°;(e)20°;(f)30°。不同角度非线性关系下得到的统计性岩石物理模型:(g)10°;(h)20°;(i) 30° |
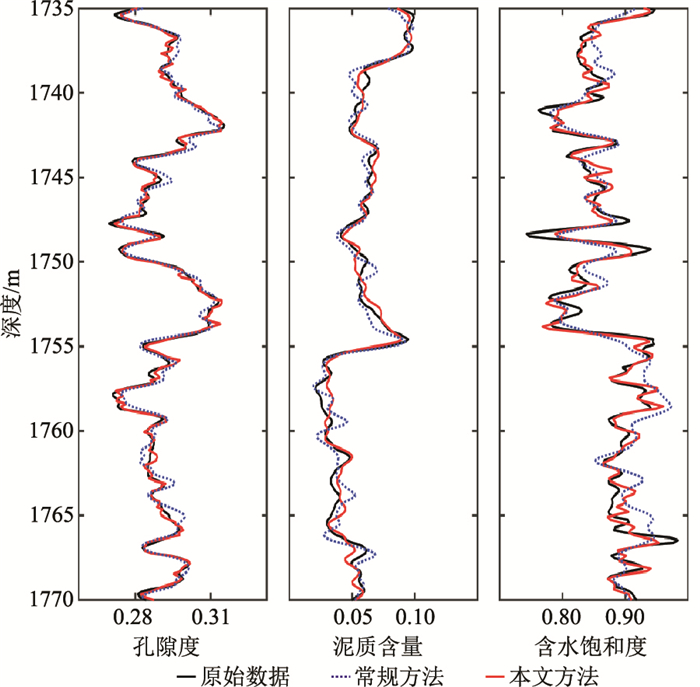
利用本文全局寻优反演方法对目标函数进行求解,反演目标层段储层物性参数。图 5为利用布谷鸟算法反演得到的储层物性参数与原始曲线对比。由图可知,利用本文方法反演得到的物性参数与原始数据整体趋势基本吻合,仅在1760~1765m处结果变化幅度较大,但反演参数误差在合理区间内,验证了本文方法的可行性。
|
图 5 不同方法物性参数反演结果对比 |
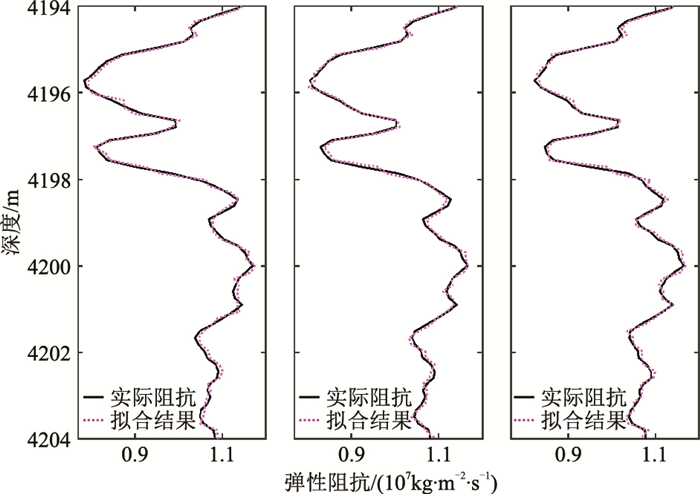
选取D工区A井实际资料对本文方法进行测试。首先进行一维实际数据(图 6)测试。在反演储层物性参数之前,需要分析实际测井数据,构建统计岩石物理模型。通过统计岩石物理模型由孔隙度、泥质含量、含水饱和度计算弹性阻抗曲线(10°、20°和30°),并与实际弹性阻抗结果进行对比(图 7)。由图可见,实际曲线与计算结果整体变化趋势相同。

|
图 6 A井实际测井曲线 |
|
图 7 A井统计岩石物理模型与阻抗方程计算结果对比 |
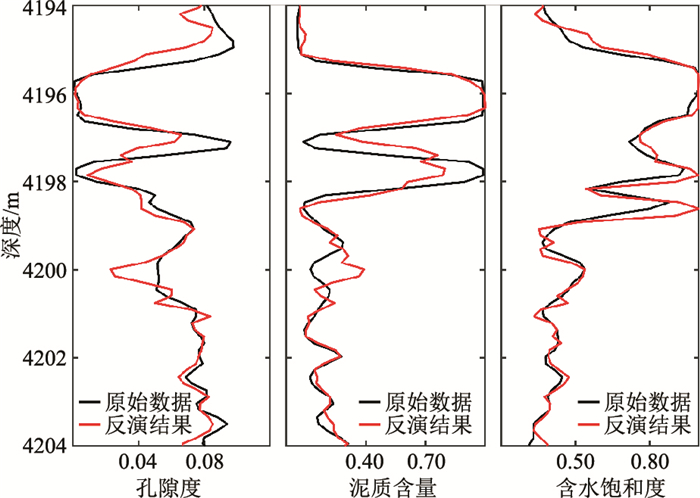
利用弹性阻抗数据反演储层物性参数(孔隙度、泥质含量、含水饱和度),结果如图 8所示。由图可见,基于布谷鸟算法反演得到的储层物性参数与测井曲线基本一致,整体变化趋势相同。其中,孔隙度相关系数为75.76%,泥质含量相关系数为80.31%,含水饱和度相关系数为84.55%。
|
图 8 A井基于布谷鸟算法的储层物性参数反演结果 |
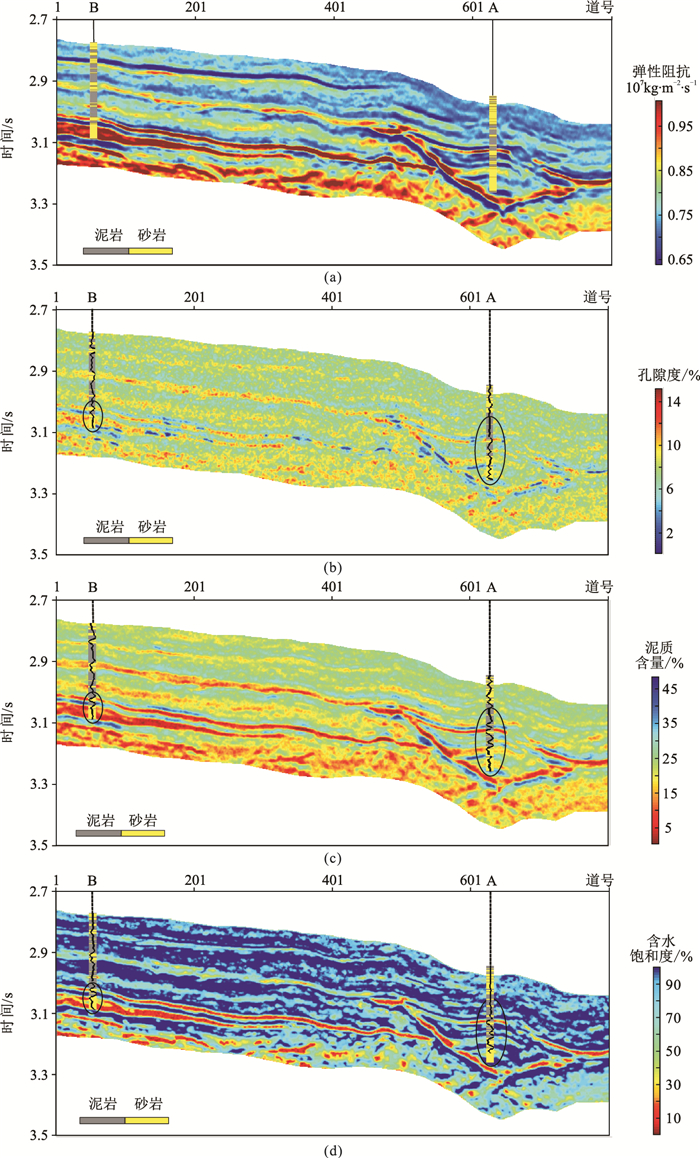
然后将本文方法拓展应用于二维测线,对图 9a进行储层物性参数反演,结果如图 9b~图 9d所示。由图可见,物性参数(孔隙度、泥质含量、含水饱和度)在横向上具有较好的连续性,大套层组间的界面较为清晰;并且在A、B两井处,与测井岩性解释结果及物性参数曲线吻合较好(黑色圆圈处)。
|
图 9 利用本文方法的不同物性参数反演结果 (a)原始数据(以中角度弹性阻抗为例);(b)孔隙度;(c)泥质含量;(d)含水饱和度 |
针对当前常规物性参数反演容易陷入局部极值的问题,本文引入元启发式算法——布谷鸟算法,提出了一种基于布谷鸟算法的储层物性参数反演方法。采用布谷鸟算法对目标函数求解,反演储层物性参数,兼具大量局部搜索及必要的全局搜索。对比利用布谷鸟算法预测得到的储层物性参数反演结果与实际测井物性参数可知,预测结果与实际测井数据具有较高的吻合度,误差较小,证明了本文算法的可行性和有效性。
Levy分布的重尾分布特征保证了布谷鸟算法的全局寻优能力,但也同样降低了该算法的计算效率。考虑全局寻优算法的计算效率下降问题,将来可进一步采取布谷鸟算法与常规全局寻优算法的结合策略,在求解精度允许范围内提高算法的计算效率,进一步提高本文方法的实用性。
| [1] |
MUKERJI T, AVSETH P, MAVKO G, et al. Statistical rock physics: Combining rock physics, information theory, and geostatistics to reduce uncertainty in seismic reservoir characterization[J]. The Leading Edge, 2001, 20(3): 313-319. DOI:10.1190/1.1438938 |
| [2] |
MUKERJI T, JØRSTAD A, AVSETH P, et al. Mapping lithofacies and pore-fluid probabilities in a North Sea reservoir: seismic inversions and statistical rock physics[J]. Geophysics, 2001, 66(4): 988-1001. DOI:10.1190/1.1487078 |
| [3] |
EIDSVIK J, AVSETH P, OMRE H, et al. Stochastic reservoir characterization using prestack seismic data[J]. Geophysics, 2004, 69(4): 978-993. DOI:10.1190/1.1778241 |
| [4] |
BACHRACH R. Joint estimation of porosity and sa-turation using stochastic rock-physics modeling[J]. Geophysics, 2006, 71(5): O53-O63. DOI:10.1190/1.2235991 |
| [5] |
邓继新, 王尚旭. 基于统计岩石物理的含气储层饱和度与孔隙度联合反演[J]. 石油天然气学报, 2009, 31(1): 48-52. DENG Jixin, WANG Shangxu. Joint inversion of sa-turation and porosity in gas reservoirs based on statistical rock physics[J]. Journal of Oil and Gas Technology, 2009, 31(1): 48-52. DOI:10.3969/j.issn.1000-9752.2009.01.012 |
| [6] |
GRANA D, ROSSA E D. Probabilistic petrophysical-properties estimation integrating statistical rock phy-sics with seismic inversion[J]. Geophysics, 2010, 75(3): O21-O37. DOI:10.1190/1.3386676 |
| [7] |
印兴耀, 崔维, 宗兆云, 等. 基于弹性阻抗的储层物性参数预测方法[J]. 地球物理学报, 2014, 57(12): 4132-4140. YIN Xingyao, CUI Wei, ZONG Zhaoyun, et al. Petrophysical property inversion of reservoir based on elastic impedance[J]. Chinese Journal of Geophysics, 2014, 57(12): 4132-4140. DOI:10.6038/cjg20141224 |
| [8] |
GUI J Y, GAO J H, YONG X S, et al. Reservoir parameter inversion based on weighted statistics[J]. Applied Geophysics, 2015, 12(4): 523-532. DOI:10.1007/s11770-015-0523-z |
| [9] |
李志勇, 钱峰, 胡光岷, 等. 储层弹性与物性参数地震叠前同步反演的确定性优化方法[J]. 地球物理学报, 2015, 58(5): 1706-1716. LI Zhiyong, QIAN Feng, HU Guangmin, et al. Pre-stack seismic joint inversion of reservoir elastic and petrophysical parameter using deterministic optimization method[J]. Chinese Journal of Geophysics, 2015, 58(5): 1706-1716. |
| [10] |
杨培杰. 砂泥岩储层孔隙度和含水饱和度同步反演[J]. 地球物理学报, 2018, 61(2): 673-682. YANG Peijie. Porosity and water saturation simultaneous inversion for sand-mudstone reservoir[J]. Chinese Journal of Geophysics, 2018, 61(2): 673-682. |
| [11] |
凌东明, 杜启振, 田军, 等. 基于岩相约束的Xu-White模型线性化近似与反演[J]. 石油地球物理勘探, 2019, 54(3): 577-586. LING Dongming, DU Qizhen, TIAN Jun, et al. The Xu-White model linearized approximation and inversion based on lithofacies constraint[J]. Oil Geophysical Prospecting, 2019, 54(3): 577-586. |
| [12] |
张佳佳, 印兴耀, 张广智, 等. 基于线性化岩石物理反演的物性参数预测方法[J]. 石油勘探与开发, 2020, 47(1): 57-64. ZHANG Jiajia, YIN Xingyao, ZHANG Guangzhi, et al. Prediction method of physical parameters based on linearized rock physics inversion[J]. Petroleum Exploration and Development, 2020, 47(1): 57-64. |
| [13] |
李坤, 印兴耀, 宗兆云. 岩石物理驱动的相约束叠前地震概率化反演方法[J]. 中国科学(地球科学), 2020, 50(6): 832-854. LI Kun, YIN Xingyao, ZONG Zhaoyun. Facies-constrained prestack seismic probabilistic inversion dri-ven by rock physics[J]. Scientia Sinica(Terrae), 2020, 50(6): 832-854. |
| [14] |
时磊, 王璞, 刘俊州, 等. 致密砂岩储层物性参数预测方法研究[J]. 石油物探, 2020, 59(1): 98-107. SHI Lei, WANG Pu, LIU Junzhou, et al. Physical properties prediction for tight sandstone reservoirs[J]. Geophysical Prospecting for Petroleum, 2020, 59(1): 98-107. DOI:10.3969/j.issn.1000-1441.2020.01.011 |
| [15] |
张健, 李景叶, 王建花, 等. 基于构造约束联合概率反演的油藏参数表征方法[J]. 石油地球物理勘探, 2021, 56(6): 1359-1369. ZHANG Jian, LI Jingye, WANG Jianhua, et al. Re-servoir parameter characterization method based on joint probability inversion with structural constraints[J]. Oil Geophysical Prospecting, 2021, 56(6): 1359-1369. |
| [16] |
田景文, 高美娟. 基于改进的模拟退火人工神经网络的薄互储层参数预测[J]. 信息与控制, 2002, 31(2): 180-184, 188. TIAN Jingwen, GAO Meijuan. Thin interbedded re-servoir parameters predicting based on improved simulated annealing artificial neural network[J]. Information and Control, 2002, 31(2): 180-184, 188. DOI:10.3969/j.issn.1002-0411.2002.02.018 |
| [17] |
FATTAHI H, KARIMPOULI S. Prediction of porosity and water saturation using pre-stack seismic attributes: a comparison of Bayesian inversion and computational intelligence methods[J]. Computational Geosciences, 2016, 20(5): 1075-1094. DOI:10.1007/s10596-016-9577-0 |
| [18] |
张冰, 郭智奇, 徐聪, 等. 基于岩石物理模型的页岩储层裂缝属性及各向异性参数反演[J]. 吉林大学学报(地球科学版), 2018, 48(4): 1244-1252. ZHANG Bing, GUO Zhiji, XU Cong, et al. Fracture properties and anisotropic parameters inversion of shales based on rock physics model[J]. Journal of Jilin University(Earth Science Edition), 2018, 48(4): 1244-1252. |
| [19] |
邢凯. 基于信息熵和布谷鸟算法的地质统计学反演方法研究[D]. 四川成都: 电子科技大学, 2020. XING Kai. Research on Geostatistical Inversion Method Based on Information Entropy and Cuckoo Algorithm[D]. University of Electronic Science and Technology of China, Chengdu, Sichuan, 2020. |
| [20] |
王鹏飞, 王书明. 改进的布谷鸟MT反演算法[J]. 石油地球物理勘探, 2020, 55(1): 217-225. WANG Pengfei, WANG Shuming. MT data inversion based on improved cuckoo search algorithm[J]. Oil Geophysical Prospecting, 2020, 55(1): 217-225. |
| [21] |
王峣钧, 邢凯, 厍斌, 等. 布谷鸟马尔科夫链蒙特卡洛混合高斯地质统计学随机反演[J]. 地球物理学报, 2021, 64(7): 2540-2553. WANG Yaojun, XING Kai, SHE Bin, et al. Mixed Gaussian stochastic inversion based on hybrid of cuckoo algorithm and Markov chain Monte Carlo[J]. Chinese Journal of Geophysics, 2021, 64(7): 2540-2553. |
| [22] |
印兴耀, 刘欣欣. 储层地震岩石物理建模研究现状与进展[J]. 石油物探, 2016, 55(3): 309-325. YIN Xingyao, LIU Xinxin. Research status and progress of the seismic rock-physics modeling methods[J]. Geophysical Prospecting for Petroleum, 2016, 55(3): 309-325. DOI:10.3969/j.issn.1000-1441.2016.03.001 |
| [23] |
崔维. 储层物性参数叠前地震反演方法研究[D]. 山东青岛: 中国石油大学(华东), 2015. CUI Wei. The Study of Petro-physical Properties Pre-Stack Seismic Inversion[D]. China University of Petroleum(East China), Qingdao, Shandong, 2015. |
| [24] |
CONNOLLY P. Elastic impedance[J]. The Leading Edge, 1999, 18(4): 438-452. DOI:10.1190/1.1438307 |
| [25] |
WHITCOMBE D N. Elastic impedance normalization[J]. Geophysics, 2002, 67(1): 60-62. DOI:10.1190/1.1451331 |
| [26] |
刘百红, 李学云, 李建华, 等. 弹性阻抗反演在储层含气性预测中的应用[J]. 石油地球物理勘探, 2012, 47(增刊1): 72-77. LIU Baihong, LI Xueyun, LI Jianhua, et al. Gas-bea-ring reservoir prediction by elastic impedance inversion[J]. Oil Geophysical Prospecting, 2012, 47(S1): 72-77. |
| [27] |
YANG X S, DEB S. Cuckoo search via Lévy flights[C]. 2009 World Congress on Nature & Biologically Inspired Computing (NaBIC), Coimbatore, India, 2009, 210-214.
|
| [28] |
YANG X S, DEB S. Multiobjective cuckoo search for design optimization[J]. Computers & Operations Research, 2013, 40(6): 1616-1624. |
| [29] |
李娜, 贺兴时. 基于粒子群算法的布谷鸟搜索算法[J]. 纺织高校基础科学学报, 2014, 27(3): 374-379, 384. LI Na, HE Xingshi. Cuckoo search algorithm based on particle swarm optimization algorithm[J]. Basic Sciences Journal of Textile Universities, 2014, 27(3): 374-379, 384. DOI:10.3969/j.issn.1006-8341.2014.03.022 |
| [30] |
王国权, 陈双全, 王恩利, 等. 粒子群优化的等效基质模量提取和横波预测方法[J]. 石油科学通报, 2020, 5(3): 316-326. WANG Guoquan, CHEN Shuangquan, WANG Enli, et al. Equivalent matrix modulus extraction and S-wave prediction based on particle swarm optimization[J]. Petroleum Science Bulletin, 2020, 5(3): 316-326. DOI:10.3969/j.issn.2096-1693.2020.03.027 |
| [31] |
CUI X F, GAO J H, ZHANG B, et al. Poststack impedance inversion using improved particle swarm optimization[C]. SEG Technical Program Expanded Abstracts, 2016, 35: 3809-3813.
|



 段治川,山东省青岛市经济技术开发区长江西路66号中国石油大学(华东)地球科学与技术学院,266580。Email:
段治川,山东省青岛市经济技术开发区长江西路66号中国石油大学(华东)地球科学与技术学院,266580。Email: