② 山东大学岩土与结构工程研究中心,山东济南 250061;
③ 华能西藏水电安全工程技术研究中心,西藏林芝 860000
② Geotechnical and Structural Engineering Research Center, Shandong University, Jinan, Shandong 250061, China;
③ Huaneng Tibet Hydropower Safety Engineering Technology Research Center, Linzhi, Tibet 860000, China
在反射波地震勘探中,偏移是利用地震记录对地下结构进行成像的重要手段。近几十年来,地球内部及近地表构造研究的需求推动了偏移技术的迅速发展。然而,当面对地震观测数据不足或不规则、地下结构复杂和波场带宽有限时,传统偏移技术如Kirchhoff偏移和逆时偏移(RTM)很难将数据偏移到准确的位置,难以满足实际地震勘探需求。
随着计算能力的飞速发展,提出了基于最小二乘优化框架的地震偏移方法,在真实速度扰动模型成像方面取得了良好的应用效果。在最小二乘偏移(LSM)中,地震偏移成像结果通常通过最小化数据残差的L2范数获得,该残差表征了正演模拟数据与实际观测数据之间的差异[1]。LSM的思想首先应用于Kirchhoff偏移[2-3],然后推广到单程波动方程偏移[4-5]。目前,该思想已应用于双程波动方程,形成了最小二乘逆时偏移(LSRTM)[6-11]。与传统的RTM成像[12-14]相比,LSRTM有助于生成高分辨率、高保真度和较少低频噪声的偏移成像结果[15-17]。
一般来说,常规的偏移方法利用地震正演算子的共轭转置而非真正意义的逆算子成像,导致由成像结果重建的地震数据与原始地震数据之间存在误差。LSM通过基于线性反演迭代的方法逼近逆算子,最终获得同预处理地震数据相匹配的地下构造模型,这种线性反演方法需要通过正演算子(或反偏移算子)和偏移算子建立地下构造模型与地震观测数据之间的线性关系[18-19],正演—偏移算子对的伴随性是影响迭代收敛和最终偏移成像结果的重要因素。通常,正演算子通过Born近似理论导出[20-21],偏移算子最常用的是RTM。然而,Xu等[22]证明了使用一阶声波方程时该算子对(Born正演和RTM)经过数值离散计算后,很难满足精确伴随关系[18]。因此,构建满足精确伴随关系的正演—偏移算子对是最小二乘逆时偏移中的一个关键步骤[23-25],也是提高偏移质量的有效手段。
针对伴随算子对存在的问题,国内外学者主要采用两种途径进行研究:一是基于伴随状态法推导连续伴随波动方程,再谨慎进行离散获得波场延拓伴随算子,保证正演—偏移算子对的精确伴随性[26-27];二是基于矩阵形式先进行离散后直接推导伴随矩阵的策略。通常采用点积测试[19]作为一种便捷的数值方法检验两个算子之间的伴随性,而点积测试最简单、直接的方法之一是利用算子矩阵的转置。不同于传统的叠后RTM算子,Ji[28]提出了一种适用于时域声波方程有限差分模拟的矩阵计算方法并推导了伴随矩阵;Yao等[29]基于矩阵形式对频率域LSRTM精确伴随算子对进行了研究;Xu等[22]详细描述了基于声波Born近似理论的精确伴随算子对的推导过程,并应用于预条件LSM。许多学者将这种基于Born正演的精确伴随算子对应用于声波[22, 30-31]、弹性波[15, 32],甚至各向异性[33-34]、黏滞介质[7, 9, 35]的LSM。由于RTM是最常用的偏移算子,因此,另一种构造精确伴随算子对的方法是先通过RTM过程的矩阵表示,再将其转置,得到RTM反偏移算子(DeRTM算子),DeRTM-RTM算子对同样有较好的成像效果[36]。此外,一些学者利用自伴随波动方程将这两种算子对混在一起,并展示了Born-RTM算子对在各种数值算例下的良好应用效果[30, 37-39]。然而,这三组伴随算子对之间的区别与联系尚不清楚,需要进一步研究和探索。
为此,本文首先在Ji[28]的研究基础上,将时域二阶声波方程离散成矩阵形式,得到Born正演和RTM过程的矩阵表示。将矩阵转置即产生两组精确伴随算子对,分别表示为Born-AdjBorn算子对和RTM-DeRTM算子对。然后,基于声波方程的自伴随离散化,对这两个算子进行混合匹配,得到了第三组精确伴随算子对,即自伴随Born-RTM算子对。最后进一步推导了这三组精确伴随算子对之间的定量关系,并通过二维数值算例进行了验证。
1 方法原理 1.1 声波波场延拓及其伴随算子矩阵形式 1.1.1 波场延拓算子一维时空域的二阶声波方程为
| $ \frac{\partial^{2} p}{\partial t^{2}}=c^{2}(z) \frac{\partial^{2} p}{\partial z^{2}} $ | (1) |
式中:p为压力场;c(z)为声波速度;t和z分别表示时间和深度。根据中心二阶有限差分格式,式(1)的离散形式可以写为
| $ \begin{aligned} p_{i, n+1}=& \alpha c_{i}^{2} p_{i-1, n}+2\left(1-\alpha c_{i}^{2}\right) p_{i, n}+\\ & \alpha c_{i}^{2} p_{i+1, n}-p_{i, n-1} \end{aligned} $ | (2) |
式中:n=1,2,…,nt,nt为时间方向样点数;i=1,2,…,nz,nz为深度方向样点数;α=Δt2/Δz2,其中Δt和Δz分别为时间间隔和深度网格间隔。将式(2)表示为矩阵形式
| $ \boldsymbol{p}_{n+1}=\left[\begin{array}{ll} -\boldsymbol{I} & \boldsymbol{T} \end{array}\right]\left[\begin{array}{c} \boldsymbol{p}_{n-1} \\ \boldsymbol{p}_{n} \end{array}\right] $ | (3) |
式中:pn=[p1, n, p2, n, …, pnz, n]T为n时刻波场的向量形式;I是单位矩阵;T是一个带状矩阵,具体为
| $ \boldsymbol{T}=\left[\begin{array}{ccccc} 2\left(1-g_{1}\right) & g_{1} & & & \\ g_{2} & 2\left(1-g_{2}\right) & g_{2} & & \\ & \ddots & \ddots & \ddots & \\ & & g_{n_{z}-1} & 2\left(1-g_{n_{z}-1}\right) & g_{n_{z}-1} \\ & & & g_{n_{z}} & 2\left(1-g_{n_{z}}\right) \end{array}\right]_{n_{z} \times n_{z}} $ | (4) |
其中gi=αci2。加入震源项s,式(3)可改写为更直接的形式
| $ \boldsymbol{B p}=\boldsymbol{s} $ | (5) |
式中:p=(p0, p1, p2, …, pnt)T;s=(s0, s1, …, snt)T为震源子波w(如Ricker子波)通过震源分布矩阵Dsrc分布在各时刻每个网格上,可表示为s=Dsrcw;B=I-A,其中
| $ \boldsymbol{A}=\left[\begin{array}{ccccc} 0 & & & & \\ \boldsymbol{T} & 0 & & & \\ -\boldsymbol{I} & \boldsymbol{T} & 0 & & \\ & \ddots & \ddots & \ddots & \\ & & -\boldsymbol{I} & \boldsymbol{T} & 0 \end{array}\right] $ | (6) |
地震记录可以通过观测矩阵D提取各时刻对应的波场。因此,观测数据可以表示为
| $ \boldsymbol{d}=\boldsymbol{D p}=\boldsymbol{D B}^{-1} \boldsymbol{s} $ | (7) |
值得注意的是,D的子矩阵Dn表示提取n时刻波场作为地震记录,其转置矩阵DnT表示将地震记录作为源在n时刻加载。这两个算子是伴随的,在LSM伴随算子对的推导和理解中起着重要的作用。
二维波场延拓算子与一维类似,详细推导见附录A。
1.1.2 波场延拓伴随算子如上所述,推导一对伴随算子最直接的方法之一是通过矩阵转置。因此,了解波场延拓算子B-1及其伴随算子B-T对于后续推导正演—偏移算子对有较大帮助。为了简单起见,只给出一维矩阵分析,对于高维可得出类似的结论。
应用线性代数方法,B-1可以显式表示为
| $ \boldsymbol{B}^{-1}=\boldsymbol{I}+\boldsymbol{A}+\boldsymbol{A}^{2}+\boldsymbol{\cdots}+\boldsymbol{A}^{n_{t}} $ | (8) |
定义一系列矩阵算子{Pn},n∈{1, 2, …, nt},将零时刻波场映射到n时刻波场。考虑式(6)中的定义,令P0=I,可得
| $ \boldsymbol{B}^{-1}=\left[\begin{array}{ccccc} \boldsymbol{P}_{0} & & & & \\ \boldsymbol{P}_{1} & \boldsymbol{P}_{0} & & & \\ \boldsymbol{P}_{2} & \boldsymbol{P}_{1} & \boldsymbol{P}_{0} & & \\ \vdots & \ddots & \ddots & \ddots & \\ \boldsymbol{P}_{n_{t}} & \cdots & \boldsymbol{P}_{2} & \boldsymbol{P}_{1} & \boldsymbol{P}_{0} \end{array}\right] $ | (9) |
因此,波场延拓p=B-1s可以写成子矩阵求和的形式
| $ \boldsymbol{p}_{n}=\sum\limits_{i=0}^{n} \boldsymbol{P}_{n_{t}-i} \boldsymbol{s}_{i} $ | (10) |
上式可以理解为,在n时刻的波场pn是由此前源项si通过Pn-i映射的所有波场的总和,这符合惠更斯原理和波场叠加原理。其伴随过程p=B-Ts,也可以表示为子阵求和形式
| $ \boldsymbol{p}_{n}=\sum\limits_{i=n}^{n_{t}} \boldsymbol{P}_{n_{t}-i}^{\mathrm{T}} \boldsymbol{s}_{i} $ | (11) |
由式(11)可知,当前的波场pn是未来源项si经PiT向后延拓的所有波场的总和。此外,矩阵PiT可以通过将式(3)中的矩阵T替换为其转置矩阵TT实现。因此,可以得到相应的伴随波动方程
| $ \frac{\partial^{2} q}{\partial t^{2}}=\frac{\partial^{2}\left(c^{2} q\right)}{\partial z^{2}}+s $ | (12) |
通过引入速度加权波场p(z, t)=c2(z)q(z, t),可以将式(12)转化为常规波动方程
| $ \frac{\partial^{2} p}{\partial t^{2}}=c^{2} \frac{\partial^{2} p}{\partial z^{2}}+c^{2} s $ | (13) |
式(13)表明伴随波场q可以通过在常规波动方程中加载速度加权源项c2s获得。在速度模型不均匀的情况下,忽略速度加权因子将导致伴随波场的计算不准确,但这与二阶声波方程自伴随的性质不一致。为了保持空间离散中的自伴随性,引入另一个中间波场u(z, t)=c-1(z)p(z, t),满足
| $ \begin{aligned} \frac{\partial^{2} u}{\partial t^{2}} &=c^{-1}(z) \frac{\partial^{2} p}{\partial t^{2}}=c(z) \frac{\partial^{2} p}{\partial z^{2}}+c^{-1}(z) s \\ &=c(z) \frac{\partial^{2}(c u)}{\partial z^{2}}+c^{-1}(z) s \end{aligned} $ | (14) |
式(14)即为自伴随波动方程,此时TT=T。根据式(9)中的定义,可以得到相应的波场延拓矩阵Bs-1和Bs-T,其子矩阵Pi为对称阵,下标“s”表示为自伴随方程的离散化矩阵。
1.2 三组精确伴随算子对 1.2.1 基于Born近似的精确伴随算子对根据Born近似理论,在小速度扰动假设下,Born正演方程为
| $ \left\{\begin{array}{l} \left(\frac{\partial^{2}}{\partial t^{2}}-c_{0}^{2} \nabla^{2}\right) \delta p=\frac{2 \delta c}{c_{0}} \frac{\partial^{2} p_{0}}{\partial t^{2}} \\ \left(\frac{\partial^{2}}{\partial t^{2}}-c_{0}^{2} \nabla^{2}\right) \frac{\partial^{2}}{\partial t^{2}} p_{0}=\frac{\partial^{2} s}{\partial t^{2}} \end{array}\right. $ | (15) |
式中:p0为背景波场;c0为背景波速;δp为扰动波场;δc为扰动波速。式(15)主要包含背景波场的计算和扰动波场的计算。引入矢量
| $ \left\{\begin{array}{l} \boldsymbol{B} \boldsymbol{p}=\ddot{\boldsymbol{p}} \odot \hat{\boldsymbol{I}} \boldsymbol{m} \\ \boldsymbol{B}\ddot{\boldsymbol{p}}=\ddot{\boldsymbol{s}} \end{array}\right. $ | (16) |
式中⊙表示Hadamard乘积。因此Born正演获得的观测数据可以表示为
| $ \boldsymbol{d}=\boldsymbol{F}_{\mathrm{Born}} \boldsymbol{m}=\boldsymbol{D} \boldsymbol{B}^{-1}\left(\boldsymbol{B}^{-1} \ddot{\boldsymbol{s}}\right) \odot \hat{\boldsymbol{I}} \boldsymbol{m} $ | (17) |
Born正演的伴随算子是式(17)中正演算子FBorn的转置,即
| $ \begin{aligned} \boldsymbol{m} &=\boldsymbol{F}_{\mathrm{AdjBorn}} \boldsymbol{d}=\boldsymbol{F}_{\mathrm{Born}}^{\mathrm{T}} \boldsymbol{d} \\ &=\hat{\boldsymbol{I}}{}^{\mathrm{T}}\left(\boldsymbol{B}^{-1} \ddot{\boldsymbol{s}}\right) \odot \boldsymbol{B}^{-\mathrm{T}} \boldsymbol{D}^{\mathrm{T}} \boldsymbol{d} \end{aligned} $ | (18) |
可以通过对于任意d和m的点积测试dTFBorn(m)=FAdjBornT(d)m检查Born正演算子FBorn及其伴随算子FAdjBorn的伴随性。其中,矩阵B-1不仅可以表示式(1),还可以代表式(14),即矩阵B-1可以被矩阵Bs-1代替,式(17)与式(18)仍然保持伴随关系。
1.2.2 基于RTM的精确伴随算子对经典的RTM过程包括正向波场延拓、逆向波场延拓和成像。利用矩阵形式表示RTM全过程是推导基于RTM精确伴随算子对的关键。正向和逆向波场延拓可表示为
| $ \left\{\begin{array}{l} \boldsymbol{B} \boldsymbol{p}_{\mathrm{f}}=\boldsymbol{s} \\ \boldsymbol{B} \boldsymbol{p}_{\mathrm{r}}=\boldsymbol{D}^{\mathrm{T}} \boldsymbol{T}_{\mathrm{re}} \boldsymbol{d} \end{array}\right. $ | (19) |
式中:pf为正传波场;pr为逆传波场;d为不含直达波的观测数据,需要将其倒置计算逆传波场。对于二维模型,这种时间反转操作可以表示为对角线矩阵Tre=diag{I, …, I},其中I是单位矩阵的镜像矩阵
| $ \overline{\boldsymbol{I}}=\left[\begin{array}{llll} & & & 1 \\ & & 1 & \\ & ⋰ & &\\ 1 & & & \end{array}\right]_{\left(n_{t}+1\right) \times\left(n_{t}+1\right)} $ | (20) |
为了实现正传波场pf和逆传波场pr的零延迟互相关过程,引入一个反对角块矩阵
| $ \tilde{\boldsymbol{I}}=\left[\begin{array}{llll} & & & \boldsymbol{I} \\ & & \boldsymbol{I} & \\ & ⋰ & &\\ \boldsymbol{I} & & & \end{array}\right] $ | (21) |
通过零延迟互相关成像条件,偏移过程可表示为
| $ \begin{aligned} \boldsymbol{m}_{\mathrm{RTM}} &=\boldsymbol{F}_{\mathrm{RTM}} \boldsymbol{d}=\hat{\boldsymbol{I}}{}^{\mathrm{T}} \boldsymbol{p}_{\mathrm{f}} \odot \tilde{\boldsymbol{I}} \boldsymbol{p}_{\mathrm{r}} \\ &=\hat{\boldsymbol{I}}{}^{\mathrm{T}}\left(\boldsymbol{B}^{-1} \boldsymbol{s}\right) \odot \widetilde{\boldsymbol{I}}\boldsymbol{B}^{-1} \boldsymbol{D}^{\mathrm{T}} \boldsymbol{T}_{\mathrm{re}} \boldsymbol{d} \end{aligned} $ | (22) |
式中FRTM为逆时偏移算子。相应的反偏移过程可表示为
| $ \begin{aligned} \boldsymbol{d} &=\boldsymbol{F}_{\mathrm{DeRTM}} \boldsymbol{m}=\boldsymbol{F}_{\mathrm{RTM}}^{\mathrm{T}} \boldsymbol{m} \\ &=\boldsymbol{T}_{\mathrm{re}}^{\mathrm{T}} \boldsymbol{D} \boldsymbol{B}^{-\mathrm{T}} \widetilde{\boldsymbol{I}}{}^{\mathrm{T}} \boldsymbol{B}^{-1} \boldsymbol{s} \odot \hat{\boldsymbol{I}}\boldsymbol{m}_{\mathrm{RTM}} \end{aligned} $ | (23) |
式中FDeRTM为逆时反偏移算子。与Born-AdjBorn算子对类似,矩阵B-1在此也可以被矩阵Bs-1替换,而不影响算子对的伴随性。
1.2.3 基于混合匹配的精确伴随算子对为了保证混合匹配后算子对的伴随性,简单直接的方法是使用式(14),而不是传统的声波方程,可以保证FBorn-s=FDeRTM-s和FAdjBorn-s=FRTM-s,即利用自伴随声波方程得到的两组伴随算子对Born-RTM和DeRTM-AdjBorn实际上是相同的。因此,在一般情况下,可以使用自伴随Born-RTM算子对作为LSM中的另一组精确伴随算子对。
综上所述,得到了LSM的三组精确伴随算子对,分别是利用常规离散波动方程的Born-AdjBorn算子对、利用常规离散波动方程的DeRTM-RTM算子对和利用自伴随离散波动方程的Born-RTM算子对。对应的LSM过程分别称为LSBM、LSRTM和自伴随LSBRTM。此外,考虑自伴随波场u、常规离散化波场p及其伴随波场q之间的关系,即u=c-1p=cq,可以得到三组精确伴随算子对成像结果之间的定量关系。
1.3 三组精确伴随算子对的定量关系首先,逐个矩阵比较Born-AdjBorn和DeRTM-RTM这两组精确伴随算子对。考虑正演与偏移算子之间的矩阵转置关系,只需要比较一半的算子对,就可以得出对整个算子对的相似结论。在附录B中,对比了偏移过程,即AdjBorn算子和RTM算子。对比式(B-1)与式(B-3),可以发现,在均匀偏移速度模型的情况下,可知B-TDTd=
因此,在大多数采用常规离散波动方程的情况下,当且仅当同一源在均匀速度模型中延拓时,Born-AdjBorn算子对和DeRTM-RTM算子对是相同的。在此条件下,Born近似正演和RTM可以作为一组精确的伴随算子对。
其次,根据附录C中的推导,可以得出以下定量结论。
(1) FBorn=FBorn-s和FAdjBorn=FRTM-s。常规离散波动方程的Born-AdjBorn算子对与自伴随离散波动方程的Born-RTM算子对相同。因此,AdjBorn结果等于自伴随RTM结果,LSBM和自伴随LSBRTM的结果是相同的。
(2) FRTM=ctop-2c2⊙FRTM-s,即传统的RTM结果等于ctop-2c2加权的基于自伴随波动方程的RTM结果(或AdjBorn结果),其中c2={ci, j2},ctop为表层速度并假设为常数。
(3) mLSBRTM-s=mLSBM=ctop-2c2⊙mLSRTM,即ctop-2m2加权的LSRTM结果等于LSBM和自伴随LSBRTM的结果。
此外,考虑到速度通常随深度增加而增加,权重因子ctop-2c2在模型深层会增大。因此,理论上RTM算子更倾向于强化成像结果的深部,对深层的成像效果比其他两种偏移算子更好。这个特征可以在Marmousi模型算例中清晰地观察到。并且,LSRTM可以看作是一个以ctop-2c2作为预条件的约束反演,速度加权后的LSRTM结果ctop-2c2⊙mLSRTM可获得真实速度扰动模型,因此,设计合理、有效的预条件算子是未来提升成像效果的研究方向。
由于式(C-6)中的Hessian矩阵通常是高度不适定的,其逆矩阵很难通过数值计算。因此,在式(C-6)中的最小二乘解通常采用迭代优化算法计算,例如本文中使用的预条件共轭梯度法。然而,由于迭代优化算法难以收敛至极小值,导致数值解可能与最小二乘解并不完全一致,式(C-7)中LSM结果之间的定量关系较难满足。
1.4 基于精确伴随算子对的LSM算法LSM的目标是速度扰动模型,该模型描述了观测数据所隐含的地下构造信息。因此求解过程通常包括正演算子、偏移算子与最小二乘算法。由于最小二乘算法在大多数LSRTM文献中都有讲述[27, 40-41],因此本文将重点关注精确伴随算子对的正确实现。
通过上述推导,得到了LSBM、LSRTM和自伴随LSBRTM伴随算子对的矩阵形式。然而,它们的矩阵运算是非常昂贵的,矩阵维度为nx×nz×nt。因此,需要将矩阵运算转化可实现的程序语言。表 1总结了各算子、矩阵的实际意义。
|
|
表 1 伴随算子对中各矩阵或算子的实际意义 |
LSM算法的目标是通过最小化目标函数求解速度扰动模型m
| $ J=\|\boldsymbol{F} \boldsymbol{m}-\boldsymbol{d}\|_{2}^{2}+\lambda\|\boldsymbol{m}\|_{2}^{2} $ | (24) |
式中F表示前面推导出的三个正演算子之一。目标函数的第一项表示数据残差,第二项是由阻尼参数λ平衡的模型正则化项,并采用了预条件共轭梯度算法获得LSBM、LSRTM和自伴随LSBRTM成像结果。
2 数值算例应用层状模型和Marmousi模型探讨和说明三组精确伴随算子对之间的定量关系,对比分析自伴随LSBRTM、LSBM、LSRTM和速度加权LSRTM(即ctop-2c2⊙mLSRTM)的成像结果。
在数值算例中,应用Ricker子波、基于这些算子对的有限差分代码计算合成数据。由于所推导的算子对不考虑任何吸收边界条件,本文通过复制模型的外边界层扩展模型,并在数值边界反射波到达之前停止波场延拓。在预条件共轭梯度算法中,阻尼参数λ设置为0.001。
2.1 层状模型为定量比较在均匀和非均匀偏移速度模型中三种伴随算子对LSM方法及ctop-2c2加权LSRTM的成像结果,设计了一个层状模型(图 1a),速度从上到下分别设置为2500、3000和3500m/s。模型网格数为200×200,网格间距为10m。震源以200m间距均匀分布在模型表面,主频为10Hz;检波器以10m间距均匀分布在模型表面。在偏移过程中采用平滑速度模型(图 1b)进行波场延拓。图 1c是LSM的收敛目标,即速度扰动模型m=2δc/c0。
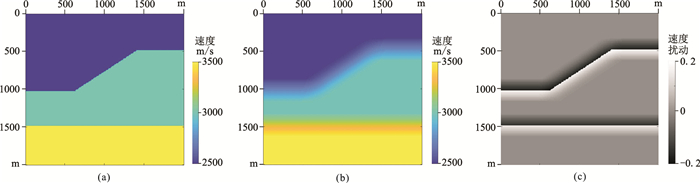
|
图 1 层状模型 (a)原始速度;(b)平滑速度;(c)速度扰动 |
自伴随LSBRTM、LSBM、LSRTM的一次迭代偏移结果分别如图 2a~图 2c所示,分别等价于自伴随RTM、传统Born偏移、传统RTM结果。LSM的30次迭代偏移结果如图 3所示。
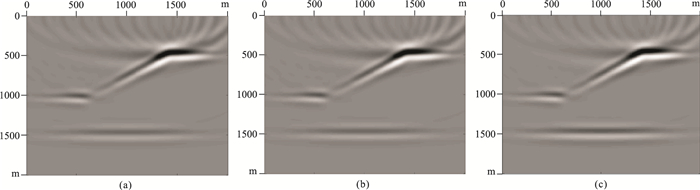
|
图 2 层状模型不同方法的一次迭代偏移结果 (a)自伴随RTM;(b)AdjBorn;(c)RTM |
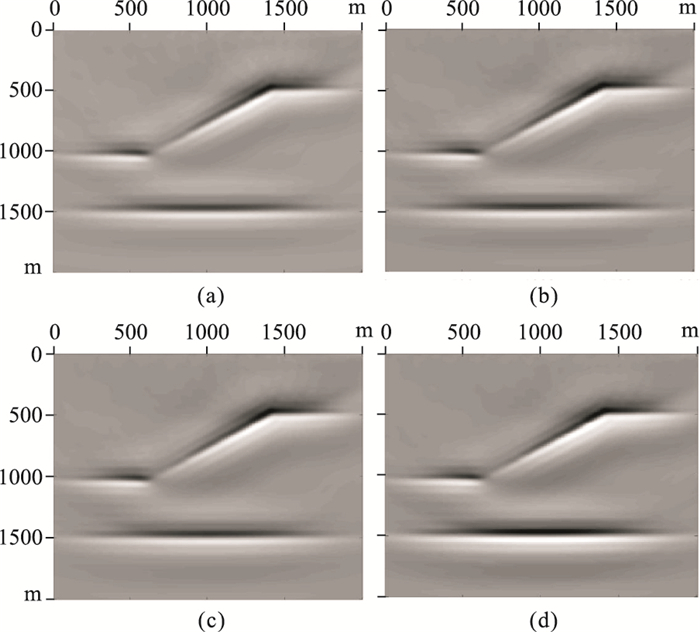
|
图 3 层状模型四种LSM方法的30次迭代结果 (a)自伴随LSBRTM;(b)LSBM;(c)LSRTM;(d)速度加权LSRTM |
与一次迭代偏移结果相比,多次迭代能够以更高的分辨率、更均衡的振幅和更少的伪影刻画出贴近真实速度扰动模型的成像结果。在波速分布由低速变化至高速的界面位置处,其速度扰动模型由负值变为正值,在一次迭代偏移结果中界面刻画均为正值—负值—正值,在LSM结果中界面均收敛为接近真实速度扰动模型的负值—正值。
为了验证三组伴随算子对结果之间的定量关系,计算了不同方法偏移成像结果的差值,如图 4所示。图 4a、图 4b和图 4d中极小的振幅证明了传统Born偏移结果(AdjBorn)与自伴随RTM的等价性、速度加权自伴随RTM与传统RTM之间的等价性以及LSBM与自伴随LSBRTM的等价性。对于自伴随LSBRTM与速度加权LSRTM结果的差异,由于存在误差,无法收敛至零,图 4e难以证明其对应的定量关系。
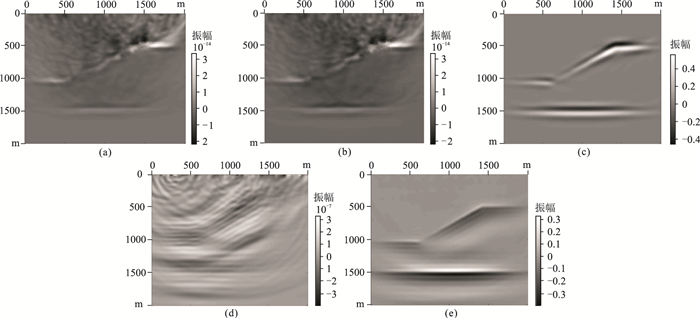
|
图 4 层状模型不同方法偏移结果的差值剖面 (a)传统Born偏移与自伴随RTM;(b)速度加权自伴随RTM与传统RTM;(c)传统RTM与自伴随RTM;(d)自伴随LSBRTM与LSBM;(e)速度加权LSRTM与自伴随LSBRTM |
此外,图 4c中的差值剖面是一个没有明显伪影的层状模型图像。然而,在图 2a和图 2c中,自伴随RTM和传统RTM结果在地表附近都存在较强的低频伪影,其与速度变化和反射结构无关,而成像结果的差异只与速度变化有关,即目标反射体。因此,这可能是一个有效减少RTM成像结果中低频伪影的策略。
在均匀偏移速度模型(2500m/s)下测试了LSBM与LSRTM,偏移成像结果如图 5所示。由于存在速度误差,第二个界面位置存在偏差,但两个偏移成像结果之间的差值为零,验证了本文的推论,即当偏移速度模型是均匀的时候,LSBM和LSRTM会呈现相同的成像结果。

|
图 5 均匀偏移速度模型下两种方法的LSM结果 (a)LSBM;(b)LSRTM |
在速度存在误差、数据含有噪声、数据有缺失的情况下,对三组精确伴随算子对进行敏感性分析。
应用平滑半径为100个网格距的偏移速度模型(图 6a),LSBM、LSRTM和自伴随LSBRTM成像结果如图 7所示,可见,在速度误差的影响下,LSBM、LSRTM和自伴随LSBRTM均可对地下层状构造较准确成像。
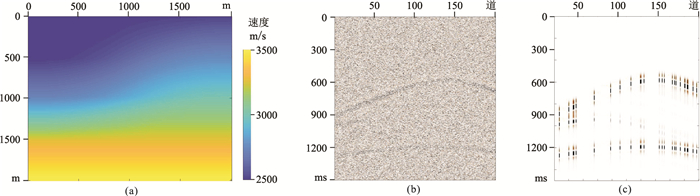
|
图 6 低精度的偏移速度速度模型(a)、震源位于1000m的含噪声数据(b)及随机缺失87.5%的道集数据(c) |

|
图 7 低精度速度模型的三种方法的LSM结果 (a)LSBM;(b)LSRTM;(c)自伴随LSBRTM |
在原始地震数据中添加白噪声,数据信噪比为-20dB(图 6b)。三组精确伴随算子对的LSM成像结果如图 8所示,受噪声的影响,均产生了较多的伪影。

|
图 8 数据含有噪声时三种方法的LSM结果 (a)LSBM;(b)LSRTM;(c)自伴随LSBRTM |
每炮地震数据随机缺失175道,即缺失87.5%(图 6c),三组精确伴随算子对的LSM成像结果如图 9所示。数据缺失对LSBM、LSRTM和自伴随LSBRTM偏移结果影响一致,均会在浅层产生些许低频噪声。

|
图 9 数据有缺失时三种方法的LSM结果 (a)LSBM;(b)LSRTM;(c)自伴随LSBRTM |
在速度存在误差、数据含有噪声、数据有缺失的情况下,LSBM与自伴随LSBRTM之间差值极小,在10-4数量级;LSBM与LSRTM、自伴随LSBRTM与LSRTM之间的差值较大,与成像结果的幅值在同一数量级。因此,速度误差、数据噪声以及数据缺失对三组精确伴随算子对之间的定量关系基本没有影响。
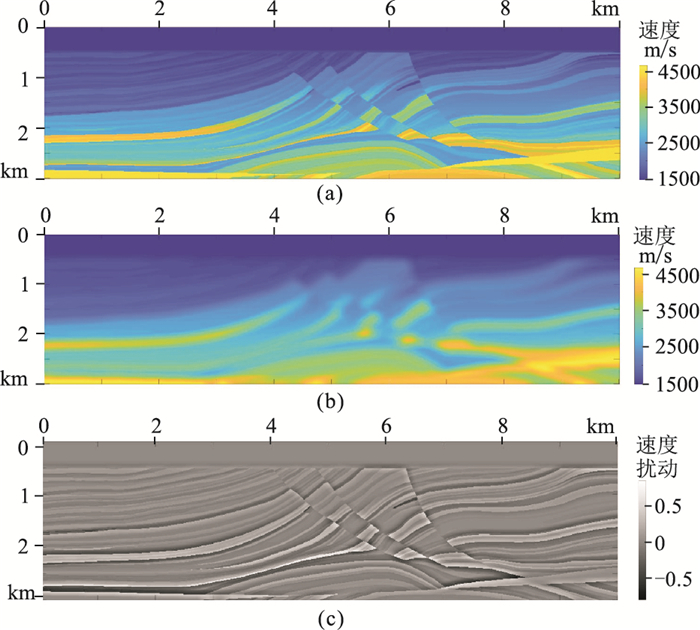
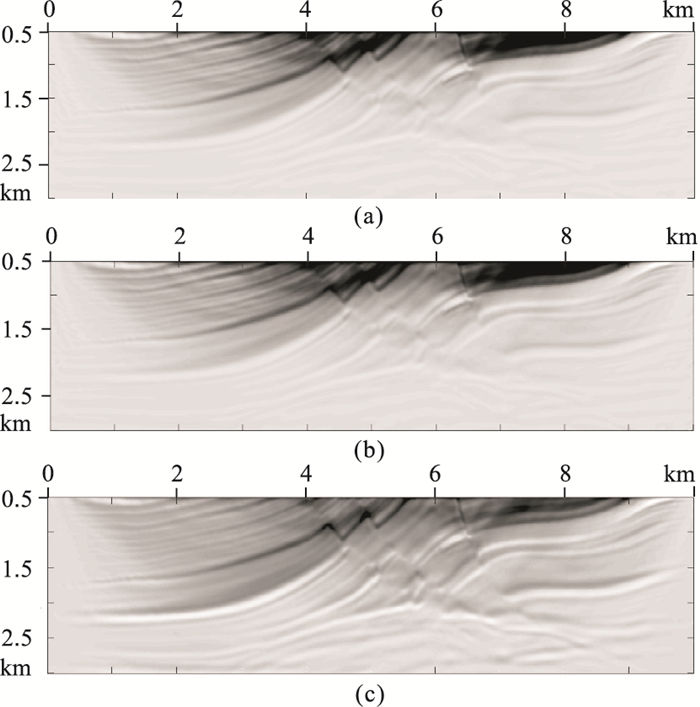
2.2 Marmousi模型应用更复杂的Marmousi模型(图 10)测试三种的精确伴随算子对。模型网格数为1000×300,网格间距为10m。50个震源均匀分布在模型表面,震源主频为10Hz。检波器以10m间距均匀分布在模型表面。一次迭代偏移结果如图 11所示,经过10次迭代,最终的LSM结果如图 12所示。
|
图 10 Marmousi模型 (a)真实速度;(b)平滑速度;(c)速度扰动 |
|
图 11 Marmousi模型不同方法的一次迭代偏移结果 (a)自伴随RTM;(b)AdjBorn;(c)RTM |

|
图 12 Marmousi模型四种LSM方法的10次迭代结果 (a)自伴随LSBRTM;(b)LSBM;(c)LSRTM;(d)速度加权LSRTM |
与层状模型结果类似,图 11和图 12中所有偏移结果符合预期,LSM结果展现了更少的低频噪声和更清晰的界面信息。图 12中红色矩形和箭头突出了成像结果之间的差异,通过与速度扰动模型进行对比可以看出,LSBM与自伴随LSBRTM更关注浅层的精细成像;LSRTM相较于LSBM和自伴随LSBRTM对深层(2km以下)成像效果更好,红色矩形中的地质构造更加清晰;并且速度加权项LSRTM对深层的照明更强,红色箭头处的地层信息与速度扰动模型基本一致。说明在Marmousi模型算例中,显式加入速度加权项后会增强深层的成像效果。
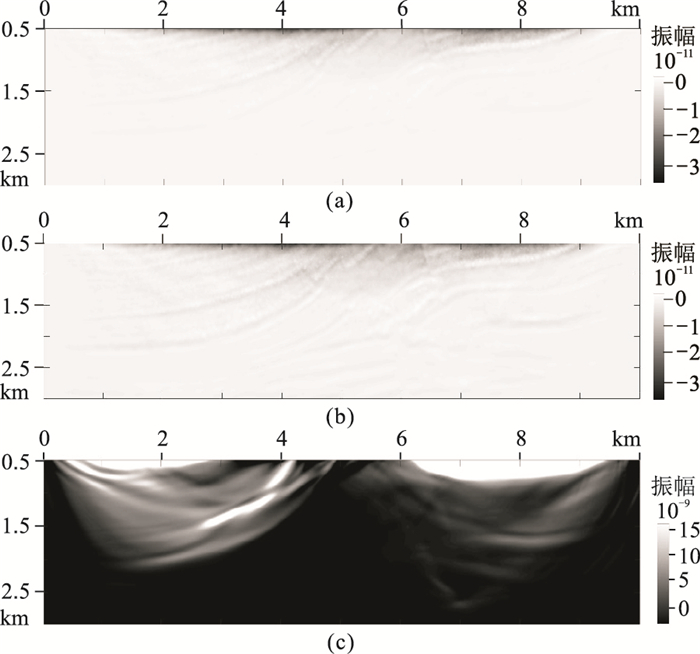
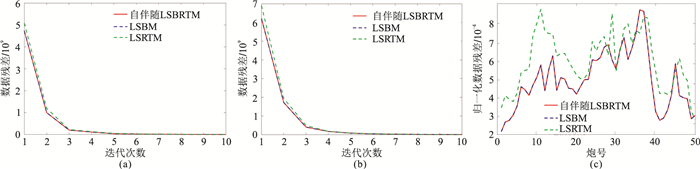
在定量关系上,图 13中极小的振幅分别验证了一次迭代偏移结果和LSM结果相应的定量关系,与层状模型算例类似,由于存在迭代误差,难以证明速度加权LSRTM与LSBM(或自伴随LSBRTM)之间的定量关系。图 14的数据收敛曲线表明三组伴随算子对的收敛速度快且相似,经过10次迭代后,三种LSM方法的归一化数据残差都小于0.001。
|
图 13 Marmousi模型不同方法偏移结果的差值剖面 (a)传统Born偏移和自伴随RTM;(b)速度加权自伴随RTM和传统RTM;(c)自伴随LSBRTM与LSBM |
|
图 14 Mairmousi模型三种LSM方法的数据残差对比 (a)第15号炮;(b)第35号炮;(c)所有50炮 |
一般认为Born正演和RTM分别是LSM的正演和偏移算子。然而,在数值离散化后,它们可能无法准确地通过点积测试。当采用非精确伴随算子对进行LSM时,会导致收敛性差或累积误差较大的偏移成像结果。因此,在声波方程矩阵表达式和矩阵运算的基础上,本文从理论上推导了基于Born近似理论和RTM过程的三组精确伴随算子对,并找出了它们之间的等价条件和定量关系。同时,开发了一套无矩阵代码,通过数值算例验证该推论。
正如在精确伴随算子对推导中所证明的,LSBM和LSRTM成像结果之间的主要区别源于相应算子对中的波场延拓矩阵B-1和B-T,即式(1)及其伴随波动方程(式(14))。后者可以进一步扩展为
| $ \frac{\partial^{2} p}{\partial t^{2}}=\frac{\partial^{2}\left(c^{2} p\right)}{\partial z^{2}}=c^{2} \frac{\partial^{2} p}{\partial z^{2}}+2 \frac{\partial c^{2}}{\partial z} \frac{\partial p}{\partial z}+p \frac{\partial^{2} c^{2}}{\partial z^{2}} $ | (25) |
式(25)意味着算子B-T实际上是传统的声波方程B-1加上与速度空间扰动有关的两项。如果偏移速度模型为均匀速度模型,即∂c2/∂z=0、∂2c2/∂z2=0,则LSBM和LSRTM会得到相同的结果。因此,可以从不同的角度对Born-AdjBorn和DeRTM-RTM伴随算子对进行对比,并得到相同的结论。并且,在二阶声波方程中(以一维情况为例),若将速度项移至方程左侧,即变为慢度项,即
| $ \frac{1}{c^{2}} \frac{\partial^{2} p}{\partial t^{2}}=\frac{\partial^{2} p}{\partial z^{2}} $ | (26) |
将该声波方程进行离散,并加载震源项s,其结果与加载速度加权源项c2s的式(13)相似。这意味着,在LSM过程中,将慢度扰动模型作为收敛目标即可利用该声波方程的自伴随性质进行波场延拓模拟。因此,在最小二乘框架下的LSM方法中,波动方程的选择及模型参数化对于迭代收敛性能和最终的偏移成像结果影响较大。
此外,不论对于连续波动方程还是波动方程的离散形式,由于Born-AdjBorn和DeRTM-RTM算子对都是与一次反射波对应的线性化算子,实际观测数据中可能包含更复杂的波场分量,如多次波或绕射波等。因此,通过正演模拟(Born正演和DeRTM过程)很难得到与实际观测数据准确匹配的合成数据,所以不应追求获得非常小的数据残差,特别是对于复杂的Marmousi模型。这使得验证LSRTM与LSBM(或自伴随LSBRTM)结果之间的定量关系(式(C-7))变得更加困难。
在实际地震勘探过程中,地震观测数据存在较严重的噪声,且实际子波与波场延拓模拟子波之间存在差异,正演地震数据与实际观测数据本身具有一定误差。若采用非精确伴随算子对进行最小二乘偏移,会引入新的误差,且在迭代收敛过程中容易累计误差,难以保证迭代收敛,导致实际资料偏移结果存在伪影、假象。因此,在偏移速度模型较为准确的前提下,采用精确伴随算子对进行最小二乘偏移成像可有效提升实际地震资料的成像质量。
4 结论最小二乘偏移需要正演和偏移两个过程实现成像结果的迭代更新,并且正演和偏移过程需满足精确伴随关系。基于Born近似理论和RTM过程,本文首先在常规离散化声波方程的基础上推导出了两对理论伴随算子。采用自伴随方法进行波动方程离散时,这两组算子对会产生另一组精确伴随算子对。这三组算子对均可通过无矩阵算法编程实现,并能准确通过点积测试。此外,还推导了这三组伴随算子对之间的定量关系,并应用二维模型进行了验证。定量关系为:采用同一源在均匀速度模型中进行波场延拓时,Born-AdjBorn算子对和DeRTM-RTM算子对是相同的;速度加权的LSRTM结果等于LSBM和自伴随LSBRTM的结果。
附录A 二维声波波场延拓算子对于时空域二维声波方程
| $ \frac{\partial^{2} p}{\partial t^{2}}=c^{2}(x, z)\left(\frac{\partial^{2} p}{\partial x^{2}}+\frac{\partial^{2} p}{\partial z^{2}}\right) $ | (A-1) |
假设Δz=Δx,其有限差分格式为
| $ \begin{aligned} p_{i, j, n+1}=& 2\left(1-2 \alpha c_{i, j}^{2}\right) p_{i, j, n}+\alpha c_{i, j}^{2}\left(p_{i-1, j, n}+\right.\\ &\left.p_{i+1, j, n}+p_{i, j-1, n}+p_{i, j+1, n}\right)-p_{i, j, n-1} \end{aligned} $ | (A-2) |
将波场表示为矩阵形式
| $ \begin{aligned} \boldsymbol{p}_{n}=& {\left[p_{1,1, n}, p_{2,1, n}, \cdots, p_{n_{z}, 1, n}, p_{1,2, n}, p_{2,2, n}, \cdots,\right.} \\ &\left.p_{n_{z}, 2, n}, \cdots, p_{1, n_{x}, n}, p_{2, n_{x}, n}, \cdots, p_{n_{z}, n_{x}, n}\right]^{\mathrm{T}} \end{aligned} $ | (A-3) |
式中nx、nz分别为x和z方向的样点数。在二维情况下,矩阵T变成了大小为(nx×nz)×(nx×nz)的三对角块矩阵
| $ \boldsymbol{T}=\left[\begin{array}{ccccc} \boldsymbol{\varGamma}_{1} & \boldsymbol{\varLambda}_{1} & & & \\ \boldsymbol{\varLambda}_{2} & \boldsymbol{\varGamma}_{2} & \boldsymbol{\varLambda}_{2} & & \\ & \ddots & \ddots & \ddots & \\ & & \boldsymbol{\varLambda}_{n_{x}-1} & \boldsymbol{\varGamma}_{n_{x}-1} & \boldsymbol{\varLambda}_{n_{x}-1} \\ & & & \boldsymbol{\varLambda}_{n_{x}} & \boldsymbol{\varGamma}_{n_{x}} \end{array}\right] $ | (A-4) |
式中:Λj=diag{αc1, j2, αc2, j2, …, αcnz, j2}是对角矩阵,j=1,2,…,nx;Γj是大小为nz×nz的三对角矩阵
| $ \boldsymbol{\varGamma}_{j}=\left[\begin{array}{ccccc} h_{1, j} & g_{1, j} & & & \\ g_{2, j} & h_{2, j} & g_{2, j} & & \\ & \ddots & \ddots & \ddots & \\ & & g_{n_{z}-1, j} & h_{n_{z}-1, j} & g_{n_{z}-1, j} \\ & & & g_{n_{z}, j} & h_{n_{z}, j} \end{array}\right] $ | (A-5) |
式中:gi, j=αci, j2,i=1,2,…,nz;hi, j=2(1-2gi, j2)。
附录B AdjBorn算子和RTM算子的等价条件将偏移过程分为以下三个步骤分析它们的等价条件。
(1) 背景波场的延拓模拟。对应的矩阵表示为式(15)中的B-1
(2) 观测数据的波场延拓模拟及其时间反转。这个过程是通过式(18)中的矩阵运算B-TDTd和式(22)中的矩阵运算
| $ \boldsymbol{B}^{-\mathrm{T}} \boldsymbol{D}^{\mathrm{T}}=\left[\begin{array}{ccccc} \boldsymbol{P}_{0}^{\mathrm{T}} & \boldsymbol{P}_{1}^{\mathrm{T}} & \boldsymbol{P}_{2}^{\mathrm{T}} & \cdots & \boldsymbol{P}_{n_{t}}^{\mathrm{T}} \\ & \boldsymbol{P}_{0}^{\mathrm{T}} & \boldsymbol{P}_{1}^{\mathrm{T}} & \ddots & \vdots \\ & & \boldsymbol{P}_{0}^{\mathrm{T}} & \ddots & \boldsymbol{P}_{2}^{\mathrm{T}} \\ & & & \ddots & \boldsymbol{P}_{1}^{\mathrm{T}} \\ & & & & \boldsymbol{P}_{0}^{\mathrm{T}} \end{array}\right]\left[\begin{array}{c} \boldsymbol{D}_{0}^{\mathrm{T}} \\ \boldsymbol{D}_{1}^{\mathrm{T}} \\ \boldsymbol{D}_{2}^{\mathrm{T}} \\ \vdots \\ \boldsymbol{D}_{n_{t}}^{\mathrm{T}} \end{array}\right]=\left[\begin{array}{c} \sum\limits_{n=0}^{n_{t}} \boldsymbol{P}_{n}^{\mathrm{T}} \boldsymbol{D}_{n}^{\mathrm{T}} \\ \sum\limits_{n=0}^{n_{t}-1} \boldsymbol{P}_{n}^{\mathrm{T}} \boldsymbol{D}_{n+1}^{\mathrm{T}} \\ \sum\limits_{n=0}^{n_{t}-2} \boldsymbol{P}_{n}^{\mathrm{T}} \boldsymbol{D}_{n+2}^{\mathrm{T}} \\ \vdots \\ \boldsymbol{P}_{0}^{\mathrm{T}} \boldsymbol{D}_{n_{t}}^{\mathrm{T}} \end{array}\right] $ | (B-1) |
| $ \tilde{\boldsymbol{I}} \boldsymbol{B}^{-1} \boldsymbol{D}^{\mathrm{T}} \boldsymbol{T}_{\mathrm{re}}=\left[\begin{array}{lllll} & & & &\boldsymbol{I} \\ & & &\boldsymbol{I} & \\ & & \boldsymbol{I} & & \\ & ⋰ & & & \\ \boldsymbol{I} & & & & \end{array}\right]\left[\begin{array}{ccccc} \boldsymbol{P}_{0} & & & & \\ \boldsymbol{P}_{1} & \boldsymbol{P}_{0} & & & \\ \boldsymbol{P}_{2} & \boldsymbol{P}_{1} & \boldsymbol{P}_{0} & & \\ \vdots & \ddots & \ddots & \ddots & \\ \boldsymbol{P}_{n_{t}} & \cdots & \boldsymbol{P}_{2} & \boldsymbol{P}_{1} & \boldsymbol{P}_{0} \end{array}\right]\left[\begin{array}{c} \boldsymbol{D}_{0}^{\mathrm{T}} {\overline{\boldsymbol{I}}} \\ \boldsymbol{D}_{1}^{\mathrm{T}} \overline{\boldsymbol{I}} \\ \boldsymbol{D}_{2}^{\mathrm{T}} \overline{\boldsymbol{I}} \\ \vdots \\ \boldsymbol{D}_{n_{t}}^{\mathrm{T}} \overline{\boldsymbol{I}} \end{array}\right]=\left[\begin{array}{c} \sum\limits_{n=0}^{n_{t}} \boldsymbol{P}_{n} \boldsymbol{D}_{n_{t}-n}^{\mathrm{T}} \overline{\boldsymbol{I}} \\ \sum\limits_{n=0}^{n_{t}-1} \boldsymbol{P}_{n} \boldsymbol{D}_{n_{t}-1-n}^{\mathrm{T}} \overline{\boldsymbol{I}} \\ \sum\limits_{n=0}^{n_{t}-2} \boldsymbol{P}_{n} \boldsymbol{D}_{n_{t}-2-n}^{\mathrm{T}} \overline{\boldsymbol{I}} \\ \vdots \\ \boldsymbol{P}_{0} \boldsymbol{D}_{0}^{\mathrm{T}} \overline{\boldsymbol{I}} \end{array}\right] $ | (B-2) |
可以看出,在Born正演中,时间反转是通过波场计算矩阵B-1的变换实现的,而在RTM中,则是通过矩阵
| $ \tilde{\boldsymbol{I}} \boldsymbol{B}^{-1} \boldsymbol{D}^{\mathrm{T}} \boldsymbol{T}_{\mathrm{re}}=\left[\begin{array}{c} \sum\limits_{n=0}^{n_{t}} \boldsymbol{P}_{n} \boldsymbol{D}_{n_{t}-n}^{\mathrm{T}} \overline{\boldsymbol{I}} \\ \sum\limits_{n=0}^{n_{t}-1} \boldsymbol{P}_{n} \boldsymbol{D}_{n_{t}-1-n}^{\mathrm{T}} \overline{\boldsymbol{I}} \\ \sum\limits_{n=0}^{n_{t}-2} \boldsymbol{P}_{n} \boldsymbol{D}_{n_{t}-2-n}^{\mathrm{T}}\overline{\boldsymbol{I}} \\ \vdots \\ \boldsymbol{P}_{0} \boldsymbol{D}_{0}^{\mathrm{T}} \overline{\boldsymbol{I}} \end{array}\right]=\left[\begin{array}{c} \sum\limits_{n=0}^{n_{t}} \boldsymbol{P}_{n} \boldsymbol{D}_{n}^{\mathrm{T}} \\ \sum\limits_{n=0}^{n_{t}-1} \boldsymbol{P}_{n} \boldsymbol{D}_{n+1}^{\mathrm{T}} \\ \sum\limits_{n=0}^{n_{t}-2} \boldsymbol{P}_{n} \boldsymbol{D}_{n+1}^{\mathrm{T}} \\ \vdots \\ \boldsymbol{P}_{0} \boldsymbol{D}_{n_{t}}^{\mathrm{T}} \end{array}\right] $ | (B-3) |
如果对于所有时刻,都有Pn=PnT,即T为对称矩阵,则在所有网格上速度保持不变(偏移速度模型均匀)的情况下,有
| $ \boldsymbol{B}^{-\mathrm{T}} \boldsymbol{D}^{\mathrm{T}} \boldsymbol{d}=\widetilde{\boldsymbol{I}} \boldsymbol{B}^{-1} \boldsymbol{D}^{\mathrm{T}} \boldsymbol{T}_{\mathrm{re}} \boldsymbol{d} $ | (B-4) |
(3) 计算所有时间步的总和,即两组算子对中的
通过上述分析可知,当且仅当采用同一震源子波,偏移速度模型均匀的情况下,AdjBorn算子和RTM算子等价,即
| $ \boldsymbol{F}_{\mathrm{AdjBorn}} =\boldsymbol{F}_{\mathrm{RTM}} $ | (B-5) |
| $ \hat{\boldsymbol{I}}{}^{\mathrm{T}}\left(\boldsymbol{B}^{-1} \ddot{\boldsymbol{s}}\right) \odot \boldsymbol{B}^{-\mathrm{T}} \boldsymbol{D}^{\mathrm{T}} =\hat{\boldsymbol{I}}{}^{\mathrm{T}}\left(\boldsymbol{B}^{-1} \boldsymbol{s}\right) \odot \widetilde{\boldsymbol{I}}\boldsymbol{B}^{-1} \boldsymbol{D}^{\mathrm{T}} \boldsymbol{T}_{\mathrm{re}} $ | (B-6) |
矩阵算子Bs-1进行波场延拓的自伴随波场u、常规离散化算子B-1延拓的波场p及其伴随波场q满足u=c-1p=cq,则有
| $ \left\{\begin{aligned} \boldsymbol{B}_{\mathrm{s}}^{-1} \boldsymbol{s} &=\boldsymbol{c}^{-1} \odot \boldsymbol{B}^{-1}(\boldsymbol{s} \odot \boldsymbol{c})=c_{\mathrm{top}} \boldsymbol{c}^{-1} \odot \boldsymbol{B}^{-1} \boldsymbol{s} \\ \boldsymbol{B}^{-\mathrm{T}} \boldsymbol{s} &=\boldsymbol{c}^{-2} \odot \boldsymbol{B}^{-1}\left(\boldsymbol{s} \odot \boldsymbol{c}^{2}\right)=c_{\mathrm{top}}^{2} \boldsymbol{c}^{-2} \odot \boldsymbol{B}^{-1} \boldsymbol{s} \\ &=\boldsymbol{c}^{-1} \odot \boldsymbol{B}_{\mathrm{s}}^{-1}(\boldsymbol{s} \odot \boldsymbol{c})=c_{\mathrm{top}} \boldsymbol{c}^{-1} \odot \boldsymbol{B}_{\mathrm{s}}^{-1} \boldsymbol{s} \end{aligned}\right. $ | (C-1) |
式中: c-1={1/ci, j};c-2={1/ci, j2}。进而可以证明基于B-1的Born-AdjBorn算子对与基于Bs-1的Born-RTM算子对的等价性。
| $ \begin{aligned} \boldsymbol{d} &=\boldsymbol{F}_{\text {Born }} \boldsymbol{m}=\boldsymbol{D} \boldsymbol{B}^{-1}\left(\boldsymbol{B}^{-1} \ddot{\boldsymbol{s}}\right) \odot \hat{\boldsymbol{I}} \boldsymbol{m} \\ &=c_{\text {top }}^{-1} \boldsymbol{D} \boldsymbol{B}^{-1}\left(c_{\text {top }} \boldsymbol{c}^{-1} \odot \boldsymbol{B}^{-1} \ddot{\boldsymbol{s}}\right) \odot \hat{\boldsymbol{I}}(\boldsymbol{m} \odot \boldsymbol{c}) \\ &=\boldsymbol{D B}_{\mathrm{s}}^{-1}\left(\boldsymbol{B}^{-1} \ddot{\boldsymbol{s}}\right) \odot \hat{\boldsymbol{I}} \boldsymbol{m}=\boldsymbol{F}_{\text {Born-s }} \boldsymbol{m}=\boldsymbol{F}_{\mathrm{DeRTM}-\mathrm{s}} \boldsymbol{m} \end{aligned} $ | (C-2) |
| $ \begin{aligned} \boldsymbol{m}=&\boldsymbol{F}_{\mathrm{AdjBorn}} \boldsymbol{d}=\boldsymbol{F}_{\mathrm{Born}}^{\mathrm{T}} \boldsymbol{d}=\hat{\boldsymbol{I}}{}^{\mathrm{T}}\left(\boldsymbol{B}^{-1} \ddot{\boldsymbol{s}}\right) \odot \boldsymbol{B}^{-\mathrm{T}} \boldsymbol{D}^{\mathrm{T}} \boldsymbol{d}\\ &=\hat{\boldsymbol{I}}{}^{\mathrm{T}}\left[c_{\text {top }}^{-1} \boldsymbol{c} \odot\left(c_{\text {top }} \boldsymbol{c}^{-1} \odot \boldsymbol{B}^{-1} \ddot{\boldsymbol{s}}\right)\right] \odot\\ &\left(c_{\text {top }} c^{-1} \odot \boldsymbol{B}_{\mathrm{s}}^{-1} \boldsymbol{D}^{\mathrm{T}} \boldsymbol{d}\right)=\hat{\boldsymbol{I}}{}^{\mathrm{T}}\left(\boldsymbol{B}_{\mathrm{s}}^{-1} \ddot{\boldsymbol{s}}\right) \odot \boldsymbol{B}_{\mathrm{s}}^{-1} \boldsymbol{D}^{\mathrm{T}} \boldsymbol{d}\\ &=\boldsymbol{F}_{\mathrm{AdjBorn-s}} \boldsymbol{d}=\boldsymbol{F}_{\mathrm{RTM}-\mathrm{s}} \boldsymbol{d} \end{aligned} $ | (C-3) |
基于B-1的DeRTM-RTM算子对和Born-AdjBorn算子对以及基于Bs-1的Born-RTM算子对之间的关系为
| $ \begin{aligned} \boldsymbol{m}=&\boldsymbol{F}_{\mathrm{RTM}} \boldsymbol{d}=\hat{\boldsymbol{I}}{}^{\mathrm{T}} \boldsymbol{p}_{\mathrm{f}} \odot \tilde{\boldsymbol{I}} \boldsymbol{p}_{\mathrm{r}}\\ &=\hat{\boldsymbol{I}}{}^{\mathrm{T}}\left(\boldsymbol{B}^{-1} \ddot{\boldsymbol{s}}\right) \odot \tilde{\boldsymbol{I}} \boldsymbol{B}^{-1} \boldsymbol{D}^{\mathrm{T}} \boldsymbol{T}_{\mathrm{re}} \boldsymbol{d}\\ &=\hat{\boldsymbol{I}}{}^{\mathrm{T}}\left\{c_{\mathrm{top}}^{-1} \boldsymbol{c} \odot\left[c_{\mathrm{top}} \boldsymbol{c}^{-1} \odot\left(\boldsymbol{B}^{-1} \ddot{\boldsymbol{s}}\right)\right]\right\} \odot\\ &\left(\tilde{\boldsymbol{I}}{c_{\text {top }}^{-1}} \boldsymbol{c} \odot c_{\mathrm{top}} \boldsymbol{c}^{-1} \odot \boldsymbol{B}^{-1} \boldsymbol{D}^{\mathrm{T}} \boldsymbol{T}_{\mathrm{re}} \boldsymbol{d}\right)\\ &=c_{\mathrm{top}}^{-2} \boldsymbol{c}^{2} \odot \hat{\boldsymbol{I}}{}^{\mathrm{T}}\left(\boldsymbol{B}_{\mathrm{s}}^{-1} \ddot{\boldsymbol{s}}\right) \odot \widetilde{\boldsymbol{I}}\boldsymbol{B}_{\mathrm{s}}^{-1} \boldsymbol{D}^{\mathrm{T}} \boldsymbol{T}_{\mathrm{re}} \boldsymbol{d}\\ &=c_{\text {top }}^{-2} \boldsymbol{c}^{2} \odot \boldsymbol{F}_{\mathrm{RTM-s}} \boldsymbol{d}\\ &=c_{\text {top }}^{-2} \boldsymbol{c}^{2} \odot \boldsymbol{F}_{\text {AdjBorn-s }} \boldsymbol{d}=c_{\text {top }}^{-2} \boldsymbol{c}^{2} \odot \boldsymbol{F}_{\mathrm{AdjBorn}} \boldsymbol{d} \end{aligned} $ | (C-4) |
| $ \begin{aligned} \boldsymbol{d}=&\boldsymbol{F}_{\mathrm{DeRTM}} \boldsymbol{m}=\boldsymbol{F}_{\mathrm{RTM}}^{\mathrm{T}} \boldsymbol{m}\\ &=\boldsymbol{T}_{\mathrm{re}}^{\mathrm{T}} \boldsymbol{D}^{-\mathrm{T}} \tilde{\boldsymbol{I}}{}^{\mathrm{T}}\left(\boldsymbol{B}^{-1} \ddot{\boldsymbol{s}}\right) \odot \hat{\boldsymbol{I}} \boldsymbol{m}\\ &=c_{\text {top }}^{-1} \boldsymbol{T}_{\mathrm{re}}^{\mathrm{T}} \boldsymbol{D}\boldsymbol{B}_{\mathrm{s}}^{-1} \widetilde{\boldsymbol{I}}{}^{\mathrm{T}} \times\\ &\left[c_{\text {top }}^{-1} \boldsymbol{c} \odot\left(c_{\text {top }} c^{-1} \odot \boldsymbol{B}^{-1} \ddot{\boldsymbol{s}}\right)\right] \odot \hat{\boldsymbol{I}}(\boldsymbol{m} \odot \boldsymbol{c})\\ &=c_{\text {top }}^{-2} \boldsymbol{T}_{\mathrm{re}}^{\mathrm{T}} \boldsymbol{D} \boldsymbol{B}_{\mathrm{s}}^{-1} \widetilde{\boldsymbol{I}}{}^{\mathrm{T}}\left(\boldsymbol{B}_{\mathrm{s}}^{-1} \ddot{\boldsymbol{s}}\right) \odot \hat{\boldsymbol{I}}\left(\boldsymbol{m} \odot \boldsymbol{c}^{2}\right)\\ &=c_{\text {top }}^{-2} \boldsymbol{F}_{\text {DeRTM-s }}\left(\boldsymbol{m} \odot \boldsymbol{c}^{2}\right)\\ &=c_{\text {top }}^{-2} \boldsymbol{F}_{\text {Born-s }}\left(\boldsymbol{m} \odot \boldsymbol{c}^{2}\right)=c_{\text {top }}^{-2} \boldsymbol{F}_{\text {Born }}\left(\boldsymbol{m} \odot \boldsymbol{c}^{2}\right)\\ &=\boldsymbol{F}_{\mathrm{Born}}\left(c_{\text {top }}^{-4} \boldsymbol{c}^{4} \odot \boldsymbol{F}_{\mathrm{AdjBorn}} \boldsymbol{d}\right) \end{aligned} $ | (C-5) |
式中c4={ci, j4}。
定义C=diag{ctop-2c2},并考虑FRTMd=ctop-2c2⊙FRTM-sd,可知FRTM=CFRTM-s。因此,C可以看作是一个正则化因子,并给出相应的最小二乘解
| $ \begin{aligned} \boldsymbol{m}_{\mathrm{LSRTM}}=&\left(\boldsymbol{F}_{\mathrm{RTM}} \boldsymbol{F}_{\mathrm{RTM}}^{\mathrm{T}}\right)^{-1} \boldsymbol{F}_{\mathrm{RTM}} \boldsymbol{d}\\ &=\left(\boldsymbol{C}_{\mathrm{RTM}-\mathrm{s}} \boldsymbol{F}_{\mathrm{RTM}-\mathrm{s}}^{\mathrm{T}} \boldsymbol{C}^{\mathrm{T}}\right)^{-1} \boldsymbol{C}_{\mathrm{RTM-s}} \boldsymbol{d}\\ &=\boldsymbol{C}^{-1}\left(\boldsymbol{F}_{\mathrm{RTM}-\mathrm{s}} \boldsymbol{F}_{\mathrm{RTM}-\mathrm{s}}^{\mathrm{T}}\right)^{-1} \boldsymbol{F}_{\mathrm{RTM}-\mathrm{s}} \boldsymbol{d}\\ &=\boldsymbol{C}^{-1} \boldsymbol{m}_{\mathrm{LSRTM}-\mathrm{s}} \end{aligned} $ | (C-6) |
因此,三种LSM结果之间的定量关系为
| $ \boldsymbol{m}_{\mathrm{LSRTM-s}}=\boldsymbol{m}_{\mathrm{LSBM}}=c_{\mathrm{top}}^{-2} \boldsymbol{c}^{2} \odot \boldsymbol{m}_{\mathrm{LSRTM}} $ | (C-7) |
| [1] |
TARANTOLA A. Inversion of seismic reflection data in the acoustic approximation[J]. Geophysics, 1984, 49(8): 1259-1266. DOI:10.1190/1.1441754 |
| [2] |
SCHUSTER G T. Least-squares cross-well migration[C]. SEG Technical Program Expanded Abstracts, 1993, 12: 110-113.
|
| [3] |
NEMETH T, WU C, SCHUSTER G T. Least-squares migration of incomplete reflection data[J]. Geophysics, 1999, 64(1): 208-221. DOI:10.1190/1.1444517 |
| [4] |
CLAPP M L, CLAPP R G, BIONDI B L. Regularized least-squares inversion for 3-D subsalt imaging[C]. SEG Technical Program Expanded Abstracts, 2005, 24: 1814-1817.
|
| [5] |
WANG J, KUEHL H, SACCHI M D. High-resolution wave-equation AVA imaging: Algorithm and tests with a data set from the Western Canadian Sedimentary Basin[J]. Geophysics, 2005, 70(5): S91-S99. DOI:10.1190/1.2076748 |
| [6] |
DONG S, CAI J, GUO M, et al. Least-squares reverse time migration: Towards true amplitude imaging and improving the resolution[C]. SEG Technical Program Expanded Abstracts, 2012, 31: 1-5.
|
| [7] |
DUTTA G, SCHUSTER G T. Attenuation compensation for least-squares reverse time migration using the viscoacoustic-wave equation[J]. Geophysics, 2014, 79(6): S251-S262. |
| [8] |
ZENG C, DONG S, WANG B. Least-squares reverse time migration: Inversion-based imaging toward true reflectivity[J]. The Leading Edge, 2014, 33(9): 962-964, 966, 968. DOI:10.1190/tle33090962.1 |
| [9] |
GUO P, MCMECHAN G. Adjoint-based least-squares reverse time migration for viscoelastic media[C]. SEG Technical Program Expanded Abstracts, 2017, 36: 4358-4363.
|
| [10] |
李庆洋, 黄建平, 李振春, 等. 优化的多震源最小二乘逆时偏移[J]. 石油地球物理勘探, 2016, 51(2): 334-341. LI Qingyang, HUANG Jianping, LI Zhenchun, et al. Optimized multi-source least-squares reverse time migration[J]. Oil Geophysical Prospecting, 2016, 51(2): 334-341. |
| [11] |
段心标, 王华忠, 邓光校. 应用反射理论的最小二乘逆时偏移成像[J]. 石油地球物理勘探, 2020, 55(6): 1305-1311. DUAN Xinbiao, WANG Huazhong, DENG Guang-xiao. Least-squares reverse-time migration based on reflection theory[J]. Oil Geophysical Prospecting, 2020, 55(6): 1305-1311. |
| [12] |
BAYSAL E, KOSLOFF D D, SHERWOOD J W C. Reverse time migration[J]. Geophysics, 1983, 48(11): 1514-1524. DOI:10.1190/1.1441434 |
| [13] |
Whitmore N D. Iterative depth migration by backward time propagation[C]. SEG Technical Program Expanded Abstracts, 1983, 2: 382-385.
|
| [14] |
LI S C, REN Y X, LIU L B, et al. Reverse time migration of seismic forward-prospecting data in tunnels based on beamforming methods[J]. Rock Mechanics and Rock Engineering, 2019, 52(9): 3261-3278. DOI:10.1007/s00603-019-01763-2 |
| [15] |
FENG Z G, SCHUSTER G T. Elastic least-squares reverse time migration[J]. Geophysics, 2017, 82(2): S143-S157. DOI:10.1190/geo2016-0254.1 |
| [16] |
方修政, 钮凤林, 吴迪. 基于逆散射成像条件的最小二乘逆时偏移[J]. 地球物理学报, 2018, 61(9): 3770-3782. FANG Xiuzheng, NIU Fenglin, WU Di. Least-squares reverse-time migration enhanced with the inverse scattering imaging condition[J]. Chinese Journal of Geophysics, 2018, 61(9): 3770-3782. |
| [17] |
黄建平, 曹晓莉, 李振春, 等. 最小二乘逆时偏移在近地表高精度成像中的应用[J]. 石油地球物理勘探, 2014, 49(1): 107-112. HUANG Jianping, CAO Xiaoli, LI Zhenchun, et al. Least square reverse time migration in high resolution imaging of near surface[J]. Oil Geophysical Prospecting, 2014, 49(1): 107-112. |
| [18] |
TARANTOLA A. Linearized inversion of seismic reflection data[J]. Geophysical Prospecting, 1984, 32(6): 998-1015. DOI:10.1111/j.1365-2478.1984.tb00751.x |
| [19] |
CLAERBOUT J F, ABMA R. Earth Soundings Ana-lysis: Processing versus Inversion[M]. Oxford: Blackwell Scientific Publications, 1991.
|
| [20] |
BEDNAR J. Conference on Inverse Scattering: Theory and Application[M]. Philaelphia: Society for Industrial and Applied Mathematics, 1983.
|
| [21] |
KEYS R G, WEGLEIN A B. Generalized linear inversion and the first Born theory for acoustic media[J]. Journal of Mathematical Physics, 1983, 24(6): 1444-1449. DOI:10.1063/1.525879 |
| [22] |
XU L N, SACCHI M D. Preconditioned acoustic least-squares two-way wave-equation migration with exact adjoint operator[J]. Geophysics, 2018, 83(1): S1-S13. DOI:10.1190/geo2017-0167.1 |
| [23] |
ZHANG Q, ZHOU H, CHEN H M, et al. Least-squares reverse time migration with and without source wavelet estimation[J]. Journal of Applied Geo-physics, 2016, 134: 1-10. |
| [24] |
SUN J Z, FDMEL S, HU J. Least-squares reverse-time migration using one-step two-way wave extrapolation by non-stationary phase shift[C]. SEG Technical Program Expanded Abstracts, 2014, 33: 3967-3973.
|
| [25] |
HOU J, SYMES W W. An approximate inverse to the extended Born modeling operator[J]. Geophy-sics, 2015, 80(6): R331-R349. |
| [26] |
BORZÌ A, SCHULZ V. Computational Optimization of Systems Governed by Partial Differential Equations[M]. Philadelphia: Society for Industrial and Applied Mathema-tics, 2011.
|
| [27] |
CHEN K, SACCHI M D. Elastic least-squares reverse time migration via linearized elastic full-waveform inversion with pseudo-Hessian preconditioning elastic LSRTM[J]. Geophysics, 2017, 82(5): S341-S358. DOI:10.1190/geo2016-0613.1 |
| [28] |
JI J. An exact adjoint operation pair in time extrapolation and its application in least-squares reverse-time migration[J]. Geophysics, 2009, 74(5): H27-H33. DOI:10.1190/1.3173894 |
| [29] |
YAO G, JAKUBOWICZ H. Least-squares reverse-time migration in a matrix-based formulation[J]. Geo-physical Prospecting, 2016, 64(3): 611-621. DOI:10.1111/1365-2478.12305 |
| [30] |
DAI W, SCHUSTER G T. Plane-wave least-squares reverse-time migration[J]. Geophysics, 2013, 78(4): S165-S177. DOI:10.1190/geo2012-0377.1 |
| [31] |
REN H R, WANG H Z, CHEN S C. Least-squares reverse time migration in frequency domain using the adjoint-state method[J]. Journal of Geophysics and Engineering, 2013, 10(3): 035002. DOI:10.1088/1742-2132/10/3/035002 |
| [32] |
REN Z M, LIU Y, SEN M K. Least-squares reverse time migration in elastic media[J]. Geophysical Journal International, 2016, 208(2): 1103-1125. |
| [33] |
李振春, 黄金强, 黄建平, 等. 基于平面波加速的VTI介质最小二乘逆时偏移[J]. 地球物理学报, 2017, 60(1): 240-257. LI Zhenchun, HUANG Jinqiang, HUANG Jianping, et al. Fast least-squares reverse time migration based on plane-wave encoding for VTI media[J]. Chinese Journal of Geophysics, 2017, 60(1): 240-257. |
| [34] |
郭旭, 黄建平, 李振春, 等. 基于一阶速度—应力方程的VTI介质最小二乘逆时偏移[J]. 地球物理学报, 2019, 62(6): 2188-2202. GUO Xu, HUANG Jinqiang, LI Zhenchun, et al. Least-squares reverse time migration based on first-order velocity-stress wave equation in VTI media[J]. Chinese Journal of Geophysics, 2019, 62(6): 2188-2202. |
| [35] |
陈汉明, 周辉, 田玉昆. 分数阶拉普拉斯算子黏滞声波方程的最小二乘逆时偏移[J]. 石油地球物理勘探, 2020, 55(3): 616-626. CHEN Hanming, ZHOU Hui, TIAN Yukun. Least-squares reverse-time migration based on a fractional Laplacian viscoacoustic wave equation[J]. Oil Geophysical Prospecting, 2020, 55(3): 616-626. |
| [36] |
XUE Z G, CHEN Y, FOMEL S, et al. Seismic imaging of incomplete data and simultaneous-source data using least-squares reverse time migration with shaping regularization[J]. Geophysics, 2016, 81(1): S11-S20. DOI:10.1190/geo2014-0524.1 |
| [37] |
ZHANG D L, SCHUSTER G T. Least-squares reverse time migration of multiples[J]. Geophysics, 2014, 79(1): S11-S21. DOI:10.1190/geo2013-0156.1 |
| [38] |
TAN S R, HUANG L J. Least-squares reverse-time migration with a wavefield-separation imaging condition and updated source wavefields[J]. Geophysics, 2014, 79(5): S195-S205. DOI:10.1190/geo2014-0020.1 |
| [39] |
LIU Y S, TENG J W, XU T, et al. An efficient step-length formula for correlative least-squares reverse time migration[J]. Geophysics, 2016, 81(4): S221-S238. DOI:10.1190/geo2015-0529.1 |
| [40] |
ZHANG Y, DUAN L, XIE Y. A stable and practical implementation of least-squares reverse time migration[J]. Geophysics, 2015, 80(1): V23-V31. DOI:10.1190/geo2013-0461.1 |
| [41] |
ZENG C, DONG S Q, WANG B. A guide to least-squares reverse time migration for subsalt imaging: Challenges and solutions[J]. Interpretation, 2017, 5(3): SN1-SN11. DOI:10.1190/INT-2016-0196.1 |



 任玉晓,山东省济南市经十路17923号山东大学齐鲁交通学院,250061。Email:
任玉晓,山东省济南市经十路17923号山东大学齐鲁交通学院,250061。Email: