② 中国石油大学(北京)油气资源与探测国家重点实验室,北京 102249
② State Key Laboratory of Petroleum Resources and Prospecting, China University of Petroleum (Beijing), Beijing 102249, China
地下介质普遍呈现各向异性,横向各向同性(TI)介质是地震勘探学界研究最广的一类各向异性模型,根据其对称轴方向可以分为VTI、HTI和TTI模型。逆时偏移技术受倾角限制小,能够适应复杂速度模型,获得高精度成像剖面,因此各向异性逆时偏移研究具有重要意义。
相比于各向异性弹性波方程,各向异性声波方程形式简单、计算量较小、波场特征明确。目前在各向异性波场模拟和偏移中主要采用伪声波方程,该类方程的一种推导思路是将耦合的各向异性P-SV波频散关系中的横波速度设置为0简化而来[1]。在此基础上,发展了多种形式的伪声波方程[2-8]。另一种伪声波方程的推导思路是基于声学近似的胡克定律[9-10]。但是当给定的各向异性参数不满足伪声波假设时,现有伪声波方程在进行P波模拟时,容易出现伪横波干扰及数值不稳定。为了彻底解决伪声波存在的问题,Liu等[11]解耦了VTI介质P-SV波频散关系,获得单独的P波和SV波方程。相比于显式表达的伪声波方程,各向异性纯声波方程包含复杂的拟微分算子,常规差分法难以直接求解。迄今为止,已经发展了多种数值算法求解纯声波方程,如伪谱法/伪解析法[12-13]、低秩分解法[14]、迭代求解法[15]、混合求解法[16]和快速泊松算法[17-18]等。目前关于纯声波方程的研究主要集中于平衡计算精度和效率方面,以及在偏移成像中的进一步应用等[19-23]。
传统逆时偏移技术对震源波场和检波点波场做互相关,结果中容易出现较强的低频噪声。Zhang等[24]采用拉普拉斯滤波压制低频噪声;Yoon等[25]、康玮等[26]利用Poynting矢量切除大角度成像结果,从而压制低频噪声;Liu等[27]提出波场分解构建逆时偏移成像条件,选择不同波场做互相关,能够较好地抑制成像噪声。在Liu等[27]的研究基础上,基于Hilbert变换构建复数波场的策略被用于提高计算效率[28-32]。波场分解成像条件已应用于各向同性声波和弹性波逆时偏移,考虑到该方法的优势,本文将其推广到各向异性介质逆时偏移。
作为对比,本文首先回顾了两种常用的TTI伪声波方程,分析了其存在的问题;然后利用最小二乘方法求取了TTI优化纯声波频散关系,并采用泊松算法和有限差分相结合的数值方案进行求解;最后结合介质各向异性特征对波场分解成像条件进行改进,将其推广至纯声波逆时偏移。相关理论和算例表明,将优化纯声波方程和波场分解成像条件联合应用于各向异性纯声波逆时偏移,能有效压制伪横波及低频噪声,获得高质量成像结果。
1 理论方法 1.1 基于限制性横波速度的TTI伪声波方程通过将原始P-SV波频散关系中的横波速度设置为0,Alkhalifah[1]推导了各向异性伪声波方程,该方程能够有效简化计算,其多种改进版本被广泛应用于各向异性波场模拟和偏移成像[2-8]。但直接将垂向横波速度设置为0并不能完全满足各向异性介质中的物理学规律,当各向异性参数不满足近似条件时(即椭圆近似条件),伪声波方程模拟容易出现SV波干扰及不稳定。为此,学者们提出了不同的解决方案,其中一种常用的基于限制性横波速度的TTI伪声波方程形式[4]为
| $ \left\{\begin{array}{l} \frac{\partial^{2} P}{\partial t^{2}}=v_{\mathrm{P} x}^{2} \frac{\partial^{2} P}{\partial \hat{x}^{2}}+v_{\mathrm{S} z}^{2} \frac{\partial^{2} P}{\partial \hat{z}^{2}}+\left(v_{\mathrm{P} z}^{2}-v_{\mathrm{S} z}^{2}\right) \frac{\partial^{2} Q}{\partial \hat{z}^{2}} \\ \frac{\partial^{2} Q}{\partial t^{2}}=\left(v_{\mathrm{P}}^{2}-v_{\mathrm{S} z}^{2}\right) \frac{\partial^{2} P}{\partial \hat{x}^{2}}+v_{\mathrm{S} z}^{2} \frac{\partial^{2} Q}{\partial \hat{x}^{2}}+v_{\mathrm{P} z}^{2} \frac{\partial^{2} Q}{\partial \hat{z}^{2}} \end{array}\right. $ | (1) |
式中:P为压力波场;Q为辅助波场;vPz为垂向P波速度;
| $ \left\{\begin{array}{l} \frac{\partial^{2}}{\partial \hat{x}^{2}}=\cos ^{2} \theta \frac{\partial^{2}}{\partial x^{2}}+\sin ^{2} \theta \frac{\partial^{2}}{\partial z^{2}}-\sin 2 \theta \frac{\partial^{2}}{\partial x \partial z} \\ \frac{\partial^{2}}{\partial \hat{z}^{2}}=\sin ^{2} \theta \frac{\partial^{2}}{\partial x^{2}}+\cos ^{2} \theta \frac{\partial^{2}}{\partial z^{2}}+\sin 2 \theta \frac{\partial^{2}}{\partial x \partial z} \end{array}\right. $ | (2) |
其中θ为对称轴倾角。特别地,通过引入限制性横波速度能够有效提高稳定性。当vSz=0时,式(1)退化为传统伪声波方程,形式为
| $ \left\{\begin{array}{l} \frac{\partial^{2} P}{\partial t^{2}}=v_{\mathrm{P} x}^{2} \frac{\partial^{2} P}{\partial \hat{x}^{2}}+v_{\mathrm{P} z}^{2} \frac{\partial^{2} Q}{\partial \hat{z}^{2}} \\ \frac{\partial^{2} Q}{\partial t^{2}}=v_{\mathrm{P}_{\mathrm{n}}}^{2} \frac{\partial^{2} P}{\partial \hat{x}^{2}}+v_{\mathrm{P} z}^{2} \frac{\partial^{2} Q}{\partial \hat{z}^{2}} \end{array}\right. $ | (3) |
采用有限差分即可求解式(1)和式(3)。图 1为两个方程计算的双层TTI模型(表 1)的波场切片,其中上、下层介质厚度均为1500m。

|
图 1 双层TTI模型式(1)(a)和式(3)方程模拟的波场切片(b) 左:模型1;中:模型2;右:模型3 |
|
|
表 1 双层TTI模型参数 |
由图 1可以看出:当介质具有椭圆各向异性特征(ε=δ)时,两种方程均可产生高精度P波响应,如图 1左所示;当各向异性参数不满足椭圆假设时(ε≠δ),两种方程会产生较强的伪横波污染,如图 1中和图 1a右所示;当ε < δ时,横波速度为0的伪声波方程(式(3))模拟出现不稳定,如图 1b右所示。
1.2 TTI优化纯声波方程及其结合泊松算法和有限差分的解法多种改进版本的各向异性伪声波方程仅能在一定程度上压制伪横波干扰,提高稳定性,但不能从根本上解决问题。众多研究表明,发展纯声波方程能够彻底消除伪横波污染及不稳定。相比于显式表达的伪声波方程,纯声波方程包含复杂的偏微分算子,常规差分法难以直接求解。考虑到计算精度和效率,本文给出一种改进的、结合泊松算法和有限差分的各向异性优化纯声波方程求解方法[17-18]。
解耦的TTI纯声波频散关系[11]为
| $ \left\{\begin{array}{l} \omega^{2}=\frac{v_{\mathrm{P} z}^{2}}{2}\left[\varPhi+\sqrt{\varPhi^{2}-8(\varepsilon-\delta) \hat{k}{}_{x}^{2} \hat{k}{}_{z}^{2}}\right] \\ \varPhi=(1+2 \varepsilon) \hat{k}{}_{x}^{2}+\hat{k}{}_{z}^{2} \end{array}\right. $ | (4) |
式中:ω为角频率;
| $ \sqrt{\varPhi^{2}-8(\varepsilon-\delta) \hat{k}{}_{x}^{2} \hat{k}{}_{z}^{2}} \approx \varPhi-\frac{4(\varepsilon-\delta) \hat{k}{}_{x}^{2} \hat{k}{}_{z}^{2}}{\varPhi} $ | (5) |
将式(5)代入式(4),可得到目前最常用的各向异性纯声波频散关系。考虑到一阶泰勒展开的精度较低,高阶泰勒展开的计算量较大,为了平衡纯声波模拟时的精度和效率,本文借鉴优化的思想[17-18]获得一种高精度的纯声波频散关系。对式(4)中的根号项做如下近似[17-18]
| $ \sqrt{\varPhi^{2}-8(\varepsilon-\delta) \hat{k}{}_{x}^{2} \hat{k}{}_{z}^{2}} \approx f_{1} \hat{k}{}_{x}^{2}+f_{2} \hat{k}{}_{z}^{2}+f_{3} \frac{\hat{k}{}_{x}^{2} \hat{k}{}_{z}^{2}}{\varPhi} $ | (6) |
式(6)相对于待求近似系数(f1,f2,f3)为线性方程,因此可以通过极小化两端的误差获得近似系数值。构建的目标函数为
| $ \begin{aligned} E=& \iint\left[\sqrt{\varPhi^{2}-8(\varepsilon-\delta) \hat{k}{}_{x}^{2} \hat{k}{}_{z}^{2}}-\right.\\ &\left.\left(f_{1} \hat{k}{}_{x}^{2}+f_{2} \hat{k}{}_{z}^{2}+f_{3} \frac{\hat{k}{}_{x}^{2} \hat{k}{}_{z}^{2}}{\Phi}\right)\right]^{2} \mathrm{~d} \hat{k}_{x} \mathrm{~d} \hat{k}_{z} \end{aligned} $ | (7) |
通过最小二乘方法求解上式,即可获得优化系数(f1,f2,f3)。
将式(6)代入式(4),整理可得优化的纯声波频散关系
| $ \omega^{2}=v_{\mathrm{P} z}^{2}\left[w_{1} \hat{k}{}_{x}^{2}+w_{2} \hat{k}{}_{z}^{2}+w_{3} \frac{\hat{k}{}_{x}^{2} \hat{k}{}_{z}^{2}}{(1+2 \varepsilon) \hat{k}{}_{x}^{2}+\hat{k}{}_{z}^{2}}\right] $ | (8) |
式中
| $ \left\{\begin{array}{l} w_{1}=\frac{1+2 \varepsilon+f_{1}}{2} \\ w_{2}=\frac{1+f_{2}}{2} \\ w_{3}=\frac{f_{3}}{2} \end{array}\right. $ | (9) |
特别地,当w1=1+2ε、w2=1、w3=-2ε-δ时,式(8)退化为常用的一阶泰勒展开纯声波频散式。式(8)在时间—空间域可写为[17]
| $ \begin{aligned} \frac{1}{v_{\mathrm{P} z}^{2}} \frac{\partial^{2} P}{\partial t^{2}}=&w_{1} \frac{\partial^{2} P}{\partial \hat{x}^{2}}+w_{2} \frac{\partial^{2} P}{\partial \hat{z}^{2}}+\\ &w_{3} \frac{\frac{\partial^{4}}{\partial \hat{x}^{2} \partial \hat{z}^{2}}}{(1+2 \varepsilon) \frac{\partial^{2}}{\partial \hat{x}^{2}}+\frac{\partial^{2}}{\partial \hat{z}^{2}}} P \end{aligned} $ | (10) |
| $ \frac{1}{v_{\mathrm{P} z}^{2}} \frac{\partial^{2} P}{\partial t^{2}}=w_{1} \frac{\partial^{2} P}{\partial \hat{x}^{2}}+w_{2} \frac{\partial^{2} P}{\partial \hat{z}^{2}}+w_{3} v_{\mathrm{P} z}^{2} \frac{\partial^{4} Q}{\partial \hat{x}^{2} \partial \hat{z}^{2}} $ | (11) |
| $ (1+2 \varepsilon) v_{\mathrm{P} z}^{2} \frac{\partial^{2} Q}{\partial \hat{x}^{2}}+v_{\mathrm{P} z}^{2} \frac{\partial^{2} Q}{\partial \hat{z}^{2}}=P $ | (12) |
式(11)为显式方程,采用常规差分即可求解。式(12)为隐式方程,其计算过程涉及线性方程组求解。Chu等[15]采用线性迭代求解隐式方程,但计算量较大。为了提高效率,本文给出一种基于泊松算法的实现策略[17]。
将式(11)和式(12)进一步整理为
| $ \begin{gathered} \frac{1}{v_{\mathrm{p} z}^{2}} \frac{\partial^{2} P}{\partial t^{2}}=\left(w_{1} \cos ^{2} \theta+w_{2} \sin ^{2} \theta\right) \frac{\partial^{2} P}{\partial x^{2}}+\left(w_{1} \sin ^{2} \theta+w_{2} \cos ^{2} \theta\right) \frac{\partial^{2} P}{\partial z^{2}}+\left(w_{2}-w_{1}\right) \sin 2 \theta \frac{\partial^{2} P}{\partial x \partial z}+\\ w_{3}\left[\cos ^{2} \theta \sin ^{2} \theta\left(\frac{\partial^{4} Q}{\partial x^{4}}+\frac{\partial^{4} Q}{\partial z^{4}}\right)+\cos ^{2} 2 \theta \frac{\partial^{4} Q}{\partial x^{2} \partial z^{2}}+\sin 2 \theta \cos 2 \theta\left(\frac{\partial^{4} Q}{\partial x^{3} \partial z}-\frac{\partial^{4} Q}{\partial x \partial z^{3}}\right)\right] \end{gathered} $ | (13) |
| $ \nabla^{2} Q=P $ | (14) |
式(13)和式(14)组成了新的TTI优化纯声波方程,其中式(13)可采用常规差分法求解。式(14)为泊松方程,基于前人研究成果,可通过泊松算法实现,计算步骤[17]如下。
(1) 采用五点差分离散式(14)
| $ Q_{i-1, j}+Q_{i+1, j}+Q_{i, j-1}+Q_{i, j+1}-4 Q_{i, j}=h^{2} P_{i, j} $ | (15) |
式中:h为网格间距;i、j分别为x、z方向网格点序号。
(2) 利用正弦变换求取波场P的傅里叶响应
| $ \hat{P}_{n, l}=\frac{1}{L_{x} L_{z}} \sum\limits_{i=1}^{L_{x}-1} \sum\limits_{j=1}^{L_{z}-1} P_{i, j} \sin \frac{i n {\rm{ \mathsf{ π} }}}{L_{x}} \sin \frac{j l {\rm{ \mathsf{ π} }}}{L_{z}} $ | (16) |
式中:Lx和Lz分别为x、z方向网格点数;n、l分别为波数域两个方向的网格点序号。
(3) 计算辅助波场Q的傅里叶响应
| $ \left\{\begin{array}{l} \hat{Q}_{n, l}=\frac{\hat{P}_{n, l}}{\lambda_{n, l}} \\ \lambda_{n, l}=4-2 \cos \frac{n {\rm{ \mathsf{ π} }}}{L_{x}}-2 \cos \frac{l {\rm{ \mathsf{ π} }}}{L_{z}} \end{array}\right. $ | (17) |
(4) 求解辅助波场Q
| $ Q_{i, j}=\sum\limits_{n=1}^{L_{x}-1} \sum\limits_{l=1}^{L_{z}-1} \hat{Q}_{n, l} \sin \frac{i n {\rm{ \mathsf{ π} }}}{L_{x}} \sin \frac{j l {\rm{ \mathsf{ π} }}}{L_{z}} $ | (18) |
通过显式差分离散式(13),通过式(15)~式(18)可实现式(14)的求解。这样能够保证纯声波方程式(13)和式(14)的高效求解。
图 2对比了一阶泰勒展开方程(式(5))和优化展开方程(式(6))对根号部分的近似精度。由图可见,与精确值(图 2a)相比,一阶泰勒展开存在较大误差(图 2b),而最小二乘优化展开能够获得更高的近似精度(图 2c)。图 3为优化纯声波方程模拟的双层TTI模型波场切片,与图 1伪声波方程的计算结果相比,纯声波方程在不同参数条件下均能产生精确有效的P波响应,同时能够完全消除伪横波和数值不稳定。

|
图 2 均匀各向异性模型的精确微分算子(a)及一阶泰勒展开误差(b)与最小二乘优化展开误差(c)的对比 模型参数为ε=0.2,δ=0.1,θ=60° |
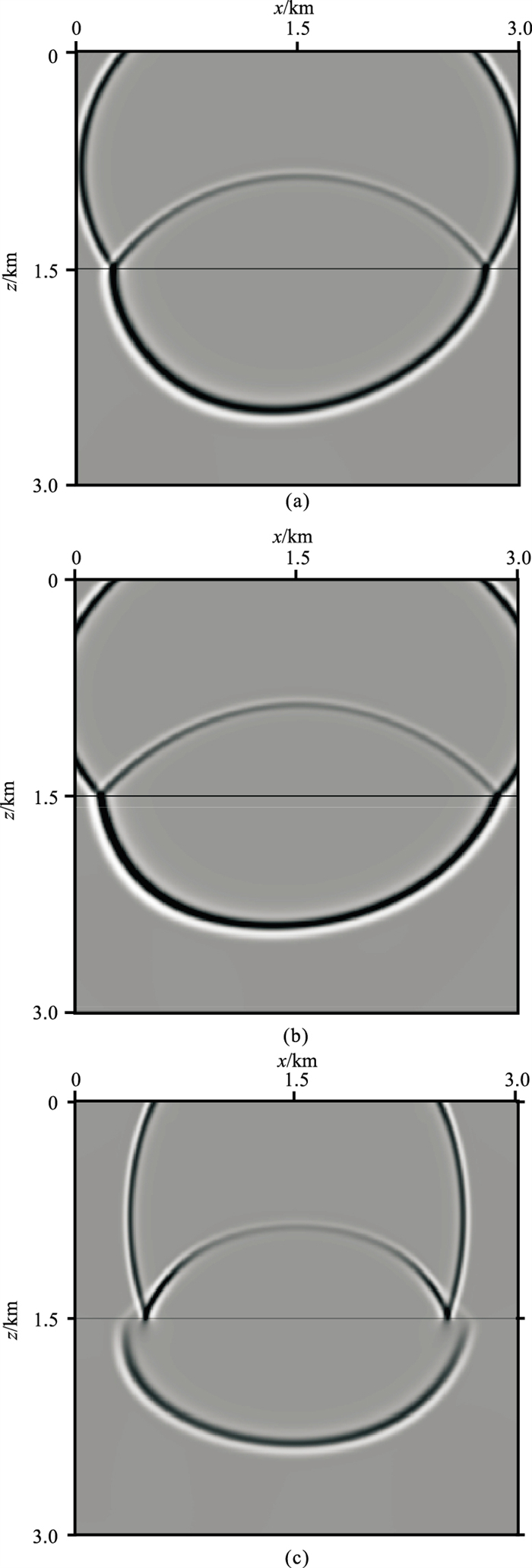
|
图 3 双层TTI模型优化纯声波方程模拟的波场切片 (a)模型1;(b)模型2;(c)模型3 |
在逆时偏移成像中,互相关成像条件具有实现简单、计算高效等优点,得到广泛应用。常规互相关成像条件[34]为
| $ I(\boldsymbol{x})=\int_{0}^{t_{\max }} P_{\mathrm{s}}(\boldsymbol{x}, t) P_{\mathrm{r}}(\boldsymbol{x}, t) \mathrm{d} t $ | (19) |
式中:x为空间坐标;I(x)为成像结果;Ps(x, t)为震源波场;Pr(x, t)为检波点波场;tmax为记录长度。
常规互相关成像条件易引起较强低频噪声,原因是互相关过程中沿所有方向传播的震源波场和检波点波场均参与成像,同向传播的波场之间互相关叠加,易形成较强的低频噪声。为了压制传统互相关成像过程中的低频噪声,除了对低频噪声进行滤波处理外[24],另一种有效策略是对参与成像的全波场沿不同方向进行分解,选取传播方向不同的分量波场参与成像,能够有效减弱低频噪声干扰[27-32]。
以二维情况为例,对式(19)中的震源波场Ps(x, t)和检波点波场Pr(x, t)进行分解
| $ \begin{aligned} P_{\mathrm{s}}(\boldsymbol{x}, t)=& P_{\mathrm{s}}^{\uparrow}(\boldsymbol{x}, t)+P_{\mathrm{s}}^{\downarrow}(\boldsymbol{x}, t)+\\ & P_{\mathrm{s}}^{\leftarrow}(\boldsymbol{x}, t)+P_{\mathrm{s}}^{\rightarrow}(\boldsymbol{x}, t) \end{aligned} $ | (20) |
| $ \begin{aligned} P_{\mathrm{r}}(\boldsymbol{x}, t)=& P_{\mathrm{r}}^{\uparrow}(\boldsymbol{x}, t)+P_{\mathrm{r}}^{\downarrow}(\boldsymbol{x}, t)+\\ & P_{\mathrm{r}}^{\leftarrow}(\boldsymbol{x}, t)+P_{\mathrm{r}}^{\rightarrow}(\boldsymbol{x}, t) \end{aligned} $ | (21) |
式中上标“↑”、“↓”、“←”、“→”分别表示上行、下行、左行和右行波场分量。
由式(19)~式(21)可知,震源波场分量与检波点波场分量之间两两互相关可得16种成像剖面。其中传播方向相反的波场分量互相关能够产生有效的成像结果,而同向传播的波场分量之间互相关主要产生低频噪声[27-32]。在前人关于波场分解成像条件的研究基础上,本文采用一种基于Hilbert变换构建复数波场的分解算法。该分解方法能够进行全波场的显式分离,目前被广泛用于各向同性介质的逆时偏移[27-32]。本文将其推广到各向异性介质的逆时偏移,实现步骤如下。
(1) 基于式(13)和式(14),震源波场的复数外推形式可以表示为
| $ \left\{\begin{array}{l} \frac{\partial^{2} P_{\mathrm{s}}(\boldsymbol{x}, t)}{\partial t^{2}}=v_{\mathrm{Pz}}^{2}(\boldsymbol{x}) \frac{\partial^{2} P_{\mathrm{s}}(\boldsymbol{x}, t)}{\partial \boldsymbol{x}^{2}}+F_{\mathrm{s}}\left(\boldsymbol{x}_{\mathrm{s}}\right) \\ \frac{\partial^{2} P_{\mathrm{s}}^{\mathrm{H}}(\boldsymbol{x}, t)}{\partial t^{2}}=v_{\mathrm{Pz}}^{2}(\boldsymbol{x}) \frac{\partial^{2} P_{\mathrm{s}}^{\mathrm{H}}(\boldsymbol{x}, t)}{\partial \boldsymbol{x}^{2}}+F_{\mathrm{s}}^{\mathrm{H}}\left(\boldsymbol{x}_{\mathrm{s}}\right) \\ \widetilde{P}_{\mathrm{s}}(\boldsymbol{x}, t)=P_{\mathrm{s}}(\boldsymbol{x}, t)+\mathrm{i} P_{\mathrm{s}}^{\mathrm{H}}(\boldsymbol{x}, t) \end{array}\right. $ | (22) |
式中:∂2Ps(x, t)/∂t2=vPz2(x)∂2Ps(x, t)/∂x2为式(13)的简写形式;Fs(xs)为震源函数,其中xs为震源坐标;上标“H”表示Hilbert变换;
(2) 基于步骤(1)构建的复数波场,以震源波场为例,上行波场可以表示为
| $ \widetilde{P}_{\mathrm{s}}^{+}\left(\hat{x}, \hat{k}_{z}, t\right)= \begin{cases}\widetilde{P}_{\mathrm{s}}\left(\hat{x}, \hat{k}_{z}, t\right) & \hat{k}_{z} \geqslant 0 \\ 0 & \hat{k}_{z}<0\end{cases} $ | (23) |
| $ P_{\mathrm{s}}^{\uparrow}(\boldsymbol{x}, t)=\operatorname{Re}\left\{\mathrm{F}^{-1}\left[\widetilde{P}{}_{\mathrm{s}}^{+}\left(\hat{x}, \hat{k}_{z}, t\right)\right]\right\} $ | (24) |
式中:Re(·)为取实运算;

|
图 4 双层TTI模型4的波场切片(a)及分离的上(b)、下(c)、左(d)、右行波场(e) |
各向异性地堑模型的尺寸为4000m×3000m,相关参数如图 5所示。网格间距为10m,时间步长为1ms,震源选用主频为28Hz的Ricker子波。

|
图 5 各向异性地堑模型 |
考虑到横波速度为0的伪声波方程存在稳定性问题,图 6为基于限制性横波速度的伪声波和优化纯声波方程模拟的波场切片,可以看出,相比于伪声波方程的模拟结果(图 6a),纯声波方程能够有效压制伪横波干扰,产生高精度P波响应(图 6b)。

|
图 6 地堑模型不同方程模拟的波场切片 (a)伪声波方程(式(1));(b)优化纯声波方程(式(13)、式(14)) |
图 7为图 6b的纯声波波场沿不同方向分解结果,可以发现,上、下、左、右行波得到了有效分离。传统互相关成像条件和波场分解成像条件的偏移结果如图 8所示。由图 8a可知,基于传统互相关条件的成像结果容易产生较强低频噪声干扰。对比部分分量波场的成像结果可见同向传播的波场之间互相关主要产生低频噪声,波场分解成像条件能够较好地将这部分干扰剔除,反向传播波场之间互相关能够产生有效的成像剖面。对图 8a中的成像剖面进行滤波处理,结果如图 8b所示。由图可知,不同剖面的低频噪音得到较好地去除。反向传播波场成像结果之和略优于传统全波场成像结果。相关结果表明,不同方向行波之间的互相关结果可以作为传统方法的补充,成像结果精度更高。

|
图 7 地堑模型分离的上(a)、下(b)、左(c)、右行波场(d) |

|
图 8 地堑模型优化纯声波方程不同条件成像结果(a)及其拉普拉斯滤波结果(b) 左:全波场互相关;中:同向传播波场互相关之和;右:反向传播波场互相关之和 |
修改的Marmousi TTI模型,如图 9所示。将计算区域剖分为500×350个网格单元。用于逆时偏移的速度场和各向异性参数场均基于五点平滑获得。图 10为各向同性声波、各向异性伪声波和优化纯声波的成像结果,相比之下,基于优化纯声波方程的逆时偏移能够获得更高精度的成像。图 11为基于优化纯声波方程的不同条件成像结果的对比,可见,传统全波场参与的互相关成像,浅层存在严重的低频噪声污染。同向传播的波场之间互相关主要产生低频成像噪声,波场分解成像条件能够较好地将低频噪声去除,反向传播波场之间互相关能够产生高精度的成像结果。相比于经过拉普拉斯滤波的成像剖面而言,基于波场分解成像条件的偏移结果不需要滤波处理,能够较好地保证振幅信息。总体而言,基于波场分解的成像方法可以作为传统方法的有效补充,以获得不同展布方向地下构造的高精度成像。

|
图 9 修改的Marmousi TTI模型 (a)vPz;(b)ε;(c)δ;(d)θ |

|
图 10 修改的Marmousi TTI模型不同方程的成像结果(拉普拉斯滤波后) (a)各向同性声波方程;(b)伪声波方程(式(1));(c)优化纯声波方程(式(13)、式(14)) |

|
图 11 修改的Marmousi TTI模型的优化纯声波方程不同条件成像结果 (a)全波场互相关;(b)同向传播波场互相关之和;(c)反向传播波场互相关之和;(d)反向传播波场互相关之和(拉普拉斯滤波后) |
本文首先回顾了TTI介质中两种常用的伪声波方程,在各向异性参数不满足声学近似时,利用该方程模拟容易产生伪横波干扰及不稳定现象。为了解决现有伪声波方程存在的问题,应用最小二乘方法获得了优化的纯声波频散关系,在此基础上采用一种泊松算法和有限差分相结合的高效精确各向异性纯声波求解算法,能够有效避免伪横波干扰及数值不稳定。将各向同性介质中基于Hilbert变换的复数波场分解成像条件推广到TTI介质优化纯声波逆时偏移成像,选择传播方向相反的分量波场参与最终成像。理论和数值算例验证了本文方法能够有效压制各向异性逆时偏移的伪横波干扰和低频噪声,获得高精度的成像结果。
| [1] |
ALKHALIFAH T. Acoustic approximations for processing in transversely isotropic media[J]. Geophy-sics, 1998, 63(2): 623-631. |
| [2] |
ZHOU H, ZHANG G, BLOOR R. An anisotropic acoustic wave equation for modeling and migration in 2D TTI media[C]. SEG Technical Program Expan-ded Abstracts, 2006, 25: 194-198.
|
| [3] |
DU X, BANCROFT J C, LINES L R. Anisotropic reverse-time migration for tilted TI media[J]. Geophysical Prospecting, 2007, 55(6): 853-869. DOI:10.1111/j.1365-2478.2007.00652.x |
| [4] |
FLETCHER R, DU X, FOWLER P. Reverse time migration in tilted transversely isotropic (TTI) media[J]. Geophysics, 2009, 74(6): WCA179-WCA187. DOI:10.1190/1.3269902 |
| [5] |
李博, 李敏, 刘红伟, 等. TTI介质有限差分逆时偏移的稳定性探讨[J]. 地球物理学报, 2012, 55(4): 1366-1375. LI Bo, LI Min, LIU Hongwei, et al. Stability of reverse time migration in TTI media[J]. Chinese Journal of Geophysics, 2012, 55(4): 1366-1375. DOI:10.6038/j.issn.0001-5733.2012.04.032 |
| [6] |
刘文卿, 王西文, 王宇超, 等. 带正则化校正的TTI介质qP波方程及其逆时偏移方法和应用[J]. 地球物理学报, 2016, 59(3): 1059-1069. LIU Wenqing, WANG Xiwen, WANG Yuchao, et al. A regularized qP-wave equation for TTI media and its application to reverse time migration[J]. Chinese Journal of Geophysics, 2016, 59(3): 1059-1069. |
| [7] |
何兵寿, 武雪峤, 高琨鹏. TI介质中qP波方程逆时偏移技术的研究现状与展望[J]. 石油物探, 2021, 60(1): 34-45. HE Bingshou, WU Xueqiao, GAO Kunpeng. Research status and prospect of qP wave reverse time migration in TI media[J]. Geophysical Prospecting for Petro-leum, 2021, 60(1): 34-45. |
| [8] |
梁锴, 曹丹平, 孙上饶, 等. 椭球各向异性介质弹性波完全解耦波动方程[J]. 石油地球物理勘探, 2021, 56(6): 1254-1261. LIANG Kai, CAO Danping, SUN Shangrao, et al. The complete decoupled wave equations for ellipsoidal anisotropic media[J]. Oil Geophysical Prospecting, 2021, 56(6): 1254-1261. |
| [9] |
DUVENECK E, MILCIK P, BAKKER P M, et al. Acoustic VTI wave equations and their application for anisotropic reverse-time migration[C]. SEG Technical Program Expanded Abstracts, 2008, 27: 2186-2190.
|
| [10] |
杨富森, 李振春, 王小丹. TTI介质一阶qP波稳定方程波场数值模拟及逆时偏移[J]. 石油地球物理勘探, 2016, 51(3): 497-505. YANG Fusen, LI Zhenchun, WANG Xiaodan. Wavefield numerical simulation and reverse-time migration based on the stable TTI first-order qP-wave equations[J]. Oil Geophysical Prospecting, 2016, 51(3): 497-505. |
| [11] |
LIU F Q, MORTON S A, JIANG S S, et al. Decoupled wave equations for P and SV waves in an acoustic VTI media[C]. SEG Technical Program Expanded Abstracts, 2009, 28: 2844-2848.
|
| [12] |
ETGEN J T, BRANDSBERG-DAHL S. The pseudo-analytical method: application of pseudo-Laplacians to acoustic and acoustic anisotropic wave propagation[C]. SEG Technical Program Expanded Abstracts, 2009, 28: 2552-2556.
|
| [13] |
CRAWLEY S, BRANDSBERG-DAHL S, MCCLEAN J, et al. TTI reverse time migration using the pseudo-analytic method[J]. The Leading Edge, 2010, 29(11): 1378-1384. DOI:10.1190/1.3517310 |
| [14] |
SONG X L, ALKHALIFAH T. Modeling of pseudo-acoustic P-waves in orthorhombic media with a low-rank approximation[J]. Geophysics, 2013, 78(4): C33-C40. DOI:10.1190/geo2012-0144.1 |
| [15] |
CHU C L, MACY B K, ANNO P D. Approximation of pure acoustic seismic wave propagation in TTI media[J]. Geophysics, 2011, 76(5): WB97-WB107. DOI:10.1190/geo2011-0092.1 |
| [16] |
杜启振, 郭成峰, 公绪飞. VTI介质纯P波混合法正演模拟及稳定性分析[J]. 地球物理学报, 2015, 58(4): 1290-1304. DU Qizhen, GUO Chengfeng, GONG Xufei. Hybrid PS/FD numerical simulation and stability analysis of pure P-wave propagation in VTI media[J]. Chinese Journal of Geophysics, 2015, 58(4): 1290-1304. |
| [17] |
LI X Y, ZHU H J. A finite-difference approach for solving pure quasi-P-wave equations in transversely isotropic and orthorhombic media[J]. Geophysics, 2018, 83(4): C161-C172. DOI:10.1190/geo2017-0405.1 |
| [18] |
ZHANG Y B, LIU Y, XU S G. Efficient modeling of optimised pure acoustic wave equation in 3D transe-versely isotropic and orthorhombic anisotropic media[J]. Exploration Geophysics, 2019, 50(5): 561-574. DOI:10.1080/08123985.2019.1643680 |
| [19] |
郭成峰, 杜启振, 张明强, 等. 改进的TTI介质纯P波方程正演模拟与逆时偏移[J]. 地球物理学报, 2017, 60(1): 258-270. GUO Chengfeng, DU Qizhen, ZHANG Mingqiang, et al. Numerical simulation and reverse time migration using an improved pure P-wave equation in tilted transversely isotropic media[J]. Chinese Journal of Geophysics, 2017, 60(1): 258-270. |
| [20] |
黄金强, 李振春. 基于Low-rank分解的复杂TI介质纯qP波正演模拟与逆时偏移[J]. 地球物理学报, 2017, 60(2): 704-721. HUANG Jinqiang, LI Zhenchun. Modeling and reverse time migration of pure quasi-P-waves in complex TI media with a low-rank decomposition[J]. Chinese Journal of Geophysics, 2017, 60(2): 704-721. |
| [21] |
胡书华, 王宇超, 刘文卿, 等. 复杂TTI介质稳定的纯qP波波场模拟方法[J]. 石油地球物理勘探, 2018, 53(2): 280-287. HU Shuhua, WANG Yuchao, LIU Wenqing, et al. Pure quasi-P wave stable simulation in complex TTI media[J]. Oil Geophysical Prospecting, 2018, 53(2): 280-287. |
| [22] |
慕鑫茹, 黄建平, 李振春, 等. 基于最佳平方逼近的TTI介质解耦qP波与qSV波逆时偏移[J]. 石油地球物理勘探, 2019, 54(6): 1280-1292. MU Xinru, HUANG Jianping, LI Zhenchun, et al. Reverse time migration of decoupled qP-and qSV-waves in TTI media with the optimal quadratic approximation[J]. Oil Geophysical Prospecting, 2019, 54(6): 1280-1292. |
| [23] |
顾汉明, 张奎涛, 刘春成, 等. 基于Low-rank一步法波场延拓的黏声各向异性介质纯qP波正演模拟[J]. 石油地球物理勘探, 2020, 55(4): 733-746. GU Hanming, ZHANG Kuitao, LIU Chuncheng, et al. Low-rank one-step wave extrapolation for pure qP-wave forward modeling in viscoacoustic anisotro-pic media[J]. Oil Geophysical Prospecting, 2020, 55(4): 733-746. |
| [24] |
ZHANG Y, SUN J. Practical issues of reverse time migration: true amplitude gathers, noise removal and harmonic-source encoding[C]. Beijing 2009 International Geophyical Conference and Exposition, Beijing, 2009.
|
| [25] |
YOON K, MARFURT K J. Reverse-time migration using the Poynting vector[J]. Exploration Geophy-sics, 2006, 37(1): 102-107. DOI:10.1071/EG06102 |
| [26] |
康玮, 程玖兵. 叠前逆时偏移假象去除方法[J]. 地球物理学进展, 2012, 27(3): 1163-1172. KANG Wei, CHENG Jiubing. Methods of suppres-sing artifacts in prestack reverse time migration[J]. Progress in Geophysics, 2012, 27(3): 1163-1172. |
| [27] |
LIU F Q, ZHANG G Q, MORTON S A, et al. An effective imaging condition for reverse-time migration using wavefield decomposition[J]. Geophysics, 2011, 76(1): S29-S39. DOI:10.1190/1.3533914 |
| [28] |
FEI T W, LUO Y, YANG J R, et al. Removing false images in reverse time migration: The concept of de-primary[J]. Geophysics, 2015, 80(6): S237-S244. DOI:10.1190/geo2015-0289.1 |
| [29] |
胡江涛, 王华忠. 基于解析时间波场外推与波场分解的逆时偏移方法研究[J]. 地球物理学报, 2015, 58(8): 2886-2895. HU Jiangtao, WANG Huazhong. Reverse time migration using analytical time wavefield extrapolation and separation[J]. Chinese Journal of Geophysics, 2015, 58(8): 2886-2895. |
| [30] |
王一博, 郑忆康, 薛清峰, 等. 基于Hilbert变换的全波场分离逆时偏移成像[J]. 地球物理学报, 2016, 59(11): 4200-4211. WANG Yibo, ZHENG Yikang, XUE Qingfeng, et al. Reverse time migration with Hilbert transform based full wavefield decomposition[J]. Chinese Journal of Geophysics, 2016, 59(11): 4200-4211. DOI:10.6038/cjg20161122 |
| [31] |
WANG E J, LIU Y. The hybrid absorbing boundary condition for one-step extrapolation and its application in wavefield decomposition-based reverse time migration[J]. Journal of Geophysics and Engineering, 2017, 14(5): 1177-1188. DOI:10.1088/1742-2140/aa7308 |
| [32] |
薛浩, 刘洋, 蔡晓慧. 基于复数波场分解的VSP逆时偏移方法研究[J]. 地球物理学进展, 2019, 34(2): 649-657. XUE Hao, LIU Yang, CAI Xiaohui. Research on VSP reverse time migration based on complex wavefield decomposition method[J]. Progress in Geophysics, 2019, 34(2): 649-657. |
| [33] |
THOMSEN L. Weak elastic anisotropy[J]. Geophy-sics, 1986, 51(10): 1954-1966. |
| [34] |
CLAERBOUT J. Toward a unified theory of reflector mapping[J]. Geophysics, 1971, 36(3): 467-481. DOI:10.1190/1.1440185 |



 徐世刚,陕西省西安市雁塔区雁塔路126号长安大学地质工程与测绘学院地球物理系,710054。Email:
徐世刚,陕西省西安市雁塔区雁塔路126号长安大学地质工程与测绘学院地球物理系,710054。Email: