② 宁夏大学数学统计学院,宁夏银川 750021;
③ 清华大学数学科学系,北京 10008;
④ 中国地质大学(武汉)地球物理与空间信息学院,湖北武汉 430074
② School of Mathematics and Statistics, Ningxia University, Yinchuan, Ningxia 750021, China;
③ Department of Mathematical Sciences, Tsinghua University, Beijing 100084, China;
④ Institute of Geophysics & Geomatics, China University of Geoscience, Wuhan, Hubei 430074, China
随着计算机技术的发展,基于地震波运动方程的伴随成像逐渐被应用于实际地震数据的成像[1-4]。在该类成像方法中,利用震源波场与接收器波场做互相关,从而构建目标函数关于模型参数的Fréchet导数。无论是震源波场的求解还是伴随波场的求解,都需要数值求解地震波运动方程,因此地震波运动方程的数值求解也成为伴随成像的关键。随着研究的深入,伴随成像的研究对象越来越复杂[5],如成像模型具有强烈起伏界面[6]、模型含有固体与液体耦合[3]。针对复杂模型的伴随成像,亟待研发适用性强、计算精度高的正演模拟方法。
关于地震波运动方程的直接求解,人们应用最早且最普遍的是有限差分方法(Finite Difference Method,FDM)[7]。FDM的主要优点包括数值格式简单、程序易于实现、计算速度快等[8-9],在实际伴随成像中得到了较广泛应用[10-11]。但FDM在模拟地震波时存在明显不足,主要表现为网格不灵活、自由边界条件难处理和数值频散强。
针对FDM的不足,人们做了大量研究,也取得了具有重要意义的成果。为了增强FDM网格的灵活性,常采用非规则曲线网格将模型离散,再通过坐标变换方式将曲线网格变换成正交网格,最后在坐标变换后的规则网格上利用FDM求解地震波动方程[12-13]。虽然通过坐标变换方式能有效解决FDM网格不灵活的缺陷,但在坐标变换后的规则网格上使用的有限差分离散格式往往只能是二阶中心差分,难以采用高阶差分格式,以至于在粗网格条件下制约了FDM数值精度。虽然采用细网格能提升数值模拟精度,但此时需要较大的计算量和存储量。此外,随着模型复杂程度的增加,曲线网格在拟合复杂地形时易发生畸变,该网格畸变会严重降低曲线网格FDM的数值稳定性[5]。
为了近似自由边界条件,可采用在自由地表之上设置虚拟层方式构造自由地表法向应力为零的自由边界条件[13-14]。虽然通过设置虚拟层可方便实现FDM对自由边界条件的近似,但该数值近似格式只具有二阶精度[14],导致地表处波场模拟精度不足,尤其是面波[15]。
为了减弱FDM的数值频散,研究者常构造优化的FDM[8, 16-21]。通过构造某种误差泛函(如差分算法误差的最小二乘泛函、相速度误差的最小二乘泛函等),利用优化方法选择有限差分系数使误差泛函极小。优化FDM相比于传统FDM的优势在于在不额外增加计算资源的条件下能有效压制数值频散。但在复杂模型中速度结构存在强烈间断或模型存在固液耦合时,优化FDM表现出较大数值误差[22]。压制FDM数值频散的另一种有效方法是利用网格点上地震波场值及其梯度共同近似空间微分算子,在这方面杨顶辉等[23-24]开展了卓有成效的研究,他们系统地发展了地震波模拟的近似解析离散方法。近似解析离散方法是FDM的推广,该方法能有效压制数值频散缘于在近似空间微分算子时近似解析离散方法不仅利用了波场信息,也利用了波场梯度信息。相比于FDM,由于差分算子包含更多的波场信息,使该方法能在粗网格条件下有效压制数值频散。然后,与FDM类似,近似解析离散方法也较难使用非规则网格。
基于傅里叶变换的伪谱法(Pseudo-Spectral Method,PSM)可在较粗网格上模拟地震波传播[25],其理论精度可达到FDM采用无穷阶差分格式时的精度[26-28]。虽然PSM相比于FDM能在粗网格条件下有效压制数值频散[24],但PSM仍存在网格不灵活、不易处理边界条件以及难以适用于固液耦合模型等不足。
基于变分原理的有限元法(Finite-Element Method,FEM)可采用任意非规则网格用于离散复杂地质模型[29-31],因此FEM能有效模拟复杂模型中地震波传播。除了模型适应性强以外,在FEM中直接令地震波动方程弱形式所包含的边界积分项为零就可满足自由地表边界条件。数值算例表明FEM能较精确近似自由地表边界条件,因此FEM能较精确模拟地震面波[15]。除以上优点外,FEM还可通过构造边界条件的方式方便实现固液耦合模型中地震波数值模拟[30]。
FEM在模拟地震波传播时具有优势,也具有明显缺点。传统FEM的缺点主要表现在计算量大和存储量大这两个方面。离散地震波动方程所得到的质量矩阵非对角性以及单元刚度矩阵稠密性决定了FEM的计算量较大[32]。较大的计算量阻碍了FEM在大尺度乃至全球尺度地震波传播模拟中的应用[33]。为了减少FEM的计算量,有效的方案是构造对角质量矩阵[34-37],从而避免求解大型线性方程组。构造对角质量矩阵主要有两种方案:第一种方案是将单元质量按一定比例分配至质量矩阵的对角线上,而将对角线之外的元素直接置为零[34-36];第二种方案是按照一定规则在离散单元内选择插值点使质量矩阵对角线上多项式的积分大于零,而对角线之外的积分为零[29, 37]。第一种质量集中方案是在假设单元内质点间惯性力解耦的情况下直接对FEM的质量矩阵对角化,该处理方式必然在一定程度上造成FEM精度损失,但理论分析和实际算例都表明集中质量FEM与常规FEM具有相同的收敛阶[36, 38],精度损失并不明显。第二种质量集中方案可在不损失FEM精度的条件下获得对角质量矩阵,但该质量集中方式需额外引入插值点,这必然增加FEM自由度。相比于传统FEM,虽然第二种方案减少了计算量,但比第一种方案引入了额外计算量[37]。FEM将地震波动方程所包含的空间微分算子离散之后,在任意离散点处空间微分算子的近似需利用到周围所有离散点信息,这就决定了FEM单元刚度矩阵的稠密性及在矩阵与向量乘积运算时计算量大的特点。单元刚度矩阵的稠密性也导致FEM需要较大的存储空间。虽然采用FEM核矩阵的思路可有效地减少FEM的存储量[16, 39],但存储核矩阵的方案需要重建单元刚度矩阵而引入了额外计算量。
相对而言,谱元法(Spectral-Element Method,SEM)是一种较为高效的地震波模拟方法[40-42],该方法结合了FEM的灵活性与谱方法的高精度性,且兼具计算量和存储量小(与FDM相当)的优点[42]。SEM的灵活性得益于其采用与FEM相同的变分原理以及单元上利用分片插值方法;SEM的高精度性主要源于其借鉴了谱方法的思想而选择正交插值多项式;SEM计算量和存储量小的原因在于插值点与积分点重合,从而质量矩阵为对角矩阵、单元刚度矩阵为稀疏矩阵[42]。SEM以其显著的优点已被运用至不同尺度地震波模拟与成像[2-3, 43-44]。值得指出的是,SEM的质量矩阵与刚度矩阵包含的积分项中多项式的最高阶数超过2N(其中N为空间插值阶数),在利用GLL(Gauss-Lobatto-Legendre)数值求积时数值积分的精度只有2N-1阶,因此GLL数值求积无法精确求取多项式积分。从而积分精度不足而影响SEM的数值精度。为了提升SEM地震波数值模拟精度,本文构造关于GLL数值积分的目标函数,通过优化算法选取GLL数值积分权系数,以提高GLL数值积分精度,最终提升SEM地震波模拟精度,得到基于优化数值积分的谱元法(简称为优化谱元法(Optimal SEM,OSEM))。
1 谱元法基本原理选取各向同性弹性波动方程简要介绍传统谱元法(Conventional SEM,CSEM)。2D非均匀各向同性弹性波方程可表示为
| $ \left\{\begin{array}{l} \rho\ddot{\boldsymbol{u}}=\nabla \cdot \boldsymbol{T}+\boldsymbol{f} \\ \boldsymbol{T}=\boldsymbol{c:} \nabla \boldsymbol{u} \end{array}\right. $ | (1) |
式中:u为位移向量;T为应力张量;c为二阶弹性张量;ρ为介质质量密度;f为震源项;▽为梯度算子。用任意测试向量v乘以式(1)的第一式,在2D空间积分,利用分部积分和格林公式可得
| $ \begin{aligned} \int_{\varOmega} \rho \boldsymbol{v} \cdot \ddot{\boldsymbol{u}} \mathrm{d}^{2} \boldsymbol{x}=&-\int_{\varOmega} \nabla \boldsymbol{v}: \boldsymbol{T} \mathrm{d}^{2} \boldsymbol{x}+\int_{\partial \varOmega} \boldsymbol{v} \cdot \boldsymbol{T} \cdot \boldsymbol{n} \mathrm{d} s+\\ & \int_{\varOmega} \boldsymbol{v} \cdot \boldsymbol{f} \mathrm{d}^{2} \boldsymbol{x} \end{aligned} $ | (2) |
式中:n为边界处的单位法向量;x=x1, x2为物理空间坐标。根据自由地表边界条件和自然边界条件,式(2)中关于边界积分项为0。将研究区域Ω离散成E个非重叠的四边形单元(三维情形为六面体单元),即
| $ \boldsymbol{x}(\xi, \eta)=\sum\limits_{a} N_{a}(\xi, \eta) \boldsymbol{x}_{a} $ | (3) |
式中:(ξ, η)为等参单元坐标;Na(ξ, η)为关于第a个差值节点的形函数。由式(3)可将式(2)所包含的物理域上的积分变换至等参域上的积分,即有
| $ \begin{aligned} \sum\limits_{e=1}^{E} \int_{\varOmega_{e}} \rho \boldsymbol{v} \cdot \boldsymbol{u} J_{e} \mathrm{~d} \xi \mathrm{d} \eta=&-\sum\limits_{e=1}^{E} \int_{\varOmega_{e}} \nabla \boldsymbol{v}: \boldsymbol{T} J_{e} \mathrm{~d} \xi \mathrm{d} \eta+\\ & \sum\limits_{e=1}^{E} \int_{\varOmega_{e}} \boldsymbol{v} \cdot \boldsymbol{f} J_{e} \mathrm{~d} \xi \mathrm{d} \eta \end{aligned} $ | (4) |
式中:
为了计算式(4),需离散各个等参单元,然后通过离散点上的u、v函数值构造多项式用于近似式(4),在计算式(4)中积分时,采用GLL数值求积[36]。在等参单元中每个方向上的离散点的坐标是通过求解以下等式的零点而得到
| $ (1-\lambda) P_{N}^{\prime}(\lambda)=0 $ | (5) |
式中PN(λ)为N阶Legendre多项式,其上标“′”表示一阶导数。通过单元上的离散点,可构造Lagrange多项式,利用Lagrange多项式可对u、v近似,即
| $ \left\{\begin{array}{l} \boldsymbol{u}^{e} \approx \sum\limits_{i=0}^{N} \sum\limits_{j=0}^{N} L_{i}(\xi) L_{j}(\eta) \boldsymbol{u}_{i j}^{e} \\ \boldsymbol{v}^{e} \approx \sum\limits_{i=0}^{N} \sum\limits_{j=0}^{N} L_{i}(\xi) L_{j}(\eta) \boldsymbol{v}_{i j}^{e} \end{array}\right. $ | (6) |
式中:L为Lagrange多项式;uije、vije分别表示位移向量和测试向量在第e单元内第(i,j)标号离散点上的离散值。利用式(6-1)及式(3)可计算应力张量T。由已计算的T及式(3)和式(6),式(4)的离散形式为
| $ \sum\limits_{e=1}^{E} \boldsymbol{M}^{e} \ddot{\boldsymbol{u}}^{e}=-\sum\limits_{e=1}^{E} \boldsymbol{K}^{e} \boldsymbol{P}^{e}+\sum\limits_{e=1}^{E} \boldsymbol{F}^{e} $ | (7) |
式中:Me为单元质量矩阵;Ke为单元刚度矩阵;Fe为单元上震源项的离散形式;Pe为离散应变张量与雅克比矩阵元素和坐标变换因子组合而成的向量。式(7)中矩阵和向量(包括震源项的离散形式)的具体形式已在文献[42]中给出,本文不赘述。
值得指出的是,得益于插值点与积分点重合,Ke为稀疏矩阵,因此SEM的计算量和存储量较小,几乎与FDM处于同一量级[42]。
2 基于优化数值积分的谱元法(OSEM)GLL数值求积的精度是2N-1阶,而式(4)中被积多项式的最高阶数超过2N阶,由于GLL数值积分无法对式(4)中积分项精确估计,这必然损失SEM精度。在保证积分点与插值点重合的条件下,本文对GLL数值求积权优化,从而提升GLL数值求积精度,进而提高SEM的精度。
构造如下目标函数
| $ F\left(w_{0}, w_{1}, \cdots, w_{N}\right)=\sum\limits_{i=0}^{N}\left(\sum\limits_{j=0}^{N} w_{j} \lambda_{j}^{2 i}-\int_{-1}^{1} \lambda^{2 i} \mathrm{~d} \lambda\right)^{2} $ | (8) |
式中:λj为式(5)的零点;wj为待优化的积分权。为了保证能量守恒和质量守恒,积分权需满足
| $ \sum\limits_{i=0}^{N} w_{i}=2 $ | (9) |
数值求积公式的积分权在对称条件下能对任意奇数次幂函数λ2i+1精确求积,因此积分权还需满足
| $ w_{i}=w_{N-i} $ | (10) |
利用共轭梯度算法(Conjugate Gradient)[45-46]求解带约束条件(式(9)和式(10))的式(8),可得到优化权系数(表 1)。考虑到对称性(式(10)),表 1只给出积分权的前半部分。由式(9)和式(10)可知,当N=1时积分权系数无法优化,故在表 1中未列出。
|
|
表 1 GLL数值求积优化权系数 |
利用平面波分析方法[36, 47],可定量给出OSEM的数值频散与稳定性。一方面,在相同网格采样条件下S波的数值频散往往大于P波[16];另一方面,S波波长小于P波。因此在空间网格一定的条件下,S波的采样率(一个波长内采样点数)大于P波。综合这两方面原因,在数值频散分析时常只需分析S波的数值频散。假设式(1)的平面波简谐解为
| $ \boldsymbol{U}_{j}=\left(\begin{array}{c} \boldsymbol{U}_{j}^{x} \\ \boldsymbol{U}_{j}^{z} \end{array}\right)=\left(\begin{array}{l} A_{j} \\ B_{j} \end{array}\right) \exp \left(\mathrm{i} \boldsymbol{k} \cdot \boldsymbol{x}_{j}-\mathrm{i} \omega t\right) $ | (11) |
式中:下标j表示空间任意网格节点编号;Aj、Bj为任意常数;k为波数;ω为圆频率。假设无限空间被离散成无穷多个正方形单元[47],离散式(7)中的时间微分采用的是二阶中心差分[48],将式(11)代入式(7),有关数值频散的分析可退化成求解以下一般特征值问题
| $ \varLambda\left[\begin{array}{cc} \widetilde{\boldsymbol{M}} & \\ & \widetilde{\boldsymbol{M}} \end{array}\right] \widetilde{\boldsymbol{U}}=\left[\begin{array}{ll} \boldsymbol{K}_{1} & \boldsymbol{K}_{2} \\ \boldsymbol{K}_{3} & \boldsymbol{K}_{4} \end{array}\right] \widetilde{\boldsymbol{U}} $ | (12) |
式中:Λ为待求解的特征值;
| $ \frac{V_{\mathrm{S}}^{\mathrm{num}}}{V_{\mathrm{S}}}=\frac{r}{{\rm{ \mathsf{ π} }} s q} \sin ^{-1}\left(\frac{q}{2} \sqrt{\varLambda}\right) $ | (13) |
选择在1附近且随采样率连续变化的频散值即可获得S波数值频散[49]。式中:VSnum、VS分别为S波的数值速度和物理速度;s为采样率的倒数;r为波速比;
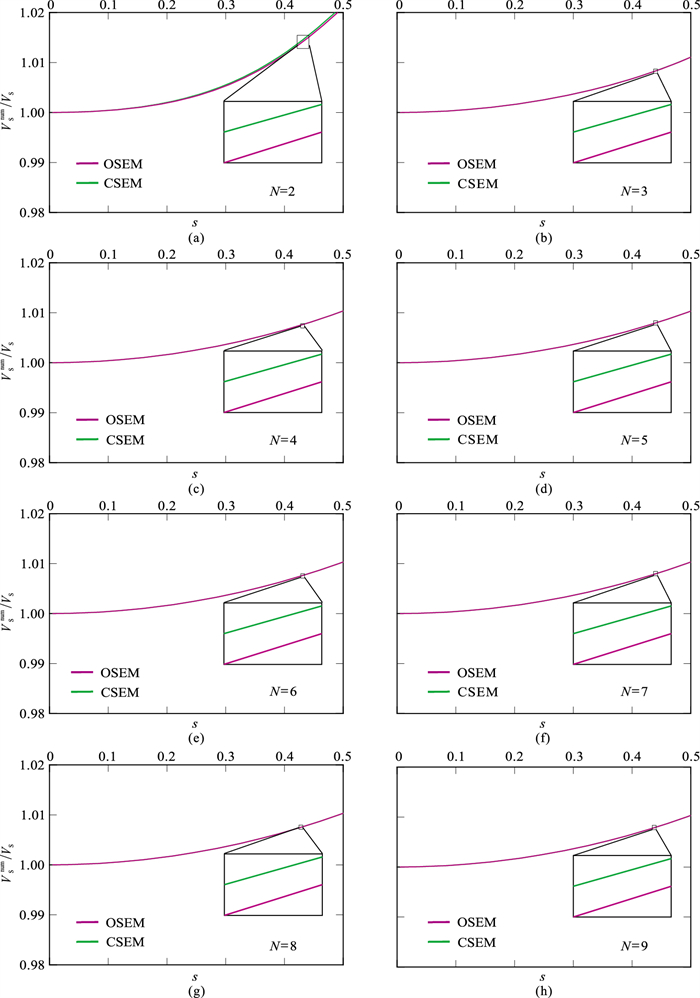
通过式(13)可计算出S波数值频散结果(图 1)。由于SEM数值频散与波传播方向几乎无关[47, 50],图 1展示q=0.25(保证2~9阶时数值格式稳定)时地震波沿与水平方向成30°方向上传播的数值频散。值得指出的是,图 1中数值速度大于物理速度,这种现象由空间离散和时间离散共同决定。
|
图 1 OSEM模拟地震波传播S波的数值频散 (a)~(h)对应于空间插值阶数分别为2~9时的数值频散曲线;局部放大图展示OSEM和CSEM局部频散特征;S波传播方向与水平方向成30°,库朗数为0.25 |
从图 1还可看出,OSEM与传统SEM总体一致,都表现出弱频散特点[44]。图 1a显示N=2时OSEM的数值频散明显小于CSEM,当空间插值阶数增加时,OSEM的数值频散与CSEM差别变小。该现象的主要原因在于,随着插值阶数的增加,优化式(8)对数值积分的贡献减弱。从图 1的局部放大图可见OSEM的数值频散小于CSEM,表明本文积分优化策略能提升SEM地震波模拟的精度。
由式(13)可知,为了保证OSEM迭代稳定,式(12)中的特征值应满足
| $ \left|\frac{q}{2} \sqrt{\varLambda}\right| \leqslant 1 $ | (14) |
对于所有特征值,在式(14)的限定条件下,q能取到的最大值即为OSEM的稳定限。根据式(12)和式(14),得到的OSEM稳定限如表 2所示。便于对比,表 2也列出了CSEM的稳定限。可见当插值阶数为2或3时,OSEM的稳定限略小于CSEM,两者的相对差别仅约为5/10000。当插值阶数大于3时,OSEM与CSEM的稳定限几乎无差别。
|
|
表 2 空间插值阶数为2~9时OSEM和CSEM的稳定限 |
选择如图 2所示的均匀介质模型用于检验OSEM地震波模拟的精度。模型尺寸为2000m×1000m,离散为边长为10m的正方形单元。介质的P波、S波速度、密度参数如图中所示。一个垂直集中力源(同时激发纵波和横波)位于(1000m,50m),其震源时间函数是主频为20Hz的Ricker子波;两个接收器R1和R2分别位于(1500m,0)和(1800m,0)处。为了防止边界截断而引起的虚假反射,在模型的左、右和下边界选用二阶位移形式的PML吸收边界条件(厚度为200m)接收反射波[16],模型上界面为自由地表。模拟时长为1s。为了减少时间离散误差,时间步长设定为0.05ms。

|
图 2 用于检验OSEM的数值精度的均匀介质模型 震源位于(1000m,50m);两接收器分列于(1500m,0)和(1800m,0) |
为了定量评估误差大小,定义误差的无穷范数max=‖u-ur‖∞和总量sum=
|
|
表 3 OSEM和CSEM模拟均匀介质中地震波传播的误差 |
从表 3可知OSEM和CSEM都能较精确模拟地震波传播,当插值阶数大于2时,OSEM和CSEM的最大相对误差均小于1%。虽然阶数为4~8时,OSEM计算得到的R1处相对误差的最大值大于CSEM,但两者的相对差别也只在1.0e-5左右,这种较小差别可能是由计算机浮点误差或时间迭代误差累积导致。对于其他情况,OSEM的误差总体上明显小于CSEM。
均匀模型中的数值测试结果表明,相比于CSEM,OSEM总体上能有效提升地震波模拟的计算精度。值得指出的是,OSEM和CSEM的差别仅在积分权重,因此只用修改CSEM代码中的积分权重值从而获得OSEM;在实际计算地震波场时,OSEM的计算时间和内存消耗量与CSEM一致。
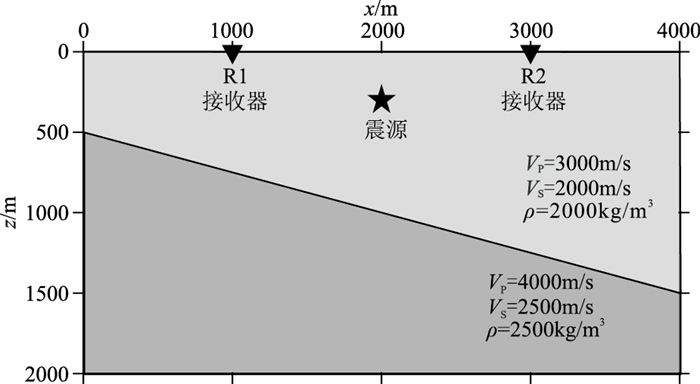
4.2 倾斜界面模型为了检验OSEM在具有非规则界面模型中的地震波模拟精度,设计了图 3所示的倾斜界面模型。模型尺寸为4000m×2000m。采用非结构化网格离散该模型,网格单元的平均尺寸为50m。倾斜界面上、下介质的P波和S波速度、密度如图中所示。一个爆炸震源(只激发纵波)位于(2000m,300m)处,其震源时间函数是主频为15Hz的Ricker子波。模型左、右和下边界设置20个单元厚度的PML吸收边界层,上界面为自由地表边界。两个接收器R1和R2分别位于(1000m,0)和(3000m,0)处。OSEM采用7阶空间插值,时间离散步长为0.1ms;参考解由10阶CSEM采用0.05ms的时间步长计算得到。
|
图 3 倾斜界面模型 震源位于(2000m,300m),接收器R1和R2分列于(1000m,0)和(3000m,0) |
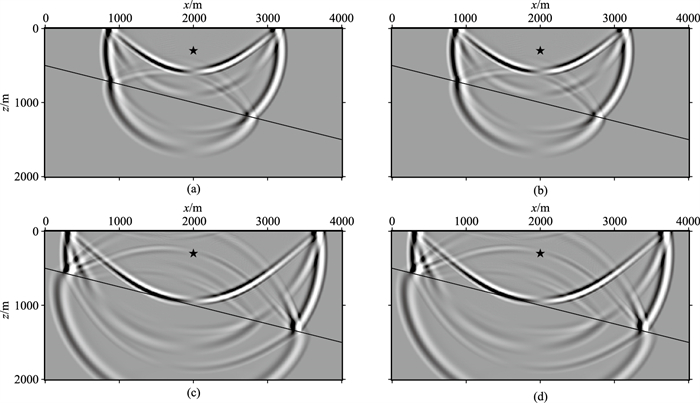
从图 4所示的位移水平分量的波场快照可见:当t=0.42s时,由于模型存在分层界面,在上层介质中除了直达波、地表反射波和转换波以外,还可看到界面的反射波,在下层介质中可看到透射P波、转换的S波(图 4a和图 4b);当t=0.60s时,由于地表反射波和转换波到达倾斜界面而进一步透射和反射,以至于图 4c和图 4d中,波场成分更复杂。从该图还可看出OSEM计算结果(图 4a和图 4c)与CSEM计算结果(图 4b和图 4d)无明显差别。
|
图 4 倾斜界面模型中地震波场快照 (a)、(b)t=0.42s时的波场快照;(c)、(d)t=0.60s时的波场快照;(a)、(c)OSEM计算得到;(b)、(d)CSEM计算得到 |
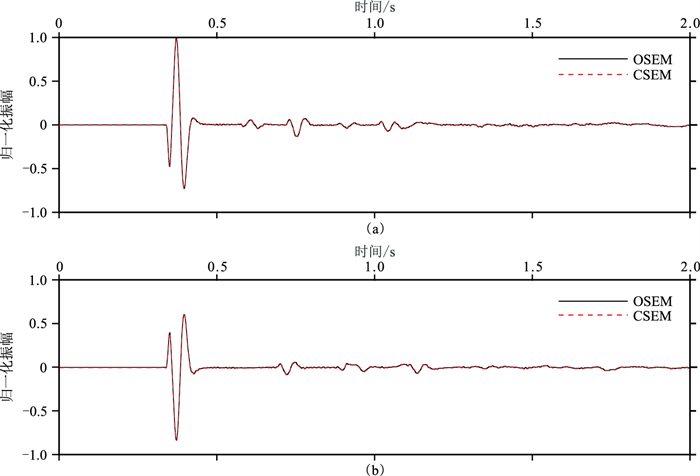
图 5显示的是R1和R2两处合成波形记录的水平分量。观察该图,除了较强的直达波以外,还可看到较强的反射和多次反射震相。从其中的合成波形也可看出,OSEM计算的波形(蓝线)与CSEM计算的波形(红色虚线)高度一致。定量对比R1与R2两处最大波形误差,发现OSEM计算波形的水平分量和垂直分量误差均小于CSEM的,最大相对误差降低了约0.3%。说明OSEM算法的精度略高于CSEM。
|
图 5 倾斜界面模型中接收器记录的波形 (a)R1处波形;(b)R2处波形 |
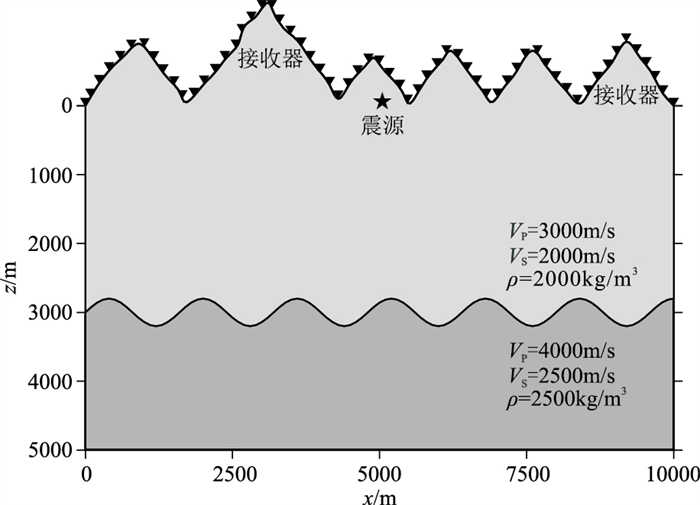
为了检验OSEM在复杂起伏介质中的模拟精度,设计了图 6所示的起伏界面模型。起伏地表的最大高程为1500m,模型水平尺度为10000m,最大深度为5000m。模型内存在由正弦函数刻画的分界面,且离散为平均单元尺寸为50m的网格,空间插值阶数为5阶。模型左、右和下边界设置20个单元厚度的PML吸收边界层,上界面为自由地表边界。分界面上、下两层介质参数同第二个算例。起伏地表之上几乎等距离分布有299个接收器,为了方便显示,图 6中展示是稀疏提取后的接收器分布。一个爆炸震源(只激发纵波)位于(5000m,100m)处,其震源时间函数是主频为15Hz的Ricker子波。
|
图 6 起伏界面模型 起伏地表最大高程为1500m,模型内分界面形状是正弦函数震源位于(2000m,100m),接收器几乎等距分布于起伏地表 |
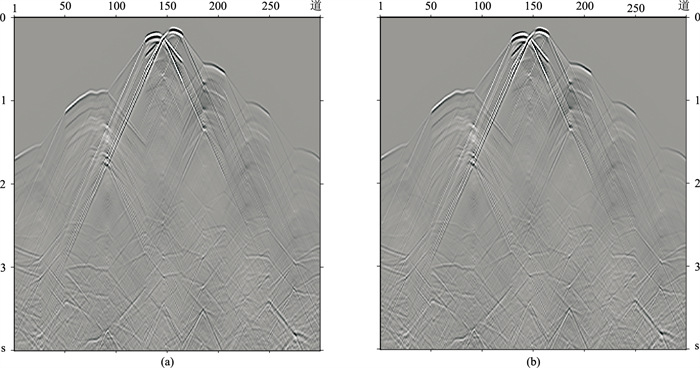
模拟结果图 7显示的是OSEM和CSEM两种方法合成位移水平分量的共炮记录。从该共炮记录中可看出明显的直达波同相轴。在2s以下,来自模型内起伏界面的反射波显得较明显。对比图 7a与图 7b可知,OSEM与CSEM模拟结果几乎一致。但对比所有接收器的误差总和,发现OSEM比CSEM的约小3%。显然,OSEM在复杂模型中的计算精度也高于CSEM。
|
图 7 OSEM(a)和CSEM(b)合成共炮记录 |
针对传统SEM数值积分精度上存在的不足,通过构造关于数值积分的误差函数,采用共轭梯度方法优化数值积分的积分权,最终提升SEM中GLL数值积分的精度,从而提升SEM的地震波模拟精度。数值频散分析证实了OSEM比CSEM更具有弱频散的特点。数值算例表明,OSEM精度总体上高于CSEM。值得指出的是,本文发展的OSEM只优化了CSEM的数值求积公式,而未改变CSEM对边界条件的适应性,因此OSEM与CSEM一样能方便地对各类边界条件(如PML吸收边界条件[30]、透射边界条件[52]和固液耦合边界条件[30]等)进行数值离散。
构造FDM优化格式提升其地震波数值模拟精度较为常见,但优化的FEM和SEM较少。虽然本文通过优化数值积分,总体上将SEM的精度提升约3%,提升幅度较小,但本文贡献在于提出了可构造优化数值积分格式提升FEM或SEM的数值精度,这为FEM或SEM的优化提供了新思路。
此外,在基于Chebyshev正交多项式的SEM(Chebyshev-SEM)中,由于Chebyshev多项式是关于加权因子
| [1] |
TROMP J, TAPE C, LIU Q Y. Seismic tomography, adjoint methods, time reversal and banana-doughnut kernels[J]. Geophysical Journal International, 2005, 160(1): 195-216. |
| [2] |
TAPE C, LIU Q Y, MAGGI A, et al. Adjoint tomography of the southern California crust[J]. Science, 2009, 325(5943): 988-992. DOI:10.1126/science.1175298 |
| [3] |
LEI W J, RUAN Y Y, BOZDA E, et al. Global adjoint tomography-model GLAD-M25[J]. Geophysical Journal International, 2020, 223(1): 1-21. DOI:10.1093/gji/ggaa253 |
| [4] |
曲英铭, 魏哲枫, 刘畅, 等. 面向高陡构造的黏声棱柱波逆时偏移[J]. 石油地球物理勘探, 2020, 55(4): 793-803. QU Yingming, WEI Zhefeng, LIU Chang, et al. Visco-acoustic reverse time migration of prismatic wave for steeply dipped structures[J]. Oil Geophysical Prospecting, 2020, 55(4): 793-803. |
| [5] |
SHRAGGE J. Reverse time migration from topography[J]. Geophysics, 2014, 79(4): S141-S152. DOI:10.1190/geo2013-0405.1 |
| [6] |
LIU Q C, ZHANG J F, GAO H W. Reverse-time migration from rugged topography using irregular, unstructured mesh[J]. Geophysical Prospecting, 2017, 65(2): 453-466. DOI:10.1111/1365-2478.12415 |
| [7] |
MADARIAGA R. Dynamics of an expanding circular fault[J]. Bulletin of the Seismological Society of America, 1976, 66(3): 639-666. DOI:10.1785/BSSA0660030639 |
| [8] |
LIU Y. Optimal staggered-grid finite-difference schemes based on least squares for wave equation modeling[J]. Geophysical Journal International, 2014, 197(2): 1033-1047. DOI:10.1093/gji/ggu032 |
| [9] |
ZHANG J H, YAO Z X. Optimized finite-difference operator for broadband seismic wave modeling[J]. Geophysics, 2013, 78(1): A13-A18. DOI:10.1190/geo2012-0277.1 |
| [10] |
CHEN P, ZHAO L, JORDAN T H. Full 3D tomography for the crustal structure of the Los Angeles region[J]. Bulletin of the Seismological Society of America, 2007, 97(4): 1094-1120. DOI:10.1785/0120060222 |
| [11] |
TONG P, ZHAO D, YANG D, et al. Wave-equation-based travel-time seismic tomography-Part 1:method[J]. Solid Earth, 2014, 5(2): 1151-1168. DOI:10.5194/se-5-1151-2014 |
| [12] |
RAO Y, WANG Y H. Seismic waveform simulation with pseudo-orthogonal grids for irregular topogra-phic models[J]. Geophysical Journal International, 2013, 194(3): 1778-1788. DOI:10.1093/gji/ggt190 |
| [13] |
ZHAO Z C, CHEN J Y, LIU X B. Frequency-domain finite-difference elastic wave modeling in the presence of surface topography[J]. Pure and Applied Geophysics, 2020, 177(6): 2821-2839. DOI:10.1007/s00024-019-02402-1 |
| [14] |
LAN H Q, ZHANG Z J. Comparative study of the free-surface boundary condition in two-dimensional finite-difference elastic wave field simulation[J]. Journal of Geophysics and Engineering, 2011, 8(2): 275-286. DOI:10.1088/1742-2132/8/2/012 |
| [15] |
苏波, 李怀良, 刘少林, 等. 修正辛格式有限元法的地震波场模拟[J]. 地球物理学报, 2019, 62(4): 1440-1452. SU Bo, LI Huailiang, LIU Shaolin, et al. Modified symplectic scheme with finite element method for seismic wavefield modeling[J]. Chinese Journal of Geophysics, 2019, 62(4): 1440-1452. |
| [16] |
LIU S L, LI X F, WANG W S, et al. A mixed-grid finite element method with PML absorbing boundary conditions for seismic wave modeling[J]. Journal of Geophysics and Engineering, 2014, 11(5): 055009. DOI:10.1088/1742-2132/11/5/055009 |
| [17] |
CHEN J B, CHAO J. An average-derivative optimal scheme for modeling of the frequency-domain 3D elastic wave equation[J]. Geophysics, 2018, 83(4): T209-T234. DOI:10.1190/geo2017-0641.1 |
| [18] |
WANG Y F, LIANG W Q, NASHED Z, et al. Seismic modeling by optimizing regularized staggered-grid finite-difference operators using a time-space domain dispersion relationship preserving method[J]. Geophysics, 2014, 79(5): T277-T285. DOI:10.1190/geo2014-0078.1 |
| [19] |
LIU S L, LANG C, YANG H, et al. A developed nearly analytic discrete method for forward modeling in the frequency domain[J]. Journal of Applied Geophysics, 2018, 149: 25-34. DOI:10.1016/j.jappgeo.2017.12.007 |
| [20] |
刘少林, 李小凡, 汪文帅, 等. 最优化辛格式广义离散奇异核褶积微分算子地震波场模拟[J]. 地球物理学报, 2013, 56(7): 2452-2462. LIU Shaolin, LI Xiaofan, WANG Wenshuai, et al. Optimal symplectic scheme and generalized discrete convolutional differentiator for seismic wave modeling[J]. Chinese Journal of Geophysics, 2013, 56(7): 2452-2462. |
| [21] |
刘少林, 刘有山, 汪文帅, 等. 最优化广义离散Shannon奇异核褶积微分算子地震波场模拟[J]. 石油地球物理勘探, 2013, 48(3): 410-416. LIU Shaolin, LIU Youshan, WANG Wenshuai, et al. Optimal generalized Shannon singular kernel convolution differentiator in seismic wavefield modeling[J]. Oil Geophysical Prospecting, 2013, 48(3): 410-416. |
| [22] |
DE BASABE J D, SEN M K. A comparison of finite-difference and spectral-element methods for elastic wave propagation in media with a fluid-solid interface[J]. Geophysical Journal International, 2015, 200(1): 278-298. DOI:10.1093/gji/ggu389 |
| [23] |
YANG D H, TENG J W, ZHANG Z J, et al. A nearly analytic discrete method for acoustic and elastic wave equations in anisotropic media[J]. Bulletin of the Seismological Society of America, 2003, 93(2): 882-890. DOI:10.1785/0120020125 |
| [24] |
YANG D H, WANG L, DENG X Y. An explicit split-step algorithm of the implicit Adams method for solving 2-D acoustic and elastic wave equations[J]. Geophysical Journal International, 2010, 180(1): 291-310. DOI:10.1111/j.1365-246X.2009.04407.x |
| [25] |
WANG Y B, TAKENAKA H. SH-wavefield simulation for a laterally heterogeneous whole-earth model using the pseudospectral method[J]. Science China-Earth Sciences, 2011, 54(12): 1940-1947. DOI:10.1007/s11430-011-4244-8 |
| [26] |
龙桂华, 李小凡, 江东辉. 基于交错网格的Fourier伪谱微分矩阵算子的地震波场模拟GPU加速方案[J]. 地球物理学报, 2010, 53(12): 2964-2971. LONG Guihua, LI Xiaofan, JIANG Donghui. Accele-rating seismic modeling with staggered-grid Fourier pseudo-spectral differentiation matrix operator me-thod on graphics processing unit[J]. Chinese Journal of Geophysics, 2010, 53(12): 2964-2971. DOI:10.3969/j.issn.0001-5733.2010.12.020 |
| [27] |
COHEN G C. Higher-order Numerical Methods for Transient Wave Equation[M]. Heidelberg: Springer-Verlag, 2002.
|
| [28] |
谭文卓, 吴帮玉, 李博, 等. 梯形网格伪谱法地震波场模拟[J]. 石油地球物理勘探, 2020, 55(6): 1282-1291. TAN Wenzhuo, WU Bangyu, LI Bo, et al. Seismic wave simulation using a trapezoid grid pseudo-spectral mehod[J]. Oil Geophysical Prospecting, 2020, 55(6): 1282-1291. |
| [29] |
MULDER W A. Higher-order mass-lumped finite ele-ments for the wave equation[J]. Journal of Computational Acoustics, 2001, 9(2): 671-680. DOI:10.1142/S0218396X0100067X |
| [30] |
KOMATITSCH D, BARNES C, TROMP J. Wave propagation near a fluid-solid interface: a spectral-element approach[J]. Geophysics, 2000, 65(2): 623-631. DOI:10.1190/1.1444758 |
| [31] |
刘少林, 李小凡, 汪文帅, 等. Lax-Wendroff集中质量有限元法地震波场模拟[J]. 石油地球物理勘探, 2015, 50(5): 905-911, 924. LIU Shaolin, LI Xiaofan, WANG Wenshuai, et al. A Lax-Wendroff lumped mass finite element method for seismic simulations[J]. Oil Geophysical Prospecting, 2015, 50(5): 905-911, 924. |
| [32] |
MARFURT K J. Accuracy of finite-difference and finite-element modeling of the scalar and elastic wave equations[J]. Geophysics, 1984, 49(5): 533-549. DOI:10.1190/1.1441689 |
| [33] |
BIELAK J, GHATTAS O, KIM E J. Parallel octree-based finite element method for large-scale earthquake ground motion simulation[J]. Computer Modeling in Engineering & Sciences, 2005, 10(2): 99-112. |
| [34] |
WU S R. Lumped mass matrix in explicit finite element method for transient dynamics of elasticity[J]. Computer Methods in Applied Mechanics and Engineering, 2006, 195(44-47): 5983-5994. DOI:10.1016/j.cma.2005.10.008 |
| [35] |
刘有山, 滕吉文, 刘少林, 等. 稀疏存储的显式有限元三角网格地震波数值模拟及其PML吸收边界条件[J]. 地球物理学报, 2013, 56(9): 3085-3099. LIU Youshan, TENG Jiwen, LIU Shaolin, et al. Explicit finite element method with triangle meshes stored by spare format and its perfectly matched la-yers absorbing boundary condition[J]. Chinese Journal of Geophysics, 2013, 56(9): 3085-3099. |
| [36] |
刘少林, 李小凡, 刘有山, 等. 三角网格有限元法声波与弹性波模拟频散分析[J]. 地球物理学报, 2014, 57(8): 2620-2630. LIU Shaolin, LI Xiaofan, LIU Youshan, et al. Dispersion analysis of triangle-based finite element method for acoustic and elastic wave simulations[J]. Chinese Journal of Geophysics, 2014, 57(8): 2620-2630. |
| [37] |
ZHEBEL E, MINISINI S, KONONOV A, et al. A comparison of continuous mass-lumped finite elements with finite differences for 3-D wave propagation[J]. Geophysical Prospecting, 2014, 62(5): 1111-1125. DOI:10.1111/1365-2478.12138 |
| [38] |
FRIED I, MALKUS D S. Finite element mass matrix lumping by numerical integration with no convergence rate loss[J]. International Journal of Solids and Structures, 1975, 11(4): 461-466. DOI:10.1016/0020-7683(75)90081-5 |
| [39] |
MENG W J, FU L Y. Seismic wavefield simulation by a modified finite element method with a perfectly matched layer absorbing boundary[J]. Journal of Geophysics and Engineering, 2017, 14(4): 852-864. DOI:10.1088/1742-2140/aa6b31 |
| [40] |
KOMATITSCH D, VILOTTE J P. The spectral element method: an efficient tool to simulate the seismic response of 2D and 3D geological structures[J]. Bulletin of the Seismological Society of America, 1998, 88(2): 368-392. |
| [41] |
KOMATITSCH D, TROMP J. Introduction to the spectral element method for three-dimensional seismic wave propagation[J]. Geophysical Journal International, 1999, 139(3): 806-822. DOI:10.1046/j.1365-246x.1999.00967.x |
| [42] |
刘少林, 杨顶辉, 徐锡伟, 等. 模拟地震波传播的三维逐元并行谱元法[J]. 地球物理学报, 2021, 64(3): 993-1005. LIU Shaolin, YANG Dinghui, XU Xiwei, et al. Three-dimensional element-by-element parallel spectral-element method for seismic wave modeling[J]. Chinese Journal of Geophysics, 2021, 64(3): 993-1005. |
| [43] |
KOMATITSCH D, RITSEMA J, TROMP J. The spectral-element method, Beowulf computing, and global seismology[J]. Science, 2002, 298(5599): 1737-1742. DOI:10.1126/science.1076024 |
| [44] |
MAGNONI F, CASAROTTI E, MICHELINI A, et al. Spectral-element simulations of seismic waves generated by the 2009 L'Aquila Earthquake[J]. Bulletin of the Seismological Society of America, 2014, 104(1): 73-94. DOI:10.1785/0120130106 |
| [45] |
HESTENES M R, STIEFEL E. Methods of conjugate gradients for solving linear systems[J]. Journal of Research of the National Bureau of Standards, 1952, 49(6): 409-436. DOI:10.6028/jres.049.044 |
| [46] |
LIU S L, SUARDI I, YANG D H, et al. Teleseismic traveltime tomography of northern Sumatra[J]. Geophysical Research Letters, 2018, 45(24): 13231-13239. |
| [47] |
DE BASABE J D, SEN M K. Grid dispersion and stability criteria of some common finite-element methods for acoustic and elastic wave equations[J]. Geophy-sics, 2007, 72(6): T81-T95. |
| [48] |
LIU S L, YANG D H, LANG C, et al. Modified symplectic schemes with nearly-analytic discrete operators for acoustic wave simulations[J]. Computer Physics Communications, 2017, 213: 52-63. DOI:10.1016/j.cpc.2016.12.002 |
| [49] |
LIU T, SEN M K, HU T Y, et al. Dispersion analysis of the spectral element method using a triangular mesh[J]. Wave Motion, 2012, 49(4): 474-483. DOI:10.1016/j.wavemoti.2012.01.003 |
| [50] |
LIU S L, YANG D H, MA J. A modified symplectic PRK scheme for seismic wave modeling[J]. Compu-ters & Geosciences, 2017, 99: 28-36. |
| [51] |
DE HOOP A T. A modification of cagniard's method for solving seismic pulse problems[J]. Applied Scientific Research, Section B, 1960, 8(1): 349-356. DOI:10.1007/BF02920068 |
| [52] |
邢浩洁, 李鸿晶. 透射边界条件在波动谱元模拟中的实现: 二维波动[J]. 力学学报, 2017, 49(4): 894-906. XING Haojie, LI Hongjing. Implementation of multi-transmitting boundary condition for wave motion si-mulation by spectral element method: two dimension case[J]. Chinese Journal of Theoretical and Applied Mechanics, 2017, 49(4): 894-906. |
| [53] |
WANG X M, GEZA S, LIN W J. Some theoretical aspects of elastic wave modeling with a recently developed spectral element method[J]. Science in China Series G: Physics, Mechanics and Astronomy, 2007, 50(2): 185-207. DOI:10.1007/s11433-007-0022-1 |



 刘少林,北京市海淀区安宁庄路1号应急管理部国家自然灾害防治研究院,100085。Email:
刘少林,北京市海淀区安宁庄路1号应急管理部国家自然灾害防治研究院,100085。Email: 