品质因子Q值是描述地下介质吸收衰减的重要物理参数。可靠准确地估计出Q值,通过反Q滤波和Q偏移能提高地震资料分辨率[1-5]。此外,Q值还与储层孔隙度、裂缝发育程度和含流体性质等因素有关,因此Q值也可应用于储层预测、油藏描述和流体检测[6-8]。总之,准确地估计Q值在油气勘探开发中具有重要意义。
为了准确地描述地层的吸收衰减特性,大量的Q值估计方法被提出,如解析信号法[9-10]、谱比法[11]、质心频移法[12-14]、峰值频率法[15]、基于衰减和补偿的Q值分析方法[16]等。这些方法都有各自的适用条件和优缺点[11]。谱比法是现今很常用的Q值估计方法之一[17-18],它是通过线性拟合对数谱比值与频率之间的线性关系估计Q值,具有较高的理论计算精度,但当地震数据存在噪声时,其稳定性随噪声的增强而迅速降低,且Q值估计结果依赖所选取的计算频段[19-20]。为此,不少学者提出了相应的改进方法:曹思远等[21]提出对数谱根式法Q值反演,其精度和抗噪性都有所提高;Wang等[22]提出了对数谱面积差法,相较于传统谱比法增强了算法的稳定性;刘国昌等通过引入整形正则化算子稳定求解不同时刻的频谱比值[23],并通过线性拟合估计出Q值[24],提高了Q值估计的稳定性;冯玮等[25]提出在频率域和时间域通过匹配方法求取Q值,该方法避免了谱比法中的谱除及线性拟合过程,同时也省去在频率域估计功率谱的环节,并将时变相位包含的吸收衰减信息加入Q值估计中,有效地提高了Q值估计的抗噪性和精度。郭锐等[26]提出改进的Capon2D Q值估计方法,与常规谱比法相比,改进方法对高频噪声不敏感,兼具压制子波干涉的能力。Blias[27]采用最优化方法对传统谱比法作了改进,可更稳定地估计Q值;Sangwan等[28]通过非线性反演振幅谱比方法获得了稳定的Q值估计结果。
迄今为止,力求提高谱比法Q值估算的稳定性依然是Q值反演估算的重要研究内容。基于谱比法Q值估计原理基础,并参考加权质心频移法[29]的思路,本文提出加权谱比法Q值估计新方法。该方法首先以高斯函数对对数谱比值进行加权处理,然后借助最小二乘线性拟合实现Q值估计。模型分析和VSP实测数据应用结果表明,该方法不仅具有良好的Q估值稳定性,而且能够降低对频段选取的依赖性。
1 基本原理当地震波在地层中传播时,由于地层的非完全弹性,地震波会产生衰减。衰减过程可用Futterman常Q模型[30]表示
| $ A(f)=C \cdot A_{0}(f) \exp \left(-\frac{{\rm{ \mathsf{ π} }} f \Delta t}{Q}\right) $ | (1) |
式中:A0(f)为震源子波振幅,其中f为频率;A(f)为接收子波振幅谱;Δt为旅行时;C表示散射衰减,在整个地震频段内与频率无关,包括几何扩散、反射、透射等。
将A(f)与A0(f)相除并取对数,据式(1)可得
| $ \ln \frac{A(f)}{A_{0}(f)}=-\frac{{\rm{ \mathsf{ π} }} f \Delta t}{Q}+\ln C $ | (2) |
式(2)是关于频率的线性函数,可改写为
| $ L(f)=k f+b $ | (3) |
显然,式中:
基于式(3),在一定频段范围内做最小二乘线性拟合,目标函数如下
| $ J=\sum\limits_{i=1}^{m}\left[L\left(f_{i}\right)-k f_{i}-b\right]^{2} \rightarrow \min $ | (4) |
式中m为频点个数。由该式即可得到直线斜率k。
根据斜率与Q值关系,得到Q值估计公式
| $ Q=-\frac{{\rm{ \mathsf{ π} }} \Delta t}{k} $ | (5) |
上述估计Q值方法称为谱比法。
地震数据中含噪声时,谱比法稳定性差且估计结果依赖所选取频段。这是由于谱比法在做最小二乘法拟合直线时采用的是等权重法,导致其拟合结果受低频和高频区异常值影响较大。为了提高谱比法的稳定性,降低其对频段选取的依赖性,本文提出了加权谱比法估计Q值。
由于子波振幅谱低频成分和高频成分有效信号强度弱,更容易受噪声干扰,使远离主频成分的振幅谱信噪比较低[14, 24]。为了降低低信噪比信号的影响,Li等[29]提出加权质心频移法提高质心频移法估计Q值的稳定性。此方法选取高斯函数作为权重因子,其中高斯函数对应的峰值频率和方差分别为震源子波的质心频率和方差,这样在计算过程中可实现高信噪比信号的参与权重大、低信噪比信号的参与权重小。参考加权质心频移法思路,本文提出的加权谱比法在拟合直线时的权重因子同样选取高斯函数,其表达式为
| $ G(f)=\exp \left[-\frac{\left(f-f_{\mathrm{s}}\right)^{2}}{2 \sigma_{\mathrm{s}}^{2}}\right] $ | (6) |
式中:fs为峰值频率;σs2为方差。定义峰值频率和方差分别为震源子波质心频率和方差,即有
| $ f_{\mathrm{s}}=\frac{\int_{f_{\min }}^{f_{\max }} f A_{0}(f) \mathrm{d} f}{\int_{f_{\min }}^{f_{\max }} A_{0}(f) \mathrm{d} f} $ | (7) |
| $ \sigma_{\mathrm{s}}^{2}=\frac{\int_{f_{\min }}^{f_{\max }}\left(f-f_{\mathrm{s}}\right)^{2} A_{0}(f) \mathrm{d} f}{\int_{f_{\min }}^{f_{\max }} A_{0}(f) \mathrm{d} f} $ | (8) |
式中fmax、fmin分别为频率上限、下限。基于式(3)做最小二乘线性拟合时,加上权重因子,目标函数为
| $ J=\sum\limits_{i=1}^{m} G\left(f_{i}\right)\left[L\left(f_{i}\right)-k f_{i}-b\right]^{2} $ | (9) |
取∂J/∂k=0和∂J/∂b=0,可得下列方程组
| $ \begin{aligned} &\left[\begin{array}{cc} \sum\limits_{i=1}^{m} G\left(f_{i}\right) & \sum\limits_{i=1}^{m} G\left(f_{i}\right) f_{i} \\ \sum\limits_{i=1}^{m} G\left(f_{i}\right) f_{i} & \sum\limits_{i=1}^{m} G\left(f_{i}\right) f_{i}^{2} \end{array}\right]\left[\begin{array}{l} b \\ k \end{array}\right]\\ &\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\left[\begin{array}{c} \sum\limits_{i=1}^{m} G\left(f_{i}\right) L\left(f_{i}\right) \\ \sum\limits_{i=1}^{m} G\left(f_{i}\right) f_{i} L\left(f_{i}\right) \end{array}\right] \end{aligned} $ | (10) |
求解该式得到加权拟合直线斜率k。根据斜率可以估计出Q值,即
上述估计Q值的方法称为加权谱比法。
2 模型测试首先选用无噪声合成衰减地震记录(图 1)验证所提方法的有效性。在合成记录中震源子波分别选用主频为45Hz的Ricker子波和可控震源Klauder子波[31](低截频和高截频分别为5Hz和85Hz),置于合成记录150ms处;在频率域计算得到衰减后的接收子波频谱,然后反傅里叶变换得到时间域的衰减接收子波,位于合成记录450ms处。合成记录从左到右Q值分别为25、50、100、200。基于图 1合成地震记录,分别利用常规谱比法和加权谱比法做Q值估计。加权谱比法选取5~100Hz频段计算震源子波的质心频率和方差,用于构建高斯函数权重因子。在估计Q值时,两种方法频段同样选为5~100Hz,估计的Q值相对误差如图 2所示。
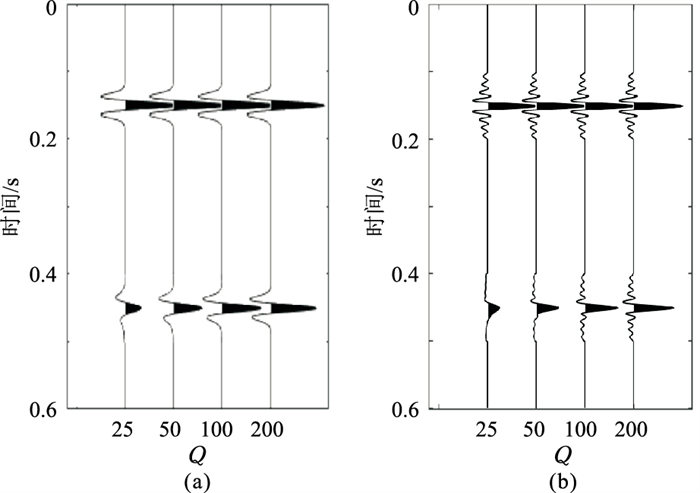
|
图 1 含衰减的Ricker子波(a)和Klauder子波(b)合成地震记录 |
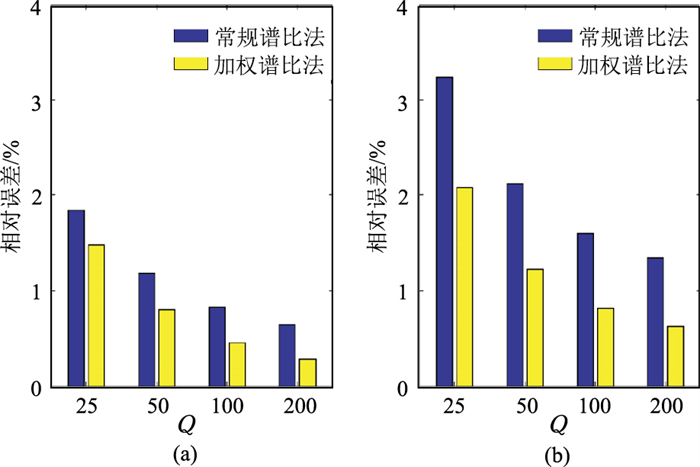
|
图 2 Ricker子波(a)和Klauder子波(b)的常规谱比法和加权谱比法Q值估计相对误差 |
从图 2可看出,不同子波在无噪声时两种方法估计结果相对误差都小于4%,表明两种方法都能较精确地估算Q值。此外,在不同Q值下加权谱比法相对误差都小于常规谱比法。测试结果表明:相较于常规谱比法,加权谱比法Q值精度更高。
由于实际地震资料中存在噪声,会影响Q值估计的稳定性。可利用含随机噪声合成地震数据对比分析常规谱比法与加权谱比法对噪声的敏感程度。每一道中加入10%随机噪声(震源子波最大振幅值10%),如图 3所示。
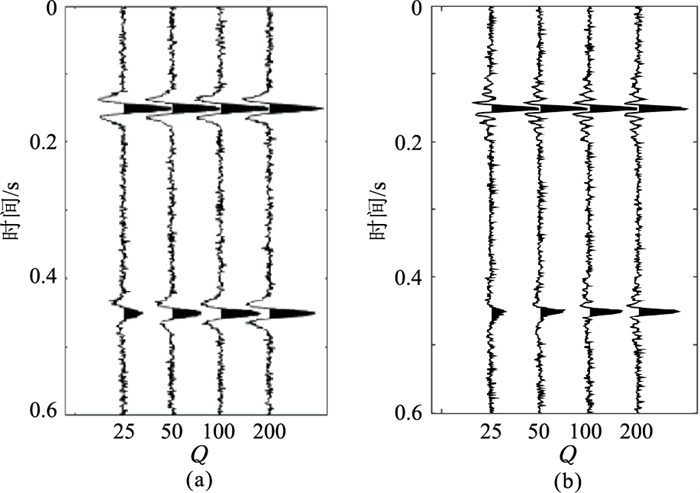
|
图 3 含10%随机噪声衰减的Ricker子波(a) 和Klauder子波(b)地震记录 |
分别以图 3a和图 3b第3道(Q=100)为例,选取频段5~100Hz,对比常规谱比法和加权谱比法Q值估计结果。绘出常规谱比法和加权谱比法拟合直线,并叠加理论曲线(Q=100)与实际对数谱比曲线(图 4)。从图 4a(震源子波对应Ricker子波)和图 4b(对应Klauder子波)中都可看出:实际对数谱比曲线(绿线)在噪声影响下存在扰动,且在低频端和高频端扰动表现得更剧烈,与无噪声情形的谱比曲线(黑线)差异较大。基于实际对数谱比曲线,常规谱比法和加权谱比法拟合的直线分别用蓝线和红线表示;可发现加权谱比法拟合直线与理论直线更接近,常规谱比法拟合结果与理论直线差异明显。
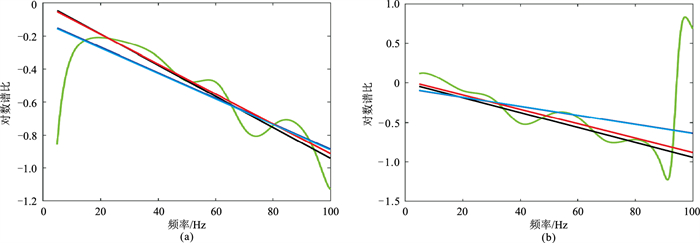
|
图 4 Ricker子波(a)和Klauder子波(b)的对数谱比曲线及不同方法拟合的直线 绿色:实际对数谱比曲线;黑色:理论Q值(Q=100)对应直线;蓝色:常规谱比法拟合直线;红色:加权谱比法拟合直线 |
通过拟合直线的斜率估计Q值。基于Ricker子波(图 4a)的常规谱比法估计的Q值为121,加权谱比法估计的Q值为104;基于Klauder子波(图 4b)的常规谱比法估计的Q值为163,加权谱比法估计的Q值为102。在不同子波类型下,加权谱比法结果都更接近理论值100。该测试结果表明,加权谱比法估计结果更接近真值,Q值估计稳定性明显好于常规谱比法,且不受子波形态影响。
随机噪声对地震数据的干扰具有随机性,通过多次试验,对常规谱比法与加权谱比法进行统计对比分析。基于图 3含噪声衰减地震记录,同样选取5~100Hz频段,进行2000次独立试验。每次试验重新生成随机噪声,将重新生成的随机噪声按震源子波最大振幅值10%的比例加入无噪声衰减地震记录中,从中估计Q值,从而得到2000个Q值估计结果,然后对其进行统计分析。
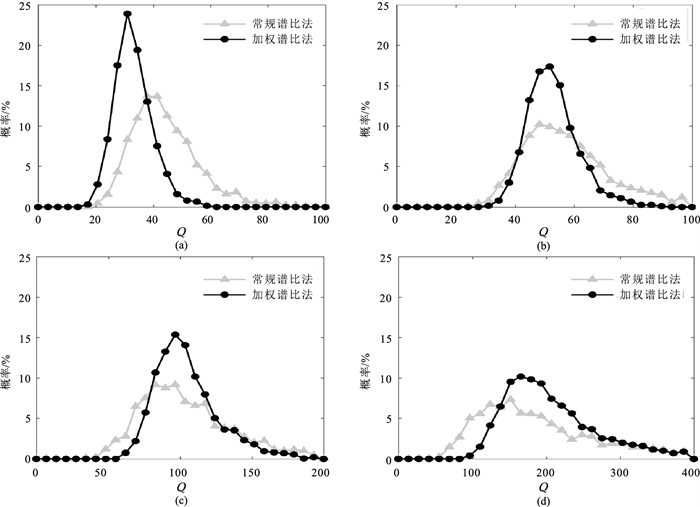
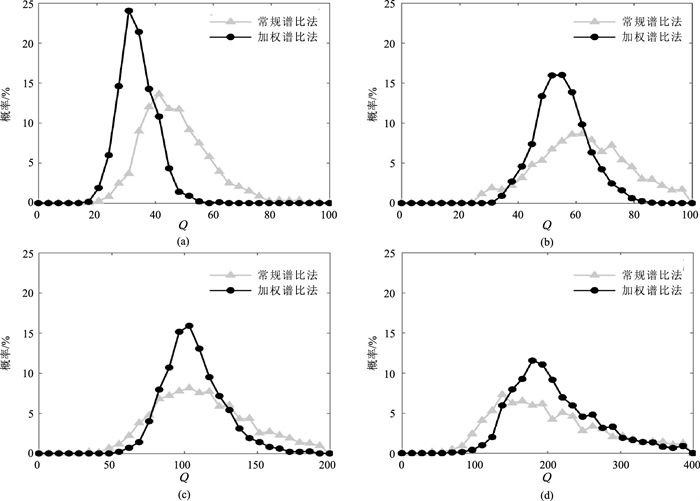
图 5和图 6分别为基于图 3a中Ricker子波和图 3b中Klauder子波估计的Q值概率分布图。从该概率分布图的形态看,加权谱比法聚焦性都明显好于常规谱比法,且其峰值对应的Q值更接近理论值。表 1为统计的均值μ和标准差σ,可见加权谱比法的均值更接近于理论值,标准差都更小。同时,从概率分布图和均值、标准差统计表中都可看出基于Ricker子波的概率分布特征与基于Klauder子波概率分布特征相似。该统计分析结果表明加权谱比法抗噪性更好,稳定性更强,同样适用于振幅谱为“门”形的地震子波。
|
图 5 基于Ricker子波估计的Q值概率分布 (a)Q=25;(b)Q=50;(c)Q=100;(d)Q=200 |
|
图 6 基于Klauder子波估计的Q值概率分布 (a)Q=25;(b)Q=50;(c)Q=100;(d)Q=200 |
|
|
表 1 估计Q值的均值μ及标准差σ |
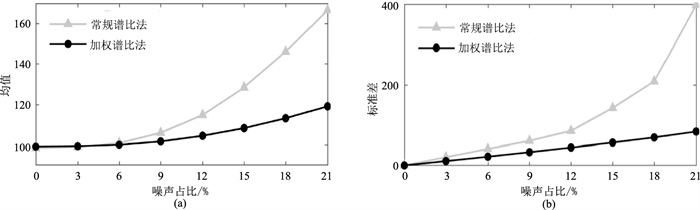
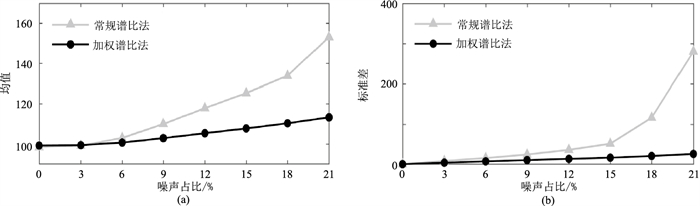
为分析不同等级噪声对常规谱比法和加权谱比法的影响,做了进一步测试。以图 1a和图 1b中第3道(Q=100)为例,加入不同等级的随机噪声,噪声占比的变化范围是0~21%。在5~100Hz频段内,进行2000次独立试验,在不同子波条件下两种方法估计的均值和标准差分别如图 7和图 8所示。从均值图(图 7a、图 8a)上可看出,噪声占比越低,Q值估计结果越精确。如在噪声占比为0时,两种方法估计结果都接近于理论值,对应的标准差为0。当噪声占比达到21%时,图 7中常规谱比法和加权谱比法估计的均值(图 7a)分别为169和120;图 8中常规谱比法的均值(图 8a)达到146,而和加权谱比法只有116。在不同等级噪声下,常规谱比法所得Q估值与理论值的差异都大于加权谱比法;且随着噪声逐渐增大,两种方法均值和标准差曲线斜率都逐渐增大,但常规谱比法斜率变化速率明显大于加权谱比法。也就是说,常规谱比法对噪声更敏感,即加权谱比法的抗噪声能力更强。
|
图 7 基于Ricker子波不同噪声条件下常规谱比法与加权谱比法估计Q值的均值(a)和标准差(b) |
|
图 8 基于Klauder子波不同噪声条件下常规谱比法与加权谱比法估计Q值的均值(a)和标准差(b) |
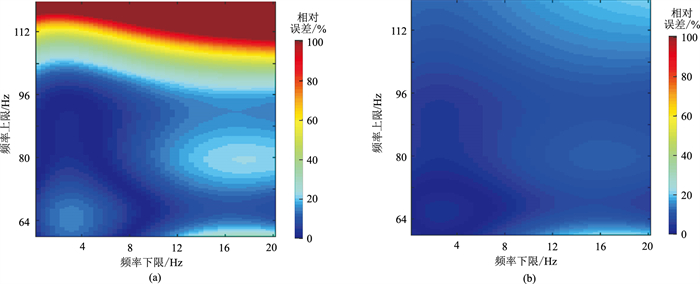
另外,由于实际地震资料普遍存在噪声,使Q估值的稳定性依赖于所选取频段。同样基于图 3a和图 3b中第3道(Q=100)含噪衰减地震记录,分别应用两种方法在不同频段内估计Q值,计算其相对误差(图 9和图 10)。将坐标横轴和纵轴对应设定为频段下限、上限,如坐标(5,90)对应的点即表示选择的频段为5~90Hz时Q估值的相对误差。从图 9a可看出,常规谱比法对频段的选取非常敏感,尤其是频段选取较宽时,会严重影响估计Q值的可靠性。如频段上限超过104Hz时,Q估值的相对误差大部分大于50%;选取的频段低截止频率越高,误差越大。然而,加权谱比法在选择相应的不同频段时,Q估值的相对误差都较小(图 9b)。当频段上限高达120Hz时,大部分Q估值的相对误差不超过30%;即使选取的积分频段为20~120Hz,其相对误差同样低于30%。加权谱比法的最大优势是在选取很宽频段时,Q估值的差异非常小,即稳定性较好。
|
图 9 基于Ricker子波不同频段的常规谱比法(a)和加权谱比法(b)估计Q值的相对误差 |
|
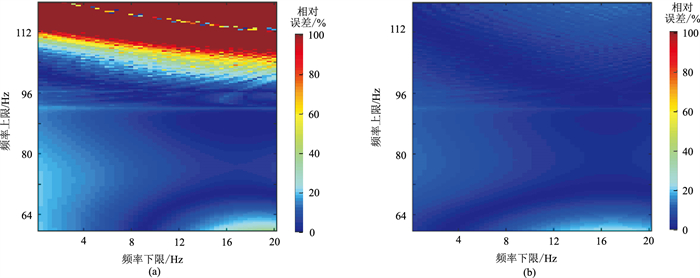
图 10 基于Klauder子波不同频段的常规谱比法(a)和加权谱比法(b)估计Q值的相对误差 |
比较图 9与图 10,可见在不同子波条件下两种Q值估算法表现出类似结果。该测试证实,加权谱比法对频段的依赖性明显弱于常规谱比法。
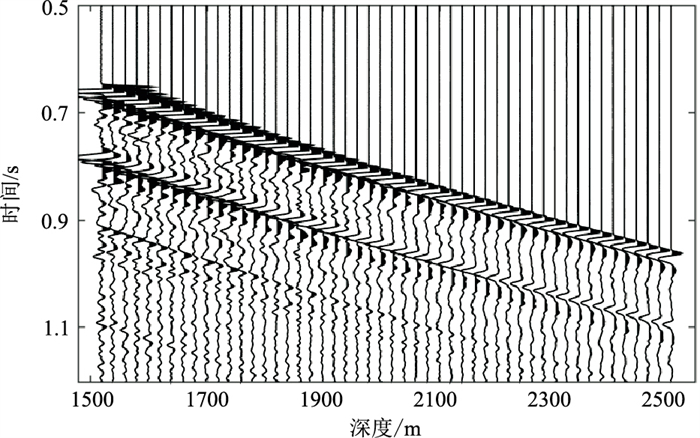
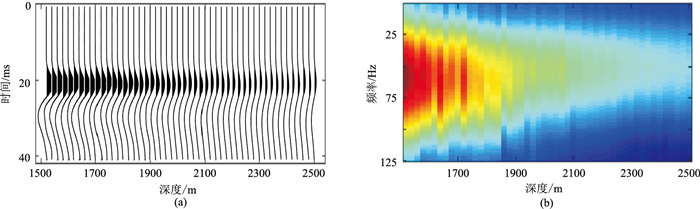
3 实际资料应用选用实际零偏VSP地震资料对比分析常规谱比法和加权谱比法的适用性。图 11为南海东部M油田实测零井源距VSP记录,采用气枪震源激发,检波器排列放置深度为1500~2500m,道间距为20m,总共51道。对原始零井源距VSP资料做波场分离得到下行波并从中截取直达初至波(图 12a)。图 12b为通过傅里叶变换得到的初至波振幅谱。在估计Q值过程中分别选取5~100Hz和10~90Hz频段用于对比。
|
图 11 M油田实际零偏VSP地震记录 |
|
图 12 VSP下行直达波初至(a)及其振幅谱(b) |
图 13是在不同频段内两种方法估计的Q值。从该图可看出,在相对较宽的频段(5~100Hz)内两种方法估计的Q值存在明显差异,常规谱比法(浅灰线)波动明显,稳定性较差;在较窄频段(10~90Hz)内两种方法估计的Q值的差异减小。

|
图 13 两种方法在5~100Hz(a)、10~90Hz(b)频段内的Q值估计结果 |
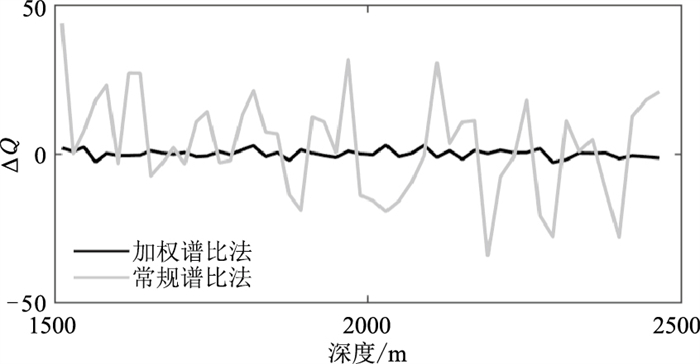
将两种方法在不同频段内估计的Q值相减,得到二者之差ΔQ(图 14)。从图中可看出,常规谱比法在不同频段内估计的ΔQ值差值明显大于加权谱比法,因其Q估算值受所选取频段范围的影响较大;加权谱比法在不同频段内估计的Q值几乎无变化,即稳定且可靠,受频段影响较小。实际VSP资料的应用效果再次证明了加权谱比法的实用性和可靠性。
|
图 14 不同频段内估计的ΔQ值 |
(1) 加权谱比法Q值估计新方法在无噪声干扰情况下,能更精确估计Q值,估计精度优于常规谱比法。
(2) 与常规谱比法相比,加权谱比法对噪声的敏感性减弱,对频段选取的依赖性较低,Q值估计结果更加稳定可靠。
| [1] |
WANG Y H. Inverse Q-filter for seismic resolution enhancement[J]. Geophysics, 2006, 71(3): V51-V60. DOI:10.1190/1.2192912 |
| [2] |
WANG S D, CHEN X H. Absorption-compensation method by L1-norm regularization[J]. Geophysics, 2014, 79(3): V107-V114. DOI:10.1190/geo2013-0206.1 |
| [3] |
WANG S D, SONG H J, YANG D F. Seismic attenuation compensation by Bayesian inversion[J]. Journal of Applied Geophysics, 2014, 111: 356-363. DOI:10.1016/j.jappgeo.2014.10.012 |
| [4] |
陈汉明, 周辉, 田玉昆. 分数阶拉普拉斯算子黏滞声波方程的最小二乘逆时偏移[J]. 石油地球物理勘探, 2020, 55(3): 616-626. CHEN Hanming, ZHOU Hui, TIAN Yukun. Least-squares reverse-time migration based on a fractional Laplacian viscoacoustic wave equation[J]. Oil Geophysical Prospecting, 2020, 55(3): 616-626. |
| [5] |
刘金涛, 王孝, 王小卫, 等. 全局约束反演多道吸收补偿方法[J]. 石油地球物理勘探, 2021, 56(2): 273-282. LIU Jintao, WANG Xiao, WANG Xiaowei, et al. Multi-channel absorption compensation method based on global constrained inversion[J]. Oil Geophysical Prospecting, 2021, 56(2): 273-282. |
| [6] |
MITTET R, SOLLIE R, HOKSTAD K. Prestack depth migration with compensation for absorption and dispersion[J]. Geophysics, 1995, 60(5): 1485-1494. DOI:10.1190/1.1443882 |
| [7] |
HICKS G J, PRATT R G. Reflection waveform inversion using local descent methods: Estimating attenuation and velocity over a gas-sand deposit[J]. Geophysics, 2001, 66(2): 598-612. DOI:10.1190/1.1444951 |
| [8] |
WINKLER K W, NUR A. Seismic attenuation: effects of pore fluids and frictional sliding[J]. Geophysics, 1982, 47(1): 1-15. DOI:10.1190/1.1441276 |
| [9] |
ENGELHARD L. Determination of seismic-wave attenuation by complex trace analysis[J]. Geophysical Journal International, 1996, 125(2): 608-622. DOI:10.1111/j.1365-246X.1996.tb00023.x |
| [10] |
刘洋, 李向阳, 杨东方. 基于线性分解的解析信号法估算品质因子Q[J]. 石油地球物理勘探, 2018, 53(4): 784-790. LIU Yang, LI Xiangyang, YANG Dongfang. Quality factor Q estimation with complex trace analysis based on linear decomposition[J]. Oil Geophysical Prospecting, 2018, 53(4): 784-790. |
| [11] |
TONN R. The determination of the seismic quality factor Q from VSP data: a comparison of different computational methods[J]. Geophysical Prospecting, 1991, 39(1): 1-27. DOI:10.1111/j.1365-2478.1991.tb00298.x |
| [12] |
QUAN Y L, HARRIS J M. Seismic attenuation tomography using the frequency shift method[J]. Geophysics, 1997, 62(3): 895-905. DOI:10.1190/1.1444197 |
| [13] |
杨登锋, 秦成岗, 汪瑞良, 等. 能量谱质心频移法Q值估计[J]. 石油地球物理勘探, 2016, 51(5): 863-867. YANG Dengfeng, QIN Chenggang, WANG Ruiliang, et al. Q factor estimation based on the centroid frequency shift of energy spectrum[J]. Oil Geophysical Prospecting, 2016, 51(5): 863-867. |
| [14] |
YANG D F, LIU J, LI J N, et al. Q-factor estimation using bisection algorithm with power spectrum[J]. Geophysics, 2020, 85(3): V233-V248. DOI:10.1190/geo2018-0403.1 |
| [15] |
ZHANG C J, ULRYCH T J. Estimation of quality factors from CMP records[J]. Geophysics, 2002, 67(5): 1542-1547. DOI:10.1190/1.1512799 |
| [16] |
WANG Y H. Stable Q analysis on vertical seismic profiling data[J]. Geophysics, 2014, 79(4): D217-D225. DOI:10.1190/geo2013-0273.1 |
| [17] |
DASGUPTA R, CLARK R A. Estimation of Q from surface seismic reflection data[J]. Geophysics, 1998, 63(6): 2120-2128. DOI:10.1190/1.1444505 |
| [18] |
REINE C, VAN DER BAAN M, CLARK R A. The robustness of seismic attenuation measurements using fixed and variable-window time-frequency transforms[J]. Geophysics, 2009, 74(2): WA123-WA135. DOI:10.1190/1.3043726 |
| [19] |
DE CASTRO NUNES B I, DE MEDEIROS W E, DO NASCIMENTO A F, et al. Estimating quality factor from surface seismic data: a comparison of current approaches[J]. Journal of Applied Geophysics, 2011, 75(2): 161-170. DOI:10.1016/j.jappgeo.2011.07.003 |
| [20] |
PICOTTI S, CARCIONE J. Estimating seismic atte-nuation (Q) in the presence of random noise[J]. Journal of Seismic Exploration, 2006, 15(1): 165-181. |
| [21] |
曹思远, 谭佳, 高明, 等. 对数谱根式法Q值反演[J]. 石油地球物理勘探, 2014, 49(1): 161-166. CAO Siyuan, TAN Jia, GAO Ming, et al. Seismic Q estimation with logarithmic spectrum equation root[J]. Oil Geophysical Prospecting, 2014, 49(1): 161-166. |
| [22] |
WANG S D, YANG D F, LI J N, et al. Q factor estimation based on the method of logarithmic spectral area difference[J]. Geophysics, 2015, 80(6): V157-V171. DOI:10.1190/geo2014-0257.1 |
| [23] |
刘国昌, 陈小宏, 杜婧, 等. 基于整形正则化和S变换的Q值估计方法[J]. 石油地球物理勘探, 2011, 46(3): 417-422. LIU Guochang, CHEN Xiaohong, DU Jing, et al. Seismic Q estimation using S-transform with regularized inversion[J]. Oil Geophysical Prospecting, 2011, 46(3): 417-422. |
| [24] |
LIU G C, CHEN X H, RAO Y. Seismic quality factor estimation using frequency-dependent linear fitting[J]. Journal of Applied Geophysics, 2018, 156: 1-8. DOI:10.1016/j.jappgeo.2018.05.007 |
| [25] |
冯玮, 胡天跃, 常丁月, 等. 基于时变子波的品质因子估计[J]. 石油地球物理勘探, 2018, 53(1): 136-146. FENG Wei, HU Tianyue, CHANG Dingyue, et al. Quality factor Q estimation based on time-varying wavelet[J]. Oil Geophysical Prospecting, 2018, 53(1): 136-146. |
| [26] |
郭锐, 林鹤, 王前, 等. 改进的Capon2D Q值估计方法及其应用[J]. 石油地球物理勘探, 2018, 53(增刊2): 182-188. GUO Rui, LIN He, WANG Qian, et al. Modified Capon2D Q value estimation method and its application[J]. Oil Geophysical Prospecting, 2018, 53(S2): 182-188. |
| [27] |
BLIAS E. Accurate interval Q-factor estimation from VSP data[J]. Geophysics, 2012, 77(3): WA149-WA156. DOI:10.1190/geo2011-0270.1 |
| [28] |
SANGWAN P, KUMAR D, CHAKRABORTY S, et al. Nonlinear approach to spectral ratio method for estimation of seismic quality factor from VSP data[J]. Journal of Applied Geophysics, 2019, 167: 33-41. DOI:10.1016/j.jappgeo.2019.04.001 |
| [29] |
LI J N, WANG S X, YANG D F. An improved Q estimation approach: the weighted centroid frequency shift method[J]. Journal of Geophysics and Engineering, 2016, 13(3): 399-411. DOI:10.1088/1742-2132/13/3/399 |
| [30] |
FUTTERMAN W I. Dispersive body waves[J]. Journal of Geophysical Research, 1962, 67(13): 5279-5291. DOI:10.1029/JZ067i013p05279 |
| [31] |
张海燕, 李庆忠. 几种常用解析子波的特性分析[J]. 石油地球物理勘探, 2010, 7(6): 651-657. ZHANG Haiyan, LI Qingzhong. Analysis on feature of common analytic wavelets[J]. Oil Geophysical Prospecting, 2010, 7(6): 651-657. |



 杨登锋,广东省深圳市南山区后海滨路(深圳湾段)3168号中海油大厦A座2005室,518000。Email:
杨登锋,广东省深圳市南山区后海滨路(深圳湾段)3168号中海油大厦A座2005室,518000。Email: