② 中海石油(中国)有限公司海南分公司,海南海口 570100;
③ 中国石油大学(华东)地球科学与技术学院,山东青岛 266580
② Hainan Branch, China National Offshore Oil Corporation (CNOOC), Haikou, Hainan 570100, China;
③ School of Geoscience, China University of Petroleum (East China), Qingdao, Shandong 266580, China
地震波从地下岩层反射回地表后,会在地表面发生下行反射,形成多次波。受海水表面强反射系数的影响,多次波是海洋地震数据中常见的干扰,对其压制是地震数据处理中的一项重要内容。Radon变换是业界多次波压制最常用的有效手段之一,同时也被广泛地应用于地震数据重建、波场分离、速度分析等领域。
抛物线Radon变换由Hampson[1]引入二维地震数据处理。Radon变换假设正常时差校正后的共中心点(CMP)道集中一次波是能被校正平的,剩余时差为零。由于对多次波做校正所用的速度是深层一次波速度,动校速度偏大,导致同相轴校正不足,产生一定的剩余时差。此时多次波时距曲线的形状由双曲线转变为抛物线,抛物线Radon变换可将CMP道集中动校平的一次波和弯曲的多次波变换到Radon域,该域中横坐标为剩余时差。由于一次波与多次波剩余时差存在差异,二者在变换域成为分离开的聚焦点。为保护有效波能量,压制多次波的常用方法是在Radon域切除一次波,并将多次波变换回时空域,得到多次波模型,之后将其从原始数据中消除。
但常规Radon变换算法受到采集空间和时间有限、离散采样等因素的影响,存在假频、分辨率低等问题,致使在变换域无法彻底分离多次波与一次波;此外,该变换只是将数据沿抛物线路径进行叠加求和,并未考虑同相轴振幅的横向变化,使分离得到的多次波与原数据中多次波的振幅存在一定差异,这些都会影响最终压制效果。
在提高变换域内一次波与多次波的可分离性方面,很多学者做了研究。如Sacchi等先后提出基于柯西范数概率密度函数的Bayes理论的高分辨率算法[2]及基于迭代共轭梯度逐次更新阻尼参数的高分辨率算法[3],Herrmann等[4]提出基于低频约束的去假频高分辨率Radon变换算法,Trad等[5]综合分析了稀疏Radon变换的算法,Chen等[6]提出了能保护地震数据弱信号、去除假频的基于地震数据特定频率解约束的非迭代高分辨率算法。近年来,也有学者提出频率—时间混合域提高分辨率的迭代收缩算法。Lu[7]提出的基于加速稀疏时不变的频率—时间混合域迭代收缩高分辨率Radon变换算法,在未显著增加计算时间的情况下,有效提高了分辨率;薛亚茹等[8]研究了基于加权迭代软阈值的频率—时间混合域高分辨率Radon变换算法;罗腾腾等[9]基于频率—时间混合域的高分辨率Radon变换算法对绕射波进行分离与成像。
在提高Radon变换的保幅性方面,也有很多学者做了相关研究。Nowak等[10]、薛昭等[11]分别分析了Radon变换及其去噪方法的保幅性;薛亚茹等[12-13]、Vyas等[14]分别给出了基于不同正交多项式的高阶Radon变换算法,增加了描述振幅变化的梯度和曲率信息,拓展了传统Radon变换算法,使其在具有振幅变化特征的数据处理中具有更高准确度;Wang等[15]给出一种能模拟道集中振幅变化的Radon变换算法,也取得了较好的保幅效果。
对于二维数据和部分三维窄方位地震数据,应用二维Radon变换方法可取得较好的效果。随着地震采集技术的进步,由于宽方位采集具有方位宽、照明充分等优势,越来越受到人们的青睐。与窄方位数据相比,宽方位地震数据存在随方位变化的特点,相同或相近炮检距、但不同方位的地震道,受不同方向地层倾角或地层各向异性的影响,可能存在较大的时差差异;当把动校正后的地震数据,按照标量炮检距从小到大的顺序排列,形成一个与二维情形类似的三维共中心点道集(Common-Cell Gathers)时,不同方位的数据由于存在一定的时差差异,相邻道时差变化剧烈,呈现同相轴样点跳动的特点,常规二维抛物线Radon算法无法精确表征该数据,更难以有效分离有效波与干扰波,即压制效果差。三维共中心点道集可分别按照x和y两个方向的炮检距大小,即矢量炮检距进行排列,形成由不同方位的小道集组成的共中心点道集;该三维共中心点道集可更直观地描述三维波场的传播;但不同方位道集形态可能存在较大差异,加之拖缆漂移、不同方位地层特性差异等的影响,不同方位的多次波时差会存在差异。显然,利用相同参数的二维变换对小道集进行多次波压制也无法取得较好效果。
为此,需要考虑三维地震波场的传播特征,利用三维Radon理论精确表征不同方位的数据,以更好地对其进行处理。
三维Radon算法考虑了波场三维传播的特点,利用x和y两个方向的曲率参数,在Radon域对动校正后的三维共中心点道集进行表征,可对时空域的三维地震数据做较好描述。基于三维地震波场传播的特点,很多学者对三维Radon算法开展了较深入的研究。Donati等[16]利用三维τ-p变换对地震数据进行插值重建;Hugonnet等[17-18]给出三维抛物线Radon变换方法并应用于宽方位地震数据处理。但常规三维变换方法在Radon域对宽方位地震数据进行表征仍存在一些与二维方法共性的问题,这缘于宽方位地震数据本身特点。如宽方位数据道集测线/炮线间距大,普通变换得到的结果存在严重的假频问题;可利用将低频运算的解作为约束的方法,或迭代阈值收缩的算法去假频,以提高分辨率。如Zhang等[19]提出一种加速三维稀疏时不变τ-p变换方法,即基于迭代收缩的高分辨率τ-p变换方法,并应用于三维叠前道集的插值重建;Cao等[20]给出基于匹配追踪的高分辨率三维τ-p变换方法,有效应对了空间假频,提高了分辨率,取得了较好插值效果。在保幅处理方面,同样可考虑利用正交多项式拟合表征地震数据的振幅。唐欢欢等[21]提出高阶高分辨率抛物线保幅Radon变换方法,并应用于三维地震数据重建;Wang等[22]也给出一种类似的三维保幅Radon变换数据重建方法。
本文系统阐述了三维Radon变换算法,并给出该变换的最小二乘解;为提高变换的分辨率,引入基于迭代阈值收缩的三维高分辨率算法;为提高算法的保幅性,引入正交多项式变换,并形成一种三维高精度保幅抛物线Radon变换算法。文中给出一套横向振幅变化的模拟数据,并基于最小二乘和高分辨率算法对其进行处理,分别对比了变换域、多次波压制后的结果,并给出了压制结果的一次波与真实一次波之间的差,表明该方法具有保幅性。最后给出海洋宽方位地震数据实例,进一步验证该方法兼具分辨率高且保幅的优势。
1 方法原理 1.1 三维抛物Radon变换原理二维抛物线Radon变换沿抛物线路径对地震数据进行求和,得到Radon域数据。类似地,三维抛物线Radon变换沿某个抛物面对地震数据进行求和,得到三维Radon域数据。设x、y分别为纵测线和非纵测线两个方向的炮检距,qx、qy分别为(变换所用的)曲率参数,时空域三维地震数据为d(t,x,y),三维Radon域数据为m(τ,qx,qy),则三维Radon反变换可表示为
| $ \boldsymbol{d}(t, x, y)=\iint \boldsymbol{m}\left(\tau=t-q_{x} x^{2}-q_{y} y^{2}, q_{x}, q_{y}\right) \mathrm{d} q_{x} \mathrm{~d} q_{y} $ | (1) |
其离散形式写成
| $ \boldsymbol{d}(t, x, y)=\sum\limits_{i=1}^{N_{q_{x}}} \sum\limits_{j=1}^{N_{q_{y}}} \boldsymbol{m}\left(\tau=t-q_{x i} x^{2}-q_{y j} y^{2}, q_{x i}, q_{y j}\right) $ | (2) |
式中Nqx、Nqy分别为曲率qx和qy的个数。对该式等号两边做傅里叶变换,再将其转变到频率域,可得
| $ \boldsymbol{D}(\omega, x, y)=\sum\limits_{i=1}^{N_{q_{x}}} \sum\limits_{j=1}^{N_{q_{y}}} \mathrm{e}^{-\mathrm{i} \omega q_{x i} x^{2}} \boldsymbol{M}\left(\omega, q_{x i}, q_{y j}\right) \mathrm{e}^{-\mathrm{i} \omega q_{y j} y^{2}} $ | (3) |
将其写成算子形式
| $ \boldsymbol{D}=\boldsymbol{L}_{x} \boldsymbol{M} \boldsymbol{L}_{y} $ | (4) |
式中Lx、Ly分别为与炮检距x、y有关的算子。
从式(4)可知,可采用与二维Radon变换类似的最小二乘方法,分别求取矩阵Lx、Ly的逆,以得到Radon域数据M。因此,在最小二乘意义下有
| $ \boldsymbol{M}=\boldsymbol{L}_{x}^{\mathrm{H}}\left(\boldsymbol{L}_{x} \boldsymbol{L}_{x}^{\mathrm{H}}+\lambda \boldsymbol{I}\right)^{-1} \boldsymbol{D}\left(\boldsymbol{L}_{y}^{\mathrm{H}} \boldsymbol{L}_{y}+\lambda \boldsymbol{I}\right)^{-1} \boldsymbol{L}_{y}^{\mathrm{H}} $ | (5) |
式中:I为单位矩阵;λ是提高矩阵求逆运算稳定性的阻尼因子,取值范围一般是0.1~1.0。
1.2 基于迭代阈值收缩的三维高分辨率Radon变换三维迭代收缩阈值方法,是提前计算矩阵Lx和Ly的最小二乘逆,并存储到大型矩阵中,在后续运算中直接调用;利用Radon域模型变换回的时空域数据与原始数据的残差,通过逐次迭代收缩阈值更新Radon域数据,达到提高分辨率的效果。
设存储Lx和Ly最小二乘逆的大型矩阵分别为BLxinv、BLyinv,则有
| $ \left\{\begin{array}{l} \boldsymbol{B}_{L_{x \text {inv }}}=\boldsymbol{L}_{x}^{\mathrm{H}}\left(\boldsymbol{L}_{x} \boldsymbol{L}_{x}^{\mathrm{H}}+\lambda \boldsymbol{I}\right)^{-1} \\ \boldsymbol{B}_{L_{y \mathrm{inv}}}=\left(\boldsymbol{L}_{y}^{\mathrm{H}} \boldsymbol{L}_{y}+\mu \boldsymbol{I}\right)^{-1} \boldsymbol{L}_{y}^{\mathrm{H}} \end{array}\right. $ | (6) |
| $ \begin{aligned} \boldsymbol{m}_{k}=& T_{\alpha}\left\{\boldsymbol{m}_{k-1}+\beta {\bf{F}}^{-1}\right.\\ & {\left.\left[\boldsymbol{B}_{\boldsymbol{L}_{x \text {inv }}}\left({\bf{F}}[\boldsymbol{d}]-\boldsymbol{L}_{x} {\bf{F}}\left[\boldsymbol{m}_{k-1}\right] \boldsymbol{L}_{y}\right) \boldsymbol{B}_{\boldsymbol{L}_{y\text {inv }}}\right]\right\} } \end{aligned} $ | (7) |
式中:Tα代表对括号内数据的一个阈值处理;mk是k次迭代后时间域的Radon模型数据;F和F-1分别是傅里叶正变换和反变换算子。由上式可看出,迭代阈值收缩算法,将地震数据与Radon域模型反变换后得到的地震数据之差,以一定比例投影到Radon域模型中,并在每次迭代处理之后,基于如下函数
| $ T_{\alpha}\{\boldsymbol{m}, k\}_{i j}=\left(\left|m_{i j}\right|-\alpha \frac{K-k}{K} \widetilde{m}_{i j}\right)_{+} \operatorname{sgn}\left(m_{i j}\right) $ | (8) |
对Radon域模型数据进行收缩、提高分辨率的运算。式中:α为介于0~1之间的系数;K为最大迭代次数;sgn为取正负号的算子;
在本算法的迭代过程中,直接调用了已有的最小二乘逆计算结果。即只需牺牲很小的存储内存,就可大大提高计算效率。
1.3 三维高分辨率保幅抛物线Radon变换Radon变换算法只是沿特定的曲线对地震数据进行求和叠加,且假设地震数据具有标准的特定形态的同相轴特征,变换过程中并未考虑地震数据振幅的横向变化;而实际上由于受地下介质复杂性的影响,地震数据一般不具有标准同相轴的特性,这样会导致变换分辨率的降低和变换的不保幅,使变换回的数据与原始数据存在一定的振幅差异,导致处理结果中有多次波残余。地震数据的保幅性是与变换的分辨率、变换算子的可逆性紧密联系的。分辨率高,会导致保幅性变差;变换算子的相对可逆,会导致分辨率降低。因此,研究三维Radon变换的保幅算法对于提高变换精度、提升最终处理效果是非常必要的。
由于CDP道集内地震数据的振幅变化平缓,Johansen等[23]采用了正交多项式对数据的AVO效应进行拟合;Xue等[13]将Radon变换与正交多项式拟合相结合,提出了保幅高阶Radon变换算法。本文采用类似思路,利用两个正交多项式系数p(x)和p(y),分别对x和y方向的地震数据振幅变化进行拟合,并将其融合到三维Radon变换算子中。
以x方向的正交多项式p(x)为例。设正交多项式系数的阶数为3,则保幅算子可由下式求取
| $ p_{i}(x)=\frac{x^{i}-\sum\limits_{l=0}^{i-1} \alpha_{i l} p_{l}(x)}{\alpha_{i i}} $ | (9) |
| $ \alpha_{i i}=\sqrt{\sum\limits_{l=0}^{N} x_{l}^{2 i}-\sum\limits_{l=0}^{i-1} \alpha_{i l}^{2}} $ | (10) |
| $ \alpha_{i l}=\sum\limits_{j=0}^{N} x_{j}^{i} p_{l}\left(x_{j}\right) $ | (11) |
式中:
将保幅算子与Radon变换算子Lx、Ly相结合,即为新的保幅Radon变换算子
| $ \left\{\begin{array}{l} \boldsymbol{L}_{x}=\mathrm{e}^{-\mathrm{i} \omega q_{x} x^{2}} \cdot p(x) \\ \boldsymbol{L}_{y}=\mathrm{e}^{-\mathrm{i} \omega q_{y} y^{2}} \cdot p(y) \end{array}\right. $ | (12) |
将式(12)代入式(5)或式(7),即可进行保幅的三维最小二乘和高分辨率Radon变换。
2 数据测试本文分别利用模拟数据和实际数据验证方法的精确度和有效性。分别展示三维Radon变换的最小二乘算法、基于迭代阈值收缩的三维高分辨率算法及保幅的三维高分辨率算法等的结果,并对变换域多次波压制结果进行了对比分析。
2.1 模拟数据测试首先生成模拟数据CDP道集。假设横测线方向共有13个CDP道集,组成三维CDP道集。利用本文三维Radon算法对该三维CDP道集展开多次波压制测试。生成模拟CDP道集时,假定纵测线炮检距范围是0~4800m,道间距为200m,纵测线方向CDP道集共有25道;横测线炮检距范围是-2400~2400m,道间距为400m,由此模拟得到三维情形下的CDP道集(图 1)。
|
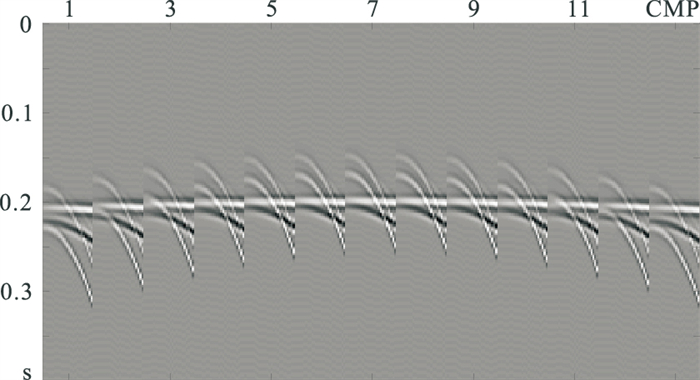
图 1 三维CDP道集 |
从所生成的数据可见,一次波和多次波在y方向都有变化,同相轴平的是一次波,其剩余时差接近于0;其余同相轴都有一定的弯曲,是多次波,四个多次波的剩余时差分别为0.043、0.080、0.080、0.020s。其中,最上部多次波振幅很弱,剩余时差都为0.080s的多次波沿y方向的变化趋势存在一定差异;最下部多次波的振幅与一次波相反,且紧邻一次波。该数据中,有与一次波同相轴十分接近、剩余时差小的多次波;也有时差差异大、能量很弱的多次波。数据x方向同相轴振幅存在变化。
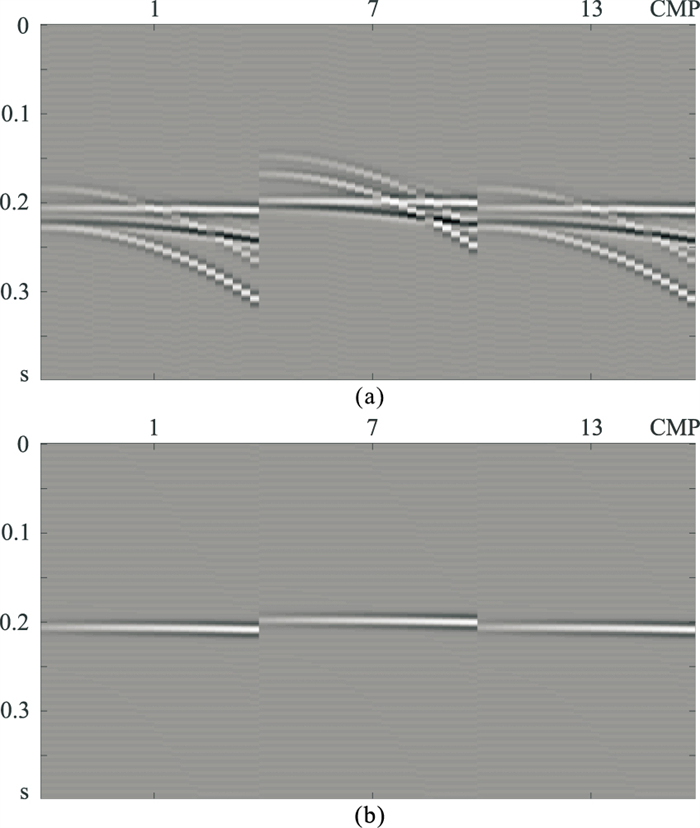
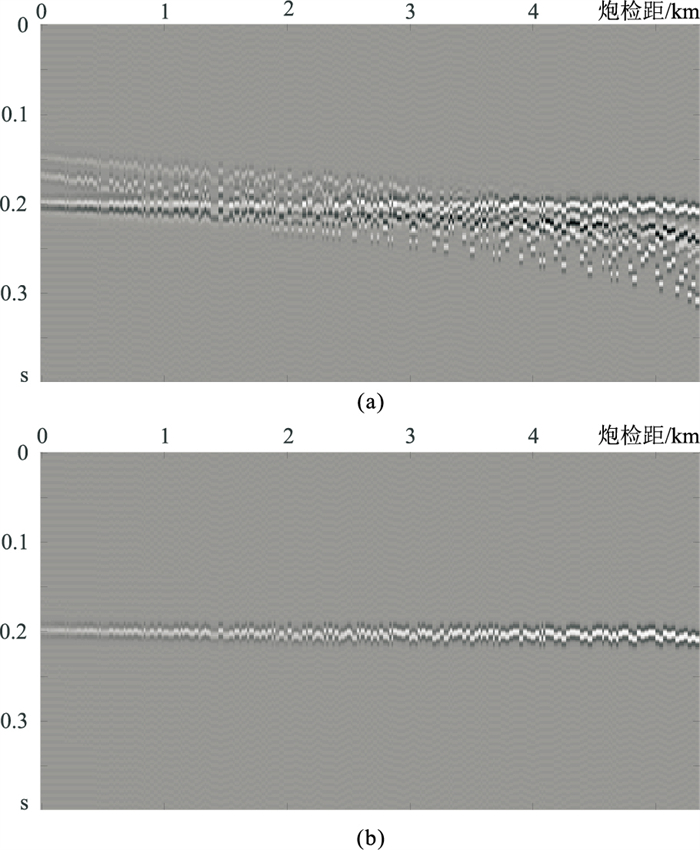
为更好地对比分析多次波的压制效果,还抽取了原始数据和一次波的第1、7和13个小面元道集(图 2)。为更直观地显示三维情形下的CDP道集,在图 3中展示了与图 1对应的沿标量炮检距方向分布的三维CDP道集。在该道集中可看到,一次波和多次波受方位各向异性的影响,同相轴有很大的抖动。基于二维Radon变换直接对其进行处理,无法得到较理想效果;同时,从图 2a中的小面元道集也可看出,不同的小道集中多次波与一次波存在不同的时差差异特点,利用相同参数对所有小道集进行处理是不可靠的。因此,需要利用上文提及的三维抛物线Radon变换对模拟数据的多次波做压制处理。
|
图 2 原始数据(a)与一次波(b)的小面元道集 |
|
图 3 沿标量炮检距方向排列的三维CDP道集 (a)含有多次波的数据;(b)真正的一次波 |
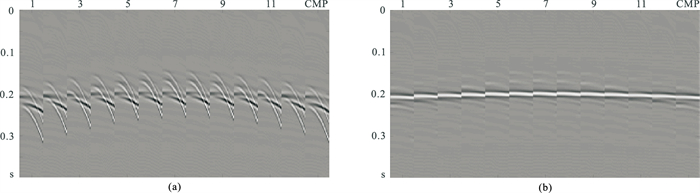
首先给出基于最小二乘理论的三维抛物线Radon变换的结果(图 4)。该Radon域结果分别展示了变换后的三维模型和单个qy切片的变换结果。可见一次波与剩余时差为0.020s的多次波存在严重的相互干涉,剩余时差为0.080s的两个多次波能量发散,但在结果中可看到能量较强。而剩余时差为0.043s的多次波,由于其能量较弱,在变换域剖面中并未呈现明显的能量团。定义的切除数值为0.010s,即在Radon域将剩余时差小于0.010s的数据切除,并将其变换回时空域,得到图 5所示的处理结果。从中可看到能量较弱的多次波(图 5a),在一次波下方也可看到有一些多次波残余(图 5b)。

|
图 4 最小二乘三维抛物线Radon变换Radon域结果 (a)三维模型;(b)单个qy的变换结果 |
|
图 5 最小二乘方法处理结果的小道集 (a)压制的多次波;(b)压制多次波后的一次波 |
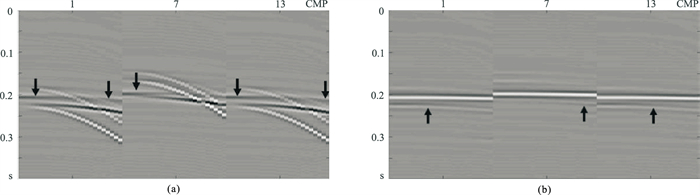
为更好地对压制结果进行对比分析,同样选取其中三个小道集进行放大展示(图 6)。从图 6a可见,由于三维最小二乘算法抛物线Radon变换的变换精度不够、分辨率低,同相轴能量无法在Radon域聚焦,切除时会产生能量泄露现象,导致变换回的多次波中有一次波的信息(箭头所指),从而使最终压制结果中一次波能量有损失;同时分辨率较低也导致多次波残余(图 6b箭头所指)。以上结果均说明最小二乘方法无法满足高精度地震数据处理的需求。
|
图 6 最小二乘方法处理结果的三个小道集 (a)压制的多次波;(b)压制多次波后的一次波 |
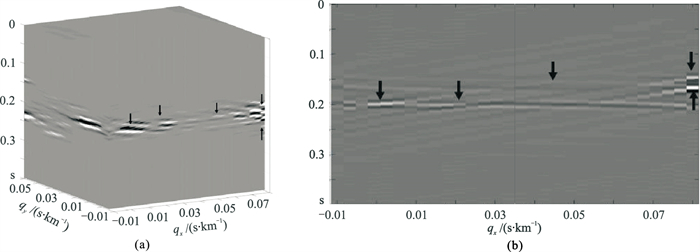
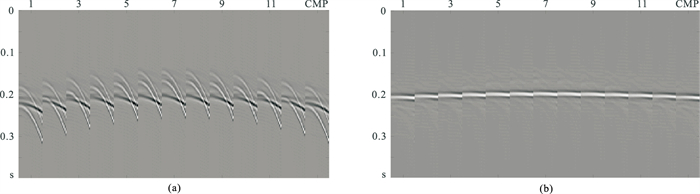
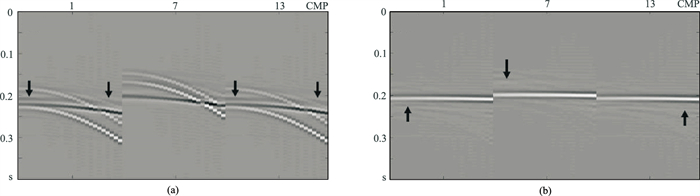
为改进多次波压制效果,利用基于迭代阈值收缩的三维高分辨率抛物线Radon变换方法对此数据进行提高分辨率处理。图 7为该方法Radon域的结果,可见该方法能大幅度提高Radon域的分辨率,在一次波与多次波交叉处,原本离散的两个点变得更聚焦;振幅较弱、剩余时差为0.043s的多次波在Radon域也可看到;但由于数据横向振幅的变化,变换域的聚焦点无法进一步集中,导致剩余时差为0的一次波与剩余时差为0.020s的多次波无法彻底分离,在变换域数据图 7上部中间0.010s处做切除,会对多次波压制带来一定影响。在Radon域将一次波对应的点切除后,变换回x-t域,并将变换回的多次波(图 8a)与原数据做相减,得到多次波压制后的结果(图 8b)。从中可见多次波压制的结果与最小二乘方法相比有明显改善。但从图 9放大的小道集剖面中可看出,多次波的压制损伤了部分有效波的能量(图 9a箭头所指)。
|
图 7 三维高分辨率抛物线Radon变换后Radon域结果 (a)三维模型;(b)单个qy的变换结果 |
|
图 8 高分辨率方法处理结果小道集 (a)压制的多次波;(b)压制多次波后的一次波 |
|
图 9 高分辨率方法处理结果(放大显示)的三个小道集 (a)压制的多次波;(b)压制多次波后的一次波 |
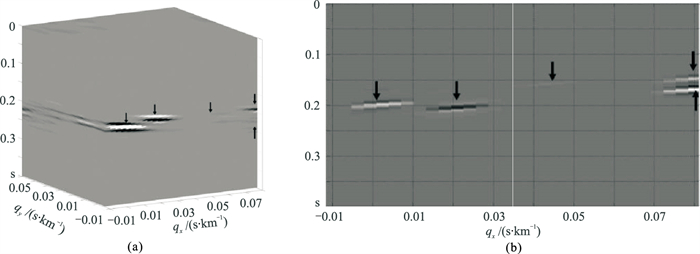
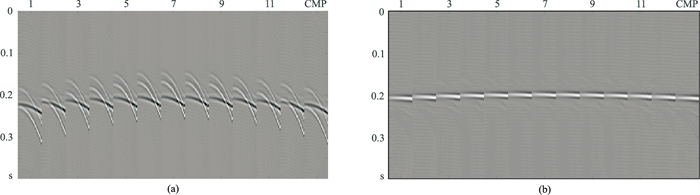
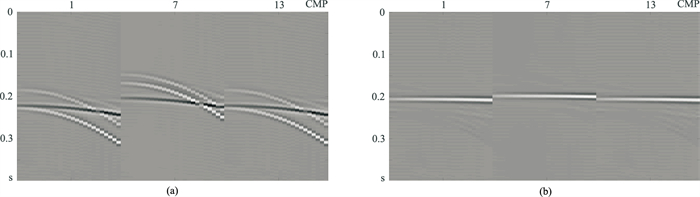
地震数据横向振幅的变化降低了高分辨率算法的聚焦性,导致有效波能量损伤,且存在多次波的残余。必须考虑横向振幅变化的影响,因此采用保幅的高分辨率算法,引入x和y方向的保幅算子对该数据进行处理。图 10为该方法变换域第二阶对应结果,从中可见一次波与多次波得到了较好的分离,且振幅较弱的多次波也有很好的聚焦效果,这有助于时空域振幅较弱多次波的有效辨别。与图 8和图 9相比,图 11、图 12中压制的多次波剖面中已经没有一次波能量;压制多次波后的一次波剖面(图 11b、图 12b)上基本没有多次波残余,压制更彻底。由于在分辨率得到提升的同时,对同相轴振幅的横向变化进行了拟合,因此多次波压制更彻底,一次波能量得到更充分保护。
|
图 10 三维保幅高分辨率抛物线Radon变换Radon域结果 (a)三维模型;(b)单个qy的变换结果 |
|
图 11 三维保幅高分辨率方法处理结果小道集 (a)压制的多次波;(b)压制多次波后的一次波 |
|
图 12 三维保幅高分辨率方法处理结果的三个小道集 (a)压制的多次波;(b)压制多次波后的一次波 |
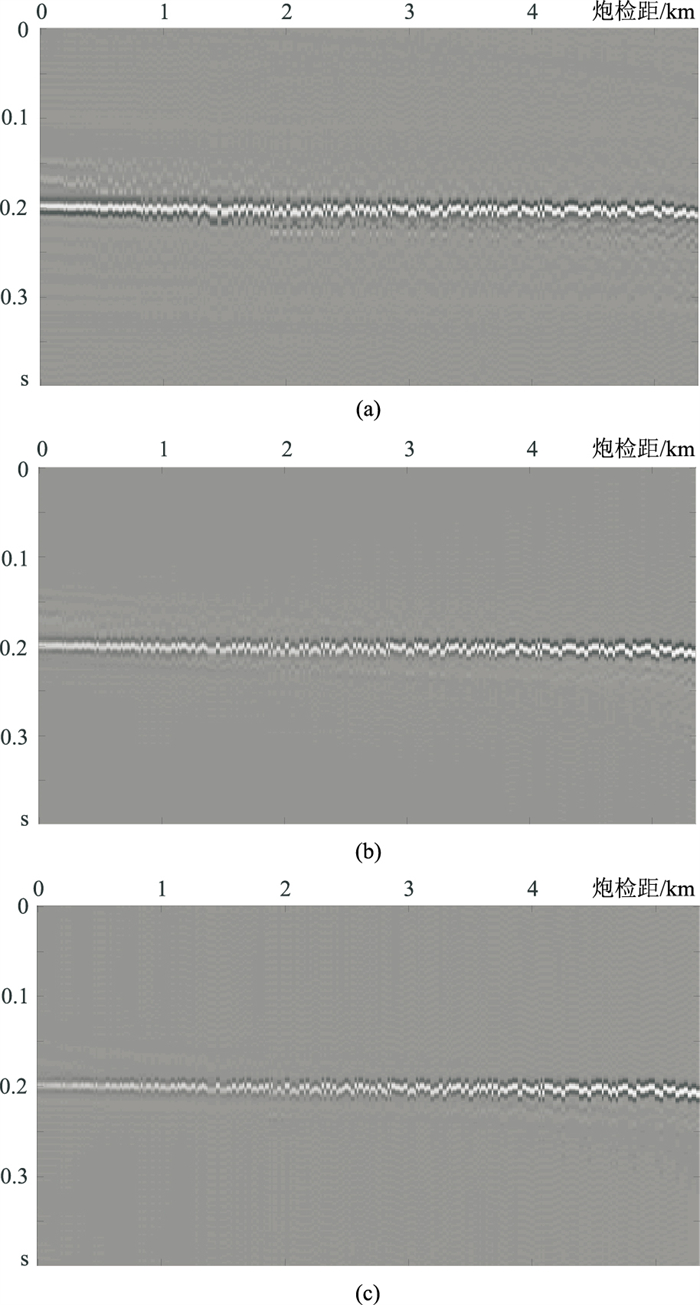
为进一步对比三种方法压制多次波的效果,将多次波压制后结果与真实一次波(图 2b)进行相减(图 13)。可明显看出,无论是最小二乘方法还是高分辨率方法,对横向振幅存在变化的数据进行处理是不保幅的,高分辨率的算法尽管会提高变换域的分辨率,但这些方法都不可避免地对横向振幅变化的一次波同相轴造成损伤。由于时空域近炮检距数据变换到三维Radon域会表现出横向拖尾假象,远炮检距数据在三维Radon域表现为纵向拖尾假象,而多次波压制是在横向某剩余时差位置对一次波与多次波进行的分离,因此多次波压制主要对近炮检距一次波数据造成了损伤。这与图 13结果相对应,压制结果与一次波之间的差值主要表现在近炮检距中。图 14为标量炮检距排列的道集压制结果对比,也可明显看出三维保幅高分辨率算法的优势。

|
图 13 不同方法多次波压制结果与真实一次波的差值 (a)最小二乘方法;(b)高分辨率方法;(c)保幅高分辨率方法 |
|
图 14 不同方法多次波压制结果对比(标量炮检距排列) (a)最小二乘方法;(b)高分辨率方法;(c)保幅高分辨率方法 |
表 1给出了对模拟数据进行处理时,最小二乘、高分辨率以及保幅高分辨率三种算法的计算时间。可看出保幅高精度算法计算量较大,约为高分辨率算法的5倍。在实际地震数据处理应用中,应权衡计算效率与计算精度,以选取最适宜算法。
|
|
表 1 各算法计算时间对比 |
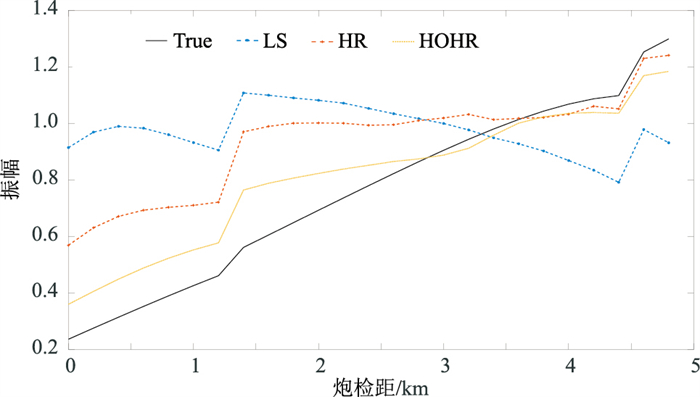
为更好地对比各算法的保幅性能,本文还给出了真实一次波和压制后结果一次波的振幅变化曲线(图 15)。可见保幅高分辨率算法(HOHR)与原始数据(True)曲线最接近,也表明本文算法对一次波能量具有良好保护性能。
|
图 15 各算法保幅性对比 |
利用某海洋实际数据CDP道集对方法进行了测试,该数据为M浅海OBC数据,经过一系列处理后,中远炮检距处有一些动校时差较小的多次波,影响了中深层的有效波信息。分别利用最小二乘、高分辨率和保幅高分辨率三种算法对该道集进行多次波压制处理。由于高分辨率Radon变换方法结果与最小二乘方法相比变化不大,在此就未给出最小二乘算法的结果。压制之前的道集、高分辨率及保幅高分辨率算法压制的小道集结果如图 16所示。
|
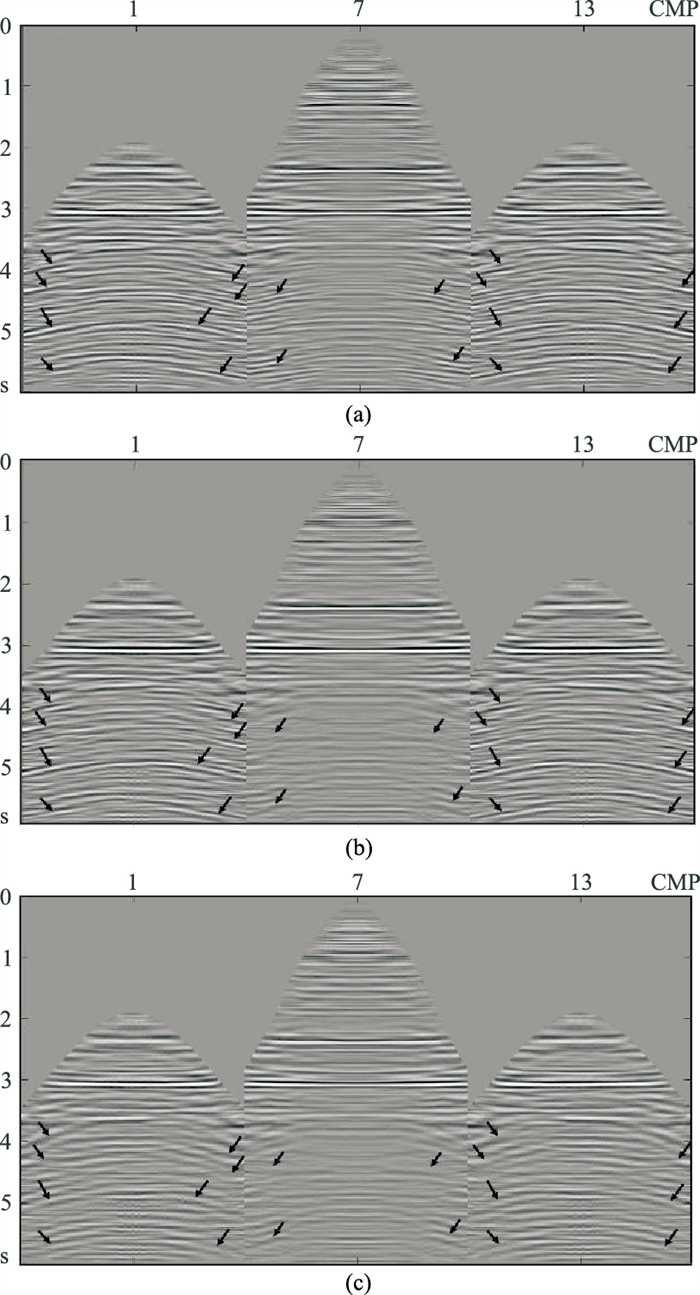
图 16 三维Radon变换压制前、后小面元道集对比 (a)原始数据;(b)高分辨率方法压制结果;(c)保幅高分辨率方法结果 |
从压制处理前、后的小道集来看,高分辨率Radon变换方法对于远缆的多次波压制效果较差。图 16b中第7个小道集为近缆数据,对应的多次波基本已被压制干净;第1和第13个小道集的远缆数据中箭头所指的多次波却因振幅与原数据存在差异,并未被彻底压制。保幅高分辨率算法(图 16c)对远缆小道集的多次波压制则较彻底。
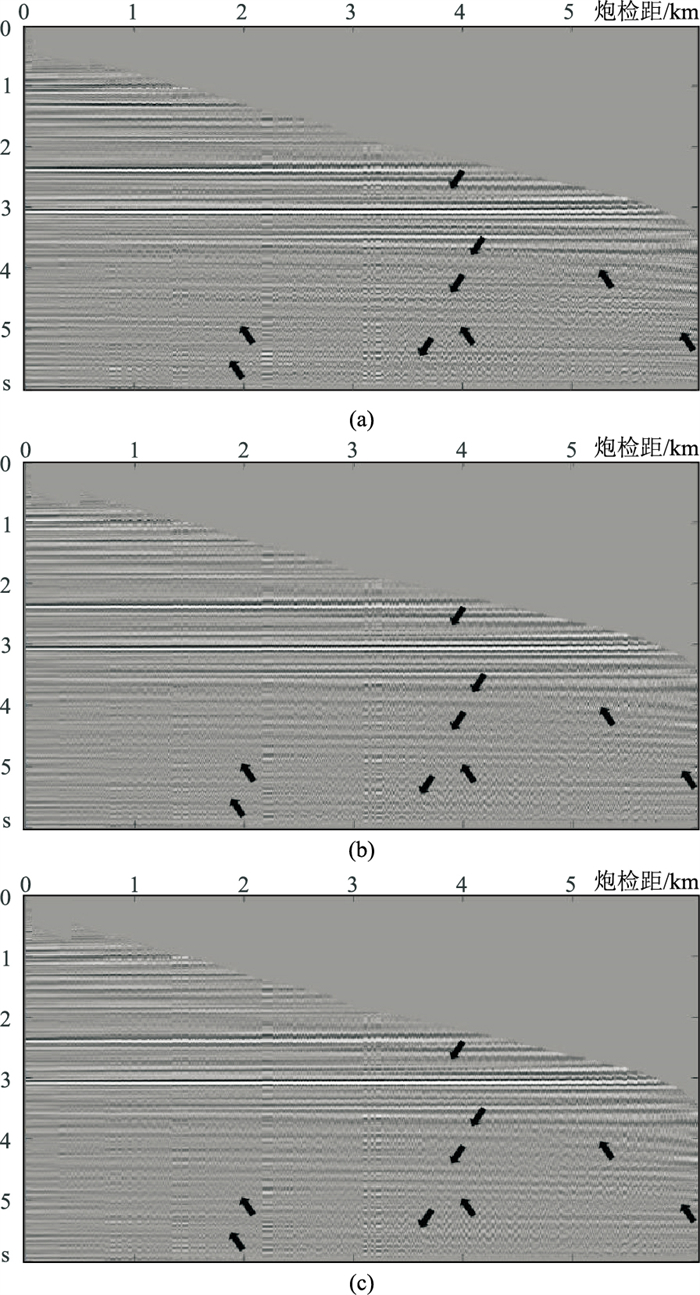
从图 17中的CDP道集对比也可看出,保幅高分辨率算法较高分辨率算法而言,可以更多地压制数据中由方位各向异性引起的抖动的多次波(向上箭头所指),即小道集中、远缆的多次波。
|
图 17 多次波压制前、后CDP道集对比 (a)原始数据;(b)高分辨率方法压制结果;(c)保幅高分辨率方法结果 |
本文对三维Radon变换多次波压制理论进行了系统论述;利用基于迭代阈值收缩的方法在时间和频率域运算,应对方法分辨率低导致的一次波与多次波分离不彻底问题;利用多项式拟合地震数据横向振幅的变化,应对方法的不保幅缺陷。针对模拟和实际数据进行了方法验证,结果表明保幅高分辨率Radon变换在多次波压制方面能取得较好效果。通过分析和研究,得出以下认识和结论:
(1) 受采集空间和时间、离散采样等因素影响,三维最小二乘Radon变换方法的分辨率较低;
(2) 迭代阈值收缩算法可提高三维Radon变换域的分辨率,提高一次波与多次波的可分离性,一定程度上提升多次波压制效果;
(3) 地震数据横向振幅的变化也会降低地震数据的分辨率,而多项式拟合可保存地震数据横向的振幅变化,高分辨率算法与多项式拟合的结合可兼顾分辨率和保幅的问题。
(4) 在本文所进行的数据处理中,为取得更接近实际的处理结果,需要对保幅高精度算法中涉及提高分辨率的多个参数进行测试。此外,与常规最小二乘算法相比,本文算法的计算量偏大,因此需在追求准确处理结果与采用适量计算耗时之间做一个权衡。
| [1] |
HAMPSON D. Inverse velocity stacking for multiple elimination[J]. Journal of the Canadian Society of Exploration Geophysicists (CSEG), 1986, 22(1): 44-55. |
| [2] |
SACCHI M D and ULRYCH T J. High-resolution velocity gathers and offset space reconstruction[J]. Geophysics, 1995, 60(4): 1169-1177. DOI:10.1190/1.1443845 |
| [3] |
SACCHI M D and PORSANI M. Fast high-resolution parabolic Radon transform[J]. SEG Technical Program Expanded Abstracts, 1999, 18: 1477-1480. |
| [4] |
HERRMANN P, MOJESKY T, MAGESAN M, et al. De-aliased, high-resolution Radon transforms[C]. SEG Technical Program Expanded Abstracts, 2000, 19: 1953-1956.
|
| [5] |
TRAD D, ULRYCH T, SACCHI M D. Latest views of the sparse Radon transform[J]. Geophysics, 2003, 68(1): 386-399. DOI:10.1190/1.1543224 |
| [6] |
CHEN Z H and LU W K. Non-iterative high resolution Radon transform[C]. Extended Abstracts of 73rd EAGE Conference and Exhibition, 2011: cp-238-00590, P234.
|
| [7] |
LU W K. An accelerated sparse time-invariant Radon transform in the mixed frequency-time domain based on iterative 2D model shrinkage[J]. Geophysics, 2013, 78(4): V147-V155. DOI:10.1190/geo2012-0439.1 |
| [8] |
薛亚茹, 郭蒙军, 冯璐瑜, 等. 应用加权迭代软阈值算法的高分辨率Radon变换[J]. 石油地球物理勘探, 2021, 56(4): 736-744, 757. XUE Yaru, GUO Mengjun, FENG Luyu, et al. High resolution Radon transform based on the reweighted-iterative soft threshold algorithm[J]. Oil Geophysical Prospecting, 2021, 56(4): 736-744, 757. |
| [9] |
罗腾腾, 徐基祥, 孙夕平. 应用迭代收缩高分辨率Radon变换的绕射波分离与成像方法[J]. 石油地球物理勘探, 2021, 56(2): 313-322. LUO Tengteng, XU Jixiang, SUN Xiping. Diffraction wave separation and imaging based on high-resolution Radon transform on an iterative model shrinking approach[J]. Oil Geophysical Prospecting, 2021, 56(2): 313-322. |
| [10] |
NOWAK E J and IMHOF M G. Amplitude preservation of Radon-based multiple-removal filters[J]. Geophysics, 2006, 71(5): V123-V126. DOI:10.1190/1.2243711 |
| [11] |
薛昭, 董良国, 单联瑜. Radon变换去噪方法的保幅性理论分析[J]. 石油地球物理勘探, 2012, 47(6): 858-867. XUE Zhao, DONG Liangguo, SHAN Lianyu. Amplitude preservation theoretical analysis of Radon transforms de-noising method[J]. Oil Geophysical Prospecting, 2012, 47(6): 858-867. |
| [12] |
薛亚茹, 陈小宏, 马继涛. 多方向正交多项式变换压制多次波[J]. 地球物理学报, 2012, 55(10): 3450-3458. XUE Yaru, CHEN Xiaohong, MA Jitao. Multiples attenuation based on directional orthogonal polynomial transform[J]. Chinese Journal of Geophysics, 2012, 55(10): 3450-3458. DOI:10.6038/j.issn.0001-5733.2012.10.028 |
| [13] |
XUE Y R, MA J T and CHEN X H. High-order sparse Radon transform for AVO-preserving data reconstruction[J]. Geophysics, 2014, 79(2): V13-V22. DOI:10.1190/geo2013-0002.1 |
| [14] |
VYAS M, ETGEN J and LIAO Q Q. Sparse Radon transform in extended domain[C]. SEG Technical Program Expanded Abstracts, 2016, 35: 4540-4544.
|
| [15] |
WANG B, SACCHI M D, YIN X Y. AVO-preserving sparse parabolic Radon transform[C]. Extended Abstracts of 73rd EAGE Conference and Exhibition, 2011: cp-238-00271, G013.
|
| [16] |
DONATI M S and MARTIN N W. Seismic reconstruction using a 3D tau-p transform[R]. CREWES Research Report, 1995, 7: 11-1-11-16.
|
| [17] |
HUGONNET P, BOELLE J L and MIHOUB M. High resolution 3D parabolic Radon filtering[C]. SEG Technical Program Expanded Abstracts, 2008, 27: 2492-2496.
|
| [18] |
HUGONNET P, BOELLE J L, MIHOUB M. 3D high resolution parabolic Radon filtering[C]. Extended Abstracts of 71st EAGE Conference and Exhibition, 2009: cp-127-00421.
|
| [19] |
ZHANG Y Q and LU W K. 2D and 3D prestack seismic data regularization using an accelerated sparse time-invariant Radon transform[J]. Geophysics, 2014, 79(5): V165-V177. DOI:10.1190/geo2013-0286.1 |
| [20] |
CAO W P and ROSS W. High-resolution 3D tau-p transform by matching pursuit[C]. SEG Technical Program Expanded Abstracts, 2017, 36: 4302-4306.
|
| [21] |
唐欢欢, 毛伟建. 3D高阶抛物Radon变换地震数据保幅重建[J]. 地球物理学报, 2014, 57(9): 2918-2927. TANG Huanhuan, MAO Weijian. Reconstruction of 3D irregular seismic data with amplitude preserved by high-order parabolic Radon transform[J]. Chinese Journal of Geophysics, 2014, 57(9): 2918-2927. |
| [22] |
WANG S, LI J Y, XUE Y R, et al. AVO-preserving data reconstruction by 3D high-order sparse-parabolic Radon transform[C]. SEG Technical Program Expanded Abstracts, 2017, 36: 4338-4342.
|
| [23] |
JOHANSEN T A, BRULAND L, LUTRO J. Tracking the amplitude versus offset (AVO) by using orthogonal polynomials[J]. Geophysical Prospecting, 1995, 43(2): 245-261. DOI:10.1111/j.1365-2478.1995.tb00134.x |



 马继涛,北京市昌平区府学路18号中国石油大学(北京)地球物理学院,102249。Email:
马继涛,北京市昌平区府学路18号中国石油大学(北京)地球物理学院,102249。Email: