② 河北省战略性关键矿产资源重点实验室,河北石家庄 050031
② Hebei Key Laboratory of Strategic Critical Mineral Resources, Shijiazhuang, Hebei 050031, China
受人类活动、仪器、环境、天气等多种因素影响,野外采集的地震数据往往含有各种噪声,严重影响速度分析和静校正、速度建模及偏移成像等处理的效果。因此,消除噪声以获取高信噪比地震数据一直是地震勘探面临的难题[1]。地震数据去噪一般依赖信号和噪声在频率、统计规律、振幅等方面的差异分离信号和噪声。地震噪声分为随机噪声和相干噪声。地震随机噪声的消除方法众多,大体上分为滤波类方法、基于变换的方法、降秩方法和深度学习方法等。
滤波类方法基于地震数据时间域分布特点构建滤波函数去除噪声,主要方法有中值滤波[2-3]、各向异性扩散滤波[4]等。基于变换的方法假设地震数据经过某个变换后的系数具有稀疏特征,选取较大的系数,通过阈值运算去掉小的系数,最后反变换到时间域实现去噪[5],常用的变换有傅里叶变换[6]、Radon变换[7]、Wavelet变换[8-10]、S变换[11]、曲波变换[12]等。
深度学习去噪方法是目前的研究热点,基本原理是利用大量的样本数据的特征,通过多层卷积的方式提取数据的时域特征,然后采用深度学习的非线性逼近能力调整网络参数,从而建立一个复杂的去噪模型实现去噪。目前卷积神经网络[13]、残差学习[14-15]、生成对抗网络[16]、降噪自编码[17]等深度学习网络被用于地震数据去噪。深度学习方法需对不同的数据大量训练,因此计算量大。
多道奇异谱分析(MSSA)是一种基于奇异值分解的降秩去噪方法,通过奇异值分解将原始数据分解为信号子空间和噪声子空间,然后将噪声子空间的能量置为零(截断),再通过反变换去噪[18]。MSSA用于多道时间序列分析,是单道奇异谱分析(SSA)的推广[19-20]。Read[21]率先将SSA拓展到多变量MSSA方法研究,基于线性同相轴的假设,利用相邻地震道的频谱相似性与可预测性组成低秩的Hankel矩阵[22],噪声破坏了数据频率切片Hankel矩阵的低秩结构[23],常用截断奇异值分解方法解决低秩近似问题。在地震信号处理领域,MSSA和Cadzow滤波是等效的但却来自不同的领域[24],即Cadzow滤波源于信号和图像去噪,MSSA则源于分析由动力系统引起的时间序列,本文采用MSSA的名称表示这类方法。Oropeza等[25]利用MSSA同时对叠前三维数据去噪和重建,数值实验表明无法完全消除随机噪声,其去噪效果有很大的提升空间。Huang等[26]将阻尼算子引入传统MSSA中,提出了阻尼多道奇异谱分析(DMSSA)算法。通过融合软阈值移动平均算子和阻尼算子的优点,Oboue等[27]利用鲁棒阻尼降秩方法提高地震数据的信噪比。阻尼降秩方法已成为一种有效的去噪方法,可以从含噪和不完备的观测数据中恢复有效信号。
对于海量地震数据来说,基于降秩的方法需要将地震数据分成不同的块,然而每个块对应的奇异值个数不同,目前需要人工估计每个块的有效奇异值个数,计算效率低,无法实现产业化。为此,本文利用Akaike信息准则自动地确定地震信号的奇异值个数,然后基于DMSSA方法去噪。首先介绍了MSSA方法的去噪原理,然后给出确定有效奇异值个数的Akaike信息准则和经验方法,经验方法可以验证Akaike信息准则的有效性。模拟和实际数据实验表明,Akaike信息准则能够自动确定有效奇异值个数,避免了人工操作,有利于实现产业化。
1 算法原理 1.1 DMSSA方法[18]假设一个含噪三维地震数据为D(x, y, t),其中x=(x1, …, xm)、y=(y1, …, yn)表示空间坐标,t=(t1, …, ts)表示时间坐标,m、n为道数,s为采样点数。根据DMSSA理论,使用以下步骤去噪。
(1) 通过离散傅里叶变换将D(x, y, t)从时间域变换为频率域数据F(x, y, ω),其中ω=(ω1, …, ωj)为离散的频率序列,j为频率切片个数。
(2) 在给定的频率范围内将不同频率切片数据排列成块Hankel矩阵。当频率为ωi(i=1, …, j)时,有
| $ \boldsymbol{F}\left(\boldsymbol{x}, \boldsymbol{y}, \omega_{i}\right)=\left(\begin{array}{cccc} F(1,1) & F(1,2) & \cdots & F(1, n) \\ F(2,1) & F(2,2) & \cdots & F(2, n) \\ \vdots & \vdots & \ddots & \vdots \\ F(m, 1) & F(m, 2) & \cdots & F(m, n) \end{array}\right) $ | (1) |
首先,将F(x, y, ωi)的每一行构造成Hankel矩阵
| $ \boldsymbol{R}_{k}=\left(\begin{array}{cccc} F(k, 1) & F(k, 2) & \cdots & F(k, h) \\ F(k, 2) & F(k, 3) & \cdots & F(k, h+1) \\ \vdots & \vdots & \ddots & \vdots \\ F(k, v) & F(k, v+1) & \cdots & F(k, n) \end{array}\right) $ | (2) |
Rk表示由F(x, y, ωi)的第k行构造的Hankel矩阵,大小为v×h,v=
| $ \boldsymbol{H}=\left(\begin{array}{cccc} \boldsymbol{R}_{1} & \boldsymbol{R}_{2} & \cdots & \boldsymbol{R}_{f} \\ \boldsymbol{R}_{2} & \boldsymbol{R}_{3} & \cdots & \boldsymbol{R}_{f+1} \\ \vdots & \vdots & \ddots & \vdots \\ \boldsymbol{R}_{l} & \boldsymbol{R}_{l+1} & \cdots & \boldsymbol{R}_{m} \end{array}\right) $ | (3) |
H为(v×l)×(h×f)阶块Hankel矩阵,
(3) 对H进行奇异值分解,并且选择和截断奇异值,是MSSA类方法的关键。如果有效信号对应的奇异值个数为N,则奇异值对角矩阵仅保留前N个奇异值,而其他所有奇异值均设置为零。对H进行奇异值分解,得到
| $ \boldsymbol{H}=\boldsymbol{U}\left(\begin{array}{ll} \boldsymbol{\varSigma} & 0 \\ 0 & 0 \end{array}\right) \boldsymbol{V}^{\mathrm{T}} $ | (4) |
其中
| $ \boldsymbol{\varSigma}=\operatorname{diag}\left(\sigma_{1}, \sigma_{2}, \cdots, \sigma_{d}\right) \quad \sigma_{1} \geqslant \sigma_{2} \geqslant \cdots \geqslant \sigma_{d} \geqslant 0 $ | (5) |
式中:U为H的左奇异值向量组成的(v×l)×(v×l)阶正交矩阵;VT为H的右奇异值向量组成的(h×f)×(h×f)阶正交矩阵;Σ为按奇异值递减顺序σ1≥σ2≥…≥σd组成的对角矩阵,非零奇异值的个数d等于H的秩。
(4) 基于截断的奇异值计算去噪结果。通过将Hankel矩阵反变换到频率域,再通过离散傅里叶逆变换得到时间—空间域去噪地震数据,即
| $ \boldsymbol{\varSigma}_{1}=\operatorname{diag}\left(\sigma_{1}, \sigma_{2}, \cdots, \sigma_{N}\right) \quad 0 \leqslant N<d $ | (6) |
| $ \boldsymbol{H}^{\mathrm{MSSA}}=\boldsymbol{U}\left(\begin{array}{cc} \boldsymbol{\varSigma}_{1} & 0 \\ 0 & 0 \end{array}\right) \boldsymbol{V}^{\mathrm{T}} $ | (7) |
对所有的频率域数据进行上述操作即可得到去噪地震数据。
若采集的地震数据中不含噪声,则Σ仅包含与有效信号相关的非零σ。若采集的地震数据中含有噪声,所有σ都会发生改变,非零σ的个数也将增加。原始MSSA方法仅保留了N个σ,对σ的大小并没有影响,因此去噪结果有很大的改进空间。Huang等[18]提出的DMSSA方法可以减小σ,因此去噪效果更好。
DMSSA方法通过添加阻尼因子减弱由噪声引起的σ增量,即
| $ \boldsymbol{T}=\boldsymbol{I}-\left(\boldsymbol{\varSigma}_{1}\right)^{-D} \sigma_{N+1}^{D} $ | (8) |
| $ \boldsymbol{H}^{\mathrm{DMSSA}}=\boldsymbol{U}\left(\begin{array}{cc} \boldsymbol{\varSigma}_{1} \boldsymbol{T} & 0 \\ 0 & 0 \end{array}\right) \boldsymbol{V}^{\mathrm{T}} $ | (9) |
式中:T为阻尼算子;I为单位矩阵;D为阻尼因子,其值越小,阻尼效果越强,反之亦然。DMSSA去噪的本质就是利用D对第N+1个σ放大或缩小,然后使用前N个σ与其求差,并对第N+1之后的σ置零,以达到压制噪声的目的。
确定N是DMSSA去噪最关键的一步,将影响噪声抑制效果和有效信号的保护程度。式(4)和式(9)是假定N已知的情况得到的,如果选择N太小,将损坏有效信号;如果选择N太大,将降低噪声压制效果。对于MSSA类方法,自动确定N是关键。面对复杂多变的实际地震数据,在没有充足的地质资料时,确定数据块中需要保留的N是一个值得研究的问题。实际数据去噪时要对数据分块,需要人工估计每个块的有效N,计算效率低,无法实现产业化。为此,首先引入一种确定有效N的经验估计方法,然后给出了一种自动确定N的方法,该方法基于Akaike信息准则自动确定有效N,有利于MSSA产业化。
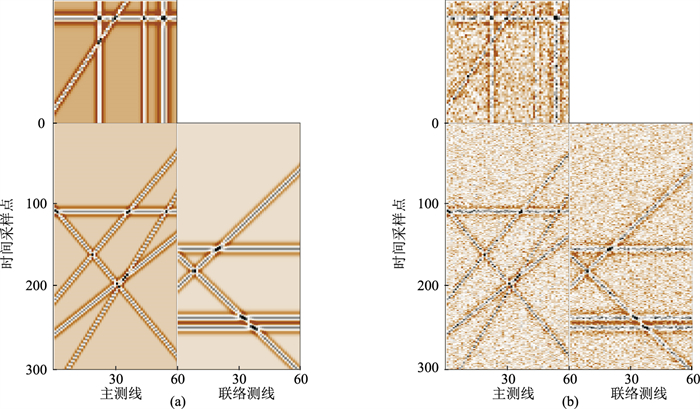
1.2 经验公式法图 1为模拟地震数据A三维视图。模拟数据使用主频为40Hz的雷克子波作为震源,信噪比(SNR)定义为
|
图 1 模拟地震数据A三维视图 (a)无噪数据;(b)加入10%随机噪声数据(信噪比为-1.322dB) 数据含有5个不同倾角的地震同相轴,时间方向有300个采样点,采样率为2ms,主测线和联络测线方向均为60个采样点 |
| $ \mathrm{SNR}=20 \lg \frac{\|\boldsymbol{d}\|_{2}}{\|\boldsymbol{r}-\boldsymbol{d}\|_{2}} $ | (10) |
式中:d为不含噪数据;r为去噪后数据。
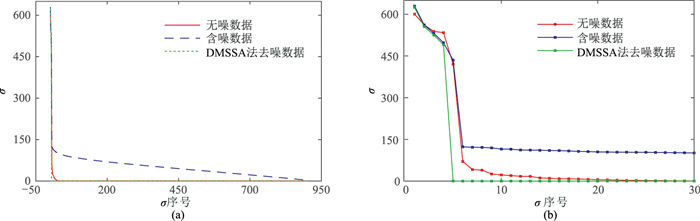
图 2为图 1数据在ω12处的σ曲线。由图可见,地震数据在无噪声时仅出现少数较大的σ且个数为N,其他σ均较小,因此σ曲线出现明显的弯折现象(图 2b红线)。从理论上来说,无噪时N以后的σ应该全部为零。数据加入噪声后,σ发生改变的同时也出现大量非零σ,因此加噪后的σ曲线下降相对平缓,但在第N和第N+1项之间,依然存在巨大的落差。
|
图 2 图 1数据在ω12处的σ曲线 (a)全部σ分布;(b)图a前30个σ分布局部放大 |
通过区分数据含噪和不含噪情况的σ,从而确定数据块中要保留的N。基于错位相除的思路,提出一种确定数据块中有效N的经验估计方法。首先将Σ的σ排列成新的向量
| $ \boldsymbol{Q}=\left(\sigma_{1}, \sigma_{2}, \cdots, \sigma_{d}\right) $ | (11) |
对Q错位相除,得
| $ q_{i}=\frac{\sigma_{i+1}}{\sigma_{i}} \quad 1 \leqslant i \leqslant d-1 $ | (12) |
定义新的向量
| $ \boldsymbol{Q}^{\prime}=\left(q_{1}, q_{2}, \cdots, q_{d-1}\right) $ | (13) |
式中Q′是基于Q的元素错位相除构造的新向量,其第i个元素等于Q的第i+1个元素除以第i个元素。若σi和σi+1的值较接近,则qi的值趋于1,否则将出现一个较小的值。对Q′取极小,并获取极小值对应的索引,有
| $ N=\arg \min \boldsymbol{Q}^{\prime}=\left(q_{1}, q_{2}, \cdots, q_{d-1}\right) $ | (14) |
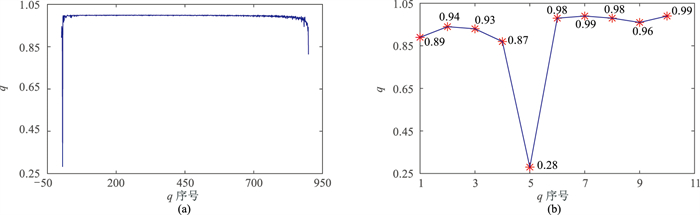
在实际处理中,只需截取Q′的前若干项即可。图 3为错位相除向量曲线。由图可见,Q′的第5个元素值明显小于第4个元素和第6个元素,说明在该频率下应该保留5个奇异值(图 3b)。
|
图 3 错位相除向量曲线 (a)完整曲线;(b)图a前10项元素的局部放大 |
为了排除偶然性,使用上述方法对数据块的主频数据进行相同的计算,并得到新向量
| $ {\bf { flag }}1=\left(\arg \min \boldsymbol{Q}_{\omega_{\mathrm{L}}}^{\prime}, \cdots, \arg \min \boldsymbol{Q}_{\omega_{\mathrm{H}}}^{\prime}\right) $ | (15) |
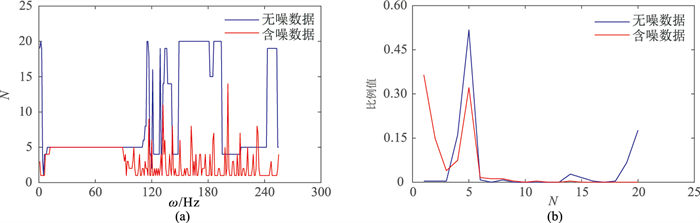
其中ωL~ωH为信号的主要频率范围。通过统计flag1中不同的N出现的占比,根据经验选择合适的N。图 4为由经验公式法确定的图 1a的σ分布。由图可见:不论是否含有噪声,在主频范围内N均为5(图 4a);含噪声数据和不含噪声数据N=5的占比分别为0.5、0.35,故确定N为5(图 4b)。因此,无论数据中是否包含噪声,利用经验公式法均可准确估计N。经验公式法所用的错位相除策略和一阶差分具有异曲同工的效果,可以验证其他方法的效果,为确定N提供了有效工具。
|
图 4 由经验公式法确定的图 1a的σ分布 (a)全频率扫描结果;(b)统计结果 |
处理海量地震数据时需要分块地震数据,然后对每个数据块去噪。但是每个数据块对应的N并不相等,人工预估方法不利于算法实施,因此需要研究自适应算法。
对σ序列Q可依据第N和第N+1个σ之间的巨大落差并伴随严重的弯折现象确定有效N。事实上,N值的选择就是检测σ序列中的拐点位置。本文利用Akaike信息准则[28-29]自动判定保留的N。首先对Q作如下变换
| $ f_{\omega_{i}}\left(\sigma_{\mu}\right)=\sigma_{\mu+1}-2 \sigma_{\mu}+\sigma_{\mu-1} \quad 1 \leqslant \mu \leqslant d $ | (16) |
式(16)实际上是求σ序列曲线的二阶导数,fωi(σμ)描述σ曲线斜率的变化率。确定频率为ωi、第R点的有效N值的Akaike信息准则为
| $ \begin{aligned} \operatorname{AIC}_{\omega_{i}}(R) &=R \lg \left[\operatorname{var}\left(f_{\omega_{i}}\left[\sigma_{i}, \sigma_{R}\right]\right)\right]+\\ &(d-R-1) \lg \left[\operatorname{var}\left(f_{\omega_{i}}\left[\sigma_{R+1}, \sigma_{d}\right]\right)\right] \end{aligned} $ | (17) |
式中:var表示数据序列的方差;AICωi(R)是长度为d的序列,其全局最小值对应的位置即为拐点,按
| $ \boldsymbol{{\rm{flag}}}2=\left(\arg \,\,\min \mathrm{AIC}_{\omega_{\mathrm{L}}}, \cdots, \arg \,\,\min \,\,\mathrm{AIC}_{\omega_{\mathrm{H}}}\right) $ | (18) |
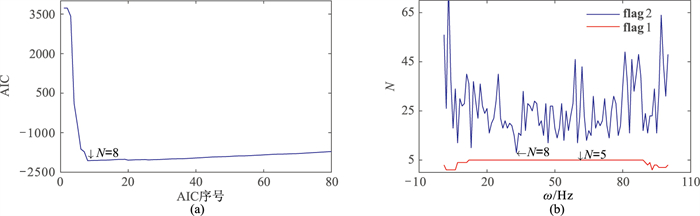
求出所有频率中的最小值。式(18)中元素最小值即是整个数据块中需要保留的N。图 5为由ADMSSA算法确定的图 1a的σ分布。由图可见:①在N=8时AICωi(R)曲线取极小值(图 5a)。由于主频范围内数值结果较稳定,其他范围则经常出现异常值,为了提高精度将频率控制在10~90Hz内。②ADMSSA算法确定的N为8(图 5b),经验公式法确定的N为5(图 4b),证明利用基于Akaike信息准则的方法去噪,可以自动地估计出与真实值较接近的N。
|
图 5 由ADMSSA算法确定的图 1a的σ分布 (a)信息准则曲线;(b)信息准则确定的结果 |
在使用上述方法确定N后,去噪过程采用DMSSA方法的框架,在ADMSSA算法中仅需要确定信号的主频范围,就可以自动地去噪。
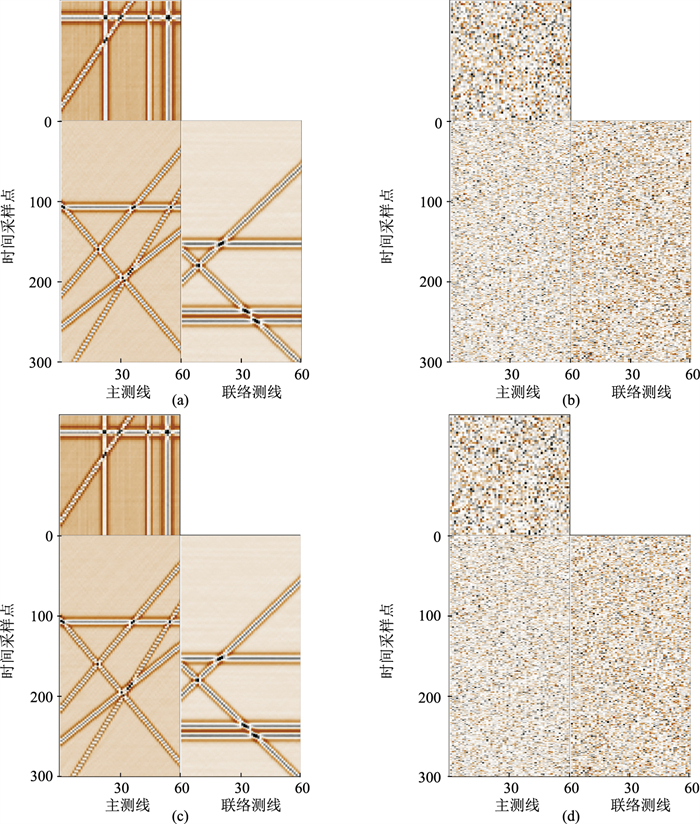
2 数值实验 2.1 模拟数据实验分别使用ADMSSA、DMSSA方法对图 1b去噪,结果(图 6)表明:由ADMSSA、DMSSA方法确定的N分别为8、5,令阻尼因子D=3,去噪结果的信噪比分别为22.110(图 6a)、22.438dB(图 6c),两者的去噪效果较接近,信噪比较高,同相轴清晰连贯,局部细节得以保留。
|
图 6 图 1b的去噪效果对比 (a)ADMSSA方法去噪结果;(b)ADMSSA方法去除的噪声;(c) DMSSA方法去噪结果;(d) DMSSA方法去除的噪声 |
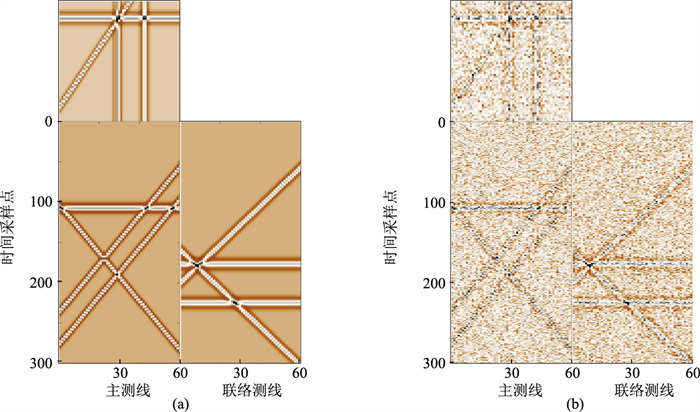
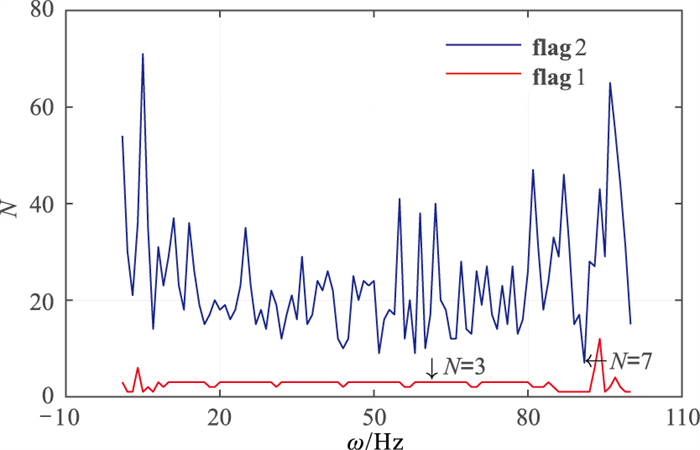
能量较强的噪声经常使地震信号发生严重畸变,导致块Hankel矩阵σ变化复杂。为了验证ADMSSA方法的有效性和对噪声的敏感程度,对含噪地震数据(图 7b)去噪,结果表明,DMSSA方法确定的N为3(图 8红色实线),ADMSSA方法确定的N为7(图 8蓝色实线)。
|
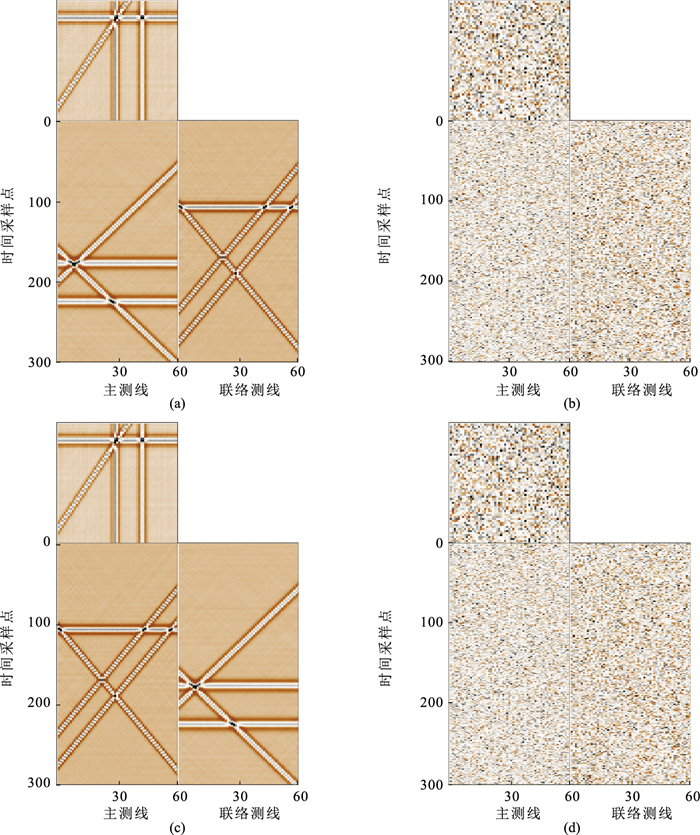
图 7 模拟地震数据B三维视图 (a)无噪数据;(b)加入15%随机噪声数据(信噪比为-4.659dB) 数据含有4个不同倾角的地震同相轴,时间方向有300个采样点,主测线和联络测线方向均为60个采样点,采用主频为40Hz的雷克子波正演 |
|
图 8 两种方法对图 7b数据确定的N |
图 9为图 7b的去噪效果对比。由图可见,令阻尼因子D=3,ADMSSA、DMSSA方法去噪结果的信噪比分别为21.263(图 9a)、21.778dB(图 9c),即前者的信噪比略低,但去噪结果的同相轴清晰,噪声残留较少(图 9b),说明ADMSSA方法高效、精确。
|
图 9 图 7b的去噪效果对比 (a)ADMSSA方法去噪结果;(b)ADMSSA方法去除的噪声;(c)DMSSA方法去噪结果;(d)DMSSA方法去除的噪声 |
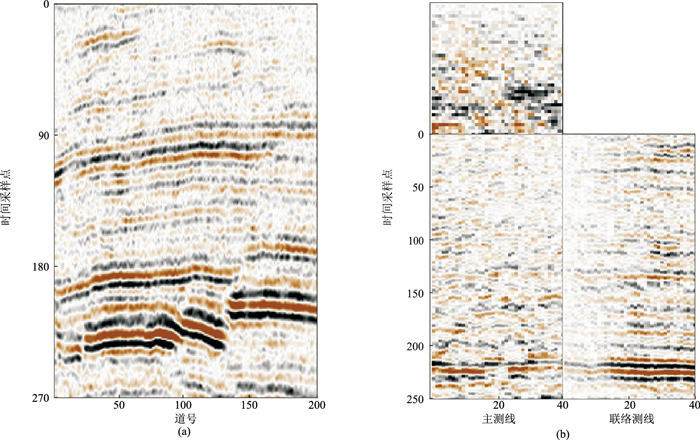
为了证明ADMSSA算法对实际地震数据的去噪效果,分别使用二维和三维叠后地震数据(图 10)验证。二维地震数据(图 10a)信噪比低,地震同相轴连续性差,随机噪声能量强,剖面中间部分以及下部存在断层,尤其是下部存在多处断裂构造。三维地震数据(图 10b)信噪比低,噪声能量较强,有效信号被噪声严重污染,中间部分同相轴出现弯曲、断裂现象。
|
图 10 二维(a)、三维(b)地震数据 图a数据共200道,每道含270个采样点,采样率为2ms;图b数据时间方向共250个采样点,采样率为2ms,主测线和联络测线方向均为40个采样点 |
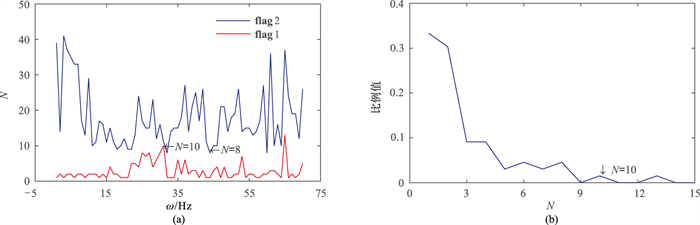
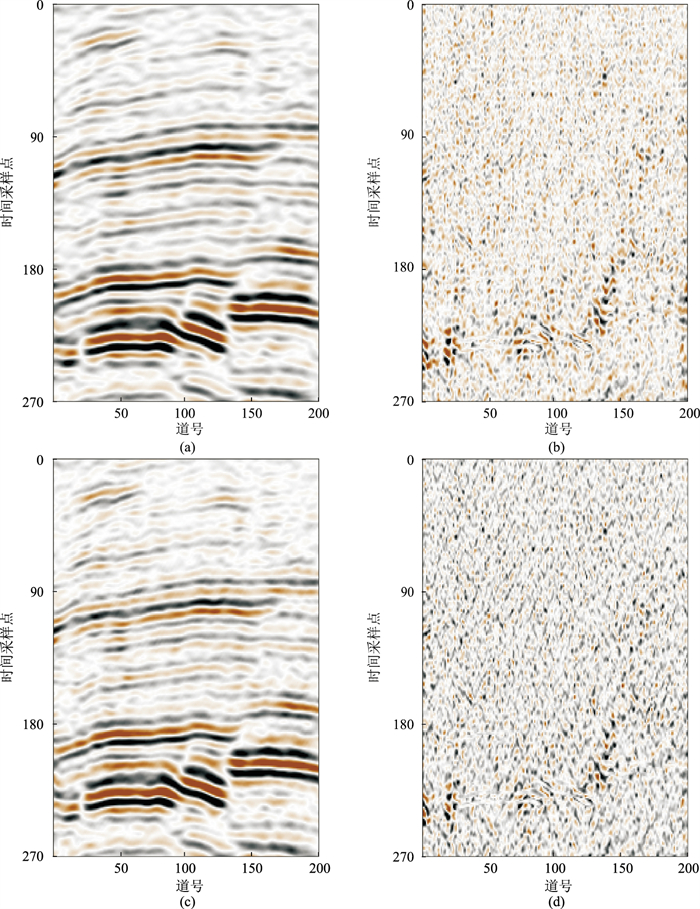
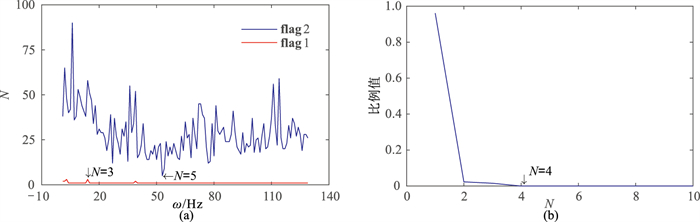
图 11为图 10a的σ分布。由图可见:ADMSSA方法确定的N为8(图 11a蓝色实线);DMSSA方法统计N出现的百分比(图 11b)确定的N为10。图 12为二维地震数据去噪效果对比。由图可见,令阻尼因子D=5,地震同相轴边缘刻画清晰,噪声去除彻底,对构造细节保护较好,去噪效果均较好。图 13为图 10b的σ分布。由图可见:ADMSSA方法确定的N为5(图 13a蓝色实线);DMSSA方法统计N出现的百分比确定的N为4(图 13b)。
|
图 11 图 10a的σ分布 (a)DMSSA、ADMSSA方法确定的N;(b)DMSSA方法统计结果 |
|
图 12 二维地震数据去噪效果对比 (a)ADMSSA方法去噪结果;(b)ADMSSA方法去除的噪声;(c)DMSSA方法去噪结果;(d)DMSSA方法去除的噪声 |
|
图 13 图 10b的σ分布 (a) DMSSA、ADMSSA方法确定的N;(b)DMSSA方法统计结果 |
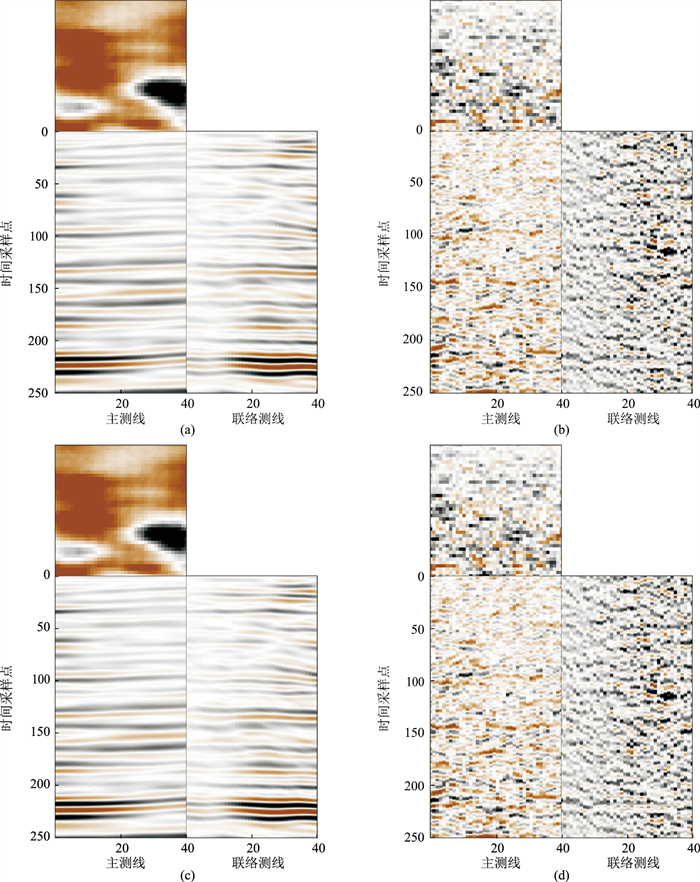
图 14为三维地震数据去噪效果对比。由图可见,两种方法去噪结果基本相同,无论是在地下结构较稳定区域还是在断点附近,ADMSSA方法的去噪结果很好地保护了构造细节(图 14a),同相轴的轮廓清晰,去噪效果很好。
|
图 14 三维地震数据去噪效果对比 (a)ADMSSA方法去噪结果;(b)ADMSSA方法去除的噪声;(c)DMSSA方法去噪结果;(d)DMSSA方法去除的噪声 |
对于MSSA类方法来说,划分的数据块的尺度对计算时间和去噪效果均有影响。ADMSSA方法同样受到划分数据块尺度的影响,因此在划分数据块时应先做试验,再确定划分尺度。ADMSSA方法需要选择一个合适的频率范围,一般取信号有效频率范围即可取得较好去噪结果。DMSSA方法受阻尼因子D的影响,当噪声能量较强时,选择D约为3,当噪声信号较弱时,应选择较大的D值。ADMSSA方法对强脉冲噪声具有一定压制作用,但是去噪结果中仍残存一些强脉冲噪声。MSSA方法对奇异值个数N依赖很强,当N较小时,会影响断层的识别。对于曲率较大的弯曲同相轴,需要合理划分数据块尺度。MSSA方法的计算量主要为奇异值分解,为了提升算法的计算效率,可以采用随机奇异值分解等方法。
DMSSA方法和ADMSSA方法确定的N存在差别,这是由于前者依靠经验公式法估计N,存在一定误差,而ADMSSA方法依靠数据信息通过概率分析提取信号特征。
降秩类去噪算法在消除随机噪声的同时会对有效信号造成一定损伤,其原因是该类方法基于线性同相轴假设,实际数据很难满足条件。因此,尽管降秩类去噪算法获得了较好效果,但是去噪效果尚有很大的提升空间。
4 结论对于MSSA类去噪方法来说,确定有效的奇异值个数是关键。目前都是依靠人工经验估计奇异值个数,不利于该类方法的产业化。本文提出了一种确定有效奇异值个数的方法,该方法基于Akaike信息准则自动区分有效信号对应的奇异值与噪声相关的奇异值,克服了人工选择奇异值个数的问题,有利于海量地震数据去噪。此外,本文还提出利用经验公式法验证ADMSSA方法的可靠性。数值实验证明,ADMSSA方法能够自动地确定可靠的奇异值个数,并且获得高信噪比的去噪结果,该算法在工业化应用中具有巨大潜力。
| [1] |
张军华, 吕宁, 田连玉, 等. 地震资料去噪方法综合评述[J]. 石油地球物理勘探, 2005, 40(增刊): 121-127, 138. |
| [2] |
王伟, 高静怀, 陈文超, 等. 基于结构自适应中值滤波器的随机噪声衰减方法[J]. 地球物理学报, 2012, 55(5): 1732-1741. WANG Wei, GAO Jinghuai, CHEN Wenchao, et al. Random seismic noise suppression via structure-adaptive median filter[J]. Chinese Journal of Geophysics, 2012, 55(5): 1732-1741. |
| [3] |
孙哲, 王建锋, 王静, 等. 基于时空变中值滤波的随机噪声压制方法[J]. 石油地球物理勘探, 2016, 51(6): 1094-1102. SUN Zhe, WANG Jianfeng, WANG Jing, et al. Random noise elimination based on the time-space variant median filtering[J]. Oil Geophysical Prospecting, 2016, 51(6): 1094-1102. |
| [4] |
杨千里, 吴国忱, 赵小龙. 三维各向异性扩散滤波在地震数据处理中的应用[J]. 地球物理学进展, 2015, 30(5): 2287-2292. YANG Qianli, WU Guochen, ZHAO Xiaolong. Application of 3D anisotropic diffusion filter in seismic data processing[J]. Process in Geophysics, 2015, 30(5): 2287-2292. |
| [5] |
李海山. 基于稀疏表示理论的地震信号处理方法研究[D]. 山东青岛: 中国石油大学(华东), 2013.
|
| [6] |
ALSORFK D. Noise reduction in seismic data using Fourier correlation coefficient filtering[J]. Geophysics, 1997, 62(5): 1617-1627. DOI:10.1190/1.1444264 |
| [7] |
TRAD D, ULRYCH T, SACCHI M. Latest view of the sparse Radon transforms[J]. Geophysics, 2003, 68(1): 386-399. DOI:10.1190/1.1543224 |
| [8] |
DONOHO D L. De-noising by soft-thresholding[J]. IEEE Transactions on Information Theory, 1995, 41(3): 613-627. DOI:10.1109/18.382009 |
| [9] |
张宇, 张关泉. 小波变换用于去除高频随机噪声[J]. 石油地球物理勘探, 1997, 32(3): 327-337. ZHANG Yu, ZHANG Guanquan. High-frequency random noise elimination using wavelet transform[J]. Oil Geophysical Prospecting, 1997, 32(3): 327-337. |
| [10] |
高静怀, 毛剑, 满蔚仕, 等. 叠前地震资料噪声衰减的小波域方法研究[J]. 地球物理学报, 2006, 49(4): 1155-1163. GAO Jinghuai, MAO Jian, MAN weishi, et al. On the denoising method of prestack seismic data in wavelet domain[J]. Chinese Journal of Geophysics, 2006, 49(4): 1155-1163. DOI:10.3321/j.issn:0001-5733.2006.04.030 |
| [11] |
曹鹏涛, 张敏, 李振春. 基于广义S变换及高斯平滑的自适应滤波去噪方法[J]. 石油地球物理勘探, 2018, 53(6): 1128-1136, 1187. CAO Pengtao, ZHANG Ming, LI Zhenchun. An adaptive filtering denoising method based on generalized S transform and Gaussian smoothing[J]. Oil Geophysical Prospecting, 2018, 53(6): 1128-1136, 1187. |
| [12] |
张华, 刁塑, 温建亮, 等. 应用二维非均匀曲波变换压制地震随机噪声[J]. 石油地球物理勘探, 2019, 54(1): 16-23. ZHANG Hua, DIAO Su, WEN Jianliang, et al. A random noise suppression with 2D non-uniform curvelet transform[J]. Oil Geophysical Prospecting, 2019, 54(1): 16-23. |
| [13] |
韩卫雪, 周亚同, 池越. 基于深度学习卷积神经网络的地震数据随机噪声去除[J]. 石油物探, 2018, 57(6): 862-869. HAN Weixue, ZHOU Yatong, CHl Yiue. Deep learning convolutional neural networks for random noise attenuation in seismic data[J]. Geophysical Prospecting for Petroleum, 2018, 57(6): 862-869. DOI:10.3969/j.issn.1000-1441.2018.06.008 |
| [14] |
WANG F, CHEN S C. Residual learning of deep convolutional neural network for seismic random noise attenuation[J]. IEEE Geoscience and Remote Sensing Letters, 2019, 16(8): 1314-1318. DOI:10.1109/LGRS.2019.2895702 |
| [15] |
李海山, 陈德武, 吴杰, 等. 叠前随机噪声深度残差网络压制方法[J]. 石油地球物理勘探, 2020, 55(3): 493-503. LI Haishan, CHEN Dewu, WU Jie, et al. Pre-stack random noise suppression with deep residual network[J]. Oil Geophysical Prospecting, 2020, 55(3): 493-503. |
| [16] |
吴学锋, 张会星. 基于循环一致性生成对抗网络的地震数据随机噪声压制方法[J]. 石油地球物理勘探, 2021, 56(5): 958-968. WU Xuefeng, ZHANG Huixing. Random noise suppression method of seismic data based on CycleGAN[J]. Oil Geophysical Prospecting, 2021, 56(5): 958-968. |
| [17] |
SONG H, GAO Y, CHEN W, et al. Seismic random noise suppression using deep convolutional autoencoder neural network[J]. Journal of Applied Geophysics, 2020. DOI:10.1016/j.jappgeo.2020.104071 |
| [18] |
HUANG W, WANG R, CHEN Y, et al. Damped multichannel singular spectrum analysis for 3D random noise attenuation[J]. Geophysics, 2015, 80(4): V261-V270. |
| [19] |
VAUTARD R, GHIL M. Singular spectrum analysis in nonlinear dynamics, with applications to paleoclimatic time series[J]. Physica D: Nonlinear Phenomena, 1989, 35(3): 395-424. DOI:10.1016/0167-2789(89)90077-8 |
| [20] |
GOLUB G, VAN LOAN C. Matrix Computations[M]. JHU Press, 2012.
|
| [21] |
READ P L. Phase portrait reconstruction using multivariate singular systems analysis[J]. Physica D: Nonlinear Phenomena, 1993, 69(3-4): 353-365. DOI:10.1016/0167-2789(93)90099-M |
| [22] |
刘朝. 基于改进曲波变换与低秩约束的地震数据去噪[D]. 黑龙江哈尔滨: 哈尔滨工业大学, 2019.
|
| [23] |
王峰. 基于深度学习的地震数据去噪和重建方法的研究[D]. 浙江杭州: 浙江大学, 2020.
|
| [24] |
TRICKETT S. F-xy Cadzow noise suppression[C]. SEG Technical Program Expanded Abstracts, 2008, 27: 2586-2590.
|
| [25] |
OROPEZA V, SACCHI M. Simultaneous seismic data denoising and reconstruction via multichannel singular spectrum analysis[J]. Geophysics, 2011, 76(3): V25-V32. DOI:10.1190/1.3552706 |
| [26] |
HUANG W, WANG R, ZHANG M, et al. Random noise attenuation for 3D seismic data by modified multichannel singular spectrum analysis[C]. Extended Abstracts of 77th EAGE Conference & Exhibition, 2015, 1-5.
|
| [27] |
OBOUE Y, CHEN W, WANG H, et al. Robust damped rank-reduction method for simultaneous denoising and reconstruction of 5-D seismic data[J]. Geo-physics, 2020, 85(1): V71-V89. |
| [28] |
MAEDA N. A method for reading and checking phase times in autoprocessing system of seismic wave data[J]. Zisin, 1985, 38(3): 365-379. DOI:10.4294/zisin1948.38.3_365 |
| [29] |
张唤兰, 朱光明, 王保利. Hankel矩阵滤波在微地震数据处理中的应用[J]. 煤田地质与勘探, 2014, 42(1): 72-75. ZHANG Huanlan, ZHU Guangming, WANG Baoli. Application of Hankel matrix filtering in microseismic data processing[J]. Coal Geology & Exploration, 2014, 42(1): 72-75. DOI:10.3969/j.issn.1001-1986.2014.01.017 |



 曹静杰,河北省石家庄市槐安东路136号河北地质大学自然资源部京津冀城市群地下空间智能探测与装备重点实验室,050031。Email:
曹静杰,河北省石家庄市槐安东路136号河北地质大学自然资源部京津冀城市群地下空间智能探测与装备重点实验室,050031。Email: