② 中国石油大学(北京)CNPC物探重点实验室,北京 102249;
③ 中国石油大学(北京)地球物理学院,北京 102249;
④ 东方地球物理公司海洋物探处,天津 300457
② CNPC Key Laboratory of Geophysical Exploration, China University of Petroleum (Beijing), Beijing 102249, China;
③ College of Geophysics, China University of Petroleum (Beijing), Beijing 102249, China;
④ BGP Offshore, CNPC, Tianjin 300457, China
稀疏炮检点采集或野外采集因素造成地震数据的不规则影响后续地震资料成像质量。基于压缩感知理论的重构方法能够有效恢复地震数据。压缩感知数据重构技术是将重构问题转化为稀疏优化问题。由于空间随机缺失的地震道引起的空间假频在稀疏域呈白噪分布,有效信号在稀疏域集中分布,可采用反演迭代的方法逐步恢复缺失的地震数据。
Ma等[1]实现了基于Fourier变换的快速迭代阈值收缩算法,在Fourier域重构地震数据;Zhang等[2]在FK域数据重构过程中引入了凸集投影(POCS)算法,在迭代过程中引入了指数衰减阈值参数。Fourier变换是全局变换,不能描述地震数据的方向特征,且稀疏度不够,数据重构精度有待提高,于是能够描述地震信号方向特征的曲波变换应用到压缩感知数据重构中。刘国昌等[3]和Yang等[4]实现了曲波域的POCS方法地震数据重构,采用指数阈值提高了迭代收敛的速度;Zhang等[5]提出了一种基于曲波变换的三维数据同步重构和噪声压制方法;Zhang等[6]提出了一种基于非等距快速离散曲波变换的三维重构方法,采用线性Bregman迭代提高反演效率;Cai等[7]在曲波域基于L1范数的谱梯度投影(SPG-L1)算法实现了数据重构;Liu等[8]提出了局部随机采样的曲波域数据重构;Wang等[9]提出了一种基于曲波变换和高分辨率Radon变换的多域稀疏约束高精度地震数据恢复方法。
曲波变换采用网格旋转方式实现方向表征,无法实现对线奇异在连续系统和离散系统的统一,而Shearlet变换克服了这个缺点,采用剪切方式代替曲波变换的旋转方式,能更加稀疏表达地震信号。冯飞等[10]提出了采用Jitter欠采样的Shearlet变换稀疏约束地震数据重构方法;张良等[11]实现了基于压缩感知的Shearlet变换地震数据重构,其重构效果优于Fourier变换、离散余弦变换、小波变换和曲波变换;刘成明等[12]采用Shearlet变换与基于Landweber加速下降迭代法进行插值,在提高计算效率的同时保证了插值精度;杨冠雨等[13]采用基于Shearlet变换的双正则化方法进行地震数据重构,同时兼顾了信号的稀疏性和地质结构的复杂性;王常波[14]在Shearlet域利用快速凸集投影(FPOCS)算法和指数阈值进行压缩感知地震数据重构,与Fourier变换、曲波变换的重构结果对比表明,Shearlet变换重构精度最高。
与固定稀疏基不同,形态分量分析(Morphological Component Analysis,MCA)框架采用不同基函数线性组合方式对地震数据稀疏表达,通过迭代方式逐一求解并重建各形态分量,最后通过合并重建后的形态分量完成数据的重构。张凯等[15-16]提出了一种Shearlet字典和离散余弦变换(DCT)字典组合的地震数据重构方法;周亚同等[17]提出在MCA框架下的基于DCT与曲波字典组合的地震信号重构方法。MCA框架的压缩感知数据重构需要迭代求解、重建各形态分量,计算效率有待提升。
本文采用Shearlet变换对地震数据稀疏表示,与常规对有缺失的地震数据进行Sheartlet变换不同,是将时空域的地震道重构转化为FK域的随机噪声压制问题。首先对有缺失的地震数据做FK变换,然后对FK域数据做Shearlet变换,通过阈值迭代法消除FK域由于地震道缺失引起的空间假频,从而实现地震道的时空域重构。与形态分量分析(MCA)框架下的地震数据重构不同,MCA认为信号由多个不同形态的分量线性组合而成,用不同的稀疏字典组合方式进行地震数据重构,本文采用的FK变换加Shearlet变换,可以看作一种新的稀疏基变换,不需要迭代求解各形态分量。
稀疏采样方法是基于压缩感知观测系统设计的重要内容。全局随机采样空间假频呈白噪分布,分段随机采样空间假频具有蓝色噪声的频谱特征,在保持采样随机性的同时,有效解决了重采样结果疏密不匀问题,提高了地震数据的重构效果。最后通过Shearlet域和全局随机采样、Shearlet域和分段随机采样、FK+Shearlet域和全局随机采样、FK+Shearlet域和分段随机采样四种数据重构结果对比,表明FK+Shearlet域和分段随机采样结合重构效果最好,信噪比和保真度最高。
1 方法原理 1.1 FK+Shearlet域联合重构方法原理考虑到传统采样定理的不足及信号的稀疏特性,Candes等[18]、Donoho[19]提出了压缩感知理论。压缩感知数据重构包括三个方面:①信号的稀疏表述,信号是稀疏的或在变换域内是稀疏的;②测量矩阵的设计,测量矩阵要与稀疏基完全不相干;③重构算法的构造,信号的有效恢复依赖高效高精度重构优化算法。
基于压缩感知的地震数据重构可表示为求解方程
| $ \boldsymbol{d}=\boldsymbol{M f} $ | (1) |
式中:f∈Rp为完整数据;d∈Rq为观测数据;M为对角采样矩阵,对角线上的元素与d对应,采样前、后数据的维数分别为p和q,且p>q。当d中地震道数据未缺失时,对应的M对角线上的元素为1;地震道数据缺失时,对应的M对角线上的元素为0。M一般选取高斯随机矩阵。
时空域的地震数据不是稀疏的,但可以通过数学变换满足稀疏特性。张良等[11]通过实验认为基于Shearlet变换的数据重构精度高于Fourier变换、DCT变换、小波变换和曲波变换。
本文利用FK+Shearlet变换对数据进行稀疏表示,将时空域不连续的地震数据重构问题转为连续FK域数据随机噪声压制问题,稀疏基为Shearlet基函数
| $ \boldsymbol{x}=\varphi \varPsi \boldsymbol{f} $ | (2) |
式中:Ψ为FK正变换;φ为Shearlet正变换;x为f的FK+Shearlet变换结果。
将式(2)代入式(1),可得
| $ \boldsymbol{d}=\boldsymbol{M} \varPsi^{-1} \varphi^{-1} \boldsymbol{x} $ | (3) |
式中:Ψ-1为FK逆变换;φ-1为Shearlet逆变换。令
| $ \boldsymbol{\theta}=\boldsymbol{M} \varPsi^{-1} \varphi^{-1} $ | (4) |
为感知矩阵。
式(3)为欠定问题,无法直接求解。感知矩阵θ只有满足有限等距性质(RIP)时,则可以求取唯一解[18-20]。高斯随机矩阵与稀疏基不相干,θ满足RIP条件。地震数据重构问题可以表示为
| $ \tilde{\boldsymbol{x}}=\min \|\boldsymbol{x}\|_{0} \quad \text { s. t. } \quad \boldsymbol{d}=\boldsymbol{\theta x} $ | (5) |
式(5)在一定的条件下,L0范数最小化求解问题可以转化为L1范数最小化问题[22],即
| $ \tilde{\boldsymbol{x}}=\min \|\boldsymbol{x}\|_{1} \quad \text { s.t. } \quad \boldsymbol{d}=\boldsymbol{\theta x} $ | (6) |
设ε为重构误差,式(6)可写为
| $ \tilde{\boldsymbol{x}}=\min \|\boldsymbol{x}\|_{1} \quad \text { s. t. } \quad\|\boldsymbol{d}-\boldsymbol{\theta} \boldsymbol{x}\|_{1}<\varepsilon $ | (7) |
关于高精度重构方法,国内外学者对Bregman迭代[6, 21]、POCS[14, 22-23]、SPG-L1[7, 24-25]、正交匹配追踪法[26-27]、交替乘子方向算法(ADMM)[13, 28]等方法进行研究或改进。温睿等[29]通过实验对比分析了POCS、IHT(Iterative Hard Thresholding)、Bregman和JRSI(Joint Reconstruction by Sparsity-promoting Inversion)四种迭代算法,认为POCS和IHT算法较为稳定,经过多次迭代能够达到较高的信噪比。本文采用POCS进行压缩感知数据重构,算法如下
| $ \boldsymbol{d}_{k+1} =\varPsi^{-1} \varphi^{-1} T_{\lambda_{k}}\left(\varphi \varPsi \overline{\boldsymbol{d}}_{k}\right) $ | (8) |
| $ \overline{\boldsymbol{d}}_{k+1} =\boldsymbol{d}^{\mathrm{obs}}+(\boldsymbol{I}-\boldsymbol{M}) \boldsymbol{d}_{k+1} $ | (9) |
式中:dobs为观测数据;Tλk为硬阈值函数,λk为阈值,k为迭代次数,dk+1为第k+1次迭代更新数据;dk+1为第k+1次迭代结果dk+1置入观测数据dobs后的重建结果,初始d1等于dobs。该方法具有较高的插值重建精度及计算效率[25]。
1.2 稀疏采样稀疏采样方法是压缩感知地震采集研究的重要内容,决定了由于地震数据缺失引起的空间假频在稀疏域的随机分布特征。相比全局随机采样,Jitter稀疏采样在保持随机性的同时,分布更均匀,减少了假频和有效信号的混叠,重建效果优于全局随机采样[10, 12, 30]。本文采用王汉闯等[31]提出的分段随机采样方法,该方法不仅具有更为优越的蓝谱特征,还突破了Jitter采样对段内样点为奇数的限制,具有更强的实用性。
以一道为例分析重采样因子对数据频谱(波数谱)的改造。对完整数据进行稀疏采样,就是对重采样因子与完整数据进行点乘,即
| $ d(t)=r(t) f(t) $ | (10) |
时间(空间)域的乘积对应频率(波数)域的褶积,即
| $ D(\omega)=R(\omega) * F(\omega) $ | (11) |
式中:f为单道完整地震数据;r为重采样因子;d为采样结果;F、R和D分别为f、r和d的Fourier变换。完全采样时,r(t)≡1。
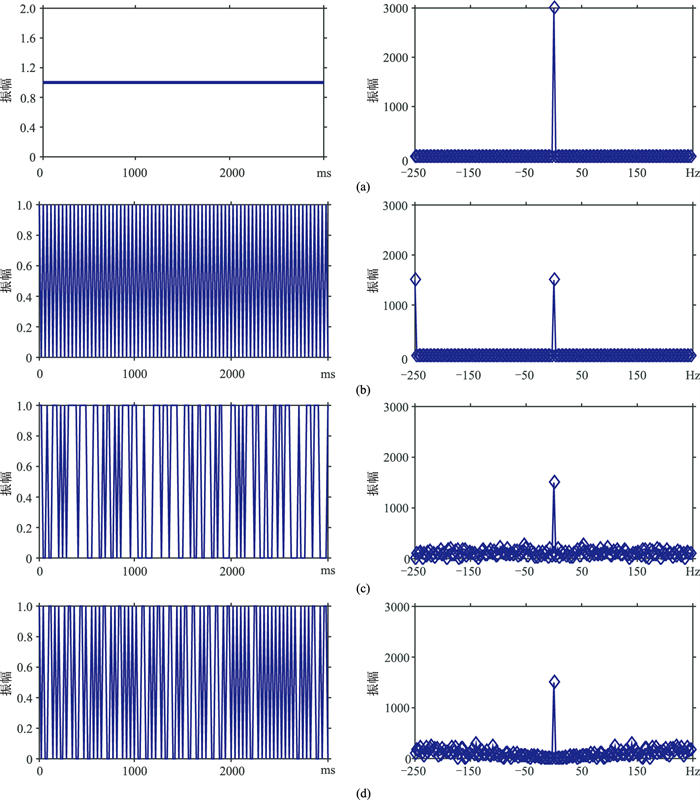
图 1为规则、全局随机、分段随机1/2采样示意图。规则采样时采样因子r中0和1规则交替出现;1/2全局随机采样的采样因子r中0和1全局随机出现;1/2分段随机采样中2个采样点为1段,每段采样因子r中0和1随机出现。假定原始数据采样间隔为2ms,采样点数为3000,则奈奎斯特频率为250Hz。图 2a为完全采样因子及其频谱,0频为有效信号频谱,频谱值为3000,不存在假频。图 2b为1/2规则采样因子及其频谱,0频处为有效信号频谱,频谱值降为原来的1/2(1500),假频在-250Hz处,与0频处有效信号频谱值相等。图 2c为1/2全局随机采样因子及其频谱,0频处谱值降为原来的1/2(1500),假频的频谱呈白噪特征,假频和有效信号混叠。图 2d为1/2分段随机采样因子及其频谱,0频处谱值降为原来的1/2(1500),假频的频谱呈蓝谱特征,假频和有效信号混叠。

|
图 1 规则(a)、全局随机(b)、分段随机(c)1/2采样示意图实心表示采样;空心表示未采样 |
|
图 2 不同稀疏采样因子(左)及其频谱(右) (a)完全采样因子;(b)1/2规则采样因子;(c)1/2全局随机采样因子;(d)1/2分段随机采样因子 |
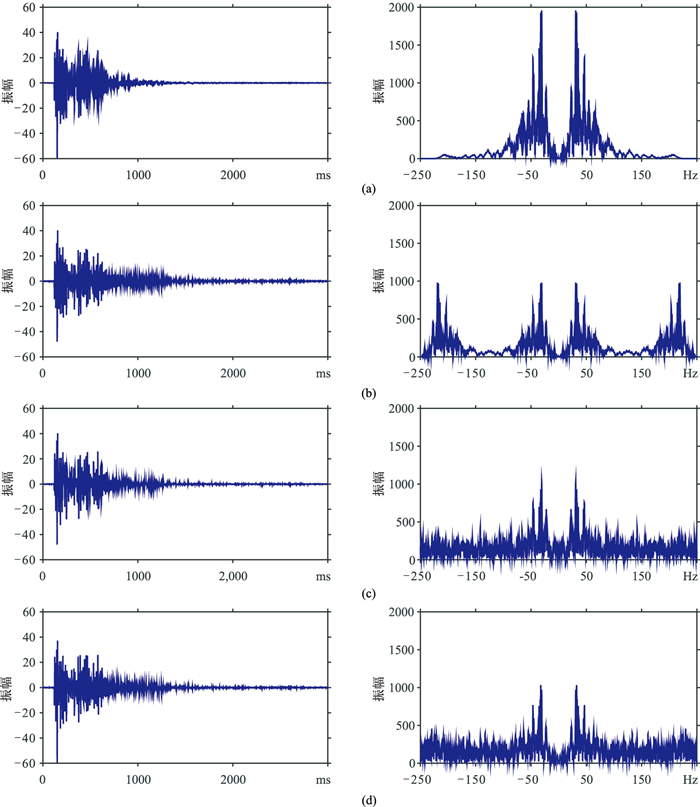
图 3a和图 3b分别为完全采样和1/2规则采样的数据及其频谱。规则采样后,如果信号频率和假频混叠,则无法保真恢复原始信号。图 3c和图 3d分别为全局1/2随机采样和分段1/2随机采样的数据和频谱。随机采样后,假频振幅值相对较小,有效数据的频谱大于假频频谱,方便后续通过反演迭代进行全频带数据恢复,理论上可以突破奈奎斯特频率的限制。但分段随机采样数据的蓝谱特征明显,由于地震数据为带限数据,分段随机更有利于后期数据重构。
|
图 3 不同稀疏采样因子采样后的数据(左)及其频谱(右) (a)完全采样因子;(b)1/2规则采样因子;(c)全局1/2随机采样因子;(d)分段1/2随机采样因子 |
信号的稀疏表示就是将信号投影到正交变换基时,有效信号对应的变换系数集中分布,系数相对较大,噪声(对地震数据重构来说,主要指由于数据缺失造成的空间假频)对应的变换系数的绝对值很小。Shearlet变换[32-34]可以有效地表示地震数据各向异性特征。由剪切方式代替了曲波变换的旋转方式,能够在离散系统和连续系统做统一处理。
对于任意二维平方可积函数b(τ),其Shearlet变换可表示为
| $ \mathrm{SH}_{\varphi} b\{j, l, m\}=\left\langle b, \varphi_{j, l, m}\right\rangle $ | (12) |
式中
| $ \varphi_{j, l, k}(\boldsymbol{\tau})=|\operatorname{det} \boldsymbol{A}|^{-\frac{1}{2}} \varphi\left[\boldsymbol{B}^{-1} \boldsymbol{A}^{-1}(\boldsymbol{\tau}-\boldsymbol{m})\right] $ | (13) |
| $ \left\{\begin{array}{l} \boldsymbol{A}=\left(\begin{array}{cc} j & 0 \\ 0 & \sqrt{j} \end{array}\right) \\ \boldsymbol{B}=\left(\begin{array}{ll} 1 & l \\ 0 & 1 \end{array}\right) \end{array}\right. $ | (14) |
其中:A为各向异性膨胀矩阵,控制尺度;B为剪切矩阵,控制方向,A和B均为2阶可逆矩阵;j为尺度参数;l为剪切参数;m为平移参数。
Shearlet变换是一类多尺度几何分析方法,通过对基函数的缩放、剪切和平移等仿射变换生成具有不同特征的剪切波函数,具有较好的地震数据的方向性描述和稀疏表达能力。
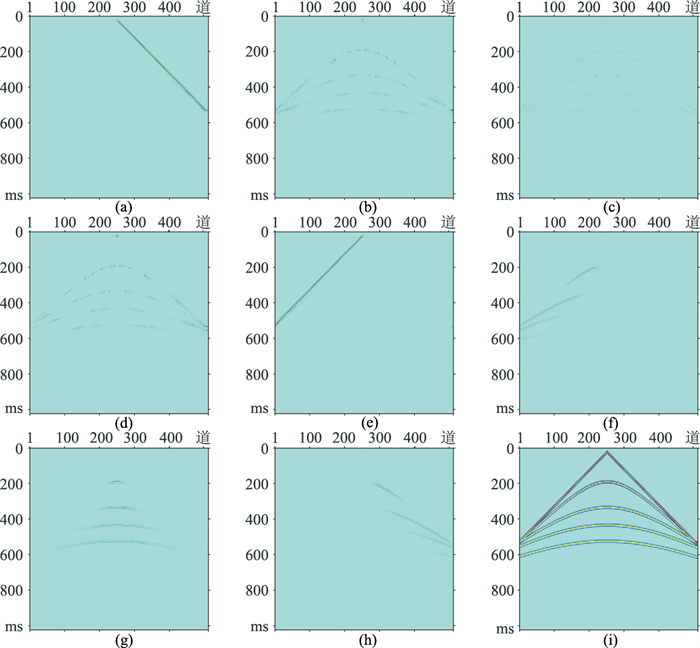
应用模拟单炮数据(采样间隔为2ms,512个样点,512道)对比Shearlet变换与FK+Shearlet变换效果。采用1尺度的Shearlet分解,将模拟单炮分解成1个不带方向特征的低频分量和8个带方向特征的高频分量。图 4为模拟单炮及FK谱,图 5为对模拟单炮进行Shearlet分解的9个系数,由于分解的8个高频系数(图 5a~图 5h)能量较弱,对其振幅放大10倍显示。
|
图 4 模拟单炮(a)及其FK谱(b) |
|
图 5 模拟单炮Shearlet分解的9个系数 (a)~(h)带方向特征的8个高频系数谱,振幅放大10倍显示;(i)不带方向特征的低频系数谱 |
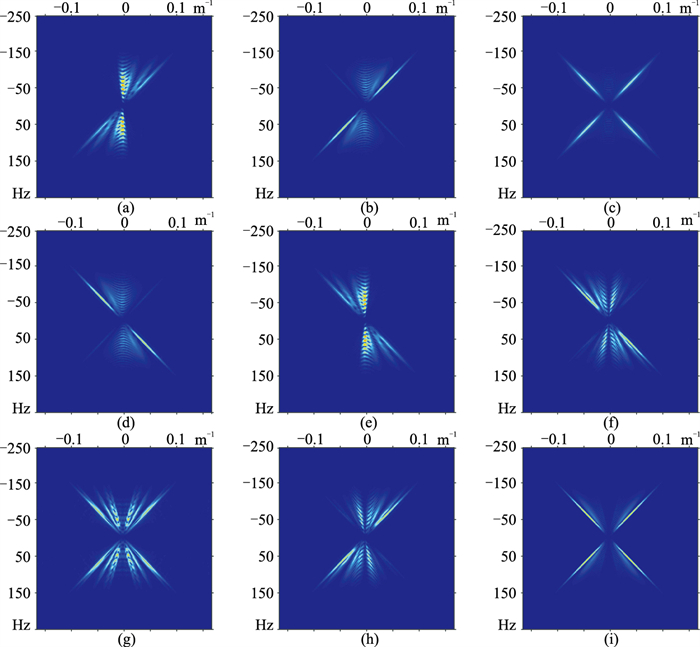
图 6为图 5的9个Shearlet域系数对应的时空域数据。图 7为对模拟单炮进行FK+Shearlet分解的9个系数谱,图 8为对模拟单炮进行FK+Shearlet分解的9个系数对应的时空域数据。表 1对比了模拟单炮不同稀疏基变换分解系数能量占比。对模拟单炮直接进行Shearlet变换,不带方向特征的低频分量系数能量占比为98.75%,8个带方向特征的高频分量系数能量占比仅为1.25%;对模拟单炮进行FK+Shearlet变换,不带方向特征的低频能量占比为8.81%,8个带方向特征的高频分量系数能量占比为91.19%,FK+Shearlet域的带有方向特征的高频系数相对Shearlet域能量更强,能更好地观测地震数据的方向(线奇异)特征。
|
图 6 图 5的9个系数对应的时空域数据 (a)~(h)带方向特征的8个高频系数谱,振幅放大10倍显示;(i)不带方向特征的低频系数谱 |
|
图 7 模拟单炮分解的FK+Shearlet域9个系数谱 (a)~(h)带方向特征的8个高频系数谱;(i)不带方向特征的低频系数谱 |

|
图 8 图 7的9个系数谱对应的时空域数据 (a)~(h)带方向特征的8个高频系数谱;(i)不带方向特征的低频系数谱 |
|
|
表 1 模拟单炮不同变换分解的系数能量占比 |
采用重构信噪比评价重构效果
| $ \mathrm{SNR}=10 \lg \frac{\|\boldsymbol{f}\|^{2}}{\left\|\boldsymbol{f}^{*}-\boldsymbol{f}\right\|^{2}} $ | (15) |
式中f*表示重构的地震数据。
应用上述模拟单炮记录对比全局随机和分段随机采样250道(采样率48.8%)在Shearlet域与FK+Shearlet域的数据重构效果。表 2为模拟单炮重构信噪比统计。
|
|
表 2 模拟单炮不同域重构信噪比统计 |
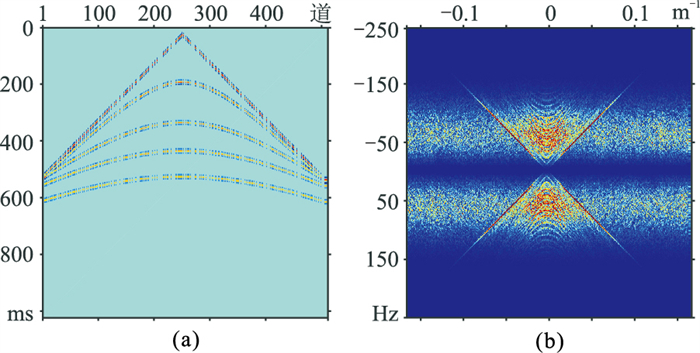
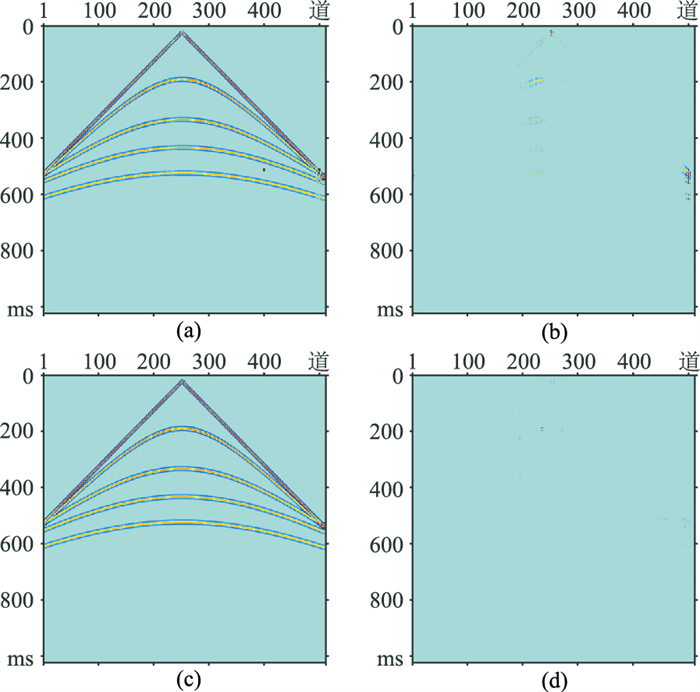
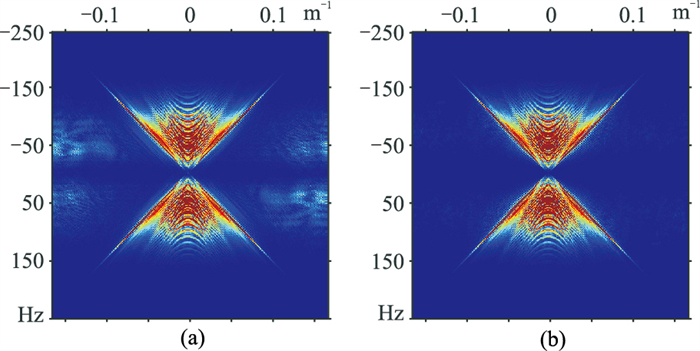
图 9为模拟单炮记录的全局随机采样结果及其FK谱。图 10为Shearlet域和FK+Shearlet域数据重构结果及误差。Shearlet域重构数据(图 10a)的信噪比为13.39dB,FK+Shearlet域重构数据(图 10c)的信噪比为21.05 dB;Shearlet域数据重构的误差(图 10b)明显大于FK+Shearlet域数据重构误差(图 10d),表明FK+Shearlet域重构效果优于Shearlet域。全局随机采样数据FK谱(图 9b)的空间假频呈白噪分布,FK+Shearlet域重构数据有效信号的FK谱(图 11b)能量的恢复及空间假频的压制效果明显优于Shearlet域重构数据的FK谱(图 11a)。
|
图 9 模拟单炮全局随机采样结果(a)及其FK谱(b) |
|
图 10 模拟单炮全局随机采样Shearlet域与FK+ Shearlet域模拟单炮重构效果分析 (a)Shearlet域重构结果;(b)Shearlet域重构误差;(c)FK+ Shearlet域重构结果;(d)FK+Shearlet域重构误差 |
|
图 11 模拟单炮全局随机采样不同域重构结果的FK谱 (a)Shearlet域;(b)FK+Shearlet域 |
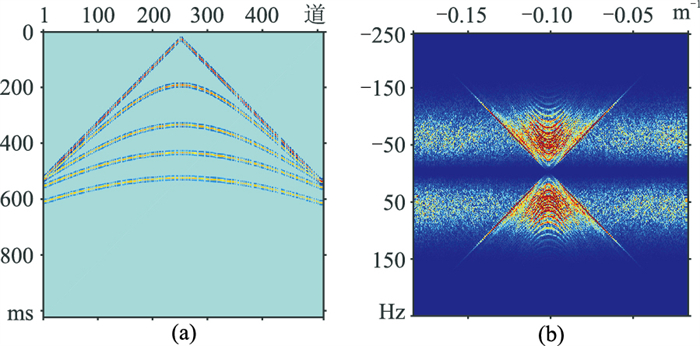
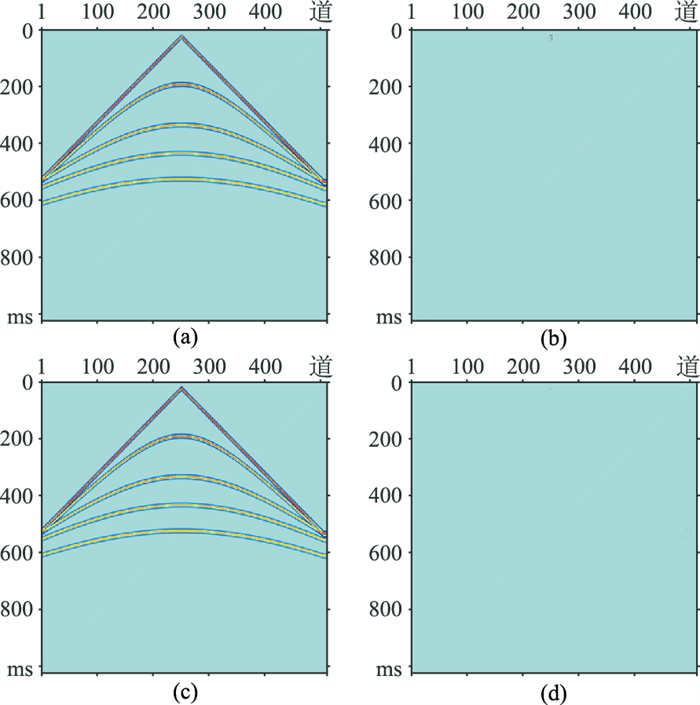
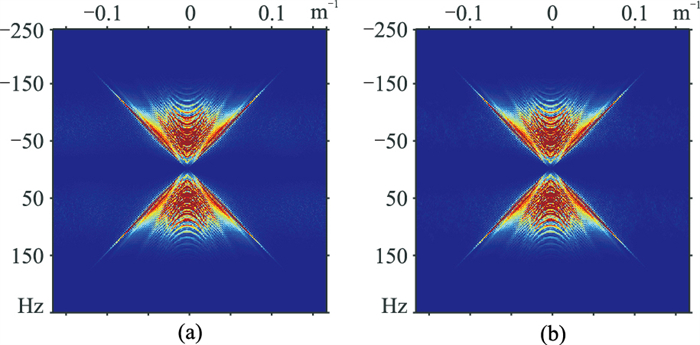
图 12为模拟单炮记录的分段随机采样结果及其FK谱。图 13为Shearlet域和FK+Shearlet域数据重构结果及误差。Shearlet域重构数据(图 13a)的信噪比为13.89dB,FK+Shearlet域重构数据(图 13c)的信噪比为23.52dB,Shearlet域数据重构的误差(图 13b)大于FK+Shearlet域数据重构误差(图 13d),FK+Shearlet域重构效果优于Shearlet域。分段随机采样数据的FK谱(图 12b)的空间假频呈蓝谱特征,空间假频与有效信号混叠相对全局随机(图 9b)要弱。FK+Shearlet域重构数据有效信号的FK谱(图 14b)的能量恢复及空间假频的压制效果优于Shearlet域重构数据的FK谱(图 14a)。从数据重构信噪比(表 2)可见,Shearlet域分段随机重构效果(图 13a)优于全局随机重构(图 10a),FK+Shearlet域分段随机重构效果(图 13c)优于全局随机重构(图 10c)。
|
图 12 模拟单炮分段随机采样结果(a)及其FK谱(b) |
|
图 13 模拟单炮分段随机采样Shearlet域与FK+Shearlet域重构效果分析 (a)Shearlet域重构结果;(b)Shearlet域重构误差;(c)FK+ Shearlet域重构结果;(d)FK+Shearlet域重构误差 |
|
图 14 模拟单炮分段随机采样不同域重构结果的FK谱 (a)Shearlet域;(b)FK+Shearlet域 |
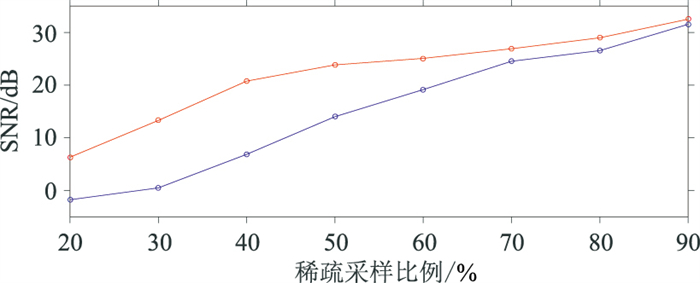
通过不同稀疏采样比例进一步验证FK+Shearlet的重构效果。图 15为分段随机采样下不同稀疏采样比例和不同稀疏基变换模拟单炮重构信噪比对比。整体上,FK+Shearlet比Shearlet域重构信噪比高。当稀疏采样比例低于60%时,FK+Shearlet比Shearlet域重构信噪比高6dB以上;当采样比例高于70%时,随着采样比例的增加,两种稀疏基重构效果逐渐接近。
|
图 15 不同稀疏采样比例FK+Shearlet(红色)与Shearlet域(蓝色)重构数据信噪比对比 |
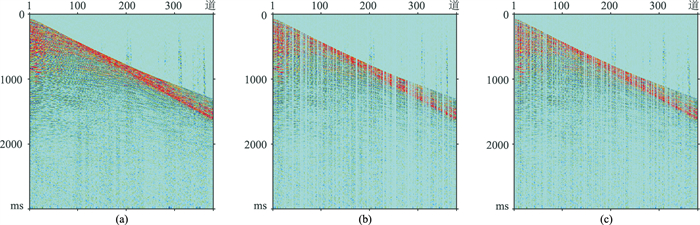
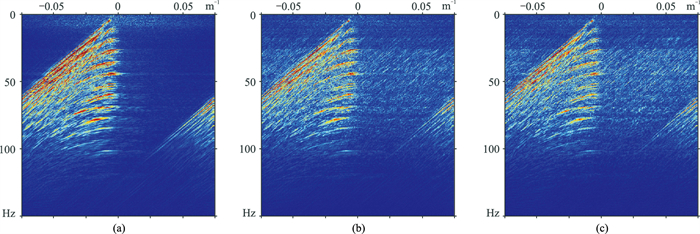
选择海域地震资料(图 16a)进行压缩感知数据重构。由于海洋资料频带较宽,同时原始数据也存在空间采样不足引起的空间假频,给数据重构带来一定难度,以70%全局随机采样(图 16b)和分段随机采样(图 16c)对比Shearlet域与FK+Shearlet域数据重构效果。图 17为原始、全局随机采样、分段随机采样数据的FK谱,分段随机采样数据FK谱(图 17c)的空间假频呈蓝谱特征,空间假频与有效信号混叠相对全局随机(图 17b)要弱。表 3为不同稀疏采样和稀疏基变换实际数据重构信噪比对比。
|
图 16 实际原始地震数据(a)及其全局(b)和分段随机采样结果(c) |
|
图 17 实际原始地震数据(a)及其全局(b)和分段随机采样结果的FK谱(c) |
|
|
表 3 实际数据的重构信噪比统计 |
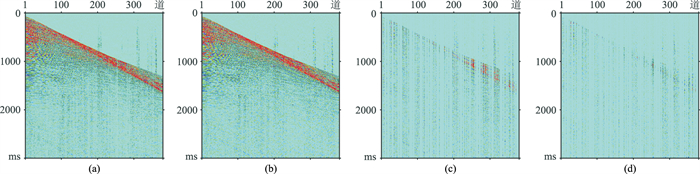
在全局随机采样情况下,Shearlet域重构数据(图 18a)的信噪比为10.08dB,FK+Shearlet域重构数据(图 18b)的信噪比为15.66dB,Shearlet域数据重构的误差(图 18c)明显大于FK+Shearlet域数据重构误差(图 18d),FK+Shearlet域重构效果优于Shearlet域重构效果。在分段随机采样情况下,Shearlet域重构数据(图 19a)的信噪比为10.47dB,FK+Shearlet域重构数据(图 19b)的信噪比为16.52dB,Shearlet域数据重构的误差(图 19c)大于FK+Shearlet域数据重构误差(图 19d),FK+Shearlet域重构效果优于Shearlet域重构。
|
图 18 实际数据全局随机采样下不同稀疏域重构结果对比 (a)Shearlet域重构结果;(b)FK+Shearlet域重构结果;(c)Shearlet域重构误差;(d)FK+Shearlet域重构误差 |
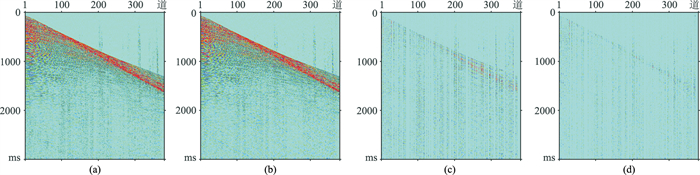
|
图 19 实际数据分段随机采样下不同稀疏域重构结果对比 (a)Shearlet域重构结果;(b)FK+Shearlet域重构结果;(c)Shearlet域重构误差;(d)FK+Shearlet域重构误差 |
在全局随机采样情况下,FK+Shearlet域重构数据有效信号的FK谱(图 20b)能量的恢复及空间假频的压制效果明显优于Shearlet域重构数据的FK谱(图 20a)。在分段随机采样情况下,FK+Shearlet域重构数据有效信号的FK谱(图 20d)能量恢复及空间假频的压制效果优于Shearlet域重构数据(图 20c)。
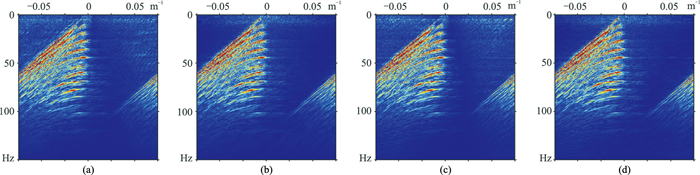
|
图 20 实际数据两种采样方式、不同域重构结果的FK谱对比 (a)全局随机,Shearlet域;(b)全局随机,FK+Shearlet域;(c)分段随机,Shearlet域;(d)分段随机,FK+Shearlet域 |
由表 3的数据重构信噪比可见,Shearlet域分段随机重构效果(图 19a)优于全局随机重构(图 18a),FK+Shearlet域分段随机重构效果(图 19b)优于全局随机重构(图 18b)。
4 结论压缩感知数据重构技术要求地震数据随机稀疏分布,由于数据缺失引起的假频在稀疏域表现为噪声,有效信号集中分布,假频和有效信号混叠,但是假频相对较弱,通过迭代的方法能进行数据重构。分段随机采样方法具有更为优越的“蓝色噪声”频谱分布,分段随机采样在保持采样随机性的同时,有效解决了重采样结果疏密不均问题。本文采用FK+Shearlet变换作为稀疏基进行分段随机采样数据重构。实验表明,FK+Shearlet域比Shearlet域能更好地描述地震数据的方向(线奇异)特征,分段随机采样FK+Shearlet域重构精度高于全局随机采样Shearlet域重构、分段随机采样Shearlet域重构和全局随机采样FK+Shearlet域重构。
| [1] |
MA X N, LI Z Y, LIANG G H, et al. Seismic data reconstruction based on compressed sensing[C]. Proceedings of the 7th International Conference on Environment and Engineering Geophysics & Summit Forum of Chinese Academy of Engineering on Enginee-ring Science and Technology, 2016, 34-37.
|
| [2] |
ZHANG H, CHEN X H, WU X M. Seismic data reconstruction based on CS and Fourier theory[J]. Applied Geophysics, 2013, 10(2): 170-180. DOI:10.1007/s11770-013-0375-3 |
| [3] |
刘国昌, 陈小宏, 郭志峰, 等. 基于Curvelet变换的缺失地震数据插值方法[J]. 石油地球物理勘探, 2011, 46(2): 237-246. LIU Guochang, CHEN Xiaohong, GUO Zhifeng, et al. Missing seismic data rebuilding by interpolation based on Curvelet transform[J]. Oil Geophysical Prospecting, 2011, 46(2): 237-246. |
| [4] |
YANG P L, GAO J H, CHEN W C. Curvelet-based POCS interpolation of nonuniformly sampled seismic records[J]. Journal of Applied Geophysics, 2012, 79(1): 90-99. |
| [5] |
ZHANG H, CHEN X H, ZHANG L Y. 3D simultaneous seismic data reconstruction and noise suppression based on the curvelet transform[J]. Applied Geophysics, 2017, 14(1): 87-95. DOI:10.1007/s11770-017-0607-z |
| [6] |
ZHANG H, DIAO S, CHEN W, et al. Curvelet reconstruction of non-uniformly sampled seismic data using the linearized Bregman method[J]. Geophysical Prospecting, 2019, 67(5): 1201-1218. DOI:10.1111/1365-2478.12762 |
| [7] |
CAI R, ZHAO Q, SHE D P, et al. Bernoulli-based random undersampling schemes for 2D seismic data regularization[J]. Applied Geophysics, 2014, 11(3): 321-330. DOI:10.1007/s11770-014-0447-z |
| [8] |
LIU W, CAO S Y, LI G F, et al. Reconstruction of seismic data with missing traces based on local random sampling and curvelet transform[J]. Journal of Applied Geophysics, 2015, 115: 129-139. DOI:10.1016/j.jappgeo.2015.02.009 |
| [9] |
WANG H C, TAO C H, CHEN S C, et al. High-precision seismic data reconstruction with multi-domain sparsity constraints based on curvelet and high-resolution Radon transforms[J]. Journal of Applied Geophysics, 2018, 162: 128-137. |
| [10] |
冯飞, 王征, 刘成明, 等. 基于Shearlet变换稀疏约束地震数据重建[J]. 石油物探, 2016, 55(5): 682-691. FENG Fei, WANG Zheng, LIU Chengming, et al. Seismic data reconstruction based on sparse constraint in the Shearlet domain[J]. Geophysical Prospecting for Petroleum, 2016, 55(5): 682-691. DOI:10.3969/j.issn.1000-1441.2016.05.007 |
| [11] |
张良, 韩立国, 许德鑫, 等. 基于压缩感知技术的Shearlet变换重建地震数据[J]. 石油地球物理勘探, 2017, 52(2): 220-225. ZHANG Liang, HAN Liguo, XU Dexin, et al. Seismic data reconstruction with Shearlet transform based on compressed sensing technology[J]. Oil Geophysical Prospecting, 2017, 52(2): 220-225. |
| [12] |
刘成明, 王德利, 胡斌, 等. Shearlet域稀疏约束地震数据重建[J]. 吉林大学学报(地球科学版), 2016, 46(6): 1855-1864. LIU Chengming, WANG Deli, HU Bin, et al. Seismic data interpolation based on sparse constraint in shearlet domain[J]. Journal of Jilin University(Earth Science Edition), 2016, 46(6): 1855-1864. |
| [13] |
杨冠雨, 栾锡武, 孟凡顺, 等. 基于Shearlet变换和广义全变分正则化的地震数据重建[J]. 地球物理学报, 2020, 63(9): 3465-3477. YANG Guanyu, LUAN Xiwu, Meng Fanshun, et al. Seismic data reconstruction based on Shearlet transform and total generalized variation regularization[J]. Chinese Journal of Geophysics, 2020, 63(9): 3465-3477. |
| [14] |
王常波. 基于Shearlet稀疏变换基的压缩感知重建技术[J]. 地球物理学进展, 2018, 33(6): 2441-2449. WANG Changbo. Compressed sensing seismic data reconstruction with Shearlet transformation[J]. Progress in Geophysics, 2018, 33(6): 2441-2449. |
| [15] |
张凯, 张医奎, 李振春, 等. MCA框架下Shearlet和DCT字典组合地震数据重建[J]. 石油地球物理勘探, 2019, 54(5): 1005-1013, 1056. ZHANG Kai, ZHANG Yikui, LI Zhenchun, et al. Seismic data reconstruction with the discrete cosine transform and Shearlet dictionaries under the morphological component analysis framework[J]. Oil Geophysical Prospecting, 2019, 54(5): 1005-1013, 1056. |
| [16] |
江萍, 张凯, 张医奎, 等. 基于形态分量分析的含噪地震数据重建方法[J]. 地球物理学进展, 2019, 34(2): 573-580. JIANG Ping, ZHANG Kai, ZHANG Yikui, et al. Noisy seismic data reconstruction method based on morphological component analysis framework[J]. Progress in Geophysics, 2019, 34(2): 573-580. |
| [17] |
周亚同, 刘志峰, 张志伟. 形态分量分析框架下基于DCT与曲波字典组合的地震信号重建[J]. 石油物探, 2015, 54(5): 560-568, 581. ZHOU Yatong, LIU Zhifeng, ZHANG Zhiwei. Seismic signal reconstruction under the morphological component analysis framework combined with DCT and curvelet dictionary[J]. Geophysical Prospecting for Petroleum, 2015, 54(5): 560-568, 581. DOI:10.3969/j.issn.1000-1441.2015.05.009 |
| [18] |
CANDES E J, ROMBERG J, TAO T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transactions on Information Theory, 2006, 52(2): 489-509. DOI:10.1109/TIT.2005.862083 |
| [19] |
DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306. DOI:10.1109/TIT.2006.871582 |
| [20] |
CANDES E J, TAO T. Decoding by linear programming[J]. IEEE Transactions on Information Theory, 2005, 51(12): 4203-4215. DOI:10.1109/TIT.2005.858979 |
| [21] |
刘洋, 张鹏, 刘财, 等. 地震数据Bregman整形迭代插值方法[J]. 地球物理学报, 2018, 61(4): 1400-1412. LIU Yang, ZHANG Peng, LIU Cai, et al. Seismic data interpolation based on Bregman shaping iteration[J]. Chinese Journal of Geophysics, 2018, 61(4): 1400-1412. |
| [22] |
王本锋, 陈小宏, 耿建华. 地震数据POCS插值重建中的一种新型质量控制准则[J]. 石油物探, 2019, 58(1): 71-77. WANG Benfeng, CHEN Xiaohong, Geng Jianhua. A novel quality control criterion in the POCS interpolation of seismic data[J]. Geophysical Prospecting for Petroleum, 2019, 58(1): 71-77. DOI:10.3969/j.issn.1000-1441.2019.01.009 |
| [23] |
GAO J J, CHEN X H, LI J Y, et al. Irregular seismic data reconstruction based on exponential threshold model of POCS method[J]. Applied Geophysics, 2010, 7(3): 229-238. DOI:10.1007/s11770-010-0246-5 |
| [24] |
李欣, 杨婷, 孙文博, 等. 一种基于光滑L1范数的地震数据插值方法[J]. 石油地球物理勘探, 2018, 53(2): 251-256. LI Xin, YANG Ting, SUN Wenbo, et al. A gradient projection method for smooth L1 norm regularization based seismic data sparse interpolation[J]. Oil Geophysical Prospecting, 2018, 53(2): 251-256. |
| [25] |
兰天维, 韩立国, 张良. 基于压缩感知的L1范数谱投影梯度算法地震数据重建[J]. 石油物探, 2019, 58(2): 219-228, 244. LAN Tianwei, HAN Liguo, ZHANG Liang. Seismic data reconstruction based on spectral projection gra-dient L1 algorithm via compressive sensing[J]. Geophy-sical Prospecting for Petroleum, 2019, 58(2): 219-228, 244. DOI:10.3969/j.issn.1000-1441.2019.02.007 |
| [26] |
兰南英, 张繁昌, 张益明, 等. 快速结构字典学习三维地震数据重建方法[J]. 石油地球物理勘探, 2020, 55(1): 1-9. LAN Nanying, ZHANG Fanchang, ZHANG Yiming, et al. 3D seismic data reconstruction based on a fast structure dictionary learning method[J]. Oil Geophysical Prospecting, 2020, 55(1): 1-9. |
| [27] |
周亚同, 王丽莉, 蒲青山. 压缩感知框架下基于K-奇异值分解字典学习的地震数据重建[J]. 石油地球物理勘探, 2014, 49(4): 652-660. ZHOU Yatong, Wang Lili, PU Qingshan. Seismic data reconstruction based on K-SVD dictionary learning under compressive sensing framework[J]. Oil Geophysical Prospecting, 2014, 49(4): 652-660. |
| [28] |
段中钰, 李婷婷, 肖勇, 等. 基于压缩感知的SR-ADMM地震数据重建[J]. 石油地球物理勘探, 2021, 56(6): 1220-1228. DUAN Zhongyu, LI Tingting, XIAO Yong, et al. Seismic data reconstruction by SR-ADMM algorithm basedon compressed sensing[J]. Oil Geophysical Prospecting, 2021, 56(6): 1220-1228. |
| [29] |
温睿, 刘国昌, 冉扬. 压缩感知地震数据重建中的三个关键因素分析[J]. 石油地球物理勘探, 2018, 53(4): 682-693. WEN Rui, LIU Guochang, RAN Yang. Three key factors in seismic data reconstruction based on compressive sensing[J]. Oil Geophysical Prospecting, 2018, 53(4): 682-693. |
| [30] |
张华, 陈小宏. 基于jitter采样和曲波变换的三维地震数据重建[J]. 地球物理学报, 2013, 56(5): 1637-1649. ZHANG Hua, CHEN Xiaohong. Seismic data reconstruction based on jittered sampling and curvelet transform[J]. Chinese Journal of Geophysics, 2013, 56(5): 1637-1649. |
| [31] |
王汉闯, 陶春辉, 陈生昌, 等. 基于稀疏约束的地震数据高效采集方法理论研究[J]. 地球物理学报, 2016, 59(11): 4246-4265. WANG Hanchuang, TAO Chunhui, CHEN Sheng-chang, et al. Study on highly efficient seismic data acquisition method and theory based on sparsity constraint[J]. Chinese Journal of Geophysics, 2016, 59(11): 4246-4265. DOI:10.6038/cjg20161126 |
| [32] |
GUO K H, LABATE D. Optimally sparse multidimensional representation using shearlets[J]. SIAM Journal on Mathematical Analysis, 2007, 39(1): 298-318. DOI:10.1137/060649781 |
| [33] |
EASLEY G, LABATE D, LIM W Q. Sparse directional image representations using the discrete shearlet transform[J]. Applied and Computational Harmonic Analysis, 2008, 25(1): 25-46. DOI:10.1016/j.acha.2007.09.003 |
| [34] |
GUO K, LABATE D. The construction of smooth Parseval frames of shearlets[J]. Mathematical Mo-delling of Natural Phenomena, 2013, 8(1): 82-105. DOI:10.1051/mmnp/20138106 |



 周辉,北京市昌平区府学路18号中国石油大学(北京)地球物理学院,102249。Email:
周辉,北京市昌平区府学路18号中国石油大学(北京)地球物理学院,102249。Email: