② 地球信息探测仪器教育部重点实验室,吉林长春 130000
② Key Laboratory of Geophysical Exploration Equipment, Ministry of Education, Changchun, Jilin 130000, China
在信号处理领域,通常采用压缩技术解决多维海量数据的存储和传输问题。Donoho[1]首先提出了压缩感知(Compressed Sensing,CS)的概念。CS理论认为,如果一个信号是稀疏的或可压缩的,那么可利用远少于奈奎斯特采样数量的测量值无失真地重建[2]。为解决地震勘探采集的地震数据因通信带宽和功耗等限制难以实时回传这一难题,应用CS理论将原始地震数据压缩后传输,从而减少地震数据的传输量,提高传输效率[3-6]。由CS理论可知:地震数据越稀疏,重构精度越高;采用不同的稀疏表示方法对地震数据进行稀疏表示,其稀疏度会有所不同[7-10]。
目前,地震数据稀疏表示方法大体上可分为两类。一类是固定变换域稀疏表示方法,如傅里叶变换、离散余弦变换及小波变换等,均是通过固定公式生成字典。这类方法构造字典的过程简单、快速,但固定基一旦确定,就不能更改,因此稀疏表示效果较差,尤其是当野外采集的地震信号含有噪声、波形比较复杂时。另一类方法是字典学习型稀疏表示法,如最优方向法(Method of Optimal Directions,MOD)和K—奇异值分解(K-Singular Value Decomposition,K-SVD)方法[11-12]等,均能学习地震数据的特点,然后根据这些特征自适应调整字典,因此对野外采集到的地震数据有较好的稀疏表示效果。MOD采用交替优化方式对模型进行求解,在字典更新阶段采用的是全局更新策略,稀疏表示过程中产生的字典性能较低;K-SVD方法采用稀疏编码和字典更新相互交替完成对信号特征的学习,得益于其单独更新字典原子的策略,对地震数据的稀疏表示效果较好,重构精度较高[13-14]。
本文采用一种改进的稀疏表示方法[15-19]对地震数据进行处理重构。该方法采用多层字典学习的方案,利用更多的数据特征去训练字典,增强稀疏表示方法的特征提取能力;同时,在稀疏编码阶段设置三个终止条件,使其可以自适应地确定不同地震数据所选择的原子数。与K-SVD方法相比,在重构算法相同的前提下,本文方法能够为基于CS的地震数据重构提供更准确的稀疏表示,对地震数据有更高的重构精度。
1 地震数据K-SVD稀疏表示 1.1 地震数据K-SVD稀疏表示法设x是长度为N的一维信号,x∈RN,R为矩阵,稀疏度为K,则有‖x‖0∈RN≤K,其中‖·‖0表示一个向量中非零向量的个数,用测量矩阵Φ∈RM×N(M<N)对原始信号x进行压缩采样,表示为y=Φx,其中y是长度为M的一维测量值,y∈RM。压缩感知问题就是在已知测量值y和测量矩阵Φ的基础上,求解欠定方程组y=Φx,以得到原始信号x。
稀疏表示理论作为CS理论的首个组成成分,为大多数信号的稀疏表示提供了新的采样形式,不同的稀疏表示方法效果不同。作为一种典型的字典学习型稀疏表示方法,K-SVD可根据不同的地震数据生成不同的稀疏表示字典,并通过稀疏编码和字典更新两个过程交替完成对地震数据的学习过程。K-SVD算法的数学表达式为
| $\begin{array}{c} {\min\limits_{\mathit{\boldsymbol{D}}, \mathit{\boldsymbol{X}}}}\left\| {\mathit{\boldsymbol{Y}} - \mathit{\boldsymbol{DX}}} \right\|_{\rm{F}}^2\quad \forall i, {\left\| {{\mathit{\boldsymbol{x}}_i}} \right\|_0} \leqslant {T_0}\\ i = 1, 2, \cdots , N \end{array}$ | (1) |
式中:Y为原始地震数据;D为经K-SVD算法训练的字典;X为稀疏系数矩阵;‖·‖F表示Frobenius范数;xi为X的第i列向量;T0为稀疏系数向量中最大非零元素个数。
K-SVD对地震数据进行稀疏表示通过以下三步进行。
(1) 初始化,即从原始地震数据中选取少部分数据作为字典的初始值。
(2) 稀疏编码,即固定初始字典D,采用正交匹配追踪算法(OMP)[20-21]求解稀疏矩阵X。求解过程可表示为
| ${\mathit{\boldsymbol{\overline x}} _i} = {\min\limits_{{x_i}}}\left( {\left\| {{\mathit{\boldsymbol{y}}_i} - \mathit{\boldsymbol{D}}{\mathit{\boldsymbol{x}}_i}} \right\|_2^2} \right)\quad \forall i, {\left\| {{\mathit{\boldsymbol{x}}_i}} \right\|_0} \leqslant {T_0}$ | (2) |
式中:xi为xi更新后的向量;yi为Y的第i列向量。
(3) 字典更新,即固定稀疏系数矩阵X,更新字典D。其过程为
| $\begin{array}{l} \overline {\mathit{\boldsymbol{D}}} = {\min\limits_{\mathit{\boldsymbol{D}}}}\left\| {{\mathit{\boldsymbol{Y}}} - {\mathit{\boldsymbol{D}}}\overline {\mathit{\boldsymbol{X}}} } \right\|_{\rm{F}}^2 = {\min\limits_{\mathit{\boldsymbol{D}}}}\left\| {{\mathit{\boldsymbol{Y}}} - \sum\limits_{i = 1}^K {{{\mathit{\boldsymbol{d}}}_i}} {{\overline {\mathit{\boldsymbol{x}}} }_i}} \right\|_{\rm{F}}^2\\ = {\min\limits_{\mathit{\boldsymbol{D}}}}\left\| {\left( {{\mathit{\boldsymbol{Y}}} - \sum\limits_{i \ne 1} {{{\mathit{\boldsymbol{d}}}_i}} {{\overline {\mathit{\boldsymbol{x}}} }_i}} \right) - {{\mathit{\boldsymbol{D}}}_j}{{\overline {\mathit{\boldsymbol{x}}} }_j}} \right\|_{\rm{F}}^2 = {\min\limits_{\mathit{\boldsymbol{D}}}}\left\| {{E_j} - {{\mathit{\boldsymbol{d}}}_j}{{\bar x}_j}} \right\|_{\rm{F}}^2 \end{array}$ | (3) |
式中:D为更新后的字典;X为更新后的稀疏系数矩阵;dj为D的第j列向量,即第j个原子;E为残差矩阵。
xj经去零操作后得到xj, R,从E中取出相对应的列向量构成Ej,R。对Ej,R进行奇异值分解
| ${\mathit{\boldsymbol{E}}_{j, {\rm{R}}}} = \mathit{\boldsymbol{U \boldsymbol{\varSigma} }}{\mathit{\boldsymbol{V}}^{\rm{T}}}$ | (4) |
式中:U为左奇异值矩阵;Σ为对角矩阵;V为右奇异值矩阵。取U的第1列更新dj,取VT的第1行与Σ中第一个元素的乘积更新xj, R。
重复步骤(2)~步骤(3),直至收敛到指定的误差或达到指定的迭代次数。
1.2 K-SVD的缺陷(1) 在K-SVD方法中,每个训练样本的K是固定的。不同样本所包含特征的信息量可能不同,对于一个包含大量特征的训练样本,如果K值太小,就没有足够的原子表示这些特征,称为欠拟合;如果K值过大,多余的原子会引起表示的过拟合,从而影响稀疏性。
(2) 在字典学习过程中,不同的目标样本会产生不同的残差,进而形成客观特征差异较大的残差层。在K-SVD方法中,由于不同的残差层采用同一个原子表示,因此,一个原子必须在不止一种类型的客观特征之间妥协,降低了CS重构的精度。
针对K-SVD方法的局限性,本文采用AMDL对地震数据进行稀疏表示。
2 地震数据AMDL稀疏表示方法AMDL方法已广泛应用于图像处理、视觉识别等领域,并获得了较理想的结果[22],但在地震勘探领域中的应用至今未见。
AMDL方法首先将字典分成若干子字典,然后分别求出每个子字典及相应的稀疏系数,最后用它们的乘积之和表示地震数据。其稀疏表示模型为
| $\mathit{\boldsymbol{Y}} = \sum\limits_{c = 1}^{{c_{\max }}} {{\mathit{\boldsymbol{D}}_c}} {\mathit{\boldsymbol{X}}_c}$ | (5) |
式中:cmax为字典的最大层数;Dc为第c层的子字典;Xc为第c层的稀疏系数矩阵。每个子字典Dc包含qh个原子,因此原子总数q=qhcmax。
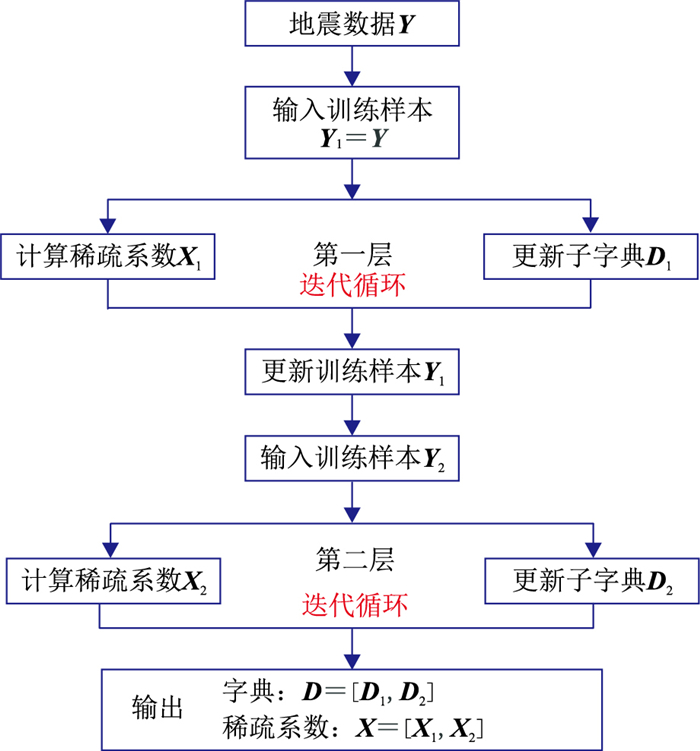
图 1给出了字典最大层数为2时的地震数据AMDL方法流程。AMDL算法在处理地震数据时,首先输入原始地震数据Y、层数cmax、每层最大稀疏水平qmax、每层最大迭代循环数tmax、系数ε以及阈值λ。第一层直接利用原始训练样本Y1=Y训练子字典D1,第一层的残差r1=Y1-D1X1,将其作为第二层子字典的训练样本Y2=r1来训练子字典D2。
|
图 1 AMDL方法地震数据稀疏表示流程 |
与K-SVD类似,AMDL方法中每层子字典的训练均分为子字典初始化、稀疏编码和字典更新三个阶段。
(1) 初始化阶段。从地震数据Y中选取少部分数据作为第一层子字典的训练样本Y1,并将Y1作为子字典D1的初始值;每层交替执行t次稀疏编码和字典更新,直至收敛到指定的误差,或达到指定的迭代次数。
(2) 稀疏编码阶段。首先,固定初始化子字典Dc,求解稀疏系数矩阵Xc,即
| ${\mathit{\boldsymbol{X}}_c} = {\left( {\left| {{\mathit{\boldsymbol{D}}_c}} \right| \times \mathit{\boldsymbol{E}}} \right)^{ - 1}}\mathit{\boldsymbol{D}}_c^*{\mathit{\boldsymbol{Y}}_c}$ | (6) |
其次,设定三个终止条件:①迭代次数t是否达到最大值tmax;②计算‖rc‖2是否小于阈值λ;③计算字典Dc与残差rc,计算内积向量p=DcTrc,找到p的最大级条目pmax,并判断是否小于ε‖rc‖2,同时判断qmax是否大于1。在③中ε为设置的系数,其值越大,选择原子需越谨慎。若满足三个条件之一,即t≥tmax、‖rc‖2<λ、pmax<ε‖rc‖2且qmax>1,则输出稀疏系数矩阵Xc,结束稀疏编码阶段,否则重复式(6)的计算,更新稀疏系数矩阵,直至达到其中一个终止条件,退出迭代。
终止条件①表示“足够的迭代周期”,保证至多选择qmax个原子;终止条件②‖rc‖2<λ表示“残差足够小”,保证在稀疏编码足够精确的情况下终止迭代,结束稀疏编码阶段,减少计算量;终止条件③pmax<ε‖rc‖2,qmax>1表示“残差与原子的相关性与第一个迭代周期”,保证在残差与剩余原子足够相关的前提下至少为本层的目标样本选择一个原子,其中,pmax<ε‖rc‖2说明子字典Dc中剩余原子与残差rc的相关性不足,qmax>1说明本层至少选取一个原子。由此可以自适应地确定每个目标样本所选择的原子数量,从而减少稀疏编码过程中的欠拟合或过拟合问题。
(3) 字典更新阶段。固定稀疏系数矩阵Xc,采用K-SVD的更新策略进行Dc的原子更新。
每层重复执行上述阶段,直至遍历设定的层数cmax,终止计算过程,最后输出更新后的字典D=[D1, D2, …, Dcmax]及与其相对应的稀疏矩阵系数X=[X1, X2, …, Xcmax]。
AMDL方法采用的多层字典学习方案除了考虑原始训练样本包含的特征外,还考虑了不同层的样本残差所包含的特征,使其能够在字典学习过程中充分利用不同层次的特征,提高地震数据的重构精度;同时,自适应策略可以确定每个地震数据在多层模式下使用原子的数量,使稀疏度自适应于每个训练样本,减少地震数据在稀疏表示过程中的欠拟合或过拟合问题,提高地震数据的稀疏性,进而提高重构精度。
K-SVD方法的目标是尽量减少表示残差。而AMDL考虑两个方面:一是尽可能减少表示残差;二是减少地震数据稀疏表示中使用的原子数。换言之,AMDL的主要任务是使用尽可能少的原子获得更精确的表示。
3 试验结果与分析压缩比(测量矩阵的行、列数之比(M/N))是描述对原始地震数据的压缩程度,压缩比越大,表示压缩程度越小,压缩后的数据越多,易于重构;反之,压缩比越小,表示压缩程度越高,压缩后的数据越少,不易于重构。本试验采用了两个地区的实测地震数据,同时采取控制变量法,利用K-SVD和AMDL两种方法在不同压缩比下分别对其进行稀疏表示,然后采用相同的重构算法进行重构,通过计算相同压缩比下的重构数据信噪比(SNR)和相对误差(Error)评价两种方法。
重构地震数据的信噪比计算公式为
| ${\rm{SNR}} = 20\lg \frac{{||\mathit{\boldsymbol{Y}}||{_2}}}{{||\mathit{\boldsymbol{\overline Y}} - \mathit{\boldsymbol{Y}}||{_2}}}$ | (7) |
重构数据的相对误差计算公式为
| ${\rm{ Error }} = \frac{{{{\left\| {\mathit{\boldsymbol{Y}} - \mathit{\boldsymbol{\overline Y}} } \right\|}_2}}}{{{{\left\| {\mathit{\boldsymbol{\overline Y}} } \right\|}_2}}}$ | (8) |
式中Y表示经稀疏表示压缩后重构的地震数据。
3.1 辽宁兴城地质走廊带实测地震数据试验选取采样率为1ms、采样时间为0.256s、总计256道的地震数据进行试验。首先,利用K-SVD方法和AMDL方法在不同压缩比下,分别对地震数据进行稀疏表示;然后,利用基追踪[23-25]重构算法进行地震数据重构。试验中,将AMDL方法中的几个参数设定为:层数cmax=4,每层最大稀疏水平qh=10,每层最大迭代循环数tmax=3,系数ε=0.5,阈值λ=0.0001。
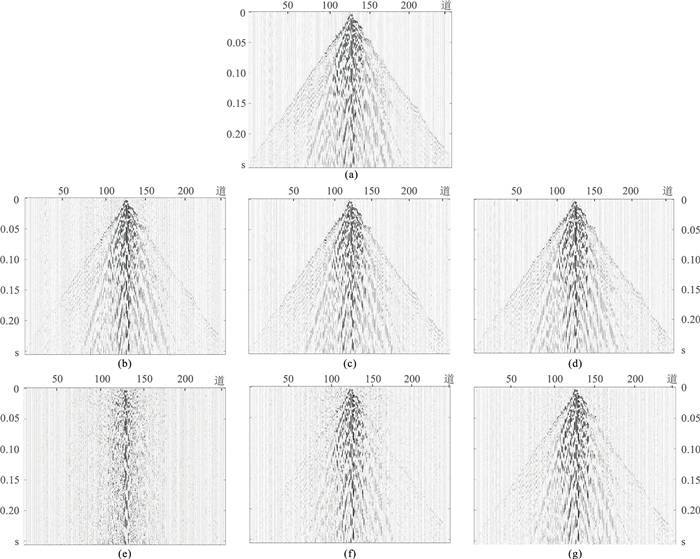
图 2a为原始地震数据,图 2b~图 2d和图 2e~图 2g分别为经过AMDL方法和K-SVD方法稀疏表示后,压缩比为0.1、0.3和0.5时的重构地震数据。可以明显看出,在压缩比为0.1时,经过K-SVD方法稀疏表示后重构的地震数据和原始地震数据相似度非常低,重构精度远低于经过AMDL方法稀疏表示后的重构精度;在压缩比为0.3时,经过K-SVD方法稀疏表示后地震数据的重构精度有明显的提升,但仍低于同压缩比下AMDL方法的重构精度;在压缩比为0.5时,经过K-SVD方法稀疏表示后重构的地震数据和原始地震数据相似度较高,重构精度与AMDL方法在压缩比为0.1时的地震数据重构精度大致相同。
|
图 2 辽宁兴城实测地震数据及两种方法在不同压缩比下稀疏表示后重构的地震数据 (a)原始地震数据;(b)AMDL法,压缩比为0.1;(c)AMDL法,压缩比为0.3;(d)AMDL法,压缩比为0.5;(e)K-SVD,压缩比为0.1;(f)K-SVD,压缩比为0.3;(g)K-SVD,压缩比为0.5 |
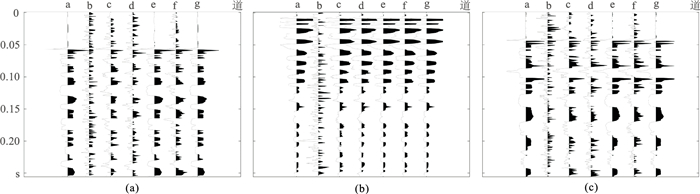
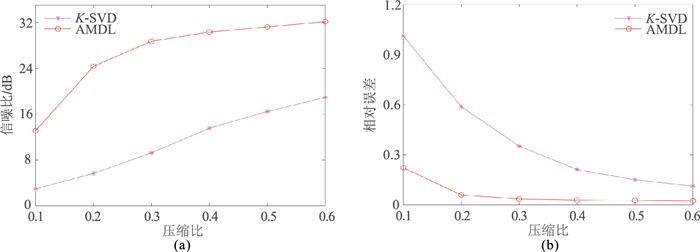
为了更加直观地展示地震数据的重构精度,从原始数据和不同压缩比下的重构数据中选取第100、125和150道数据进行波形对比。图 3a~图 3c分别为原始地震数据和在不同压缩比下经过两种方法稀疏表示后重构地震数据中第100道、125道和150道数据的波形对比图,a代表原始地震数据,b、d和f分别代表压缩比为0.1、0.3和0.5时经过K-SVD方法稀疏表示后重构地震数据,c、e和g分别代表压缩比为0.1、0.3和0.5时经过AMDL方法稀疏表示后重构地震数据。图 4a、图 4b分别为地震数据经过两种不同方法稀疏表示后,在不同压缩比下重构信噪比和相对误差的对比图。可以看出,压缩比为0.1时,AMDL方法的重构信噪比比K-SVD方法高约10dB,提高了近3.5倍,重构误差比K-SVD方法低约0.8,降低了近80%;在压缩比为0.2时,信噪比提高约20dB,提高了近3.5倍,且重构误差减小约0.53,重构误差降低了近90%;在其它压缩比下,信噪比提高了约1~2倍,重构误差降低了80%~90%。可见,在相同压缩比下且使用相同的重构算法前提下,AMDL方法对地震数据稀疏表示后重构的地震数据信噪比更高,相对误差更小。
|
图 3 辽宁兴城实测地震数据不同道波形与两种方法在不同压缩比下稀疏表示后重构数据波形的对比 (a)第100道;(b)第125道;(c)第150道 |
|
图 4 辽宁兴城实测地震数据在不同压缩比下两种方法稀疏表示后的重构数据的信噪比(a)和相对误差(b)对比 |
为进一步证明两种方法的稀疏表示效果,选取甘肃金昌铜镍矿的实测地震数据做了相同的对比试验,本数据由500N的轻便小型可控震源产生,且该实测地震数据经过预处理。数据的采样率为1ms,采样时间为2s,道数为72道。同样利用不同压缩比下两种方法分别对地震数据进行稀疏表示。然后利用基追踪重构算法进行数据重构。AMDL方法的参数与3.1相同。
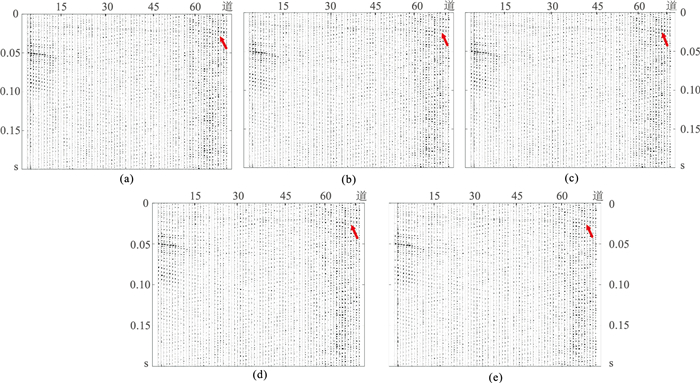
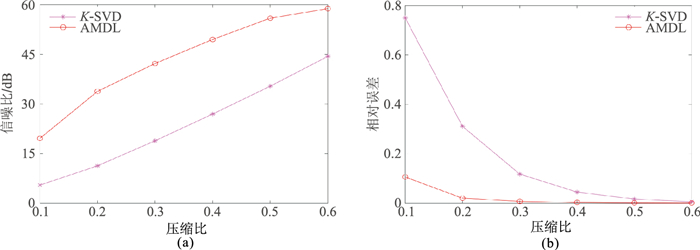
图 5a为原始地震数据。图 5b~图 5c分别为经AMDL方法稀疏表示后压缩比分别为0.1和0.3时的重构地震数据。图 5d~图 5e分别为经过K-SVD方法稀疏表示后、压缩比分别为0.1和0.3时的重构地震数据。由图可见,压缩比在0.1时,经过AMDL方法稀疏表示后重构的地震数据具有很高的重构精度,可清楚地看出反射层的位置(图 5b箭头所示),而经过K-SVD方法稀疏表示后重构的地震数据与原始地震数据相似度较低,只能隐约看出反射层的位置(图 5d箭头所示)。而压缩比为0.3时,经过K-SVD方法稀疏表示后地震数据的重构精度有明显提升,也可以清晰看出反射层位置(图 5e箭头所示),且重构精度与AMDL方法在压缩比为0.1时的地震数据重构精度几乎相同。图 6a和图 6b分别为经两种不同方法稀疏表示后、在不同压缩比下重构的地震数据信噪比和相对误差的对比,同样可以看出,压缩比相同时,AMDL算法对地震数据稀疏表示后重构的地震数据信噪比更高、相对误差更小。
|
图 5 甘肃金昌实测地震数据与两种方法在不同压缩比下稀疏表示后重构数据的对比 (a)原始地震数据;(b)AMDL法,压缩比为0.1;(c)AMDL法,压缩比为0.3;(d)K-SVD,压缩比为0.1;(e)K-SVD,压缩比为0.3 |
|
图 6 甘肃金昌实测数据不同压缩比时两种方法稀疏表示后的重构数据的信噪比(a)和相对误差(b)对比 |
两组数据的试验结果可以证明,在处理相同的实测地震数据,且使用相同重构算法的前提下,相比于K-SVD方法,AMDL方法对地震数据的稀疏表示精度更高、效果更好。
4 结束语本文将自适应多层字典学习(AMDL)方法用于地震数据的稀疏表示,旨在字典学习过程中利用不同的特征层训练字典,且自适应地确定每个训练样本使用的原子数,不仅可利用更多的特征训练字典,而且字典不会受到其他特征层的影响,同时避免了稀疏表示过程中出现的欠拟合和过拟合问题。实测地震数据重构试验结果表明,AMDL方法具有较强的稀疏表示能力,相比于K-SVD方法,其在地震数据稀疏表示方面更具优越性。
| [1] |
DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306. DOI:10.1109/TIT.2006.871582 |
| [2] |
CANDES E J, WAKIN M B. An introduction to compressive sampling[J]. IEEE Signal Processing Ma-gazine, 2008, 25(2): 21-30. DOI:10.1109/MSP.2007.914731 |
| [3] |
HERRMANN F J. Randomized sampling and sparsity: getting more information from fewer samples[J]. Geophysics, 2010, 75(6): WB173-WB187. DOI:10.1190/1.3506147 |
| [4] |
HERRMANN F J, FRIEDLANDER M P, YILMAZ O. Fighting the curse of dimensionality: compressive sensing in exploration seismology[J]. IEEE Signal Processing Magazine, 2012, 29(3): 88-100. DOI:10.1109/MSP.2012.2185859 |
| [5] |
黄小刚. 海上压缩感知地震仿真采集设计与处理[J]. 石油地球物理勘探, 2020, 55(2): 248-256. HUANG Xiaogang. A simulation of acquisition design and data processing for offshore compressive sensing seismic[J]. Oil Geophysical Prospecting, 2020, 55(2): 248-256. |
| [6] |
宋维琪, 吴彩端. 利用压缩感知方法提高地震资料分辨率[J]. 石油地球物理勘探, 2017, 52(2): 214-219. SONG Weiqi, WU Caiduan. Seismic data resolution improvement based on compressed sensing[J]. Oil Geophysical Prospecting, 2017, 52(2): 214-219. |
| [7] |
MA J W, PLONKA G, CHAURIS H. A new sparse representation of seismic data using adaptive easy-path wavelet transform[J]. IEEE Geoscience and Remote Sensing Letters, 2010, 7(3): 540-544. DOI:10.1109/LGRS.2010.2041185 |
| [8] |
陈祖斌, 王丽芝, 宋杨, 等. 基于压缩感知的小波域地震数据实时压缩与高精度重构[J]. 石油地球物理勘探, 2018, 53(4): 674-681, 693. CHEN Zubin, WANG Lizhi, SONG Yang, et al. Seismic data real-time compression and high-precision reconstruction in the wavelet domain based on the compressed sensing[J]. Oil Geophysical Prospecting, 2018, 53(4): 674-681, 693. |
| [9] |
TIAN X, ABDI A, LIU E T, et al. Memory-assisted seismic signal compression based on dictionary lear-ning and sparse coding[C]//2017 IEEE Global Conference on Signal and Information Processing (Global SIP), 2017: 358-362.
|
| [10] |
赵子越, 李振春, 张敏. 利用压缩感知技术的离散正交S变换地震数据重建[J]. 石油地球物理勘探, 2020, 55(1): 29-35. ZHAO Ziyue, LI Zhenchun, ZHANG Min. Seismic data Reconstruction using discrete orthonormal S-Transform based on compressive sensing[J]. Oil Geophysical Prospecting, 2020, 55(1): 29-35. |
| [11] |
AHARON M, ELAD M, BRUCKSTEIN A. K-SVD: an algorithm for designing overcomplete dictionaries for sparse representation[J]. IEEE Transactions on Signal Processing, 2006, 54(11): 4311-4322. DOI:10.1109/TSP.2006.881199 |
| [12] |
LIU Z X, WAN W G. Image inpainting algorithm based on KSVD and improved CDD[C]. 2018 International Conference on Audio, Language and Image Processing (ICALIP), 2018: 413-417.
|
| [13] |
SUN H M, JIA R S, ZHANG X L, et al. Reconstruction of missing seismic traces based on sparse dictionary learning and the optimization of measurement matrices[J]. Journal of Petroleum Science and Engi-neering, 2019, 175: 719-727. DOI:10.1016/j.petrol.2019.01.016 |
| [14] |
YU C X, ZHAO J T, WANG Y F. Seismic detection method for small-scale discontinuities based on dictionary learning and sparse representation[J]. Journal of Applied Geophysics, 2017, 137: 55-62. DOI:10.1016/j.jappgeo.2016.12.005 |
| [15] |
SMITH L N, ELAD M. Improving dictionary lear-ning: multiple dictionary updates and coefficient reuse[J]. IEEE Signal Processing Letters, 2013, 20(1): 79-82. DOI:10.1109/LSP.2012.2229976 |
| [16] |
NAZZAL M, YEGANLI F, OZKARAMANLI H. A strategy for residual component-based multiple structured dictionary learning[J]. IEEE Signal Processing Letters, 2015, 22(11): 2059-2063. DOI:10.1109/LSP.2015.2456071 |
| [17] |
CHEN B, POLATKAN G, SAPIRO G, et al. Deep learning with hierarchical convolutional factor analysis[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(8): 1887-1901. DOI:10.1109/TPAMI.2013.19 |
| [18] |
TARIYAL S, MAJUMDAR A, SINGH R, et al. Deep dictionary learning[J]. IEEE Access, 2016, 4: 10096-10109. DOI:10.1109/ACCESS.2016.2611583 |
| [19] |
FU J, YUAN H K, ZHAO R Q, et al. Adaptive multilayered dictionary learning for compressive-sensing-based image reconstruction[J]. IEEE Access, 2019, 7: 105922-105936. DOI:10.1109/ACCESS.2019.2932098 |
| [20] |
TROPP J A, GILBERT A C. Signal recovery from random measurements via orthogonal matching pursuit[J]. IEEE Transactions on Information Theory, 2007, 53(12): 4655-4666. DOI:10.1109/TIT.2007.909108 |
| [21] |
TROPP J A. Greed is good: algorithmic results for sparse approximation[J]. IEEE Transactions on Information Theory, 2004, 50(10): 2231-2242. DOI:10.1109/TIT.2004.834793 |
| [22] |
GAO Z, XUAN H Z, ZHANG H, et al. Adaptive fusion and category-level dictionary learning model for multiview human action recognition[J]. IEEE Internet of Things Journal, 2019, 6(6): 9280-9293. DOI:10.1109/JIOT.2019.2911669 |
| [23] |
姚振岸, 孙成禹, 李红星, 等. 基于基追踪的时变子波提取与地震反射率反演[J]. 石油地球物理勘探, 2019, 54(1): 137-144. YAO Zhen'an, SUN Chengyu, LI Hongxing, et al. Time-variant wavelet extraction and seismic reflectivity inversion based on basis pursuit[J]. Oil Geophysical Prospecting, 2019, 54(1): 137-144. |
| [24] |
CHEN S S, DONOHO D L, SAUNDERS M A. Atomic decomposition by basis pursuit[J]. SIAM Review, 2001, 43(1): 129-159. DOI:10.1137/S003614450037906X |
| [25] |
RAUHUT H. Stability results for random sampling of sparse trigonometric polynomials[J]. IEEE Transactions on Information Theory, 2008, 54(12): 5661-5670. DOI:10.1109/TIT.2008.2006382 |



 王俊秋,吉林省长春市朝阳区西民主大街938号吉林大学,130000。Email:
王俊秋,吉林省长春市朝阳区西民主大街938号吉林大学,130000。Email: