② 西安交通大学信息与通信工程学院,陕西西安 710049;
③ 西安交通大学人工智能学院,陕西西安 710049;
④ 西安交通大学数学与统计学院,陕西西安 710049
② School of Information and Communications Engineering, Xi'an Jiaotong University, Xi'an, Shaanxi 710049, China;
③ College of Artificial Intelligence, Xi'an Jiaotong University, Xi'an, Shaanxi 710049, China;
④ School of Mathematics and Statistics, Xi'an Jiaotong University, Xi'an, Shaanxi 710049, China
断层解释的精度和效率对油气藏的勘探与开发非常重要。早期主要依靠人工在地震剖面上解释断层[1-2],这极大地依赖于解释人员的经验,断层解释精度和效率难以满足实际生产需要。随着信号处理等方法的拓展以及计算机技术的飞速发展,越来越多的数据处理方法应用于断层识别,提高了断层解释的准确性和效率。
相干体分析技术常用于描述地质体的不连续性,可用于断层解释。相干体是指由地震数据体经过相关性计算而得到的一种新的属性数据体,利用该数据体,不连续的断层信息能够从三维地震资料中突显出来。Bahorich等[3]提出了第一代相干体技术(C1)并用于断层识别,该算法计算量小,但易受相干噪声干扰。在C1的基础上,Marfurt等[4]基于多道相似原理,提出了第二代相干体技术(C2),弥补了C1因采样地震道少而导致的抗噪性差的不足。随后,Gersztenkorn等[5]提出了基于本征结构的第三代相干体技术(C3),可更精细地描述断层特征。此后,很多学者对相干体技术进行了发展和推广。王西文等[6]在相干分析中引入小波变换,提高了小断层的识别能力。Li等[7]结合倾角扫描与超道技术,提高了相干体技术对大倾角地质结构的适用性。杨培杰等[8]提出了方向性边界保持断层增强技术以提高地震资料分辨率。郑静静等[9]则在Curvelet变换的基础上进行多尺度相干分析,同样在断层识别方面效果较好。Yang等[10]在C3的基础上引入互信息率和信息散度,提高了相干体计算的效率和不连续地质体的解释精度。
借助上述相干体技术可以进行自动或半自动的断层解释,与人工标注方法相比,提高了断层识别的准确性和效率,但是解释精度易受地震资料中其他不连续特征(如噪声和地质体等)的影响。
另一种常用的断层解释方法是源于仿生学理论的蚂蚁追踪技术。该技术首先由Colorni等[11]提出,在引入断层识别领域后得到了进一步的推广和发展。Bullnheimer等[12]改进了“蚂蚁体”的行程。Merkle等[13]提出多群蚂蚁算法,利用多个蚂蚁群体同时对地震断层进行追踪。刘财等[14]基于加权一致性,改进了蚂蚁算法,进一步提升了蚂蚁算法的抗噪性能。
BP神经网络是实现断层自动识别的另一种途径,能够将预测值与真实值之间的误差逆向传播,并可以不断调整网络权值,具有较好的泛化能力。然而,BP神经网络存在网络收敛慢的缺点,即使对于简单问题也可能需要上千次的学习,这意味着训练过程中需要大量地震资料以及较多的运算资源。此外,BP神经网络也对初始权重较为敏感,多次训练结果可能存在较大差异。
近年来,深度学习技术是机器学习领域的重要研究方向之一,它的出现极大地推动了人工智能技术的发展。常见的深度学习算法有:堆栈自编码网络(SA)、深度置信网络(DBN)以及卷积神经网络(CNN)等。相较于BP神经网络,CNN引入了卷积和池化两种运算方式,在精简网络模型参数的同时使模型性能也有所提升。学者们将其应用于断层等地质结构的智能识别与解释,如Xiong等[15]利用实际数据以及对应的断层标签,训练CNN模型并用于断层智能化识别,取得了初步效果。Wu等[16]使用带标签的合成三维地震数据样本,进行U-Net模型训练,最终将训练模型用于三维实际地震数据的断层智能解释。Liu等[17]搭建了Res-Unet,并利用训练模型进行宽方位角地震数据断层智能解释,提出了新思路。常德宽等[18]利用多个深度CNN模块,构建了用于地震数据断层识别的SeisFault-Net模型。
边缘检测作为一种常用的图像处理方法,目的是标识图像属性显著变化的位置[19-20]。断层发生在相对位移显著的岩层的边缘,在地震图像上多表现为同相轴的高度不连续特征。因此,本文引入深度学习边缘检测算法——整体嵌套边缘检测(Holistically-Nested Edge Detection,HED)网络[21],并将其推广至三维形式,即三维HED模型;根据地震数据和断层特点对三维HED模型进行改进和优化,提出了三维改进HED(Improved HED,IHED)模型;利用三维合成地震数据及其标签数据进行训练,将训练模型用于三维实际地震数据进行断层智能解释,并与常规算法进行对比、分析,验证了三维IHED模型的准确性和有效性。
1 HED网络 1.1 HED网络结构HED网络由Xie等[21]提出,用于解决图像处理领域中的边缘检测问题。该网络具有多尺度的结构,其中骨干网络结构来源于VGG16网络[22]。HED网络保留了VGG16网络主体的卷积层和池化层,舍弃了用于分类的全连接层。HED网络在每一个尺度的卷积块的最后各引出一个侧输出(Side Output),分别生成特征图,最终将所得的不同尺度的特征图和对这些特征图进行融合操作所得到的融合特征图共同作为网络的输出。
具体而言,HED网络是在VGG16网络的每一个尺度的最后一个卷积层之后各引出一个侧输出,共计引出5个不同尺寸的侧输出。以输入数据矩阵尺寸128×128×1为例,此时5个侧输出前端特征图的尺寸分别为128×128×64、64×64×128、32×32×256、16×16×512、8×8×512。由于每一个模块引出特征图的尺寸不同,HED网络采用了转置卷积(Transposed Convolution)对每一组得到的数据集合进行反卷积运算,分别将第二~第五组得到特征图的尺寸扩大了2~16倍,第一组特征图的尺寸保持不变。至此,网络在每个尺度上得到了相同尺寸的特征图。为了将每一组特征图合并成一个反映图像当前尺度特征的单一图像,需要将生成的特征数据集合的深度降至一维,因此引入了输出通道数为1、卷积核尺寸为1×1的卷积操作,以实现特征图的“去”深度。最终各个输出层都得到了矩阵尺寸为128×128×1的特征图像,从而完成了5个不同尺度特征图像的提取。
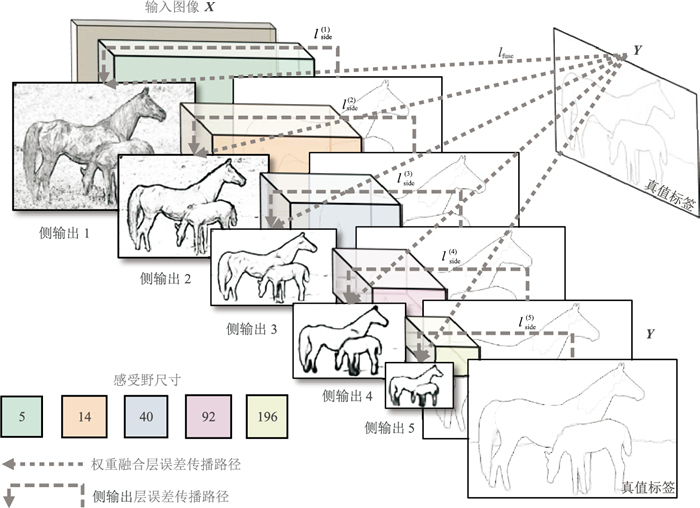
将这5个特征图像叠加,可以得到尺寸为128× 128×5的特征数据集合。因为期望最终输出结果通道数与原图一致,因此引入了输出通道数为1、卷积核尺寸为1×1的卷积操作,以得到通道数为1的输出,且各权值可以通过网络训练自主学习,逐步接近最优的权值配比。该加权得到的输出就是HED网络学习和训练得到的最佳边缘特征结果。HED网络结构[21]如图 1所示。
|
图 1 HED网络结构示意图(据文献[21]) X为输入图像;Y为真值标签;l为网络损失,下标side、fuse分别为侧输出、融合输出 |
VGG16网络具有强大的特征提取能力,HED主体网络结构是基于VGG16网络设计的,可以通过多次池化操作缩小图像的处理尺寸,从而获得更深的模型架构,这使其在保持图像多层次、多维度特征提取能力的同时减少了计算量的增加。
HED网络的核心是融合5个源于不同尺度的特征图像,其中浅层网络的感受野较小,可以提供准确的位置信息,且充分保留了局部细节信息。然而,随着网络的加深,深层网络由于感受野的逐步扩大,对位置信息的敏感度下降,并在池化过程中损失了大部分细节信息且降低了图像分辨率;但是与此同时,深层网络通过对数据特征不断抽象,语义信息逐步丰富。而HED网络对不同层次的特征图像进行融合的优势在于同时利用浅层网络准确的位置信息与深层网络丰富的语义信息,以获得最佳的边缘特征图像。
在图像边缘检测中,Xie等[21]将HED网络训练结果与优化过的Canny算子进行比较,可直观地展示HED网络的优势:可以在不同的尺度分别得到该尺度独特的边缘结果并加以融合;HED模型能进行多尺度的特征学习和整体图片的训练、预测。这是它相较常规边缘检测算法的两大优势。因此,本文充分利用HED模型的多尺度信息提取能力,进行多尺度断层智能解释。
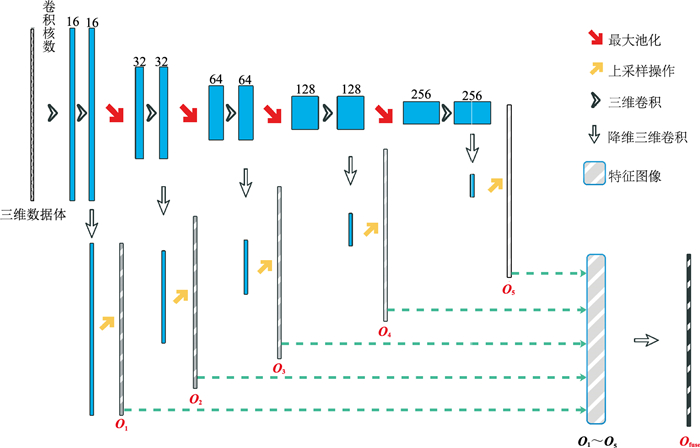
2 三维IHED网络模型 2.1 三维HED网络搭建原始HED网络是一个二维图像处理网络,在对三维地震数据体进行断层智能解释时表现欠佳,这是因为在使用二维卷积神经网络处理三维数据体时,需要对每个二维地震剖面分别进行预测,未考虑相邻剖面之间的空间关系,从而丢失了断层的三维空间信息,最终导致断层智能识别精度不高。因此,本文借鉴原始二维HED网络的思想,将卷积、池化等操作变为三维形式,提出了三维HED网络模型。利用该三维模型可以将一个三维数据体作为整体进行网络模型训练,从而充分利用三维训练数据集提供的断层空间信息,解决上述二维断层智能解释面临的断层空间信息缺失问题(图 2)。
|
图 2 三维HED网络结构 |
边缘通常表现为属性局部的急剧变化,例如颜色、梯度、亮度等的变化。鉴于边缘的微观特性,人们通常运用一阶或者二阶微分算子对其进行检测,如Canny[23]的常规边缘检测算法。HED浅层网络与Canny等常规检测算法相似,感受野较小,只考虑图像局部的急剧变化。但仅靠这些局部特征难以勾勒出完整的主体轮廓,在主体存在内部纹理或背景杂乱的条件下,浅层网络的识别精度不高。因此,HED网络利用深度学习的优势,引入嵌套的卷积池化操作,逐级对图像特征进行浓缩、提取,并通过加入深层的语义信息对图像边缘进行鲁棒性更强的检测。但究其根本,HED网络解决常规边缘检测问题的核心依旧是通过浅层网络的特征输出(图 2中O1、O2)提取到图像在小尺度中具有强烈反差的特征信息,从而获得初步的边缘检测结果。而深层网络的特征输出(图 2中O3、O4、O5)仅提供优化边缘结果的辅助作用。
断层是断裂面两侧岩层发生显著相对位移的构造,具有一定规模,大者可连续延伸数百千米。断层通常在二维、三维的地震数据中以连续的断层线、断层面的形式存在,而不是离散孤立的断层点。这表明了断层是地质结构中的一种宏观构造,仅凭借局部特征并不能有效地识别断层,对某点是否为断层点的预测通常需要综合考量该点周边范围的地质结构特征。
由于实际断层本身形式多样,又加之复杂的地震噪声,局部像素信息具有很强的随机性,这使断层智能解释与常规边缘检测问题不同,仅依据局部像素信息很难得到有效的边缘预测结果。图 3和图 4分别展示了图像边缘检测和地震断层解释这两种问题的代表性图、局部图像、局部的期望预测结果。图像边缘检测时,仅仅利用局部像素特征即可检测图像边缘(图 3b、图 3c)。但在进行断层解释时,仅依据局部像素特征很难得到准确的断层预测结果,如图 4a中红色矩形框正处在实际地震数据的断层线上,但图 4b中局部像素特征不能正确表征断层信息,即仅利用局部像素信息不能得到图 4c中的断层期望解释结果。

|
图 3 常规图像局部边缘检测示意图 (a)动物图像;(b)图a红框局部放大图;(c)图a红框局部边缘检测期望 |

|
图 4 地震数据局部断层解释示意图 (a)实际地震数据;(b)图a红框局部放大图;(c)图a红框局部断层期望 |
对于图 2所示的HED网络结构,浅层网络只有5×5的感受野范围,因此仅凭小尺度(局部)的像素信息难以得到准确的断层预测结果。因此,本文在图 2所示三维HED模型的基础上,根据地震数据和断层特征进一步优化。基于前文的理论分析,重新调整三维HED网络的拓扑结构,提出了一种改进的三维HED网络结构——IHED模型,即在浅层网络中加入拥有更大感受野的深层网络的信息,改善三维HED边缘检测技术在断层智能解释领域的适用性。
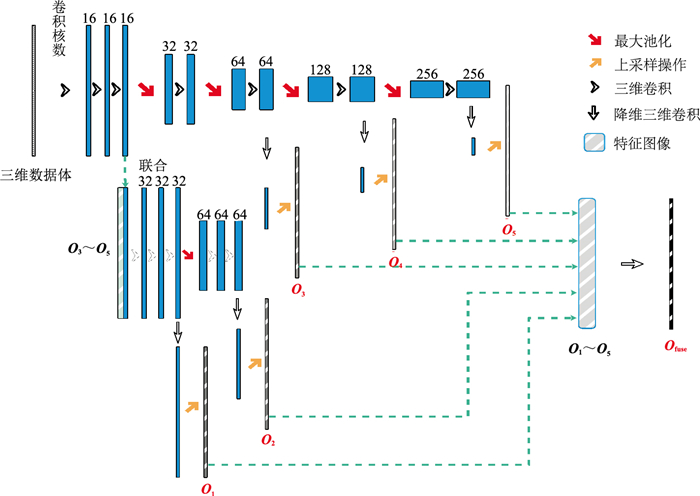
本文提出的三维IHED网络结构如图 5所示。该网络取消了浅层网络预测失灵的侧输出及侧输出特征图(O1、O2),只通过感受野更大的深层网络提取地震数据特征,并分析语义信息,最后输出有效的断层识别特征图(O3、O4、O5)。此时,浅层网络不再直接对断层进行预测,而是通过卷积处理预先对地震特征进行增强,以提取断层特征,辅助深层网络进行断层智能解释。
|
图 5 三维IHED网络结构示意图 |
深层网络随着感受野的扩大,数据特征不断抽象,语义信息逐步丰富,但同时也随着池化过程而损失了部分细节信息,所得深层网络特征图(O3、O4、O5)断层分辨率较低,即断层线“粗”,断层边缘模糊。鉴于此,三维IHED网络将深层特征图重新加入到浅层网络中进行训练。由于结合了大感受野的深层网络信息,浅层网络也能提取到全面的断层特征,最终可得到具有高分辨率的侧输出特征图(O1、O2),弥补了深层网络特征图在分辨率方面的不足。
最后,将O1~O5这5个特征图像叠加,并加权得到网络输出(Ofuse),作为三维IHED模型学习得到的最终断层智能识别结果。
3 三维IHED模型训练 3.1 训练集在断层智能识别领域,神经网络模型需要判断待预测像素点是否为断层点的二分类任务,需要大量的地震数据及其对应的断层标签。但是,在实际地震数据中,手动标记或解释断层非常耗时且主观程度很高,断层的三维特性和空间特征也增加了人工解释断层的复杂度,容易产生断层标记的纰漏,从而误导深度网络学习和训练过程。故本文采用了合成地震数据集作为训练集,即将地质模型的反射系数与地震子波褶积、正演得到三维合成地震记录[16],用于模型训练。
原始合成地震数据集共包含200个三维合成地震数据体及其对应的二值断层标签(1为断层点,0为非断层点),每个三维合成地震数据体的尺寸均为128×128×128。此外,另有20个三维合成地震数据体和断层标签数据体作为验证集。如若对该数据体作归一化处理,并映射至0~255的灰度范围,可得如图 6所示灰度图像。

|
图 6 三维合成地震数据集及断层标签(红色)示例图 |
为了使不同工区的地震数据互相兼容,需要在网络训练前对地震数据进行预处理。常用的数据预处理方式是将地震数据做标准化处理,标准化方式的选择会影响神经网络的学习和训练过程。
本文在数据预处理方法选取方面,分别对比了(0, 1)标准化、(-0.5, 0.5)标准化和Z-Score标准化三种方式,并设置未标准化处理作为空白对照组。对四种不同方法处理后的合成数据集进行网络模型训练,并分别计算各自的评价指标。本文选取准确率、精确率、召回率和F1分数作为定量评价指标,其定义如下。
(1) 准确率。指所有预测正确的样本占全部样本的比例。
(2) 精确率。指预测为正(负)的正类(负类)样本占所有被预测为正类(负类)样本的比例。本文将断层作为正类样本、非断层作为负类样本。
(3) 召回率。指预测为正(负)的正类(负类)样本占所有正类(负类)样本的比例。
(4) F1分数。是精确率和召回率的调和平均结果。F1分数同时兼顾了精确率和召回率。
不同方式训练得到的网络模型对应的准确率、精确率、召回率和F1分数等如表 1所示。
|
|
表 1 不同处理方式训练的网络模型评价指标 |
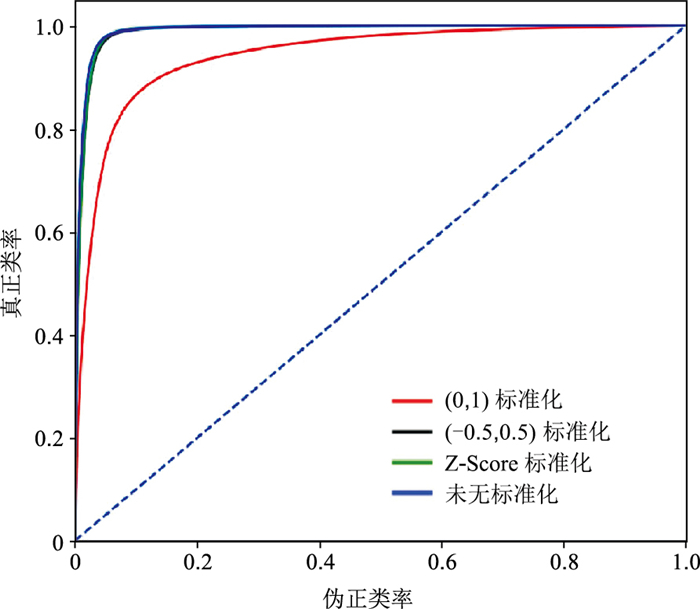
另外,本文引入了ROC曲线和AUC值作为模型评价指标。ROC曲线也称为接收者操作特征曲线,是反映敏感性和特异性连续变量的综合指标。ROC曲线的横坐标为伪正类率(False Positive Rate,FPR),指预测为正但实际为负的样本占所有负类样本的比例;纵坐标是真正类率(True Positive Rate,TPR),指预测为正且实际为正的样本占所有正类样本的比例。AUC值是指ROC曲线下的面积,通常0.5<AUC<1.0。ROC曲线越趋近(0, 1)点,对应AUC值越大,则模型分类结果越好。可见,AUC值能够更直观地反映ROC曲线的优劣,从而可用于评判模型的性能。
由图 7可见,未标准化网络的AUC值(为0.9906)最接近1,断层分类性能最优;Z-Score标准化方式次之(AUC值为0.9890);(0, 1)标准化结果最差(AUC值为0.9419)。从表 1中的数据同样可以得到相同结论,即未标准化对照组的所有评价指标均为最优,推测原因可能是因为标准化处理会损失部分数据特征信息。但是,在利用实际地震数据进行断层智能解释时,不同工区地震数据幅值范围往往不尽相同,因此为使所训练网络模型兼容多个工区实际地震数据,必须引入标准化处理以使训练数据与预测数据的幅值范围相同,为断层精确解释提供保障。在除对照组(未标准化处理)外的三种标准化处理方式中,Z-Score标准化的各评价指标均最高,因此本文选择其进行数据预处理。
|
图 7 不同处理方式训练的网络模型的ROC曲线 |
本文IHED模型基于Python3.6实现,通过搭建Cuda11下的Tensorflow2.3环境,利用GeForce RTX 3090GPU训练,采用Adam优化器,并设置初始学习率为0.0001,且该学习率可以随着迭代次数的增加而动态下降。
网络模型和训练数据的匹配程度会随训练迭代次数的增加而不断变化。如果模型训练的迭代次数太少,模型将无法充分拟合训练集数据而产生欠拟合;如果训练迭代次数过多,模型将因过度依赖训练集数据的分布而产生过拟合。过拟合的模型将会倾向于学习噪声特征而忽略了断层的典型特征,导致网络泛化能力下降。在网络学习中,通常将测试集的损失值作为评价网络是否达到最佳拟合状态的重要指标。测试集的损失值与该网络模型在实际场景中的预测效果呈负相关,故大致可以推断在测试集的损失值最小时网络性能达到最优。因此,本文最终将测试集损失值最小的训练模型加以保存。
3.4 模型验证由表 1可知,选择Z-Score标准化处理的IHED网络的预测准确率达到95.07%,其他评价指标也比较高,在一定程度上证明了该模型的有效性。
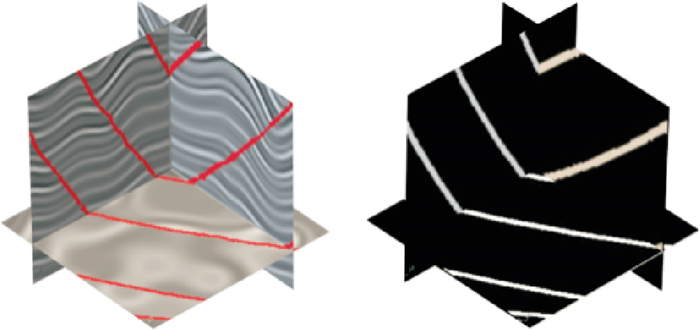
本文选取测试集中的一个三维合成地震数据体进行验证。由图 8可见,IHED模型对测试集数据的断层预测走势与标签结果高度吻合,定性地验证了本文所提出模型的有效性。
|
图 8 测试集地震数据体(左)与IHED网络断层智能解释结果(右) |
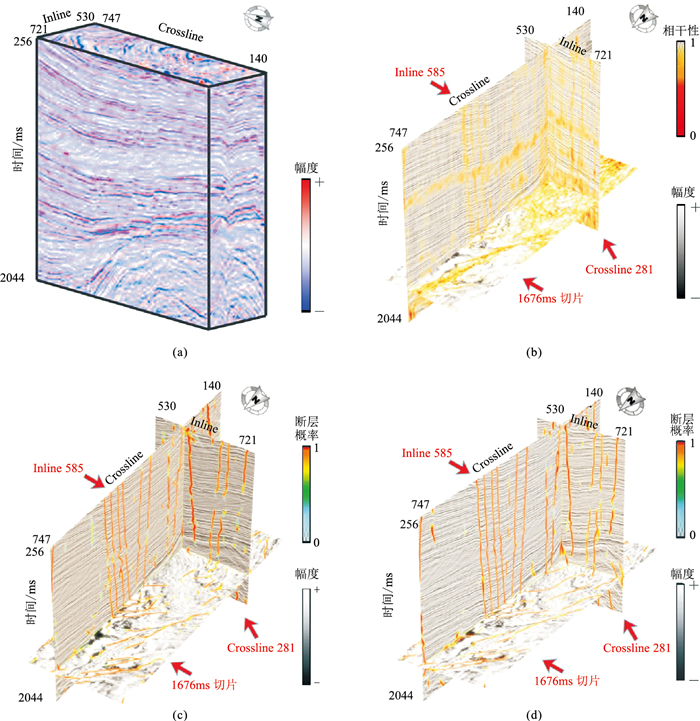
使用上述训练的IHED模型对Kerry-3D数据体进行断层自动解释,该三维实际地震数据体为New Zealand Petroleum and Minerals公司提供的时间偏移叠后地震数据(图 9a)。同时,引入了一种改进的适用于断层智能解释的U-Net网络模型[17]和第三代相干体(C3)方法作为对比,最终得到的三维断层解释结果如图 9所示。
|
图 9 Kerry-3D三维数据体不同方法断层解释结果 (a)地震数据体;(b)相干体方法;(c)U-Net模型;(d)IHED模型 |
由图 9可知,三种方法均可揭示地震数据不连续的位置,但相干体方法结果(图 9b)较为模糊,尤其是时间切片,可见相干体方法不能从地震反射不连续性中精确识别断层位置;U-Net模型(图 9c)和IHED模型(图 9d)对断层的识别和定位效果优于相干体方法,证明了深度学习算法在断层智能解释中的有效性;IHED模型识别的断层更为连续,且不连续点(散点)更少,这说明IHED模型在识别不同尺度断层信息的能力上要优于U-Net模型。
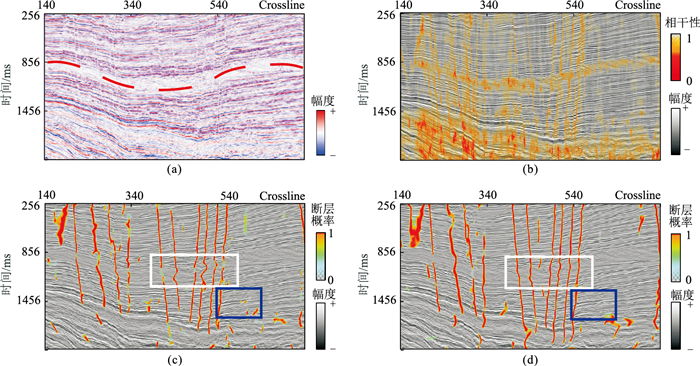
同样,可以利用Kerry-3D数据体中的Inline 585地震剖面(图 10)进一步分析本文IHED模型在断层智能解释方面的优势。与相干体识别结果(图 10b)相比,两种深度学习模型(图 10c、图 10d)均能有效地识别断层的所在位置,且识别出的断层连续性较高;同时,两种模型识别出的断层边缘清晰、光滑,不存在明显的毛刺,且断层与非断层部分特征对比明显,验证了深度学习模型的优越性。相比U-Net模型,IHED模型的断层智能解释结果背景区域更干净,断层预测散点较少,如图 10c和图 10d中蓝色矩形所示。这说明IHED模型对地震背景噪声的抗干扰能力较强。此外,与U-Net模型相比,IHED模型的断层预测分类更加明确,预测的断层概率取值主要集中在1(图 10d中红色)附近,介于断层点和非断层点间的分类不明确的预测结果(图中呈现为黄、绿、蓝的部分)较少出现,进一步证明了本文模型对断层智能解释的有效性和准确性。
|
图 10 Kerry-3D三维数据体Inline 585地震剖面不同方法断层解释结果 (a)地震剖面;(b)相干体方法;(c)U-Net模型;(d)IHED模型 |
另外,从细节方面看,本文IHED模型识别的主要断层连续性更好。由于原始地震数据中部分区域同相轴的不连续性特征不显著(如图 10a中红色虚线附近),导致U-Net模型难以准确识别该处的断层特征,即本该连续的断层在纵向上不连续(如图 10c中白色矩形框所示)。鉴于HED模型多尺度的特性,该模型对部分数据缺失或局部噪声的抗干扰性更强,因此IHED模型依然能够准确识别该区域的断层特征(图 10d中白色矩形框所示)。
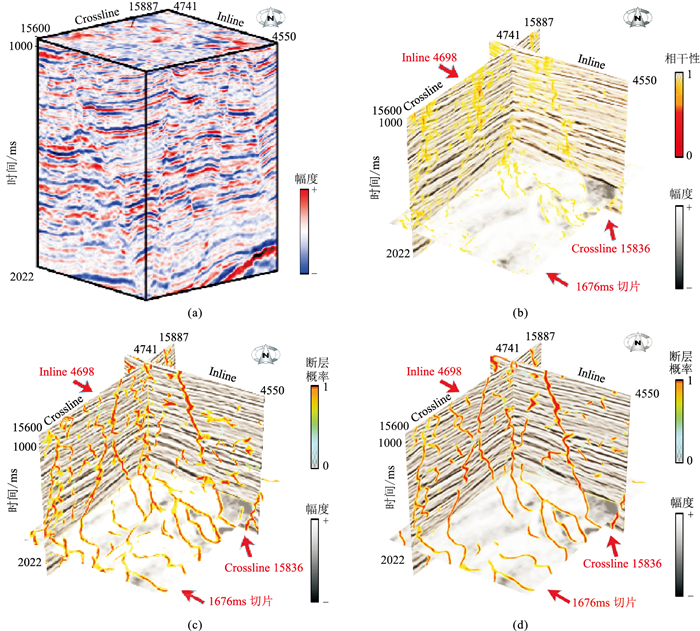
4.2 渤海B工区三维实际地震数据体断层识别为进一步验证本文模型的泛化性,选取渤海B工区的一个三维地震数据体进行断层识别。将本文IHED模型与U-Net模型、C3相干体方法作对比,得到的三维断层解释结果如图 11所示。由图可见,三种方法识别的断层的分布特征大致相同,但相干体方法识别的有效断层较少且较为混乱;两种深度学习模型由于使用相同训练集进行模型训练,断层预测结果的相似程度较高,并且断层的识别和定位效果均优于相干体方法;IHED模型比U-Net模型识别的断层更为清晰,且散点更少。
|
图 11 渤海B工区三维数据体不同方法断层解释结果 (a)地震数据体;(b)相干体方法;(c)U-Net模型;(d)IHED模型 |
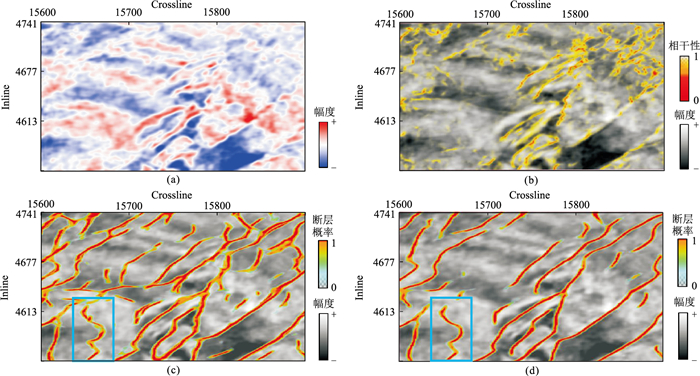
为了进一步展示IHED模型在断层智能解释方面的优势,结合原始地震数据时间切片与不同方法断层解释结果进行对比和分析。由图 12可见,两种深度学习模型的断层检测结果中,IHED模型识别的断层背景区域更干净,断层散点更少,断层连续性也更高;IHED模型的断层分类结果更加明确,介于断层点和非断层点间的预测结果出现较少(如图 12c蓝色矩形框中呈现蓝、绿色部分的断层点)。
|
图 12 渤海B工区1808ms地震时间切片不同方法断层解释结果 (a)地震剖面;(b)相干体方法;(c)U-Net模型;(d)IHED模型 |
根据三维地震数据和断层的特点,本文将整体嵌套边缘检测网络应用于断层识别,提出了一种新的三维改进嵌套边缘检测网络模型。相比传统的嵌套边缘检测网络模型,三维改进嵌套边缘检测网络模型具有如下优点:
(1) 将二维嵌套边缘检测网络模型推广为三维嵌套边缘检测,可以直接处理三维地震数据体,进行断层智能解释;
(2) 将浅层网络中加入拥有更大感受野的深层网络的信息,可以在更多尺度上捕捉不同规模断层的连续性特征,从而提高断层智能解释的精度。
在Kerry-3D和渤海B工区的两个三维实际地震工区的应用效果表明,与相干体算法、U-Net模型对比,本文提出的改进嵌套边缘检测模型预测断层更准确,连续性更好。三维改进嵌套边缘检测网络模型为地震断层智能识别提供了一种可靠途径。
| [1] |
李书兵. 断层在地震剖面上的图示法[J]. 西南石油学院学报, 1993, 15(增刊1): 78-79. LI Shubing. Graphic method of fault on seismic section[J]. Journal of Southwest Petroleum Institute, 1993, 15(S1): 78-79. |
| [2] |
梁顺军. 地震剖面上的断层分析及相关意义[J]. 石油地球物理勘探, 1999, 34(5): 560-568. LIANG Shunjun. Fault analysis and fault correlation in seismic section[J]. Oil Geophysical Prospecting, 1999, 34(5): 560-568. |
| [3] |
BAHORICH M S, FARMER S L. 3-D seismic discontinuity for faults and stratigraphic features: The coherence cube[C]. SEG Technical Program Expanded Abstracts, 1995, 14: 93-96.
|
| [4] |
MARFURT K J, KIRLIN L, FARMER S H, et al. 3-D seismic attributes using a semblance-based coherency algorithm[J]. Geophysics, 1998, 63(4): 1150-1165. DOI:10.1190/1.1444415 |
| [5] |
GERSZTENKORN A, MARFURT K J. Eigenstructure-based coherence computations as an aid to 3-D structural and stratigraphic mapping[J]. Geophysics, 1999, 64(5): 1468-1479. DOI:10.1190/1.1444651 |
| [6] |
王西文, 苏明军, 刘军迎, 等. 基于小波变换的地震相干体算法及其应用[J]. 石油物探, 2002, 41(3): 334-338. WANG Xiwen, SU Mingjun, LIU Junying, et al. Computation of seismic coherence cube based on wavelet transform and its application[J]. Geophysical Prospecting for Petroleum, 2002, 41(3): 334-338. DOI:10.3969/j.issn.1000-1441.2002.03.018 |
| [7] |
LI Y D, LU W K, XIAO H Q, et al. Dip-scanning coherence algorithm using eigenstructure analysis and supertrace technique[J]. Geophysics, 2006, 71(3): V61-V66. DOI:10.1190/1.2194899 |
| [8] |
杨培杰, 穆星, 张景涛. 方向性边界保持断层增强技术[J]. 地球物理学报, 2010, 53(12): 2992-2997. YANG Peijie, MU Xing, ZHANG Jingtao. Orientational edge preserving fault enhance[J]. Chinese Journal of Geophysics, 2010, 53(12): 2992-2997. DOI:10.3969/j.issn.0001-5733.2010.12.023 |
| [9] |
郑静静, 印兴耀, 张广智. 基于Curvelet变换的多尺度分析技术[J]. 石油地球物理勘探, 2009, 44(5): 543-547. ZHENG Jingjing, YIN Xingyao, ZHANG Guangzhi. Multi-scale analysis technique based on Curvelet transform[J]. Oil Geophysical Prospecting, 2009, 44(5): 543-547. DOI:10.3321/j.issn:1000-7210.2009.05.004 |
| [10] |
YANG L Y, GAO J H, LIU N H, et al. A coherence algorithm for 3D seismic data analysis based on the mutual information[J]. IEEE Geoscience and Remote Sensing Letters, 2019, 16(6): 967-971. DOI:10.1109/LGRS.2018.2886768 |
| [11] |
COLORNI A, DORIGO M, MANIEZZO V. Distributed optimization by ant colonies[C]. Proceedings of ECAL91 - European Conference on Artificial Life, Milano, Italy, 1991, 134-142.
|
| [12] |
BULLNHEIMER B, HARTL R F, STRAUSS C. Applying the ant System to the Vehicle Routing Problem[M]. Boston: Springer, 1999: 285-296.
|
| [13] |
MERKLE D, MIDDENDORF M. Modeling the dynamics of ant colony optimization[J]. Evolutionary Computation, 2002, 10(3): 235-262. DOI:10.1162/106365602760234090 |
| [14] |
刘财, 刘海燕, 彭冲, 等. 基于加权一致性的蚁群算法在断层检测中的应用[J]. 地球物理学报, 2016, 59(10): 3859-3868. LIU Cai, LIU Haiyan, PENG Chong, et al. Application of the ant colony algorithm based on weighted coherence to fault detection[J]. Chinese Journal of Geophysics, 2016, 59(10): 3859-3868. DOI:10.6038/cjg20161029 |
| [15] |
XIONG W, JI X, MA Y, et al. Seismic fault detection with convolutional neural network[J]. Geophysics, 2018, 83(5): O97-O103. DOI:10.1190/geo2017-0666.1 |
| [16] |
WU X M, LIANG L M, SHI Y Z, et al. FaultSeg3D: using synthetic data sets to train an end-to-end convolutional neural network for 3D seismic fault segmentation[J]. Geophysics, 2019, 84(3): IM35-IM45. DOI:10.1190/geo2018-0646.1 |
| [17] |
LIU N H, HE T, TIAN Y J, et al. Common-azimuth seismic data fault analysis using residual U-Net[J]. Interpretation, 2020, 8(3): SM25-SM37. DOI:10.1190/INT-2019-0173.1 |
| [18] |
常德宽, 雍学善, 王一惠, 等. 基于深度卷积神经网络的地震数据断层识别方法[J]. 石油地球物理勘探, 2021, 56(1): 1-8. CHANG Dekuan, YONG Xueshan, WANG Yihui, et al. Seismic fault interpretation based on deep convolutional neural networks[J]. Oil Geophysical Prospecting, 2021, 56(1): 1-8. |
| [19] |
吕丙南, 陈学华, 徐赫, 等. 空间与加窗二维希尔伯特变换在三维地震资料体边缘检测中的应用[J]. 石油地球物理勘探, 2020, 55(3): 661-668. LYU Bingnan, CHEN Xuehua, XU He, et al. Application of spatial-windowed 2D Hilbert transform in vo-lumetric edge detection of 3D seismic data[J]. Oil Geophysical Prospecting, 2020, 55(3): 661-668. |
| [20] |
杨午阳, 杨佳润, 陈双全, 等. 基于U-Net深度学习网络的地震数据断层检测[J]. 石油地球物理勘探, 2021, 56(4): 688-697. YANG Wuyang, YANG Jiarun, CHEN Shuangquan, et al. Seismic data fault detection based on U-Net deep learning network[J]. Oil Geophysical Prospecting, 2021, 56(4): 688-697. |
| [21] |
XIE S N, TU Z W. Holistically-nested edge detection[J]. International Journal of Computer Vision, 2017, 125(1): 3-18. |
| [22] |
SIMONYAN K, ZISSERMAN A. Very deep convolutional networks for large-scale image recognition[DB/OL]. (2014-09-04)[2021-07-13]. https://arxiv.org/abs/1409.1556.
|
| [23] |
CANNY J. A computational approach to edge detection[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1986, PAMI-8(6): 679-698. DOI:10.1109/TPAMI.1986.4767851 |



 王治国,陕西省西安市碑林区咸宁西路28号西安交通大学数学与统计学院,710049。Email:
王治国,陕西省西安市碑林区咸宁西路28号西安交通大学数学与统计学院,710049。Email: