② 东华理工大学放射性地质与勘探技术国防重点学科实验室, 江西南昌 330013
② Fundamental Science on Radioactive Geology and Exploration Technology Laboratory, East China University of Technology, Nanchang, Jiangxi 330013, China
由于地球物理场的等效性、观测数据集的有限性和数据观测存在误差等,地球物理反问题不可避免地存在多解性[1]。正则化技术[2]作为减小反问题多解性的有效策略之一,广泛应用于地球物理反演。该技术通过在数据和模型权重矩阵引入先验信息,降低反问题的不适定性;当拥有足够的先验信息时,可有效提高反演的稳定性。相反,当先验信息不足甚至错误时,将会增加产生错误结果的可能性;降低反问题多解性的另一途径是提高观测数据集的数量和质量[3],但无法改变地球物理场等效性造成的反演多解性。此外,减少反演未知数数量是有效降低反问题不适定性的另一重要途径[4],但是以牺牲反演分辨率为代价;另一方面,如果离散的反演网格无法真实构建实际异常体,也可能会导致反演的多解性、影响反演分辨率[5]。高质量的反演网格应该在确保反演效果的同时减少反演单元数,进而从一定程度上降低反问题的不适定性。
提高地球物理反演离散网格质量是一个亟需解决的问题,但是实际的反问题由于缺乏地下结构边界、尺寸和形状等先验信息,难以建立理想的初始反演网格[5]。虽然可以通过全局网格加密,实现对反演目标体更好的逼近,但这无疑会过多地增加单元数量,对反演效率和稳定性造成不利影响。Böhm等[6]提出了一种变网格反演方案,即先使用粗网格进行反演迭代,并将粗网格反演结果作为先验信息,对粗网格进行加密与合并获取更高质量的反演网格,然后重新反演以提高反演分辨率。Ascher等[7]对Böhm等的方案进行了深入研究,发展了一种自适应反演方案,并证明了粗网格选择的正则化因子在细网格是可以延续使用的;此外,交叉检验与L曲线正则化因子选取方法在自适应反演中依然适用[8]。很多学者在地震层析成像[6, 9-12]、图像重建[13-15]、医学成像[16]、电阻率成像[17]以及电磁法反演[18-19]、磁测数据反演[20-21]等方面开展了自适应反演方案的研究。自适应反演方案中,最重要的是选择网格并对选定网格进行细化,理论上网格细化最有效的方案就是分析灵敏度矩阵的奇异值和海森矩阵的特征值,但这两种方法的计算量过大,对于二维、三维反演问题难于实用。目前较为实用的网格细化标准有物性变化[17]、物性梯度变化[16]和物性相关的给定函数[22]等;此外,基于小波技术的自适应反演方案成功应用于直流电阻率反演[23]。在自适应反演过程中,当网格细化过程中允许网格结点位置发生改变时,对于简单模型的反演效果明显[9],但可能会产生局部过小的网格[12],约束网格面积能在一定程度上避免此问题。
本文以二维MT反演为例,研究了自适应网格细化反演算法。在反演初期使用粗网格,通过减少反演单元数的方式降低反问题的不适定性;基于网格细化策略,随反演迭代的进行,网格自适应加密,以提高正则化反演效果。反演过程中,细化网格反演以前一重网格的反演结果作为参考模型与初始模型,确保反演沿正确的方向进行,同时提高反演稳定性,逐步改善反演效果。采用四种网格细化方案进行自适应反演,对比分析了四种网格细化方案的特点和反演效果,并通过Hessian矩阵的特征值分布分析了这四种方案对反演结果的影响。最后,开展了理论模型和实测数据试算,结果表明反演过程稳定,自适应反演算法具有较好的实用性。
1 渐近自适应正则化反演 1.1 二维MT正演对于大地电磁问题,考虑地下电阻率变化,取时谐因子为e-iωt。假设地下电性结构为二维,取走向为z轴,电导率只在(x,y)平面变化,则走向方向的电场和磁场的偏微分方程可分别表示为
| $ \frac{1}{{\rm{i}} \omega \mu}\left(\frac{\partial^{2} E_{z}}{\partial x^{2}}+\frac{\partial^{2} E_{z}}{\partial y^{2}}\right)+(\sigma-{\rm{i}} \omega \varepsilon) E_{z}=0 $ | (1) |
| $ \frac{1}{\sigma-{\rm{i}} \omega \varepsilon}\left(\frac{\partial^{2} H_{z}}{\partial x^{2}}+\frac{\partial^{2} H_{z}}{\partial y^{2}}\right)+{\rm{i}} \omega \mu H_{z}=0 $ | (2) |
式中:σ为电导率;μ为磁导率;ε为介电常数;ω为角频率;i为虚数单位;Ez为电场的z分量;Hz为磁场的z分量。采用非结构化三角单元对研究区域进行离散,考虑空气层的边界条件,式(1)和式(2)对应的变分问题可通过有限单元法[24]转化为求解大型稀疏线性方程组
| $ \boldsymbol{K} \boldsymbol{U}=\boldsymbol{P} $ | (3) |
式中:K为刚度矩阵;U为节点上的场值;P为由边界条件形成的源项。通过求解式(3)的线性方程组可得主场分量,通过麦克斯韦方程可求得辅助场分量,最后可计算视电阻率和相位
| $ \rho_{\mathrm{s}}=\frac{|Z|^{2}}{\omega \mu} $ | (4) |
| $ \varphi=\arctan \frac{\operatorname{Im}(Z)}{\operatorname{Re}(Z)} $ | (5) |
式中:ρs为视电阻率;Z为阻抗;φ为相位;Im(·)表示取复数虚部;Re(·)表示取复数实部。
1.2 正则化反演目标函数建立二维MT正则化反演目标函数,其中模型稳定函数采用Zhdanov的一般表达式[25],则有
| $ \begin{aligned} \varPhi(\boldsymbol{m}) &=\lambda \varPhi_{\mathrm{m}}(\boldsymbol{m})+\varPhi_{\mathrm{d}}(\boldsymbol{m}) \\ &=\lambda\left\|\boldsymbol{W}_{\mathrm{m}}\left(\boldsymbol{m}-\boldsymbol{m}^{\mathrm{apr}}\right)\right\|_{2}^{2}+\\ &\left\|\boldsymbol{W}_{\mathrm{d}}\left[\boldsymbol{d}^{\mathrm{obs}}-\boldsymbol{A}(\boldsymbol{m})\right]\right\|_{2}^{2} \end{aligned} $ | (6) |
式中:m为离散模型;Φd(m)为数据误差函数;λ为正则化因子;Φm(m)为模型稳定函数,本文采用最小结构稳定函数[26],非结构化网格模型粗糙度采用最小二乘算法计算[27];Wm为模型权重矩阵;mapr为先验模型;Wd为数据权重矩阵;dobs为观测数据;A(m)为与m相关的正演算子。自适应反演过程中考虑到粗网格正演存在误差,则Wd可表示为
| $ \boldsymbol{W}_{\mathrm{d}}=\operatorname{diag}\left(\frac{1}{\xi_{1}^{\mathrm{obs}}+\xi_{1}^{\mathrm{cal}}}, \frac{1}{\xi_{2}^{\mathrm{obs}}+\xi_{2}^{\mathrm{cal}}}, \ldots, \frac{1}{\xi_{{N}}^{\mathrm{obs}}+\xi_{{N}}^{\mathrm{cal}}}\right) $ | (7) |
式中:ξobs为观测数据误差;ξcal为正演计算误差,通过网格细化后的正演数据评估得到;N为观测数据个数。
1.3 目标函数优化采用高斯—牛顿最优化法求解目标函数(式(6)),并基于迭代法求解高斯—牛顿方程。为了获得模型参数,取mn=mn-1+Δm,其中n为迭代次数,对A(m)进行一阶泰勒展开,则
| $ \boldsymbol{A}\left(\boldsymbol{m}_{n-1}+\Delta \boldsymbol{m}\right) \approx \boldsymbol{A}\left(\boldsymbol{m}_{n-1}\right)+\frac{\partial \boldsymbol{A}\left(\boldsymbol{m}_{n-1}\right)}{\partial \boldsymbol{m}_{n-1}} \Delta \boldsymbol{m} $ | (8) |
对式(6)关于Δm求偏导并令其为0,可得高斯—牛顿迭代方程
| $ \boldsymbol{H}_{n-1} \Delta \boldsymbol{m}=-\nabla \varPhi\left(\boldsymbol{m}_{n-1}\right) $ | (9) |
| $ \boldsymbol{H}_{n-1}=\boldsymbol{J}^{\mathrm{T}} \boldsymbol{W}_{\mathrm{d}}^{\mathrm{T}} \boldsymbol{W}_{\mathrm{d}} \boldsymbol{J}+\lambda \boldsymbol{W}_{\mathrm{m}}^{\mathrm{T}} \boldsymbol{W}_{\mathrm{m}} $ | (10) |
| $ \begin{gathered} \nabla \varPhi\left(\boldsymbol{m}_{n-1}\right)=\lambda \boldsymbol{W}_{\mathrm{m}}^{\mathrm{T}} \boldsymbol{W}_{\mathrm{m}}\left(\boldsymbol{m}_{n-1}-\boldsymbol{m}^{\mathrm{apr}}\right)- \\ \boldsymbol{J}^{\mathrm{T}} \boldsymbol{W}_{\mathrm{d}}^{\mathrm{T}} \boldsymbol{W}_{\mathrm{d}}\left[\boldsymbol{d}^{\mathrm{obs}}-\boldsymbol{A}\left(\boldsymbol{m}_{n-1}\right)\right] \end{gathered} $ | (11) |
式中:J为灵敏度矩阵,表示正演算子对m的偏导数;Δm为模型改变量;H为海森矩阵。采用互换定理[28]计算J,采用稳定双共轭梯度法[29](BICGSTAB)求解式(9)。最后可得新的模型参数
| $ \boldsymbol{m}_{n}=\boldsymbol{m}_{n-1}+\alpha \Delta \boldsymbol{m} $ | (12) |
式中α为改进量的搜索步长[25]。
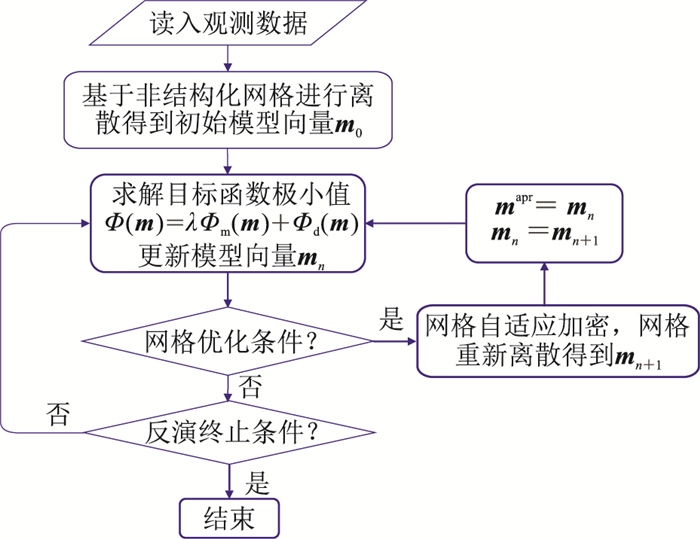
1.4 自适应反演算法自适应反演算法在整个反演过程中采用可变网格。在反演初期使用粗网格,在反演迭代过程中基于网格优化方案进行自适应加密,细化网格的反演以前一重网格的反演结果作为初始模型和参考模型以确保反演的准确性和稳定性。自适应反演流程(图 1)如下:
|
图 1 自适应反演流程 |
(1) 设置反演网格最大细化次数及自适应反演中每一重网格最大迭代次数,根据反演需求设置每重网格细化的单元比例和最小单元面积约束等;
(2) 采用非结构化三角单元进行网格离散生成网格,为确保正演精度,在测量点周围采用局部加密技术;
(3) 对当前网格,采用高斯—牛顿最优化法求解目标函数,直至达到当前重网格的最大反演迭代次数;
(4) 根据网格优化方案计算单元优化参考信息,并根据优化比例选择优化单元,然后对网格自适应加密;
(5) 以细化后的网格作为下次反演的网格,设置反演的初始模型与参考模型,并返回第三步开始当前网格反演,判断是否达到反演中止条件,若达到,则终止反演。
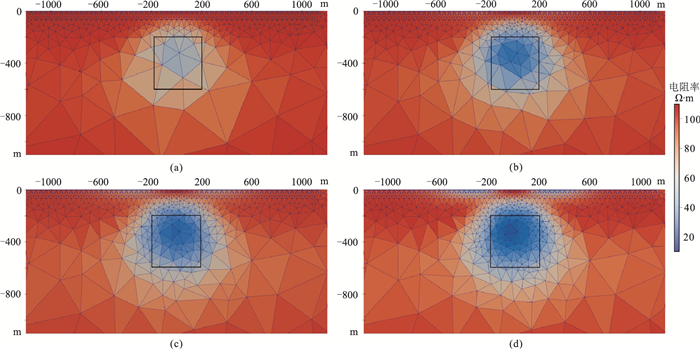
应用低阻体模型说明自适应反演过程。在围岩电阻率为100Ω·m均匀半空间,设置一个尺寸为400m×400m、电阻率为10Ω·m的低阻异常体,其顶部埋深为200m,在0.1~100Hz频段以10为底的对数等间距取10个频点,测点距为40m,共60个测点。在反演过程中基于模型梯度信息进行网格细化,每次细化比例为反演总网格数量的2%。图 2为前三次网格细化结果及基于模型梯度信息优化方案的自适应反演结果,每一重网格反演的初始正则化因子为200,迭代过程中以0.9的速率下降。为防止网格在某些区域过度细化,初始最小面积约束设为以测点间距为正方形的单元面积,并随网格细化高于最小面积约束的单元面积以2为倍数增加。图 2中黑色正方形为实际异常体边界,可见自适应反演方案在反演初期使用粗网格,随反演迭代进行,基于网格细化策略对网格自适应加密,反演分辨率得到有效提高,反演目标体的位置空间信息也更为清晰。
|
图 2 各重网格自适应反演结果 (a)第一重网格;(b)第二重网格;(c)第三重网格;(d)第四重网格 |
在自适应反演过程中网格优化策略对反演至关重要,不同网格优化策略的网格加密位置有所差异,最后的反演效果会有所不同。为此,本文研究了四种网格优化方案,对它们的网格加密特点进行了对比;此外,为了分析四种优化方案在网格加密过程中对反演的影响,对各自的Hessian矩阵进行SVD,并对归一化特征值分布进行分析。四种网格优化方案的参数分别为模型灵敏度矩阵J[29]、模型改变量Δmi、模型梯度信息η和“边—角”检测参数R[22]。J、Δmi、η、R具体为
| $ J_{j}=\sqrt{\frac{1}{N} \sum\limits_{i=1}^{N} G_{i j}^{2}} $ | (13) |
| $ \Delta m_{i}=\left|m_{i}-m_{i}^{\mathrm{apr}}\right| $ | (14) |
| $ \eta_{i}=\left(\frac{\partial m_{i}}{\partial x}\right)^{2}+\left(\frac{\partial m_{i}}{\partial y}\right)^{2} $ | (15) |
| $ R=\operatorname{det}(\boldsymbol{M})-k[\operatorname{trace}(\boldsymbol{M})]^{2} $ | (16) |
| $ \boldsymbol{M}=\left[\begin{array}{c} \left(\frac{\partial m_{i}}{\partial x}\right)^{2} & \frac{\partial m_{i}}{\partial x} \frac{\partial m_{i}}{\partial y} \\ \frac{\partial m_{i}}{\partial x} \frac{\partial m_{i}}{\partial y} & \left(\frac{\partial m_{i}}{\partial y}\right)^{2} \end{array}\right] $ | (17) |
式中:
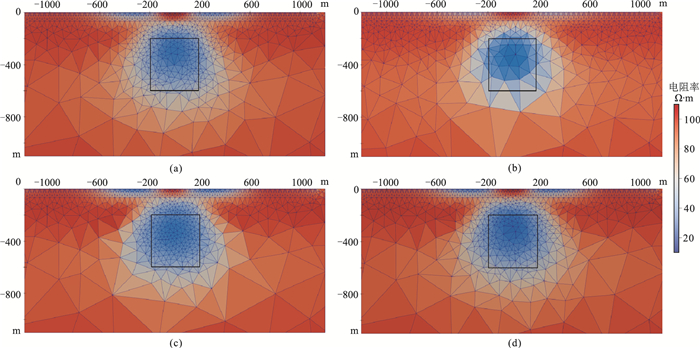
为说明不同网格优化方案的加密特点,对上述低阻模型采用四种优化方案进行自适应反演,整个反演过程网格共细化4次,图 3为四种优化方案的最后一重网格细化结果及反演结果。由图 3a和图 3d对比可知,基于“边—角”检测和梯度信息的网格优化方案类似,主要在异常体边界加密,能够有效提高反演的效果。图 3b为基于灵敏度细化方案的反演结果,一般近地表的单元灵敏度较大,此方案会由近地表逐渐向深部加密,因此该方案具有对反演区域整体优化的特点;图 3c为基于模型改变量方案的反演结果,该方案加密区域集中于异常体内部。
|
图 3 不同方案网格细化结果及反演结果对比 (a)基于“边—角”检测;(b)基于灵敏度信息;(c)基于模型改变量;(d)基于梯度信息 |
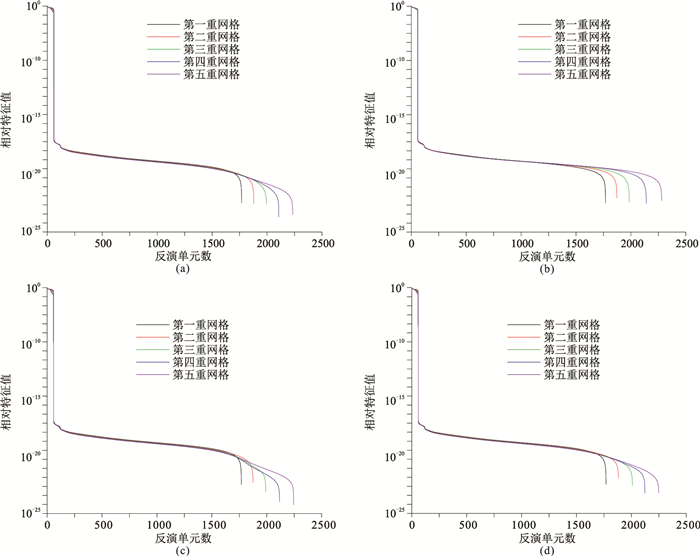
为分析上述四种网格优化方案对反演的影响,对Hessian矩阵的归一化特征值分布进行分析,在不考虑先验信息的情况下Hessian矩阵可近似表示为JTJ。在反问题中,Hessian矩阵的特征值分布分为主成分特征值(接近0)和离群值两部分,其中主成分特征值与网格尺寸无关,网格数量增加只会提高主成分特征值的数量[31-33];此外,线性问题的病态特征与Hessian矩阵特征值衰减为0的速度有关,在相同条件下衰减速率越快说明不适定性越强[31-32, 34];Hessian矩阵特征值分布有时也会出现极小值,与主成分特征值相差数个数量级,这种情况被认为是由于零空间的存在引起的[35-36]。因此本文对自适应反演中每一重网格最后一次迭代的Hessian矩阵的特征值进行归一化分析,如图 4所示,可见整个特征值分布出现两部分极值,即极大和极小特征值部分,中间较平滑部分可认为是主成分特征值。对于基于模型灵敏度的网格优化方案,随网格的增加,主成分特征值的衰减速率基本没有变化,说明此方案对反演的不适定性影响较小,因此不仅可以用于进行自适应反演,也可以用于生成高质量的初始反演网格;对于基于模型梯度信息和“边—角”检测的网格优化方案,在第一次网格加密后特征值衰减速率基本不变,但随着网格数持续增加特征值衰减速率增加,意味着反演的不适定性增强;对于基于模型改变量的网格优化方案,在第一次网格加密后特征值衰减速率基本不变,但随着网格数继续增加,特征值衰减速率明显增加,相比其他方案反演不适定性增加速率更快。
|
图 4 不同网格细化方案的自适应反演的Hessian矩阵特征值分布 (a)基于“边—角”检测;(b)基于灵敏度信息;(c)基于模型改变量;(d)基于梯度信息 |
由图 3和图 4可知,基于灵敏度信息加密方式具有全局优化加密的特点;而其他三种网格优化方案,网格加密均直接与反演异常体分布区域相关,在异常体分布区域进行网格适量加密,对异常体逼近程度提高时,反问题的不适定性受到的影响不大,但持续增加后反问题的不适定性会快速增加,模型改变量尤为明显。总体上看,反演单元数越大,反问题的不适定性越强,在自适应反演过程中应尽量避免冗余网格的产生。
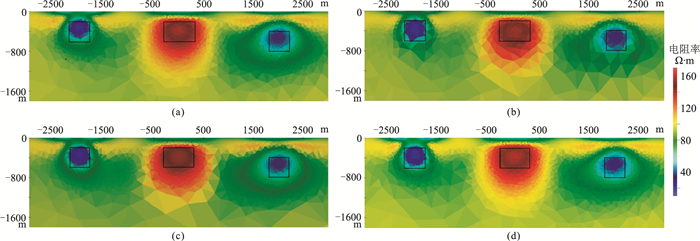
2 模型试算 2.1 水平地形模型在背景电阻率为100Ω·m的均匀半空间下设置三个异常体,其中两个为正方形低阻异常体,尺寸为400m×400m,电阻率为10Ω·m,顶面深度分别为200m和400m;另一个为矩形高阻异常体,尺寸为600m×400m,顶面深度为200m,电阻率为1000Ω·m。异常体的实际位置在反演结果中以黑色矩形框标识。在0.1~100Hz频段以10为底的对数等间距取10个频点,测点距为20m,共540个测点,反演区域为测线长度与地下2000m形成的矩形区。每一重网格初始正则化因子均为500,以0.95的速率下降,整个反演过程中网格共细化四次,每次优化比例为反演总网格的2%,基于四种网格优化策略进行反演;为避免某些区域过度细化,初始最小面积约束设为以测点间距为正方形的单元面积,并随网格细化,以2为倍数增加。图 5为四种网格优化方案反演结果。
|
图 5 四种细化方案的自适应反演结果 (a)基于“边—角”检测;(b)基于灵敏度信息;(c)基于模型改变量;(d)基于梯度信息 |
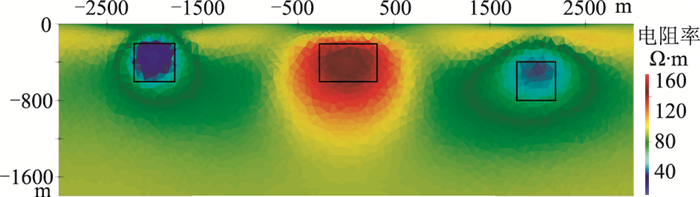
为验证自适应反演算法的反演效果,采用固定网格的方案进行反演,并与自适应反演的效果进行对比。在固定网格的反演中,整个反演区域采用均匀网格离散,最大单元面积为5000m2,反演单元数为18100,反演过程中采用经验选取的方法选择正则化因子,初始正则化因子为500。整个反演过程中共进行了34次迭代,图 6为固定网格反演结果。
|
图 6 固定网格反演结果 |
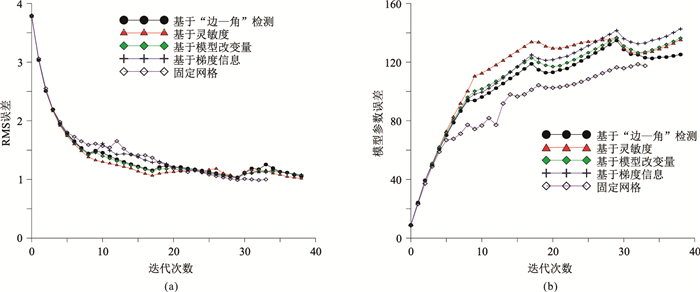
图 7a为五种反演方案的数据均方根(RMS)误差曲线,图 7b为模型参数误差曲线;表 1为四种方案的网格变化。由图 7可知,四种优化方案的自适应反演,初始RMS均快速下降,整个自适应反演过程中RMS误差均呈稳定下降趋势并逐渐趋近于1,以及模型参数误差的稳定上升说明反演过程稳定[25];固定网格方案反演RMS误差呈稳定下降趋势并逐渐趋近于1,说明反演过程稳定,但下降速率较自适应反演略慢,说明粗网格较细网格的反演迭代收敛要快。根据表 1和图 5可知,四种优化方案最后的网格数量接近,网格数量较初始网格增加了约六分之一,四种网格细化策略都能较好地反演出异常体,其中低阻物性接近真值,证明了四种网格加密方案在自适应反演中的有效性。基于“边—角”检测技术与物性梯度信息的网格加密方式都以物性两个方向的梯度变化为基础,两者网格加密方式较为相似,反演结果相近;基于模型灵敏度的加密方式,反演区域整体由上至下逐渐加密,这是由于地表观测的地球物理方法模型灵敏度由浅到深逐渐减小;基于模型改变量的网格加密能够有效在高、低阻异常区进行网格加密,异常体周围网格较大,能够有效反演出异常体。
|
图 7 水平地形模型五种方案的反演参数随迭代次数的变化曲线 (a)数据的RMS误差;(b)模型参数误差 |
|
|
表 1 水平地形模型四种自适应加密方案的单元数 |
由图 5a、图 5c、图 5d和图 6可知,基于“边—角”检测技术、物性梯度信息和模型改变量的局部网格加密方案对顶面深度为200m的低阻体边界描述较固定网格方案略好,顶面深度为400m的低阻体物性恢复得更好,且反演单元数约为固定网格的77%。说明基于局部网格加密的自适应反演方案能在保证反演效果的同时减小反演单元数,从而减少内存消耗。
2.2 起伏地形模型为测试自适应反演方案在带地形反演中的效果,在起伏地形下加入三个异常体,其中两个低阻异常体,尺寸为400m×400m,顶面深度为400m,电阻率为10Ω·m;一个高阻异常体尺寸为400m×400m,顶面深度为400m,电阻率为1000Ω·m,取地下背景电阻率为100Ω·m。异常体的实际位置在反演结果中以黑色矩形框标识。在0.1~100Hz频段以10为底的对数等间距取15个频点,测点距为20m,共240个测点。每一重网格初始正则化因子为300,以0.95的速率下降,整个反演过程中网格共细化四次,每次优化比例为反演总网格的3%。限于篇幅只讨论基于模型梯度信息和模型改变量两种网格优化方案的自适应反演。
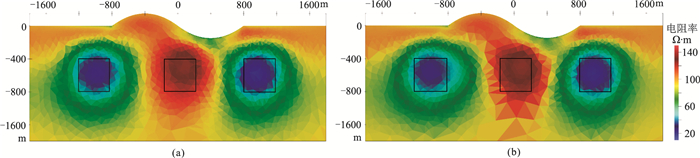
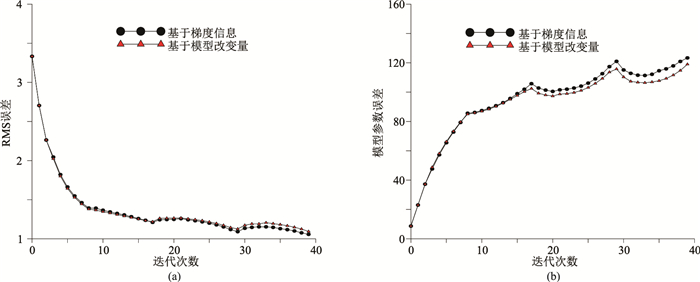
图 8为基于模型梯度信息和模型改变量网格优化方案的反演结果,图 9为数据的RMS误差和模型参数误差曲线,表 2为两种方案的网格变化。由图 9可知,两种优化方案反演初始RMS快速下降,整个自适应反演过程中RMS总体呈下降的趋势并逐渐趋近于1,说明反演过程稳定。根据表 2和图 8可知:两种优化方案最后的网格数量接近,网格数量较初始网格增加了约四分之一,两种方案都能较好地反演出目标体,其中低阻物性接近真值,且与真实位置相一致;高阻物体受地形影响,反演位置与实际位置略有偏移;此外,基于模型改变量网格加密方案在高阻物体周围网格加密相对较少,网格明显偏大,这与模型改变量优先细化异常明显区域有关。模型梯度信息的方案可有效避免这种情况。
|
图 8 起伏地形模型两种方案的自适应反演结果 (a)基于梯度信息;(b)基于模型改变量 |
|
图 9 起伏地形模型两种方案的反演参数随迭代变化曲线 (a)数据的RMS误差;(b)模型参数误差 |
|
|
表 2 起伏地形模型两种方案的自适应反演单元数 |
选择A花岗岩区一条MT实测剖面验证自适应反演方案能力。该测线长约为7km,点距约为50m,采用四种网格细化方案进行自适应反演。初始正则化因子设为4000,以0.9的速率下降。每次网格优化比例为反演总网格的5%,采用相同的网格面积约束方案。图 10为四种网格细化方案反演结果,图 11为数据RMS误差和模型参数误差的变化曲线,表 3为四种方案的网格变化。由表 3可知最后四种网格优化方案的网格数量接近,由图 11可知四种方案的反演参数变化曲线大致相同,RMS误差平稳下降,模型误差单调上升,说明算法具有较好的稳定性。四种网格优化自适应反演都能识别出横向0~2.0km和4.5~6.5km的地下高阻地质体,且左侧的电阻率更大。基于“边—角”检测和模型梯度信息网格细化方案能够清晰地刻画出地质体边界;基于模型灵敏度的网格加密方案,地质体边界网格较大,边界分辨率略低;基于模型改变量的网格加密方案在地质体内部明显加密,但目标体边界网格明显大于梯度信息和“边—角”检测方案,对边界的描述与基于模型灵敏度的加密方案相当。此外,基于“边—角”检测的反演方案能够对两个方向的模型梯度信息进行重新平衡,减小异常值之间的差异,避免网格在异常大的地质体单元周围过度加密。

|
图 10 实测数据四种方案自适应反演结果 (a)基于“边—角”检测;(b)基于灵敏度信息;(c)基于模型改变量;(d)基于梯度信息 |

|
图 11 实际数据两种方案的反演参数随迭代变化曲线 (a)数据的RMS误差;(b)模型参数误差 |
|
|
表 3 实际数据四种方案自适应反演的网格单元数 |
综上所述,实际的地质情况往往较为复杂,且可能存在较大的地质体,因此在实测数据反演中基于模型梯度信息和“边—角”检测网格优化的自适应反演在刻画地质体边界方面更具优势。
4 结论本文研究了自适应渐进网格细化反演算法,并应用于二维MT反演,得到以下结论。
(1) 自适应反演方案,在反演初期使用粗网格,通过减小反演单元数能够有效降低反问题的不适定性;随反演迭代进行,基于网格优化方案自适应加密网格,能够逐步改善反演效果。
(2) 对基于模型灵敏度、模型改变量、模型梯度、“边—角”检测的四种网格细化方案形成的Hessian矩阵特征值分布研究表明:总体上,反问题不适定性会随网格数量增加而提高,基于模型灵敏度的网格优化方案,随网格的增加对反演不适定性的影响相比其他三种方法小。
(3) 四种网格优化方案有三种主要特点,其中基于模型梯度方法与“边—角”检测的特征相似,集中在异常体边界加密,能够有效提高对异常体边界刻画的效果;基于模型改变量方案主要对异常体分布区进行加密,对异常不明显区域识别较差;基于模型灵敏度方案具有一定的全局加密特点。
在反演中,可根据网格优化特点综合应用多种方案进一步改善反演效果。基于灵敏度的方法可以用于反演的初期,以提高网格总体质量甚至可用于初始网格生成,基于梯度与“边—角”检测的方案有利于得到精确的异常边界,基于模型改变量的方案可以用于中期以提高异常体响应精度。以后将进一步研究多种优化方案的组合技术。此外,本文只采用了由粗到细的优化方案,由细到粗的反向优化策略是进一步的研究方向。
| [1] |
王家映. 地球物理反演理论[M]. 北京: 高等教育出版社, 2002. WANG Jiaying. Geophysical Inversion Theory[M]. Beijing: Higher Education Press, 2002. |
| [2] |
TIKHONOV A N, ARSENIN V Y. Solutions of Ill-posed Problems[M]. Winston, Washington, 1977.
|
| [3] |
MAURER H, CURTIS A, BOERNER D E. Recent advances in optimized geophysical survey design[J]. Geo-physics, 2010, 75(5): 75A177-75A194. |
| [4] |
MENKE W. Geophysical Data Analysis: Discrete Inverse Theory[M]. San Diego: Academic Press, 1989.
|
| [5] |
BANGERTH W. A framework for the adaptive finite element solution of large-scale inverse problems[J]. SIAM Journal on Scientific Computing, 2008, 30(6): 2965-2989. DOI:10.1137/070690560 |
| [6] |
BÖHM G, VESNAVER A L. In quest of the grid[J]. Geophysics, 1999, 64(4): 1116-1125. DOI:10.1190/1.1444618 |
| [7] |
ASCHER U M, HABER E. Grid refinement and sca-ling for distributed parameter estimation problems[J]. Inverse Problems, 2001, 17(3): 571-590. DOI:10.1088/0266-5611/17/3/314 |
| [8] |
BRENDEL M, MARQUARDT W. An algorithm for multivariate function estimation based on hierarchically refined sparse grids[J]. Computing and Visualization in Science, 2009, 12(4): 137-153. DOI:10.1007/s00791-008-0085-1 |
| [9] |
MICHELINI A. An adaptive-grid formalism for tra-veltime tomography[J]. Geophysical Journal International, 1995, 121(2): 489-510. DOI:10.1111/j.1365-246X.1995.tb05728.x |
| [10] |
CURTIS A, SNIEDER R. Reconditioning inverse problems using the genetic algorithm and revised parameterization[J]. Geophysics, 1997, 62(5): 1524-1532. DOI:10.1190/1.1444255 |
| [11] |
ZHANG H J, THURBER C. Adaptive mesh seismic tomography based on tetrahedral and Voronoi diagrams: application to Parkfield, California[J]. Journal of Geophysical Research-Solid Earth, 2005. DOI:10.1029/2004JB003186 |
| [12] |
AJO-FRANKLIN J B, URBAN J A, HARRIS J M. Using resolution-constrained adaptive meshes for traveltime tomography[J]. Journal of Seismic Exploration, 2006, 14: 371-392. |
| [13] |
SCHUMACHER H, HELDMANN S, HABER E, et al. Iterative Reconstruction of SPECT Images Using Adaptive Multi-Level Refinement[M]//Tolxdorff T, Braun J, Deserno TM, et al. Bildverarbeitung für die Medizin 2008. Berlin, Heidelberg: Springer-Verlag Berlin Heidelberg, 2008, 318-322.
|
| [14] |
HABER E, HELDMANN S, MODERSITZKI J. Adaptive mesh refinement for nonparametric image registration[J]. SIAM Journal on Scientific Computing, 2008, 30(6): 3012-3027. DOI:10.1137/070687724 |
| [15] |
GOKSEL O, ESKANDARI H, SALCUDEAN S E. Mesh adaptation for improving elasticity reconstruction using the FEM inverse problem[J]. IEEE Tran-sactions on Medical Imaging, 2013, 32(2): 408-418. DOI:10.1109/TMI.2012.2228664 |
| [16] |
MOLINARI M, BLOTT B H, COX S J, et al. Optimal imaging with adaptive mesh refinement in electrical impedance tomography[J]. Physiological Measurement, 2002, 23(1): 121-128. DOI:10.1088/0967-3334/23/1/311 |
| [17] |
KIM B S, KIM K Y, KIM S. Image reconstruction using adaptive mesh refinement based on adaptive thresholding in electrical impedance tomography[J]. Nuclear Engineering and Design, 2014, 270: 421-426. DOI:10.1016/j.nucengdes.2013.12.063 |
| [18] |
HABER E, HELDMANN S, ASCHER U. Adaptive finite volume method for distributed non-smooth parameter identification[J]. Inverse Problems, 2007, 23(4): 1659. DOI:10.1088/0266-5611/23/4/017 |
| [19] |
HABER E, OLDENBURG D, SCHWARZBACH C, et al. An adaptive mesh method for electromagnetic inverse problems[C]. SEG Technical Program Expanded Abstracts, 2012, 31: SEG-2012-0828.
|
| [20] |
DAVIS K, LI Y G. Fast solution of geophysical inversion using adaptive mesh, space-filling curves and wavelet compression[J]. Geophysical Journal International, 2011, 185(1): 157-166. DOI:10.1111/j.1365-246X.2011.04929.x |
| [21] |
DAVIS K, LI Y G. Efficient 3D inversion of magnetic data via octree-mesh discretization, space-filling curves, and wavelets[J]. Geophysics, 2013, 78(5): J61-J73. DOI:10.1190/geo2012-0192.1 |
| [22] |
CHOU T K, CHOUTEAU M, DUBÉ J S. Intelligent meshing technique for 2D resistivity inverse problems[J]. Geophysics, 2016, 81(4): IM45-IM56. DOI:10.1190/geo2015-0177.1 |
| [23] |
PLATTNER A, MAURER H R, VORLOEPER J, et al. 3-D electrical resistivity tomography using adaptive wavelet parameter grids[J]. Geophysical Journal International, 2012, 189(1): 317-330. DOI:10.1111/j.1365-246X.2012.05374.x |
| [24] |
KEY K, WEISS C. Adaptive finite-element modeling using unstructured grids: the 2D magnetotelluric example[J]. Geophysics, 2006, 71(6): G291-G299. DOI:10.1190/1.2348091 |
| [25] |
ZHDANOV M. Geophysical Inverse Theory and Regu-larization Problems[M]. Elsevier Science, Amsterdam, Netherlands Cambridge, MA, 2002.
|
| [26] |
OLDENBURG D W, LI Y G. Inversion of induced polarization data[J]. Geophysics, 1994, 59(9): 1327-1341. DOI:10.1190/1.1443692 |
| [27] |
LELIōVRE P G, FARQUHARSON C G. Gradient and smoothness regularization operators for geophysical inversion on unstructured meshes[J]. Geophysical Journal International, 2013, 195(1): 330-341. DOI:10.1093/gji/ggt255 |
| [28] |
RODI W L. A technique for improving the accuracy of finite element solutions for magnetotelluric data[J]. Geophysical Journal International, 1976, 44(2): 483-506. DOI:10.1111/j.1365-246X.1976.tb03669.x |
| [29] |
周勇, 张志勇, 张大洲, 等. 自适应网格直流电阻率三维反演[J]. 石油地球物理勘探, 2019, 54(5): 1174-1180. ZHOU Yong, ZHANG Zhiyong, ZHANG Dazhou, et al. 3D DC resistivity inversion based on inversion-oriented adaptive meshes[J]. Oil Geophysical Prospecting, 2019, 54(5): 1174-1180. |
| [30] |
HARRIS C, STEPHENS M. A combined corner and edge detector[C]. Alvey Vision Conference, 1988, 147-152.
|
| [31] |
BUI-THANH T, GHATTAS O. Analysis of the Hessian for inverse scattering problems: Ⅰ.Inverse shape scattering of acoustic waves[J]. Inverse Problems, 2012, 28(5): 055001. DOI:10.1088/0266-5611/28/5/055001 |
| [32] |
BUI-THANH T, GHATTAS O. Analysis of the Hessian for inverse scattering problems: Ⅱ.Inverse medium scattering of acoustic waves[J]. Inverse Problems, 2012, 28(5): 055002. DOI:10.1088/0266-5611/28/5/055002 |
| [33] |
SAGUN L, EVCI U, GUNEY V U, et al.Empirical analysis of the hessian of over-parametrized neural networks[DB/OL].(2017-06-14). https://arxiv.org/abs/1706.04454.
|
| [34] |
RIVAS C, BARBONE P, OBERAI A. Divergence of finite element formulations for inverse problems treated as optimization problems[J]. Journal of Physics-Conference Series, 2008, 135: 012088. DOI:10.1088/1742-6596/135/1/012088 |
| [35] |
BLOME M, MAURER H, GREENHALGH S. Geoelectric experimental design-efficient acquisition and exploitation of complete pole-bipole data sets[J]. Geophysics, 2011, 76(1): F15-F26. DOI:10.1190/1.3511350 |
| [36] |
WIESE T, GREENHALGH S, ZHOU B, et al. Resistivity inversion in 2-D anisotropic media: numerical experiments[J]. Geophysical Journal International, 2015, 201(1): 247-266. DOI:10.1093/gji/ggv012 |



 张志勇, 江西省南昌市广兰大道418号东华理工大学地球物理与测控技术学院, 330013。Email:
张志勇, 江西省南昌市广兰大道418号东华理工大学地球物理与测控技术学院, 330013。Email: 