② 非常规油气省部共建协同创新中心, 湖北武汉 430100
② Cooperative Innovation Center of Unconventional Oil and Gas, Wuhan, Hubei 430100, China
近年来,随着油气资源需求的急剧增加,剩余油气勘探及油气藏动态监测新技术、新方法成为业内研究热点。时移地球物理方法作为油气藏动态监测的有效途径之一,逐渐应用于石油开发领域,取得了良好的效果[1-3]。时移地震技术是目前发展最为成熟的时移地球物理方法[4-6],但对于多数油气储层,油气藏被流体驱替引起的声波阻抗差异较小,致使时移地震监测资料解释困难,且该方法经济成本高,对储层条件、注采方式等要求严苛。然而,在油气藏开采过程中,油气藏被流体驱替后引起的储层电性变化明显,这为时移电磁方法应用于油气藏动态监测提供了地球物理基础。
随着地球物理勘探方法的快速发展,电磁勘探方法逐渐向高维发展,并成为地震勘探方法的重要补充。电性源瞬变电磁法作为电磁法的重要分支,相比于可控源电磁(CSEM)法和大地电磁(MT)法,具有探测效率高、勘探深度大、信噪比高等优点,广泛应用于环境调查、油气、矿产、地热资源勘探及深部地壳研究等领域[7-14]。电磁资料的合理、精细解释离不开可靠的正、反演技术,而正演模拟作为反演的关键步骤,一直是地球物理工作者的研究重点。Edwards等[15]采用频时转换方法研究了电偶源在海水、基底双层介质中产生的阶跃、脉冲响应特征。Commer等[16]基于直流电法,通过求解泊松方程得到初始电场,进而实现长偏移距瞬变电磁三维正演,并研究了层状介质中油气储层的电磁场响应特征。Avdeeav等[17]基于有限差分法对比了频域和时间域海洋可控源电磁法对浅海油气储层的探测能力,发现时间域方法具有更好的勘探效果。Um等[18]采用隐式时间步长,基于一阶后退欧拉算法实现了非结构化网格的电性源瞬变电磁三维正演,并提出了一种自适应时间步长算法提高计算精度,极大地促进了隐式时间步长方法在瞬变电磁非结构有限元三维模拟中的应用。此后,随着地电模型复杂程度的增加,基于隐式时间步长的非结构有限元瞬变电磁法正、反演得到快速发展,并广泛应用于航空、半航空、地面、井中、海洋时域电磁法的数值计算[19-26]。
时移电磁法作为一种有效的地下介质电性变化监测手段,在油气藏、地热、地下水动态监测等方面具有良好的应用前景,相关研究取得了一定的进展,但整体上其理论方法、仪器研发、采集方式、数据解释等仍处于初始阶段。
考虑到时域电磁法勘探能力优于频域电磁法,本文基于非结构化网格矢量有限元法进行电性源瞬变电磁三维正演,并采用一种二阶后退欧拉算法(BDF2)变步长差分格式,避免了迭代过程中需向前查找上一个时间点。该方法实现简单,理论上可更准确地计算电场对时间的导数项,计算精度较高。本文对二阶后退欧拉法定步长、变步长差分格式的电性源瞬变电磁数值结果与解析解结果进行比对,对三维复杂地电模型数值结果与有限体积法计算结果进行对比分析,以验证本文算法的有效性与精度。最后,通过计算复杂油藏模型及实际页岩气压裂模型的动态监测平行电场分量,分析相对异常的变化,验证了电性源瞬变电磁法对陆地油气藏监测的有效性。
1 正演算法 1.1 非结构网格时域矢量有限元法对于设定有限区域的地电模型,时域电磁法电场扩散方程为[18]
| $ \nabla \times\left[\frac{1}{\mu} \nabla \times \boldsymbol{E}(\boldsymbol{r}, t)\right]+\sigma \frac{\partial \boldsymbol{E}(\boldsymbol{r}, t)}{\partial t}+\frac{\partial \boldsymbol{j}_{\mathrm{s}}(\boldsymbol{r}, t)}{\partial t}=0 $ | (1) |
式中:E(r, t)和js(r, t)分别为时刻t、任意位置r上的电场和发射源电流密度,下标“s”表示外部电流源;μ为介质磁导率;σ为电导率。
采用非结构四面体网格对地电模型进行剖分(图 1),并引入矢量插值基函数,将自由度赋予棱边上,则任意四面体单元内的电场可展开为
| $ \boldsymbol{E}^{e}(\boldsymbol{r}, t)=\sum\limits_{i=1}^{6} \boldsymbol{E}_{i}^{e}(t) \boldsymbol{n}_{i}^{e}(\boldsymbol{r}) $ | (2) |

|
图 1 四面体单元e的矢量电场分布图 |
式中:Eie为单元e的第i条棱边上的电场;nie(r)为矢量插值基函数,其定义为
| $ \boldsymbol{n}_{i}^{e}(\boldsymbol{r})=\left(L_{i_{1}}^{e} \nabla L_{i_{2}}^{e}-L_{i_{2}}^{e} \nabla L_{i_{1}}^{e}\right) l_{i}^{e} $ | (3) |
式中:Li1e和Li2e分别是单元e第i条棱边上节点i1和i2的标量插值基函数,i取1~6;lie为单元e的第i条棱边的长度。由上式可知,nie(r)自动满足散度为零的条件,即单元分界面上电场切向分量保持连续性[27]。
利用Galerkin方法离散式(1),得到单元e的残差矢量
| $ \begin{aligned} \boldsymbol{R}^{e}(\boldsymbol{r}, t)=& \nabla \times\left[\frac{1}{\mu} \nabla \times \boldsymbol{E}^{e}(\boldsymbol{r}, t)\right]+\\ & \sigma \frac{\partial \boldsymbol{E}^{e}(\boldsymbol{r}, t)}{\partial t}+\frac{\partial \boldsymbol{j}_{\mathrm{s}}^{e}(\boldsymbol{r}, t)}{\partial t} \end{aligned} $ | (4) |
并确保该单元的加权余量为零
| $ \boldsymbol{G}^{e}=\iiint\limits_{V^{e}} \boldsymbol{n}^{e} \cdot \boldsymbol{R}^{e}(\boldsymbol{r}, t) \mathrm{d} V=0 $ | (5) |
将所有四面体单元加权余量组合,可得
| $ \boldsymbol{G}=\sum\limits_{e=1}^{M} \boldsymbol{G}^{e}=\boldsymbol{A} \frac{\mathrm{d} \boldsymbol{E}(t)}{\mathrm{d} t}+\boldsymbol{B} \boldsymbol{E}(t)+\boldsymbol{S}=0 $ | (6) |
式中:V表示四面体单元体积;M是四面体单元总数;A表示单元质量矩阵;B表示单元刚度矩阵;S表示电流源项。对于四面体单元e,Ae、Be和Se的积分表达式分别为
| $ \boldsymbol{A}_{i, j}^{e} =\iiint\limits_{V^{e}} \sigma^{e} \boldsymbol{n}_{i}^{e}(\boldsymbol{r}) \boldsymbol{n}_{j}^{e}(\boldsymbol{r}) \mathrm{d} V $ | (7) |
| $ \boldsymbol{B}_{i, j}^{e} =\frac{1}{\mu^{e}} \iiint\limits_{V^{e}}\left[\nabla \times \boldsymbol{n}_{i}^{e}(\boldsymbol{r})\right] \cdot\left[\nabla \times \boldsymbol{n}_{j}^{e}(\boldsymbol{r})\right] \mathrm{d} V $ | (8) |
| $ \boldsymbol{S}_{i}^{e} =\iiint\limits_{V^{e}} \boldsymbol{n}_{i}^{e}(\boldsymbol{r}) \cdot \frac{\partial \boldsymbol{j}_{\mathrm{s}}(\boldsymbol{r}, t)}{\partial t} \mathrm{~d} V $ | (9) |
式中i、j均取1~6,为单元棱边索引。
利用非结构四面体网格离散灵活的特点,将长导线源分解为多段,每段导线可近似为电偶极子,每个电偶极子的电流密度可表示为[28]
| $ \boldsymbol{j}_{\mathrm{s}}(\boldsymbol{r}, t)=\delta\left(\boldsymbol{r}-\boldsymbol{r}_{\mathrm{s}}\right) \boldsymbol{I}(t) \mathrm{d} l $ | (10) |
式中:δ是脉冲函数;rs为电偶源位置;I是电流矢量;dl是电偶极子长度。
1.2 二阶后退欧拉变步长差分格式求解式(6)需对时间进行离散,本文采用精度较高的二阶后退欧拉法[18],经Taylor展开得到
| $ \frac{\mathrm{d} \boldsymbol{E}(t)^{(k)}}{\mathrm{d} t}=\frac{1}{2 \Delta t}\left[3 \boldsymbol{E}(t)^{(k)}-4 \boldsymbol{E}(t)^{(k-1)}+\boldsymbol{E}(t)^{(k-2)}\right] $ | (11) |
式中:Δt为时间步长;k为迭代次数。将式(11)代入式(6)可得
| $ \begin{aligned} (3 \boldsymbol{A}+2 \Delta t \boldsymbol{B}) \boldsymbol{E}(t)^{(k)}=& \boldsymbol{A}\left[4 \boldsymbol{E}(t)^{(k-1)}-\right.\\ &\left.\boldsymbol{E}(t)^{(k-2)}\right]-2 \Delta t \boldsymbol{S}^{(k)} \end{aligned} $ | (12) |
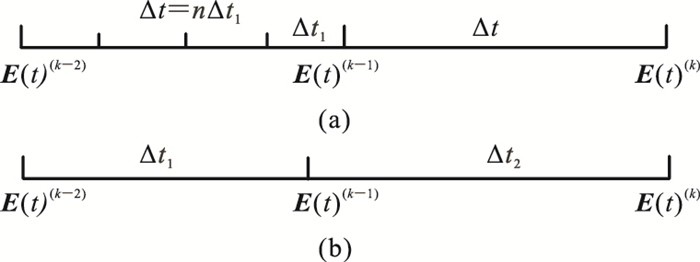
上式左端项系数矩阵与时间步长Δt相关。当使用直接求解器(Pardiso)时,若Δt保持不变,只需更新方程右端项,重复将储存的矩阵分解结果带回右端项求解(图 2a);若Δt是变化的,需向前查找上一个时刻nΔt1的电场值,重新分解系数矩阵并带入右端项求解。本文采用一种二阶后退欧拉变步长差分格式(图 2b)[29],此方法仅需利用第k个时间道的前两个时间步长(Δt1、Δt2)的结果进行计算(为更直观地表示变步长差分格式,用Δt2替代定步长差分格式的Δt),具有较高的精度和良好的稳定性,比使用定步长差分格式更有效,其具体表达式为
| $ \begin{cases}\frac{\mathrm{d} \boldsymbol{E}(t)^{(k)}}{\mathrm{d} t}= & \frac{1}{\Delta t_{2}}\left[\frac{1+2 \gamma^{(k)}}{1+\gamma^{(k)}} \boldsymbol{E}(t)^{(k)}-\right. \\ & \left.\left(1+\gamma^{(k)}\right) \boldsymbol{E}(t)^{(k-1)}+\frac{\left[\gamma^{(k)}\right]^{2}}{1+\gamma^{(k)}} \boldsymbol{E}(t)^{(k-2)}\right] \\ \gamma=\frac{\Delta t_{2}}{\Delta t_{1}}\end{cases} $ | (13) |
|
图 2 时间步长离散示意图 (a)定步长差分格式;(b)变步长差分格式 |
将式(13)代入式(6),得
| $ \begin{aligned} &\left(\frac{1+2 \gamma^{(k)}}{1+\gamma^{(k)}} \boldsymbol{A}+\Delta t_{2} \boldsymbol{B}\right) \boldsymbol{E}(t)^{(k)}= \\ &\boldsymbol{A}\left[\left(1+\gamma^{(k)}\right) \boldsymbol{E}(t)^{(k-1)}-\frac{\left[\gamma^{(k)}\right]^{2}}{1+\gamma^{(k)}} \boldsymbol{E}(t)^{(k-2)}\right]-\Delta t_{2} \boldsymbol{S}^{(k)} \end{aligned} $ | (14) |
当Δt1=Δt2时,式(13)和式(14)退化为与式(11)和式(12)相同的结果,后文对该差分格式的效果进行了验证。
1.3 初始电场计算当电性源采用上升沿(Step-on)激发时,初始电场为零;当采用下降沿(Step-off)激发时,初始电场E(0)由长导线源所在位置的电场分布Es(0)与电极供电形成的稳定直流场EDC(0)两部分组成,即
| $ \boldsymbol{E}^{(0)}=\boldsymbol{E}_{\mathrm{s}}^{(0)}+\boldsymbol{E}_{\mathrm{DC}}^{(0)} $ | (15) |
Es(0)可通过欧姆定律求取,EDC(0)可通过直流电阻率三维正演所得电位的梯度求取[18]。
直流电法的电位u满足三维Poisson方程
| $ \nabla \cdot(\sigma \nabla u)=-I \delta\left(\boldsymbol{r}-\boldsymbol{r}_{0}\right) $ | (16) |
式中:r0为发射源位置;I为电流强度。
为保证空气电场切向分量不为零,采取总场方法求解式(16),并采用与时间域电磁场同一套非结构化网格及对应的Dirichlet边界条件
| $ \left.u\right|_{\boldsymbol{\varGamma}}=0 $ | (17) |
使直流电场与矢量电场在边界Г上保持一致性,得到四面体节点电位后,计算每条棱边对应节点电位的梯度即可得到稳定的直流电场EDC(0)。
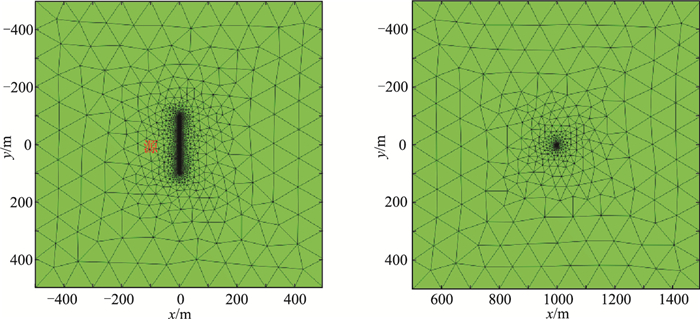
2 数值模拟 2.1 解析解验证本算例开展正演计算的工作站配置为:处理器AMD Ryzen 9-5950,CPU主频3.4GHz,内存96GB。为验证本文算法的正确性,对比后退欧拉法定步长与变步长差分格式的计算精度。设计一个均匀半空间模型进行数值计算,均匀半空间的介质电阻率为100Ω·m,空气电阻率为1×108Ω·m,电性源长度为200m,沿y方向布设,发射电流为1A。测点也沿y方向布设,与源的偏移距为1000m。将长导线等间距分割为100段电偶极子,为保证计算精度,对发射源与接收点处的网格进行局部加密,最终生成201906个四面体、32983个节点、235656条棱边(图 3)。计算时间为2×10-7~4s,离散为1122个时间道,分别计算二阶后退欧拉法定步长、变步长差分格式在测点处平行电场分量Ey的响应曲线,并与解析解对比。利用下式计算相对误差
| $ \operatorname{Error}=\frac{E_{\mathrm{N}}-E_{\mathrm{A}}}{E_{\mathrm{A}}} $ | (18) |
|
图 3 发射源区域(左)与测点区域(右)网格局部加密示意图 |
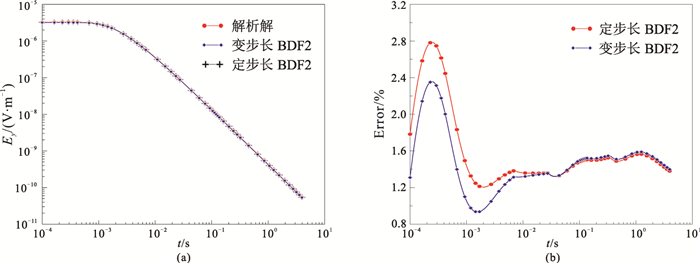
结果见图 4。式中:EN表示有限元数值解;EA表示解析解或有限体积解。
|
图 4 不同步长差分格式Ey计算结果(a)及其与数值解的相对误差(b) |
由图 4可见,两种差分格式的计算结果均与解析解拟合较好,变步长法在早期的计算精度高于定步长法,晚期基本一致,说明变步长差分格式具有较高的精度和稳定性。整体而言,两种方法均可以高精度地计算电场响应,表明本文算法的可行性,适用于电性源瞬变电磁的三维正演模拟。
2.2 三维模型验证为验证二阶后退欧拉法变步长差分格式对复杂地电模型的计算精度,设计一个三维模型[20]进行计算,模型切面如图 5a所示。电性源长度为1000m,沿y方向布设,中心点位于地表(0, 0, 0)处,发射电流为1A。将长导线等间距分割为400段电偶极子。沿x负方向布置12个测点,对发射源和测点区域进行局部网格加密,最终生成1255209个网格、202819个节点、1458795条棱边(图 5b)。
|
图 5 三维复杂模型切面图(a)和测点区域网格剖分示意图(b) |
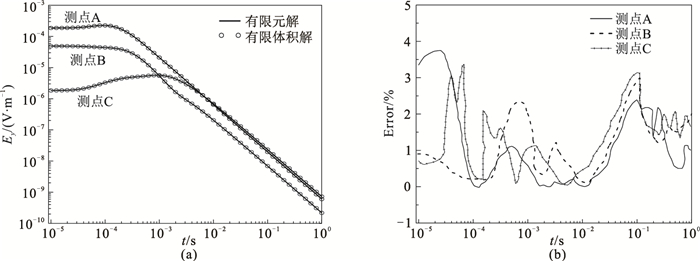
计算该模型占用内存10.5G,总耗时为3296s。图 6a为测点A(-500m, 0, 0)、测点B(-1050m, 0, 0)、测点C(-2000m, 0, 0)的电场分量Ey数值计算结果与Liu等[20]有限体积计算结果对比。由图可见,二阶后退欧拉法变步长差分格式的矢量有限元解与有限体积解吻合良好。图 6b为误差曲线,可见这三个测点的计算结果相对误差均低于5%,证明了本文算法的正确性,可用于电性源瞬变电磁法油气藏动态监测数值研究。
|
图 6 电性源瞬变电磁法三维模型Ey分量数值计算结果(a)及三个测点的相对误差曲线(b) |
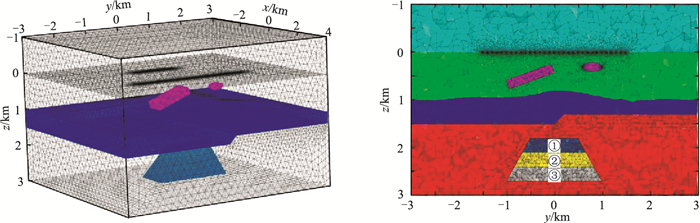
为从理论上研究电性源瞬变电磁法对油藏动态监测的响应能力,设计图 7所示的复杂油藏模型。空气电阻率设为1×108Ω·m。发射源沿y向布设,长度为1000m,发射电流为1A。将长导线源等间距分割为400段电偶极子。在地表沿y方向从-1500m到1500m共布置31个测点,点距为100m,测线与源的偏移距为2000m。在近地表存在两个异常体作为对油气藏动态监测过程的干扰区域:一个是长方体异常体,大小为1000m×1000m×200m,倾角为20°,异常体中心埋深为400m,电阻率为2000Ω·m;另一个是椭球状异常体,x、y、z方向的半轴长度分别为200、200、100m,中心埋深为200m,电阻率为10Ω·m。假设一个金字塔状的油藏,基底边长为2000m,顶部边长为1000m,高为900m,油藏顶面距地表2000m,电阻率为500Ω·m。模型背景为三层复杂起伏地层,从上至下电阻率分别为1000、200、100Ω·m。对发射源、测点、异常体周围的网格进行局部加密,最终生成1547756个网格、249739个节点、1798262条棱边(图 7b)。按照图中序号,分三个阶段进行电性源瞬变电磁法监测,每个阶段盐水驱油后储层电阻率变为10Ω·m,由下至上每次驱油深度300m。该模型计算占用内存13.1G,总求解时间为3823s。
|
图 7 复杂地质油藏模型3D示意图(左)和局部网格剖分示意图(右) 右图中序号①~③为盐水驱替油层顺序,长方体与椭球体为浅地表异常干扰区域 |
图 8为利用以下公式计算的三段水驱油动态监测相对异常
| $ R_{\mathrm{a}}=\frac{E_{\mathrm{al}}-E_{\mathrm{bd}}}{E_{\mathrm{bd}}} $ |
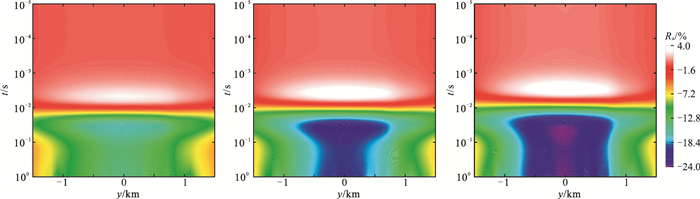
|
图 8 水驱油动态监测过程阶段①~③(左,中,右)相对异常Ra剖面 |
式中:Ebd、Eal分别表示水驱油或压裂前、后的电场响应。由图可见,随着水驱油过程中地下介质电阻率的不断降低,电场响应的相对异常Ra不断增大,最大可达24.00%(绝对值),且相对异常基本不受地下起伏界面及其他异常体的干扰,可以清晰地反映油藏动态监测过程。还可以看出,相对异常区域的顶边界随盐水驱油过程在时间道上向上移动。根据电磁理论,电性源瞬变电磁数据的早期时间道勘探深度小、晚期时间道勘探深度大,时间道与深度由晚期到早期、由深至浅互相对应,很好地反映了盐水驱油由下至上的动态过程。由于近地表异常体产生的电性干扰没有发生变化,油藏监测过程中干扰区域的电磁场可作为背景场(Ebd)从总场中减去。因此,近地表异常干扰对油藏动态监测基本没有影响(图 8)。此例计算结果表明,利用时移电磁法对油藏进行动态监测具有良好的应用前景。
2.4 实际应用基于涪陵页岩气田区焦页30井测井资料,Liu等[30]设计了图 9所示的页岩气储层模型,并采用可控源电磁法在理论上对该地区页岩气压裂监测进行了可行性论证。本文基于Liu等建立的模型,采用电性源瞬变电磁法对页岩气压裂模型的动态监测效果进行分析。

|
图 9 涪陵焦页30井页岩气储层电阻率模型 |
发射源沿y方向布设,中心点位于地表(0, 0, 0),长度为1000m,发射电流为100A。将长导线源等间距分割为400段电偶极子。在地表沿y方向-800~800m区域共布置41个测点,间距为40m,测线偏移距为5000m。图 9中页岩气规模为2300m×840m×300m,电阻率为42Ω·m,压裂后电阻率变为5Ω·m。对发射源、测点、页岩气藏区域进行局部网格加密,最终生成1914330个网格、305778个节点和2221195条棱边。
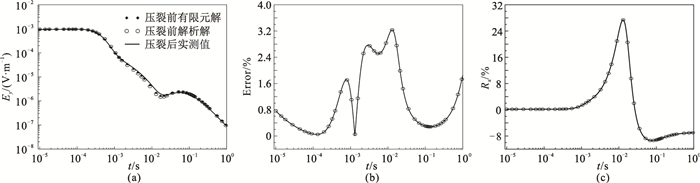
该模型计算占用内存14.6G,总求解时间为4075s。图 10a为测线中点(5000,0,0)压裂前电场Ey的解析解、有限元数值解(均匀层状储层模型)及页岩气压裂后的电场Ey;图 10b为压裂前均匀层状储层模型有限元数值解相对于解析解的相对误差曲线,可见误差不大于3.50%,具有较高的计算精度;图 10c为压裂前、后有限元数值解的相对异常,可以看出相对异常最大达27.39%,可以清楚地反映出页岩气藏压裂引起的电性变化。
|
图 10 页岩气层状储层模型测点(5000m,0,0)压裂前、后的Ey曲线及相对误差 (a)压裂前有限元解和解析解及压裂后的响应曲线;(b)压裂前有限元解与解析解的相对误差;(c)压裂后响应与压裂前有限元解的相对异常 |
图 11a为页岩气储层压裂前、后测线上不同时间道的电场Ey分量相对异常等值线,可以明显看出压裂引起的电性异常,但同时也伴随着假异常(图中虚线框区域)的出现,这是由于压裂过程中,随着压裂液的侵入,压裂区的电阻率会降低,电流在低阻体中形成明显的电流通道效应,致使压裂区域电场出现较大变化,最终表现为正、负异常特征。图 11b为压裂前、后总场残差(Eal-Ebd)等值线图,同样可以看出页岩气藏压裂导致的电场残差出现正、负特征。总之,页岩气藏压裂前、后电场异常响应明显,证实了利用时移电磁法对油气藏动态监测的有效性和可行性。
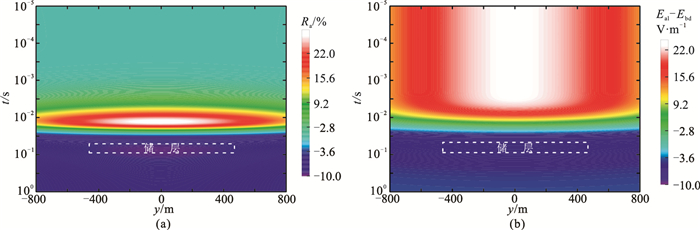
|
图 11 页岩气层状储层压裂前、后Ey相对异常Ra(a)及总场残差(Eal-Ebd)(b) |
本文将非结构化网格矢量有限元法应用于电性源瞬变电磁法油气藏动态监测的正演模拟,得到以下结论。
(1) 采用二阶后退欧拉法变步长差分格式离散时间步长,可有效提高数值计算精度。对比复杂地电模型的有限体积解,有限元解可有效保证数值结果的稳定性,适于复杂油气藏模型动态监测数值模拟。
(2) 对理论油藏模型与实际页岩气模型的数值分析表明,电性源时移电磁法的相对异常响应基本不受地层中其它异常体的影响,可有效刻画油(气)藏驱替(压裂)前、后的电性差异,实现高精度油气藏动态监测。
电性源时移电磁法对油气藏、地下水、金属等资源动态监测是有效的。作为时移地震勘探的重要补充,时移电磁法目前还处于起步阶段,借助本文算法可分析电性源瞬变电磁法对矿产资源动态监测的规律,为实际矿产资源动态监测提供理论指导。
| [1] |
BLACK N, ZHDANOV M S. Chapter 8-active geophysical monitoring of hydrocarbon reservoirs using EM methods[J]. Handbook of Geophysical Exploration: Seismic Exploration, 2010, 40: 135-159. |
| [2] |
HE Z X, HU Z Z, GAO Y, et al. Field test of monitor-ing gas reservoir development using time-lapse continuous electromagnetic profile method[J]. Geophy-sics, 2015, 80(2): WA127-WA134. |
| [3] |
YAN L J, CHEN X X, TANG H, et al. Continuous TDEM for monitoring shale hydraulic fracturing[J]. Applied Geophysics, 2018, 15(1): 26-34. DOI:10.1007/s11770-018-0661-1 |
| [4] |
REY A, BHARK E, GAO K, et al. Streamline-based integration of time-lapse seismic and production data into petroleum reservoir models[J]. Geophysics, 2012, 77(6): M73-M87. DOI:10.1190/geo2011-0346.1 |
| [5] |
PETERSON B, GERHARDT A. Pluto gas field: successful placement of an infill well based on 4D seismic monitoring[J]. The Leading Edge, 2020, 39(7): 464-470. DOI:10.1190/tle39070464.1 |
| [6] |
王波, 聂其海, 陈进娥, 等. 四维多波地震在油藏动态监测中的应用[J]. 石油地球物理勘探, 2021, 56(2): 340-345. WANG Bo, NIE Qihai, CHEN Jin'e, et al. Application of 4D multi-component seismic survey in dynamic reservoir monitoring[J]. Oil Geophysical Prospecting, 2021, 56(2): 340-345. |
| [7] |
STRACK K M. The deep transient electromagnetic soun-ding technique: first field test in Australia[J]. Exploration Geophysics, 1984, 15(4): 251-259. DOI:10.1071/EG984251 |
| [8] |
KELLER G V, PRITCHARD J I, JACOBSON J J, et al. Megasource time-domain electromagnetic sounding methods[J]. Geophysics, 1984, 49(7): 993-1009. DOI:10.1190/1.1441743 |
| [9] |
HÖRDT A, DRUSKIN V L, KNIZHNERMAN L A, et al. Interpretation of 3-D effects in long-offset transient electromagnetic (LOTEM) soundings in the Münsterland area, Germany[J]. Geophysics, 1992, 57(9): 1127-1137. DOI:10.1190/1.1443327 |
| [10] |
MVLLER M, HÖRDT A, NEUBAUER F M. Internal structure of Mount Merapi, Indonesia, derived from long-offset transient electromagnetic data[J]. Journal of Geophysical Research-Solid Earth, 2002, 107(B9): ECV2-1-ECV2-14. DOI:10.1029/2001JB000148 |
| [11] |
MITSUHATA Y, UCHIDA T, AMANO H. 2.5-D inversion of frequency-domain electromagnetic data ge-nerated by a grounded-wire source[J]. Geophysics, 2002, 67(6): 1753-1768. DOI:10.1190/1.1527076 |
| [12] |
COMMER M, HELWIG S L, HÖRDT A, et al. New results on the resistivity structure of Merapi Volcano (Indonesia), derived from three-dimensional restricted inversion of long-offset transient electromagnetic data[J]. Geophysical Journal International, 2006, 167(3): 1172-1187. DOI:10.1111/j.1365-246X.2006.03182.x |
| [13] |
HAROON A, ADRIAN J, BERGERS R, et al. Joint inversion of long-offset and central-loop transient electromagnetic data: application to a mud volcano exploration in Perekishkul, Azerbaijan[J]. Geophysical Prospecting, 2015, 63(2): 478-494. DOI:10.1111/1365-2478.12157 |
| [14] |
何继善, 薛国强. 短偏移距电磁探测技术概述[J]. 地球物理学报, 2018, 61(1): 1-8. HE Jishan, XUE Guoqiang. Review of the key techniques on short-offset electromagnetic detection[J]. Chinese Journal of Geophysics, 2018, 61(1): 1-8. DOI:10.3969/j.issn.1672-7940.2018.01.001 |
| [15] |
EDWARDS R N, CHAVE A D. A transient electric dipole-dipole method for mapping the conductivity of the sea floor[J]. Geophysics, 1986, 51(4): 984-987. DOI:10.1190/1.1442156 |
| [16] |
COMMER M, NEWMAN G. A parallel finite-diffe-rence approach for 3D transient electromagnetic modeling with galvanic sources[J]. Geophysics, 2004, 69(5): 1192-1202. DOI:10.1190/1.1801936 |
| [17] |
AVDEEVA A, COMMER M, NEWMAN G A. Hydrocarbon reservoir detectability study for marine CSEM methods: time domain versus frequency domain[C]. SEG Technical Program Expanded Abstracts, 2007, 26: 628-632.
|
| [18] |
UM E S, HARRIS J M, ALUMBAUGH D L. 3D time-domain simulation of electromagnetic diffusion phenomena: a finite-element electric-field approach[J]. Geophysics, 2010, 75(4): F115-F126. DOI:10.1190/1.3473694 |
| [19] |
LIU Y H, YIN C C. Electromagnetic divergence correction for 3D anisotropic EM modeling[J]. Journal of Applied Geophysics, 2013, 96: 19-27. DOI:10.1016/j.jappgeo.2013.06.014 |
| [20] |
LIU Y J, YOGESHWAR P, HU X Y, et al. Effects of electrical anisotropy on long-offset transient electromagnetic data[J]. Geophysical Journal International, 2020, 222(1): 1074-1089. |
| [21] |
LI J H, FARQUHARSON C G, HU X Y, et al. 3D vector finite-element electromagnetic forward mode-ling for large loop sources using a total-field algorithm and unstructured tetrahedral grids[J]. Geophysics, 2017, 82(1): E1-E16. DOI:10.1190/geo2016-0004.1 |
| [22] |
OLDENBURG D W, HABER E, SHEKHTMAN R. Three dimensional inversion of multisource time domain electromagnetic data[J]. Geophysics, 2013, 78(1): E47-E57. DOI:10.1190/geo2012-0131.1 |
| [23] |
YIN C C, QI Y F, LIU Y H. 3D time-domain airborne EM modeling for an arbitrarily anisotropic earth[J]. Journal of Applied Geophysics, 2016, 131: 163-178. DOI:10.1016/j.jappgeo.2016.05.013 |
| [24] |
惠哲剑, 殷长春, 刘云鹤, 等. 基于非结构有限元的时间域海洋电磁三维反演[J]. 地球物理学报, 2020, 63(8): 3167-3179. HUI Zhejian, YIN Changchun, LIU Yunhe, et al. 3D inversions of time-domain marine EM data based on unstructured finite-element method[J]. Chinese Journal of Geophysics, 2020, 63(8): 3167-3179. |
| [25] |
殷长春, 惠哲剑, 张博, 等. 起伏海底地形时间域海洋电磁三维自适应正演模拟[J]. 地球物理学报, 2019, 62(5): 1942-1953. YIN Changchun, HUI Zhejian, ZHANG Bo, et al. 3D adaptive forward modeling for time-domain marine CSEM over topographic seafloor[J]. Chinese Journal of Geophysics, 2019, 62(5): 1942-1953. |
| [26] |
王显祥, 底青云, 邓居智. 多通道瞬变电磁法油气藏动态检测[J]. 石油地球物理勘探, 2016, 51(5): 1021-1030. WANG Xianxiang, DI Qingyun, DENG Juzhi. Reservoir dynamic detection based on multi-channel transient electromagnetic[J]. Oil Geophysical Prospecting, 2016, 51(5): 1021-1030. |
| [27] |
JIN J M. The Finite Element Method in Electromagnetics[M]. John Wiley & Sons, New York, USA, 2002.
|
| [28] |
JAHANDARI H, FARQUHARSON C G. A finite-vo-lume solution to the geophysical electromagnetic forward problem using unstructured grids[J]. Geophy-sics, 2014, 79(6): E287-E302. |
| [29] |
CELAYA E A, AGUIRREZABALA J J A, CHAT-ZIPANTELIDIS P. Implementation of an adaptive BDF2 formula and comparison with the MATLAB ode15s[J]. Procedia Computer Science, 2014, 29: 1014-1026. DOI:10.1016/j.procs.2014.05.091 |
| [30] |
LIU R, LIU J X, WANG J X, et al. A time-lapse CSEM monitoring study for hydraulic fracturing in shale gas reservoir[J]. Marine and Petroleum Geology, 2020, 120: 104545. DOI:10.1016/j.marpetgeo.2020.104545 |



 严良俊, 湖北省武汉市蔡甸区大学路111号长江大学武汉校区石油科技大楼d309, 430100。Email:
严良俊, 湖北省武汉市蔡甸区大学路111号长江大学武汉校区石油科技大楼d309, 430100。Email: 