② 东方地球物理公司综合物化探处, 河北涿州 072751
② GME & Geochemical Surveys of BGP, CNPC, Zhuozhou, Hebei 072751, China
近年来,非地震勘探在川西地区火成岩、深层结构和断裂研究方面发挥了一定的指导作用,尤其是时频电磁法在寻找火山通道、探索火山岩形成机制方面效果良好[1-3]。
时频电磁法[4-8]是一种可控源电磁测深方法,该方法是基于油气藏或矿藏的激发极化特性以及其与围岩之间的电性差异,采用大功率、高精度人工源多频激发,将时间域电磁方法与频率域电磁方法有机结合,利用激发极化特性和电性综合异常检测和识别油气藏。相较于天然电磁法,可控源电磁法采用人工场源激发,即便在有工业干扰的地区,也能获得较高信噪比的数据。
时频电磁法基于原始资料分析和弱异常信息提取,通过精细反演,可寻找火山通道,探索火山岩形成机制;通过精细建模、针对火山岩约束反演,可刻画火山岩电阻率的平面变化,并结合不同岩性火山岩的电阻率变化特征,优选有利火山岩储集相带,有效区分火山碎屑岩与玄武岩,为地震勘探对火山岩岩性的识别提供了依据。
时频电磁法所采用的人工场源会导致非平面波效应、阴影效应以及场源附加效应,增加数据反演的多解性,使反演成像的质量偏低、甚至造成假异常,致使地质解释出现错误[9-10]。本文利用时频电磁法多分量联合反演解决上述问题。
国内外学者做了大量关于可控源电磁勘探的多分量正、反演研究工作。陈明生等[11]深入研究了二维模型条件下可控线电流源的瞬变电磁响应;王若等[12]开展了二维模型中CSAMT的正演计算;陈小斌等[13]利用有限元直接迭代算法正演计算了二维电性模型频率域有限长线源响应;Li等[14]采用三角形剖分、有限元离散、背景场与散射场分离等方法消除场源处的奇异性,计算了海水中有限长线源产生的电磁响应。
可控源电磁数据的反演研究也取得了一定的成果。Key[15]在Constable等[16]的大地电磁法Occam反演算法的基础上,提出了适用于海洋可控源电磁数据的多分量反演算法;师学明等[17]将最优化非线性反演方法和模拟退火方法引入电磁勘探数据多分量联合反演,取得了良好的效果;王若等[18-19]实现了CSAMT全资料反演;何梅兴等[20]基于Occam方法实现了CSAMT一维全资料反演;邱卫忠等[21]详细介绍了电流源瞬变电磁法利用不同电磁场分量实现地下目标体的精确探测;王志刚等[22]利用模拟退火法,实现了时频电磁法的多分量反演,并在实际数据处理中取得了好的效果;何展翔等[23]基于人工鱼群算法实现了TFEM的水平电场和垂直磁场的联合约束反演,有效降低了反演结果的非唯一性,提高了反演精度。
实践中,如何平衡不同分量之间(如电道与磁道振幅)数量级的差异,防止出现绝对值较大或较小的数据在反演过程中占据主导地位、而其他分量起次要作用或不起作用的情况,是多分量联合反演成败的关键。为此,本文提出了在反演过程中增加动态平衡系数的方法,校正迭代搜索方向和模型更新步长,并对理论模型和实际数据进行了测试。
1 时频电磁二维正演理论时频电磁法正演控制表达式为
| $ \nabla \times \boldsymbol{E}=-\hat{z} \boldsymbol{H} $ | (1) |
| $ \nabla \times \boldsymbol{H}=-\hat{y} \boldsymbol{E}+\boldsymbol{J}_{\mathrm{s}} $ | (2) |
式中:E表示电场;H表示磁场;Js表示源电流密度;
假设地电模型沿x方向延伸,该模型可简化为一个关于y和z的函数
| $ \sigma=\sigma(y, z) $ | (3) |
从式(2)可以看出右边存在一个源项Js,由于在源处存在奇异性,很难对其进行数值模拟。为了消除源项引起的奇异性,可借鉴Li等[14]提出的背景场与散射场分离方法。
2 控制方程有限差分离散有限差分法是一种经典的数值模拟计算方法,其基本原理是用差商替代微商,将待求解的连续微分方程变换为离散的差分方程,并通过求解差分方程得到源微分方程的近似解。其优点是方法简便、易于实现。
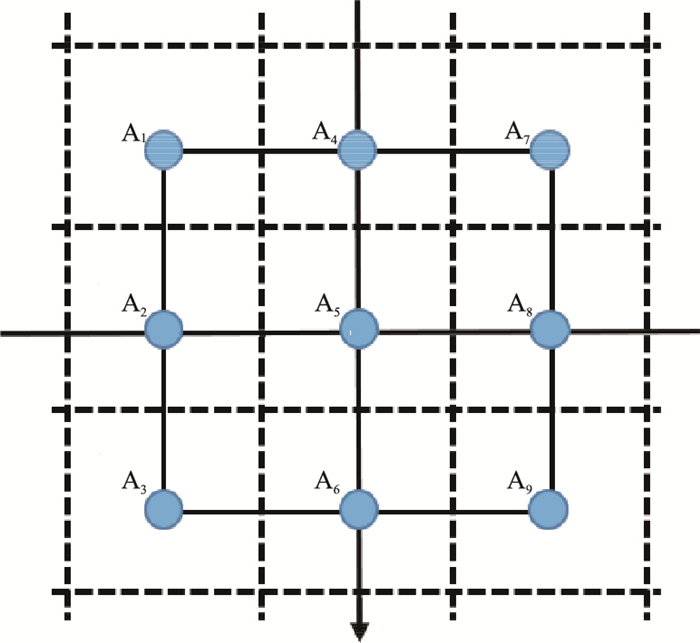
模型的网格剖分采用矩形剖分,如图 1所示。设横向剖分节点数为N+1,即横向网格数为N;纵向剖分为M+1个节点,即纵向网格数为M。总计N×M个网格。将网格按照从上至下、从左至右的方式顺序自然编号。设待求解的电、磁场分量分别为U=Exi, i=1, 2, …, N×M, V={Hxi, i=1, 2, …, N×M},计算点位于网格的中心位置。采用九点差分格式进行离散,并对局部节点进行自然顺序编号(A1~A9),如图 2所示。

|
图 1 模型矩形网格剖分示意图 |
|
图 2 九点差分格式示意图 |
将局部离散方程组装并加上狄里克莱边界条件,形成一个大型稀疏线性方程
| $ \bf{K} \cdot \bf{X}=\boldsymbol{S} $ | (4) |
式中:K表示与频率和电阻率有关的复对称矩阵;S是与频率和电阻率有关的向量;X表示电场或者磁场分量。求解该方程组,即可得到电、磁场响应。
3 多分量联合反演原理本文采用正则化反演原理实现时频电磁多分量联合反演。首先,构造一个反演目标泛函数(简称目标泛函)。目标泛函一般由两部分组成,其中一个是反演过程稳定函数,简称稳定函数。稳定函数有多种实现方式,本文采用Occam算法所采用的模型导数作为稳定函数[15-16],其一般形为
| $ \|\partial \mathit{\boldsymbol{m}}\|^{2}=\min $ | (5) |
式中:∂为正则化反演模型稳定器,一般为加权求导矩阵算子形式;m为反演模型参数;min表示取最小值。另一个是惩罚函数,用于度量反演模型的响应与观测数据之间的偏差,其一般形为
| $ \|\boldsymbol{W} \boldsymbol{d}-\boldsymbol{W} f(\boldsymbol{m})\|^{2}=\min $ | (6) |
式中:d为参与反演的观测数据;f为正演响应计算函数;W为观测数据的权重。利用拉格朗日乘子理论可求得反演目标泛函
| $ \begin{aligned} T(\boldsymbol{m}) &=\|\partial \boldsymbol{m}\|^{2}+\xi^{-1}\left[\|\boldsymbol{W} \boldsymbol{d}-\boldsymbol{W} f(\boldsymbol{m})\|^{2}-\chi^{2}\right] \\ &=\min \end{aligned} $ | (7) |
式中:ξ为拉格朗日乘子,用于反演过程中平衡惩罚函数与稳定函数;χ为期望拟合差。
时频电磁的响应函数一般为最小相位系统,其振幅与相位之间存在一定的联系,即振幅包含的信息等价于相位包含的信息,故时频电磁反演一般采用振幅数据。
时频电磁的电场分量Ex与磁场分量Bz的振幅量级差异较大,一般相差4个量级。如果直接将两个分量的振幅数据代入反演目标函数,可能会导致某个分量的数据占优,而另一分量的数据在反演过程中不能对反演模型的修改发挥作用,这种现象称为数据间的相互“淹没”。
为了克服不同分量数据的量级差异,笔者认为可以有两种方法解决这一问题:一是将不同分量的振幅转换为视电阻率,一般采用可控源电磁全区视电阻率,这点将另文论述,本文不做详细讨论;另一种是将两类分量数据(包括振幅和相位)分别作为两个数据集合代入目标函数
| $ \begin{aligned} T(\boldsymbol{m})=&\|\partial \boldsymbol{m}\|^{2}+\xi^{-1}\left[\left\|\boldsymbol{W} \boldsymbol{d}_{E_{x}}-\boldsymbol{W} f(\boldsymbol{m})\right\|^{2}+\right.\\ &\left.\beta\left\|\boldsymbol{W} \boldsymbol{d}_{B_{z}}-\boldsymbol{W} f(\boldsymbol{m})\right\|^{2}-\chi^{2}\right]=\min \end{aligned} $ | (8) |
式中β为不同分量数据量级差异的平衡因子,后文简称平衡因子。
β可以采取固定赋值的方法,即处理人员根据经验设置,但是实际数据Ex与Bz的振幅量级差异是变化的,需要处理人员不断测试平衡因子的有效取值范围,工作量大,且人为因素多,故本文不采用这种方法。正则化反演是一种迭代寻优的数学过程,本文采用动态统计估算平衡算法,即在每一次迭代过程中,利用当前迭代反演模型的响应,利用下式
| $ \beta=\frac{\operatorname{median}\left[\left\|\boldsymbol{W} \boldsymbol{d}_{E_{x}}-\boldsymbol{W} f(\boldsymbol{m})\right\|^{2}\right]}{\operatorname{median}\left[\left\|\boldsymbol{W} \boldsymbol{d}_{B_{z}}-\boldsymbol{W} f(\boldsymbol{m})\right\|^{2}\right]} $ | (9) |
估算平衡因子β。式中median是中值函数。
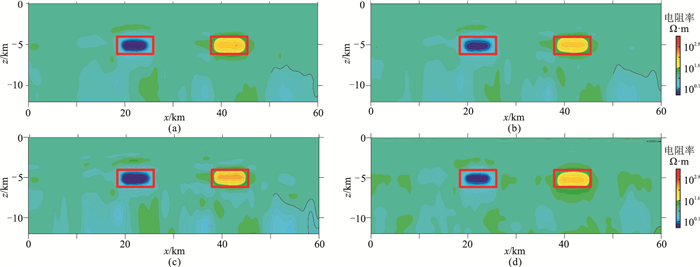
4 算法测试 4.1 合成数据测试为了验证算法的正确性,设计包含两个异常体的二维理论模型(图 3a),正演得到合成测试数据。模型背景为均匀介质,电阻率为10Ω·m。模型中有两个目标体,左边的低阻目标体电阻率为1Ω·m,右边的高阻目标体电阻率为100Ω·m。反演初始模型为10Ω·m的均匀半空间。

|
图 3 理论模型及电阻率反演剖面 (a)理论电阻率模型; (b)Ex振幅反演结果; (c)Bz振幅反演结果; (d)Ex和Bz振幅联合反演结果 |
首先,分别进行单分量(Ex和Bz)数据反演,结果见图 3b和图 3c;然后,对Ex和Bz进行联合反演,结果见图 3d。由图 3可见:①Ex数据单独反演结果(图 3b)对低阻目标的形态恢复较好,对高阻目标成像效果不佳,在高阻目标下方形成了明显的假异常;②Bz数据单独反演结果(图 3c)对高阻目标的形态恢复较好,但低阻目标下方形成了明显的假异常;③Ex和Bz联合反演结果(图 3d)较好地克服了Ex或Bz单独反演结果中的假异常现象。该理论模型反演结果证明了本文提出的联合反演算法的正确性和有效性。
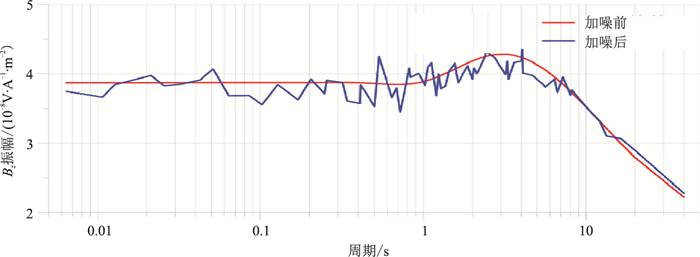
4.2 反演收敛的一致性为了验证算法收敛的一致性,抽取上节中的一道磁场振幅数据,并加入5%的高斯白噪声,如图 4所示。分别从四个不同的初始模型开始反演,以验证本文算法的收敛一致性。这四个初始模型都是均匀半空间,其电阻率分别为1、10、30、50Ω·m,Ex和Bz联合反演结果见图 5。可以发现,本文算法对不同的反演初始模型都能达到一致收敛的效果,对加噪数据能有效恢复出理论模型的形态。
|
图 4 理论模型磁场数据及加噪数据 |
|
图 5 初始模型电阻率为1Ω·m(a)、10Ω·m(b)、30Ω·m(c)、50Ω·m(d)的加噪数据Ex和Bz的振幅联合反演电阻率剖面 |
为了验证算法收敛的稳定性,分别在上节磁道数据中加入2%、5%、10%和20%的高斯白噪声进行反演,以研究噪声水平的变化对反演结果的影响,结果见图 6。由图可见, 随着噪声水平的增大,反演模型与真实模型的偏差越来越大, 但是反演电阻率剖面仍能清晰地反映异常体的位置及其电阻率的高、低特征,即使噪声水平超过10%时,剖面上异常体的位置也能准确识别,这说明了本文算法的收敛稳定性。

|
图 6 加入2%(a)、5%(b)、10%(c)、20%(d)白噪声数据的反演结果 |
近年来,川西地区YT1井二叠系获高产气流,开辟了火山岩勘探新领域。YT1井储层主要包括火山碎屑岩和玄武岩两大类。其中火山碎屑熔岩发育厚层孔隙型储层,平均孔隙度超过10%,厚度超过100m,是该区油气主力储层。火山碎屑熔岩储集空间以脱玻化溶蚀微孔、残余气孔为主,裂缝发育程度较低。玄武岩岩性致密,孔隙不发育,储集空间主要为裂缝。储层在区内分布面积较大,达6000km2,勘探潜力巨大。地震反射总体表现为丘状杂乱反射,特征不明显,储层识别难度较大。该区储层与围岩的电性特征差异明显,这是利用电磁法在川西地区开展火山岩、深层结构和断裂研究的良好物性基础,为此部署了时频电磁勘探。
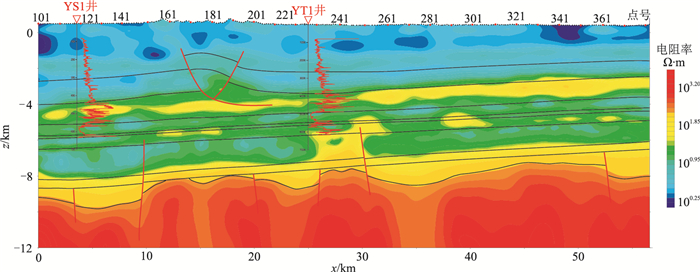
此次勘探的部分测点位于三维地震区内,对过地震三维区内的时频测线进行了多分量联合约束反演,选取其中一条典型剖面进行时频电磁多分量联合反演,结果见图 7。可以看出,该剖面纵向上可划分为电阻率高低变化的多套电性层,纵向上的电性特征与电阻率测井曲线规律一致,说明时频电磁多分量联合反演结果较真实地反映了研究区电性结构。剖面中部偏移距25~30km范围的深部高阻层是火山通道断裂发育的表现,这里的断裂不仅是火山喷发通道,而且沿断裂还有侵入岩发育,这点已得到YT1井区钻探结果(图 7中电测井曲线)的证实。
|
图 7 川西地区时频电磁多分量联合反演剖面 红色线段是解释的断层;黑线是解释的地层界面;红线是电阻率测井曲线 |
为了进一步验证时频电磁多分量联合反演的效果,对YS1井和YT1井(位置见图 7)附近的点进行Ex分量单独反演及Ex与Bz联合反演,并与这两口井的电测井曲线进行对比,结果见图 8。根据钻井信息,这两口井都钻遇了二叠系火山岩。可以看出,单分量反演和联合反演的电阻率与电阻率测井曲线的变化趋势吻合较好,但多分量联合反演比Ex分量单独反演结果的纵向分辨率更高,能够更好地揭示不同岩性火山岩引起的电阻率变化细节。

|
图 8 YS1井(左)和YT1井(右)电测井曲线与反演电阻率曲线对比 |
本文基于正则化反演原理,开发了适用于时频电磁Ex、Bz分量的联合反演方法。理论模型合成数据测试结果表明,相对于单分量数据反演,Ex与Bz数据联合反演对高阻、低阻目标体的形态恢复更好,可解决单分量反演对特定电性特征的目标形态恢复不佳的问题。另外,模型理论数据加噪测试结果表明该算法稳定、有效。实测数据反演结果表明,时频电磁多分量联合反演剖面较好地反映了火山岩的分布及火山通道(断裂)的存在,与该区电测井数据较吻合。
理论模型和实测数据的计算结果表明,时频电磁法基于电阻率空间分布特征,结合不同岩性火山岩电阻率变化规律,可有效刻画火山岩的分布,为优选有利火山岩储集相带提供有效信息,是一种兼具经济性、可靠性的勘探手段。
另外,激发极化特征也是研究火山岩的重要物理基础,笔者后续将在本文研究的基础上,进一步开展基于Cole-Cole模型的激发极化正、反演研究。
| [1] |
马新华, 李国辉, 应丹琳, 等. 四川盆地二叠系火成岩分布及含气性[J]. 石油勘探与开发, 2019, 46(2): 216-225. MA Xinhua, LI Guohui, YING Danlin, et al. Distribution and gas-bearing properties of Permian igneous rocks in Sichuan Basin, SW China[J]. Petroleum Exploration and Development, 2019, 46(2): 216-225. |
| [2] |
马新华, 杨雨, 张健, 等. 四川盆地二叠系火山碎屑岩气藏勘探重大发现及其启示[J]. 天然气工业, 2019, 39(2): 1-8. MA Xinhua, YANG Yu, ZHANG Jian, et al. A major discovery in Permian volcanic rock gas reservoir exploration in the Sichuan Basin and its implications[J]. Natural Gas Industry, 2019, 39(2): 1-8. |
| [3] |
张光荣, 张宇生, 赵晓红, 等. 时频电磁在川西南部火山岩勘探中的初步探索[C]. 中国石油学会2019年物探技术研讨会论文集, 成都, 2019, 1044-1047. ZHANG Guangrong, ZHANG Yusheng, ZHAO Xiaohong, et al. Time-frequency electromagnetic (TFEM) method in volcanic rock exploration in southwestern Sichuan[C]. Proceedings of 2019 Geophysical Exploration Technology Seminar of China Petroleum Society, Chengdu, 2019, 1044-1047. |
| [4] |
何展翔, 王绪本. 油气藏电性异常模式与电磁法油气检测[J]. 石油地球物理勘探, 2007, 42(1): 102-106. HE Zhanxiang, WANG Xuben. Geo-electrical anomalous pattern of reservoir and oil/gas detection by electromagnetic survey[J]. Oil Geophysical Prospecting, 2007, 42(1): 102-106. DOI:10.3321/j.issn:1000-7210.2007.01.020 |
| [5] |
HE Z X, HU W B, DONG W B. Petroleum electromagnetic prospecting advances and case studies in China[J]. Surveys in Geophysics, 2010, 31(2): 207-224. DOI:10.1007/s10712-009-9093-z |
| [6] |
何展翔, 杨国世, 陈思琪, 等. 时频电磁(TFEM)技术: 数据采集参数设计[J]. 石油地球物理勘探, 2019, 54(4): 908-914. HE Zhanxiang, YANG Guoshi, CHEN Siqi, et al. Time-frequency electromagnetic (TFEM) method: data acquisition design[J]. Oil Geophysical Prospecting, 2019, 54(4): 908-914. |
| [7] |
何展翔, 陈忠昌, 任文静, 等. 时频电磁(TFEM)勘探技术: 数据采集系统[J]. 石油地球物理勘探, 2020, 55(5): 1131-1138. HE Zhanxiang, CHEN Zhongchang, REN Wenjing, et al. Time-frequency electromagnetic (TFEM) method: data acquisition system and its application[J]. Oil Geophysical Prospecting, 2020, 55(5): 1131-1138. |
| [8] |
ZHAO Z, HE Z X, LI D C, et al. Detecting favorable oil and gas targets with time-frequency electromagnetic method-case studies[C]. 72nd EAGE Confe-rence and Exhibition Incorporating SPE EUROPEC 2010, 2010.
|
| [9] |
NABIGHIAN M N. Electromagnetic methods in applied geophysics: volume 1: theory[M]. Society of Exploration Geophysicists, Tulsa, Oklahoma, 1988.
|
| [10] |
傅良魁. 电法勘探教程[M]. 北京: 地质出版社, 1983.
|
| [11] |
陈明生, 闫述, 石显新, 等. 二维地质体的瞬变电磁场响应特征[J]. 地震地质, 2001, 23(2): 252-256. CHEN Mingsheng, YAN Shu, SHI Xianxin, et al. Time-domain behavior of transient electromagnetic field for 2D model[J]. Seismology and Geology, 2001, 23(2): 252-256. DOI:10.3969/j.issn.0253-4967.2001.02.018 |
| [12] |
王若, 王妙月, 卢元林. 三维三分量CSAMT法有限元正演模拟研究初探[J]. 地球物理学进展, 2007, 22(2): 579-585. WANG Ruo, WANG Miaoyue, LU Yuanlin. Preliminary study on 3D3C CSAMT method modeling using finite element method[J]. Progress in Geophysics, 2007, 22(2): 579-585. DOI:10.3969/j.issn.1004-2903.2007.02.035 |
| [13] |
陈小斌, 胡文宝. 有限元直接迭代算法及其在线源频率域电磁响应计算中的应用[J]. 地球物理学报, 2002, 45(1): 119-130. CHEN Xiaobin, HU Wenbao. Direct iterative finite ele-ment (DIFE) algorithm and its application to electromagnetic response modeling of line current source[J]. Chinese Journal of Geophysics, 2002, 45(1): 119-130. DOI:10.3321/j.issn:0001-5733.2002.01.015 |
| [14] |
LI Y G, KEY K. 2D marine controlled-source electromagnetic modeling: part 1-an adaptive finite-element algorithm[J]. Geophysics, 2007, 72(2): WA51-WA62. DOI:10.1190/1.2432262 |
| [15] |
KEY K. 1D inversion of multicomponent, multifrequency marine CSEM data: methodology and synthetic stu-dies for resolving thin resistive layers[J]. Geophysics, 2009, 74(2): F9-F20. DOI:10.1190/1.3058434 |
| [16] |
CONSTABLE S C, PARKER R L, CONSTABLE C G. Occam's inversion: a practical algorithm for generating smooth models from electromagnetic sounding data[J]. Geophysics, 1987, 52(3): 289-300. DOI:10.1190/1.1442303 |
| [17] |
师学明, 王家映. 一维层状介质大地电磁模拟退火反演法[J]. 地球科学, 1998, 23(5): 542-546. SHI Xueming, WANG Jiaying. One dimensional magnetotelluric sounding inversion using simulated annealing[J]. Earth Science, 1998, 23(5): 542-546. |
| [18] |
王若, 王妙月. 可控源音频大地电磁数据的反演方法[J]. 地球物理学进展, 2003, 18(2): 197-202. WANG Ruo, WANG Miaoyue. Inversion method of controlled source audio-frequency magnetotelluric data[J]. Progress in Geophysics, 2003, 18(2): 197-202. DOI:10.3969/j.issn.1004-2903.2003.02.004 |
| [19] |
王若, 王妙月. 一维全资料CSAMT反演[J]. 石油地球物理勘探, 2007, 42(1): 107-114. WANG Ruo, WANG Miaoyue. Inversion of 1-D full CSAMT data[J]. Oil Geophysical Prospecting, 2007, 42(1): 107-114. DOI:10.3321/j.issn:1000-7210.2007.01.021 |
| [20] |
何梅兴, 胡祥云, 陈玉萍, 等. CSAMT奥克姆一维反演的应用[J]. 工程地球物理学报, 2008, 5(4): 439-443. HE Meixing, HU Xiangyun, CHEN Yuping, et al. Application of 1D Occam's inversion to CSAMT[J]. Chinese Journal of Engineering Geophysics, 2008, 5(4): 439-443. DOI:10.3969/j.issn.1672-7940.2008.04.011 |
| [21] |
邱卫忠, 闫述, 薛国强, 等. CSAMT的各分量在山地精细勘探中的作用[J]. 地球物理学进展, 2011, 26(2): 664-668. QIU Weizhong, YAN Shu, XUE Guoqiang, et al. Action of CSAMT field components in mountainous fine prospecting[J]. Progress in Geophysics, 2011, 26(2): 664-668. DOI:10.3969/j.issn.1004-2903.2011.02.035 |
| [22] |
王志刚, 何展翔, 覃荆城, 等. 时频电磁技术的新进展及应用效果[J]. 石油地球物理勘探, 2016, 51(增刊1): 144-151. WANG Zhigang, HE Zhanxiang, QIN Jincheng, et al. Advances of TFEM technique and its application[J]. Oil Geophysical Prospecting, 2016, 51(S1): 144-151. |
| [23] |
何展翔, 胡祖志, 王志刚, 等. 时频电磁(TFEM)技术: 数据联合约束反演[J]. 石油地球物理勘探, 2020, 55(4): 898-905. HE Zhanxiang, HU Zuzhi, WANG Zhigang, et al. Time-frequency electromagnetic (TFEM) technique: step-by-step constraint inversion based on artificial fish swarm algorithm[J]. Oil Geophysical Prospecting, 2020, 55(4): 898-905. |



 曹杨, 河北省涿州市范阳中路307号东方地球物理公司国际部大楼, 072751。Email: caoyang01.cnpc.com.cn
曹杨, 河北省涿州市范阳中路307号东方地球物理公司国际部大楼, 072751。Email: caoyang01.cnpc.com.cn