郭旭升等[1-2]研究涪陵气田焦石坝、平桥地区五峰组—龙马溪组页岩后认为,裂缝是影响页岩气产能的关键因素。随着页岩气勘探向深层领域迈进,页岩储层裂缝对工程压裂的积极作用逐渐体现。天然裂缝具有良好的结构弱面,强度较低,导致存在天然裂缝的地层更易于压裂,是影响压裂效果的关键因素[3]之一。因此,高精度裂缝预测在页岩气勘探中具有重要意义。在地震数据处理中每一个炮检距向量片(Offset Vector Tile,OVT)都有自己的方位角信息,偏移后能够保留方位角信息。因此,OVT地震道集资料在叠前各向异性裂缝预测中具有明显优势[4-6],为高精度裂缝预测奠定了良好的数据基础[7-9]。
Hudson[10-11]、Thomsen[12]认为,含裂缝地层具有明显的各向异性特征,基于方位各向异性的裂缝预测已经成为当前的主流技术。目前的裂缝预测方法主要分为两类。第一类方法基于方位地震数据的振幅或振幅导出属性(频率、衰减等)预测裂缝。Mallick等[13]认为,反射振幅随方位的变化曲线大致是一条周期为π的余弦曲线,可据此预测裂缝。Rüger[14]建立了HTI介质方位AVO反射系数近似方程,为各向异性研究奠定了基础。Al-Marzong等[15]在极坐标系下将不同方位的AVO梯度随观测方位的变化关系拟合为椭圆,并利用椭圆率表征裂缝发育密度,椭圆长轴指示裂缝走向。Downton等[16-18]利用傅里叶级数展开Rüger的方位AVO反射系数近似方程,根据二阶傅里叶系数预测裂缝。印兴耀等[19]基于叠前方位道集,利用各向异性梯度反演方法预测裂缝。王康宁等[20]对比了傅里叶级数与椭圆展开法,认为二者预测结果等价。第一类方法得到的裂缝各向异性信息实际是界面两侧地层裂缝信息的综合响应,无法确定上覆、下伏地层的裂缝信息。第二类方法基于方位AVO叠前地震反演获得不同方位的弹性参数,进而利用椭圆拟合法预测裂缝,或者直接反演各向异性参数。王建花等[21]利用方位杨氏模量椭圆拟合预测裂缝。陈怀震[22]、Pan等[23]基于岩石物理模型驱动研究了各向异性参数反演,并取得一定效果。第二类方法可直接求取目的层内的裂缝信息,在理论上精度更高。虽然宽方位地震勘探已成为现阶段地震勘探技术发展的主流方向之一,为方位AVO叠前反演提供了高品质的五维道集资料[5],但待反演参数维度高(一般为5~6个),且各向异性参数值较弹性参数值小得多,反演稳定性有待提升。
第一类方法仅能得到界面两侧地层的综合响应,无法确定上覆、下伏地层的裂缝信息,影响实际勘探评价,精度偏低。为此,本文基于Rüger的方位AVO反射系数近似方程[14],首先推导了方位弹性阻抗方程,将裂缝介质的界面信息转化为地层内部的弹性信息,方位弹性阻抗差异体现了地层的各向异性。其次,利用傅里叶级数展开方位弹性阻抗方程求取二阶傅里叶系数,通过方位弹性阻抗与余弦函数的互相关求取裂缝法向。最后,通过模型验证方法的有效性与抗噪性,利用川东南DS-DX地区页岩气实际资料验证方法的精度,并利用裂缝预测结果简单评估压裂施工情况。
1 方位弹性阻抗方程傅里叶级数展开在HTI介质中,非零入射角的不同方位地震波速度存在差异,因此地震振幅随方位变化。Rüger[14]根据一阶扰动理论给出了HTI介质方位反射系数近似方程
| $ \begin{aligned} R(\theta, \phi)=& \frac{\Delta Z_{\mathrm{P}}}{2 \bar{Z}_{\mathrm{P}}}+\frac{1}{2}\left\{\frac{\Delta V_{\mathrm{P}}}{\bar{V}_{\mathrm{P}}}-4 g \frac{\Delta \mu}{\bar{\mu}}+\right.\\ & {\left.\left[\Delta \delta^{(\mathrm{v})}+8 g \Delta \gamma\right] \cos ^{2} \phi\right\} \sin ^{2} \theta+} \\ & \frac{1}{2}\left[\frac{\Delta V_{\mathrm{P}}}{\bar{V}_{\mathrm{P}}}+\Delta \varepsilon^{(\mathrm{v})} \cos ^{4} \phi+\right.\\ &\left.\Delta \delta^{(\mathrm{v})} \sin ^{2} \phi \cos ^{2} \phi\right] \sin ^{2} \theta \tan ^{2} \theta \end{aligned} $ | (1) |
式中:R(θ, ϕ)为反射系数,θ为入射角,ϕ=φ-φN(φ为观测方位角,φN为裂缝面法向方位角)为测线方向与裂缝面法向的夹角;g=(VS/VP)2,VS、VP分别为横波速度、纵波速度;ZP、μ分别为介质的纵波阻抗、剪切模量;ε(v)、δ(v)、γ分别为介质的Thomsen弱各向异性参数;“Δ(·)”表示取界面下、上介质参数的差值;“
Downton等[16]利用傅里叶级数展开式(1),并利用二阶傅里叶系数预测裂缝
| $ R(\theta, \phi)=r_{0}+r_{2}(\theta) \cos 2 \phi+r_{4}(\theta) \cos 4 \phi $ | (2) |
式中r0、r2、r4分别为基于反射系数的零阶、二阶、四阶傅里叶系数。
基于式(2)的裂缝预测结果是界面两侧介质的综合响应,无法确定上覆、下伏地层的裂缝信息。为了消除这种不确定性,首先根据Connolly[24]与Whitcombe[25]建立弹性阻抗的思想,将式(1)转换为方位弹性阻抗方程
| $ \begin{aligned} \operatorname{AEI}(\theta, \phi)=& \bar{\rho} \bar{V}_{\mathrm{P}}\left(\frac{V_{\mathrm{P}}}{\bar{V}_{\mathrm{P}}}\right)^{\sec ^{2} \theta} \times \\ &\left(\frac{V_{\mathrm{S}}}{\bar{V}_{\mathrm{S}}}\right)^{-8 g \sin ^{2} \theta}\left(\frac{\rho}{\bar{\rho}}\right)^{1-4 g \sin ^{2} \theta} \times \\ & \exp \left[\varepsilon^{(\mathrm{v})} \cos ^{4} \phi \sin ^{2} \theta \tan ^{2} \theta\right] \times \\ & \exp \left[\sin ^{2} \theta \cos ^{2} \phi\left(1+\tan ^{2} \theta \sin ^{2} \phi\right) \times\right.\\ &\left.\delta^{(\mathrm{v})}\right] \times \exp \left(4 g \gamma \sin ^{2} \theta \cos ^{2} \phi\right) \end{aligned} $ | (3) |
式中:AEI(θ, ϕ)为方位弹性阻抗;ρ为密度,ρ为界面两侧密度的平均值。AEI(θ, ϕ)表征了地层的弹性信息,则不同方位的AEI(θ, ϕ)变化表征地层的裂缝发育特征。
由于式(3)是非线性的,为了方便求解,进一步对其线性化处理。首先令
| $ A(\theta)=\frac{\bar{\rho} \bar{V}_{\rm P}}{\bar{V}_{\rm P}^{\sec ^{2} \theta} \bar{V}_{\mathrm{S}}^{-8 g \sin ^{2} \theta} \bar{\rho}^{1-4 g \sin ^{2} \theta}} $ | (4) |
将式(3)等式两端同时除以A(θ),并令EIA (θ, ϕ)=AEI(θ, ϕ)/A(θ),再对等式两边取对数,即可得到线性化方位弹性阻抗方程
| $ \begin{aligned} \ln \mathrm{EI}_{A}(\theta, \phi) &=\sec ^{2} \theta \ln V_{\mathrm{P}}-8 g \sin ^{2} \theta \ln V_{\mathrm{S}}+\\ &\left(1-4 g \sin ^{2} \theta\right) \ln \rho+\varepsilon^{(\mathrm{v})} \cos ^{4} \phi \sin ^{2} \theta \tan ^{2} \theta+\\ & \delta^{(\mathrm{v})} \sin ^{2} \theta \cos ^{2} \phi\left(1+\sin ^{2} \phi \tan ^{2} \theta\right)+\\ & 4 g \gamma \sin ^{2} \theta \cos ^{2} \phi \end{aligned} $ | (5) |
由于裂缝的各向异性特征与方位有关,且式(5)中的方位信息均为三角函数幂的形式。通过傅里叶级数展开,进而可以得到方位弹性阻抗的傅里叶级数展开式
| $ \ln \left[\mathrm{EI}_{A}(\theta, \phi)\right]=A_{0}+A_{2} \cos 2 \phi+A_{4} \cos 4 \phi $ | (6) |
其中
| $ \begin{aligned} A_{0}=& \sec ^{2} \theta \ln V_{\mathrm{P}}-8 g \sin ^{2} \theta \ln V_{\mathrm{S}}+\\ &\left(1-4 g \sin ^{2} \theta\right) \ln \rho+\frac{\delta^{(\mathrm{v})}}{2} \sin ^{2} \theta+2 g \gamma \sin ^{2} \theta+\\ & \frac{3 \varepsilon^{(v)}}{8} \sin ^{2} \theta \tan ^{2} \theta+\frac{\delta^{(\mathrm{v})}}{8} \sin ^{2} \theta \tan ^{2} \theta \end{aligned} $ | (7) |
| $ A_{2}=\frac{\varepsilon^{(\mathrm{v})}}{2} \sin ^{2} \theta \tan ^{2} \theta+\frac{\delta^{(\mathrm{v})}}{2} \sin ^{2} \theta+2 g \gamma \sin ^{2} \theta $ | (8) |
| $ A_{4}=\frac{\varepsilon^{(\mathrm{v})}}{8} \sin ^{2} \theta \tan ^{2} \theta-\frac{\delta^{(\mathrm{v})}}{8} \sin ^{2} \theta \tan ^{2} \theta $ | (9) |
式中:A0为基于方位弹性阻抗的零阶傅里叶系数,为背景项,与观测方位无关,包含弱各向异性信息;A2与A4分别为基于方位弹性阻抗的二阶与四阶傅里叶系数,只与入射角和各向异性参数有关,反映了裂缝的各向异性特征。通常θ<30°,则sin2θtan2θ≈0,A4≈0。
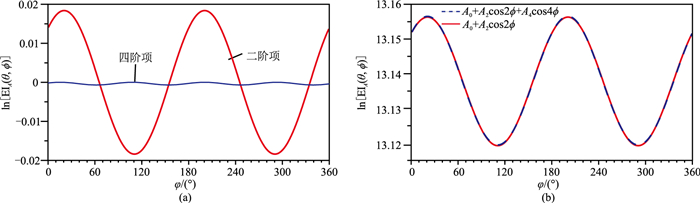
根据川东南地区五峰组—龙马溪组页岩特征设计了两层模型(表 1)分析式(6)的精度(图 1)。可见:二阶项随方位呈周期性变化明显,四阶项接近于0,且四阶项幅值远小于二阶项(图 1a);式(6)取三项与前两项的曲线几乎重合(图 1b),因此第三项A4cos4ϕ可以忽略。
|
|
表 1 两层介质模型参数 |
|
图 1 式(6)精度分析 (a)二阶项与四阶项;(b)两项与三项展开 |
上述分析表明,式(6)可以简化为
| $ \ln \left[\mathrm{EI}_{A}(\theta, \phi)\right] \approx A_{0}+A_{2} \cos 2 \phi $ | (10) |
其中
| $ A_{2} \approx \frac{\delta^{(v)}}{2} \sin ^{2} \theta+2 g \gamma \sin ^{2} \theta $ | (11) |
根据各向异性参数与裂缝密度的关系[26]
| $ \delta^{(\rm v)}=-\frac{8}{3}\left[1+\frac{g(1-2 g)}{(3-2 g)(1-g)}\right] e $ | (12) |
| $ \gamma=-\frac{8 e}{3(3-2 g)} $ | (13) |
将式(12)、式(13)代入式(11),得
| $ A_{2} \approx \frac{\delta^{(\rm v)}}{2} \sin ^{2} \theta+2 g \gamma \sin ^{2} \theta \propto e \sin ^{2} \theta $ | (14) |
式中e为裂缝密度。
由式(14)可知:θ越大,|A2|越大,因此通常使用较大入射角的地震数据预测裂缝;当θ一定时,|A2|与e成正比,因此|A2|反映了裂缝密度。
2 傅里叶系数提取与裂缝面法向预测准确求取傅里叶系数与裂缝面法向即可准确预测裂缝。将ϕ=φ-φN代入式(10),得
| $ \begin{aligned} \ln \left[\mathrm{EI}_{A}(\theta, \phi)\right] \approx & A_{0}+A_{2} \cos 2 \varphi_{\mathrm{N}} \cos 2 \varphi+\\ & A_{2} \sin 2 \varphi_{\mathrm{N}} \sin 2 \varphi \end{aligned} $ | (15) |
待求的φN不随观测方位变化,可以视为常数,因此可以将A2cos2φN、A2sin2φN分别视为cos2φ、sin2φ的系数。由于正弦函数与余弦函数均具有正交性,因此对于N个方位弹性阻抗即可利用
| $ m=A_{2} \cos 2 \varphi_{\mathrm{N}}=\frac{1}{{\rm{ \mathit{ π} }}} \sum\limits_{i=1}^{N} \ln \left[\mathrm{EI}_{A}\left(\theta, \varphi_{i}\right)\right] \cos 2 \varphi_{i} \Delta \varphi $ | (16) |
| $ n=A_{2} \sin 2 \varphi_{\mathrm{N}}=\frac{1}{{\rm{ \mathit{ π} }}} \sum\limits_{i=1}^{N} \ln \left[\mathrm{EI}_{A}\left(\theta, \varphi_{i}\right)\right] \sin 2 \varphi_{i} \Delta \varphi $ | (17) |
| $ A_{2} =\sqrt{m^{2}+n^{2}} $ | (18) |
| $ \varphi_{\mathrm{N}} =\frac{1}{2} \arctan \frac{n}{m} $ | (19) |
快速求取A2与φN,式中Δφ为观测方位角的变化量。然而,Downton等[16]指出,由于arctan函数的值域为[0,180°],利用式(19)得到的φN的值域为[0,90°],当实际裂缝面的φN大于90°时,则无法准确预测φN。为此,Ma等[27]提出利用成像测井裂缝方位信息进行约束,可以解决井点附近裂缝方位预测不准的问题,但对于远离井点的位置,可能存在较大预测误差。
由式(10)可见,ln[EIA(θ, ϕ)]随ϕ的变化由cos2ϕ控制,通过求取ln[EIA(θ, ϕ)]与cos2φ的互相关系数求取φN,即将cos2φ从左向右平移φN后,计算cos2φ与ln[EIA(θ, ϕ)]的相关系数
| $ \operatorname{RE}\left(\varphi_{\mathrm{N}}\right)=\sum\limits_{i=1}^{N} \ln \left[\mathrm{EI}_{A}\left(\theta, \varphi_{i}\right)\right] \cos \left[2\left(\varphi_{i}-\varphi_{\mathrm{N}}\right)\right] $ | (20) |
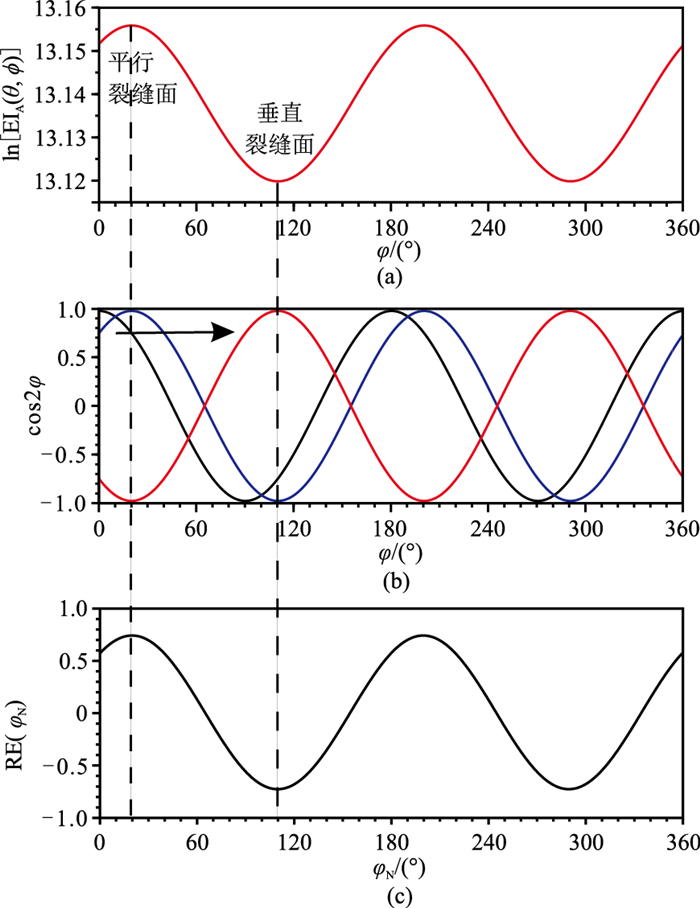
为了准确预测裂缝面法向,进一步利用表 1数据分析式(10),寻求准确的预测裂缝方法。图 2为ln[EIA(θ, ϕ)]与cos2φ的互相关分析,由图可见:①ln[EIA(θ, ϕ)]随φ的变化曲线(图 2a)与cos2φ随φ的变化曲线(图 2b蓝线)具有明显的相关性,且存在一定相位差。②当φ=20°(平行裂缝面)时,ln[EIA(θ, ϕ)]最大,随着φ逐渐增大,ln[EIA(θ, ϕ)]逐渐减小,当φ=110°(垂直裂缝面)时,ln[EIA(θ, ϕ)]达到最小(图 2a)。③将cos2φ从φ=0°开始向右平移,当φ=20°时,cos[2(φ-20π/180)](图 2b蓝线)与ln[EIA(θ, ϕ)]形态一致,RE(φN)达到最大(图 2c);cos2φ再向右平移,RE(φN)逐渐减小直至负值,当φ=110°(垂直裂缝面)时(图 2b红线),RE(φN)达到最小,且RE(φN)曲线呈周期性变化,周期为π(图 2c)。因此只需找出一个周期内RE(φN)最小时对应的平移角度φN,即可确定裂缝面的法向
| $ \begin{aligned} \varphi_{\mathrm{N}}=& \underset{\varphi_{\mathrm{N}} \in[0, 180]}{\arg \min }\left\{\sum\limits_{i=1}^{N} \ln \left[\mathrm{EI}_{A}\left(\theta, \varphi_{i}\right)\right] \times\right.\\ &\left.\cos \left[2\left(\varphi_{i}-\varphi_{\mathrm{N}}\right)\right]\right\} \end{aligned} $ | (21) |
|
图 2 ln[EIA(θ, ϕ)]与cos2φ互相关分析 (a)ln[EIA(θ, ϕ)]随φ变化曲线;(b)cos2φ随φ变化曲线;(c)RE(φN)随φN变化曲线 |
根据上述分析建立了基于方位弹性阻抗傅里叶级数的裂缝预测流程(图 3)。首先,将方位叠前地震道集划分为N个方位道集,将每个方位道集分为小、中、大入射角地震数据并进行部分叠加;其次,对N个方位的大入射角地震数据开展系数脉冲反演得到N个大入射角弹性阻抗数据体;然后,将N个方位弹性阻抗数据体除以A(θ)并取对数,进而利用式(15)~式(18)求取A2表征裂缝密度;最后,利用互相关方法求取裂缝法向,进而准确预测裂缝。

|
图 3 基于方位弹性阻抗傅里叶级数的裂缝预测流程 |
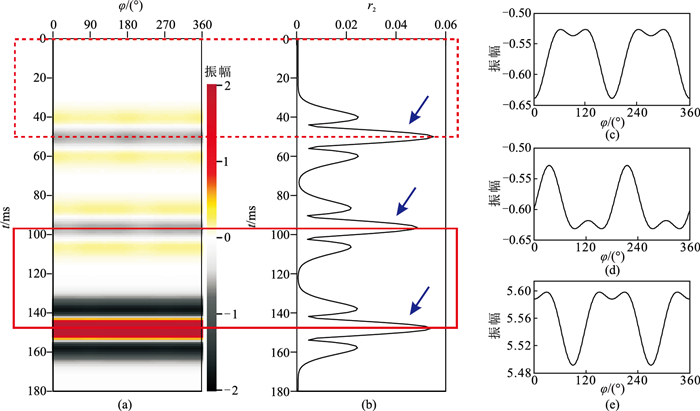
为了验证方法的有效性,设计了四层模型(表 2),利用40Hz的雷克子波作为震源进行正演,得到θ=30°的方位地震道集(图 4a),基于地震数据的傅里叶级数展开预测裂缝(图 4)。可见,各界面的振幅随φ的变化曲线(图 4c~图 4e)清晰地展示了各向异性特征,但直接利用振幅的预测结果只能反映界面的各向异性特征(图 4b箭头处),无法反映地层的裂缝发育特征(图 4b红色虚线框与实线框分别指示第1层、第3层),无法确定上覆、下伏地层的裂缝信息。
|
|
表 2 四层介质模型参数 |
|
图 4 基于地震数据的傅里叶级数展开裂缝预测结果 (a)θ=30°的方位道集合成记录;(b)r2;(c)界面1振幅随φ变化曲线;(d)界面2振幅随φ变化曲线;(e)界面3振幅随φ变化曲线 |
图 5为无噪声时基于方位弹性阻抗的傅里叶级数展开裂缝预测结果。由图可见:①θ=30°的方位弹性阻抗(图 5a)清晰地展示了第1层与第3层的弹性阻抗随φ的变化。②A2(图 5b)指示第1层与第3层的裂缝发育强度一致,第2层与第4层裂缝不发育。③常规方法(图 5c)得到的第1层的φN准确(与模型一致), 第3层的φN不准确(35°, 与模型相差90°)。④本文方法得到的第1层与第3层的φN较准确(图 5d)。由于受噪声影响,通常不能得到精确的方位弹性阻抗。图 6为含噪声(信噪比为40)时基于方位弹性阻抗的傅里叶级数展开裂缝预测结果,由图可见,裂缝预测结果与不含噪声时一致。

|
图 5 无噪声时基于方位弹性阻抗的傅里叶级数展开裂缝预测结果 (a)θ=30°方位弹性阻抗;(b)A2;(c)常规方法的φN;(d)本文方法的φN |
|
图 6 含噪声时基于方位弹性阻抗的傅里叶级数展开裂缝预测结果(信噪比为40) (a)θ=30°方位弹性阻抗;(b)A2;(c)常规方法的φN;(d)本文方法的φN |
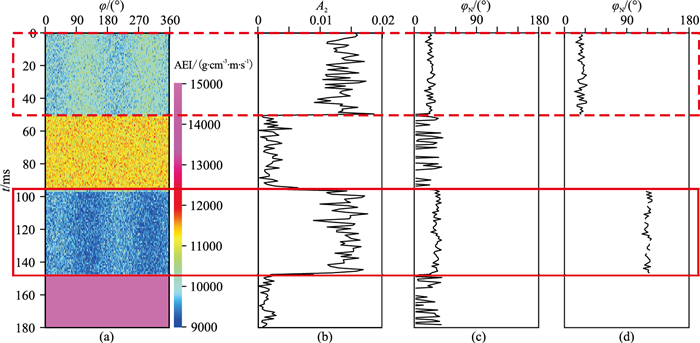
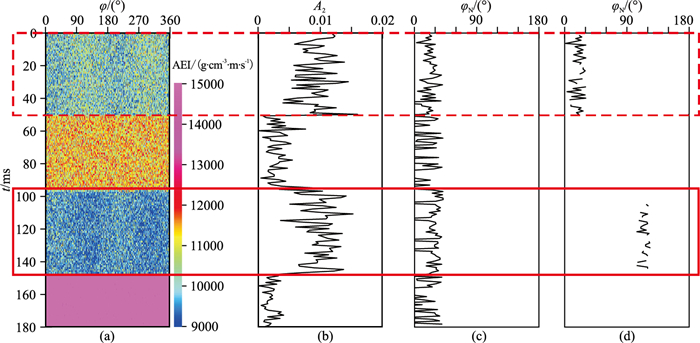
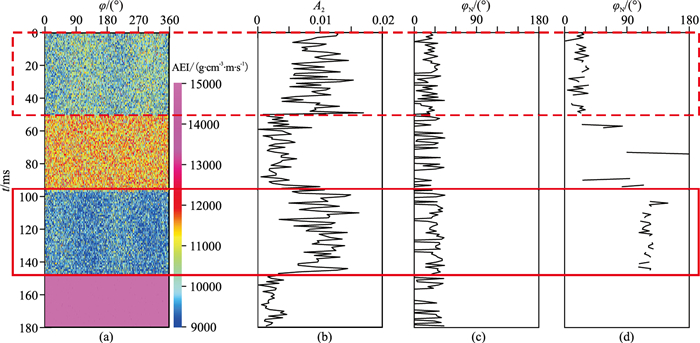
进一步在方位弹性阻抗中加入不同强度的噪声(信噪比分别为20、10),分别得到基于方位弹性阻抗的傅里叶级数展开裂缝预测结果(图 7、图 8)。可见,由于方位弹性阻抗受噪声影响较大,随着噪声强度增加对裂缝预测结果的影响也增大(图 8),但仍能清楚地指示第1层与第3层的裂缝发育特征,预测的φN抖动剧烈,但裂缝预测结果与不含噪声时基本一致。
|
图 7 含噪声时基于方位弹性阻抗的傅里叶级数展开裂缝预测结果(信噪比为20) (a)θ=30°方位弹性阻抗;(b)A2;(c)常规方法的φN;(d)本文方法的φN |
|
图 8 含噪声时基于方位弹性阻抗的傅里叶级数展开裂缝预测结果(信噪比为10) (a)θ=30°方位弹性阻抗;(b)A2;(c)常规方法的φN;(d)本文方法的φN |
模型测试表明,基于方位弹性阻抗傅里叶级数展开的裂缝预测方法能较好地预测裂缝发育情况以及裂缝法向,精度较高且抗噪性较强。
4 实际资料应用 4.1 预测精度对比川东南DS-DX地区是页岩气勘探的重点地区,钻井资料揭示,该区五峰组(O3w)—龙马溪组一段一亚段(S1l11)为典型的深水陆棚沉积,发育了一套以黑色碳质泥岩、黑色含碳泥岩为主的优质页岩[28]。该区DY4井岩心(图 9)与成像测井(图 10a)表明,该区页岩气层内高角度裂缝较发育。该区开展了OVT处理,获得了高品质的五维叠前道集数据。图 11为井旁道OVT道集以及目的层均方根振幅随方位角变化。由图可见:井旁道OVT叠前道集(图 11a)反映了振幅随炮检距、方位角变化;在远炮检距(即大入射角)O3w底界振幅随方位角变化更显著(图 11b),各向异性响应更显著,因此利用大炮检距数据预测裂缝。

|
图 9 DY4岩心 |

|
图 10 DY4井成像测井、DY4井旁大入射角不同方位地震、弹性阻抗数据对比 (a)成像测井;(b)、(c)、(d)入射角27°时,方位角分别为0°~30°、30°~60°、60°~90°的部分叠加剖面;(e)、(f)、(g)入射角27°时,方位角分别为0°~30°、30°~60°、60°~90°的方位弹性阻抗反演剖面 |
|
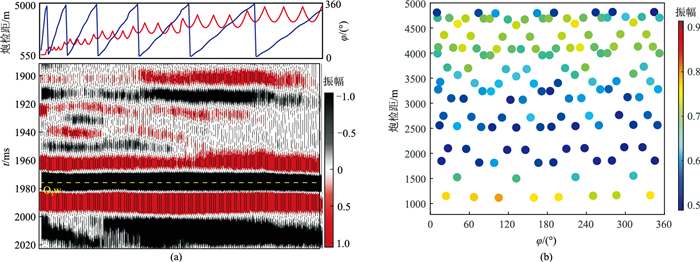
图 11 井旁道OVT叠前道集(a)以及目的层均方根振幅随方位角变化(b) 图a中红色曲线为炮检距变化曲线,蓝色曲线为方位角变化曲线,黑色虚线为五峰组底界(O3w) |
综合各方位覆盖次数、最大炮检距,进而将OVT叠前道集划分为6个方位角道集,每个方位角道集划分为中心角度9°、18°、27°共3组入射角数据并进行部分叠加,由于大入射角地震数据的各向异性特征更明显,因此利用入射角为27°地震数据预测裂缝。成像测井(图 10a)表明,在O3w-S1l11裂缝发育程度最高,理论上应具有最强的各向异性。由入射角为27°,方位角分别为0°~30°、30°~60°、60°~90°的部分叠加剖面(图 10b~图 10d)可以观察到石牛栏组(S1sh)底界、S1l1上部由裂缝引起的振幅方位各向异性差异,但O3w-S1l11振幅较强,振幅的各向异性较弱。O3w-S1l11为优质页岩层段,速度较低,O3w下部为奥陶系灰岩,速度较高,由于界面两侧速度差异较大,O3w底界为强波峰反射,各向异性较弱,被掩盖在强反射之下,预测难度较大。上部为龙马溪组(S1l)内部地层,地层岩性、速度差异均较小,振幅较O3w底界弱,各向异性较明显。因此,利用振幅信息预测裂缝精度偏低。
由入射角27°,方位角分别为0°~30°、30°~60°、60°~90°的方位弹性阻抗反演剖面(图 10e~图 10g)可见,O3w-S1l11优质页岩层段不同方位弹性阻抗的差异显著,明显体现了方位各向异性特征(图 10a),为进一步利用傅里叶级数展开预测裂缝提供了良好的数据基础。
图 12展示了DY4井裂缝密度预测效果。由图可见:由于O3w-S1l底部裂缝密度最大,上部裂缝密度较小,因此O3w底界强反射掩盖了裂缝各向异性信息,导致基于方位振幅的O3w-S1l11裂缝预测结果(图 12a)与裂缝密度曲线不符,精度较低;基于方位弹性阻抗的O3w-S1l11的裂缝密度较高(图 12b),上覆地层裂缝密度小,与裂缝密度曲线一致性较好,预测精度较高。DY4井实测裂缝走向(图 13a)与预测裂缝走向(图 13b)均为近东西向,与成像测井裂缝走向基本一致,精度较高。

|
图 13 DY4井实测裂缝走向(a)与预测裂缝走向(b) |
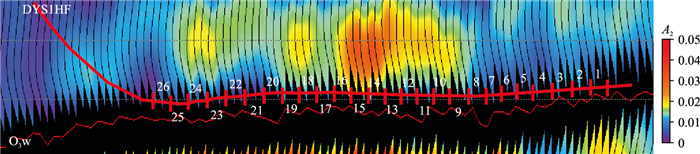
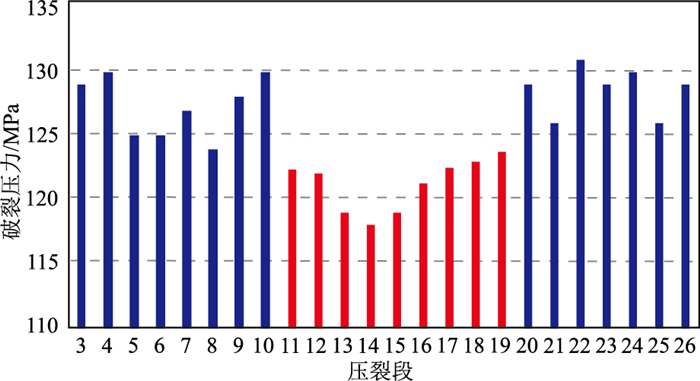
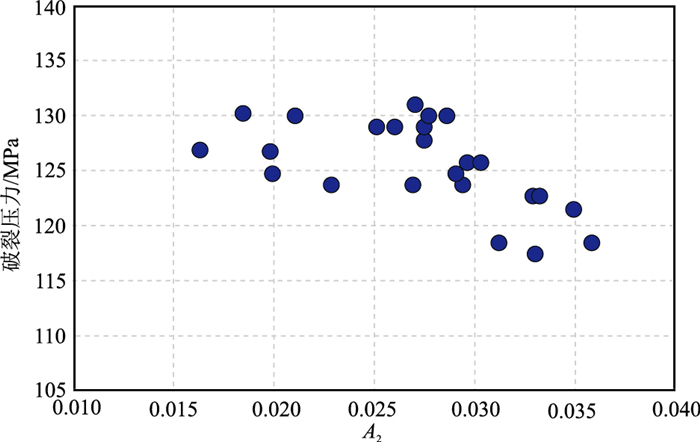
页岩气勘探逐渐走向深层领域(埋深大于4000m),地应力增加,地层压裂难度增加,施工难度较大。若地层中裂缝发育,地层更容易破裂,降低了压裂施工的破裂压力。图 14为DS-DX地区过DYS1HF井裂缝预测剖面。由图可见,水平井轨迹在优质页岩层段穿行,其中1~9段以及20~26段裂缝密度较低,中部10~19段裂缝较发育。DYS1HF井区预测裂缝平面分布图(图 15)同样表明DYS1HF井10~19段裂缝较发育。图 16为DYS1HF井3~26段破裂压力直方图。对比图 14、图 15与图 16发现,裂缝发育段(11~19段)地层破裂压力相对其他段较低(图 16),其中14~16段裂缝密度最大(图 15),破裂压力最低。DYS1HF井破裂压力与A2交会分析表明,裂缝密度与破裂压力呈负相关,即裂缝越发育,破裂压力越低(图 17)。因此,本文提出的裂缝预测方法精度较高,裂缝预测结果可为页岩气井位部署、水平井设计等提供可靠的参考依据。
|
图 14 DS-DX地区过DYS1HF井裂缝预测剖面 |

|
图 15 DYS1HF井区预测裂缝平面分布图 |
|
图 16 DYS1HF井3~26段破裂压力直方图 |
|
图 17 DYS1HF井破裂压力与A2交会图 |
文中提出了基于方位弹性阻抗傅里叶级数展开的裂缝预测方法。首先通过方程推导建立方位弹性阻抗方程,将地震界面各向异性信息转化为地层内部各向异性信息,进而对方位弹性方程进行傅里叶级数展开,去除与方位无关的背景项,提取反映裂缝各向异性的二阶傅里叶系数预测裂缝发育情况。所提方法与基于方位地震振幅数据的方法相比,能够直接反映地层内部裂缝发育情况。为了准确预测裂缝面法向,提出了互相关裂缝法向预测方法,解决了当实际裂缝面法向方位角大于90°时,无法准确预测的难题。模型数据预测结果与真实模型基本一致,实际数据预测结果与成像测井结果一致,具有较高精度。
| [1] |
郭旭升, 胡东风, 魏祥峰, 等. 四川盆地焦石坝地区页岩裂缝发育主控因素及对产能的影响[J]. 石油天然气与地质, 2016, 37(6): 799-808. GUO Xusheng, HU Dongfeng, WEI Xiangfeng, et al. Main controlling factors on shale fractures and their influences on production capacity in Jiaoshiba area, the Sichuan Basin[J]. Oil & Gas Geology, 2016, 37(6): 799-808. |
| [2] |
郭旭升. 四川盆地涪陵平桥页岩气田五峰组—龙马溪组页岩气富集主控因素[J]. 天然气地球科学, 2019, 30(1): 1-10. GUO Xusheng. Controlling factors on shale gas accumulations of Wufeng-Longmaxi Formations in Pingqiao shale gas field in Fuling area, Sichuan Basin[J]. Natural Gas Geoscience, 2019, 30(1): 1-10. |
| [3] |
DAESHY A A. Hydraulic fracture propagation in the presence of planes of weakness[C]. SPE European Spring Meeting, 1974, SPE-4852-MS.
|
| [4] |
VEMEER G J O. Creating image gathers in the absence of proper common-offset gathers[J]. Exploration Geophysics, 1998, 29(3-4): 636-642. DOI:10.1071/EG998636 |
| [5] |
印兴耀, 张洪学, 宗兆云. OVT数据域五维地震资料解释技术研究现状与进展[J]. 石油物探, 2018, 57(2): 155-178. YIN Xingyao, ZHANG Hongxue, ZONG Zhaoyun. Research status and progress of 5D seismic data interpretation in OVT domain[J]. Geophysical Prospecting for Petroleum, 2018, 57(2): 155-178. DOI:10.3969/j.issn.1000-1441.2018.02.001 |
| [6] |
赵邦六, 张宇生, 曾忠, 等. 川中地区侏罗系沙溪庙组致密气处理和解释关键技术与应用[J]. 石油地球物理勘探, 2021, 56(6): 1370-1380. ZHAO Bangliu, ZHANG Yusheng, ZENG Zhong, et al. Key technology and application of processing and interpretation of tight gas in Jurassic Shaximiao Formation in Central Sichuan Basin[J]. Oil Geophysical Prospecting, 2021, 56(6): 1370-1380. |
| [7] |
夏亚良, 魏小东, 王中凡, 等. OVT域方位各向异性技术在中非花岗岩裂缝预测中的应用研究[J]. 石油物探, 2018, 57(1): 140-147. XIA Yaliang, WEI Xiaodong, WANG Zhongfan, et al. Application of azimuthally anisotropy by OVT gather for granite fracture prediction in Central Africa[J]. Geophysical Prospecting for Petroleum, 2018, 57(1): 140-147. DOI:10.3969/j.issn.1000-1441.2018.01.018 |
| [8] |
姜晓宇, 张研, 甘利灯, 等. 花岗岩潜山裂缝地震预测技术[J]. 石油地球物理勘探, 2020, 55(3): 694-704. JIANG Xiaoyu, ZHANG Yan, GAN Lideng, et al. Seismic techniques for predicting fractures in granite buried hills[J]. Oil Geophysical Prospecting, 2020, 55(3): 694-704. |
| [9] |
何峰, 龙凡, 韩刚, 等. 基于宽方位地震数据的纵、横波速度方位各向异性对比研究[J]. 石油地球物理勘探, 2021, 56(2): 289-294, 301. HE Feng, LONG Fan, HAN Gang, et al. Comparision of azimuthal anisotropy of P-wave and S-wave velocity based on wide azimuth seismic data[J]. Oil Geophysical Prospecting, 2021, 56(2): 289-294, 301. |
| [10] |
HUDSON J A. A higher order approximation to the wave propagation constants for a cracked solid[J]. Geophysical Journal International, 1986, 87(1): 265-274. DOI:10.1111/j.1365-246X.1986.tb04556.x |
| [11] |
HUDSON J A. Overall properties of a cracked solid[J]. Mathematical Proceedings of the Cambridge Philo-sophical Society, 1980, 88(2): 371-384. DOI:10.1017/S0305004100057674 |
| [12] |
THOMSEN L. Elastic anisotropy due to aligned cracks in porous rock[J]. Geophysical Prospecting, 1995, 43(6): 805-829. DOI:10.1111/j.1365-2478.1995.tb00282.x |
| [13] |
MALLICK S, CRAFT K L, MEISTER L J, et al. Determination of the principal directions of azimuthal anisotropy from P-wave seismic data[J]. Geophysics, 1998, 63(2): 692-706. DOI:10.1190/1.1444369 |
| [14] |
RÜGER A. Reflection Coefficients and Azimuthal AVO Analysis in Anisotropic Media[M]. Society of Exploration Geophysicists, 2002.
|
| [15] |
Al-MARZONG A M, NEVES F A, KIM J J, et al. P-wave anisotropy from azimuthal AVO and velocity estimates using 3D seismic data from Saudi Arabia[J]. Geophysics, 2006, 71(2): E7-E11. DOI:10.1190/1.2187724 |
| [16] |
DOWNTON J, ROURE B. Interpreting azimuthal Fourier coefficients for anisotropic and fracture parameters[J]. Interpretation, 2015, 3(3): ST9-ST27. DOI:10.1190/INT-2014-0235.1 |
| [17] |
DOWNTON J, ROURE B, HUNT L. Azimuthal Fou- rier coefficients[J]. CSEG Recorder, 2011, 36(10): 22-36. |
| [18] |
DOWNTON J, ROURE B. Azimuthal simultaneous elastic inversion for fracture detection[C]. SEG Technical Program Expanded Abstracts, 2010, 29: 263-267.
|
| [19] |
印兴耀, 刘志国, 李春鹏, 等. 裂缝型储层预测的稳定方位AVO梯度无约束反演方法研究[J]. 石油物探, 2014, 53(6): 683-691. YIN Xingyao, LIU Zhiguo, LI Chunpeng, et al. Fracture formation prediction with a steady azimuth AVO gradient unconstrained inversion method[J]. Geophysical Prospecting for Petroleum, 2014, 53(6): 683-691. DOI:10.3969/j.issn.1000-1441.2014.06.008 |
| [20] |
王康宁, 孙赞东, 侯昕晔. 基于傅里叶级数展开的纵波方位各向异性裂缝预测[J]. 石油物探, 2015, 54(6): 755-761. WANG Kangning, SUN Zandong, HOU Xinye. Fracture prediction by P-wave azimuthal anisotropy based on Fourier series decomposition[J]. Geophysical Prospecting for Petroleum, 2015, 54(6): 755-761. DOI:10.3969/j.issn.1000-1441.2015.06.014 |
| [21] |
王建花, 张金淼, 吴国忱. 宽方位杨氏模量反演和裂缝预测方法及应用——以渤中凹陷H构造潜山勘探为例[J]. 石油地球物理勘探, 2021, 56(3): 593-602. WANG Jianhua, ZHANG Jinmiao, and WU Guochen. Wide-azimuth Young's modulus inversion and fracture prediction: An example of H structure in Bozhong sag[J]. Oil Geophysical Prospecting, 2021, 56(3): 593-602. |
| [22] |
陈怀震. 基于岩石物理的裂缝型储层叠前地震反演方法研究[D]. 山东青岛: 中国石油大学(华东), 2015.
|
| [23] |
PAN X P, ZHANG G Z, YIN X Y. Azimuthally anisotropic elastic impedance inversion for fluid indicator driven by rock physics[J]. Geophysics, 2017, 82(6): C211-C227. DOI:10.1190/geo2017-0191.1 |
| [24] |
CONNOLLY P. Elastic impedance[J]. The Leading Edge, 1999, 18(4): 438-452. DOI:10.1190/1.1438307 |
| [25] |
WHITCOMBE D N. Elastic impedance normalization[J]. Geophysics, 2002, 67(1): 60-62. DOI:10.1190/1.1451331 |
| [26] |
宗兆云. 基于模型驱动的叠前地震反演方法研究[D]. 山东青岛: 中国石油大学(华东), 2013.
|
| [27] |
MA Z Q, YIN X Y, ZONG Z Y, et al. Azimuthally variation of elastic impedances for fracture estimation[J]. Journal of Petroleum Science and Engineering, 2019. DOI:10.1016/j.petrol.2019.05.063 |
| [28] |
魏祥峰, 赵正宝, 王庆波, 等. 川东南綦江丁山地区上奥陶统五峰组—下志留统龙马溪组页岩气地质条件综合评价[J]. 地质论评, 2017, 63(1): 153-164. WEI Xiangfeng, ZHAO Zhengbao, WANG Qingbo, et al. Comprehensive evaluation on geological conditions of the shale gas in Upper Ordovician Wufeng Formation-Lower Silurian Longmaxi Formation in Dingshan Area, Qijiang, Southeastern Sichuan[J]. Geological Review, 2017, 63(1): 153-164. |



 刘晓晶, 四川省成都市高新区吉泰路688号中国石油化工股份有限公司勘探分公司物探研究院,610041。Email:
刘晓晶, 四川省成都市高新区吉泰路688号中国石油化工股份有限公司勘探分公司物探研究院,610041。Email: 
