② 中国石油大学(华东)深层油气重点实验室, 山东青岛 266580;
③ 中国石化胜利油田分公司勘探开发研究院, 山东东营 257015;
④ 中国石化胜利油田分公司物探研究院, 山东东营 257022
② Key labortory of Deep Oil and Gas, China University of Petroleum (East China), Qingdao, Shandong 266580, China;
③ Exploration and Development Research Institute, Shengli Oilfield Branch Company, SINOPEC, Dongying, Shandong 257015, China;
④ Geophysical Research Institute, Shengli Oilfield Branch Company, SINOPEC, Dongying, Shandong 257022, China
利用地震资料研究薄层一直是难点,其中强屏蔽使下伏储层信号变弱,导致难以精细描述与预测储层。去除强屏蔽的方法包括四类:
(1) 去相似背景的方法,通过分离地震记录的背景信息和有用信息,从而去除与地层特性无关的信息,由汪恩华等[1]首先提出。赵铭海[2]、李军亮[3]用于提取薄层反射特征。
(2) 多子波变换方法,将地震道分解成多个不同频率、振幅、相位的子波成分,然后根据实际需要重构子波,舍弃强屏蔽层对应的子波,从而达到去强屏蔽的效果。赵爽等[4]利用地震信号不同尺度的子波分解与重构去除煤层强屏蔽。张军华等[5]应用多子波分解重构方法剥离强屏蔽层,提高了储层预测精度。向龙斌等[6]利用多子波分解和地震旋回分析方法剥离火成岩强反射。金成志等[7]引进子波主成分分解思想,基于长、短旋回分解在Wheeler域提取并剥离了高频短旋回强屏蔽信息。江馀等[8]提出变分模态分解方法消除强反射层,分辨率高、分解完备并避免了模态混叠效应。
(3) 基于匹配追踪的方法,基于投影追踪、逐步递推的小波算法,通过将每一次迭代得到的残差信号不断地进行最佳匹配实现。Wang[9]提出了基于自由多尺度的匹配追踪去除强屏蔽方法,利用地震时频谱分解剥离强屏蔽;随后,采用多道匹配追踪算法解决强屏蔽的横向连续性问题[10]。李海山等[11]成功地应用匹配追踪算法分离煤系地层强屏蔽。张在金等[12]引入沿层信息,利用匹配追踪技术在横向定位强屏蔽层并剥离,再利用低频伴影现象验证剥离效果。
(4) 基于反演的方法,基于已知先验信息,将地震数据按照某种基函数分解而获得反射系数。Levy等[13]提出了稀疏脉冲地震反演方法,可提高强反射之下薄层弱反射的分辨率。Chopra等[14]、Puryear等[15]提出了基于反射系数的薄层反演理论,可较好地分辨薄储层。张锐等[16]引进压缩感知理论在深度域反演薄层反射系数,提高了储层识别精度。陈祖庆等[17]基于压缩感知理论结合谱反演,利用地震资料部分谱信息恢复反射系数(稀疏反演),改善了资料的分辨率。顾雯等[18]利用地震波形指示反演技术精确地预测了强屏蔽之下的薄储层。宋维琪等[19]基于较大反射信号约束的观测矩阵,联合应用局部压缩感知和区域压缩感知的处理方法提高地震资料分辨率,从而增强弱信号。夏红敏等[20]基于压缩感知的谱反演,通过梯度投影稀疏重构实现地震谱反演,反演结果的信噪比高和横向连续性好。
第四类方法是目前的研究热点,尤其是压缩感知[21-24]是一种稀疏采样重构方法,具有很好的稀疏表征能力,根据地震资料可得到高分辨率的反射系数信息。常规的压缩感知方法均基于反射系数稀疏反演提高地震资料分辨率,而对于强屏蔽层信息和储层弱信息耦合叠加情况而言,效果并不理想,原因在于在剥离强反射层的同时往往会损失弱反射层的信息,从而不能有效预测储层。
本文利用反射系数域分辨率高和不存在子波重叠的优势,提出了基于压缩感知的反射系数域沿层L2范数约束去强屏蔽方法,该方法基于压缩感知理论,先根据时域反射系数域稀疏特性利用沿层信息分离强屏蔽与弱信号,再进行稀疏反演,最后将去强屏蔽后的反射系数与原子波褶积,从而获得去强屏蔽层的高分辨率结果。理论模型测试和实际资料应用取得了较好效果,证明了方法的可行性。
1 算法 1.1 基本原理设N×1维反射系数r(t)(t为时间)可以分解为n个采样点处反射系数幅值αn和延时τn的线性组合[17]
| $ \mathit{\boldsymbol{r}}(t) = \sum\limits_{n = 1}^N {} {\alpha _n}\cdot{\rm{ \mathsf{ δ} }} (t{\rm{ - }}{\tau _n}) $ | (1) |
式中:N为地震数据的采样点个数;δ(·)为脉冲函数。引入强屏蔽层信息(一般通过人工拾取同相轴得到),r(t)可以分解为
| $ \mathit{\boldsymbol{r}}(t) = \sum\limits_{n = 1 \atop n \ne k }^N {\alpha _n}\cdot{\rm{ \mathsf{ δ} }} (t{\rm{ - }}{\tau _n}) + {\alpha _k}\cdot{\rm{ \mathsf{ δ} }} (t{\rm{ - }}{\tau _k}) $ | (2) |
式中k表示强屏蔽层位置信息。
设子波为w(t),噪声为n(t),则合成记录为
| $ \begin{array}{l} \mathit{\boldsymbol{s}}(t) = \mathit{\boldsymbol{w}}(t){\rm{*}}\mathit{\boldsymbol{r}}(t) + \mathit{\boldsymbol{n}}(t) = \\ \;\;\;\;\;\;\;\;\;\;\sum\limits_{n = 1 \atop n \ne k }^N {} [{\alpha _n}w\left( {t{\rm{ - }}{\tau _n}} \right) + {\alpha _k}w(t{\rm{ - }}{\tau _k})] + \mathit{\boldsymbol{n}}(t) \end{array} $ | (3) |
对式(3)进行傅里叶变换,得
| $ \begin{array}{l} \mathit{\boldsymbol{S}}(f) = \sum\limits_{n = 1 \atop n \ne k }^N {} {\alpha _n} \times \mathit{\boldsymbol{W}}(f){{\rm{e}}^{{\rm{ - i}}2{\rm{ \mathsf{ π} }}f{\tau _n}}} + {\alpha _k} \times \\ \;\;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{W}}(f){{\rm{e}}^{ - {\rm{i}}2{\rm{ \mathsf{ π} }}f{\tau _k}}} + \mathit{\boldsymbol{N}}(f) \end{array} $ | (4) |
式中αk和τk分别为强屏蔽层位置处的反射系数幅值和时间位置。针对不同的频率分量fm(m=1,…,M,M≥k),将上式离散化,即
| $ \begin{array}{l} {{S}}({f_m}) = \sum\limits_{n = 1 \atop n \ne k }^N {} {\alpha _n} \times W({f_m}){{\rm{e}}^{{\rm{ - i}}2{\rm{ \mathsf{ π} }}{f_m}{\tau _n}}} + {\alpha _k} \times \\ \;\;\;\;\;\;\;\;\;\;\;W({f_m}){{\rm{e}}^{{\rm{ - i}}2{\rm{ \mathsf{ π} }}{f_m}{\tau _k}}} + N({f_m}) \end{array} $ | (5) |
记Amn=W(fm)e-i2πfmτn,由于e-i2πfmτn表示部分傅里叶矩阵,因此Amn为子波对角矩阵W(fm)与e-i2πfmτn的乘积组合。由于e-i2πfmτn和W(fm)均具有两两不相关特性,故Amn满足有限约束条件(Restricted Isometry Property,RIP),可以利用压缩感知进行信号稀疏表示再重构。
将式(5)写成矩阵形式
| $ \begin{array}{l} {\left( \begin{array}{l} {S_{{f_1}}}\\ {S_{{f_2}}}\\ \;\; \vdots \\ {S_{{f_M}}} \end{array} \right)_{M \times 1}} = {\left( {\begin{array}{*{20}{c}} {{A_{11}}}&{{A_{12}}}& \cdots &{{A_{1N}}}\\ {{A_{21}}}&{{A_{22}}}& \cdots &{{A_{2N}}}\\ {}&{}& \vdots &{}\\ {{A_{M1}}}&{{A_{M2}}}& \cdots &{{A_{MN}}} \end{array}} \right)_{M \times N}}{\left( \begin{array}{l} {\alpha _1}\\ \; \vdots \\ {0_k}\\ \; \vdots \\ {\alpha _M} \end{array} \right)_{N \times 1}}{\rm{ + }}\\ {\left( {\begin{array}{*{20}{c}} {{A_{11}}}&{{A_{12}}}& \cdots &{{A_{1N}}}\\ {{A_{21}}}&{{A_{22}}}& \cdots &{{A_{2N}}}\\ {}&{}& \vdots &{}\\ {{A_{M1}}}&{{A_{M2}}}& \cdots &{{A_{MN}}} \end{array}} \right)_{M \times N}} \times \\ {\left( {\begin{array}{*{20}{c}} {{0_{11}}}&{}&{}\\ {}&{{1_{kk}}}&{}\\ {}&{}&{{0_{NN}}} \end{array}} \right)_{N \times N}}{\left( \begin{array}{l} {\alpha _1}\\ \; \vdots \\ {\alpha _k}\\ \; \vdots \\ {\alpha _N} \end{array} \right)_{N \times 1}} + N\left( {{f_m}} \right) \end{array} $ | (6) |
令Sfm(m=1, 2, …, M)=y,αn(n=1, 2, …, N)=x, αn(n=1, 2, …, N, 且n≠k)=x′,A=
| $ \mathit{\boldsymbol{y}} = \mathit{\boldsymbol{Ax}}^\prime + \mathit{\boldsymbol{ALx}} + \mathit{\boldsymbol{N}} $ | (7) |
根据压缩感知理论,通过L1范数最小化策略,可得
| $ \mathop {{\rm{min}}}\limits_\mathit{\boldsymbol{x}} \frac{1}{2}\left\| {\mathit{\boldsymbol{y}}{\rm{ - }}\mathit{\boldsymbol{ALx}}{\rm{ - }}\mathit{\boldsymbol{Ax}}^\prime } \right\|_2^2 + \lambda {\left\| {\mathit{\boldsymbol{x}}^\prime } \right\|_1} $ | (8) |
式中λ为正则项,可控制L1范数所占比重。本文创新性地引入沿层信息ALx,在反演的同时利用高分辨率的反射系数分离耦合叠加的强屏蔽层信号与储层弱信号,有利于强屏蔽层的拾取和剥离。由式(8)可见:第一项为沿层L2范数约束项或误差估计项,表示利用沿层控制去强屏蔽层,也使迭代结果收敛;第二项是稀疏约束项,促进结果的稀疏程度。
为了更好地约束层信息,引入窗函数,其宽度为T,则改进后的沿层对角矩阵为
| $ {\mathit{\boldsymbol{L}}_{\rm{a}}} = {\rm{diag}}{({l_i})_{N \times N}} $ | (9) |
式中
由于式(8)中的x未知,通过引进迭代思路求解,构成以下目标函数
| $ \left\{ \begin{array}{l} \mathop {{\rm{min}}}\limits_\mathit{\boldsymbol{x}} \frac{1}{2}\left\| {\mathit{\boldsymbol{y}}{\rm{ - }}\mathit{\boldsymbol{Ax}}} \right\|_2^2 + \lambda {\left\| \mathit{\boldsymbol{x}} \right\|_0}\\ \mathop {{\rm{min}}}\limits_{\mathit{\boldsymbol{x}}^\prime } \frac{1}{2}\left\| {\mathit{\boldsymbol{y}} - \mathit{\boldsymbol{ALx}} - \mathit{\boldsymbol{Ax}}^\prime } \right\|_2^2 + \lambda {\left\| {\mathit{\boldsymbol{x}}^\prime } \right\|_1} \end{array} \right. $ | (10) |
依次迭代求解x和x′。本文采用快速迭代阈值算法[25]求解目标函数,正则化初始值设为最大振幅的10%。
根据褶积公式,去强屏蔽后的反射系数x′与原始子波重构可以得到去强屏蔽的处理结果
| $ {\mathit{\boldsymbol{s}}^*} = \mathit{\boldsymbol{x}}^\prime *\mathit{\boldsymbol{w}}(t) $ | (11) |
具体实现过程如下:
(1) 输入信号y、矩阵A、层位信息L,设定参数λ和正则化初始值;
(2) 计算x和x′,利用快速迭代阈值算法求解x,再求解x′;
(3) 将x′与子波褶积进行重构,s*=x′*w(t);
(4) 输出最优化解s*。
本文方法沿层按列处理地震数据剥离强屏蔽层,即利用强屏蔽层信息(对应向量的一个位置)与反射系数的乘积剥离该列的强屏蔽层信息,特别在处理多道地震剖面时,采用三列加权平均方法提取子波,保证列与列之间的横向连续性。
2 理论模型测试 2.1 一维模型测试为了证明本文方法的去强屏蔽效果,首先建立一维含强屏蔽盖层的薄互层正演模型(图 1a),共201个采样点,采样率为2ms,选用30Hz零相位雷克子波作为震源进行正演模拟得到一维模型处理结果(图 1)。可见:在褶积模型中储层弱反射被强屏蔽盖层干扰,无法识别储层(图 1a);去强屏蔽反射系数将强屏蔽盖层与储层分离(图 1c),而且没有损失储层信息;去强屏蔽地震记录的波形后移,波谷能量减弱,增强和凸显了储层信息(图 1d黑色箭头处)。图 2为一维模型去强屏蔽前、后时频谱。由图可见:去强屏蔽前,强能量团凸显,掩盖了下部储层弱信息(图 2a);去强屏蔽后,强屏蔽层下部110ms处的残留弱能量团对应储层弱信息,说明本文方法在去除强屏蔽的同时保留了储层弱反射信息,而且方法的抗噪性较强。
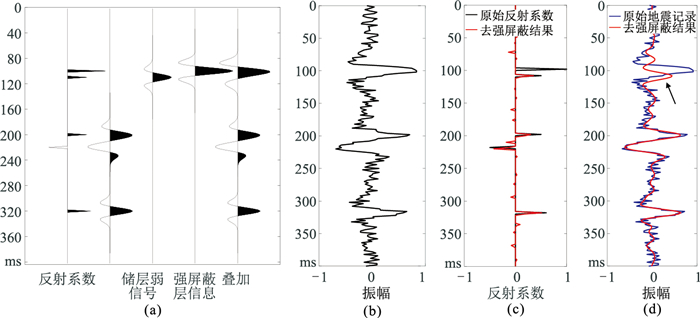
|
图 1 一维模型处理结果
(a)褶积模型;(b)含30%噪声地震记录;(c)去强屏蔽反射系数;(d)去强屏蔽地震记录 本例是单道地震资料,沿层信息在100ms处,窗函数宽度为4ms |

|
图 2 含30%噪声地震记录(a)、去强屏蔽地震记录(b)时频谱 |
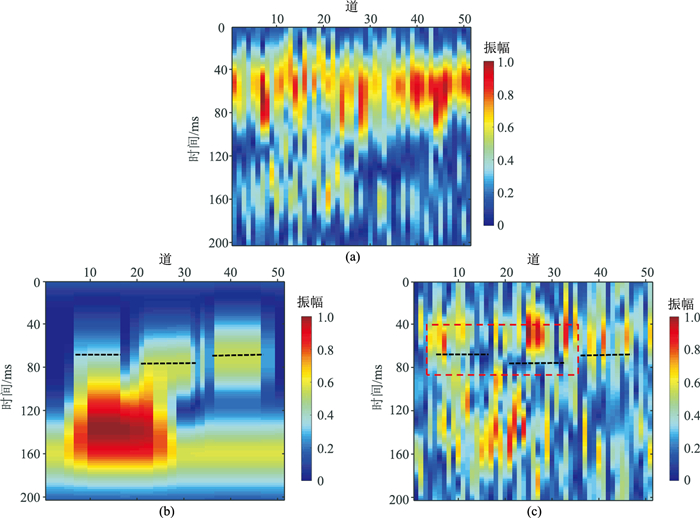
为验证本文方法的横向连续性,设计了一个上部为强屏蔽盖层的砂体反射系数模型(图 3a),共51道,101个采样点,采样率为2ms,选用30Hz雷克子波作为震源进行正演模拟得到二维模型处理结果(图 3)。在实际处理过程中,采用逐列处理方式,并利用三列加权平均方法提取子波,以保证列与列之间的横向连续性。可见,含30%高斯随机噪声地震记录中强屏蔽盖层反射和噪声影响储层弱反射的识别(图 3c),去强屏蔽地震记录中储层弱反射清晰可见,也增强了其他层的反射(图 3e)。
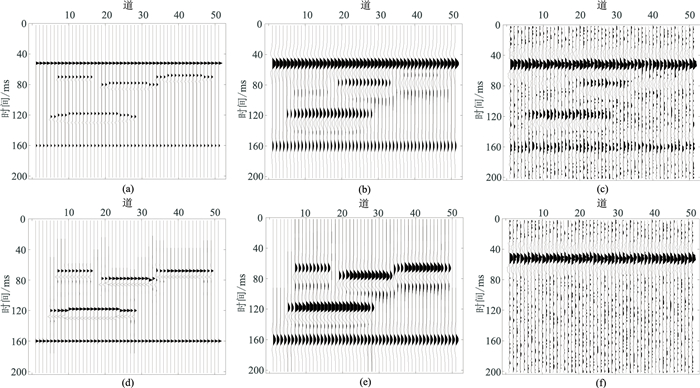
|
图 3 二维模型处理结果 (a)反射系数模型;(b)图a的合成地震记录;(c)含30%高斯随机噪声地震记录;(d)去强屏蔽反射系数;(e)去强屏蔽地震记录;(f)图3c与图3e的差。强屏蔽层位置均为50ms,窗函数宽度取4ms |
为了考察本文方法的有效性,采用匹配追踪算法对图 3c进行去强屏蔽层处理(图 4)。对比匹配追踪方法去除的强屏蔽信息(图 4b)和图 3f发现,匹配追踪算法去除的强屏蔽层位置出现偏差(图 4b红色虚线框),而本文方法剥离的强屏蔽层位置准确(图 3f)。分别对两种方法的处理结果进行时频分析(图 5)。可见:原始地震记录30Hz时频切片(图 5a)中强屏蔽层下方低频能量团被覆盖;经本文方法去强屏蔽层后,强屏蔽层下方60ms处的弱能量团显现,其余位置的能量团也相对增强(图 5b的黑色虚线对应弱反射位置);匹配追踪方法去强屏蔽后,残留强反射能量,没有显现强屏蔽层下方的弱能量团(图 5c红色虚线框)。时频分析结果说明本文方法较匹配追踪方法去除强屏蔽层的效果更好,且不会损失弱反射信息。

|
图 4 匹配追踪方法对图 3c去强屏蔽处理结果 (a)匹配追踪方法去强屏蔽结果;(b)匹配追踪方法去除的强屏蔽信息 |
3 实际地震资料应用
本文方法是基于压缩感知的稀疏重构方法,在处理实际地震数据过程中,子波提取是非常重要的环节,因为子波的作用体现在以下两方面:①基于压缩感知对地震记录进行稀疏反演,就是要消除子波信息干扰,从窄频带信息的地震记录重构宽频带反射系数信息,子波会影响反演精度,而实际资料的原始子波是未知的,会造成反演误差;②利用反射系数进行拓频处理,尤其是基于褶积模型拓展高频信息,要以原始子波为基础,通过对比频谱信息范围选取宽频带子波进行拓频,因此子波会影响拓频效果。本文针对实际资料采用多道加权复赛谱提取子波技术,该方法基于同态反褶积技术,对多道复赛谱序列叠加后求平均,反射系数的平均复赛谱会趋于零,而子波的复赛谱保持不变。根据该原理,通过滤波分离反射系数和子波,从而提取子波。
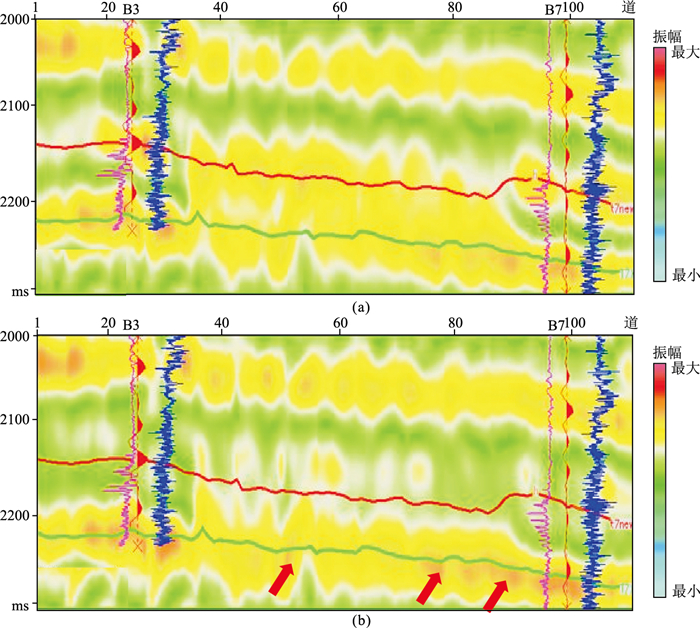
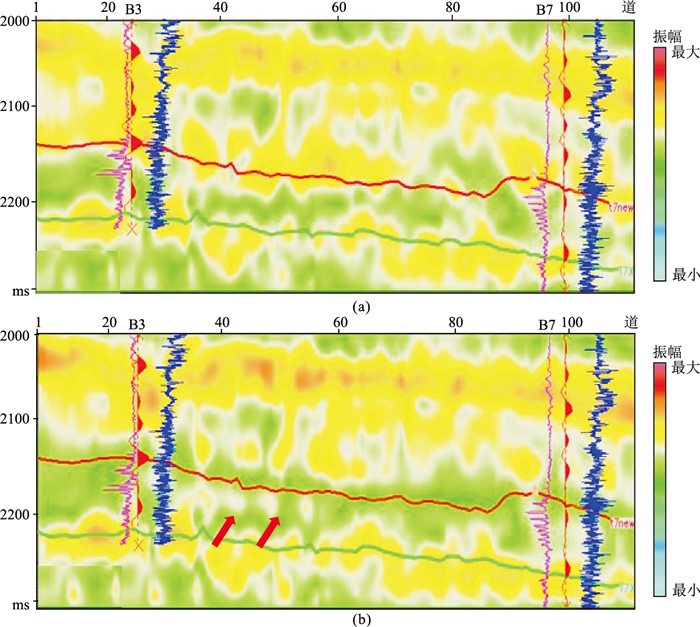
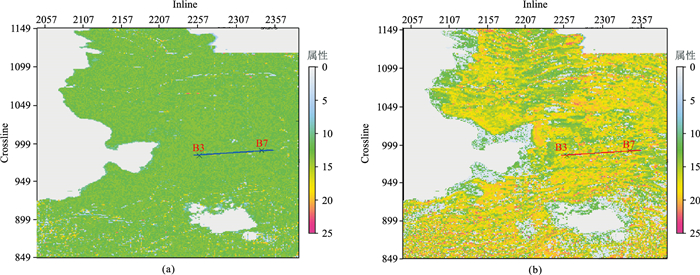
将本文方法应用于A区,图 6为过井原始地震剖面和本文方法去除强屏蔽层处理结果。由图可见,去强屏蔽层后,强屏蔽层位置振幅减弱,强屏蔽层下方出现弱反射信息(图 6b红色箭头处),并且与井曲线对应较好。图 7和图 8分别为去强屏蔽层前、后的20Hz和34Hz时频切片。由图可见:在去强屏蔽层后的20Hz时频切片上,强反射同相轴下方能量团增强,出现低频伴影现象(图 7b红色箭头处);在去强屏蔽层后的34Hz时频切片上,强反射同相轴下方也出现储层弱能量团信息(图 8b红色箭头处)。图 9为去强屏蔽层前、后沿层能量半时属性切片。由图可见,去强屏蔽层前沿层能量半时属性值基本不变,无法展示下伏滩坝砂体弱反射储层(图 9a);经去强屏蔽层处理,井点及整个储层的相关性变好,可以有效识别有利储层区域(图 9b)。
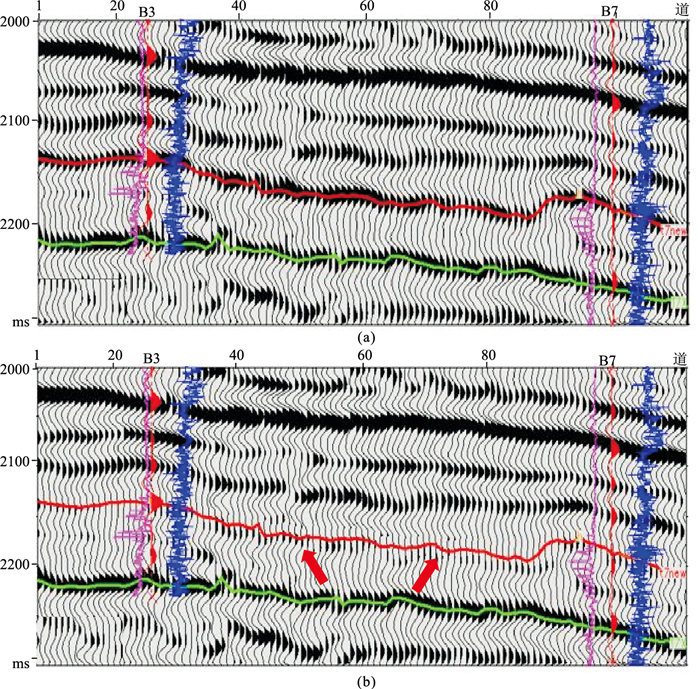
|
图 6 过井原始地震剖面(a)和本文方法去除强屏蔽层处理结果(b) 选取的地震数据时间范围为2000~2300ms,采样率为2ms。红线表示强屏蔽层位置,绿线为另一个标志层位置,下同。沿层信息通过人工解释层位获得 |
|
图 7 去强屏蔽层前(a)、后(b)的20Hz时频切片 |
|
图 8 去强屏蔽层前(a)、后(b)的34Hz时频切片 |
|
图 9 去强屏蔽层前(a)、后(b)沿层能量半时属性切片(上、下开窗10ms) |
当上覆地层存在厚层烃源岩等特殊层位时,在地震剖面上会呈现强振幅特征,此类强屏蔽层往往会掩盖下伏储层的信息,不利于准确预测储层。为了有效去除强屏蔽层的影响,本文提出了基于压缩感知的反射系数域沿层L2范数约束去强屏蔽方法。该方法基于压缩感知理论,首先根据时域反射系数域稀疏特性,利用沿层信息分离强屏蔽层与储层,再进行稀疏反演;最后将去强屏蔽后的反射子波与原子波褶积,从而获得去强屏蔽层的高分辨率结果,其优势在于高分辨率的反射系数能够分离强屏蔽层与储层的信息,有利于拾取和剥离强屏蔽层。理论模型测试和实际地震资料应用的结果表明,文中方法的计算步骤以及参数选取较简单,处理后的地震数据可以有效凸显强屏蔽层以下的储层弱反射信息,证明了本文方法的有效性和和可行性。
在实际应用中,以下两点需要关注:
(1) 为了更好地进行层位约束,引进了一个窗函数,其宽度会影响强屏蔽层的剥离效果,在实际应用中,要具体分析地震数据,一般根据强屏蔽层的厚度确定窗函数宽度;
(2) 本文方法的难点在于沿层准确拾取强屏蔽层位置,目前方法大多基于人工追踪层位,存在一定的不确定性,而且难以保证精度。因此在应用文中方法时,要尽量结合井位信息,确保层位拾取的准确性。
| [1] |
汪恩华, 万忠宏. 相似地震背景分离提高分辨率处理方法与效果[C]. CPS/SEG2004国际地球物理会议论文集, 2004, 274-276.
|
| [2] |
赵铭海. 地震相似背景分离技术在东营凹陷的应用[J]. 油气地质与采收率, 2004, 11(4): 25-27. ZHAO Minghai. Application of separation technology in seismic similar background to Dongying sag[J]. Petroleum Geology and Recovery Efficiency, 2004, 11(4): 25-27. DOI:10.3969/j.issn.1009-9603.2004.04.009 |
| [3] |
李军亮. 相似背景目标分离技术在滩坝砂储层预测中的应用——以济阳坳陷东营凹陷沙四段为例[J]. 工程地球物理学报, 2008, 5(3): 332-336. LI Junliang. The application of separation technology in seismic semblance background to reservoir prediction of beach-bar sandbody: Case of Es4 sandbody in the area of Dongying sag of Jiyang depression[J]. Chinese Journal of Engineering Geophysics, 2008, 5(3): 332-336. DOI:10.3969/j.issn.1672-7940.2008.03.013 |
| [4] |
赵爽, 李仲东, 许红梅, 等. 多子波分解技术检测含煤砂岩储层[J]. 天然气工业, 2007, 27(9): 44-47. ZHAO Shuang, LI Zhongdong, XU Hongmei, et al. Using multiple wavelet decomposition technique to detect the sandstone reservoir with coal layer[J]. Na-tural Gas Industry, 2007, 27(9): 44-47. DOI:10.3321/j.issn:1000-0976.2007.09.013 |
| [5] |
张军华, 刘振, 刘炳杨, 等. 强屏蔽层下弱反射储层特征分析及识别方法[J]. 特种油气藏, 2012, 19(1): 23-26. ZHANG Junhua, LIU Zhen, LIU Bingyang, et al. Analysis and identification of reservoir characteristics of weak reflectors under strong shielding layer[J]. Special Oil & Gas Reservoirs, 2012, 19(1): 23-26. DOI:10.3969/j.issn.1006-6535.2012.01.004 |
| [6] |
向龙斌, 李东安. 基于多子波分解和旋回分析法去火成岩地震反射屏蔽[J]. 地质科技情报, 2016, 35(3): 210-215. XIANG Longbin, LI Dong'an. Eliminating seismic shielding of igneous rock using wavelet decomposition and seismic cycle analysis[J]. Geological Science and Technology Information, 2016, 35(3): 210-215. |
| [7] |
金成志, 秦月霜. 利用长、短旋回波形分析法去除地震强屏蔽[J]. 石油地球物理勘探, 2017, 52(5): 1042-1048, 1111. JIN Chengzhi, QIN Yueshuang. Seismic strong shield removal based on the long and short cycle ana-lysis[J]. Oil Geophysical Prospecting, 2017, 52(5): 1042-1048, 1111. |
| [8] |
江馀, 张军华, 韩宏伟, 等. 优化变分模态分解方法消除强反射影响——以东营凹陷沙四段滩坝砂目标处理为例[J]. 石油地球物理勘探, 2020, 55(1): 147-152, 166. JIANG Yu, ZHANG Junhua, HAN Hongwei, et al. Elimination of strong reflection influence based on optimized variational mode decomposition method: a case study of the target processing of beach bar sand of Es4 in Dongying Sag[J]. Oil Geophysical Prospecting, 2020, 55(1): 147-152, 166. |
| [9] |
WANG Y H. Seismic time-frequency spectral decomposition by matching pursuit[J]. Geophysics, 2007, 72(1): V13-V20. DOI:10.1190/1.2387109 |
| [10] |
WANG Y H. Multichannel matching pursuit for seismic trace decomposition[J]. Geophysics, 2010, 75(4): V61-V66. DOI:10.1190/1.3462015 |
| [11] |
李海山, 杨午阳, 田军, 等. 匹配追踪煤层强反射分离方法[J]. 石油地球物理勘探, 2014, 49(5): 866-870. LI Haishan, YANG Wuyang, TIAN Jun, et al. Coal seam strong reflection separation with matching pursuit[J]. Oil Geophysical Prospecting, 2014, 49(5): 866-870. |
| [12] |
张在金, 张军华, 李军, 等. 煤系地层地震强反射剥离方法研究及低频伴影分析[J]. 石油地球物理勘探, 2016, 51(2): 376-383. ZHANG Zaijin, ZHANG Junhua, LI Jun, et al. A method for stripping coal seam strong reflection and low-frequency shadow analysis[J]. Oil Geophysical Prospecting, 2016, 51(2): 376-383. |
| [13] |
LEVY S, FULLAGAR P K. Reconstruction of a sparse spike train from a portion of its spectrum and application to high-resolution deconvolution[J]. Geophysics, 1981, 46(9): 1235-1243. DOI:10.1190/1.1441261 |
| [14] |
CHOPRA S, CASTAGNA J, PORTNIAGUINE O. Thin-bed reflectivity inversion[C]. SEG Technical Program Expanded Abstracts, 2006, 25: 2057-2061.
|
| [15] |
PURYEAR C I, CASTAGNA J P. An algorithm for calculation of bed thickness and reflection coefficients from amplitude spectrum[J]. SEG Technical Program Expanded Abstracts, 2006, 25: 1767-1770. |
| [16] |
张锐, 张奎. 基于压缩感知理论的深度域薄层反演[C]. SPG/SEG北京2016国际地球物理会议电子论文集, 2016, 528-530. ZHANG Rui, ZHANG Kui. Compressed sensing inversion for thin-bed resolution in depth domain[C]. Proceedings of SPG/SEG Beijing 2016 International Geophysical Conference, Beijing, China, 2016, 528-530. |
| [17] |
陈祖庆, 王静波. 基于压缩感知的稀疏脉冲反射系数谱反演方法研究[J]. 石油物探, 2015, 54(4): 459-466. CHEN Zuqing, WANG Jingbo. A spectral inversion method of sparse-spike reflection coefficients based on compressed sensing[J]. Geophysical Prospecting for Petroleum, 2015, 54(4): 459-466. DOI:10.3969/j.issn.1000-1441.2015.04.013 |
| [18] |
顾雯, 章雄, 徐敏, 等. 强屏蔽下薄储层高精度预测研究——以松辽盆地三肇凹陷为例[J]. 石油物探, 2017, 56(3): 439-448. GU Wen, ZHANG Xiong, XU Min, et al. High precision prediction of thin reservoir under strong shielding effect and its application: a case study from Sanzhao Depression, Songliao Basin[J]. Geophysical Prospecting for Petroleum, 2017, 56(3): 439-448. DOI:10.3969/j.issn.1000-1441.2017.03.014 |
| [19] |
宋维琪, 吴彩端. 利用压缩感知方法提高地震资料分辨率[J]. 石油地球物理勘探, 2017, 52(2): 214-219. SONG Weiqi, WU Caiduan. Seismic data resolution improvement based on compressed sensing[J]. Oil Geophysical Prospecting, 2017, 52(2): 214-219. |
| [20] |
夏红敏, 刘兰锋, 张显辉, 等. 地震数据谱反演压缩感知算法实现及应用[J]. 石油地球物理勘探, 2021, 56(2): 295-301. XIA Hongwei, LIU Lanfeng, ZHANG Xianhui, et al. Implementation and application of compressed sensing algorithm for seismic spectrum inversion[J]. Oil Geophysical Prospecting, 2021, 56(2): 295-301. |
| [21] |
DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306. DOI:10.1109/TIT.2006.871582 |
| [22] |
CANDES E J, ROMBERG J, TAO T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transactions on Information Theory, 2006, 52(2): 489-509. DOI:10.1109/TIT.2005.862083 |
| [23] |
BARANIUK R G. Compressive sensing[J]. IEEE Signal Processing Magazine, 2007, 24(4): 118-121. DOI:10.1109/MSP.2007.4286571 |
| [24] |
CANDES E J, WAKIN M B. An introduction to compressive sampling[J]. IEEE Signal Processing Magazine, 2008, 25(2): 21-30. DOI:10.1109/MSP.2007.914731 |
| [25] |
BECK A, TEBOULLE M. A fast iterative shrinkage-thresholding method for linear inverse problem[J]. SIAM Journal on Imaging Sciences, 2009, 2(1): 183-202. DOI:10.1137/080716542 |



 张军华, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院,266580。Email:
张军华, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院,266580。Email: