② 中国石油天然气集团有限公司物联网重点实验室, 甘肃兰州 730030
② Key Laboratory of Internet of Things, CNPC, Lanzhou, Gansu 730030, China
逆时偏移(RTM)互相关成像条件可阐述为:对正传得到的震源波场和反传得到的接收波场进行互相关,得到地下反射界面的构造图像[1]。实际上,该成像条件是Born正演算子的伴随算子[2]。当炮检距有限、数据不完美(带限、含噪、缺失)时,常规RTM很难得到满意的成像结果,无法满足复杂构造和岩性油气藏的地震成像需求。
解决上述问题的一种严格做法是将地震成像看作最小二乘意义下的最优化问题,通过最优化算法最小化Born正演数据和观测反射地震数据之间的差异,得到最佳匹配观测数据的地下模型估计,即最小二乘偏移[3-6]。在最小二乘偏移中,可以选择不同的Born正演/偏移算子,其中最精确的是双程波算子,即最小二乘逆时偏移(LSRTM)[7-9]。LSRTM每次迭代大概需要两次所有共炮点道集的RTM,通常需要迭代近十次,因此计算成本极高。目前主要有两类方法可以降低计算成本:一类方法是利用炮编码技术对叠前炮集数据进行压缩[10-22],降低Born正演和RTM的计算成本,如随机相位编码、平面波相位编码、振幅编码、确定性炮编码等;另一类方法是利用预条件算子加快迭代的收敛速度,减少迭代次数,例如近似Hessian对角矩阵[23-24]、去模糊化滤波器[25-26]、Hessian矩阵近似逆[27]、构造导向滤波[28-29]等。
本文从人工智能领域引入自适应矩估计(A-dam)方法[30]解决LSRTM的效率问题。Adam方法结合了深度学习中两种常用方法的优势:一种是自适应梯度(AdaGrad)方法[31],该方法能够自适应地对梯度进行归一化,改善稀疏特征的更新效果;另一种是均方根传播(RMSProp)方法[32],该方法利用之前迭代的计算结果,对当前迭代的更新量和归一化向量进行平滑处理,提高迭代收敛的稳定性,在梯度非稳态时效果显著。相应地,在LSRTM中,Adam方法有潜力压制随机选取部分炮集数据进行偏移而引入的成像噪声,并补偿观测系统有限和复杂速度模型带来的照明不均匀问题。另外,Adam方法也有潜力压制炮编码LSRTM中存在的串扰噪声。最后通过SEG/EAGE盐丘模型验证了Adam方法对LSRTM的有效性。
1 方法和理论 1.1 逆时偏移在常密度声波介质中,地震波的传播过程可用频率域波动方程描述
| $ \left[\nabla^{2}+\omega^{2} m(\boldsymbol{x})\right] u(\boldsymbol{x}, \omega)=f(\omega) {\rm{ \mathsf{ δ} }}\left(\boldsymbol{x}-\boldsymbol{x}_{\mathrm{s}}\right) $ | (1) |
式中:x表示空间位置坐标;xs为炮点坐标;m(x)为模型慢度场的平方;u(x, ω)是频率为ω的地震波场;f(ω)为震源函数谱。
将模型m(x)分解成两部分
| $ m(\boldsymbol{x})=b(\boldsymbol{x})+r(\boldsymbol{x}) $ | (2) |
式中:b(x)为背景模型,是对m(x)平滑后的结果,只影响地震波场的走时,而不影响地震波场的振幅,且不会产生反射波;r(x)为扰动模型,不影响地震波场的走时,但入射波场遇到反射界面会产生反射波,且反射波的振幅与反射系数的大小有关,因此扰动模型反映的是地下模型的层位构造信息。为描述简化起见,本文将扰动模型称为反射系数模型。与模型分解相对应,地震波场u(x, ω)也可以分解成两部分:透射波场u0(x, ω)和反射波场Δu(x, ω)。经线性近似,式(1)可分解为
| $ {\left[\nabla^{2}+\omega^{2} b(\boldsymbol{x})\right] u_{0}(\boldsymbol{x}, \omega)=f(\omega) {\rm{ \mathsf{ δ} }}\left(\boldsymbol{x}-\boldsymbol{x}_{\mathrm{s}}\right)} $ | (3) |
| $ {\left[\nabla^{2}+\omega^{2} b(\boldsymbol{x})\right] \Delta u(\boldsymbol{x}, \omega)=-\omega^{2} r(\boldsymbol{x}) u_{0}(\boldsymbol{x}, \omega)} $ | (4) |
式(3)的解可以用Green函数表示为
| $ u_{0}(\boldsymbol{x}, \omega)=f(\omega) G\left(\boldsymbol{x}, \boldsymbol{x}_{\mathrm{s}}, \omega\right) $ | (5) |
式中G(x, xs, ω)为炮点位于xs的Green函数。反射地震数据d(xr, xs, ω)可以通过求解式(4)的Δu(x, ω)并在接收点xr采样得到。数学上,该过程可表示为
| $ \begin{aligned} d\left(\boldsymbol{x}_{\mathrm{r}}, \boldsymbol{x}_{\mathrm{s}}, \omega\right)=&-\omega^{2} f(\omega) \times \\ & \int \mathrm{d} \boldsymbol{x} G\left(\boldsymbol{x}_{\mathrm{r}}, \boldsymbol{x}, \omega\right) r(\boldsymbol{x}) G\left(\boldsymbol{x}, \boldsymbol{x}_{\mathrm{s}}, \omega\right) \end{aligned} $ | (6) |
该式即为线性Born正演公式。对应地,线性Born正演的共轭算子可表示为
| $ \begin{aligned} r(\boldsymbol{x})=&-\int \mathrm{d} \boldsymbol{x}_{\mathrm{s}} \mathrm{d} \boldsymbol{x}_{\mathrm{r}} \mathrm{d} \omega \omega^{2} f^{*}(\omega) \times \\ & G^{*}\left(\boldsymbol{x}_{\mathrm{s}}, \boldsymbol{x}, \omega\right) G^{*}\left(\boldsymbol{x}, \boldsymbol{x}_{\mathrm{r}}, \omega\right) d\left(\boldsymbol{x}_{\mathrm{r}}, \boldsymbol{x}_{\mathrm{s}}, \omega\right) \end{aligned} $ | (7) |
式中上标“*”表示共轭。式(7)即为互相关成像条件,也证明了互相关成像条件为线性Born正演的共轭。
1.2 炮编码逆时偏移从式(7)可以看出,RTM的计算成本和共炮点道集个数成正比。为了减少计算量,炮编码技术可以对叠前共炮点道集进行压缩。目前常见的炮编码技术有随机相位编码、平面波相位编码、振幅编码等。Krebs等[33]的数值结果表明单点随机时间相位编码可以取得较好的收敛效果,因此本文将采用这种编码方式对数据进行压缩。该方法的编码函数定义为
| $ \alpha\left(\boldsymbol{x}_{\mathrm{s}}, p_{\mathrm{s}}\right)=\frac{1}{\sqrt{N}} \gamma\left(\boldsymbol{x}_{\mathrm{s}}, p_{\mathrm{s}}\right) $ | (8) |
式中:ps为炮编码实现次数的索引;N为炮编码实现的总次数;γ是随机符号序列,取值为+1或-1。经过炮编码后的地震数据为
| $ \widetilde{d}{}^{\mathrm{obs}}\left(\boldsymbol{x}_{\mathrm{r}}, p_{\mathrm{s}}, \omega\right)=\int \mathrm{d} \boldsymbol{x}_{\mathrm{s}} \alpha\left(\boldsymbol{x}_{\mathrm{s}}, p_{\mathrm{s}}\right) d^{\mathrm{obs}}\left(\boldsymbol{x}_{\mathrm{r}}, \boldsymbol{x}_{\mathrm{s}}, \omega\right) $ | (9) |
式中dobs为观测数据。对应地,相同的编码函数也用于编码震源。由于波传播算子和震源函数为线性关系,因此炮编码后的震源波场可表示为
| $ \begin{aligned} S\left(\boldsymbol{x}, p_{\mathrm{s}}, \omega\right)=& \int \mathrm{d} \boldsymbol{x}_{\mathrm{s}} \alpha\left(\boldsymbol{x}_{\mathrm{s}}, p_{\mathrm{s}}\right) f(\omega) \times \\ & {\rm{ \mathsf{ δ} }}\left(\boldsymbol{x}-\boldsymbol{x}_{\mathrm{s}}\right) G\left(\boldsymbol{x}, \boldsymbol{x}_{\mathrm{s}}, \omega\right) \end{aligned} $ | (10) |
同样地,线性Born正演和输入震源也是线性关系,因此只需要修改震源函数即可完成炮编码下的线性Born正演,即
| $ \begin{aligned} \tilde{d}\left(\boldsymbol{x}_{\mathrm{r}}, p_{\mathrm{s}}, \omega\right)=&-\omega^{2} \int \mathrm{d} \boldsymbol{x} \times \\ & G\left(\boldsymbol{x}_{\mathrm{r}}, \boldsymbol{x}, \omega\right) r(\boldsymbol{x}) S\left(\boldsymbol{x}, p_{\mathrm{s}}, \omega\right) \end{aligned} $ | (11) |
对应的炮编码RTM公式为
| $ \begin{aligned} r(\boldsymbol{x})=&-\int \mathrm{d} p_{\mathrm{s}} \mathrm{d} \boldsymbol{x}_{\mathrm{r}} \mathrm{d} \omega \times \\ & \omega^{2} S^{*}\left(p_{\mathrm{s}}, \boldsymbol{x}, \omega\right) G^{*}\left(\boldsymbol{x}, \boldsymbol{x}_{\mathrm{r}}, \omega\right) \tilde{d}\left(\boldsymbol{x}_{\mathrm{r}}, p_{\mathrm{s}}, \omega\right) \end{aligned} $ | (12) |
从上式可以看出,炮编码RTM的计算成本与炮编码的次数成正比,而炮编码次数往往远小于炮数,因此经过炮编码后线性Born正演和RTM的计算成本都得到大幅降低。
1.3 基于Adam方法的最小二乘逆时偏移由于一次反射波地震数据与反射系数呈线性关系,因此线性Born正演公式(式(6))可以写成矩阵形式
| $ \boldsymbol{d}=\boldsymbol{L m} $ | (13) |
式中:d为Born正演数据;m为模型参数;L为线性Born正演算子。LSRTM目标函数可表示为
| $ \min \limits_{\boldsymbol{m}} J=\frac{1}{2}\left\|\boldsymbol{L m}-\boldsymbol{d}^{\text {obs }}\right\|_{2}^{2} $ | (14) |
式中:dobs为离散化后的观测反射地震数据;‖·‖2表示L2范数。
式(14)的反问题可以通过梯度下降(GD)法求解。在深度学习领域,一种更加有效的最优化算法是小批量梯度下降法。与GD法相比,该算法随机地打乱样本集,然后只使用样本集的一部分样本(即“小批量”的来历)计算梯度,从而快速地更新网络参数。在深度神经网络学习过程中,往往需要大量的训练样本以避免过拟合,小批量梯度下降法只需要使用小部分样本就可以对模型参数进行更新,相比全样本集GD法,效率往往高很多。
但是小批量GD往往容易剧烈震荡。为解决这一问题,动量法应运而生。该方法考虑了之前迭代的梯度信息,对当前迭代次数中的梯度进行平滑。更准确地说,动量法采用指数加权函数对前面所有的梯度进行平均,得到新的梯度,即
| $ \boldsymbol{v}_{t}=\beta_{1} \boldsymbol{v}_{t-1}+\left(1-\beta_{1}\right) \frac{\partial J}{\partial \boldsymbol{m}} $ | (15) |
式中vt-1、vt分别表示第t-1和第t次迭代的梯度;β1是控制梯度平滑程度的超级参数,β1∈[0, 1)。β1越大,更新方向越平滑。如果β1=0,上式就退化为常规的梯度下降法;如果β1太大,就会平滑掉一些有用的更新信息。大多数情况下,β1=0.9是一个比较合理的选择。
式(15)通常会产生边界效应,需对平滑后的梯度进行校正。校正后的梯度为
| $ \boldsymbol{v}_{\mathrm{c}}=\frac{\boldsymbol{v}_{t}}{1-\beta_{1}^{t}} $ | (16) |
式(16)的校正后更新方向梯度没有考虑非稳态性。具体到LSRTM方法,它没有考虑计算的梯度方向存在照明不均匀的问题。RMSProp方法应用梯度平方的指数加权平均近似照明矩阵
| $ \boldsymbol{s}_{t}=\beta_{2} \boldsymbol{s}_{t-1}+\left(1-\beta_{2}\right)\left(\frac{\partial J}{\partial \boldsymbol{m}}\right)^{2} $ | (17) |
式中:st-1、st分别表示第t-1和第t次迭代的照明矩阵;β2为控制照明矩阵平滑程度的超级参数,与β1类似,一般取0.9。同样地,也需要校正边界效应
| $ \boldsymbol{s}_{\mathrm{c}}=\frac{\boldsymbol{s}_{t}}{1-\beta_{2}^{t}} $ | (18) |
然后,利用RMSProp估计的照明矩阵归一化校正后的梯度(式(16)),得到模型的更新量
| $ \Delta \boldsymbol{m}=\frac{-\boldsymbol{v}_{\mathrm{c}}}{\sqrt{\boldsymbol{s}_{\mathrm{c}}}+\varepsilon} $ | (19) |
式中ε为稳定因子,以保证除法的稳定性。最终,反射系数模型更新可表示为
| $ \boldsymbol{m}_{t}=\boldsymbol{m}_{t-1}+\lambda \Delta \boldsymbol{m} $ | (20) |
式中λ在深度学习中称为学习率,在数值优化中称为步长。步长可以随着迭代次数的增加逐步减小
| $ \lambda_{t}=\frac{\lambda_{t-1}}{1+t \eta} $ | (21) |
式中:λt-1、λt分别为第t-1和第t次迭代的步长;η为衰减率,本文将其设置为1。
图 1为Adam法LSRTM计算流程。该算法共有3层循环:①最内层循环是使用每个小批量共炮点道集数据计算梯度;②中层循环则是利用Adam方法更新反射系数模型;③最外层循环执行的是打乱并划分的共炮点道集数据,以及自适应地减小步长。

|
图 1 Adam法LSRTM计算流程 |
在动态炮编码LSRTM的每次迭代过程中,虽然更新了炮编码,但是经过偏移后提供的有效梯度信息具有相干性,而动态编码引入的串扰噪声不相干。由于Adam法采用指数加权平均对前面所有迭代步中计算得到的梯度和近似照明矩阵进行平滑,因此Adam法具有压制串扰噪声的能力。为此,本文修改Adam法以适用于炮编码LSRTM。修改后的计算流程和梯度下降法动态炮编码LSRTM类似,唯一的不同之处在于Adam方法采用自适应矩估计法计算梯度。完整的算法流程如图 2所示。
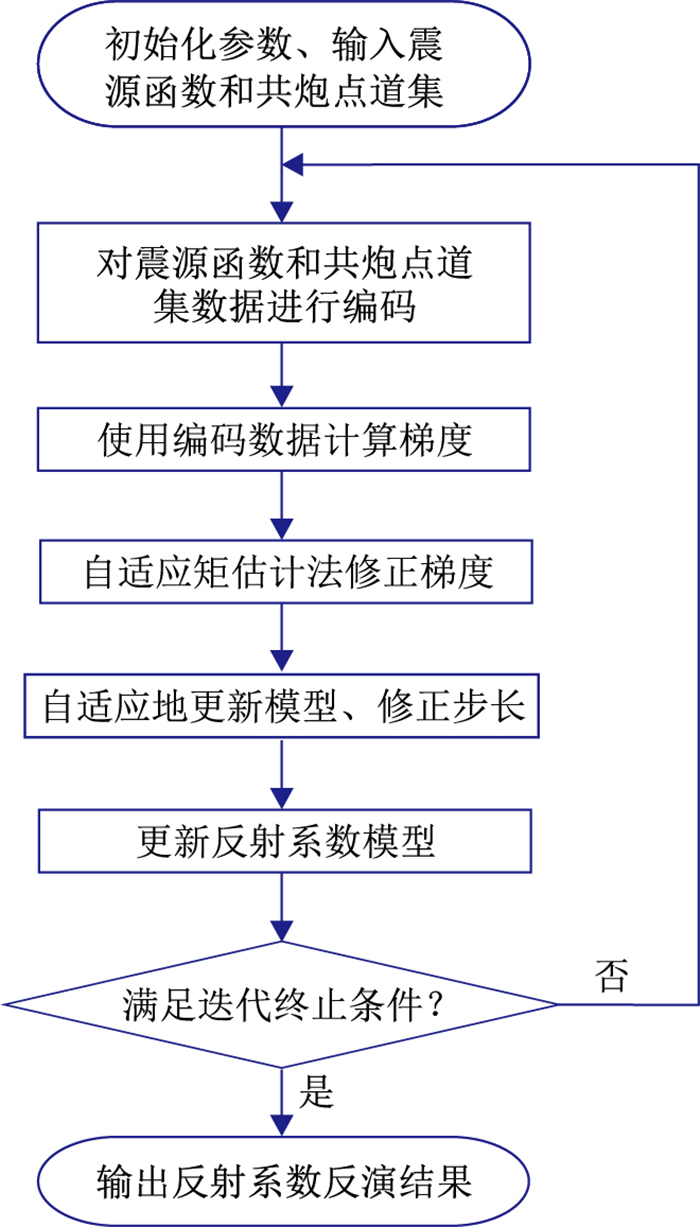
|
图 2 炮编码Adam法LSRTM计算流程 |
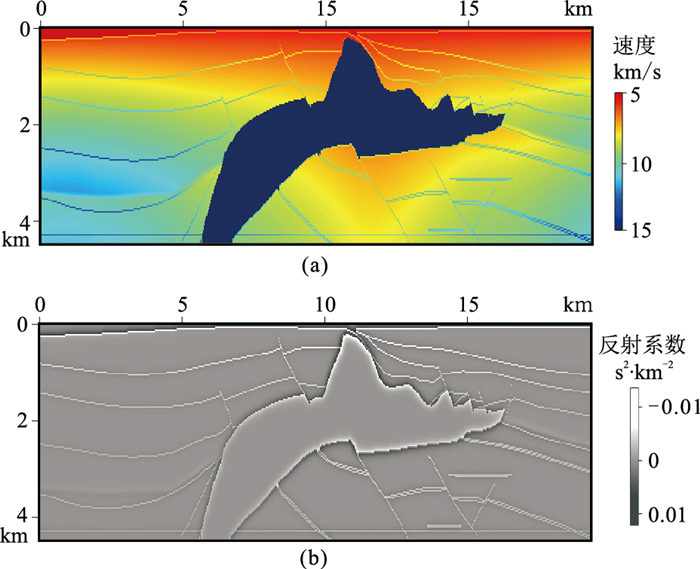
采用SEG/EAGE盐丘模型测试本文提出的算法。该模型的横向和纵向空间采样间隔均为30m。图 3a为该模型的速度场,由式(2)可计算其反射系数模型(图 3b)。采用主频为15Hz、时间采样间隔为1ms的Ricker子波进行有限差分线性Born正演。总共正演了163炮,起始炮点位于(0,0),间隔为120m;采用645个接收点的固定排列接收,起始点位于(0,0),接收点间隔为30m。
|
图 3 盐丘速度(a)和反射系数(b)模型 |
图 4a为RTM经拉普拉斯滤波后的结果,可以看出成像结果分辨率较低,且盐下成像振幅较弱。图 4b为迭代10次后共轭梯度(CG)法的LSRTM结果,与图 4a相比,提高了分辨率,而且一定程度上恢复了盐下的反射振幅,但仍然与真实反射系数(图 3b)相差较远。通过迭代更多次数,可以进一步改善LSRTM的成像结果,但10次迭代的计算成本已相当于20次全部共炮点道集的RTM。图 4c和图 4d均为迭代10次后的Adam法LSRTM成像结果,其中前者的批量参数为16,后者为4,后者的成像结果远优于前者,说明批量参数对成像效果影响很大。对不同批量参数进行测试,最终选择成像效果最好的批量参数4。对比图 4d与图 4b可以看出,在相同的迭代次数下,Adam法的效果远优于CG法,从而验证了Adam法比共轭梯度法的收敛速度快得多。

|
图 4 RTM和LSRTM结果对比 (a)RTM+拉普拉斯滤波;(b)CG法LSRTM;(c)Adam法LSRTM(批量参数为16);(d)Adam法LSRTM(批量参数为4) |
图 5是CG法、批量参数为16的Adam法、批量参数为4的Adam法的LSRTM数据拟合误差曲线和模型误差曲线,可见批量参数为4时Adam算法具有最快的收敛速度。进一步对比三种方法LSRTM结果在横向10km处的反射系数波形(图 6),批量参数为4时的Adam法偏移结果最接近于真实反射系数模型。

|
图 5 三种LSRTM法的误差曲线对比 (a)数据拟合误差;(b)反射系数平方误差 |

|
图 6 三种方法LSRTM结果与真实 反射系数的单道波形对比 |
结合Adam方法和炮编码可以进一步提高LSRTM的计算效率。图 7a为应用炮编码GD法进行LSRTM迭代163次后的成像结果,其计算成本相当于2次全部共炮点道集的RTM,但已经优于迭代10次的LSRTM结果(图 4b)。图 7b为应用炮编码Adam法进行LSRTM迭代163次的成像结果。两种方法的计算成本大致相同,但炮编码Adam法LSRTM的结果要优于GD法,计算结果十分接近真实的反射系数模型。

|
图 7 炮编码LSRTM反射系数成像结果 (a)GD法;(b)Adam法 |
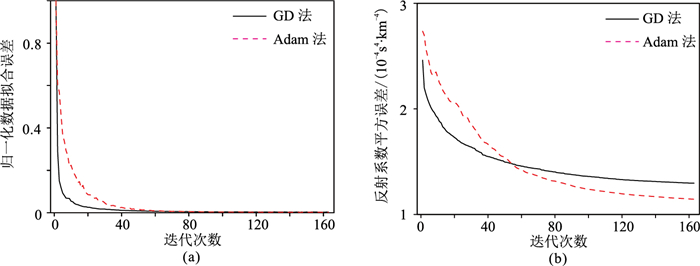
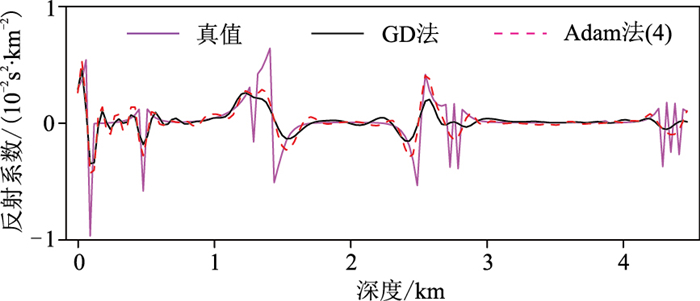
图 8为炮编码LSRTM的数据拟合误差曲线和模型误差曲线,可以看出,相比于GD法,炮编码Adam法LSRTM具有更快的收敛速度。进一步对比横向10km处的反射系数波形,炮编码Adam法LSRTM的成像结果更接近于真实反射系数模型(图 9)。
|
图 8 炮编码两种方法LSRTM法的误差曲线对比 (a)数据拟合误差;(b)反射系数平方误差 |
|
图 9 炮编码两种方法LSRTM结果与 真实反射系数的单道波形对比 |
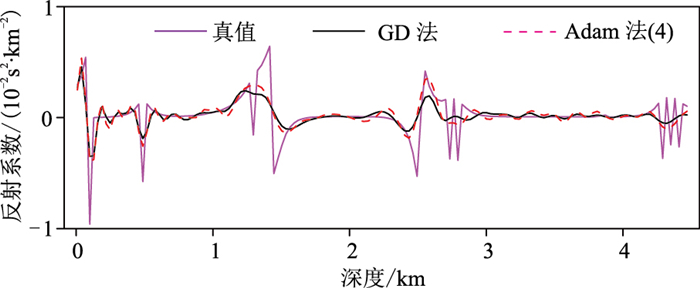
对原始Born正演数据加入随机噪声,其信噪比为-7.7dB。图 10为加噪数据的炮编码GD法和Adam法LSRTM的结果,可见Adam算法的盐下成像结果更清晰,整体分辨率更高。图 11为两种方法的数据拟合误差曲线和模型误差曲线,可以看出Adam算法的收敛速度更快。两种方法成像结果在横向10km处的反射系数波形与真实反射系数的对比如图 12所示,可见在数据存在噪声的情况下,炮编码Adam法LSRTM成像结果更接近于真实反射系数模型。需要注意的是,反演类成像方法对数据的信噪比一般要求较高,因此建议在反演成像之前对数据做去噪处理,以尽可能减小噪声对反演结果的影响。

|
图 10 含噪数据炮编码两种方法LSRTM结果 (a)GD法;(b)Adam法 |

|
图 11 含噪数据炮编码两种方法LSRTM法的误差曲线对比 (a)数据拟合;(b)反射系数 |
|
图 12 含噪数据炮编码两种方法LSRTM结果与 真实反射系数的单道波形对比 |
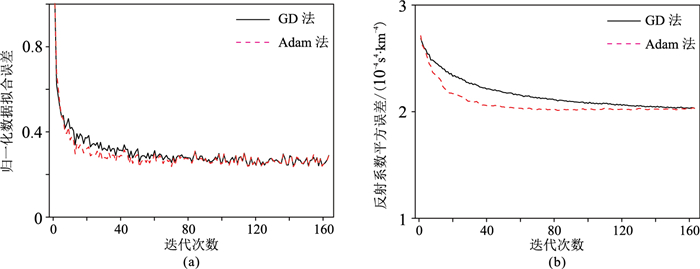
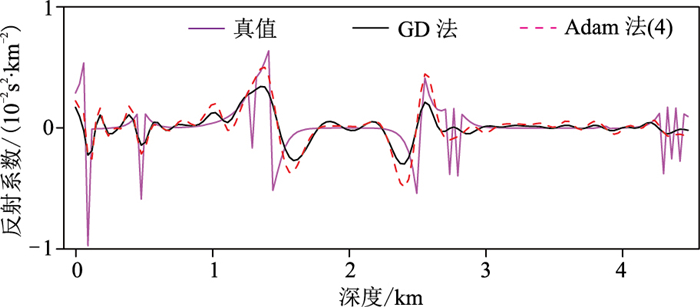
应用声波方程有限差分法正演数据作为观测数据分析炮编码GD法和Adam法LSRTM对正演算子误差的敏感性。图 13为两种方法的成像结果,可见Adam算法的对盐下成像结果更清晰,整体的分辨率更高。图 14为这两种方法的数据拟合误差曲线和模型误差曲线,可以看出Adam算法的收敛速度更快。对比横向10km处的两种方法的反射系数波形(图 15),可见炮编码Adam法LSRTM反演结果更接近真实反射系数模型。

|
图 13 有限差分法正演数据炮编码两种方法LSRTM结果 (a)GD法;(b)Adam法 |
|
图 14 有限差分法正演数据炮编码两种方法LSRTM的误差曲线对比 (a)数据拟合;(b)反射系数 |
|
图 15 有限差分法正演数据两种方法炮编码LSRTM结果 与真实反射系数的单道波形对比 |
使用偏移速度为准确速度的95%测试炮编码GD法和Adam法LSRTM的对速度误差的敏感性。图 16为两种方法对Born正演数据的成像结果。可以看出,不管是GD法还是Adam法,都无法对盐丘模型准确成像,表明LSRTM对速度精度要求很高。

|
图 16 偏移速度有误差时炮编码两种方法LSRTM结果 (a)GD法;(b)Adam法 |
本文首次采用深度学习领域中的优化算法——Adam算法解决LSRTM的计算成本问题。SEG/EAGE盐丘模型数值实验表明,通过结合Adam算法和炮编码技术,只需要消耗大约两次完整炮集数据RTM的计算成本,就能够得到比RTM分辨率更高、更精确的反射系数结果,从而使LSRTM应用于实际地震数据的成像成为可能,为复杂构造成像提供更完善的信息。
另外,本文进一步分析了Adam法LSRTM对随机噪声、正演算子误差、速度误差的敏感性,结果表明:在存在随机噪声和正演误差的情况下,Adam方法的收敛速度都要优于GD法;但是在速度存在误差的情况下,Adam方法与其他方法一样,都无法得到准确的成像结果。
值得注意的是,直接从实际数据中的波形信息估计反射系数模型十分困难。深度学习也许能够从地震数据中提取更可靠的特征,提供对地下岩性参数更加有效的估计,这也是下一步的研究方向。
| [1] |
CLAERBOUT J F. Toward a unified theory of reflector mapping[J]. Geophysics, 1971, 36(3): 467-481. DOI:10.1190/1.1440185 |
| [2] |
LAILLY P. The seismic inverse problem as a sequence of before stack migrations[C]. Conference on Inverse Scattering, Theory and Applications, Society for Industrial and Applied Mathematics, 1983, 206-220.
|
| [3] |
NEMETH T, WU C J, SCHUSTER G T. Least-squares migration of incomplete reflection data[J]. Geophy-sics, 1999, 64(1): 208-221. |
| [4] |
KVHL H, SACCHI M D. Least-squares wave-equation migration for AVP/AVA inversion[J]. Geophy-sics, 2003, 68(1): 262-273. |
| [5] |
CLAPP M L, CLAPP R G, BIONDI B L. Regularized least-squares inversion for 3-D subsalt imaging[C]. SEG Technical Program Expanded Abstracts, 2005, 24: 1814-1817.
|
| [6] |
VALENCIANO A A, BIONDI B, GUITTON A. Target-oriented wave-equation inversion[J]. Geophysics, 2006, 71(4): A35-A38. DOI:10.1190/1.2213359 |
| [7] |
王华忠, 盛燊. 走向精确地震勘探的道路[J]. 石油物探, 2021, 60(5): 693-708, 720. WANG Huazhong, SHENG Shen. Pathway toward accurate seismic exploration[J]. Geophysical Prospecting for Petroleum, 2021, 60(5): 693-708, 720. |
| [8] |
段心标, 王华忠, 邓光校. 应用反射理论的最小二乘逆时偏移成像[J]. 石油地球物理勘探, 2020, 55(6): 1305-1311. DUAN Xinbiao, WANG Huazhong, DENG Guangxiao. Least-squares reverse-time migration based on reflection theory[J]. Oil Geophysical Prospecting, 2020, 55(6): 1305-1311. |
| [9] |
陈汉明, 周辉, 田玉昆. 分数阶拉普拉斯算子黏滞声波方程的最小二乘逆时偏移[J]. 石油地球物理勘探, 2020, 55(3): 616-626. CHEN Hanming, ZHOU Hui, TIAN Yukun. Least-squares reverse-time migration based on a fractional Laplacian viscoacoustic wave equation[J]. Oil Geophysical Prospecting, 2020, 55(3): 616-626. |
| [10] |
MORTON S A, OBER C C. Faster shot-record depth migrations using phase encoding[C]. SEG Technical Program Expanded Abstracts, 1998, 17: 13-17.
|
| [11] |
ROMERO L A, GHIGLIA D C, OBER C C, et al. Phase encoding of shot records in prestack migration[J]. Geophysics, 2000, 65(2): 426-436. DOI:10.1190/1.1444737 |
| [12] |
ZHANG Y, SUN J, NOTFORS C, et al. Delayed-shot 3D depth migration[J]. Geophysics, 2005, 70(5): E21-E28. DOI:10.1190/1.2057980 |
| [13] |
LIU F Q, HANSON D W, WHITMORE N D, et al. Toward a unified analysis for source plane-wave migration[J]. Geophysics, 2006, 71(4): S129-S139. DOI:10.1190/1.2213933 |
| [14] |
TANG Y X. Target-oriented wave-equation least-squares migration/inversion with phase-encoded Hessian[J]. Geophysics, 2009, 74(6): WCA95-WCA107. DOI:10.1190/1.3204768 |
| [15] |
GODWIN J, SAVA P. Blended source imaging by amplitude encoding[C]. SEG Technical Program Expanded Abstracts, 2010, 29: 3125-3129.
|
| [16] |
GAO F C, ATLE A, Williamson P. Full waveform inversion using deterministic source encoding[C]. SEG Technical Program Expanded Abstracts, 2010, 29: 1013-1017.
|
| [17] |
SCHUSTER G T, WANG X, HUANG Y, et al. Theo-ry of multisource crosstalk reduction by phase-encoded statics[J]. Geophysical Journal International, 2011, 184(3): 1289-1303. DOI:10.1111/j.1365-246X.2010.04906.x |
| [18] |
HERRMANN F, LI X. Efficient least-squares imaging with sparsity promotion and compressive sensing[J]. Geophysical Prospecting, 2012, 60(4): 696-712. DOI:10.1111/j.1365-2478.2011.01041.x |
| [19] |
LIU Y J, SYMES W W, LI Z C. Multisource least-squares extended reverse time migration with preconditioning guided gradient method[C]. SEG Technical Program Expanded Abstracts, 2013, 32: 3709-3715.
|
| [20] |
刘玉金, 李振春. 扩展成像条件下的最小二乘逆时偏移[J]. 地球物理学报, 2015, 58(10): 3771-3782. LIU Yujin, LI Zhenchun. Least-squares reverse-time migration with extended imaging condition[J]. Chinese Journal of Geophysics, 2015, 58(10): 3771-3782. |
| [21] |
李庆洋, 黄建平, 李振春, 等. 优化的多震源最小二乘逆时偏移[J]. 石油地球物理勘探, 2016, 51(2): 334-341. LI Qingyang, HUANG Jianping, LI Zhenchun, et al. Optimized multi-source least-squares reverse time migration[J]. Oil Geophysical Prospecting, 2016, 51(2): 334-341. |
| [22] |
TANG Y X, LEE S. Preconditioning full waveform inversion with phase-encoded Hessian[C]. SEG Technical Program Expanded Abstracts, 2010, 29: 1034-1038.
|
| [23] |
PRATT R G. Seismic waveform inversion in the frequency domain, part 1:theory and verification in a physical scale model[J]. Geophysics, 1999, 64(3): 888-901. DOI:10.1190/1.1444597 |
| [24] |
SHIN C, JANG S, MIN D J. Improved amplitude preservation for prestack depth migration by inverse scattering theory[J]. Geophysical Prospecting, 2001, 49(5): 592-606. DOI:10.1046/j.1365-2478.2001.00279.x |
| [25] |
AOKI N, SCHUSTER G T. Fast least-squares migration with a deblurring filter[J]. Geophysics, 2009, 74(6): WCA83-WCA93. DOI:10.1190/1.3155162 |
| [26] |
姚振岸, 孙成禹, 喻志超, 等. 融合点扩散函数的预条件黏声最小二乘逆时偏移[J]. 石油地球物理勘探, 2019, 54(1): 73-83. YAO Zhen'an, SUN Chengyu, YU Zhichao, et al. Preconditioned visco-acoustic least-squares reverse time migration integrated with point spread function[J]. Oil Geophysical Prospecting, 2019, 54(1): 73-83. |
| [27] |
HOU J, SYMES W W. Accelerating extended least-squares migration with weighted conjugate gradient iteration[J]. Geophysics, 2016, 81(4): S165-S179. DOI:10.1190/geo2015-0499.1 |
| [28] |
MA Y, HALE D, MENG Z B, et al. Full waveform inversion with image-guided gradient[C]. SEG Technical Program Expanded Abstracts, 2010, 29: 1003-1007.
|
| [29] |
刘梦丽, 黄建平, 李闯, 等. 基于角度滤波成像的最小二乘逆时偏移[J]. 石油地球物理勘探, 2018, 53(3): 469-477. LIU Mengli, HUANG Jianping, LI Chuang, et al. Least-squares reverse time migration based on the angular filtering imaging condition[J]. Oil Geophysical Prospecting, 2018, 53(3): 469-477. |
| [30] |
KINGMA D P, BA J. Adam: a method for stochastic optimization[DB/OL]. [2014-12-22], https://arxiv.org/abs/1412.6980.
|
| [31] |
DUCHI J, HAZAN E, SINGER Y. Adaptive subgradient methods for online learning and stochastic optimization[J]. The Journal of Machine Learning Research, 2011, 12(7): 2121-2159. |
| [32] |
TIELEMAN T, HINTON G. Rmsprop: divide the gradient by running average of its recent magnitude//Courser A: Neural Networks for Machine Learning[EB/OL]. https://open.163.com/newview/movie/free?pid=UEV4DEHJP&mid=VEV4DEIUQ.
|
| [33] |
KREBS J R, ANDERSON J E, HINKLEY D, et al. Fast full-wavefield seismic inversion using encoded sources[J]. Geophysics, 2009, 74(6): WCC177-WCC188. |



 吴丹, 北京市海淀区花园北路环星大厦D座3层中国石油勘探开发研究院西北分院计算机研究所,100191。Email:
吴丹, 北京市海淀区花园北路环星大厦D座3层中国石油勘探开发研究院西北分院计算机研究所,100191。Email: