常规砂岩储层主要发育粒间孔,孔隙类型单一,储层相对均质。而复杂储层发育溶蚀孔、生物孔、晶间孔、铸模孔、微裂缝等,孔隙类型多样,孔隙结构复杂,非均质性强。复杂储层中普遍存在孔隙度相近而渗透率(K)差异较大的现象。目前尚未见孔隙连通性的评价和连通孔隙度(φc)的计算模型等方面的研究成果。基于总孔隙度(φ)[1-3]、孔隙结构参数[4-7]计算渗透率的一系列方法在复杂储层中均未获得理想的效果。另外,在基于核磁共振测井的方法中,尽管针对孔径组分、双截止值、T2谱分别建立了渗透率评价方法[8-12],但未能建立具有普适性的孔隙度指数模型及核磁共振T2模型。采用机器学习算法及地震曲率预测渗透率[13-16]并不适用于复杂储层。在实际应用中,为了减小核磁共振T2模型的评价误差,往往是基于适当的岩心实验标定,选择适用于不同类型储层的孔隙度指数,但均未阐明孔隙度指数变化的根本原因。
针对上述问题,本文首先采用铸体薄片、核磁共振、CT扫描成像等实验方法求取岩心的连通孔隙度,再从岩石孔隙空间“连通”和“导电”的角度出发,以导电孔隙度(φf)为桥梁,建立连通孔隙度的计算模型,分析十二种不同类型岩石中连通孔隙度与总孔隙度的关系。基于连通孔隙度的计算模型,改进核磁共振T2模型,形成复杂储层渗透率的定量计算方法。然后以石灰岩储层为例,在相近孔隙度条件下,从不同类型岩石渗透率之间的差异出发,推导、建立孔隙度指数模型和适用于石灰岩储层核磁共振T2模型。实际结果表明,基于孔隙度指数模型建立的核磁共振T2模型能更准确地评价石灰岩储层的渗透率。因此,连通孔隙度模型、孔隙度指数模型及普适性的核磁共振T2模型对于复杂储层连通孔隙度评价与渗透率定量计算具有一定的理论价值和实际意义。
1 连通孔隙度的实验测定在复杂储层中,孔隙结构是渗透率的一个主控因素,连通孔隙度是决定渗透率大小的一个重要参数[17-22]。岩石内孔隙连通性可以通过铸体薄片、核磁共振、CT扫描成像等实验进行评价。其中,铸体薄片实验可以在平面上直观显示不同类型孔隙之间的连通性,但不能定量计算连通孔隙度;核磁共振实验可以定量计算连通孔隙度,但不能直观显示不同类型孔隙之间的连通性[21];CT扫描成像实验不仅可以在空间上直观显示不同类型孔隙之间的连通性,而且可以定量计算连通孔隙度[23-24]。
1.1 铸体薄片实验两块白云岩岩心样品的铸体薄片如图 1所示。根据孔隙充填的程度可知,两块样品的孔喉半径、总孔隙度均相近,但连通性不同,导致渗透率存在较大差异。

|
图 1 两块白云岩岩心样品的铸体薄片 (a)样品1:孔喉半径为0.37μm,总孔隙度为6.5%,渗透率为2.00mD;(b)样品2:孔喉半径为0.37μm,总孔隙度为6.7%,渗透率为0.37mD |
尽管铸体薄片可以在平面上直观显示两块样品的连通孔隙度存在差异,但无法定量给出连通孔隙度的大小。
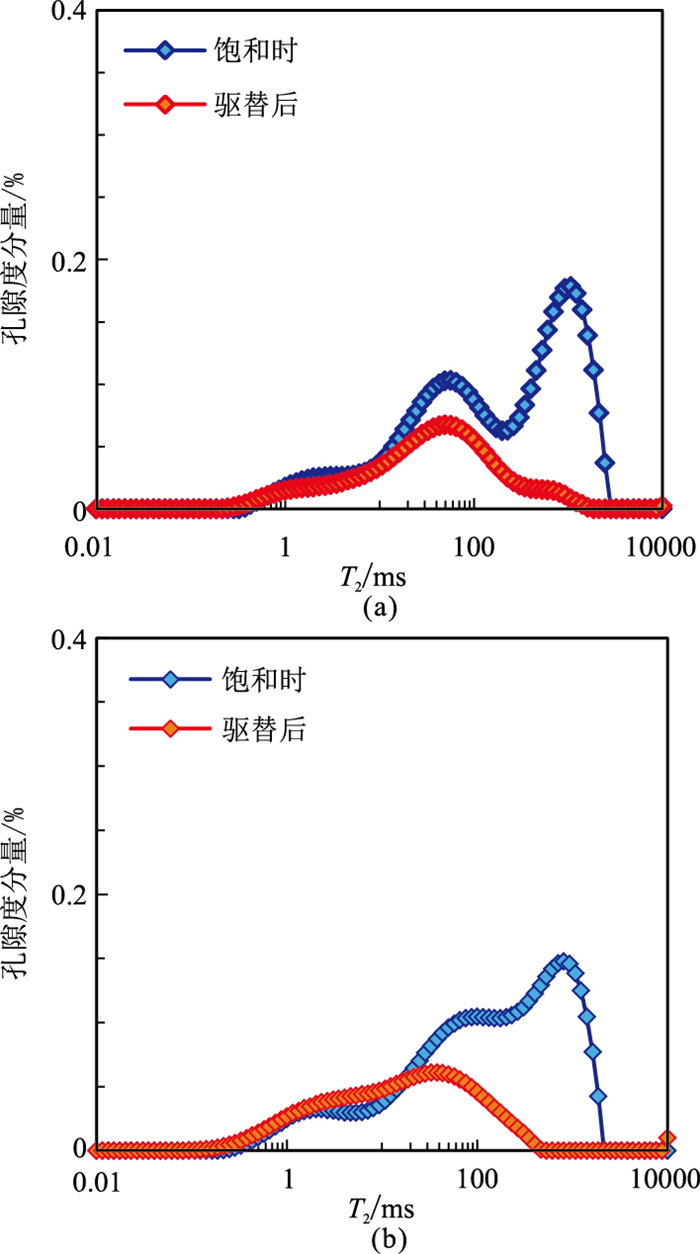
1.2 核磁共振实验两块白云岩岩心样品饱和时与驱替后的横向弛豫时间T2谱如图 2所示。岩心样品饱和时的核磁孔隙度可以认为是总孔隙度,驱替后的核磁孔隙度可以认为是不连通孔隙度,二者之差即为连通孔隙度。因此,岩心样品1的连通孔隙度为2.62%,连通孔隙占比为59.82%;岩心样品2的连通孔隙度为0.69%,连通孔隙占比为15.83%。
|
图 2 两块白云岩岩心样品饱和时与驱替后的核磁共振横向弛豫时间T2谱分布图 (a)样品1饱和时、驱替后的核磁孔隙度(计算蓝线、红线所围面积而得)分别为4.38%、1.76%;(b)样品2饱和时、驱替后的核磁孔隙度分别为4.36%、3.67% |
尽管核磁共振实验可以定量给出岩心样品连通孔隙度的大小,但无法在平面上或空间上直观显示不同类型孔隙之间的连通性。
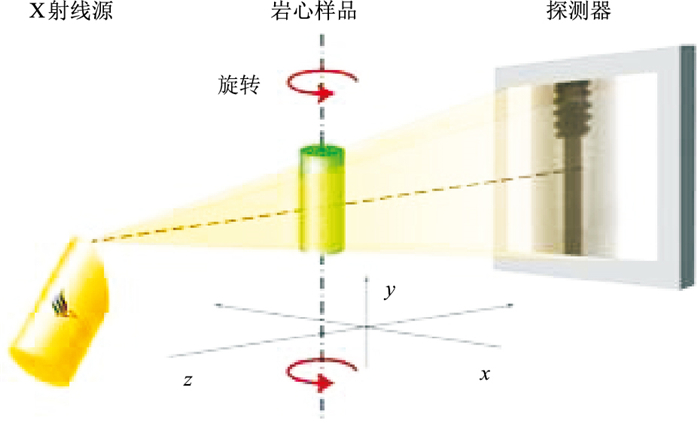
1.3 CT扫描成像实验典型的X射线CT扫描成像布局如图 3所示。其中X射线源与探测器分别置于岩心样品转台的两侧,X射线穿透放置在转台上的岩心样品后被探测器接收,岩心样品可以进行纵向、横向平移或垂直升降运动。当岩心样品纵向距X射线源越近,岩心样品放大倍数越大,内部细节同时会被放大,因而图像分辨率越高,可探测的区域越小;相反,岩心样品纵向距X射线源越远,岩心样品放大倍数越小,图像分辨率越低,可探测区域越大。岩心样品的横向平移和垂直升降可用于改变扫描区域,但不改变图像分辨率。将旋转360°后所获得的一系列投影图像进行重构后,便可得到岩心样品CT扫描的三维图像。
|
图 3 岩心样品CT扫描成像布局图 |
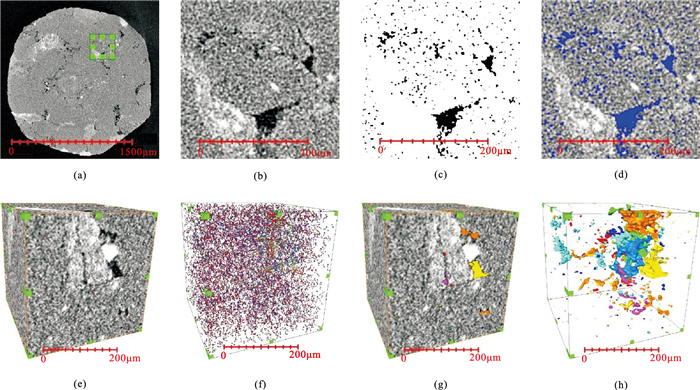
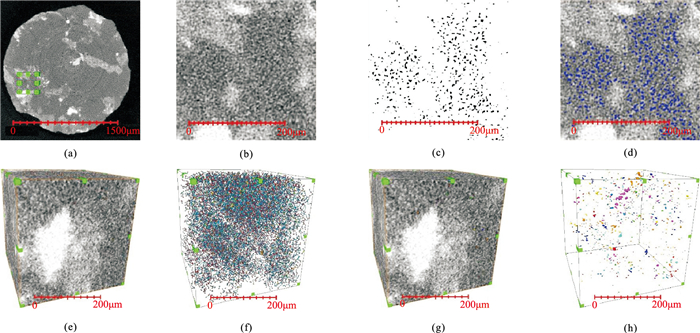
通过钻取岩心样品、滤波降噪、二值化分割、孔隙填涂,重建岩心样品的三维数字模型,并建立孔喉球棍(体)模型和孔隙连通(体)模型,可展示岩心样品的三维内部结构(图 4、图 5)。
|
图 4 岩心样品1的CT扫描成果图 (a)截取位置;(b)滤波降噪;(c)二值化分割;(d)孔隙填涂;(e)孔喉球棍体模型;(f)孔喉球棍模型;(g)孔隙连通体模型;(h)孔隙连通性模型。岩心样品的扫描精度为0.99μm;深黑色区域代表样本内的孔隙,灰色和白色区域均代表岩心样品的基质;图f和图h的不同颜色表示不同类型的孔隙,图 5同 |
|
图 5 岩心样品2的CT扫描成果图 (a)截取位置;(b)滤波降噪;(c)二值化分割;(d)孔隙填涂;(e)孔喉球棍体模型;(f)孔喉球棍模型;(g)孔隙连通体模型;(h)孔隙连通性模型 |
对比图 4h与图 5h可知,岩心样品1的孔隙连通性明显好于岩心样品2。岩心样品的CT扫描成果(表 1)揭示,两块岩心样品的总孔隙度、孔喉半径、孔隙数量、孔隙体积均相近,但孔隙连通体积百分比和连通孔隙度的差异较大。
|
|
表 1 岩心样品的CT扫描成果 |
另外,由于铸体薄片、核磁共振、CT扫描成像实验中岩心样品的尺寸相差甚大,且白云岩储层非均质性强,因而不同方法所测定的连通孔隙度、总孔隙度之间存在着一定的差异。
2 连通孔隙度的计算模型铸体薄片、核磁共振、CT扫描成像等实验可以显示岩石内连通孔隙的分布情况,但难以建立连通孔隙度的计算模型。
从“连通”的角度来看,岩石孔隙空间可以被分为连通孔隙和不连通孔隙;从“导电”的角度来看,岩石孔隙空间则可以被分为导电孔隙和不导电孔隙。由于连通孔隙与导电孔隙所表征的孔隙空间是相同的,因此,可以认为连通孔隙度等于导电孔隙度。基于Maxwell方程,地层因素与导电孔隙度之间的关系为[25-29]
| $ \left\{\begin{array}{l} F=\frac{(z+1)-\varphi_{\mathrm{f}}}{z \varphi_{\mathrm{f}}}=1+\frac{G\left(1-\varphi_{\mathrm{f}}\right)}{\varphi_{\mathrm{f}}} \\ G=\frac{1+z}{z} \end{array}\right. $ | (1) |
式中:F为地层因素;G、z为孔隙几何形状参数。
通过假设函数关系并设置相应的边界条件之后[30],可以得出
| $ \varphi_{\mathrm{f}}=\frac{\varphi-\varphi_{\mathrm{s}}}{1-\varphi_{\mathrm{s}}} $ | (2) |
式中φs为不导电孔隙度。联立式(1)、式(2),便能得到
| $ \varphi=\frac{G(1-\varphi)}{F-1}+\varphi_{\mathrm{s}} $ | (3) |
以(1-φ)/(F-1)为横坐标、φ为纵坐标,可求取直线的斜率G。将其代入式(1),便能求解导电孔隙度φf,从而得到连通孔隙度φc。
基于上述方法,本文分别计算了十二种岩性的连通孔隙度,并建立了总孔隙度与连通孔隙度之间的函数关系(表 2)。
|
|
表 2 十二种岩性的总孔隙度、连通孔隙度及它们之间的函数关系 |
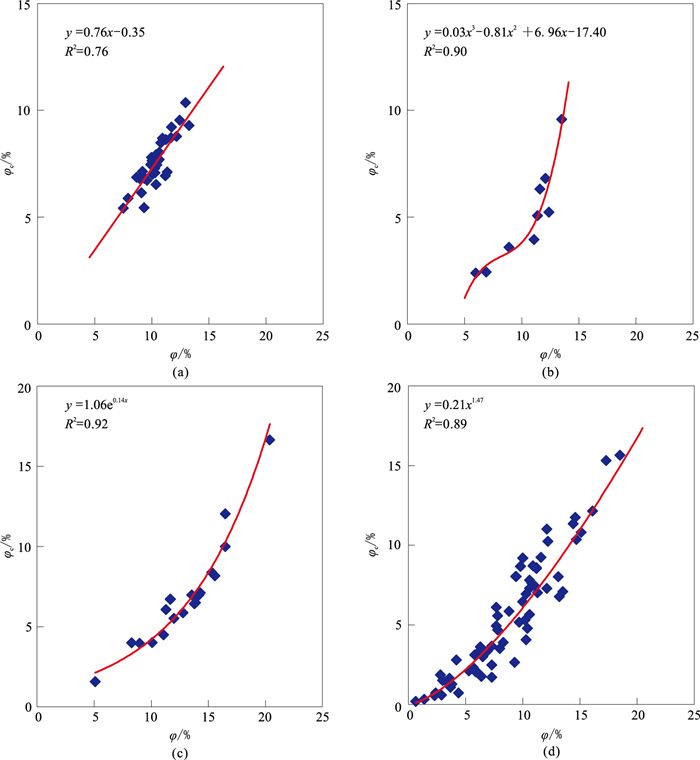
在十二种岩性中,连通孔隙度与总孔隙度的四种典型函数关系分别为线性、多项式、乘幂和指数(图 6)。由表 2、图 6可知:①与砾岩相比,角砾岩磨圆度极低且分选很差,角砾岩的总孔隙度与连通孔隙度呈现更为复杂的函数关系;②不同类型的岩石连通孔隙度与总孔隙度之间的函数关系存在较大差异,即使总孔隙度相近,连通孔隙度也会存在较大差异。这也就解释了在一些岩石中,尽管总孔隙度相近,但渗透率却存在较大差异,根本原因是连通孔隙度不同。
|
图 6 四种典型的φc与φ函数关系 (a)致密砂岩;(b)角砾岩;(c)砾岩;(d)安山岩 |
连通孔隙度主要与总孔隙度、岩石类型相关,因此复杂储层连通孔隙度的计算模型为
| $ \varphi_{\mathrm{c}}=f(\varphi, L) $ | (4) |
式中L代表岩石类型。
基于核磁共振、CT扫描实验所测定的连通孔隙度,结合连通孔隙度与总孔隙度函数关系,可以综合评价所计算连通孔隙度的准确性。
3 渗透率的定量计算方法基于核磁共振T2模型,常规砂岩储层渗透率的计算公式为[30]
| $ K=a T_{2 \mathrm{gm}}{}^{2} \varphi^{4} $ | (5) |
式中:a为经验常数;T2gm是横向弛豫时间T2分布的几何平均值。
在复杂储层中,复杂的孔隙结构导致φc与φ存在较大差异,而对渗透率起主要贡献的是φc。因此,本文将复杂储层渗透率的计算公式修改为
| $ K_{\text {comp }}=a T_{\rm{2 g m-c o m p}}^{2} \varphi_{\mathrm{c}}^{4} $ | (6) |
式中:Kcomp为复杂储层的渗透率;T2gm-comp是复杂储层横向弛豫时间T2分布的几何平均值。
φc与φ呈乘幂(φc=bφd)、指数(φc=bedφ)、线性(φc=bφ+d)和多项式(φc=b1φ3+b2φ2+b3φ+d)四种典型函数关系,相应四种复杂储层渗透率的计算公式分别为
| $ K_{\text {comp }}=a T_{2 \mathrm{gm}-\mathrm{comp}}^{2}\left(b \varphi^{d}\right)^{4} $ | (7) |
| $ K_{\text {comp }}=a T_{2 \mathrm{gm}-\mathrm{comp}}^{2}\left(b \mathrm{e}^{d \varphi}\right)^{4} $ | (8) |
| $ K_{\text {comp }}=a T_{2 \mathrm{gm}-\mathrm{comp}}^{2}(b \varphi+d)^{4} $ | (9) |
| $ K_{\text {comp }}=a T_{2 \mathrm{gm}-\text { comp }}^{2}\left(b_{1} \varphi^{3}+b_{2} \varphi^{2}+b_{3} \varphi+d\right)^{4} $ | (10) |
式中b、b1、b2、b3、d均为系数。
基于式(7)~式(10),复杂储层渗透率的计算公式表达为
| $ K_{\text {comp }}=c T_{2 \text {gm-comp }}^{2} f(\varphi) $ | (11) |
式中c为系数。
进一步简化式(11),可以得到
| $ K_{\text {comp }}=c T_{\rm{2 g m-c o m p}}^{2} \varphi^{x} $ | (12) |
式中x为储层的孔隙度指数。如果计算砂岩的渗透率,则x取为4。而石灰岩储层渗透率的计算公式为
| $ K_{\text {lime }}=c T_{2 \text { gm-lime }}^{2} \varphi^{x} $ | (13) |
式中:Klime为石灰岩储层的渗透率;T2gm-lime是石灰岩储层T2分布的几何平均值。
石灰岩储层具强非均质性,即使在相近的孔隙度条件下,石灰岩储层的渗透率与常规砂岩储层的渗透率也会存在较大差异。因此,假定相近孔隙度条件下,石灰岩与常规砂岩的储层渗透率的比值
| $ \frac{K_{\text {lime }}}{K_{\text {sand }}}=\frac{T_{2 \mathrm{gm-lime }}^{2} \varphi^{x}}{T_{2 \mathrm{gm} \text {-sand }}^{2} \varphi^{4}}=y $ | (14) |
式中:Ksand为砂岩储层的渗透率;T2gm-sand是砂岩储层T2分布的几何平均值。
由式(14)可以得到石灰岩储层孔隙度指数
| $ x=4+\frac{\ln y-2\left(\ln T_{2 \mathrm{gm}-\mathrm{lime}}-\ln T_{2 \mathrm{gm}-\mathrm{sand}}\right)}{\ln \varphi} $ | (15) |
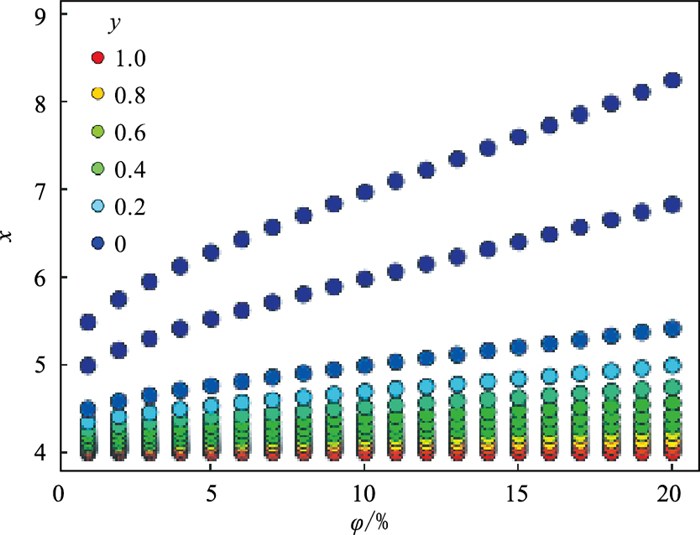
在相近孔隙度条件(孔隙度小于20%)下,当T2gm-lime=T2gm-sand,y小于1时,φ、x、y之间的关系如图 7所示。由图可知,x的分布范围为4.0~8.3;φ逐渐变大,x逐渐变大;y逐渐变小,x逐渐变大。
|
图 7 T2相同时,φ、x与y之间的关系 |
在相近孔隙度条件(孔隙度小于20%)下,当T2gm-lime明显大于T2gm-sand,即T2gm-lime≠T2gm-sand时,φ、x、y之间的关系如图 8所示,可见x的分布范围为5.9~13.7。

|
图 8 T2不同时,φ、x与y之间的关系 |
联立式(13)和式(15)可以得到石灰岩储层渗透率的计算公式
| $ K_{\text {lime }}=c T_{2 \mathrm{gm}-\operatorname{lime}}^{2} \varphi^{\left[\frac{\ln y-2\left(\ln T_{2 \mathrm{gm}-\operatorname{lime}}-\ln T_{2 \mathrm{gm}-\mathrm{sand}}\right)}{\ln \varphi}\right]} $ | (16) |
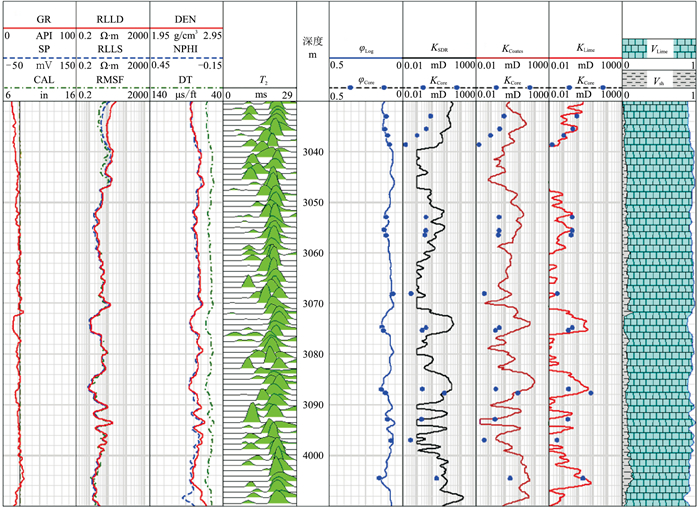
选用A井部分层段石灰岩储层(图 9)测试本文方法应用效果。
|
图 9 A井部分层段石灰岩储层渗透率处理成果 GR为自然伽马,SP为自然电位,RLLD为深侧向电阻率,RLLS为浅侧向电阻率,RMSF为冲洗带电阻率,DEN为密度,NPHI为中子孔隙度,DT为声波时差,φLog为根据测井资料计算的孔隙度,φcore为岩心孔隙度,KSDR为T2模型估算渗透率,KCore为岩心渗透率,KCoates为自由流体模型估算渗透率,Vlime、Vsh分别为石灰岩、泥岩含量 |
由图 9可见,基于测井曲线所计算的孔隙度(φLog)与岩心分析的孔隙度(φCore)之间的吻合程度较高;基于核磁共振T2模型所计算的渗透率(KSDR)与岩心分析的渗透率(KCore)之间误差相对较大,平均绝对误差为20.41mD;基于核磁共振自由流体模型所计算的渗透率(KCoates)与KCore之间误差相对较大,平均绝对误差为21.75mD;基于核磁共振测井、采用式(16)所计算的渗透率(Klime)与KCore之间误差相对较小,平均绝对误差为0.83mD。因此,基于连通孔隙度的渗透率定量计算方法可以提高石灰岩储层渗透率预测的精度。
5 结论本文研究了复杂储层连通孔隙度评价与渗透率定量计算方法,并建立了连通孔隙度模型、孔隙度指数模型及普适性的核磁共振T2模型。主要结论如下。
(1) 核磁共振实验可以定量计算连通孔隙度,但不能直观显示不同类型孔隙之间的连通性;CT扫描成像不仅可以在空间上直观显示不同类型孔隙之间的连通性,也可以定量计算连通孔隙度。
(2) 由于导电孔隙度与连通孔隙度所表征的孔隙空间相同,因此以导电孔隙度为桥梁,建立了连通孔隙度的计算模型,明确了不同类型岩石中连通孔隙度与总孔隙度的函数关系。二者的函数形式不尽相同,主要表现为线性、多项式、乘幂和指数等。这揭示了总孔隙度相近、连通孔隙度不同是导致渗透率存在较大差异的根本原因。
(3) 采用连通孔隙度的计算模型改进了核磁共振T2模型,形成了复杂储层渗透率的定量计算方法,大幅度地提高了石灰岩储层渗透率的计算精度。
| [1] |
NELSON P H. Permeability-porosity relationships in sedimentary rocks[J]. The Log Analyst, 1994, 35(3): 38-62. |
| [2] |
DZIUBA T T. Improved permeability prediction in carbonates[C]. SPWLA 37th Annual Logging Symposium, New Orleans, Louisiana, 1996, SPWLA-1996-H.
|
| [3] |
RUSSEL D, GOURNAY J, RICHTER P, et al. Porosity partitioning and permeability quantification in vuggy carbonate using wireline logs, Permian Basin, West Texas[C]. SPWLA 46th Annual Logging Symposium, New Orleans, Louisiana, 2005, SPWLA-2005-JJ.
|
| [4] |
PERMADI P, SUSILO A. Permeability prediction and characteristics of pore structure and geometry as inferred from core data[C]. SPE/EAGE Reservoir Characterization and Simulation Conference, Abu Dhabi, UAE, 2009, SPE-125350-MS.
|
| [5] |
孙海, 姚军, 张磊, 等. 基于孔隙结构的页岩渗透率计算方法[J]. 中国石油大学学报(自然科学版), 2014, 38(2): 92-98. SUN Hai, YAO Jun, ZHANG Lei, et al. A computing method of shale permeability based on pore structures[J]. Journal of China University of Petroleum(Edition of Natural Science), 2014, 38(2): 92-98. DOI:10.3969/j.issn.1673-5005.2014.02.014 |
| [6] |
杨泽皓, 董明哲, 宫厚健, 等. 测量页岩径向渗透率和孔隙度的新方法[J]. 石油学报, 2015, 36(4): 482-489. YANG Zehao, DONG Mingzhe, GONG Houjian, et al. A new method to measure radial permeability and porosity of shale[J]. Acta Petrolei Sinica, 2015, 36(4): 482-489. |
| [7] |
甘利灯, 王峣钧, 罗贤哲, 等. 基于孔隙结构参数的相控渗透率地震预测方法[J]. 石油勘探与开发, 2019, 46(5): 883-890. GAN Lideng, WANG Yaojun, LUO Xianzhe, et al. A permeability prediction method based on pore structure and lithofacies[J]. Petroleum Exploration and Development, 2019, 46(5): 883-890. |
| [8] |
郑炀, 徐锦绣, 刘欢, 等. 基于随钻核磁测井的渗透率评价方法及其应用——以渤海锦州油田古近系沙河街组为例[J]. 中国海上油气, 2019, 31(2): 69-75. ZHENG Yang, XU Jinxiu, LIU Huan, et al. A permea-bility evaluation method based on NMR logging while drilling and its application: taking Paleogene Shahejie formation in Jinzhou oilfield of Bohai sea as an example[J]. China Offshore Oil and Gas, 2019, 31(2): 69-75. |
| [9] |
韩玉娇, 周灿灿, 范宜仁, 等. 基于孔径组分的核磁共振测井渗透率计算新方法——以中东A油田生物碎屑灰岩储集层为例[J]. 石油勘探与开发, 2018, 45(1): 170-178. HAN Yujiao, ZHOU Cancan, FAN Yiren, et al. A new permeability calculation method using nuclear magnetic resonance logging based on pore sizes: A case study of bioclastic limestone reservoirs in the A oilfield of the Mid-East[J]. Petroleum Exploration and Development, 2018, 45(1): 170-178. |
| [10] |
范宜仁, 刘建宇, 葛新民, 等. 基于核磁共振双截止值的致密砂岩渗透率评价新方法[J]. 地球物理学报, 2018, 61(4): 1628-1638. FAN Yiren, LIU Jianyu, GE Xinmin, et al. Permeability evaluation of tight sandstone based on dual T2 cutoff values measured by NMR[J]. Chinese Journal of Geophysics, 2018, 61(4): 1628-1638. |
| [11] |
张超. 利用核磁共振T2谱计算致密砂岩储层渗透率新方法[J]. 测井技术, 2018, 42(5): 550-556. ZHANG Chao. A new method for calculating permeability of tight sandstone reservoir by using NMR T2 spectrum[J]. Well logging Technology, 2018, 42(5): 550-556. |
| [12] |
李志愿, 崔云江, 关叶钦, 等. 基于孔径分布和T2谱的低孔渗储层渗透率确定方法[J]. 中国石油大学学报(自然科学版), 2018, 42(4): 34-40. LI Zhiyuan, CUI Yunjiang, GUAN Yeqin, et al. Permeability confirmation method of low porosity and permeability reservoirs based on pore distribution and T2 spectrum[J]. Journal of China University of Petroleum(Edition of Natural Science), 2018, 42(4): 34-40. DOI:10.3969/j.issn.1673-5005.2018.04.004 |
| [13] |
谷宇峰, 张道勇, 鲍志东. 测井资料PSO-XGBoost渗透率预测[J]. 石油地球物理勘探, 2021, 56(1): 26-37. GU Yufeng, ZHANG Daoyong, BAO Zhidong. Permeability prediction using PSO-XGBoost based on logging data[J]. Oil Geophysical Prospecting, 2021, 56(1): 26-37. |
| [14] |
王谦, 谭茂金, 石玉江, 等. 径向基函数神经网络法致密砂岩储层相对渗透率预测与含水率计算[J]. 石油地球物理勘探, 2020, 55(4): 864-872. WANG Qian, TAN Maojin, SHI Yujiang, et al. Prediction of relative permeability and calculation of water cut of tight sandstone reservoir based on radial basis function neural network[J]. Oil Geophysical Prospecting, 2020, 55(4): 864-872. |
| [15] |
王俊, 曹俊兴, 尤加春, 等. 基于门控循环单元神经网络的储层孔渗饱参数预测[J]. 石油物探, 2020, 59(4): 616-627. WANG Jun, CAO Junxing, YOU Jiachun, et al. Prediction of reservoir porosity, permeability, and saturation based on a gated recurrent unit neural network[J]. Geophysical Prospecting for Petroleum, 2020, 59(4): 616-627. DOI:10.3969/j.issn.1000-1441.2020.04.012 |
| [16] |
陈龙伟, 汪关妹, 冯小英, 等. 沁水盆地LB区块煤系地层渗透率预测[J]. 石油地球物理勘探, 2020, 55(增刊1): 85-91. CHEN Longwei, WANG Guanmei, FENG Xiaoying, et al. Permeability prediction of coal strata in block LB, Qinshui Basin[J]. Oil Geophysical Prospecting, 2020, 55(S1): 85-91. |
| [17] |
郭振华, 李光辉, 吴蕾, 等. 碳酸盐岩储层孔隙结构评价方法——以土库曼斯坦阿姆河右岸气田为例[J]. 石油学报, 2011, 32(3): 459-465. GUO Zhenhua, LI Guanghui, WU Lei, et al. Pore texture evaluation of carbonate reservoirs in gasfield A, Turkmenistan[J]. Acta Petrolei Sinica, 2011, 32(3): 459-465. |
| [18] |
VERWER K, EBERLIG P, WEGER R J. Effect of pore structure on electrical resistivity in carbonates[J]. AAPG Bulletin, 2011, 95(2): 175-190. DOI:10.1306/06301010047 |
| [19] |
HOLLIS C, VAHRENKAMP V, TULL S, et al. Pore system characterization in heterogeneous carbonates: An alternative approach to widely-used rock-typing methodologies[J]. Marine and Petroleum Geology, 2010, 27(4): 772-793. DOI:10.1016/j.marpetgeo.2009.12.002 |
| [20] |
GHAFOORI M R, ROOSTAEIAN M, SAJJADIAN V A. Secondary porosity: A key parameter controlling the hydrocarbon production in heterogeneous carbonate reservoirs (case study)[J]. Petrophysics, 2009, 50(1): 67-78. |
| [21] |
李滔, 李闽, 荆雪琪, 等. 孔隙尺度各向异性与孔隙分布非均质性对多孔介质渗透率的影响机理[J]. 石油勘探与开发, 2019, 46(3): 569-579. LI Tao, LI Min, JING Xueqi, et al. Influence mechanism of pore-scale anisotropy and pore distribution heterogeneity on permeability of porous media[J]. Petroleum Exploration and Development, 2019, 46(3): 569-579. |
| [22] |
王京悉. 基于分形理论的导电模型及应用[J]. 石油地球物理勘探, 2019, 54(2): 456-460. WANG Jingxi. A fractal-based electrical conductivity model and the application[J]. Oil Geophysical Prospecting, 2019, 54(2): 456-460. |
| [23] |
张凤生, 隋秀英, 段朝伟, 等. 高孔隙度低渗透率碳酸盐岩储层岩心核磁共振实验研究[J]. 测井技术, 2018, 42(5): 497-502, 529. ZHANG Fengsheng, SUI Xiuying, DUAN Chaowei, et al. NMR experimental study on carbonate reservoirs with high porosity and low permeability[J]. Well logging Technology, 2018, 42(5): 497-502, 529. |
| [24] |
李宁, 王克文, 张宫, 等. 应用CT分析及核磁测井预测碳酸盐岩产气量[J]. 石油勘探与开发, 2015, 42(2): 150-157. LI Ning, WANG Kewen, ZHANG Gong, et al. Prediction of gas production in carbonates based on CT analysis and nuclear magnetic resonance (NMR) logging[J]. Petroleum Exploration and Development, 2015, 42(2): 150-157. |
| [25] |
李雄炎, 秦瑞宝, 毛志强, 等. 高精度胶结指数模型的建立与应用[J]. 石油学报, 2014, 35(1): 76-84. LI Xiongyan, QIN Ruibao, MAO Zhiqiang, et al. Establishment and application of a high-precision cementation exponent model[J]. Acta Petrolei Sinica, 2014, 35(1): 76-84. DOI:10.3969/j.issn.1001-8719.2014.01.012 |
| [26] |
MENDOZA-ROMERO G, PREZ-RESALES C. New relationship between formation resistivity factor and primary and secondary porosities[C]. SPWLA 26th Annual Logging Symposium, Dallas, Texas, 1985, SPWLA-1985-D.
|
| [27] |
PEREZ-ROSALES C. On the relationship between formation resistivity factor and porosity[J]. Society of Petroleum Engineers Journal, 1982, 22(4): 531-536. DOI:10.2118/10546-PA |
| [28] |
PEREZ-ROSALES C. Generalization of the Maxwell equation for formation resistivity factors[J]. Journal of Petroleum Technology, 1976, 28(7): 819-824. DOI:10.2118/5502-PA |
| [29] |
WYLLIE M R J, GREGORY A R. Formation factors of unconsolidated porous media influence of particle shape and effect of cementation[J]. Journal of Petroleum Technology, 1953, 5(4): 103-110. DOI:10.2118/223-G |
| [30] |
COATES G, 肖立志, PRAMMER M. 核磁共振测井原理与应用[M]. 北京: 石油工业出版社, 2007: 50-178. COATES G, XIAO Lizhi, PRAMMER M. Principles and Application of Nuclear Magnetic Resonance Logging[M]. Beijing: Petroleum Industry Press, 2007: 50-178. |



 李雄炎,北京市朝阳区太阳宫南街6号院海油大厦,100028。Email:
李雄炎,北京市朝阳区太阳宫南街6号院海油大厦,100028。Email: 