② 中国石化勘探分公司, 四川成都 610041
② SINOPEC Exploration Branch Co., Chengdu, Sichuan 610041, China
地层压力是油气勘探领域的重要研究内容,无论是对钻井工程还是地质评价,都有十分重要的意义。尤其近年来页岩气勘探开发的实践表明,页岩气产量与压力系数呈正相关关系,高流体压力有利于页岩孔隙的保持,同时降低页岩储层有效应力,有利于压裂改造,因而压力系数的预测及研究对页岩气的成功勘探至关重要[1-4]。
地震预测是实现地层压力钻前预测的有效手段,但其影响因素多,准确预测的难度大。利用地震信息进行压力预测逐步由经验公式法发展到岩石物理方法。早期形成的经验公式主要以“欠压实”理论为核心,基于“正常趋势线”及低速度特征形成了一系列方法,称为传统方法,代表性的有等效深度公式计算法、Eaton法[5]、Fillippone法[6-7]、云美厚法等[8]。基于“正常趋势线”的压力预测方法适用范围小,受构造、剥蚀及岩性变化影响,实际应用中难以准确地建立正常压实趋势线,且带有主观性;以速度—地层孔隙压力的统计特征为基础的压力预测方法预测精度往往较低,主要原因是速度影响因素多,包括岩性、埋深、物性等诸多因素,难以解耦得到速度对压力的影响。Terzaghi[9]提出“有效应力定理”,基于该理论发展了一系列技术方法。影响声波传播速度的因素主要有孔隙度、泥质含量和有效应力[10],基于此一些研究者给出了纵波速度经验模型。樊洪海[11]将该模型改写为适应性更广的形式;Singh等[12]给出了地震波速度与孔隙度、有效应力和泥岩含量的另一更简洁实用的公式;Khazanehdari等[13]总结前人的经验和方法,将各种可利用数据综合起来对地层压力进行预测。这些方法的共同不足是参数多、地震反演难度大。
近年来,针对页岩储层,结合岩石物理特征的研究取得了一些新成果。马霄一等[14]根据三轴压缩实验和纵、横波速度测试,分析了页岩弹性模量、泊松比和纵、横波速度在不同方向、不同围压下的变化。刘财等[15]应用Bacus平均方法将模型从测井尺度粗化至地震尺度,应用各向异性传播矩阵模拟页岩含油储层的地震响应。刘致水等[16]构建了一种新的富有机质岩石横波速度预测方法。Lei等[17]提出一种基于岩石物理模型的弹性模量孔隙压力预测方法,将Eaton法中的正常压实速度替换为体积模量,进一步导出孔隙压力与体积模量的关系从而实现压力预测。巫芙蓉等[18]提出了改进的页岩气地震约束多因素孔隙压力预测方法。
基于岩石物理的方法依赖适用的岩石物理模型,但往往存在一定误差;改进的多因素孔隙压力地震预测方法的影响因素较多,且需大量样本数据,难以推广到其他地区。
页岩气储层富含有机质及有机质孔隙,相比常规储层,其矿物组分及微观结构更复杂。本文结合页岩储层微观结构特征,针对支撑矿物的差异性,建立了一种适用于海相页岩的岩石物理模型;通过计算背景矿物体积模量与饱和流体等效体积模量的差异,建立了地震预测模型,并开展叠前地震反演,实现页岩地层体积模量及压力系数定量预测,结果与实钻井及后验井高度吻合。
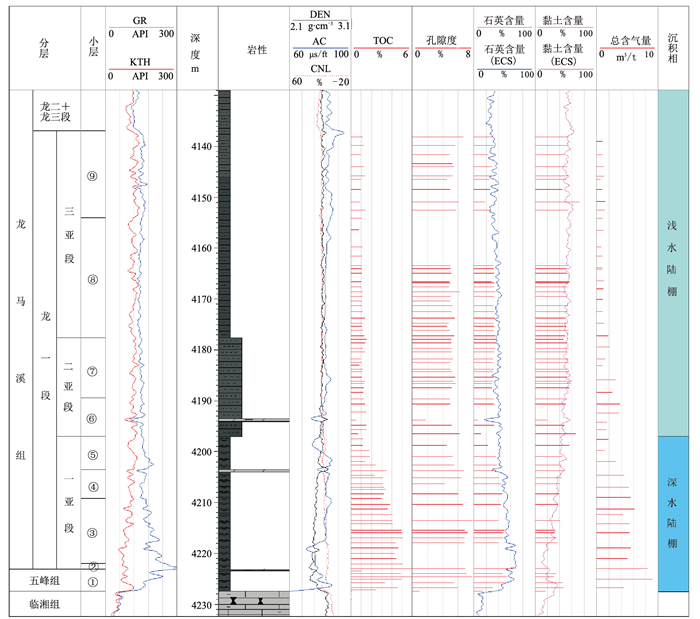
1 岩石物理建模 1.1 页岩储层微观结构及岩石物理特征五峰—龙马溪组海相页岩是目前中国四川盆地页岩气勘探开发的主力层系,本次研究区位于川东南DS-DX区块,DYS1井在该层系获得重大突破,测试获日产31.18万方工业气流。该井页岩气层为五峰—龙马溪组一段,对其开展了详细的化验分析(图 1):纵向上划分为三个亚段和九个小层,由上而下TOC、硅质矿物含量、孔隙度及含气量均具有不断增大的特征。其中五峰—龙马溪组一段一亚段为优质页岩储层(①~⑤号层),即主力开发层段,为深水陆棚沉积,表现为高TOC、高硅质矿物含量、高孔隙度及高含气量特征(表 1);同时电测井曲线上具有显著的高GR、低密度、中声波时差特征。龙马溪组一段二~三亚段(⑥~⑨号层)为较差页岩储层,是浅水陆棚沉积,TOC及含气量相对较低,黏土矿物含量较高;同时电测曲线上具有显著的中GR、相对高密度及高声波时差特征。
|
图 1 DYS1井综合柱状图 测井缩写名称:GR,自然伽马;KTH,无铀伽马;DEN,密度;AC,声波时差;CNL,中子;ECS,元素扫描测井 |
|
|
表 1 DYS1井页岩储层参数(括号内为相应均值) |
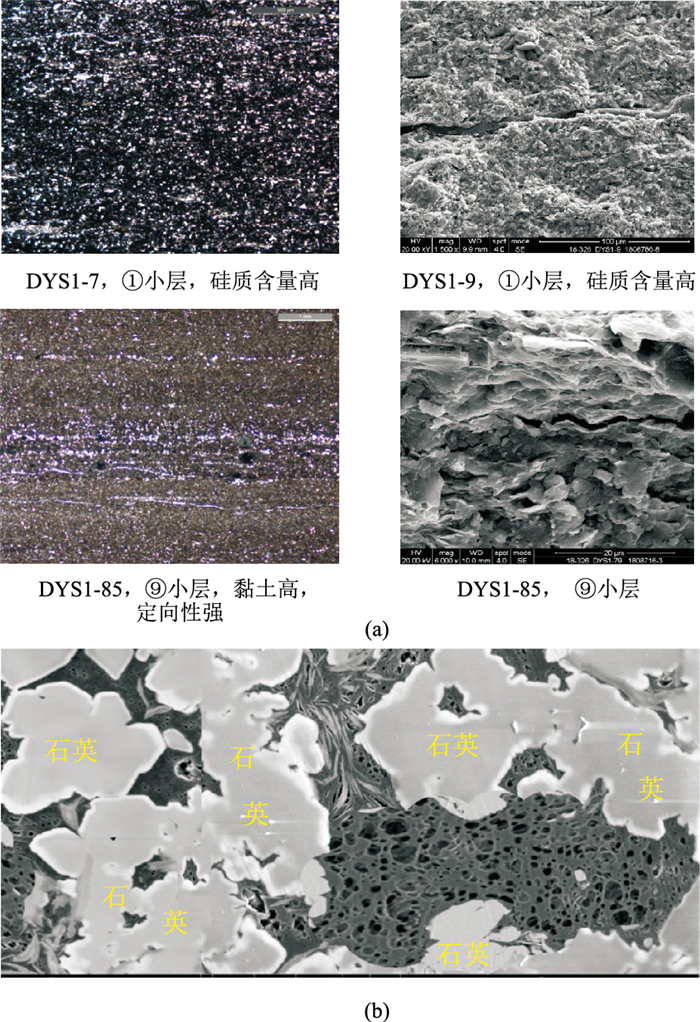
郭旭升等[19]结合涪陵页岩气的勘探实践,明确了深水陆棚页岩具有高TOC、高硅质的“二高”耦合特征,硅质主要为生物化学成因;而浅水陆棚页岩则表现出硅质矿物与黏土矿物混合分布的特征,硅质主要为陆源输入(图 2a),不同小层页岩矿物组分及结构差异显著。相比常规储层,五峰—龙马溪组海相页岩矿物组分及微观结构更复杂,黏土和硅质矿物是岩石的主要矿物,尤其富含有机质,同时发育大量有机质孔隙。
|
图 2 五峰—龙马溪组页岩储层微观照片及硅质格架结构示意(据文献[20]) (a)①、⑨小层页岩扫描电镜照片;(b)页岩氩离子抛光扫描电镜照片 |
郭旭升等[20]通过进一步研究认为,深水陆棚相生物成因的硅质(蛋白石A)在埋藏成岩早期转化成高硬度晶态硅质,伴生形成大量微米级粒间孔隙,而生物成因的硅质格架抗压性强,为早期原油充注及纳米级蜂窝状有机孔隙的发育和保持提供了空间和保护(图 2b),针对该特殊的微观结构特征需开展相应的岩石物理建模研究。
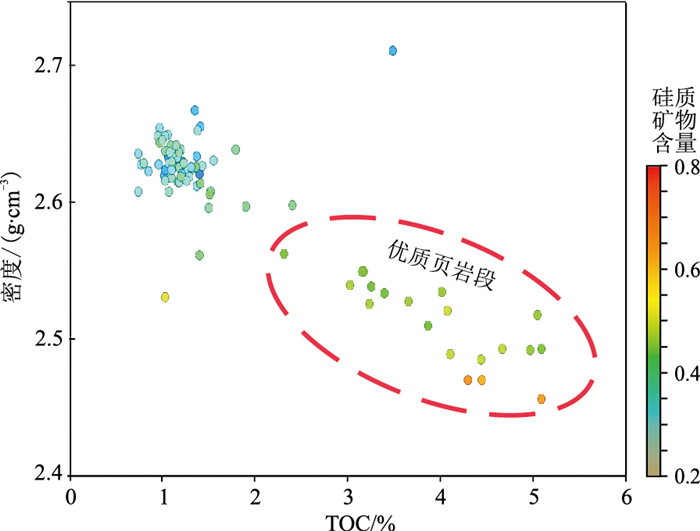
本文基于DYS1井储层分析化验数据及测井速度数据开展研究,对比分析发现优质页岩储层(①~⑤号层)与非优质页岩储层(⑥~⑨号层)差异显著。首先分析了TOC与密度的相关性(图 3):优质页岩段TOC与硅质矿物共生耦合,TOC越高、硅质矿物含量越高,与密度呈现良好的负相关性;而非优质页岩段,其相关性较差。
|
图 3 岩石矿物组分与测井曲线相关分析 |
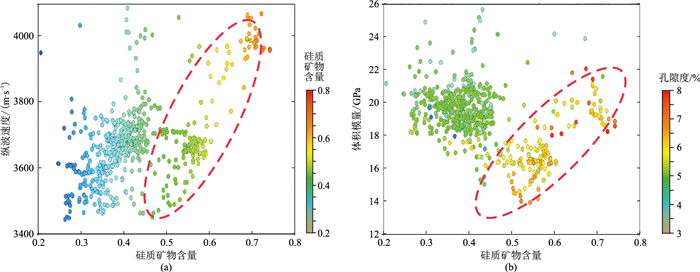
从硅质矿物含量与纵波速度交会分析(图 4a)发现:硅质矿物含量与速度相关性差异显著,优质页岩段为明显的正相关性,表明硅质是速度的主要影响因素;非优质页岩黏土矿物含量高,硅质矿物含量并非速度的主要影响因素。通过体积模量与硅质矿物含量及孔隙度的交会(图 4b)分析发现:优质页岩段硅质矿物含量越高,体积模量越大,正相关较明显,但与孔隙度只略有相关性;而非优质页岩段孔隙度多为黏土矿物间孔及微裂隙,为软孔隙特征,对体积模量影响相对更大。
|
图 4 纵波速度相关分析 (a)硅质矿物含量与纵波速度交会图;(b)体积模量与硅质矿物含量和孔隙度交会图 |
微观结构特征(图 2)研究表明,优质页岩段硅质属生物化学成因,为岩石的骨架矿物,此时较“硬”硅质颗粒作为弹性波传播的载体,造成速度相对较高;同时,格架间在力学性质上具有硬孔隙特征,有机质及黏土为其充填物,孔隙度、TOC及流体可能为次要影响因素。陆源碎屑硅质为主的非优质页岩,以黏土颗粒和硅质矿物等共同作为岩石骨架,较“软”的黏土颗粒及孔隙作为弹性波传播的载体,使得介质速度相对较低;两者微观结构特征的变化决定了速度及模量与硅质含量相关关系的差异性。
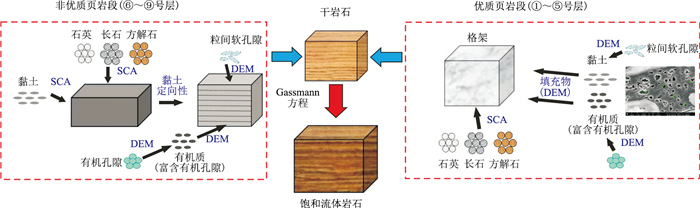
1.2 岩石物理建模技术及流程岩石物理主要研究岩石的力学、弹性、波传播、孔隙结构等特征及其引起的地球物理响应。本文通过分析页岩复杂的矿物成分、储集空间、流体特征等方面对页岩的弹性响应的影响,建立具有针对性的页岩岩石物理模型。基于所构建模型对页岩气储层压力系数的敏感参数进行分析,可为页岩地层压力系数地震预测奠定良好的理论基础。结合储层微观结构及岩石物理特征的认识,形成针对五峰—龙马溪组海相页岩的岩石物理建模流程(图 5)。
|
图 5 海相页岩岩石物理建模流程 |
第一步:针对两种不同成因的硅质矿物及页岩储层发育段,需采用不同的模型得到背景介质等效模量。Berryman[21]给出了N相混合物的自洽(SCA) 模型,适用于多种矿物共同作为岩石骨架,非优质页岩段(⑥~⑨号层)即符合该模型。该模型充分考虑了各组分之间的相互作用,将硅质矿物、黏土矿物、碳酸盐岩矿物及软孔隙共同混合得到背景介质等效模量,公式如下
| ${\sum\limits_{i = 1}^N {{x_i}\left( {{K_i} - {K^*}} \right)P_i^ * = 0} }$ | (1) |
| ${\sum\limits_{i = 1}^N {{x_i}\left( {{\mu _i} - {\mu ^*}} \right)Q_i^ * = 0} }$ | (2) |
式中:xi指第i种矿物体积分数,本文选取石英、长石、方解石、白云石和黄铁矿等主要矿物,即N=5;Ki、μi分别为第i种矿物的体积模量和剪切模量;K*、μ*分别为等效体积模量和剪切模量;Pi*和Qi*是第i种矿物的模量和形状相关的几何因子。该两式是耦合的,须通过同时迭代的方法求解。
微分等效介质模型(DEM)通过向一种固体相中逐步递增地加入另一种充填物,直至完全加入的过程来模拟双相混合物。优质页岩段(①~⑤号层)硅质矿物为骨架矿物,需采用DEM模型,通过向主相固体矿物中逐渐加入充填物模拟混合物,其中充填物主要为有机质及黏土。具体方程如下
| ${\left( {1 - y} \right)\frac{{\rm{d}}}{{{\rm{d}}y}}\left[ {{K^*}\left( y \right)} \right] = \left( {{K_2} - {K^*}} \right)P_2^ * \left( y \right)}$ | (3) |
| ${\left( {1 - y} \right)\frac{{\rm{d}}}{{{\rm{d}}y}}\left[ {{\mu ^*}\left( y \right)} \right] = \left( {{\mu _2} - {\mu ^*}} \right)Q_2^ * \left( y \right)}$ | (4) |
该公式初始条件为K*(0)=K1、μ*(0)=μ1。式中:K1、K2、K*分别表示岩石主相矿物、充填物和DEM模型计算的等效介质的体积模量;μ1、μ2、μ*分别表示相应的剪切模量;y表示充填物的体积分数。
建模过程中通过获得总有机质含量、成烃生物构成及其有机孔隙的发育程度(面孔率),综合可得页岩有机孔隙占比[22]。其他关键点如下:①将有机质孔隙以DEM模型加入有机质中,无机孔隙为典型软孔隙以DEM模型加入黏土矿物中,分别形成等效模量;②针对优质页岩段,等效有机质(含有机孔隙)和等效黏土矿物(含无机孔隙)作为充填物,再利用DEM模型,加入到背景介质中;③针对非优质页岩段,黏土作为主要矿物之一,利用SCA模型与硅质矿物及碳酸盐岩矿物等形成背景模量,然后添加有机质和无机孔隙。
第二步:页岩地层广泛存在各向异性特征,导致各向异性的主要成因是黏土矿物的定向排列及发育的裂缝等。其中黏土矿物的水平层状定向排列是导致强VTI各向异性的主因。利用各向异性SCA-DEM模型向上述等效岩石中添加黏土矿物(横纵比为0.5),计算得到等效各向异性介质刚度张量
| $\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{C}}_{{\rm{VTI}}}} = \sum\limits_{i = 1}^N {{x_i}{\mathit{\boldsymbol{C}}_i}{{\left[ {\mathit{\boldsymbol{I}} + \mathit{\boldsymbol{\hat G}}\left( {{\mathit{\boldsymbol{C}}_i} - {\mathit{\boldsymbol{C}}_{{\rm{VTI}}}}} \right)} \right]}^{ - 1}} \times } }\\ {\;\;\;\;\;\;\;\;{{\left\{ {\sum\limits_{i = 1}^N {} {x_i}{{\left[ {{\rm{I}} + \mathit{\boldsymbol{\hat G}}\left( {{\mathit{\boldsymbol{C}}_i} - {\mathit{\boldsymbol{C}}_{{\rm{VTI}}}}} \right)} \right]}^{ - 1}}} \right\}}^{ - 1}}} \end{array}$ | (5) |
式中:I是单位张量;Ci是第i种矿物成分的刚度张量;
第三步:由于页岩的致密性及孔隙的非连通性,饱和流体具有高频非弛豫特征,将Gassmann方程应用于预测饱和岩石的弹性模量,表达式为
| $K_{{\rm{sat}}}^ * = K_{{\rm{dry}}}^ * + \frac{{{{\left( {1 - \frac{{K_{{\rm{dry}}}^ * }}{{K_{\rm{m}}^ * }}} \right)}^2}}}{{\left( {\frac{\phi }{{{K_{{\rm{fl}}}}}} + \frac{{1 - \phi }}{{K_{\rm{m}}^ * }} - \frac{{K_{{\rm{dry}}}^ * }}{{K_{\rm{m}}^{ * \;2}}}} \right)}}K_{{\rm{dry}}}^ * $ | (6) |
| ${\mu _{{\rm{sat}}}^ * = \mu _{{\rm{dry}}}^ * }$ | (7) |
式中:Ksat*、μsat*分别为饱和岩石的等效体积、剪切模量;Kdry*、μdry*分别为干岩石骨架的相应模量;Km*、Kfl分别为基质和流体的体积模量;ϕ为孔隙度。
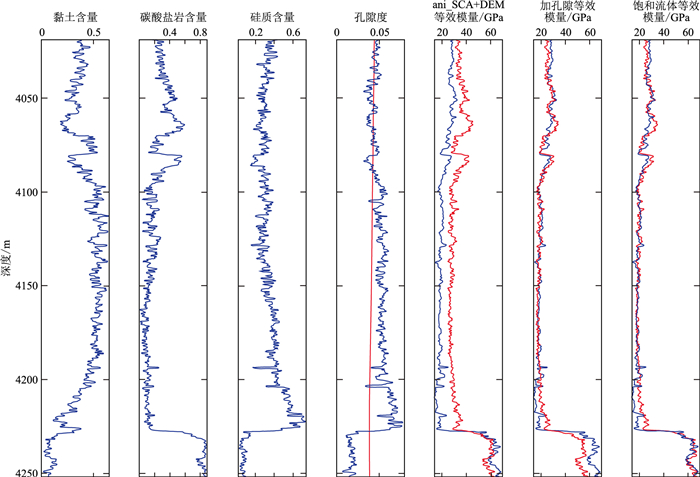
基于ECS元素测井可获取黏土矿物、硅质矿物及碳酸盐岩矿物的含量,在利用总孔隙度及有机孔隙体积比,将这些关键曲线加入建模流程,完成了DYS1井的等效模量计算(图 6)。可见通过每一步计算的等效体积模量(蓝线),最后得到的饱和流体等效体积模量与实测曲线(红色)吻合度较好。
|
图 6 DYS1井岩石物理建模及等效体积模量 |
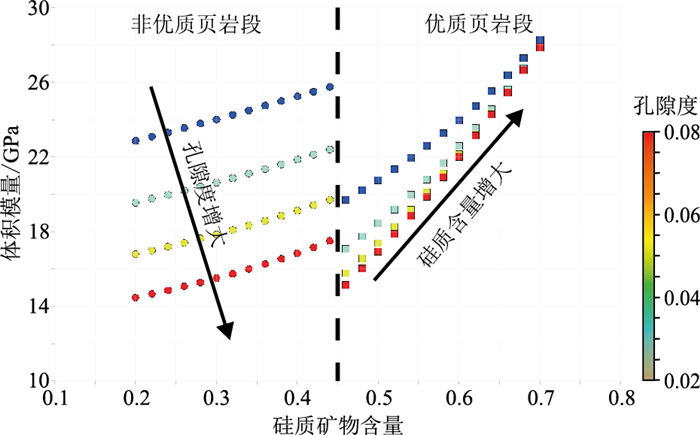
利用该岩石物理模型,构建了体积模量随硅质矿物含量及孔隙度变化的岩石物理量板(图 7)。图中相关关系差异显著,优质页岩段体积模量与硅质矿物含量呈明显的正相关关系,且随着孔隙度增大,体积模量略有降低;非优质页岩段体积模量主要随孔隙度的增大而降低,与硅质矿物含量略有相关性。该量板反映的规律与图 4b实测曲线结果基本一致,与背景骨架矿物及孔隙结构的差异认识一致。而优质页岩由于硅质矿物含量较大,对体积模量有显著影响,因而压力等甜点参数的地震预测中需结合该影响因素加以分析。
|
图 7 岩石物理量板 |
本文基于岩石物理模型,直接根据体积模量分析其对压力系数的影响。利用文中提到的岩石物理建模方法,计算多种矿物组合背景介质等效体积模量Km*(图 6中曲线ani_SCA+DEM),该模量不受孔隙、流体及压力的影响;然后加载孔隙及流体,计算得到饱和流体等效体积模量Ksat*,同时定义Km*与Ksat*之差为扰动体积模量
| $\Delta K = K_{\rm{m}}^ * - K_{{\rm{sat}}}^ * $ | (8) |
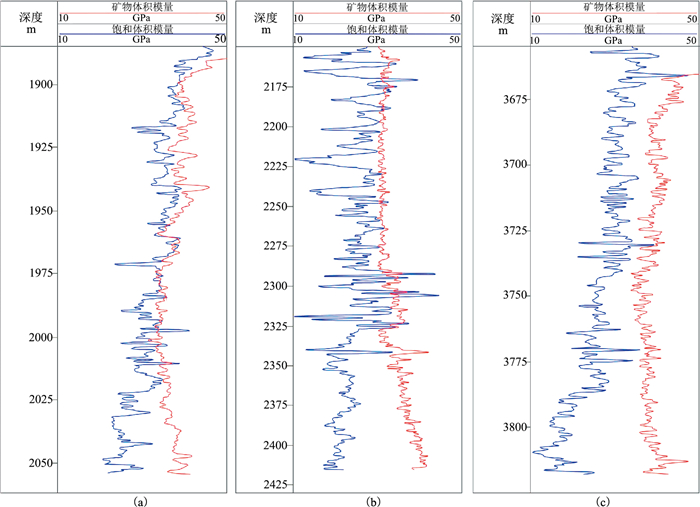
利用工区内多口井进一步测试该岩石物理模型。对比DY1(图 8a)、JY1(图 8b)、DY5(图 8c)三口井饱和流体等效体积模量Ksat*(蓝线)与背景介质等效体积模量Km*(红线),其中DY1井五峰—龙马溪组压力系数为0.98,为常压页岩气钻井,JY1井和DY5井压力系数分别为1.45和1.55,为高压页岩气钻井。可见随着压力系数增加,背景介质体积模量与饱和流体体积模量之间的差异(扰动体积模量)逐渐增加,表明可通过从饱和流体体积模量中消除岩性变化对等效模量的影响,进一步提取地层孔隙压力的响应特征。
|
图 8 川东南地区钻井饱和流体体积模量(蓝线)与背景介质体积模量(红线)对比 (a)DY1井(常压,压力系数为0.98);(b)JY1井(高压,压力系数为1.45);(c)DY5井(高压,压力系数为1.55) |
对研究区更多实钻井资料开展压力系数与扰动体积模量交会分析(图 9)。选取分布于川东南探区不同区块的12口典型井做拟合,同时利用位于不同区块的两口常压(焦石坝的JY5及白马的JY6井)及两口高压页岩气井(平桥的JY8及东溪的DYS3井)作为验证井。从交会结果可见,实钻井压力系数与扰动体积模量呈对数正相关关系,相关系数达0.9,验证井预测相对误差小于10%,表明压力系数预测模型颇具普适性。由此可建立该区基于扰动体积模量的压力系数预测模型
| ${P_{\rm{c}}} = a \times \ln \Delta K + b$ | (9) |

|
图 9 川东南地区多口井扰动体积模量与压力系数交会图 |
式中:Pc为压力系数;a、b为回归系数,可由交会图拟合得到。
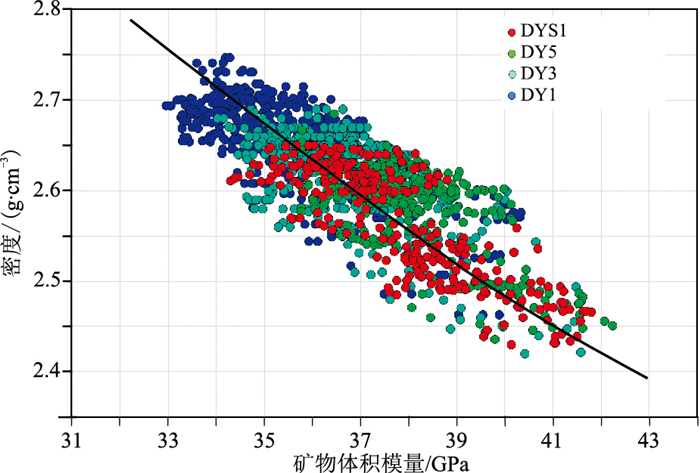
饱和流体等效体积模量Ksat*与背景介质等效体积模量Km*是压力预测的关键参数,叠前AVO反演是实现等效体积模量Ksat*地震反演的有效手段。通过区内多口井密度与背景介质体积模量交会分析(图 10)可知,两者呈现良好的负相关关系,据此建立Km*的地震预测模型
| $K_{\rm{m}}^ * = a\rho + b$ | (10) |
|
图 10 研究区多口井密度与背景介质矿物体积模量交会图 |
式中ρ为密度。
3 地震反演及预测 3.1 反演方法通过叠前AVO反演技术可实现饱和流体体积模量的预测,基于Zoeppritz方程或其近似式的AVO反演结果稳定、分辨率高,人们还针对不同介质类型做了大量研究。
Gray等[23]将Aki-Richards近似式写成用ΔK/K、Δμ/μ及Δρ/ρ形式的表达式
| $\begin{array}{*{20}{l}} {{R_{{\rm{pp}}}}\left( \theta \right) = \left( {\frac{1}{4} - \frac{{{\beta ^2}}}{{3{\alpha ^2}}}} \right){\rm{se}}{{\rm{c}}^2}\theta \frac{{\Delta K}}{K} + }\\ {\;\;\;\;\;\;\;\;\;\;\;\;\frac{{{\beta ^2}}}{{{\alpha ^2}}}\left( {\frac{1}{3}{\rm{se}}{{\rm{c}}^2}\theta - 2{{\sin }^2}\theta } \right)\frac{{\Delta \mu }}{\mu } + }\\ {\;\;\;\;\;\;\;\;\;\;\;\;\left( {\frac{1}{2} - \frac{1}{4}{\rm{se}}{{\rm{c}}^2}\theta } \right)\frac{{\Delta \rho }}{\rho }} \end{array}$ | (11) |
式中:RPP(θ)为反射系数,其中θ为入射角;α为纵波速度;β为横波速度。
Connolly[24]将叠后方法应用于叠前数据,并从Aki-Richards近似公式导出弹性阻抗公式,将AVO界面信息转化为层内信息。由于弹性阻抗与常规声阻抗在量纲和数量级上有很大差别,Whitcombe等[25]又做了标准化处理。借用Connolly及Whitcombe等的思路,提出了基于Gray近似的弹性阻抗公式
| ${\rm{EI}}\left( \theta \right) = {A_0}{\left( {\frac{K}{{{K_0}}}} \right)^{a(\theta )}}{\left( {\frac{\mu }{{{\mu _0}}}} \right)^{b(\theta )}}{\left( {\frac{\rho }{{{\rho _0}}}} \right)^{c(\theta )}}$ | (12) |
式中:K0、μ0、ρ0分别为平均体积模量、平均剪切模量、平均密度;A0为标准化参数。且有
| $ \begin{array}{*{20}{l}} {{A_0} = {{\left( {6{K_0}{\mu _0}{\rho _0}} \right)}^{\frac{1}{4}}}}\\ {a\left( \theta \right) = \left( {\frac{1}{2} - \frac{2}{3}\frac{{{\beta ^2}}}{{{\alpha ^2}}}} \right){\rm{se}}{{\rm{c}}^2}\theta }\\ {b\left( \theta \right) = \frac{{{\beta ^2}}}{{{\alpha ^2}}}\left( {\frac{2}{3}{\rm{se}}{{\rm{c}}^2}\theta - 4{{\sin }^2}\theta } \right)}\\ {c\left( \theta \right) = 1 - \frac{1}{2}{\rm{se}}{{\rm{c}}^2}\theta } \end{array} $ |
因为式(12)是非线性的,直接求解方程难度较大。对式(12)两边同时求对数,并做线性化处理,进而基于Gray公式的弹性阻抗方程可提取体积模量、剪切模量和密度。即先做弹性阻抗反演,再联立三个角度(θ1、θ2、θ3)的弹性阻抗形成方程组,并通过阻尼最小二乘算法求解弹性矩阵,提取弹性参数
| $\left\{ {\begin{array}{*{20}{l}} {\ln \frac{{{\rm{EI}}\left( {{\theta _1}} \right)}}{{{A_0}}} = a\left( {{\theta _1}} \right)\ln \frac{K}{{{K_0}}} + b\left( {{\theta _1}} \right)\ln \frac{\mu }{{{\mu _0}}} + c\left( {{\theta _1}} \right)\ln \frac{\rho }{{{\rho _0}}}}\\ {\ln \frac{{{\rm{EI}}\left( {{\theta _2}} \right)}}{{{A_0}}} = a\left( {{\theta _2}} \right)\ln \frac{K}{{{K_0}}} + b\left( {{\theta _2}} \right)\ln \frac{\mu }{{{\mu _0}}} + c\left( {{\theta _2}} \right)\ln \frac{\rho }{{{\rho _0}}}}\\ {\ln \frac{{{\rm{EI}}\left( {{\theta _3}} \right)}}{{{A_0}}} = a\left( {{\theta _3}} \right)\ln \frac{K}{{{K_0}}} + b\left( {{\theta _3}} \right)\ln \frac{\mu }{{{\mu _0}}} + c\left( {{\theta _3}} \right)\ln \frac{\rho }{{{\rho _0}}}} \end{array}} \right.$ | (13) |
研究区具有良好的数据基础,区内共有6口探井,压力系数分布于1.0~1.8。开展OVT处理后叠前地震道集近炮检距和远炮检距的能量得到明显补偿,AVO信息保真性更好。将优化预处理后的叠前道集做分角度叠加,同时进行井震标定并提取不同角度叠加数据体的子波,结合井旁道测井计算结果,以地震解释层位为横向约束建立低频模型,将分角度叠加数据体、子波、低频模型作为数据输入,开展不同角度弹性阻抗反演。
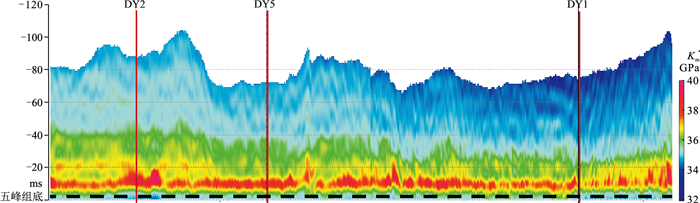
在不同角度弹性阻抗反演基础上,利用式(13)通过阻尼最小二乘算法求解弹性矩阵,提取体积模量、剪切模量及密度等参数。基于密度反演结果和式(10),实现背景介质等效体积模量的地震预测(图 11),从所得剖面可见纵向上自上而下脆性矿物增加,底部优质页岩段背景介质体积模量最大。
|
图 11 矿物体积模量反演剖面 |
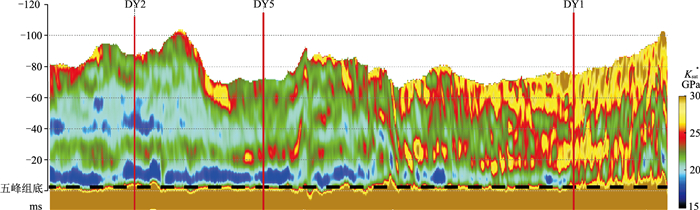
基于公式(13)实现了饱和流体体积模量的直接反演,减小了通过常规AVO反演纵波速度、横波速度及密度再计算体积模量的累计误差;同时利用了弹性阻抗反演稳定的特征,进一步提高了预测精度。图 12为饱和流体体积模量Ksat*反演结果,由DY1井到DY2井方向地层埋深逐渐增加,目的层优质页岩段的饱和流体体积模量呈明显减小趋势。
|
图 12 饱和流体体积模量反演剖面 |
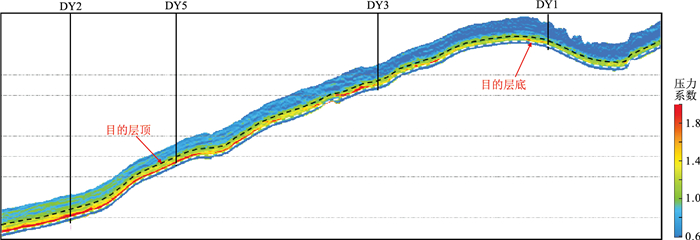
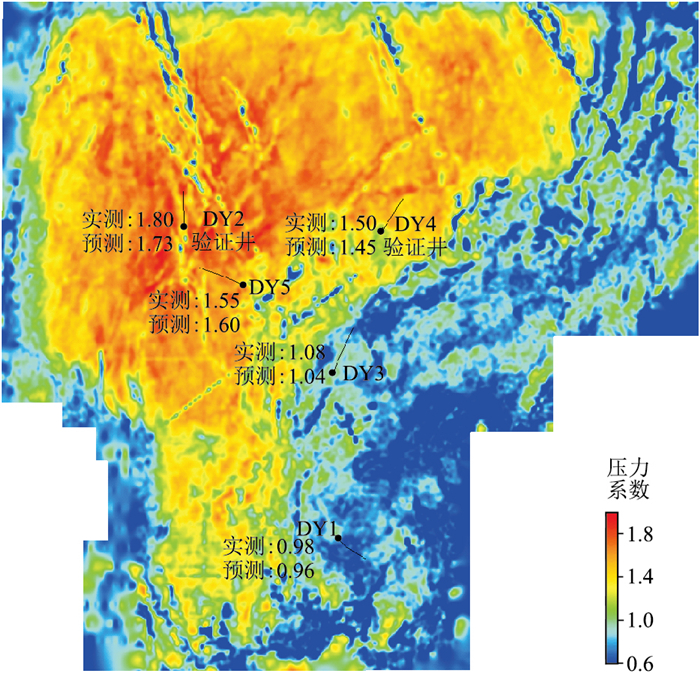
利用反演得到的Ksat*与Km*计算ΔK,并将其代入式(9),即可实现基于ΔK的压力系数地震预测。图 13为最终压力系数预测过井剖面,图 14为目的层压力系数预测平面图。由图可见本文方法压力预测结果与钻井实测结果基本一致,相对误差整体小于5%,其中未参与建模的验证井DY2井及DY4井预测相对误差均小于4%,可见基于扰动体积模量的压力系数地震预测方法具有较好的应用效果。
|
图 13 基于扰动体积模量的压力系数预测剖面图 |
|
图 14 研究区目的层压力系数预测平面图 |
本文针对四川盆地五峰—龙马溪组海相页岩,构建了一种适用的岩石物理模型及相应页岩地层压力系数预测技术,获得以下认识和结论。
(1) 优质页岩段硅质属生物化学成因,为岩石的骨架矿物,此时较“硬”硅质颗粒作为弹性波传播的载体,同时格架间在力学性质上具有硬孔隙特征;非优质页岩以黏土颗粒和硅质矿物等共同作为岩石骨架,较“软”的黏土颗粒及孔隙作为弹性波传播的载体。
(2) 支撑矿物及微观结构有明显差异,需分别采用SCA和DEM模型计算背景介质等效模量。结合岩石物理模型,发现背景介质体积模量及饱和流体等效岩石体积模量的差异与实钻井压力系数具有良好正相关关系,据此建立的压力系数预测模型精度较高。
(3) 推导建立了基于Gray近似的弹性阻抗体积模量直接反演方法,实现了页岩地层体积模量及压力系数的定量预测;经实际数据试验,预测结果与实钻井及后验井吻合度高。
| [1] |
郭旭升. 南方海相页岩气"二元富集"规律——四川盆地及周缘龙马溪组页岩气勘探实践认识[J]. 地质学报, 2014, 88(7): 1209-1218. GUO Xusheng. Rules of Two-factor enrichiment for marine shale gas in southern China-understanding from the Longmaxi formation shale gas in Sichuan basin and its surrounding area[J]. Acta Geologica Sinica, 2014, 88(7): 1209-1218. |
| [2] |
郭旭升, 胡东风, 黄仁春, 等. 四川盆地深层—超深层天然气勘探进展与展望[J]. 天然气工业, 2020, 40(5): 1-14. GUO Xusheng, HU Dongfeng, HUANG Renchun, et al. Deep and ultra-deep natural gas exploration in the Sichuan Basin: progress and prospect[J]. Natural Gas Industry, 2020, 40(5): 1-14. |
| [3] |
何治亮, 聂海宽, 胡东风, 等. 深层页岩气有效开发中的地质问题——以四川盆地及其周缘五峰组—龙马溪组为例[J]. 石油学报, 2020, 41(4): 379-391. HE Zhiliang, NIE Haikuan, HU Dongfeng, et al. Geological problems in the effective development of deep shale gas: a case study of Upper Ordovician Wufeng-Lower Silurian Longmaxi formations in Sichuan basin and its periphery[J]. Acta Petrolei Sinica, 2020, 41(4): 379-391. |
| [4] |
黄仁春, 魏祥峰, 王强. 四川盆地东南缘丁山地区页岩气成藏富集的关键控制因素[J]. 海相油气地质, 2017, 22(2): 25-30. HUANG Renchun, WEI Xiangfeng, WANG Qiang. Key factors of shale gas accumulation in Dingshan area of southeastern Sichuan basin[J]. Marine Origin Petroleum Geology, 2017, 22(2): 25-30. |
| [5] |
EATON B A. The equation for geopressure prediction from well logs[C]. Fall Meeting of the Society of Petroleum Engineers of AIME, Dallas, Texas, 1975, SPE-5544-MS.
|
| [6] |
EBERHART-PHILLIPS D, HAN D H, ZOBACK M D. Empirical relationships among seismic velocity, effective pressure, porosity, and clay content in sandstone[J]. Geophysics, 1989, 54(1): 82-89. DOI:10.1190/1.1442580 |
| [7] |
FILLIPPONE W R. Estimation of formation parameters and the prediction of overpressures from seismic data[C]. SEG Technical Program Expanded Abstracts, 1982, 1: 502-503.
|
| [8] |
云美厚. 地震地层压力预测[J]. 石油地球物理勘探, 1996, 31(4): 575-586. YUN Meihou. Formation pressure prediction using seismic data[J]. Oil Geophysical Prospecting, 1996, 31(4): 575-586. DOI:10.3321/j.issn:1000-7210.1996.04.017 |
| [9] |
TERZAGHI K. Theoretical Soil Mechanics[M]. New York: J.Wiley and Sons, Inc, 1943.
|
| [10] |
HAN D H, NUR A, MORGAN D. Effects of porosity and clay content on wave velocities in sandstones[J]. Geophysics, 1986, 51(11): 2093-2107. DOI:10.1190/1.1442062 |
| [11] |
樊洪海. 异常地层压力分析方法与应用[M]. 北京: 科学出版社, 2016. FAN Honghai. Analysis methods and applications of abnormal formation pressures[M]. Beijing: Science Press, 2016. |
| [12] |
SINGH R, RAI C, SONDERGELD C. Pressure depen-dence of elastic wave velocities in sandstones[C]. SEG Technical Program Expanded Abstracts, 2006, 25: 1883-1887.
|
| [13] |
KHAZANEHDARI J, DUTTA N. High-resolution pore pressure prediction using seismic inversion and velocity analysis[C]. SEG Technical Program Expanded Abstracts, 2006, 25: 1540-1544.
|
| [14] |
马霄一, 李呈呈, 白俊, 等. 基于超声测试的页岩岩石物理特征分析[J]. 石油地球物理勘探, 2021, 56(4): 801-808. MA Xiaoyi, LI Chengcheng, BAI Jun, et al. Analysis of physical characteristics of shale rock based on ultrasonic testing[J]. Oil Geophysical Prospecting, 2021, 56(4): 801-808. |
| [15] |
刘财, 邓馨卉, 郭智奇, 等. 基于岩石物理的页岩储层各向异性表征[J]. 石油地球物理勘探, 2018, 53(2): 339-346. LIU Cai, DENG Xinhui, GUO Zhiqi, et al. Shale reservoir anisotropic characterization based on rock physics[J]. Oil Geophysical Prospecting, 2018, 53(2): 339-346. |
| [16] |
刘致水, 刘俊州, 董宁, 等. 富有机质岩石横波速度预测方法[J]. 石油地球物理勘探, 2021, 56(1): 127-136, 154. LIU Zhishui, LIU Junzhou, DONG Ning, et al. Investigation to shear-wave velocity prediction method for organic-rich rock[J]. Oil Geophysical Prospecting, 2021, 56(1): 127-136, 154. |
| [17] |
LEI T, YIN X Y, ZONG Z Y. Pore pressure prediction in orthotropic medium based on rock physics modeling of shale gas[J]. Journal of Natural Gas Science and Engineering, 2020, 74: 103091. |
| [18] |
巫芙蓉, 周诗雨, 邓小江, 等. 一种改进的页岩气地震约束多因素孔隙压力预测方法[J]. 天然气工业, 2021, 41(1): 198-204. WU Furong, ZHOU Shiyu, DENG Xiaojiang, et al. An improved seismic-constrained multi-factor pore pressure prediction method for shale gas reservoirs[J]. Natural Gas Industry, 2021, 41(1): 198-204. |
| [19] |
郭旭升, 胡东风, 李宇平, 等. 涪陵页岩气田富集高产主控地质因素[J]. 石油勘探与开发, 2017, 44(4): 481-491. GUO Xusheng, HU Dongfeng, LI Yuping, et al. Geological factors controlling shale gas enrichment and high production in Fuling shale gas field[J]. Petro-leum Exploration and Development, 2017, 44(4): 481-491. |
| [20] |
郭旭升, 李宇平, 腾格尔, 等. 四川盆地五峰组—龙马溪组深水陆棚相页岩生储机理探讨[J]. 石油勘探与开发, 2020, 47(1): 193-201. GUO Xusheng, LI Yuping, BORJIGEN Tenger, et al. Hydrocarbon generation and storage mechanisms of deep-water shelf shales of Ordovician Wufeng Formation-Silurian Longmaxi Formation in Sichuan Basin, China[J]. Petroleum Exploration and Development, 2020, 47(1): 193-201. |
| [21] |
BERRYMAN J G. Long-wavelength propagation in composite elastic media Ⅰ.spherical inclusions[J]. The Journal of the Acoustical Society of America, 1980, 68(6): 1809-1819. |
| [22] |
张光荣, 聂海宽, 唐玄, 等. 基于有机孔和生物成因硅优选页岩气富集高产层段的方法及应用——以四川盆地及其周缘五峰组—龙马溪组页岩为例[J]. 天然气地球科学, 2021, 32(6): 888-898. ZHANG Guangrong, NIE Haikuan, TANG Xuan, et al. Optimization method and application of shale gas enrichment layer based on biogenic silica and organic matter pore: case study of Wufeng-Longmaxi formations shale in the Sichuan basin and its periphery[J]. Natural Gas Geoscience, 2021, 32(6): 888-898. |
| [23] |
GRAY D, GOODWAY B, CHEN T W. Bridging the gap: using AVO to detect changes in fundamental elastic constants[C]. SEG Technical Program Expanded Abstracts, 1999, 18: 852-855.
|
| [24] |
CONNOLLY P. Elastic impedance[J]. The Leading Edge, 1999, 18(4): 438-452. |
| [25] |
WHITCOMBE D N. Elastic impedance normalization[J]. Geophysics, 2002, 67(1): 60-62. |



 陈超,四川省成都市高新区吉泰路688号中国石化西南科研办公基地,610041。Email:
陈超,四川省成都市高新区吉泰路688号中国石化西南科研办公基地,610041。Email: