② 海洋国家实验室海洋矿产资源评价与探测技术功能实验室, 山东青岛 266071
② Laboratory for Marine Mineral Resources, Qingdao National Laboratory for Marine Science and Technology, Qingdao, Shandong 266071, China
近年来,油气勘探的目标储层日趋复杂,勘探难度逐步增加,复杂(岩性)油气藏渐渐成为研究与开发的重点。煤系地层在中国分布范围广阔[1],包括沁水盆地、鄂尔多斯盆地、四川盆地、东海盆地等,是油气勘探的重要领域[2-4]。煤系烃源岩生烃潜力大。根据源岩有机碳含量从高到低顺序将其划分为煤岩、碳质泥岩和暗色泥岩等类型[5-6]。煤成气理论拓展了中国油气勘探的领域,且促进了天然气工业的大发展。根据地质资料可知,煤系地层中的煤层一般具有层数多、厚度薄、横向分布广、垂向分布散等特点[7],为储层预测带来了极大挑战。煤层相较于常规的砂、泥岩,在测井响应上具有低密度、高声波时差和高中子值等特征[8]。目前针对煤系地层岩石物理性质的研究相对较少,无法有效地阐述地层弹性参数与物性参数之间的关系。
地层物性参数是描述地下介质的重要信息,通过地震岩石物理建模可有效地将物性信息过渡到岩石的弹性特征,使得地层物理性质在地震响应中有所体现。岩石的性质主要受矿物组分、体积占比、排列方式、孔隙度、孔隙几何形状、流体分布及周围环境等因素影响[9]。当地震波长足够大时,地下岩石可视为均匀物体,就能利用等效介质理论和孔隙弹性理论构建地震岩石物理模型,量化物性参数与弹性参数之间的关系。在岩石物理建模方面,人们针对矿物岩性、孔隙结构、流体性质等做了大量研究[10-13],分析了物性参数对弹性性质的影响。经典的Xu-White模型将石英和黏土作为碎屑岩的背景矿物,并综合考虑了孔隙和流体的影响[14],得到了广泛应用。在Xu-White模型基础上,改变背景矿物并将孔隙类型替换为裂缝、粒间孔和溶洞,可构建适用于碳酸盐岩地层的岩石物理模型[15]。随着页岩气的大力开发,众多学者聚焦于页岩的物理性质研究[16-18],充分考虑干酪根等有机物的形态与孔隙特点,计算岩石的等效模量。在实际应用中,常缺少横波测井资料,利用岩石物理模型计算横波速度等弹性参数已经是一种常用手段[19-21]。此外,从岩石物理角度,建立物性参数与地震响应之间的联系,可为储层预测奠定基础[22-25]。因此,针对煤系地层的岩石物理模型构建及其性质研究对油气储层的有效开发具有重要意义。
本文充分考虑地层含煤对地震弹性参数的影响,基于VRH平均模型[26]、K-T骨架模型[27-28]、SCA模型[29-30]和Gassmann方程[31],构建了一种煤系地层的地震岩石物理模型。在煤系地层等效介质基础上,进一步计算多种岩石弹性参数,分析多种微观物性参数变化对不同弹性参数的影响,得到区分不同岩性的敏感参数。最后,在测井资料反演约束下构建目标泛函,形成一种煤系地层岩石弹性参数非线性计算方法。利用该方法求得的横波速度的(预测)误差较小且呈正态分布,在煤层处与实测横波速度吻合度较高,表明煤系地层地震岩石物理模型构建的有效性。
1 岩石物理建模根据煤系地层地质特点和相关背景,构建了考虑煤层影响的油气储层地震岩石物理模型,具体过程分为四个部分,依次为背景岩石基质构建、孔隙填充、煤层耦合、流体替换(图 1)。

|
图 1 煤系地层岩石物理模型构建示意图 |
首先利用VRH平均模型将石英、黏土等背景矿物按照各成分体积含量进行混合,VRH模型[26]是通过求取等应力平均与等应变平均的均值来表征矿物基质的等效岩石模量,具体表达式为
| $ K_{\mathrm{m}} =\frac{\sum\limits_{i=1}^{N} f_{i} K_{i}+\left(\sum\limits_{i=1}^{N} \frac{f_{i}}{K_{i}}\right)^{-1}}{2} $ | (1) |
| $ \mu_{\mathrm{m}} =\frac{\sum\limits_{i=1}^{N} f_{i} \mu_{i}+\left(\sum\limits_{i=1}^{N} \frac{f_{i}}{\mu_{i}}\right)^{-1}}{2} $ | (2) |
式中:Km、μm分别为混合后的矿物基质体积模量和剪切模量;fi、Ki、μi分别为第i种矿物组分的体积含量、体积模量以及剪切模量;N为不同矿物类型的数目。
1.2 孔隙填充K-T模型[27-28]基于散射理论,可得到矿物基质包含不同形状孔隙时的骨架等效模量
| $ \left(K_{\mathrm{KT}}-K_{\mathrm{m}}\right) \frac{K_{\mathrm{m}}+\frac{4 \mu_{\mathrm{m}}}{3}}{K_{\mathrm{KT}}+\frac{4 \mu_{\mathrm{m}}}{3}}=\sum\limits_{i=1}^{N} x_{i}\left(K_{i}-K_{\mathrm{m}}\right) P_{\mathrm{m} i} $ | (3) |
| $ \left(\mu_{\mathrm{KT}}-\mu_{\mathrm{m}}\right) \frac{\mu_{\mathrm{m}}+\zeta_{\mathrm{m}}}{\mu_{\mathrm{KT}}+\zeta_{\mathrm{m}}}=\sum\limits_{i=1}^{N} x_{i}\left(\mu_{i}-\mu_{\mathrm{m}}\right) Q_{\mathrm{m} i} $ | (4) |
| $ \zeta_{\mathrm{m}}=\frac{\mu_{\mathrm{m}}}{6} \frac{8 \mu_{\mathrm{m}}+9 K_{\mathrm{m}}}{2 \mu_{\mathrm{m}}+K_{\mathrm{m}}} $ | (5) |
式中:KKT、μKT分别为加入孔隙后的岩石骨架等效体积模量和剪切模量;xi为不同孔隙所占的体积分量,若为干燥孔隙,则Ki=μi=0,若为流体饱和,则μi=0;Pmi、Qmi反映的是不同形状的孔隙对矿物基质的作用。
K-T模型仅适用于较低孔隙度的岩石模量估算,常与微分等效介质模型结合使用。Keys等[32]对此模型进行改进,假定骨架的泊松比为常数,推导出岩石骨架等效体积模量和剪切模量表达式
| $ K(\phi)=K_{\mathrm{m}}(1-\phi)^{p} $ | (6) |
| $ \mu(\phi)=\mu_{\mathrm{m}}(1-\phi)^{q} $ | (7) |
式中:K(ϕ)、μ(ϕ)分别代表加入孔隙后的骨架体积模量和剪切模量;ϕ表示孔隙度;p、q为几何因子,与背景介质和孔隙形状相关。
1.3 煤层耦合SCA模型[29-30]是计算多相混合物介质模量的有效模型,向骨架中以包含物形式加入煤层(图 2),通过调整背景介质参数计算耦合煤后的岩石剪切模量和体积模量,具体表达如下
| $ \sum\limits_{i=1}^{N} f_{i}\left(K_{i}-K_{\mathrm{d}}\right) P_{i}^{*}=0 $ | (8) |
| $ \sum\limits_{i=1}^{N} f_{i}\left(\mu_{i}-\mu_{\mathrm{d}}\right) Q_{i}^{*}=0 $ | (9) |

|
图 2 煤层耦合示意图 |
式中:fi在此处特指背景骨架或煤的体积含量;Kd、μd是加入煤层后的干岩石模量;Pi*和Qi*是与(包含)煤的形状、性质以及骨架背景有关的几何因数,当煤的形状不同时,Pi*和Qi*的表达式也会相应改变。上述两式均为耦合的,需利用迭代方式求解。
在建模过程中,煤层的耦合使用的是SCA模型,煤层占比及孔隙度均较低。假设在理想情况下,煤层以包含物的形式添加时,不会替换掉孔隙,此时得到的背景介质模量依旧为干岩石骨架模量。分析煤层和孔隙度的不同添加顺序对岩石骨架弹性模量的影响(图 3),可见在不同煤层占比情况下,先加孔隙后加煤层(图 3a)与先加煤层后加孔隙(图 3b)得到的体积模量和剪切模量较接近,说明煤层和孔隙的建模顺序对数值计算结果影响较小。但岩石物理建模只是对地下岩石构成的一种等效近似,并不能表征实际岩石形成过程,煤层和孔隙的具体建模顺序可依据目标工区实际情况做调整。

|
图 3 先加孔隙后加煤层(a)与相反次序(b)所得骨架模量对比 |
Gassmann[31]将地下介质简化为均匀各向同性,在一定假设前提下,建立了饱和岩石等效模量与流体类型、矿物基质、岩石骨架之间的关系,推导出含煤层骨架填充流体后的体积模量和剪切模量
| $ K_{\mathrm{s}}=K_{\mathrm{d}}+\alpha^{2} K_{\mathrm{f}} /\left[\phi+(\alpha-\phi) K_{\mathrm{f}} / K_{\mathrm{m}}\right] $ | (10) |
| $ \mu_{\mathrm{s}}=\mu_{\mathrm{d}} $ | (11) |
式中:Ks、μs分别为流体替换后的岩石等效体积模量和剪切模量;α=1-Kd/Km;Kf为流体等效体积模量,这里可利用Reuss平均求取。
针对上面构建的煤系地层地震岩石物理模型,推导得到岩石等效体积模量和剪切模量,再进一步计算多种岩石弹性参数。本文利用实际测井数据验证模型的合理性。
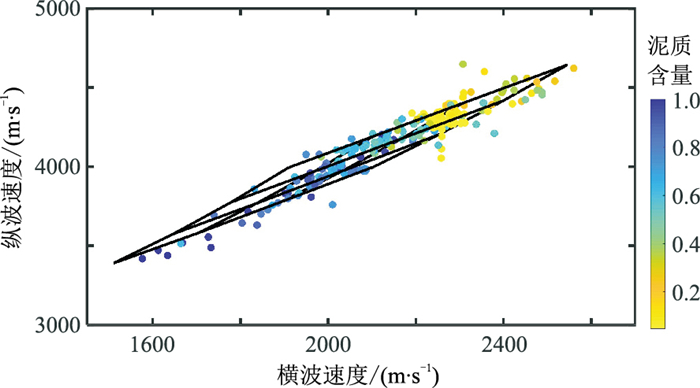
图 4中黑线是根据所建模型得到的纵、横波速度范围,彩色圆点为实测纵、横波速度样点。样点泥质含量高其速度偏低;泥质含量低则速度较高。可见二者吻合性较好,证明了模型构建的可靠性。
|
图 4 实测(样点)与建模(线框)的纵、横波速度对比图 |
岩石物理方法在物性参数与弹性参数之间起到了桥梁的作用,分析岩石弹性参数对物性参数变化的响应十分重要。因此,针对煤系地层特点,本文分析了煤层占比、泥质含量、孔隙度、含水饱和度等物性参数的渐变对不同弹性参数的影响。在所建模型中,主要矿物为石英、黏土及煤三相矿物混合,包含的孔隙主要为刚性孔和柔性孔两种类型,分别设定其孔隙纵横比为0.220和0.025。
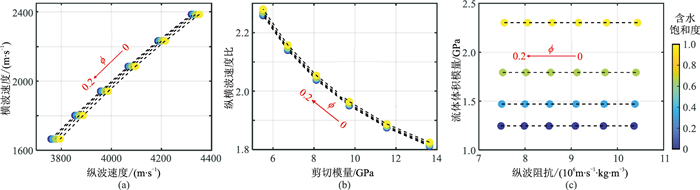
图 5为多种弹性参数随孔隙度和含水饱和度的变化趋势,其中孔隙度变化范围是0~0.2(箭头指向增大方向),含水饱和度变化范围是0~1.0。可见横波速度随含水饱和度变化幅度较小,主要是受流体密度变化的影响;剪切模量的变化不受含水饱和度影响,是因为孔隙中流体饱和程度不会改变岩石骨架的性质;流体体积模量不受孔隙度影响,但随含水饱和度变化明显;除纵横波速度比外,其余弹性参数均随孔隙度增大而减小,且均受含水饱和度的影响较小。
|
图 5 多种弹性参数随孔隙度和含水饱和度的变化趋势 (a)纵波速度和横波速度;(b)剪切模量和纵横波速度比;(c)纵波阻抗和流体体积模量 |
图 6为不同弹性参数随泥质含量和煤层占比(Vcoal)的变化趋势,其中煤层占比变化范围是0~0.1(箭头指向增大方向),泥质含量变化范围是0~0.5。可见泥质含量固定(即颜色相同)时,随着煤层占比的增大,拉梅常数、纵波阻抗、纵波速度、弹性阻抗及横波速度等参数均呈明显减小趋势;泊松阻抗[33](泊松比与密度的乘积)受煤层占比影响较小,变化幅度微弱。图中同一条虚线上的点具有相同的煤层占比,从0开始沿箭头方向以0.025的幅度增大。当煤层占比固定时,随着泥质含量的增加(即由蓝变黄),除了泊松阻抗和拉梅常数增大外,其余弹性参数均减小。

|
图 6 多种弹性参数随泥质含量和煤层占比的变化趋势 (a)纵波阻抗和拉梅常数;(b)泊松阻抗和纵波速度;(c)弹性阻抗和横波速度 |
在煤系地层中,储层预测受煤层的影响较大,煤层的分离与砂岩的识别一直是煤系地层油气勘探的难点与重点,因此需优选出较敏感的弹性参数区分煤层和储层。通过分析,主要研究纵波速度、横波速度、剪切模量、小角度(6°)弹性阻抗、泊松阻抗、纵横波速度比等参数对煤层占比和泥质含量的敏感度。
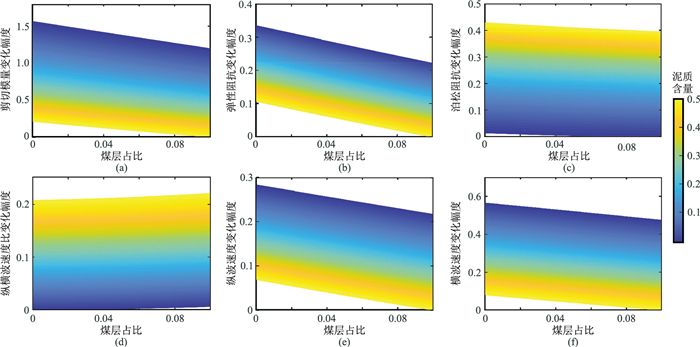
图 7是各弹性参数随煤层占比和泥质含量的变化情况。斜率越大,说明该弹性参数对煤层占比越敏感;颜色跨度越大,证明该弹性参数受泥质含量影响越大,变化越明显。进一步分析可知,6种弹性参数中,剪切模量对煤层敏感性最高,泊松阻抗受煤层占比影响十分微弱,但对泥质含量变化敏感,据此可分别作为区分煤层和砂岩的敏感因子。
|
图 7 各弹性参数随煤层占比和泥质含量的变化幅度 (a)剪切模量;(b)弹性阻抗;(c)泊松阻抗;(d)纵横波速度比;(e)纵波速度;(f)横波速度 |
在实际应用中,将各弹性参数的敏感性系数[34]定义为,表达式为
| $ C=\left|\frac{P_{\text {mean }}-P_{\text {mean }}^{0}}{P_{\mathrm{std}}}\right| $ | (12) |
式中:C为敏感系数,数值越高说明对应的弹性参数越敏感;Pmean是目标岩性的弹性参数均值;Pmean0是其他岩性的弹性参数均值;Pstd是目标岩性的弹性参数标准差。
|
|
表 1 不同岩性的弹性参数的均值与标准差 |
为进一步验证上述结论的正确性,利用东海盆地M区实际测井资料进行弹性参数敏感性计算测试。当目标岩性为砂岩时,背景岩性为泥岩和煤层,当目标岩性为煤层时,背景岩性为砂岩和泥岩。
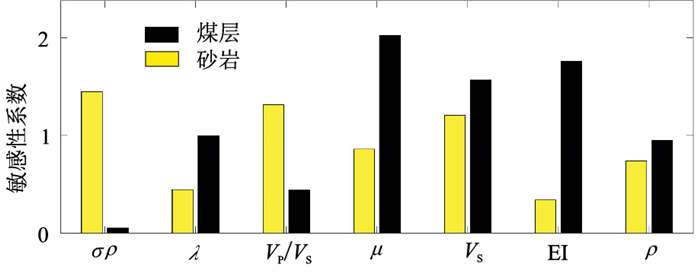
图 8是泊松阻抗、拉梅参数、纵横波速度比、剪切模量、横波速度、弹性阻抗、密度等不同参数对煤层和砂岩的敏感性分析。可以看出:泊松阻抗对砂岩更敏感,可作为储层预测的敏感参数;剪切模量对煤层更敏感,可用于识别煤层。
|
图 8 不同弹性参数对煤层和砂岩的敏感性分析 |
针对煤系地层,基于岩石物理模型,可定量表征煤系地层弹性参数与物性参数之间的关系,其中纵、横波速度与体积模量、剪切模量间的关系为
| $ V_{\mathrm{P}}=\sqrt{\left(K+\frac{4}{3} \mu\right) / \rho} $ | (13) |
| $ V_{\mathrm{S}}=\sqrt{\frac{\mu}{\rho}} $ | (14) |
式中ρ为密度。
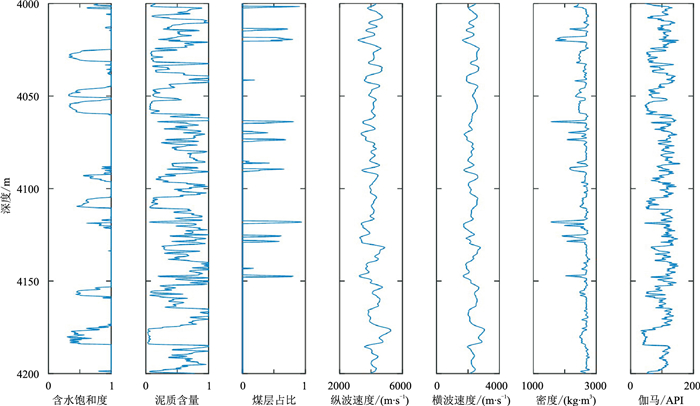
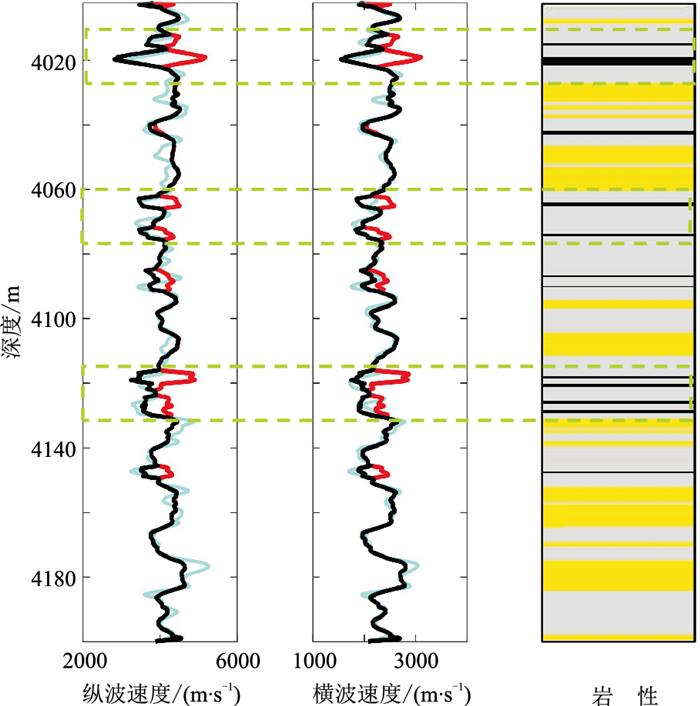
实际应用中,横波速度实测资料较少,常规岩石物理建模时未考虑煤层的影响,估算速度时无法得到煤层对应的低值异常,难以适用于煤系地层。以M工区实际测井X为例,该井测得的地质背景曲线如图 9所示,可见煤层处具有较明显的低速度、低密度特征。利用所建模型直接计算纵、横波速度,图 10是建模时考虑煤层与否得到的测井X纵、横波速度对比。从绿色虚线框可看到,在煤层处考虑煤层后建模计算的速度曲线(黑线)与实际测井数据(蓝线)吻合较好,常规建模计算的纵、横波速度曲线(红线)明显高于实测纵、横波速度(蓝线),证明建模时已有效地将煤层加入到地震岩石物理模型中。
|
图 9 地质背景参数曲线 |
|
图 10 测井X纵、横波速度计算结果对比图 蓝线为原始纵、横波速度测井曲线,红线为常规建模计算的纵、横波速度曲线,黑线为考虑煤层后建模计算的速度曲线;岩性解释中黄色代表砂岩、灰色代表泥岩、黑色代表煤层 |
由于岩石弹性参数受多种因素影响,很难建立其与物性参数的显式表达,本文利用所建模型构建了一种煤系地层弹性模量非线性预测方法。以实测纵波速度为约束,密度、孔隙度、含水饱和度、泥质含量等测井数据依据所建模型的岩石物理关系参与计算,对测井解释物性参数与纵波速度不相匹配的位置做局部修正。最终目标是利用煤系地层地震岩石物理模型及局部修正的储层物性参数,计算井曲线中常缺失的横波速度等参数。利用模拟退火算法逐点修正模型参数,建立目标泛函
| $ \begin{aligned} \boldsymbol{m}^{*}=& \operatorname{argmin} \| V_{\mathrm{P}}^{\text {mea }}-\\ & V_{\mathrm{P}}^{\text {cal }}\left(\boldsymbol{K}, \boldsymbol{\mu}, V_{\text {sh }}, V_{\text {coal }}, \rho, \phi, S_{\mathrm{w}}, \boldsymbol{a}\right) \|_{2}^{2} \end{aligned} $ | (15) |
式中:m*=[Vsh,Vcoal,ϕ,a]为物性参数,其中Vsh、Vcoal分别为泥质含量和煤层占比,a为不同孔隙类型的孔隙纵横比;VPmea为测量的纵波速度;VPcal(K,μ,Vsh,Vcoal,ρ,ϕ,Sw,a)为实际计算得到的纵波速度;K、μ分别为各组分的体积模量和剪切模量;Sw为含水饱和度。模拟退火算法跳出了局部搜索的局限性,可在解空间内趋于全局最优。本文反演仅是对实际测井解释物性参数进行修正,是分参数逐个反演的,以孔隙度和泥质含量为主。各物性参数进行反演时,参数每扰动一次,就会随机产生一种新状态,以Metropolis准则判断是否接受新状态,最终通过大量次数迭代得到满足终止条件的解(图 11)。

|
图 11 模拟退火方法流程示意图 |
将本文方法应用于东海盆地M区,对测井Z进行纵波速度和横波速度估算。模型中孔隙度类型设定为泥质孔隙(软孔)和砂质孔隙(硬孔)两种,对应的孔隙度为ϕc=ϕVsh、ϕs=ϕ-ϕc(其中ϕc为泥质孔隙,ϕs为砂质孔隙),输入参数包括泥质含量、含水饱和度、纵波速度、横波速度、孔隙度、密度、煤层占比、不同矿物组分及所含流体的模量等,对比并分析模型预测效果。
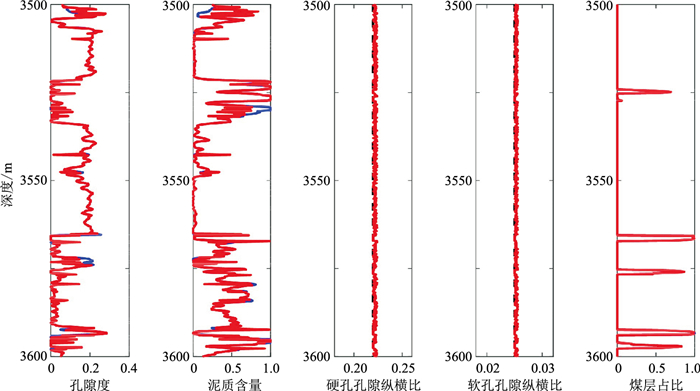
在纵波速度约束下,利用模拟退火算法对孔隙度、泥质含量、孔隙纵横比、煤层占比等物性参数做修正。其中,硬孔和软孔的孔隙纵横比是根据实际工区储层发育特征预先分别给定的,如0.220和0.025。对比图 12中的修正曲线(红线)与实际数据(蓝线),可见除孔隙度和泥质含量曲线进行了轻微修正之外,其余数据与原始曲线高度近似,也进一步证明了所构建模型的有效性。
|
图 12 物性参数对比图 |
图 13为测井Z纵、横波速度预测结果与实际测井曲线的对比。可看出纵波速度和横波速度的计算结果(红线)与真实测井曲线(蓝线)的变化趋势基本一致,且在煤层低值处具有较高的吻合度。

|
图 13 基于煤系地层模型的纵(a)、横(b)波速度预测 |
图 14为纵、横波速度相对误差分析。可见纵波速度误差在0.05以内,横波速度误差集中在0.10以内,整体速度误差较小且呈正态分布,证明了所构建的地震岩石物理模型在煤系地层的适用性。

|
图 14 纵(a)、横(b)波速度相对误差分析结果 |
地层含煤对岩石弹性模量的影响较大,在建模过程中不可忽略。本文根据实际地震资料及地质背景,构建了一种煤系地层地震岩石物理模型;充分考虑地层含煤对地震响应的影响,分析微观物性参数对弹性参数的作用。理论分析和实例研究均表明:剪切模量对煤层变化敏感,可作为煤层的指示因子;泊松阻抗随煤层变化幅度小,但受泥质含量影响大,可为后续储层反演做贡献。
根据相关地震岩石物理理论计算,可先后得到背景矿物、干岩石骨架及含流体孔隙介质的体积模量和剪切模量。在实际测井资料约束下,构建反演目标泛函,形成一种煤系地层岩石横波速度非线性计算方法,提高了储层岩石弹性模量预测的精度,完善了不同储层类型的横波速度计算方法。将该方法应用于实际工区测井的速度预测,预测结果与测井数据吻合度较高,进一步验证了本文方法的有效性和实用性。
| [1] |
戴金星, 秦胜飞, 胡国艺, 等. 新中国天然气勘探开发70年来的重大进展[J]. 石油勘探与开发, 2019, 46(6): 1037-1046. DAI Jinxing, QIN Shengfei, HU Guoyi, et al. Major progress in the natural gas exploration and development in the past seven decades in China[J]. Petroleum Exploration and Development, 2019, 46(6): 1037-1046. |
| [2] |
丁文龙, 梅永贵, 尹帅, 等. 沁水盆地煤系地层孔—裂隙特征测井反演[J]. 煤炭科学技术, 2015, 43(2): 53-57. DING Wenlong, MEI Yonggui, YIN Shuai, et al. Logging inversion on pore-crack features of coal measure strata in Qinshui Basin[J]. Coal Science and Techno-logy, 2015, 43(2): 53-57. |
| [3] |
陶士振, 邹才能. 东海盆地西湖凹陷天然气成藏及分布规律[J]. 石油勘探与开发, 2005, 32(4): 103-110. TAO Shizhen, ZOU Caineng. Accumulation and distribution of natural gases in Xihu sag, East China Sea Basin[J]. Petroleum Exploration and Development, 2005, 32(4): 103-110. DOI:10.3321/j.issn:1000-0747.2005.04.017 |
| [4] |
杨鹏程, 刘峰, 沈珊, 等. 西湖凹陷平北地区平湖组煤系烃源岩生烃潜力研究[J]. 海洋地质与第四纪地质, 2020, 40(4): 139-147. YANG Pengcheng, LIU Feng, SHEN Shan, et al. A study on the hydrocarbon generation potential of the coal-bearing source rocks in the Pinghu formation of Pingbei area, the Xihu depression[J]. Marine Geology & Quaternary Geology, 2020, 40(4): 139-147. |
| [5] |
廖前进, 于学敏, 何咏梅, 等. 大港探区上古生界煤系烃源岩特征及资源潜力[J]. 天然气地球科学, 2003, 14(4): 250-253. LIAO Qianjin, YU Xuemin, HE Yongmei, et al. The characteristics and resource potential of coal-bearing formations in Upper Paleozoic in Dagang oilfield[J]. Natural Gas Geoscience, 2003, 14(4): 250-253. DOI:10.3969/j.issn.1672-1926.2003.04.004 |
| [6] |
秦建中, 李志明, 张志荣. 不同类型煤系烃源岩对油气藏形成的作用[J]. 石油勘探与开发, 2005, 32(4): 131-136, 141. QIN Jianzhong, LI Zhiming, ZHANG Zhirong. Contribution of various coal measures source rocks to oil and gas reservoir formation[J]. Petroleum Exploration and Development, 2005, 32(4): 131-136, 141. DOI:10.3321/j.issn:1000-0747.2005.04.022 |
| [7] |
张兰, 汪文基, 何贤科, 等. 东海西湖凹陷平湖组富煤环境相控储层预测技术[J]. 现代地质, 2019, 33(2): 337-344. ZHANG Lan, WANG Wenji, HE Xianke, et al. A new phase-controlled reservoir prediction technique for coal-rich environment in the Pinghu formation of the Xihu sag, the East China Sea[J]. Geoscience, 2019, 33(2): 337-344. |
| [8] |
姚军朋, 司马立强, 张玉贵. 构造煤地球物理测井定量判识研究[J]. 煤炭学报, 2011, 36(增刊1): 94-98. YAO Junpeng, SIMA liqiang, ZHANG Yugui. Quantitative identification of deformed coals by geophysical logging[J]. Journal of China Coal Society, 2011, 36(S1): 94-98. |
| [9] |
印兴耀, 刘欣欣. 储层地震岩石物理建模研究现状与进展[J]. 石油物探, 2016, 55(3): 309-325. YIN Xingyao, LIU Xinxin. Research status and progress of the seismic rock-physics modeling methods[J]. Geophysical Prospecting for Petroleum, 2016, 55(3): 309-325. DOI:10.3969/j.issn.1000-1441.2016.03.001 |
| [10] |
XU M M, YIN X Y, ZONG Z Y, et al. Rock-physics model of volcanic rocks, an example from Junggar Basin of China[J]. Journal of Petroleum Science and Engineering, 2020, 195: 107003. DOI:10.1016/j.petrol.2020.107003 |
| [11] |
印林杰, 印兴耀, 宗兆云, 等. 基于微纳米孔隙理论的页岩气储层岩石物理建模方法[J]. 地球物理学报, 2020, 63(4): 1642-1653. YIN Linjie, YIN Xingyao, ZONG Zhaoyun, et al. A new rock physics model method for shale on the theory of micro-nanopores[J]. Chinese Journal of Geophysics, 2020, 63(4): 1642-1653. |
| [12] |
ZHANG L, BA J, CARCIONE J M. A rock-physics model to determine the pore microstructure of cracked porous rocks[J]. Geophysical Journal International, 2020, 223(1): 622-631. DOI:10.1093/gji/ggaa327 |
| [13] |
MAVKO G, SAXENA N. Rock-physics models for hete-rogeneous creeping rocks and viscous fluids[J]. Geophysics, 2016, 81(4): D427-D440. DOI:10.1190/geo2015-0531.1 |
| [14] |
XU S Y, WHITE R E. A new velocity model for clay-sand mixtures[J]. Geophysical Prospecting, 1995, 43(1): 91-118. DOI:10.1111/j.1365-2478.1995.tb00126.x |
| [15] |
张广智, 李呈呈, 印兴耀, 等. 基于修正Xu-White模型的碳酸盐岩横波速度估算方法[J]. 石油地球物理勘探, 2012, 47(5): 717-722. ZHANG Guangzhi, LI Chengcheng, YIN Xingyao, et al. A shear velocity estimation method for carbonate rocks based on the improved Xu-White model[J]. Oil Geophysical Prospecting, 2012, 47(5): 717-722. |
| [16] |
桂俊川, 马天寿, 陈平. 横观各向同性页岩岩石物理模型建立——以龙马溪组页岩为例[J]. 地球物理学报, 2020, 63(11): 4188-4204. GUI Junchuan, MA Tianshou, CHEN Ping. Rock physics modeling of transversely isotropic shale: an example of the Longmaxi formation in the Sichuan Basin[J]. Chinese Journal of Geophysics, 2020, 63(11): 4188-4204. DOI:10.6038/cjg2020N0294 |
| [17] |
张天炬, 刘明阳, 李东哲, 等. 页岩岩石物理建模研究[J]. 海洋石油, 2019, 39(1): 11-16. ZHANG Tianju, LIU Mingyang, LI Dongzhe, et al. Research on shale rock physics modeling[J]. Offshore Oil, 2019, 39(1): 11-16. DOI:10.3969/j.issn.1008-2336.2019.01.011 |
| [18] |
钱恪然, 张峰, 李向阳, 等. 基于网格分析法的页岩储层等效孔隙纵横比反演[J]. 石油物探, 2015, 54(6): 724-734. QIAN Keran, ZHANG Feng, LI Xiangyang, et al. Inversion of effective pore aspect ratio for shale reservoir using grid search method[J]. Geophysical Prospecting for Petroleum, 2015, 54(6): 724-734. DOI:10.3969/j.issn.1000-1441.2015.06.011 |
| [19] |
刘致水, 刘俊州, 董宁, 等. 富有机质岩石横波速度预测方法[J]. 石油地球物理勘探, 2021, 56(1): 127-136, 154. LIU Zhishui, LIU Junzhou, DONG Ning, et al. Investigation to shear-wave velocity prediction method for organic-rich rock[J]. Oil Geophysical Prospecting, 2021, 56(1): 127-136, 154. |
| [20] |
林凯, 贺振华, 熊晓军, 等. 基于基质矿物模量自适应提取横波速度反演方法[J]. 石油地球物理勘探, 2013, 48(2): 262-267. LIN Kai, HE Zhenhua, XIONG Xiaojun, et al. S-wave velocity inversion based on adaptive extraction of matrix mineral modulus[J]. Oil Geophysical Prospecting, 2013, 48(2): 262-267. |
| [21] |
张秉铭, 刘致水, 刘俊州, 等. 富有机质泥页岩岩石物理横波速度预测方法研究[J]. 石油物探, 2018, 57(5): 658-667. ZHANG Bingming, LIU Zhishui, LIU Junzhou, et al. A new S-wave velocity estimation method for organic-enriched shale[J]. Geophysical Prospecting for Petroleum, 2018, 57(5): 658-667. DOI:10.3969/j.issn.1000-1441.2018.05.004 |
| [22] |
李坤, 印兴耀, 宗兆云. 岩石物理驱动的相约束叠前地震概率化反演方法[J]. 中国科学(地球科学), 2020, 50(6): 832-854. LI Kun, YIN Xingyao, ZONG Zhaoyun. Facies-constrained prestack seismic probabilistic inversion driven by rock physics[J]. Scientia Sinica(Terrae), 2020, 50(6): 832-854. |
| [23] |
宗兆云, 印兴耀, 吴国忱. 基于叠前地震纵横波模量直接反演的流体检测方法[J]. 地球物理学报, 2012, 55(1): 284-292. ZONG Zhaoyun, YIN Xingyao, WU Guochen. Fluid identification method based on compressional and shear modulus direct inversion[J]. Chinese Journal of Geophysics, 2012, 55(1): 284-292. DOI:10.6038/j.issn.0001-5733.2012.01.028 |
| [24] |
郭同翠, 姜明军, 纪迎章, 等. 叠前地质统计学反演在页岩甜点和薄夹层预测中的应用——以西加拿大盆地W区块为例[J]. 石油地球物理勘探, 2020, 55(1): 167-175. GUO Tongcui, JIANG Mingjun, JI Yingzhang, et al. The application of prestack geostatistical inversion in the prediction of shale sweet spots and thin interbeds: a case study of block W in western Canada Basin[J]. Oil Geophysical Prospecting, 2020, 55(1): 167-175. |
| [25] |
唐建明, 徐天吉, 程冰洁, 等. 四川盆地深层页岩气"甜点"预测与钻井工程辅助设计技术[J]. 石油物探, 2021, 60(3): 479-487. TANG Jianming, XU Tianji, CHENG Bingjie, et al. Sweet-spot prediction and aided design for drilling engineering: application to deep shale gas reservoirs in the Sichuan Basin[J]. Geophysical Prospecting for Petroleum, 2021, 60(3): 479-487. DOI:10.3969/j.issn.1000-1441.2021.03.014 |
| [26] |
HILL R. The elastic behaviour of a crystalline aggregate[J]. Proceedings of the Physical Society.Section A, 1952, 65(5): 349. DOI:10.1088/0370-1298/65/5/307 |
| [27] |
KUSTER G T, TOKSOZ M N. Velocity and attenuation of seismic waves in two-phase media: part Ⅰ, theoretical formulations[J]. Geophysics, 1974, 39(5): 587-606. DOI:10.1190/1.1440450 |
| [28] |
KUSTER G T, TOKSOZ M N. Velocity and attenuation of seismic waves in two-phase media: part Ⅱ, experimental results[J]. Geophysics, 1974, 39(5): 607-618. DOI:10.1190/1.1440451 |
| [29] |
BERRYMAN J G. Long-wavelength propagation in composite elastic media Ⅰ.Spherical inclusions[J]. The Journal of the Acoustical Society of America, 1980, 68(6): 1809. DOI:10.1121/1.385171 |
| [30] |
BERRYMAN J G. Long-wavelength propagation in composite elastic media Ⅱ.Ellipsoidal inclusions[J]. The Journal of the Acoustical Society of America, 1980, 68(6): 1820. DOI:10.1121/1.385172 |
| [31] |
GASSMANN F. Elastic waves through a packing of spheres[J]. Geophysics, 1951, 16(4): 673-685. DOI:10.1190/1.1437718 |
| [32] |
KEYS R G, XU S Y. An approximation for the Xu-White velocity model[J]. Geophysics, 2002, 67(5): 1406-1414. DOI:10.1190/1.1512786 |
| [33] |
ZONG Z, YIN X. Direct inversion of Young's and Poi-sson impedances for fluid discrimination[J]. Geo-fluids, 2016, 16(5): 1006-1016. |
| [34] |
ZONG Z Y, YIN X Y, WU G C. Geofluid discrimination incorporating poroelasticity and seismic reflection inversion[J]. Surveys in Geophysics, 2015, 36(5): 659-681. DOI:10.1007/s10712-015-9330-6 |



 印兴耀,山东省青岛市经济技术开发区长江西路66号中国石油大学(华东)地球科学与技术学院,266580。Email:
印兴耀,山东省青岛市经济技术开发区长江西路66号中国石油大学(华东)地球科学与技术学院,266580。Email: