② 海洋国家实验室海洋矿产资源评价与探测技术功能实验室, 山东青岛 266071
② Laboratory for Marine Mineral Resources, Qingdao National Laboratory for Marine Science and Technology, Qingdao, Shandong 266071, China
模拟地震波的传播对理解地下介质中的复杂波现象具有重要意义。有限差分法的模拟结果能反映完整的地震波场信息,且模拟过程相对简单、高效,因而得到广泛应用。频率域波动方程有限差分数值模拟相对于时间域具有独特优势,如可灵活地选择计算频段、各单频分量相互独立、适于多震源模拟、适于频率相关介质的地震波模拟等[1]。密度是地下岩石的一个重要弹性参数,对油气藏描述具有重要意义,因此进行包括密度参数的正演模拟是必不可少的[2]。现有关于声波方程频率域正演研究的文献很少考虑密度的空间变化,因此本文考虑空间变密度对波传播的影响,构建了基于交错网格的高阶有限差分模拟算法的一般框架,并应用于频率域非均质声波正演。
在频率域有限差分模拟中,大规模稀疏矩阵的结构直接影响矩阵方程的求解[3],而矩阵结构的复杂度又依赖于空间导数的近似方法。Luo等[4]提出频率域声波方程有限差分的二阶交错网格简化式,该式只涉及二阶波动方程中的压力场。Pratt等[5-6]针对声波和弹性波方程,采用中心有限差分得到声波方程的五点格式和弹性波方程的九点格式。Jo等[7]提出的最优化九点方法由经典笛卡尔坐标系和45°旋转坐标系上二阶导数算子的两种离散方法线性组合而成,这两种离散方法的结合降低了网格的各向异性,进一步结合质量加速度项的加权平均,可得到一个具有最佳各向异性和频散特性的紧凑模板,然后利用相速度频散最小优化方法,得到最优权重系数(下文将该方法称为混合网格法)。Stekl等[8]将混合网格法推广到弹性波方程,在弹性情况下须考虑矢量场,因而该方法更复杂。为使混合网格适应流体情况,只能使用旋转网格框架下的离散方法。Shin等[9]对混合网格法做第二次扩展,即在对声波方程模拟时运用一个25点的模板,每个波长需要的最少网格点数减至2.5,阻抗矩阵的带宽保持不变,所需核心存储单元的数量仅为原来的四分之一。
针对频率域波动方程正演模拟,人们也进行了诸多研究。吴国忱等[10]将25点优化差分算子应用于频率—空间域正演,模拟弹性波在TTI介质中的传播。殷文等[11]做了频率—空间域二维弹性波方程高精度25点有限差分正演模拟研究。梁锴等[12]基于TTI介质做了频率—空间域qP波方程的波场传播特性研究。吴建鲁等[13]研究了上覆液相频率域声—弹耦合正演并推广到全波形反演。李青阳等[14]提出准规则网格高阶有限差分法非均值弹性波波场模拟方法。张衡等[15]发展了一种基于平均导数方法(Average-derivative method,简称ADM)的25点有限差分格式以实现声波方程频率域高精度正演。刘璐等[16]综合利用加权平均算子、平均加速度项和优化系数三种方法,提出了优化15点差分格式。马晓娜等[17]从频散关系、计算效率和存储量三方面对比分析了四种差分方法,为高精度数值模拟和声波频率域全波形反演提供方法选择上的参考。范娜等[18]提出一种通用差分系数优化方法,只要给定差分模板形式,即可直接构造频散方程,求取优化系数。
基于以上频率—空间域波动方程正演模拟研究相关方法和思想,本文构建了基于稀疏交错网格法离散频域二阶声波变密度方程的一般框架,且提供了一种适用于该差分框架的完全匹配层(Perfectly matched layers,PML)吸收边界条件[19]。通过经典谐波分析比较了混合网格和四阶交错网格的频散特性,结果表明四阶交错网格模板的精度略高于混合网格模板。比较几种模板阻抗矩阵的结构,混合网格法的计算效率显著优于四阶交错网格法,这是由于使用四阶交错网格法时扩大了矩阵带宽。另外,基于其紧凑性,混合网格模板在CPU和RAM性能方面是最佳的。
1 非均质声波传播理论在各向同性介质假设下,时间域声波方程可表示为如下二阶双曲偏微分方程
| $ \rho(x, z) \frac{\partial^{2} u(x, z, t)}{\partial t^{2}}=\nabla[K(x, z) \nabla \cdot u(x, z, t)] $ | (1) |
式中:ρ(x,z)是介质密度的空间分布函数;u(x,z,t)=[u1(x,z,t),u3(x,z,t)]为质点位移,且u1(x,z,t)和u3(x,z,t)分别表示u(x,z,t)在x、z方向的位移分量;K(x,z)为弹性介质体积模量。
式(1)可分解为以下两个标量方程
| $ \left\{\begin{array}{l} \rho(x, z) \frac{\partial^{2} u_{1}(x, z, t)}{\partial t^{2}}= \\ \quad \frac{\partial}{\partial x}\left[K(x, z)\left(\frac{\partial u_{1}(x, z, t)}{\partial x}+\frac{\partial u_{3}(x, z, t)}{\partial z}\right)\right] \\ \rho(x, z) \frac{\partial^{2} u_{3}(x, z, t)}{\partial t^{2}}= \\ \quad \frac{\partial}{\partial z}\left[K(x, z)\left(\frac{\partial u_{1}(x, z, t)}{\partial x}+\frac{\partial u_{3}(x, z, t)}{\partial z}\right)\right] \end{array}\right. $ | (2) |
为降低方程阶数并简化后续离散过程,定义
| $ \left\{\begin{array}{l} P(x, z, t)=K(x, z)\left[\frac{\partial u_{1}(x, z, t)}{\partial x}+\frac{\partial u_{3}(x, z, t)}{\partial z}\right] \\ Q(x, z)=\frac{\partial u_{1}(x, z, t)}{\partial t} \\ S(x, z)=\frac{\partial u_{3}(x, z, t)}{\partial t} \end{array}\right. $ | (3) |
式中:P(x,z,t)为声压场;Q(x,z,t)和S(x,z,t)分别为x、z方向质点速度。式(3-1)对时间求一阶导数,并结合式(2)和式(3),可得时间域二维声波方程的一阶形式
| $ \left\{\begin{array}{l} \frac{\partial P(x, z, t)}{\partial t}=K(x, z)\left[\frac{\partial Q(x, z, t)}{\partial x}+\frac{\partial S(x, z, t)}{\partial z}\right] \\ \rho(x, z) \frac{\partial Q(x, z, t)}{\partial t}=\frac{\partial P(x, z, t)}{\partial x} \\ \rho(x, z) \frac{\partial S(x, z, t)}{\partial t}=\frac{\partial P(x, z, t)}{\partial z} \end{array}\right. $ | (4) |
对该式做傅里叶变换,得到频域的二维声波变密度方程
| $ \left\{\begin{array}{l} -\mathrm{i} \omega P(x, z, \omega)= \\ \ \ \ \ K(x, z)\left[\frac{\partial Q(x, z, \omega)}{\partial x}+\frac{\partial S(x, z, \omega)}{\partial z}\right] \\ -\mathrm{i} \omega Q(x, z, \omega) \rho(x, z)=\frac{\partial P(x, z, w)}{\partial x} \\ -\mathrm{i} \omega S(x, z, \omega) \rho(x, z)=\frac{\partial P(x, z, w)}{\partial z} \end{array}\right. $ | (5) |
式中:i为虚数单位;ω为角频率。针对该式即可利用交错网格进行后续离散。
地震波数值模拟只能处理有限区域,为减弱人工边界造成的虚假反射,需在模拟过程中添加边界条件,现应用最广泛的是PML吸收边界条件,该边界理论上对任意角度、任意频率的波场都能完全吸收。
针对频率域声波方程,首先将P(x,z,ω)分解为Px(x,z,ω)和Pz(x,z,ω),即式(5)分裂为
| $ \left\{\begin{array}{l} -\mathrm{i} P_{x}(x, z, \omega)=K(x, z) \frac{\partial Q(x, z, \omega)}{\partial x} \\ -\mathrm{i} \omega P_{z}(x, z, \omega)=K(x, z) \frac{\partial Q(x, z, \omega)}{\partial z} \\ -\mathrm{i} \omega Q(x, z, \omega) \rho(x, z)= \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \frac{\partial P_{x}(x, z, \omega)}{\partial x}+\frac{\partial P_{z}(x, z, \omega)}{\partial x} \\ -\mathrm{i} \omega S(x, z, \omega) \rho(x, z)= \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \frac{\partial P_{x}(x, z, \omega)}{\partial z}+\frac{\partial P_{z}(x, z, \omega)}{\partial z} \end{array}\right. $ | (6) |
为加入PML吸收边界条件,可在频率域对坐标进行复延伸,以x方向为例
| $ \left(\frac{\partial}{\partial x}\right)^{\prime}=\frac{1}{1+\mathrm{i} \frac{\gamma(x)}{\omega}} \frac{\partial}{\partial x} $ | (7) |
衰减函数取
| $ \gamma(x)=c_{\mathrm{PML}}\left[1-\cos \left(\frac{{\rm{ \mathsf{ π} }}}{2} \frac{x}{D_{\mathrm{PML}}}\right)\right] $ | (8) |
式中:DPML为层宽度;x表示PML域内质点水平位置;系数cPML为实验选取经验值。定义衰减系数
| $ \xi_{x}(x)=1+\mathrm{i} \frac{\gamma(x)}{\omega} $ | (9) |
得到具有PML吸收边界条件的频率—空间域二维声波变密度方程
| $ \left\{\begin{array}{l} -\mathrm{i} \omega \xi_{x} P_{x}(x, z, \omega)=K(x, z) \frac{\partial Q(x, z, \omega)}{\partial x} \\ -\mathrm{i} \omega \xi_{z} P_{z}(x, z, \omega)=K(x, z) \frac{\partial Q(x, z, \omega)}{\partial z} \\ -\mathrm{i} \omega \xi_{x} Q(x, z, \omega) \rho(x, z)= \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \frac{\partial P_{x}(x, z, \omega)}{\partial x}+\frac{\partial P_{z}(x, z, \omega)}{\partial x} \\ -\mathrm{i} \omega \xi_{z} S(x, z, \omega) \rho(x, z)= \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \frac{\partial P_{x}(x, z, \omega)}{\partial z}+\frac{\partial P_{z}(x, z, \omega)}{\partial z} \end{array}\right. $ | (10) |
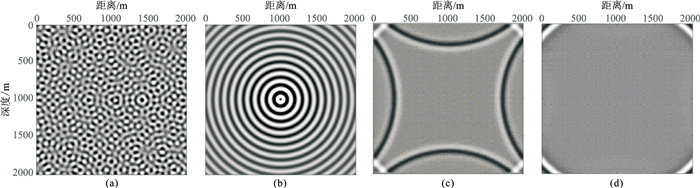
为说明该PML边界对人工边界反射的吸收效果,在简单二维半空间介质中进行模拟实验(图 1),可知该PML边界吸收效果良好。
|
图 1 最佳匹配层(PML)边界吸收效果示意图 (a)和(b)分别表示添加边界前、后的频率切片(50Hz);(c)和(d)分别表示添加边界前、后的波场快照(250ms) |
由前文易得具有PML吸收边界条件的频率—空间域二维声波变密度方程
| $ \left\{\begin{array}{l} \frac{-\mathrm{i} \omega \xi_{x}(x)}{K(x, z)} P_{x}(x, z, \omega)=\frac{\partial Q(x, z, \omega)}{\partial x} \\ \frac{-\mathrm{i} \omega \xi_{z}(z)}{K(x, z)} P_{z}(x, z, \omega)=\frac{\partial S(x, z, \omega)}{\partial z} \\ -\mathrm{i} \omega \xi_{x}(x) \rho(x, z) Q(x, z, \omega)=\frac{\partial P(x, z, \omega)}{\partial x} \\ -\mathrm{i} \omega \xi_{z}(z) \rho(x, z) S(x, z, \omega)=\frac{\partial P(x, z, \omega)}{\partial z} \end{array}\right. $ | (11) |
利用二阶交错网格做模拟,其差分格式如图 2所示。
采用二阶中心差分格式将式(11)离散化
| $ \left[\frac{\partial Q}{\partial x}\right]_{i, j} \approx \frac{1}{d}\left(Q_{i+1 / 2, j}-Q_{i-1 / 2, j}\right) $ | (12) |
式中:d为步长;i、j分别表示差分中心点在x、z方向的坐标。其余一阶导数差分格式依此类推。
将该离散公式代入式(11),并按Luo等[4]给出的化简技巧(Parsimonious technique)将式中的Q、S消掉,再合并,得到二阶声压差分方程
| $ \begin{aligned} \frac{-\omega^{2}}{K_{i, j}} P_{i, j}=& \frac{1}{\xi_{x, i}} \frac{1}{d^{2}}\left[\frac{1}{\xi_{x, i+1 / 2}} \frac{1}{\rho_{i+1 / 2, j}}\left(P_{i+1, j}-P_{i, j}\right)-\right.\\ &\left.\frac{1}{\xi_{x, i-1 / 2}} \frac{1}{\rho_{i-1 / 2, j}}\left(P_{i, j}-P_{i-1, j}\right)\right]+\\ & \frac{1}{\xi_{z, j}} \frac{1}{d^{2}}\left[\frac{1}{\xi_{z, j+1 / 2}} \frac{1}{\rho_{i, j+1 / 2}}\left(P_{i, j+1}-P_{i, j}\right)-\right.\\ &\left.\frac{1}{\xi_{z, j-1 / 2}} \frac{1}{\rho_{i, j-1 / 2}}\left(P_{i, j}-P_{i, j-1}\right)\right] \end{aligned} $ | (13) |
对该式按图 2所示5点差分格式整理,可得
| $ \begin{aligned} C_{1} P_{i, j}&+C_{2} P_{i-1, j}+C_{3} P_{i+1, j}+ \\ &C_{4} P_{i, j-1}+C_{5} P_{i, j+1}=-S_{i, j} \end{aligned} $ | (14) |
其中各系数分别如下
| $ \left\{\begin{aligned} C_{1}=& \frac{\omega^{2}}{K_{i, j}}-\frac{1}{\xi_{x, i} d^{2}}\left(\frac{1}{\xi_{x, i+1 / 2}} \frac{1}{\rho_{i+1 / 2, j}}+\frac{1}{\xi_{x, i-1 / 2}} \frac{1}{\rho_{i-1 / 2, j}}\right) \\ &-\frac{1}{\xi_{z, j} d^{2}}\left(\frac{1}{\xi_{z, j+1 / 2}} \frac{1}{\rho_{i, j+1 / 2}}+\frac{1}{\xi_{z, j-1 / 2}} \frac{1}{\rho_{i, j-1 / 2}}\right) \\ C_{2}=& \frac{1}{\xi_{x, i} d^{2}} \frac{1}{\xi_{x, i-1 / 2}} \frac{1}{\rho_{i-1 / 2, j}} \\ C_{3}=& \frac{1}{\xi_{x, i} d^{2}} \frac{1}{\xi_{x, i+1 / 2}} \frac{1}{\rho_{i+1 / 2, j}} \\ C_{4}=& \frac{1}{\xi_{z, j} d^{2}} \frac{1}{\xi_{z, j-1 / 2}} \frac{1}{\rho_{i, j-1 / 2}} \end{aligned}\right. $ | (15a) |
| $ C_{5}=\frac{1}{\xi_{z, j} d^{2}} \frac{1}{\xi_{z, j+1 / 2}} \frac{1}{\rho_{i, j+1 / 2}} $ | (15b) |
由以上系数点阵构造阻抗矩阵,并求解线性方程组,即可进行频率域声波变密度波场模拟。
为降低数值频散,提高模拟精度,在利用二阶交错网格做模拟的基础上,自然想到通过提高差分阶数的方法达到此目的,四阶交错网格差分格式如图 3所示。
|
图 3 声波变密度四阶交错网格示意图 |
采用四阶交错网格差分格式将式(11)离散化
| $ \begin{aligned} {\left[\frac{\partial Q}{\partial x}\right]_{i, j} \approx } & \frac{1}{d}\left[\frac{9}{8}\left(Q_{i+1 / 2, j}-Q_{i-1 / 2, j}\right)-\right.\\ &\left.\frac{1}{24}\left(Q_{i+3 / 2, j}-Q_{i-3 / 2, j}\right)\right] \end{aligned} $ | (16) |
其余一阶导数差分格式依此类推。将离散式(16)代入式(11)并按Luo等[4]的方法将式中的Q、S消掉,合并得到四阶声压差分方程
| $ \begin{aligned} \frac{-\omega^{2}}{K_{i, j}} P_{i, j}=& \frac{1}{\xi_{x, i}} \frac{1}{d^{2}}\left\{\frac { 9 } { 8 } \left[\frac{1}{\xi_{x, i+1 / 2}} \frac{1}{\rho_{i+1 / 2, j}}\left(\frac{9}{8}\left(P_{i+1, j}-P_{i, j}\right)-\frac{1}{24}\left(P_{i+2, j}-P_{i-1, j}\right)\right)-\right.\right.\\ &\left.\frac{1}{\xi_{x, i-1 / 2}} \frac{1}{\rho_{i-1 / 2, j}}\left(\frac{9}{8}\left(P_{i, j}-P_{i-1, j}\right)-\frac{1}{24}\left(P_{i+1, j}-P_{i-2, j}\right)\right)\right]-\\ & \frac{1}{24}\left[\frac{1}{\xi_{x, i+3 / 2}} \frac{1}{\rho_{i+3 / 2, j}}\left(\frac{9}{8}\left(P_{i+2, j}-P_{i+1, j}\right)-\frac{1}{24}\left(P_{i+3, j}-P_{i, j}\right)\right)-\right.\\ &\left.\left.\frac{1}{\xi_{x, i-3 / 2}} \frac{1}{\rho_{i-3 / 2, j}}\left(\frac{9}{8}\left(P_{i-1, j}-P_{i-2, j}\right)-\frac{1}{24}\left(P_{i, j}-P_{i-3, j}\right)\right)\right]\right\}+\\ & \frac{1}{\xi_{z, j}} \frac{1}{d^{2}}\left\{\frac { 9 } { 8 } \left[\frac{1}{\xi_{z, j+1 / 2}} \frac{1}{\rho_{i, j+1 / 2}}\left(\frac{9}{8}\left(P_{i, j+1}-P_{i, j}\right)-\frac{1}{24}\left(P_{i, j+2}-P_{i, j-1}\right)\right)-\right.\right.\\ &\left.\frac{1}{\xi_{x, i-1 / 2}} \frac{1}{\rho_{i-1 / 2, j}}\left(\frac{9}{8}\left(P_{i, j}-P_{i, j-1}\right)-\frac{1}{24}\left(P_{i, j+1}-P_{i, j-2}\right)\right)\right]-\\ & \frac{1}{24}\left(\frac{1}{\xi_{z, j+3 / 2}} \frac{1}{\rho_{i, j+3 / 2}}\left(\frac{9}{8}\left(P_{i, j+2}-P_{i, j+1}\right)-\frac{1}{24}\left(P_{i, j+3}-P_{i, j}\right)\right)-\right.\\ &\left.\left.\frac{1}{\xi_{x, i-3 / 2}} \frac{1}{\rho_{i-3 / 2, j}}\left(\frac{9}{8}\left(P_{i, j-1}-P_{i, j-2}\right)-\frac{1}{24}\left(P_{i, j}-P_{i, j-3}\right)\right)\right]\right\} \end{aligned} $ | (17) |
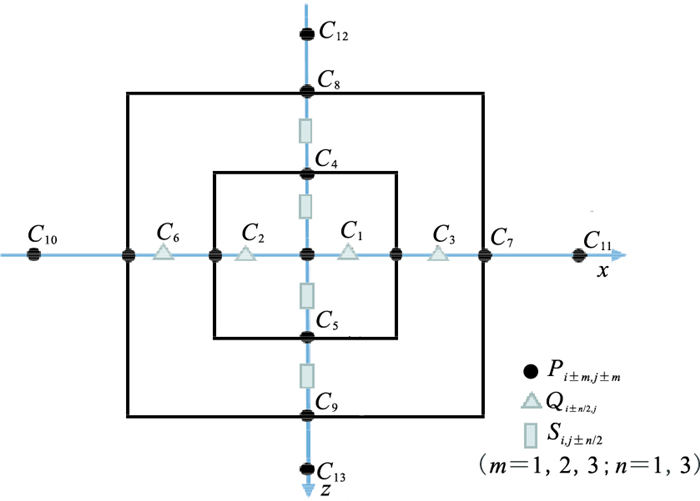
对该式按图 3所示13点差分格式整理可得
| $ \begin{gathered} C_{1} P_{i, j}+C_{2} P_{i-1, j}+C_{3} P_{i+1, j}+C_{4} P_{i, j-1}+C_{5} P_{i, j+1}+C_{6} P_{i-2, j}+C_{7} P_{i+2, j}+C_{8} P_{i, j-2}+ \\ C_{9} P_{i, j+2}+C_{10} P_{i-3, j}+C_{11} P_{i+3, j}+C_{12} P_{i, j-3}+C_{13} P_{i, j+3}=-S_{i, j} \end{gathered} $ | (18) |
其中各系数对应如下
| $ \left\{\begin{aligned} &C_{1}=\frac{\omega^{2}}{K_{i, j}}-\frac{1}{d^{2} \xi_{x, i}}\left[\frac{9}{8} \frac{9}{8}\left(\frac{1}{\xi_{x, i+1 / 2} \rho_{i+1 / 2, j}}+\frac{1}{\xi_{x, i-1 / 2} \rho_{i-1 / 2, j}}\right)+\frac{1}{24} \frac{1}{24}\left(\frac{1}{\xi_{x, i+3 / 2} \rho_{i+3 / 2, j}}+\frac{1}{\xi_{x, i-3 / 2} \rho_{i-3 / 2, j}}\right)\right]-\\ &\ \ \ \ \ \ \ \ \ \ \frac{1}{d^{2} \xi_{z, j}}\left[\frac{9}{8} \frac{9}{8}\left(\frac{1}{\xi_{z, j+1 / 2} \rho_{i, j+1 / 2}}+\frac{1}{\xi_{z, j-1 / 2} \rho_{i, j-1 / 2}}\right)+\frac{1}{24} \frac{1}{24}\left(\frac{1}{\xi_{z, j+3 / 2} \rho_{i, j+3 / 2}}+\frac{1}{\xi_{z, j-3 / 2} \rho_{i, j-3 / 2}}\right)\right]\\ &C_{2}=\frac{1}{d^{2}} \frac{1}{\xi_{x, i}}\left(\frac{9}{8} \frac{9}{8} \frac{1}{\xi_{x, i-1 / 2} \rho_{i-1 / 2, j}}+\frac{9}{8} \frac{1}{24} \frac{1}{\xi_{x, i+1 / 2} \rho_{i+1 / 2, j}}+\frac{1}{24} \frac{9}{8} \frac{1}{\xi_{x, i-3 / 2} \rho_{i-3 / 2, j}}\right)\\ &C_{3}=\frac{1}{d^{2}} \frac{1}{\xi_{x, i}}\left(\frac{9}{8} \frac{9}{8} \frac{1}{\xi_{x, i+1 / 2} \rho_{i+1 / 2, j}}+\frac{9}{8} \frac{1}{24} \frac{1}{\xi_{x, i-1 / 2} \rho_{i-1 / 2, j}}+\frac{1}{24} \frac{9}{8} \frac{1}{\xi_{x, i+3 / 2} \rho_{i+3 / 2, j}}\right)\\ &C_{4}=\frac{1}{d^{2}} \frac{1}{\xi_{z, j}}\left(\frac{9}{8} \frac{9}{8} \frac{1}{\xi_{z, j-1 / 2} \rho_{i, j-1 / 2}}+\frac{9}{8} \frac{1}{24} \frac{1}{\xi_{z, j+1 / 2} \rho_{i, j+1 / 2}}+\frac{1}{24} \frac{9}{8} \frac{1}{\xi_{z, j-3 / 2} \rho_{i, j-3 / 2}}\right)\\ &C_{5}=\frac{1}{d^{2}} \frac{1}{\xi_{z, j}}\left(\frac{9}{8} \frac{9}{8} \frac{1}{\xi_{z, j+1 / 2} \rho_{i, j+1 / 2}}+\frac{9}{8} \frac{1}{24} \frac{1}{\xi_{z, j-1 / 2} \rho_{i, j-1 / 2}}+\frac{1}{24} \frac{9}{8} \frac{1}{\xi_{z, j+3 / 2} \rho_{i, j+3 / 2}}\right)\\ &C_{6}=-\frac{1}{d^{2}} \frac{1}{\xi_{x, i}}\left(\frac{9}{8} \frac{1}{24} \frac{1}{\xi_{x, i-1 / 2} \rho_{i-1 / 2, j}}+\frac{1}{24} \frac{9}{8} \frac{1}{\xi_{x, i-3 / 2} \rho_{i-3 / 2, j}}\right) \\ &C_{7}=-\frac{1}{d^{2}} \frac{1}{\xi_{x, i}}\left(\frac{9}{8} \frac{1}{24} \frac{1}{\xi_{x, i+1 / 2} \rho_{i+1 / 2, j}}+\frac{1}{24} \frac{9}{8} \frac{1}{\xi_{x, i+3 / 2} \rho_{i+3 / 2, j}}\right) \\ &C_{8}=-\frac{1}{d^{2}} \frac{1}{\xi_{z, j}}\left(\frac{9}{8} \frac{1}{24} \frac{1}{\xi_{z, j-1 / 2} \rho_{i, j-1 / 2}}+\frac{1}{24} \frac{9}{8} \frac{1}{\xi_{z, j-3 / 2} \rho_{i, j-3 / 2}}\right) \\ &C_{9}=-\frac{1}{d^{2}} \frac{1}{\xi_{z, j}}\left(\frac{9}{8} \frac{1}{24} \frac{1}{\xi_{z, j+1 / 2} \rho_{i, j+1 / 2}}+\frac{1}{24} \frac{9}{8} \frac{1}{\xi_{z, j+3 / 2} \rho_{i, j+3 / 2}}\right)\\ &C_{10}=\frac{1}{d^{2}} \frac{1}{\xi_{x, i}}\left(\frac{1}{24} \frac{1}{24} \frac{1}{\xi_{x, i-3 / 2} \rho_{i-3 / 2, j}}\right) \\ &C_{11}=\frac{1}{d^{2}} \frac{1}{\xi_{x, i}}\left(\frac{1}{24} \frac{1}{24} \frac{1}{\xi_{x, i+3 / 2} \rho_{i+3 / 2, j}}\right) \\ &C_{12}=\frac{1}{d^{2}} \frac{1}{\xi_{z, j}}\left(\frac{1}{24} \frac{1}{24} \frac{1}{\xi_{z, j-3 / 2} \rho_{i, j-3 / 2}}\right) \\ &C_{13}=\frac{1}{d^{2}} \frac{1}{\xi_{z, j}}\left(\frac{1}{24} \frac{1}{24} \frac{1}{\xi_{z, j+3 / 2} \rho_{i, j+3 / 2}}\right) \end{aligned}\right. $ | (19) |
由以上系数点阵构造阻抗矩阵,并求解线性方程组,即可进行频率域声波变密度波场模拟。
进而,由前述二阶(式(13))、四阶(式(17))声压差分方程,可推广至交错网格任意阶声压差分方程
| $ \begin{array}{l} \frac{-\omega^{2}}{K_{i, j}} P_{i, j}=\frac{1}{\xi_{x, i}} \frac{1}{d^{2}}\left\{\sum\limits_{h=1}^{N} a_{h}\left[\frac{\sum\limits_{m=1}^{N} a_{m}\left(P_{i+m+h-1, j}^{n}-P_{i-m+h, j}^{n}\right)}{\xi_{i+(2 h-1) / 2, j}^{n} \rho_{i+(2 h-1) / 2, j}^{n}}-\frac{\sum\limits_{m=1}^{N} a_{m}\left(P_{i+m-h, j}^{n}-P_{i-m-h+1, j}^{n}\right)}{\xi_{i-(2 h-1) / 2, j}^{n} \rho_{i-(2 h-1) / 2, j}^{n}}\right]\right\}+ \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \frac{1}{\xi_{z, j}} \frac{1}{d^{2}}\left\{\sum \limits_ { h = 1 } ^ { N } a _ { h } \left[\frac{\sum\limits_{m=1}^{N} a_{m}\left(P_{i, j+m+h-1}^{n}-P_{i, j-m+h}^{n}\right)}{\xi_{i, j+(2 h-1) / 2}^{n} \rho_{i, j+(2 h-1) / 2}^{n}}-\frac{\sum\limits_{m=1}^{N} a_{m}\left(P_{i, j+m-h}^{n}-P_{i, j-m-h+1}^{n}\right)}{\left.\left.\xi_{i, j-(2 h-1) / 2}^{n} \rho_{i, j-(2 h-1) / 2}^{n}\right]\right\}}\right.\right. \end{array} $ | (20) |
式中:ah和am是差分系数;N表示差分阶数。表 1给出十阶以内对应的差分系数。
|
|
表 1 十阶以内差分系数 |
不同差分阶数的方程对应不同差分系数,将差分系数代入式(20)并按相应差分格式构造系数点阵,进一步构造阻抗矩阵并求解,即可进行频率—空间域声波变密度方程交错网格高阶有限差分模拟。
2.2 混合网格法Jo等[7]提出一种最优化9点有限差分格式,该方法将每个波长需要的最小网格点数减至约4个,它由经典笛卡尔坐标系和45°旋转坐标系上二阶导数算子的两个离散方法线性组合而成。据此,本文总结一种混合网格有限差分法,利用两种二阶交错网格的混合,实现频率域非均匀介质声波场的高精度数值模拟。混合网格差分格式如图 4所示。
|
图 4 声波变密度混合网格示意图 菱形表示45°方向质点速度 |
将传统二阶网格与旋转45°网格结合,得到具有PML吸收边界条件的混合网格频率域二维声波变密度方程
| $ \left\{\begin{array}{l} \frac{-\mathrm{i} \omega \xi_{x}(x)}{K(x, z)} P_{x}(x, z, \omega)=a \frac{\partial Q(x, z, \omega)}{\partial x}+ \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (1-a) \frac{\partial Q^{\prime}\left(x^{\prime}, z^{\prime}, \omega\right)}{\partial x^{\prime}} \\ \frac{-\mathrm{i} \omega \xi_{z}(z)}{K(x, z)} P_{z}(x, z, \omega)=a \frac{\partial S(x, z, \omega)}{\partial z}+ \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (1-a) \frac{\partial S^{\prime}\left(x^{\prime}, z^{\prime}, \omega\right)}{\partial z^{\prime}} \\ -\mathrm{i} \omega \xi_{x}(x) \rho(x, z) Q(x, z, \omega)=\frac{\partial P(x, z, \omega)}{\partial x} \\ -\mathrm{i} \omega \xi_{z}{(z)} \rho(x, z) S(x, z, \omega)=\frac{\partial P(x, z, \omega)}{\partial z} \\ -\mathrm{i} \omega \xi_{x}{ }^{\prime}\left(x^{\prime}\right) \rho\left(x^{\prime}, z^{\prime}\right) Q^{\prime}(x, z, \omega)=\frac{\partial P\left(x^{\prime}, z^{\prime}, \omega\right)}{\partial x^{\prime}} \\ -\mathrm{i} \omega \xi_{z}{ }^{\prime}\left(z^{\prime}\right) \rho\left(x^{\prime}, z^{\prime}\right) Q^{\prime}(x, z, \omega)=\frac{\partial P\left(x^{\prime}, z^{\prime}, \omega\right)}{\partial z^{\prime}} \end{array}\right. $ | (21) |
式中a为加权系数。
旋转网格框架与传统网格框架下偏导数关系为
| $ \left\{\begin{array}{l} \frac{\partial Q^{\prime}\left(x^{\prime}, z^{\prime}, \omega\right)}{\partial x^{\prime}}=\frac{\sqrt{2}}{2}\left[\frac{\partial Q(x, z, \omega)}{\partial x^{\prime}}+\frac{\partial Q(x, z, \omega)}{\partial z^{\prime}}\right] \\ \frac{\partial S^{\prime}\left(x^{\prime}, z^{\prime}, \omega\right)}{\partial z^{\prime}}=\frac{\sqrt{2}}{2}\left[\frac{\partial S(x, z, \omega)}{\partial x^{\prime}}+\frac{\partial S(x, z, \omega)}{\partial z^{\prime}}\right] \end{array}\right. $ | (22) |
采用二阶中心差分格式将式(21)离散化
| $ \left[\frac{\partial Q}{\partial x}\right]_{i, j} \approx \frac{1}{d}\left(Q_{i+1 / 2, j}-Q_{i-1 / 2, j}\right) $ | (23) |
其余一阶导数差分格式依此类推。将该离散式代入式(21),并按Luo等[4]的方法将式中的Q、S消掉,合并得到混合四阶声压差分方程
| $ \begin{aligned} \frac{-\omega^{2}}{K_{i, j}} P_{i, j}=& \frac{a}{\xi_{x, i} d^{2}}\left[\frac{1}{\xi_{x, i+1 / 2}} \frac{1}{\rho_{i+1 / 2, j}}\left(P_{i+1, j}-P_{i, j}\right)-\frac{1}{\xi_{x, i-1 / 2}} \frac{1}{\rho_{i-1 / 2, j}}\left(P_{i, j}-P_{i-1, j}\right)\right]+\\ & \frac{a}{\xi_{z, j} d^{2}}\left[\frac{1}{\xi_{z, j+1 / 2}} \frac{1}{\rho_{i, j+1 / 2}}\left(P_{i, j+1}-P_{i, j}\right)-\frac{1}{\xi_{z, j-1 / 2}} \frac{1}{\rho_{i, j-1 / 2}}\left(P_{i, j}-P_{i, j-1}\right)\right]+\\ & \frac{1-a}{\xi_{x, i} 2 d^{2}}\left\{\left[\frac{1}{\xi_{x, i+1 / 2}} \frac{1}{\rho_{i+1 / 2, j-1 / 2}}\left(P_{i+1, j-1}-P_{i, j}\right)-\frac{1}{\xi_{x, i-1 / 2}} \frac{1}{\rho_{i-1 / 2, j+1 / 2}}\left(P_{i, j}-P_{i-1, j+1}\right)\right)+\right.\\ &\left.\left[\frac{1}{\xi_{x, i+1 / 2}} \frac{1}{\rho_{i+1 / 2, j+1 / 2}}\left(P_{i+1, j+1}-P_{i, j}\right)-\frac{1}{\xi_{x, i-1 / 2}} \frac{1}{\rho_{i-1 / 2, j-1 / 2}}\left(P_{i, j}-P_{i-1, j-1}\right)\right]\right\}+ \\ &\frac{1-a}{\xi_{z, j} 2 d^{2}}\left\{\left[\frac{1}{\xi_{z, j+1 / 2}} \frac{1}{\rho_{i+1 / 2, j-1 / 2}}\left(P_{i+1, j-1}-P_{i, j}\right)-\frac{1}{\xi_{z, i-1 / 2}} \frac{1}{\rho_{i-1 / 2, j+1 / 2}}\left(P_{i, j}-P_{i-1, j+1}\right)\right]+\right. \\ &\left.\left[\frac{1}{\xi_{z, j+1 / 2}} \frac{1}{\rho_{i+1 / 2, j+1 / 2}}\left(P_{i+1, j+1}-P_{i, j}\right)-\frac{1}{\xi_{z, i-1 / 2}} \frac{1}{\rho_{i-1 / 2, j-1 / 2}} \frac{1}{d}\left(P_{i, j}-P_{i-1, j-1}\right)\right]\right\} \end{aligned} $ | (24) |
同时对质量加速度项按9点格式加权分配,可得
| $ \begin{aligned} \frac{\omega^{2}}{K(x, z)} P_{i, j}=& \frac{\omega^{2}}{K_{i, j}}\left[c P_{i, j}+e\left(P_{i+1, j}+P_{i-1, j}+P_{i, j+1}+P_{i, j-1}\right)+\right.\\ &\left.\frac{1-c-4 e}{4}\left(P_{i+1, j+1}+P_{i-1, j+1}+P_{i+1, j-1}+P_{i-1, j-1}\right)\right] \end{aligned} $ | (25) |
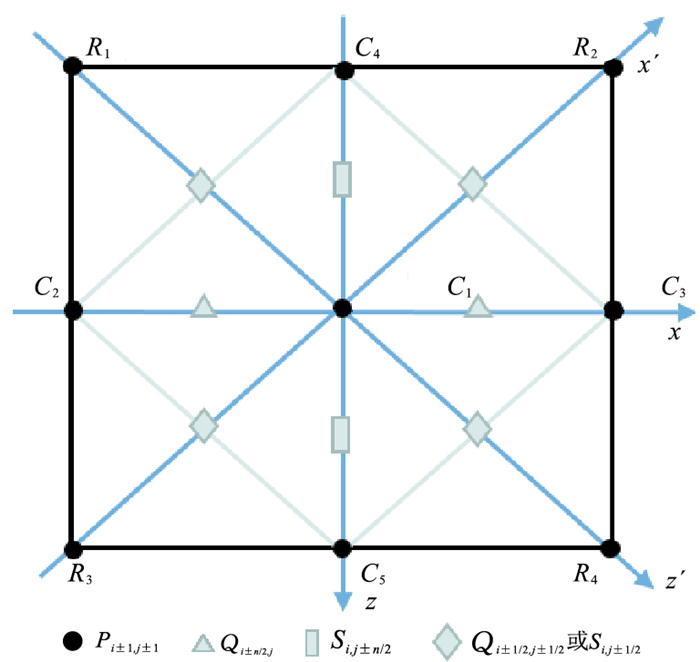
式中c、e为加权平均系数。结合以上两式,按图 4所示旋转混合9点差分格式整理,可得
| $ \begin{aligned} C_{1} P_{i, j}+& C_{2} P_{i-1, j}+C_{3} P_{i+1, j}+C_{4} P_{i, j-1}+C_{5} P_{i, j+1}+\\ & R_{1} P_{i-1, j-1}+R_{2} P_{i+1, j-1}+R_{3} P_{i-1, j+1}+R_{4} P_{i+1, j+1}=-S_{i, j} \end{aligned} $ | (26) |
其中各系数对应如下
| $ \left\{\begin{aligned} &\begin{aligned} C_{1}=& \frac{\omega^{2}}{K_{i, j}} c-\frac{a}{\xi_{x, i} d^{2}}\left(\frac{1}{\xi_{x, i+1 / 2}} \frac{1}{\rho_{i+1 / 2, j}}+\frac{1}{\xi_{x, i-1 / 2}} \frac{1}{\rho_{i-1 / 2, j}}\right)-\frac{a}{\xi_{z, j} d^{2}}\left(\frac{1}{\xi_{z, j+1 / 2}} \frac{1}{\rho_{i, j+1 / 2}}+\frac{1}{\xi_{z, j-1 / 2}} \frac{1}{\rho_{i, j-1 / 2}}\right)+\\ & \frac{(1-a)}{4 d^{2}}\left[\frac{1}{\rho_{i+1 / 2, j-1 / 2}}\left(\frac{1}{\xi_{x, i} \xi_{x, i+1 / 2}}+\frac{1}{\xi_{z, j} \xi_{z, j-1 / 2}}\right)+\frac{1}{\rho_{i-1 / 2, j+1 / 2}}\left(\frac{1}{\xi_{x, i} \xi_{x, i-1 / 2}}+\frac{1}{\xi_{z, j} \xi_{z, j+1 / 2}}\right)+\right.\\ &\left.\frac{1}{\rho_{i+1 / 2, j+1 / 2}}\left(\frac{1}{\xi_{x, i} \xi_{x, i+1 / 2}}+\frac{1}{\xi_{z, j} \xi_{z, j+1 / 2}}\right)+\frac{1}{\rho_{i-1 / 2, j-1 / 2}}\left(\frac{1}{\xi_{x, i} \xi_{x, i-1 / 2}}+\frac{1}{\xi_{z, j} \xi_{z, j-1 / 2}}\right)\right] \end{aligned}\\ &C_{2}=-\frac{a}{d^{2}} \frac{b_{i-1 / 2, j}}{\xi_{x, i} \xi_{x, i-1 / 2}}-\frac{(1-a)}{4 d^{2}}\\ &\left[\frac{1}{\rho_{i-1 / 2, j+1 / 2}}\left(\frac{1}{\xi_{x, i} \xi_{x, i-1 / 2}}-\frac{1}{\xi_{z, j} \xi_{z, j+1 / 2}}\right)+\frac{1}{\rho_{i-1 / 2, j-1 / 2}}\left(\frac{1}{\xi_{x, i} \xi_{x, i-1 / 2}}-\frac{1}{\xi_{z, j} \xi_{z, j-1 / 2}}\right)\right]-\frac{\omega^{2}}{K_{i, j}} e \\ &C_{3}=-\frac{a}{d^{2}} \frac{b_{i+1 / 2, j}}{\xi_{x, i} \xi_{x, i+1 / 2}}-\frac{(1-a)}{4 d^{2}}\\ &\left[\frac{1}{\rho_{i+1 / 2, j-1 / 2}}\left(\frac{1}{\xi_{x, i} \xi_{x, i+1 / 2}}-\frac{1}{\xi_{z, j} \xi_{z, j-1 / 2}}\right)+\frac{1}{\rho_{i+1 / 2, j+1 / 2}}\left(\frac{1}{\xi_{x, i} \xi_{x, i+1 / 2}}-\frac{1}{\xi_{z, j} \xi_{z, j+1 / 2}}\right)\right]-\frac{\omega^{2}}{K_{i, j}} e \\ &C_{4}=-\frac{a}{d^{2}} \frac{b_{i, j-1 / 2}}{\xi_{z, j} \xi_{z, j-1 / 2}}-\frac{(1-a)}{4 d^{2}}\\ &\left[\frac{1}{\rho_{i+1 / 2, j-1 / 2}}\left(\frac{1}{\xi_{z, j} \xi_{z, j-1 / 2}}-\frac{1}{\xi_{x, i} \xi_{x, i+1 / 2}}\right)+\frac{1}{\rho_{i-1 / 2, j-1 / 2}}\left(\frac{1}{\xi_{z, j} \xi_{z, j-1 / 2}}-\frac{1}{\xi_{x, i} \xi_{x, i-1 / 2}}\right)\right]-\frac{\omega^{2}}{K_{i, j}} e \\ &C_{5}=-\frac{a}{d^{2}} \frac{b_{i, j+1 / 2}}{\xi_{z, j} \xi_{z, j+1 / 2}}-\frac{(1-a)}{4 d^{2}}\\ &\left[\frac{1}{\rho_{i-1 / 2, j+1 / 2}}\left(\frac{1}{\xi_{z, j} \xi_{z, j+1 / 2}}-\frac{1}{\xi_{x, i} \xi_{x, i-1 / 2}}\right)+\frac{1}{\rho_{i+1 / 2, j+1 / 2}}\left(\frac{1}{\xi_{z, j} \xi_{z, j+1 / 2}}-\frac{1}{\xi_{x, i} \xi_{x, i+1 / 2}}\right)\right]-\frac{\omega^{2}}{K_{i, j}} e\\ &R_{1}=-\frac{(1-a)}{4 d^{2}} \frac{1}{\rho_{i-1 / 2, j-1 / 2}}\left(\frac{1}{\xi_{x, i} \xi_{x, i-1 / 2}}+\frac{1}{\xi_{z, j} \xi_{z, j-1 / 2}}\right)-\frac{1-c-4 e}{4} \frac{\omega^{2}}{K_{i, j}} \\ &R_{2}=-\frac{(1-a)}{4 d^{2}} \frac{1}{\rho_{i+1 / 2, j-1 / 2}}\left(\frac{1}{\xi_{x, i} \xi_{x, i+1 / 2}}+\frac{1}{\xi_{z, j} \xi_{z, j-1 / 2}}\right)-\frac{1-c-4 e}{4} \frac{\omega^{2}}{K_{i, j}} \\ &R_{3}=-\frac{(1-a)}{4 h^{2}} \frac{1}{\rho_{i-1 / 2, j+1 / 2}}\left(\frac{1}{\xi_{x, i} \xi_{x, i-1 / 2}}+\frac{1}{\xi_{z, j} \xi_{z, j+1 / 2}}\right)-\frac{1-c-4 e}{4} \frac{\omega^{2}}{K_{i, j}} \\ &R_{4}=-\frac{(1-a)}{4 h^{2}} \frac{1}{\rho_{i+1 / 2, j+1 / 2}}\left(\frac{1}{\xi_{x, i} \xi_{x, i+1 / 2}}+\frac{1}{\xi_{z, j} \xi_{z, j+1 / 2}}\right)-\frac{1-c-4 e}{4} \frac{\omega^{2}}{K_{i, j}} \end{aligned}\right. $ | (27) |
式中系数a=0.5461,c=0.6248,e=0.09381。
优化求取方法参照Jo等[7]方法,由以上系数点阵构造阻抗矩阵,并求解线性方程组,即可做频率域声波变密度波场模拟。进一步地,由二阶混合差分方程(式(27))格式,可推广至混合格式任意阶声压差分方程
| $ \begin{aligned} \frac{-\omega^{2}}{K_{i, j}} P_{i, j}=& \frac{a}{\xi_{x, i} d^{2}}\left\{\sum\limits_{h=1}^{N} a_{h}\left[\frac{\sum\limits_{m=1}^{N} a_{m}\left(P_{i+m+h-1, j}^{n}-P_{i-m+h, j}^{n}\right)}{\xi_{i+(2 h-1) / 2, j}^{n} \rho_{i+(2 h-1) / 2, j}^{n}}-\frac{\sum\limits_{m=1}^{N} a_{m}\left(P_{i+m-h, j}^{n}-P_{i-m-h+1, j}^{n}\right)}{\xi_{i-(2 h-1) / 2, j}^{n} \rho_{i-(2 h-1) / 2, j}^{n}}\right]\right\}+\\ & \frac{a}{\xi_{z, j} d^{2}}\left\{\sum\limits_{h=1}^{N} a_{h}\left[\frac{\sum\limits_{m=1}^{N} a_{m}\left(P_{i, j+m+h-1}^{n}-P_{i, j-m+h}^{n}\right)}{\xi_{i, j+(2 h-1) / 2}^{n} \rho_{i, j+(2 h-1) / 2}^{n}}-\frac{\sum\limits_{m=1}^{N} a_{m}\left(P_{i, j+m-h}^{n}-P_{i, j-m-h+1}^{n}\right)}{\xi_{i, j-(2 h-1) / 2}^{n} \rho_{i, j-(2 h-1) / 2}^{n}}\right]\right\}+\\ & \frac{1-a}{\xi_{x, i} 2 d^{2}}\left\{\sum\limits_{h=1}^{N} a_{h}\left[\frac{\sum\limits_{m=1}^{N} a_{m}\left(P_{i+m+h-1, j-m-h+1}^{n}-P_{i-m+h, j}^{n}\right)}{\xi_{i+(2 h-1) / 2, j-(2 h-1) / 2}^{n} \rho_{i+(2 h-1) / 2, j-(2 h-1) / 2}^{n}}-\frac{\sum\limits_{m=1}^{N} a_{m}\left(P_{i+m-h, j}^{n}-P_{i-m-h+1, j+m+h-1}^{n}\right)}{\xi_{i-(2 h-1) / 2, j+(2 h-1) / 2}^{n} \rho_{i-(2 h-1) / 2, j+(2 h-1) / 2}^{n}}\right]+\right.\\ & \left.\sum\limits_{h=1}^{N} a_{h}\left[\frac{\sum\limits_{m=1}^{N} a_{m}\left(P_{i+m+h-1, j+m+h-1}^{n}-P_{i-m+h, j}^{n}\right)}{\xi_{i+(2 h-1) / 2, j+(2 h-1) / 2}^{n} \rho_{i+(2 h-1) / 2, j+(2 h-1) / 2}^{n}}-\frac{\sum\limits_{m=1}^{N} a_{m}\left(P_{i+m-h, j}^{n}-P_{i-m-h+1, j-m-h+1}^{n}\right)}{\xi_{i-(2 h-1) / 2, j-(2 h-1) / 2}^{n} \rho_{i-(2 h-1) / 2, j-(2 h-1) / 2}^{n}}\right]\right\}+\\ & \frac{1-a}{\xi_{z, j} 2 d^{2}}\left\{\sum\limits_{h=1}^{N} a_{h}\left[\frac{\sum\limits_{m=1}^{N} a_{m}\left(P_{i+m+h-1, j-m-h+1}^{n}-P_{i-m+h, j}^{n}\right)}{\xi_{i+(2 h-1) / 2, j-(2 h-1) / 2}^{n} \rho_{i+(2 h-1) / 2, j-(2 h-1) / 2}^{n}}-\frac{\sum\limits_{m=1}^{N} a_{m}\left(P_{i+m-h, j}^{n}-P_{i-m-h+1, j+m+h-1}^{n}\right)}{\xi_{i-(2 h-1) / 2, j+(2 h-1) / 2}^{n} \rho_{i-(2 h-1) / 2, j+(2 h-1) / 2}^{n}}\right]+\right.\\ & \left.\sum\limits_{h=1}^{N} a_{h}\left[\frac{\sum\limits_{m=1}^{N} a_{m}\left(P_{i+m+h-1, j+m+h-1}^{n}-P_{i-m+h, j}^{n}\right)}{\xi_{i+(2 h-1) / 2, j+(2 h-1) / 2}^{n} \rho_{i+(2 h-1) / 2, j+(2 h-1) / 2}^{n}}-\frac{\sum\limits_{m=1}^{N} a_{m}\left(P_{i+m-h, j}^{n}-P_{i-m-h+1, j-m-h+1}^{n}\right)}{\xi_{i-(2 h-1) / 2, j-(2 h-1) / 2}^{n} \rho_{i-(2 h-1) / 2, j-(2 h-1) / 2}^{n}}\right]\right\} \end{aligned} $ | (28) |
频率—空间域二维声波方程解析解为
| $ G_{2}(x, z, \omega)=\frac{\mathrm{i}}{4} H_{0}^{(1)}(k|r|) $ | (29) |
式中:G2表示频率域解析波场;r满足r2=(x-xs)2 +(z-zs)2,且(xs,zs)为震源位置坐标;H0(1)=J0+iY0为第一类0阶Hankel函数,其中J0、Y0为第一、第二类Bessel函数。
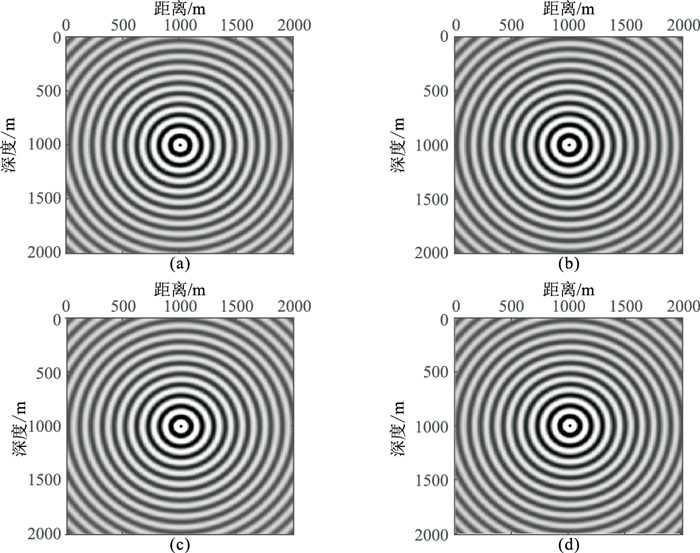
将二阶交错网格法和混合网格法的数值模拟结果与解析解结果进行对比(图 5和图 6),可知二阶交错网格法和混合网格法的模拟精度与解析解结果总体相差不大,具有较高模拟精度,且混合网格法的模拟精度明显好于二阶交错网格法。
|
图 5 二阶交错(a)、四阶(b)、混合(c)三种网格及解析法(d)得到的频率切片(f=30Hz)对比 |
|
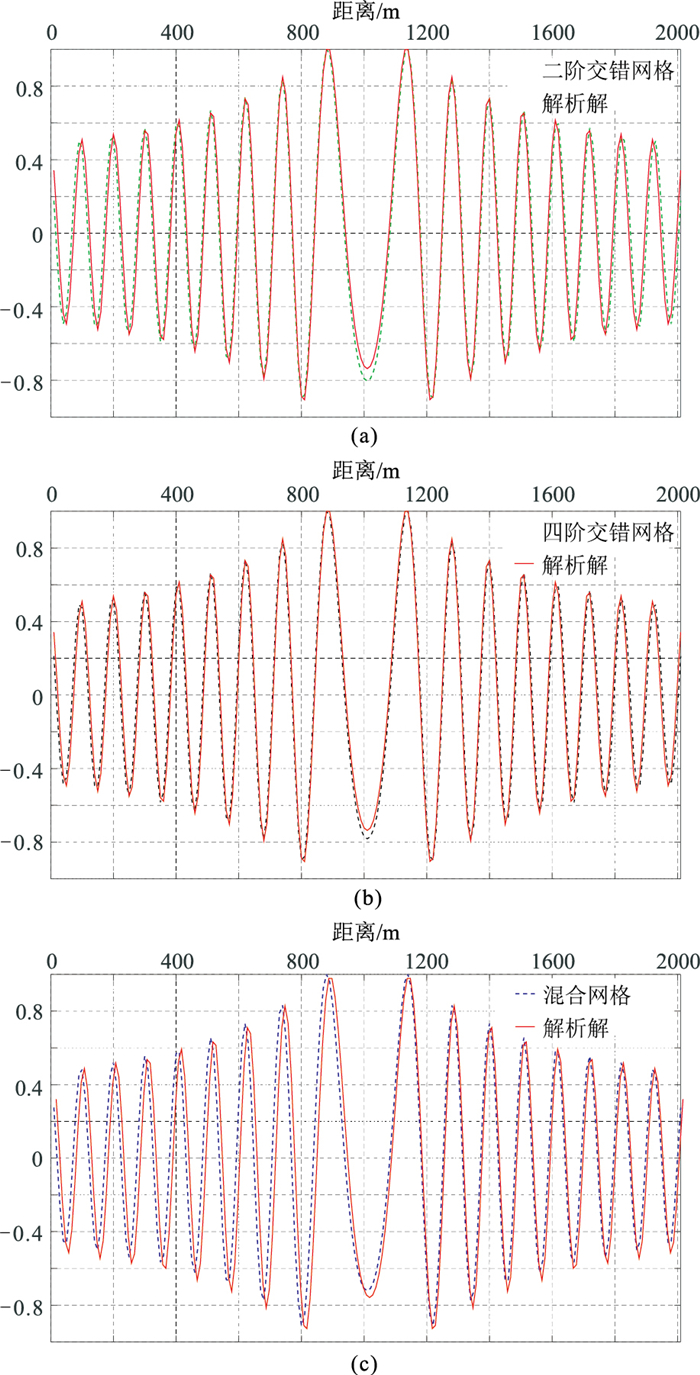
图 6 二阶交错(a)、四阶交错(b)、混合(c)三种网格及其解析解的频率切片抽道(第81道)对比 |
为有效压制数值模拟过程中的频散现象,同时提高模拟精度和效率,须通过频散分析确定合适的模拟参数。以四阶交错网格差分法为例,将平面简谐波解P=P0e-i(kx+kz)(e为自然常数)代入式(17)所示四阶交错网格离散方程,并假设dx=dz=d,其中dx、dz分别为x和z方向的空间采样间隔,θ为传播角度,k为波数,α1=9/8、α2=-1/24为差分系数,离散情况下有Pi,j=P0e-idk(isinθ+jcosθ),得到频散方程
| $ \begin{aligned} \omega^{2}&(k)=\frac{v^{2}}{d^{2}}\left[4 \alpha_{1} \alpha_{1}-2 \alpha_{1} \alpha_{1} \cos (k d \sin \theta)+\right. \\ &4 \alpha_{1} \alpha_{2} \cos (k d \sin \theta)-4 \alpha_{1} \alpha_{2} \cos (2 k d \sin \theta)- \\ &2 \alpha_{2} \alpha_{2} \cos (3 k d \sin \theta)+4 \alpha_{2} \alpha_{2}-2 \alpha_{1} \alpha_{1} \cos (k d \cos \theta)+ \\ &4 \alpha_{1} \alpha_{2} \cos (k d \cos \theta)-4 \alpha_{1} \alpha_{2} \cos (2 k d \cos \theta)- \\ &\left.2 \alpha_{2} \alpha_{2} \cos (3 k d \cos \theta)\right] \end{aligned} $ | (30) |
定义数值相速度和群速度分别为vph=ω/k和vgr=∂ω/∂k,可得
| $ \begin{aligned} \frac{v_{\mathrm{ph}}^{2}}{v^{2}}=& \frac{G^{2}}{4 {\rm{ \mathsf{ π} }}^{2}}\left[4 \alpha_{1} \alpha_{1} \sin ^{2}\left(\frac{{\rm{ \mathsf{ π} }}}{G} \sin \theta\right)+8 \alpha_{1} \alpha_{2} \sin ^{2}\left(\frac{{\rm{ \mathsf{ π} }}}{G} \sin \theta\right)-\right.\\ & 8 \alpha_{1} \alpha_{2} \sin ^{2}\left(2 \frac{{\rm{ \mathsf{ π} }}}{G} \sin \theta\right)+4 \alpha_{2} \alpha_{2} \sin ^{2}\left(3 \frac{{\rm{ \mathsf{ π} }}}{G} \sin \theta\right)+\\ & 4 \alpha_{1} \alpha_{1} \sin ^{2}\left(\frac{{\rm{ \mathsf{ π} }}}{G} \cos \theta\right)+8 \alpha_{1} \alpha_{2} \sin ^{2}\left(\frac{{\rm{ \mathsf{ π} }}}{G} \cos \theta\right)-\\ &\left.8 \alpha_{1} \alpha_{2} \sin ^{2}\left(2 \frac{{\rm{ \mathsf{ π} }}}{G} \cos \theta\right)+4 \alpha_{2} \alpha_{2} \sin ^{2}\left(3 \frac{{\rm{ \mathsf{ π} }}}{G} \cos \theta\right)\right] \end{aligned} $ | (31) |
式中G=λ/d=2π/(k/d),为每个波长内的网格数。
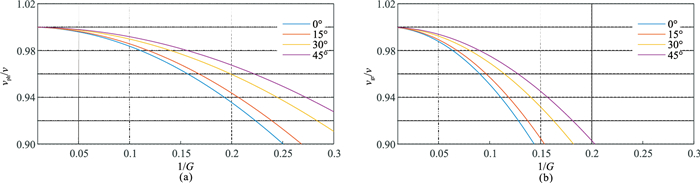
同理,可对二阶交错网格法及混合网格法进行分析,得到如图 7~图 9所示归一化相速度和群速度频散曲线。由图可知相同采样间隔情况下四阶交错网格法和混合网格法的数值频散情况远优于二阶交错网格。
|
图 7 二阶交错网格法求取的归一化相速度(a)和归一化群速度(b)频散曲线 |
|
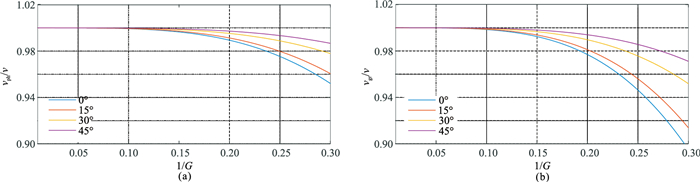
图 8 四阶交错网格法求取的归一化相速度(a)和归一化群速度(b)频散曲线 |
|
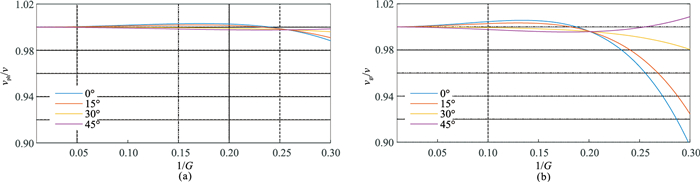
图 9 混合网格法求取的归一化相速度(a)和归一化群速度(b)频散曲线 |
在频率域有限差分模拟过程中,大规模稀疏矩阵的结构直接影响矩阵方程的求解,而矩阵结构的复杂度与空间导数的近似方法密切相关。表 2对比了三种差分格式对应的阻抗矩阵特征,其中nx为水平方向的网格点数。从非零条带的分布可以看出相较于二阶交错网格,混合网格非零条带分布复杂程度稍有增加,而四阶交错网格非零条带分布复杂度大大增加,这也相应的反映在了计算时间上。
|
|
表 2 三种差分格式对应的阻抗矩阵特征 |
图 10对比了三种差分格式对应的阻抗矩阵示意图,其中模型网格尺寸为15×15,即对应于一个225阶矩阵。图中可见,相较于二阶格式矩阵,四阶格式的带宽增加了三倍,而混合网格格式的矩阵带宽仅稍有增加,这极大降低求解相应线性方程组的计算量和内存耗用量。

|
图 10 二阶(a)、四阶(b)、混合(c)三种差分格式对应的阻抗矩阵示意图 |
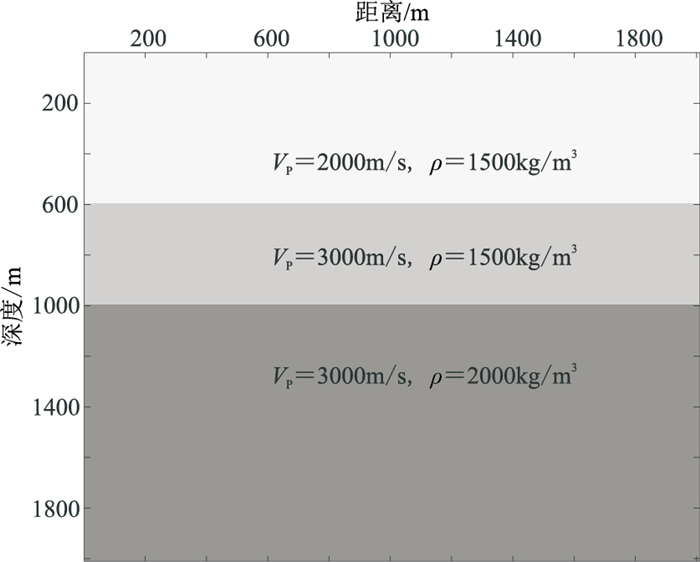
构建一个200×200网格单元的简单层状模型(图 11),震源在(1010m,210m)处,空间步长统一为10m,震源采用主频为20Hz的雷克子波(图 11)。
|
图 11 层状模型 |
图 12为层状介质模型得到的30Hz频率切片,可观察到速度界面和密度界面反射现象。
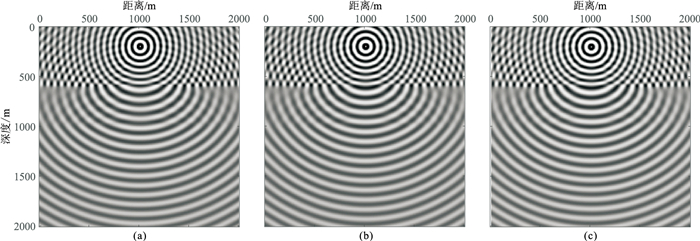
|
图 12 二阶交错(a)、四阶交错(b)、混合(c)三种网格对应的层状模型f=30Hz频率切片 |
图 13为频率切片经傅里叶逆变换得到的时间域t=500ms波场快照,速度层界面和密度层界面反射波明显,从中可见二阶交错网格法得到的时间域波场存在明显频散现象,模拟精度低,相比之下四阶交错网格法和混合网格法得到的波场快照显示数值频散得到有效压制,模拟精度明显提高。

|
图 13 二阶交错(a)、四阶交错(b)、混合(c)三种网格对应的层状模型t=500ms波场快照 |
图 14为层状介质模型得到的共中心点道集,其中直达波、速度层反射波和密度层反射波同相轴明显,二阶交错网格法得到的道集中数值频散干扰明显,而四阶交错网格和混合网格法则有效压制了数值频散。
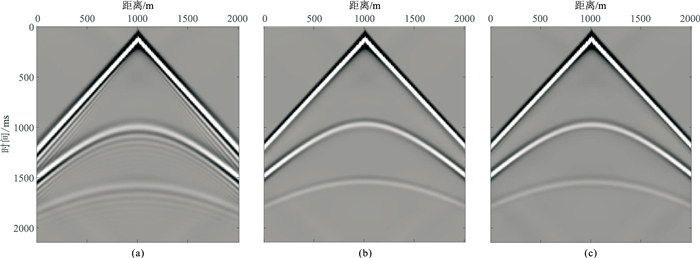
|
图 14 二阶交错(a)、四阶交错(b)、混合(c)三种网格对应的层状模型地震记录 |
图 15是对三个共中心点道集抽取第81道记录对比,结果显示四阶交错网格法和混合网格法模拟精度接近且远高于二阶交错网格法,二阶交错网格法在反射波处存在明显数值频散现象。

|
图 15 二阶交错(红)、四阶交错(黑)、混合(绿)三种网格对应的层状模型地震记录抽道对比(第81道) |
因此,对层状模型的正演模拟测试说明了方法的精度和准确性。
4.2 Marmousi模型为进一步验证和说明本文方法对复杂模型的适用性和稳定性,采用复杂Marmousi模型(图 16)进行测试。模型尺寸为500×250,网格间距为10m,震源采用主频为20Hz的雷克子波,震源激发点位于坐标(2510m,251m)处,检波器置于模型表面。

|
图 16 纵波速度(a)和密度(b)表征的Marmousi模型 |
图 17为由该模型得到的30Hz频率切片,从中可观察到界面反射现象。

|
图 17 二阶交错(a)、四阶交错(b)、混合(c)三种网格对应的Marmousi模型f=30Hz频率切片 |
图 18为频率片经过傅里叶逆变换得到的时间域t=500ms波场快照,其界面反射波明显,且可见二阶交错网格法得到的时间域波场存在明显的频散现象,模拟精度低,相比之下四阶交错网格法和混合网格法得到的波场快照显示数值频散得到有效压制,模拟精度明显提高。

|
图 18 二阶交错(a)、四阶交错(b)、混合(c)三种网格对应的Marmousi模型t=500ms波场快照 |
图 19为由模型得到的共中心点道集,其中直达波、反射波同相轴明显,二阶交错网格法所得道集中数值频散干扰明显,而四阶交错网格法和混合网格法则有效压制了数值频散。
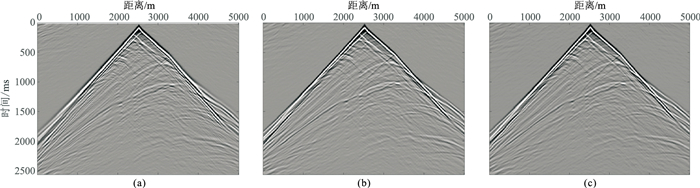
|
图 19 二阶交错(a)、四阶交错(b)、混合(c)三种网格对应的Marmousi模型共中心点道集记录 |
总之,对Marmousi模型进行正演模拟测试验证了方法的稳定性和可靠性。
5 结论针对频率—空间域非均匀声介质中地震波有限差分正演模拟问题,本文运用交错网格思想,分别用笛卡尔坐标系提高差分阶数和结合45°旋转坐标系提高差分阶数两种方式提高模拟精度,导出两类方法的有限差分公式,对比分析了两类方法的计算精度和效率,并通过模型测试验证了方法的精度和稳定性,得到如下认识。
(1) 考虑密度参数在油气地球物理勘探中的重要性,本文研究频率—空间域非均匀声介质地震波有限差分正演模拟,并构建了分别应用两种方式提高正演模拟精度的一般框架,得到了任意阶数下两种方法的一般差分公式,对后续正演和反演研究都具有现实意义。
(2) 对交错网格和混合网格模型的数值频散分析表明,混合网格的相速度和群速度的数值离散度都小于二阶交错网格,因为混合网格法将笛卡尔坐标系和旋转坐标系上的两种二阶交错网格模板线性组合,同时对质量加速度项进行了加权平均,加强了两种交错网格模板之间的耦合。
(3) 几种差分方法的计算效率由矩阵结构复杂度决定,也就是由离散模板几何的紧凑性控制,构建网格时涉及的周围点越少越好。二阶的混合网格模板需9个网格点,四阶近似的交错网格模板需13个网格点,因此用于矩阵分解的内存需求和浮点运算显著增加。在内存占用和计算效率两方面,混合网格策略对于二维频率域有限差分建模均展现出明显的优越性。
| [1] |
任浩然, 王华忠, 龚婷. 标量地震波频率—空间域有限差分法数值模拟[J]. 石油物探, 2009, 48(1): 20-26, 15. REN Haoran, WANG Huazhong, GONG Ting. Seismic modeling of scalar seismic wave propagation with finite difference scheme in frequency-space domain[J]. Geophysical Prospecting for Petroleum, 2009, 48(1): 20-26, 15. DOI:10.3969/j.issn.1000-1441.2009.01.004 |
| [2] |
李青阳, 吴国忱, 段沛然, 等. 基于互相关目标函数的反射波波形反演[J]. 石油地球物理勘探, 2020, 55(4): 754-765. LI Qingyang, WU Guochen, DUAN Peiran, et al. Reflection waveform inversion based on cross-correlation misfit function[J]. Oil Geophysical Prospecting, 2020, 55(4): 754-765. |
| [3] |
HUSTEDT B, OPERTO S, VIRIEUX J. Mixed-grid and staggered-grid finite-difference methods for frequency-domain acoustic wave modelling[J]. Geophysical Journal International, 2004, 157(3): 1269-1296. DOI:10.1111/j.1365-246X.2004.02289.x |
| [4] |
LUO Y, SCHUSTER G. Parsimonious staggered grid finite-differencing of the wave equation[J]. Geophysical Research Letters, 1990, 17(2): 155-158. DOI:10.1029/GL017i002p00155 |
| [5] |
PRATT G R, WORTHINGTON M H. Inverse theory applied to multi-source cross-hole tomography.part 1:acoustic wave-equation method[J]. Geophysical Prospecting, 1990, 38(3): 287-310. DOI:10.1111/j.1365-2478.1990.tb01846.x |
| [6] |
PRATT R G. Inverse theory applied to multi-source cross-hole tomography.part 2:elastic wave-equation method[J]. Geophysical Prospecting, 1990, 38(3): 311-329. DOI:10.1111/j.1365-2478.1990.tb01847.x |
| [7] |
JO C H, SHIN C, SUH J H. An optimal 9-point, finite-difference, frequency-space, 2-D scalar wave extrapolator[J]. Geophysics, 1996, 61(2): 529-537. DOI:10.1190/1.1443979 |
| [8] |
ŠTEKL I, PRATT R G. Accurate viscoelastic mode-ling by frequency-domain finite differences using rotated operators[J]. Geophysics, 1998, 63(5): 1779-1794. DOI:10.1190/1.1444472 |
| [9] |
SHIN C, SOHN H. A frequency-space 2-D scalar wave extrapolator using extended 25-point finite-difference operator[J]. Geophysics, 1998, 63(1): 289-296. DOI:10.1190/1.1444323 |
| [10] |
吴国忱, 梁锴. VTI介质频率—空间域准P波正演模拟[J]. 石油地球物理勘探, 2005, 40(5): 535-545. WU Guochen, LIANG Kai. Quasi P-wave forward modeling in frequency-space domain in VTI media[J]. Oil Geophysical Prospecting, 2005, 40(5): 535-545. DOI:10.3321/j.issn:1000-7210.2005.05.010 |
| [11] |
殷文, 印兴耀, 吴国忱, 等. 高精度频率域弹性波方程有限差分方法及波场模拟[J]. 地球物理学报, 2006, 49(2): 561-568. YIN Wen, YIN Xingyao, WU Guochen, et al. The method of finite difference of high precision elastic wave equations in the frequency domain and wave-field simulation[J]. Chinese Journal of Geophysics, 2006, 49(2): 561-568. DOI:10.3321/j.issn:0001-5733.2006.02.032 |
| [12] |
梁锴, 吴国忱, 印兴耀. TTI介质qP波方程频率—空间域加权平均有限差分算子[J]. 石油地球物理勘探, 2007, 42(5): 516-525. LIANG Kai, WU Guochen, YIN Xingyao. Weighted mean finite-difference operator of qP wave equation in frequency-space domain for TTI medium[J]. Oil Geophysical Prospecting, 2007, 42(5): 516-525. DOI:10.3321/j.issn:1000-7210.2007.05.007 |
| [13] |
吴建鲁, 吴国忱. 频率域声—弹耦合地震波波动方程有限差分方法[J]. 地球物理学报, 2018, 61(6): 2396-2408. WU Jianlu, WU Guochen. Finite difference method for acoustic-elastic coupled equations of seismic waves in the frequency domain[J]. Chinese Journal of Geophysics, 2018, 61(6): 2396-2408. |
| [14] |
李青阳, 吴国忱, 段沛然. 准规则网格高阶有限差分法非均质弹性波波场模拟[J]. 石油地球物理勘探, 2019, 54(3): 539-550. LI Qingyang, WU Guochen, DUAN Peiran. Elastic wavefield forward modeling in heterogeneous media based on the quasi-regular grid high-order finite difference[J]. Oil Geophysical Prospecting, 2019, 54(3): 539-550. |
| [15] |
张衡, 刘洪, 刘璐, 等. 基于平均导数方法的声波方程频率域高阶正演[J]. 地球物理学报, 2014, 57(5): 1599-1611. ZHANG Heng, LIU Hong, LIU Lu, et al. Frequency domain acoustic equation high-order modeling based on an average-derivative method[J]. Chinese Journal of Geophysics, 2014, 57(5): 1599-1611. |
| [16] |
刘璐, 刘洪, 刘红伟. 优化15点频率—空间域有限差分正演模拟[J]. 地球物理学报, 2013, 56(2): 644-652. LIU Lu, LIU Hong, LIU Hongwei. Optimal 15-point finite difference forward modeling in frequency-space domain[J]. Chinese Journal of Geophysics, 2013, 56(2): 644-652. |
| [17] |
马晓娜, 李志远, 谷丙洛, 等. 2D声波频率域数值模拟中几种有限差分方法的对比分析[J]. 地球物理学进展, 2015, 30(2): 878-888. MA Xiaona, LI Zhiyuan, GU Bingluo, et al. Comparisons and analysis of several optimization finite-differencing schemes in 2D acoustic frequency-domain numerical modeling[J]. Progress in Geophysics, 2015, 30(2): 878-888. |
| [18] |
范娜, 成景旺, 秦雷, 等. 一种优化的频率域三维声波有限差分模拟方法[J]. 地球物理学报, 2018, 61(3): 1095-1108. FAN Na, CHENG Jingwang, QIN Lei, et al. An optimal method for frequency-domain finite-difference solution of 3D scalar wave equation[J]. Chinese Journal of Geophysics, 2018, 61(3): 1095-1108. |
| [19] |
BERENGER J P. A perfectly matched layer for the absorption of electromagnetic waves[J]. Journal of Computational Physics, 1994, 114(2): 185-200. DOI:10.1006/jcph.1994.1159 |
| [20] |
VIRIEUX J. SH-wave propagation in heterogeneous media: velocity-stress finite-difference method[J]. Exploration Geophysics, 1984, 15(4): 265. |
| [21] |
SAENGER E H, GOLD N, SHAPIRO S A. Mode-ling the propagation of elastic waves using a modified finite-difference grid[J]. Wave Motion, 2000, 31(1): 77-92. |



 吴国忱,山东省青岛市经济技术开发区长江西路66号中国石油大学(华东)地球科学与技术学院,266580。Email:
吴国忱,山东省青岛市经济技术开发区长江西路66号中国石油大学(华东)地球科学与技术学院,266580。Email:
