地下介质普遍具有非弹性和各向异性特征,对地震波的传播速度、振幅和相位等产生影响,因此研究介质的各向异性和黏滞性对于地震波场数值模拟、偏移成像和波形反演具有重要意义。
TI(Transversely Isotropic,横向各向同性)介质是一种常用的地球介质近似模型,按照对称轴的方向可以划分为VTI(垂直对称轴)、HTI(水平对称轴)和TTI(倾斜对称轴)三种类型。由于各向异性弹性波方程涉及波场变量多、计算效率低、多波信息复杂等,因此目前主要采用伪声波方程进行相关计算,该类方程是直接将TI介质耦合频散关系中的横波速度置为0简化而来[1]。基于该思想,导出了多种改进版本的各向异性伪声波方程[2-6]。但是当介质参数不满足椭圆假设时,大多数伪声波方程模拟容易出现噪声干扰及数值不稳定。发展各向异性纯声波方程能够较好地解决伪声波方程存在的问题,其核心思想是从原始的TI介质P-SV波频散关系中解耦出纯P波频散关系,获得对应的纯声波方程,采用不同数值算法求解,以获得纯声波响应[7-10]。相比传统伪声波方程,纯声波方程能够彻底消除伪横波干扰及数值不稳定,近年来在各向异性波场模拟及成像中受到较多关注[11-15]。目前关于各向异性纯声波方程的研究主要集中于模拟精度和计算效率的相互平衡,以及如何进一步的推广应用。
在考虑地下介质各向异性特征的同时,地层的黏滞性容易引起地震波的振幅衰减和相位畸变。在地震频带内,广义标准线性体和常Q模型被广泛用于描述介质的衰减特性[16-19]。多位学者利用差分法求解了基于标准线性体推导的黏声或黏弹方程[20-23]。杜启振等[24]采用有限元法求解黏弹各向异性波动方程;Zhu等[25]采用差分法求解了基于标准线性体的黏声和黏弹波动方程,并与常Q理论计算的参考解进行对比分析。相比于标准线性体模型,常Q模型对介质衰减描述更准确,但是相应的理论推导和数值计算更复杂[25]。Carcione[26]采用伪谱法求解了均匀介质中常Q黏声波方程;Zhu等[27]利用伪谱法模拟了振幅和衰减项相互独立的常Q黏声波方程。为了同时兼顾常Q黏滞声波方程的计算精度和效率,不同学者提出了相应的解决策略[28-29]。
基于标准线性体理论,本文首先介绍了各向同性介质中能表征振幅衰减和相位畸变的三维黏滞声波方程;其次,将泊松算子和有限差分联合用于求解三维TTI介质纯声波方程;最后,结合各向同性黏滞声波方程和TTI介质纯声波方程,推导了适用于各向异性介质、同时考虑振幅衰减和相位畸变的三维TTI黏滞介质纯声波方程。数值算例表明本文方法能够同时考虑地震波的振幅衰减和相位畸变,模拟精度高,适用于复杂模型的P波模拟。
1 理论方法 1.1 各向同性介质三维黏滞声波方程地球介质对地震波的衰减作用不仅体现在对振幅的衰减,同样会引起相位的畸变[16-23]。在各向同性介质中,基于标准线性体理论的黏滞声波方程,Wang等[20]推导了一种同时包含振幅衰减和相位畸变的简化黏滞声波方程,其三维形式为
| $ \begin{gathered} \frac{\partial^{2} P}{\partial t^{2}}=v^{2} \nabla^{2} P-\frac{\tau v}{2} \sqrt{-\nabla^{2}} \frac{\partial}{\partial t} P- \\ \frac{1-\sqrt{Q^{2}+1}}{Q^{2}} v^{2} \nabla^{2} P \end{gathered} $ | (1) |
式中:P为纵波波场;v为纵波速度;∇2为三维拉普拉斯算子;Q为品质因子;τ为与应力和应变松弛时间τσ、τε相关的参数
| $ \left\{\begin{array}{l} \tau=\frac{\tau_{\varepsilon}}{\tau_{\sigma}}-1 \\ \tau_{\varepsilon}=\frac{1}{\omega_{0} Q}\left(\sqrt{Q^{2}+1}+1\right) \\ \tau_{\sigma}=\frac{1}{\omega_{0} Q}\left(\sqrt{Q^{2}+1}-1\right) \end{array}\right. $ | (2) |
其中ω0为参考角频率。
将式(1)分解为以下三个方程[20]
| $ \frac{\partial^{2} P}{\partial t^{2}}=v^{2} \nabla^{2} P $ | (3) |
| $ \frac{\partial^{2} P}{\partial t^{2}}=v^{2} \nabla^{2} P-\frac{1-\sqrt{Q^{2}+1}}{Q^{2}} v^{2} \nabla^{2} P $ | (4) |
| $ \frac{\partial^{2} P}{\partial t^{2}}=v^{2} \nabla^{2} P-\frac{\tau v}{2} \sqrt{-\nabla^{2}} \frac{\partial}{\partial t} P $ | (5) |
式(3)为传统的声波方程,式(4)为仅包含相位畸变项的黏滞声波方程,式(5)是仅包含振幅衰减项的黏滞声波方程。
采用有限差分离散式(1)中的拉普拉斯算子,采用伪谱法求解算子
| $ \begin{aligned} P_{0,0,0}^{1}=& 2 P_{0,0,0}^{0}-P_{0,0,0}^{-1}-\frac{\tau v \Delta t^{2}}{2} \times \\ & F^{-1}\left[|\boldsymbol{k}| F\left(\frac{P_{0,0,0}^{0}-P_{0,0,0}^{-1}}{\Delta t}\right)\right]+\\ & \frac{v^{2} \Delta t^{2}}{h^{2}}\left(1-\frac{1-\sqrt{Q^{2}+1}}{Q^{2}}\right) \times \\ & {\left[3 c_{0} P_{0,0,0}^{0}+\sum\limits_{I=1}^{M} c_{I}\left(P_{-I, 0,0}^{0}+P_{I, 0,0}^{0}+\right.\right.} \\ &\left.\left.P_{0,-I, 0}^{0}+P_{0, I, 0}^{0}+P_{0,0,-I}^{0}+P_{0,0, I}^{0}\right)\right] \end{aligned} $ | (6) |
式中:F和F-1分别表示傅里叶正、反变换;k为波数矢量;h为空间采样间隔;Δt为时间采样间隔;M为有限差分算子长度的一半;cI为有限差分系数。式(3)~式(5)可以采用类似的递推格式求解。
采用三维各向同性层状模型对上述方程进行测试。模型尺寸为2km×2km×2km,上层速度为2400m/s,品质因子为20,厚度为1km;下层速度为3000m/s,品质因子为40。震源是主频为26Hz的Ricker子波,位于(1.0km,1.0km,0.9km)。图 1为声波(式(3))、仅含相位畸变黏滞声波(式(4))、仅含振幅衰减黏滞声波(式(5))和同时考虑相位畸变和振幅衰减黏滞声波方程(式(1))模拟的波场切片,图 2为四个方程模拟的单道波形对比。由图 1和图 2可以看出:与声波方程的计算结果相比,仅含相位畸变黏滞声波方程仅能模拟相移而无明显振幅差异;仅含振幅损失黏滞声波方程仅能模拟振幅衰减而无明显相移;同时考虑相位畸变和振幅损失的黏滞声波方程能够同时模拟振幅衰减和相位畸变,更精确地描述了黏滞介质的吸收衰减效应。

|
图 1 三维各向同性层状模型四种方程模拟的切片对比 (a)xz平面,y=0.5km;(b)xy平面,z=0.5km;(c)yz平面,x=1km。由左往右依次为式(3)、式(4)、式(5)、式(1) |

|
图 2 四个方程模拟的(x=1.0km,y=0.5km)处波形对比 |
迄今为止,TI介质中常用的声波方程主要是基于伪声波近似推导的,该类方程在各向异性参数不满足近似条件时模拟结果会出现伪横波干扰,甚至模拟过程不稳定[1],尤其是TTI介质。多种改进版本的TI伪声波方程仅能在一定程度上压制干扰,提高稳定性,但不能从根本上解决问题[2-6]。众多研究表明,发展各向异性纯声波方程能够有效消除伪横波污染和不稳定现象[7-15]。相比于显式表达的伪声波方程,纯声波方程通常包含复杂的偏微分算子,常规差分方法很难直接求解。考虑到计算精度与效率,本文应用泊松算子和优化有限差分相结合的方法求解三维各向异性纯声波方程[10]。在TI介质中,为了便于计算,通常采用一阶泰勒展开对解耦后的纯声波频散关系进行近似,三维TTI介质近似纯声波频散关系可以简化为[7-12]
| $ \begin{aligned} \frac{\omega^{2}}{v_{\mathrm{P} 0}^{2}}=&(1+2 \varepsilon)\left(\hat{K}{}_{x}^{2}+\hat{K}{}_{y}^{2}\right)+\hat{K}{}_{z}^{2}-\\ &\frac{2(\varepsilon-\delta)\left(\hat{K}{}_{x}^{2}+\hat{K}{}_{y}^{2}\right) \hat{K}{}_{z}^{2}}{\hat{K}{}_{x}^{2}+\hat{K}{}_{y}^{2}+\hat{K}{}_{z}^{2}} \end{aligned} $ | (7) |
式中:vP0为沿对称轴方向的纵波速度;ω为角频率;ε和δ为各向异性参数;旋转波数
| $ \left\{\begin{array}{l} \hat{K}_{x}=K_{x} \cos \theta \cos \varphi+K_{y} \cos \theta \sin \varphi-K_{z} \sin \theta \\ \hat{K}_{y}=-K_{x} \sin \varphi+K_{y} \cos \varphi \\ \hat{K}_{z}=K_{x} \sin \theta \cos \varphi+K_{y} \sin \theta \sin \varphi+K_{z} \cos \theta \end{array}\right. $ | (8) |
其中:Kx、Ky和Kz为正交波数;θ为对称轴倾角;φ为对称轴方位角。
将式(7)变换到时间—空间域,有
| $ \begin{gathered} \frac{1}{v_{\mathrm{P} 0}^{2}} \frac{\partial^{2} P}{\partial t^{2}}=(1+2 \varepsilon)\left(R_{x} P+R_{y} P\right)+R_{z} P- \\ 2(\varepsilon-\delta) \frac{\left(R_{x}+R_{y}\right) R_{z}}{R_{x}+R_{y}+R_{z}} P \end{gathered} $ | (9) |
式中算子Rx、Ry和Rz的形式为
| $ \begin{aligned} R_{x}=& \cos ^{2} \theta \cos ^{2} \varphi \frac{\partial^{2}}{\partial x^{2}}+\cos ^{2} \theta \sin ^{2} \varphi \frac{\partial^{2}}{\partial y^{2}}+\\ & \sin ^{2} \theta \frac{\partial^{2}}{\partial z^{2}}+\cos ^{2} \theta \sin 2 \varphi \frac{\partial^{2}}{\partial x \partial y}-\\ & \sin 2 \theta \cos \varphi \frac{\partial^{2}}{\partial x \partial z}-\sin 2 \theta \sin \varphi \frac{\partial^{2}}{\partial y \partial z} \end{aligned} $ | (10) |
| $ R_{y}=\sin ^{2} \varphi \frac{\partial^{2}}{\partial x^{2}}+\cos ^{2} \varphi \frac{\partial^{2}}{\partial y^{2}}-\sin 2 \varphi \frac{\partial^{2}}{\partial x \partial y} $ | (11) |
| $ \begin{aligned} R_{z}=& \sin ^{2} \theta \cos ^{2} \varphi \frac{\partial^{2}}{\partial x^{2}}+\sin ^{2} \theta \sin ^{2} \varphi \frac{\partial^{2}}{\partial y^{2}}+\\ & \cos ^{2} \theta \frac{\partial^{2}}{\partial z^{2}}+\sin ^{2} \theta \sin 2 \varphi \frac{\partial^{2}}{\partial x \partial y}+\\ & \sin 2 \theta \cos \varphi \frac{\partial^{2}}{\partial x \partial z}+\sin 2 \theta \sin \varphi \frac{\partial^{2}}{\partial y \partial z} \end{aligned} $ | (12) |
引入辅助波场H,式(9)可分解为两个方程[8]
| $ v_{\mathrm{P} 0}^{2}\left(R_{x}+R_{y}+R_{z}\right) H=P $ | (13) |
| $ \begin{aligned} \frac{1}{v_{\mathrm{P} 0}^{2}} \frac{\partial^{2} P}{\partial t^{2}}=&(1+2 \varepsilon)\left(R_{x}+R_{y}\right) P+R_{z} P-\\ & 2(\varepsilon-\delta) v_{\mathrm{P} 0}^{2}\left(R_{x} R_{z}+R_{y} R_{z}\right) H \end{aligned} $ | (14) |
式(13)为隐式方程,其运算过程需要求解线性方程组。为了提高效率,本文结合泊松算子实现[10]。
将式(13)和式(14)整理为
| $ \nabla^{2} H=P $ | (15) |
| $ \begin{aligned} \frac{\partial^{2} P}{\partial t^{2}}=&(1+2 \varepsilon) v_{\mathrm{P} 0}^{2}\left(R_{x}+R_{y}\right) P+v_{\mathrm{P} 0}^{2} R_{z} P-\\ & 2(\varepsilon-\delta) v_{\mathrm{P} 0}^{2}\left(R_{x} R_{z}+R_{y} R_{z}\right) H \end{aligned} $ | (16) |
式(15)和式(16)组成新的TTI介质三维纯声波方程,后者可采用优化有限差分求解。前者为泊松方程,基于前人的研究,可以通过泊松算子求解,其实现流程可分为以下步骤[10]。
(1) 基于五点差分法离散式(15)
| $ \begin{aligned} &6 H_{i, j, k}-H_{i+1, j, k}-H_{i-1, j, k}-H_{i, j+1, k}-H_{i, j-1, k}- \\ &\ \ \ \ H_{i, j, k+1}-H_{i, j, k-1}=-h^{2} P_{i, j, k} \end{aligned} $ | (17) |
式中:i、j、k分别为x、y、z方向网格点序号。
(2) 采用正弦变换计算输入波场P的傅里叶响应
| $ \begin{aligned} \hat{P}_{l, m, n}=&-\frac{1}{N_{x} N_{y} N_{z}} \sum\limits_{i=1}^{N_{x}} \sum\limits_{j=1}^{N_{y}} \sum\limits_{k=1}^{N_{z}} P_{i, j, k} \sin \frac{i l {\rm{ \mathsf{ π} }}}{N_{x}} \times \\ & \sin \frac{j m {\rm{ \mathsf{ π} }}}{N_{y}} \sin \frac{k n {\rm{ \mathsf{ π} }}}{N_{z}} \end{aligned} $ | (18) |
式中:Nx、Ny和Nz为三个方向的网格点数;l、m、n为波数域三个方向的网格点序号。
(3) 结合步骤(2)获得的波场响应
| $ \left\{\begin{array}{l} \hat{H}_{l, m, n}=\hat{P}_{l, m, n} / \lambda_{l, m, n} \\ \lambda_{l, m, n}=6-2 \cos \frac{l {\rm{ \mathsf{ π} }}}{N_{x}}-2 \cos \frac{m {\rm{ \mathsf{ π} }}}{N_{y}}-2 \cos \frac{n {\rm{ \mathsf{ π} }}}{N_{z}} \end{array}\right. $ | (19) |
(4) 基于波场响应
| $ \begin{aligned} H_{i, j, k}=& \sum\limits_{l=1}^{N_{x}} \sum\limits_{m=1}^{N_{y}} \sum\limits_{n=1}^{N_{z}} \hat{H}_{l, m, n} \sin \frac{i l {\rm{ \mathsf{ π} }}}{N_{x}} \times \\ & \sin \frac{j m {\rm{ \mathsf{ π} }}}{N_{y}} \sin \frac{k n {\rm{ \mathsf{ π} }}}{N_{z}} \end{aligned} $ | (20) |
通过以上四步,可实现泊松方程式(15)的求解。采用优化有限差分可实现显式方程式(16)的求解。上述流程能够保证纯声波方程式(15)和式(16)的高效精确求解。
采用三维各向异性层状模型对横波速度为0的伪声波方程[3]、限制性横波速度的伪声波方程[4]和本文的纯声波方程进行测试。模型上层介质参数为:厚度为1.2km,vP0=2400m/s,ε=0.10,δ=0.05,θ=0°,φ=0°;下层介质参数为:厚度为0.8km,vP0=3000m/s,ε=0.10,δ =-0.12,θ=45°,φ=60°。震源是主频为26Hz的Ricker子波,位于(1.0km,1.0km,0.9km)。图 3为不同方程计算的波场切片,可知,基于横波速度为0的伪声波方程和限制性横波速度的伪声波方程不可避免地会出现伪横波干扰,而纯声波方程能够获得高精度P波响应。

|
图 3 三维TTI层状模型中三种方程模拟的切片对比
(a)基于横波速度为0的伪声波方程;(b)基于限制性横波速度的伪声波方程;(c)本文纯声波方程 从左到右依次为:xz平面,y=1.0km;xy平面,z=0.9km;yz平面,x=1.0km |
现有黏滞声波方程主要是针对各向同性介质设计的。对于各向异性介质,尤其是各向异性纯声波方程,相应的黏滞声波方程研究较少。本文将三维各向同性黏滞声波方程与TTI纯声波方程进行结合,推导了适用于三维TTI介质的黏滞声波方程。
纯声波方程式(16)可写为
| $ \frac{\partial^{2} P}{\partial t^{2}}=v_{\mathrm{P} 0}^{2} S(P) $ | (21) |
式中算子S可表述为
| $ \begin{aligned} S(P)=&(1+2 \varepsilon)\left(R_{x}+R_{y}\right) P+R_{z} P-\\ & 2(\varepsilon-\delta)\left(R_{x} R_{z}+R_{y} R_{z}\right) H \end{aligned} $ | (22) |
式(1)中的算子∇2和式(21)中的算子S均是由波场相关的不同偏导数组合而成,因此将各向同性黏滞声波方程式(1)与TTI介质纯声波方程结合,即用算子S替换∇2,可以得到三维TTI介质中简化的黏滞纯声波方程
| $ \begin{aligned} \frac{\partial^{2} P}{\partial t^{2}}=& v_{\mathrm{P} 0}^{2} S(P)-\frac{\tau v_{\mathrm{P} 0}}{2} \sqrt{-\nabla^{2}} \frac{\partial}{\partial t} P-\\ & \frac{1-\sqrt{Q^{2}+1}}{Q^{2}} v_{\mathrm{P} 0}^{2} S(P) \end{aligned} $ | (23) |
类似地,可将式(23)分解为三个方程
| $ \frac{\partial^{2} P}{\partial t^{2}}=v_{\mathrm{P} 0}^{2} S(P) $ | (24) |
| $ \frac{\partial^{2} P}{\partial t^{2}}=v_{\mathrm{P} 0}^{2} S(P)-\frac{1-\sqrt{Q^{2}+1}}{Q^{2}} v_{\mathrm{P} 0}^{2} S(P) $ | (25) |
| $ \frac{\partial^{2} P}{\partial t^{2}}=v_{\mathrm{P} 0}^{2} S(P)-\frac{\tau v_{\mathrm{P} 0}}{2} \sqrt{-\nabla^{2}} \frac{\partial}{\partial t} P $ | (26) |
式(24)为三维TTI纯声波方程,式(25)为仅包含相位畸变的TTI黏滞纯声波方程,式(26)是仅包含振幅衰减的TTI黏滞纯声波方程。利用式(23)即可实现三维TTI黏滞纯声波方程数值模拟。相应的离散方案与前文所述类似。
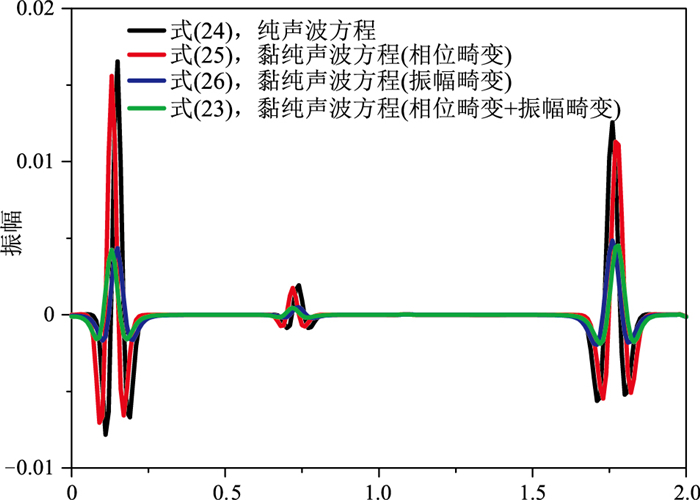
应用三维TTI层状黏滞模型对比式(23)~式(26)数值模拟结果(图 4、图 5)。模型上层介质参数为:厚度为1.2km,vP0=2400m/s,ε=0.10,δ=0.05,θ=0°,φ=0°,Q=20;下层介质参数为:vP0=3000m/s,ε=0.10,δ=-0.12,θ=45°,φ=60°,Q=40。震源是主频为26Hz的Ricker子波,位于(1.0km,1.0km,0.9km)。由图 4、图 5可以看出,与TTI纯声波方程(式(24))的模拟结果相比,仅含相位畸变TTI黏滞纯声波方程(式(25))仅能模拟时移,仅含振幅损失TTI黏滞纯声波方程(式(26))仅能模拟振幅衰减,同时考虑相位畸变和振幅损失TTI黏滞纯声波方程(式(23))能够同时模拟振幅衰减和相位畸变,更精确地描述了三维TTI介质中黏滞纯声波的吸收衰减属性。
|
图 4 三维TTI黏滞层状模型中四个方程模拟的(x=1.0km,y=1.0km)处波形曲线对比 |

|
图 5 三维TTI黏滞层状模型不同方程模拟的波场快照对比 (a)xz平面,y=1.0km;(b)xy平面,z=0.9km;(c)yz平面,x=1.0km。由左往右依次为式(24)、式(25)、式(26)、式(23) |
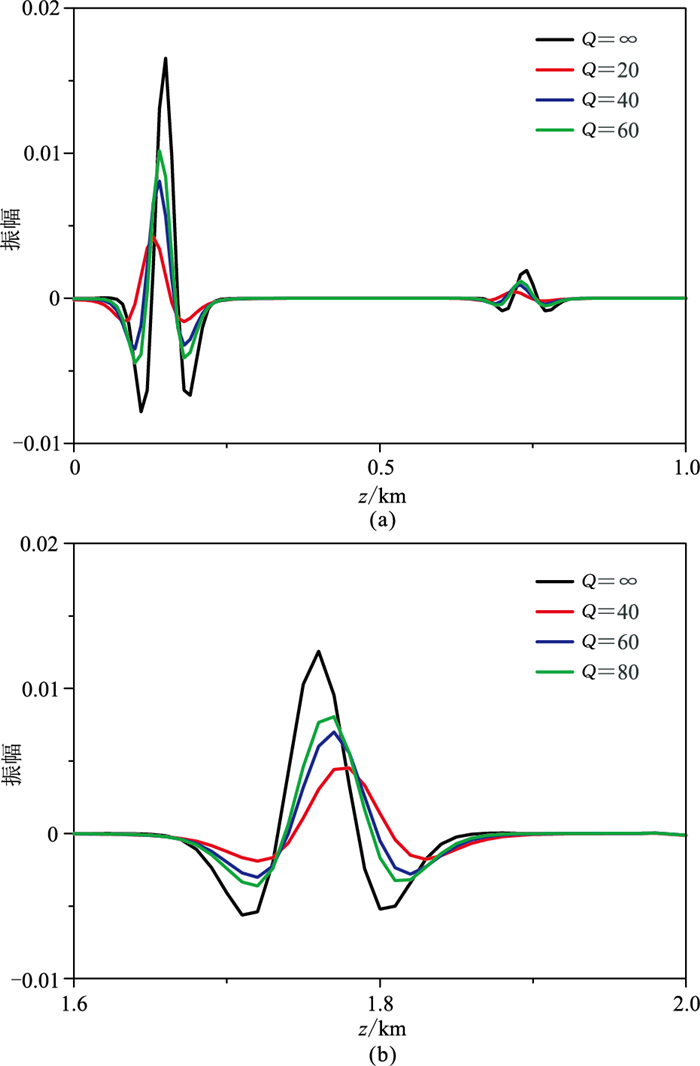
将三维TTI层状黏滞模型上下层品质因子由(20,40)变为(40,60)和(60,80),分析品质因子对波场模拟结果的影响(图 6、图 7)。由图 6、图 7可见,相比于纯声波方程的计算结果(图 4、图 5左),随着品质因子的增大,吸收衰减效应导致地震波的振幅减弱、相位变化的程度降低(图 5右、图 6)。

|
图 6 三维TTI黏滞层状不同Q值模型的简化黏滞纯声波方程模拟的波场快照 (a)xz平面,y=1.0km;(b)xy平面,z=0.9km;(c)yz平面,x=1.0km。左:上下层介质Q为(40,60);右:上下层介质Q为(60,80) |
|
图 7 三维TTI层状不同Q值模型简化黏滞纯声波方程模拟的在(x=1.0km,y=1.0km)处波形对比 (a)上层介质;(b)下层介质 |
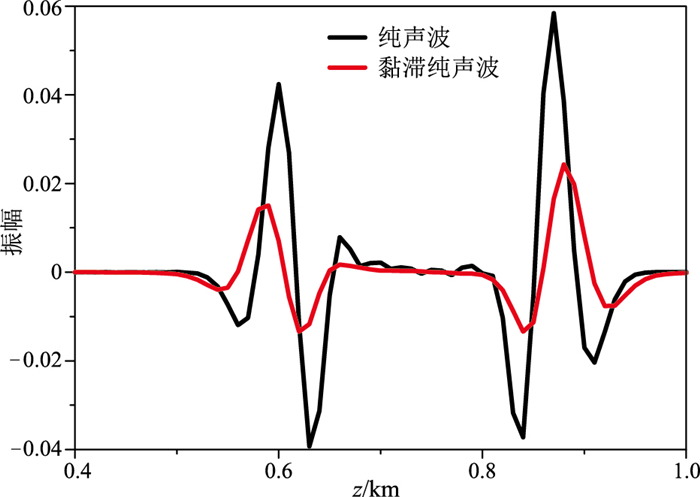
首先采用修改的三维各向异性楔状体模型进行测试。模型尺寸为1.5m×1.5m×1.5m,图 8为该模型xz平面示意图,沿y方向直接延拓可得其三维形式。模型A区的参数为:vP0=1500m/s,ε=0,δ=0,θ=-25°,φ=45°,Q=34.2;B区的参数为:vP0=1500m/s,ε=0.30,δ=0.02,θ=-25°,φ=45°,Q=34.2;C区的参数为:vP0=4500m/s,ε=0.10,δ=0.01,θ=60°,φ=45°,Q=382.9;D区的参数为:vP0=3500m/s,ε=0.05,δ=0.01,θ=10°,φ=45°,Q=220.2。震源是主频为20Hz的Ricker子波,位于(0.75km,0.75km,0.15km)。图 9对比了伪声波和纯声波方程的模拟结果,可以看出,相比于伪声波方程的模拟结果,纯声波方程能够较好地消除伪横波干扰。图 10为黏滞纯声波方程模拟波场快照,与纯声波方程的模拟结果(图 9c)相比,能量明显减弱、分辨率降低,有明显的振幅和相位差异(图 11)。

|
图 8 各向异性楔状体模型xz平面切片 |

|
图 9 三维TTI楔状体模型不同方程模拟的波场快照
(a)基于横波速度为0的伪声波方程;(b)基于限制性横波速度的伪声波方程;(c)本文纯声波方程。 从左到右依次为:xz平面,y=0.75km;xy平面,z=0.40km;yz平面,x=0.75km |

|
图 10 三维TTI楔状体模型黏滞纯声波模拟的波场快照 (a)xz平面,y=0.75km;(b)xy平面,z=0.40km;(c)yz平面,x=0.75km |
|
图 11 三维TTI楔状体模型的纯声波和黏滞纯声波方程模拟结果的(x=0.75km,y=0.75km)处波形对比 |
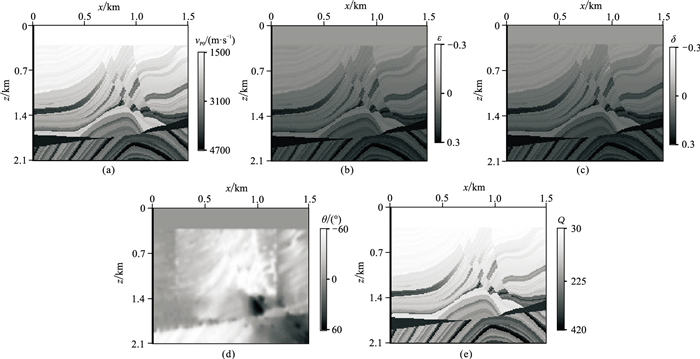
采用修改的三维Marmousi TTI模型验证本文方法对复杂模型的适应性。模型尺寸为1.5km×1.5km×2.1km,图 12为该改进模型的xz平面示意图,沿y方向直接延拓可得三维形式,对称轴方位角固定为30°。震源选用主频为20Hz的Ricker子波,置于(0.74km,0.74km,0.18km)。图 13和图 14分别为纯声波和黏滞纯声波方程模拟的波场快照,图 15为两种方程模拟波形曲线对比,可以看出,与纯声波方程的模拟结果相比,基于黏滞纯声波方程的模拟结果能量显著减弱,出现明显的振幅降低和相位畸变。该算例表明,本文的TTI黏滞纯声波方程可以适应复杂各向异性黏滞介质模型的P波波场模拟。
|
图 12 修改的Marmousi TTI模型的xz切片 (a)vP0;(b)ε;(c)δ;(d)θ;(e)Q |

|
图 13 三维Marmousi TTI模型纯声波方程模拟的波场快照 左:xz平面,y=0.74km;中:xy平面,z=0.18km;右:yz平面,x=0.74km |

|
图 14 三维Marmousi TTI模型黏滞纯声波方程模拟的波场快照 左:xz平面,y=0.74km;中:xy平面,z=0.18km;右:yz平面,x=0.74km |
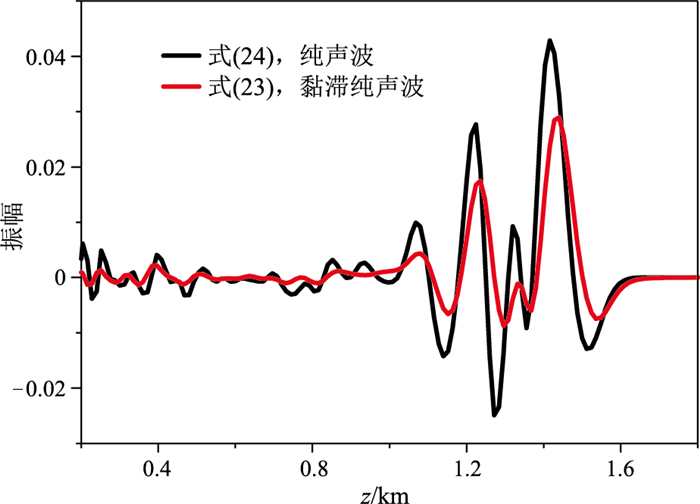
|
图 15 三维Marmousi TTI模型纯声波和黏滞纯声波方程模拟的(x=0.74km, y=0.74km)处波形对比 |
本文首先介绍了一种三维各向同性介质中同时考虑振幅衰减和相位畸变的黏滞声波方程。针对各向异性介质传统伪声波方程模拟容易产生伪横波干扰及出现数值不稳定,结合泊松算子和有限差分法给出了一种适用于三维TTI介质的纯声波求解算法,有效消除了伪声波方程模拟结果存在的干扰及数值不稳定。基于各向同性黏滞声波方程和TTI介质纯声波方程,推导了一种针对三维TTI介质的黏滞纯声波方程,该方程能够同时考虑黏滞各向异性介质中的地震波振幅衰减和相位畸变属性。
应用三维TTI层状模型模型验证了本文方法的模拟精度;TTI楔状体和Marmousi模型验证了方法的有效性和适用性。
| [1] |
ALKHALIFAH T. An acoustic wave equation for anisotropic media[J]. Geophysics, 2000, 65(4): 1239-1250. DOI:10.1190/1.1444815 |
| [2] |
ZHOU H B, BLOOR R, ZHANG G Q. An anisotropic acoustic wave equation for modeling and migration in 2D TTI media[C]. SEG Technical Program Expanded Abstracts, 2006, 25: 194-198.
|
| [3] |
DU X, BANCROFT J C, LINES L R. Anisotropic reverse-time migration for tilted TI media[J]. Geophy-sical Prospecting, 2007, 55(6): 853-869. DOI:10.1111/j.1365-2478.2007.00652.x |
| [4] |
FLETCHER R P, DU X, FOWLER P J. Reverse time migration in tilted transversely isotropic (TTI) media[J]. Geophysics, 2009, 74(6): WCA179-WCA187. DOI:10.1190/1.3269902 |
| [5] |
李博, 李敏, 刘红伟, 等. TTI介质有限差分逆时偏移的稳定性探讨[J]. 地球物理学报, 2012, 55(4): 1366-1375. LI Bo, LI Min, LIU Hongwei, et al. Stability of reverse time migration in TTI media[J]. Chinese Journal of Geophysics, 2012, 55(4): 1366-1375. DOI:10.6038/j.issn.0001-5733.2012.04.032 |
| [6] |
杨富森, 李振春, 王小丹. 稳定的TTI介质拟声波逆时偏移及伪横波的联合压制策略[J]. 地球物理学进展, 2016, 31(1): 396-402. YANG Fusen, LI Zhenchun, WANG Xiaodan. Stable TTI pseudo-acoustic wave reverse time migration and joint suppression strategy of pseudo-qSV wave[J]. Progress in Geophysics, 2016, 31(1): 396-402. |
| [7] |
LIU F Q, MORTON S A, JIANG S S, et al. Decoupled wave equations for P and SV waves in an acoustic VTI media[C]. SEG Technical Program Expanded Abstracts, 2009, 28: 2844-2848.
|
| [8] |
CHU C L, MACY B K, ANNO P D. Approximation of pure acoustic seismic wave propagation in TTI media[J]. Geophysics, 2011, 76(5): WB97-WB107. DOI:10.1190/geo2011-0092.1 |
| [9] |
杜启振, 郭成锋, 公绪飞. VTI介质纯P波混合法正演模拟及稳定性分析[J]. 地球物理学报, 2015, 58(4): 1290-1304. DU Qizhen, GUO Chengfeng, GONG Xufei. Hybrid PS/FD numerical simulation and stability analysis of pure P-wave propagation in VTI media[J]. Chinese Journal of Geophysics, 2015, 58(4): 1290-1304. |
| [10] |
LI X Y, ZHU H J. A finite-difference approach for solving pure quasi-P-wave equations in transversely isotropic and orthorhombic media[J]. Geophysics, 2018, 83(4): C161-C172. DOI:10.1190/geo2017-0405.1 |
| [11] |
黄金强, 李振春. 基于Low-rank分解的复杂TI介质纯qP波正演模拟与逆时偏移[J]. 地球物理学报, 2017, 60(2): 704-721. HUANG Jinqiang, LI Zhenchun. Modeling and reverse time migration of pure quasi-P-waves in complex TI media with a low-rank decomposition[J]. Chinese Journal of Geophysics, 2017, 60(2): 704-721. |
| [12] |
胡书华, 王宇超, 刘文卿, 等. 复杂TTI介质稳定的纯qP波波场模拟方法[J]. 石油地球物理勘探, 2018, 53(2): 280-287. HU Shuhua, WANG Yuchao, LIU Wenqing, et al. Pure quasi-P wave stable simulation in complex TTI media[J]. Oil Geophysical Prospecting, 2018, 53(2): 280-287. |
| [13] |
慕鑫茹, 黄建平, 李振春, 等. 基于最佳平方逼近的TTI介质解耦qP波与qSV波逆时偏移[J]. 石油地球物理勘探, 2019, 54(6): 1280-1292. MU Xinru, HUANG Jianping, LI Zhenchun, et al. Reverse time migration of decoupled qP- and qSV-waves in TTI media with the optimal quadratic approximation[J]. Oil Geophysical Prospecting, 2019, 54(6): 1280-1292. |
| [14] |
顾汉明, 张奎涛, 刘春成, 等. 基于Low-rank一步法波场延拓的黏声各向异性介质纯qP波正演模拟[J]. 石油地球物理勘探, 2020, 55(4): 733-746. GU Hanming, ZHANG Kuitao, LIU Chuncheng, et al. Low-rank one-step wave extrapolation for pure qP-wave forward modeling in viscoacoustic anisotropic media[J]. Oil Geophysical Prospecting, 2020, 55(4): 733-746. |
| [15] |
何兵寿, 武雪峤, 高琨鹏. TI介质中qP波方程逆时偏移技术的研究现状与展望[J]. 石油物探, 2021, 60(1): 34-45, 69. HE Bingshou, WU Xueqiao, GAO Kunpeng. Research status and prospect of qP wave reverse time migration in TI media[J]. Geophysical Prospecting for Petro-leum, 2021, 60(1): 34-45, 69. |
| [16] |
CARCIONE J M, KOSLOFF D, Kosloff R. Wave propagation simulation in a linear viscoacoustic medium[J]. Geophysical Journal International, 1988, 93(2): 393-401. DOI:10.1111/j.1365-246X.1988.tb02010.x |
| [17] |
吾拉力·胡尔买提, 曲英铭, 李振春, 等. 双相黏弹VTI介质一阶速度—应力方程正演模拟及双程波照明研究[J]. 石油地球物理勘探, 2021, 56(3): 505-518. WORRAL Qurmet, QU Yingming, LI Zhenchun, et al. First-order velocity-stress equation forward mode-ling and two-way wave illumination in two-phase viscoelastic VTI media[J]. Oil Geophysical Prospecting, 2021, 56(3): 505-518. |
| [18] |
BAI J Y, YINGST D, BLOOR R, et al. Viscoacoustic waveform inversion of velocity structures in the time domain[J]. Geophysics, 2014, 79(3): R103-R119. DOI:10.1190/geo2013-0030.1 |
| [19] |
LI G F, ZHENG H, ZHU W L, et al. Tomographic inversion of near-surface Q factor by combining surface and cross-hole seismic surveys[J]. Applied Geophy-sics, 2016, 13(1): 93-102. DOI:10.1007/s11770-016-0544-2 |
| [20] |
WANG E J, LIU Y, JI Y X, et al. Q full-waveform inversion based on the viscoacoustic equation[J]. Applied Geophysics, 2019, 16(1): 77-91. DOI:10.1007/s11770-019-0749-2 |
| [21] |
蔡瑞乾, 孙成禹, 伍敦仕, 等. 黏声波动方程变机制数有限差分正演[J]. 石油地球物理勘探, 2019, 54(3): 529-538. CAI Ruiqian, SUN Chengyu, WU Dunshi, et al. Finite-difference numerical modeling with variable mechanisms for viscoacoustic wave equation[J]. Oil Geophysical Prospecting, 2019, 54(3): 529-538. |
| [22] |
汪勇, 徐佑德, 高刚, 等. 二维黏滞声波方程的优化组合型紧致有限差分数值模拟[J]. 石油地球物理勘探, 2018, 53(6): 1152-1164. WANG Yong, XU Youde, GAO Gang, et al. Numerical simulation of 2D visco-acoustic wave equation with an optimized combined compact difference scheme[J]. Oil Geophysical Prospecting, 2018, 53(6): 1152-1164. |
| [23] |
XU W C, YANG G Q, LI H Z, et al. Pure viscoacoustic equation of TTI media and applied it in anisotropic RTM[C]. SEG Technical Program Expanded Abstracts, 2015, 34: 525-529.
|
| [24] |
杜启振, 杨慧珠. 方位各向异性黏弹性介质波场有限元模拟[J]. 物理学报, 2003, 52(8): 2010-2014. DU Qizhen, YANG Huizhu. Finite-element methods for viscoelastic and azimuthally anisotropic media[J]. Acta Physica Sinica, 2003, 52(8): 2010-2014. DOI:10.3321/j.issn:1000-3290.2003.08.034 |
| [25] |
ZHU T Y, CARCIONE J M, HARRIS J M. Approximating constant-Q seismic propagation in the time domain[J]. Geophysical Prospecting, 2013, 61(5): 931-940. DOI:10.1111/1365-2478.12044 |
| [26] |
CARCIONE J M. A generalization of the Fourier pseu-dospectral method[J]. Geophysics, 2010, 75(6): A53-A56. DOI:10.1190/1.3509472 |
| [27] |
ZHU T Y, HARRIS J M. Modeling acoustic wave pro-pagation in heterogeneous attenuating media using decoupled fractional Laplacians[J]. Geophysics, 2014, 79(3): T105-T116. DOI:10.1190/geo2013-0245.1 |
| [28] |
SUN J Z, ZHU T Y, FOMEL S. Viscoacoustic mode-ling and imaging using low-rank approximation[J]. Geophysics, 2015, 80(5): A103-A108. DOI:10.1190/geo2015-0083.1 |
| [29] |
CHEN H M, ZHOU H, LI Q Q, et al. Two efficient modeling schemes for fractional Laplacian viscoacoustic wave equation[J]. Geophysics, 2016, 81(5): T233-T249. DOI:10.1190/geo2015-0660.1 |



 徐世刚,陕西省西安市雁塔区雁塔路126号长安大学地质工程与测绘学院地球物理系,710054。Email:
徐世刚,陕西省西安市雁塔区雁塔路126号长安大学地质工程与测绘学院地球物理系,710054。Email: