② 东华理工大学核科学与技术学院, 江西南昌 33001;
③ 东华理工大学核资源与环境国家重点实验室, 江西南昌 330013
② School of Nuclear Science and Engineering, East China University of Technology, Nanchang, Jiangxi 330013, China;
③ State Key Laboratory of Nuclear Resources and Environment, East China University of Technology, Nanchang, Jiangxi 330013, China
地震波在黏弹性介质中传播时会产生速度频散和能量衰减[1-2],而品质因子Q作为测量速度频散和能量衰减的一个重要参数[3-4],在地震数据处理和解释中起重要作用。一方面,品质因子Q是反Q滤波必不可少的参数,可提高地震成像的纵向分辨率[5-6]。另一方面,品质因子Q与岩石类型、流体饱和度和渗透率等有关,常被应用于储层预测和油气识别[7-8]。
近年来,由于品质因子Q值的作用日趋显著,Q值估计方法也得到了快速发展。最早的估计方法是时域估计方法,如上升时间[9]、脉冲振幅法[10]。由于该类算法仅适用于无噪声的地震记录,未能得到广泛的应用。随着快速傅里叶变换技术的发展,人们相继提出了一系列的频域方法,如对数谱比法(Logical Spectrum Ratio,LSR)[11]、中心频移法(Centroid Frequency Shift,CFS)[12]、小波域包络峰值瞬时频率法(Wavelet Envelope Peak Instanta-neous Frequency,WEPIF)[13]。但这些方法的Q值估计准确程度通常受噪声、时窗、带宽、子波干涉等因素影响[14-16]。因此,针对Q估计的鲁棒性和准确性,人们提出了一系列稳键的频域方法。
赵宁等[17]采用一阶、二阶泰勒级数展开理论计算质心频率,进一步提高了Q值估计的精度和抗噪性。Wang等[18]提出对数谱面积差法(Logarithmic Spectral Area Difference,LSAD),提高了Q估计的稳定性。王静等[19]基于频谱拟合法实现VSP地震数据的准确Q值估计。刘国昌等[20]在谱比法的理论基础上,利用局部斜率相同的反射波形进行Q值估计,得到了较好的Q值估计结果。苏勤等[21]基于地表一致性原理,通过引入表层相对衰减系数,推导出表层相对品质因子Q值的计算公式,并将相应方法应用于实际数据Q值估计,取得了较好的应用效果。
本文对描述大地滤波作用的地震波振幅衰减因子进行二阶泰勒级数展开,从不同时刻地震子波振幅谱的积分差值与Q值关系出发,推导出基于泰勒展开振幅谱积分差值(Amplitude Spectral Integral Difference,ASID)的Q值估计方法;并通过频带宽度、时窗宽度及噪声干扰试验,测试了本文方法的有效性,同时与LSR、CFS和LSAD三种Q值估计方法进行对比分析以说明ASID法的优越性。
1 方法原理忽略地震波在地下传播过程中的球面扩散和透射损失作用,地层的“大地滤波作用”可用频域一维波动方程的解析解描述[3]
| $\begin{array}{*{20}{l}} {U\left( {r + \Delta r, f} \right) = U\left( {r, f} \right) \times }\\ {\;\;\;\;\;\;\;\exp \left[ { - 2{\rm{ \mathsf{ π} i}}\frac{{f\Delta r}}{{v\left( {r, f} \right)}}} \right] \times \exp \left[ { - \frac{{{\rm{ \mathsf{ π} }}f\Delta r}}{{Qv\left( {r, f} \right)}}} \right]} \end{array}$ | (1) |
式中:i为虚数单位;f为频率;r为传播距离;Δr为传播距离增量;U(r,f)和U(r+Δr,f)对应传播距离分别为r和r+Δr的波场;Q是传播距离r与r+Δr之间的地层品质因子;v(r,f)是相速度,可由Kjartansson相速度模型[4]表示为
| $v\left( {r, f} \right) = v(r, {f_0}){\left| {\frac{f}{{{f_0}}}} \right|^\gamma }$ | (2) |
| $\gamma = \frac{2}{{\rm{ \mathsf{ π} }}}{\tan ^{ - 1}}\frac{1}{{2Q}} \approx \frac{1}{{\pi Q}}$ | (3) |
式中:f0为地震波主频;v(r, f0)是频率f0的地震波在r处的相速度;γ是与Q有关的频率指数项。另外,若主频为f0的地震波在Δr之内的相速度v(r, f0)保持不变,则Δr可由v(r, f0)表示为
| $\Delta r = v(r, {f_0})\Delta t$ | (4) |
式中Δt是地震波通过Δr的旅行时间。
| $\begin{array}{*{20}{c}} {U\left( {t + \Delta t, f} \right) = U\left( {t, f} \right)\exp \left( { - 2{\rm{ \mathsf{ π} i}}{{\left| {\frac{f}{{{f_0}}}} \right|}^{ - \gamma }}f\Delta t} \right) \times }\\ {\exp \left( {- {{\left| {\frac{f}{{{f_0}}}} \right|}^{-\gamma }}\frac{{{\rm{ \mathsf{ π} }}f\Delta t}}{Q}} \right)} \end{array}$ | (5) |
当频率在f0附近时,有|f/f0|-(1/πQ)
| $\begin{array}{*{20}{c}} {U\left( {t + \Delta t, f} \right) = U\left( {t, f} \right)\exp \left( { - 2{\rm{ \mathsf{ π} i}}f\Delta t} \right) \times }\\ {\exp \left( { - \frac{{{\rm{ \mathsf{ π} }}\Delta tf}}{Q}} \right)} \end{array}$ | (6) |
从该式发现Q只影响实数部分,因此不同时刻地震子波振幅谱的关系[16, 25]可表示为
| $A(t + \Delta t, f) = A\left( {t, f} \right)\exp \left( { - \frac{{{\rm{ \mathsf{ π} }}\Delta t}}{Q}f} \right)$ | (7) |
式中A(t+Δt, f)和A(t, f)分别是t+Δt和t时刻的振幅谱。定义旅行时t处振幅谱积分为
| $G\left( t \right) = {\int _F}A\left( {t, f} \right){\rm{d}}f$ | (8) |
式中F为频率积分区间,可预先给定,且该区间通常选取包含主频的频段。同理,t+Δt时刻的振幅谱积分为
| $\begin{array}{*{20}{l}} {G\left( {t + \Delta t} \right) = {\int _F}A\left( {t + \Delta t, f} \right){\rm{d}}f}\\ {\;\;\;\;\;\;\;\;\;\;\;\;\;\; = {\int _F}A\left( {t, f} \right)\exp \left( { - \frac{{{\rm{ \mathsf{ π} }}\Delta tf}}{Q}} \right){\rm{d}}f} \end{array}$ | (9) |
基于二阶泰勒级数展开,式(9)指数项可表示为
| $\begin{array}{*{20}{l}} {\exp \left( { - \frac{{{\rm{ \mathsf{ π} }}\Delta t}}{Q}f} \right) = 1 - \frac{{{\rm{ \mathsf{ π} }}\Delta t}}{Q}f + }\\ {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{1}{2}{{\left( {\frac{{{\rm{ \mathsf{ π} }}\Delta t}}{Q}} \right)}^2}{f^2} + {R_n}\left( {\frac{{{\rm{ \mathsf{ π} }}\Delta tf}}{Q}} \right)} \end{array}$ | (10) |
式中Rn(πΔtf/Q)是泰勒公式的余项,与旅行时t、频率f和品质因子Q有关。当πΔtf/Q<1时,可认为该余项接近于0。因此,估算Q时选取的旅行时差Δt不宜过大。当忽略余项时,式(9)可改写为
| $G(t + \Delta t) \cong {\int _F}A\left( {t, f} \right)\left[ {1 - \frac{{{\rm{ \mathsf{ π} }}\Delta t}}{Q}f + \frac{1}{2}{{\left( {\frac{{{\rm{ \mathsf{ π} }}\Delta t}}{Q}} \right)}^2}{f^2}} \right]{\rm{d}}f$ | (11) |
两个接收点之间的振幅谱积分差值为
| $\begin{array}{*{20}{l}} {\Delta G = G\left( t \right) - G\left( {t + \Delta t} \right)}\\ {\;\;\;\;\;\; = {\int _F}A\left( {t, f} \right){\rm{d}}f - {\int _F}A\left( {t, f} \right)\exp \left( { - \frac{{{\rm{ \mathsf{ π} }}\Delta tf}}{Q}} \right){\rm{d}}f}\\ {\;\;\;\;\;\; \cong {\int _F}A\left( {t, f} \right){\rm{d}}f - }\\ {\;\;\;\;\;\;{\int _F}A\left( {t, f} \right)\left[ {1 - \frac{{{\rm{ \mathsf{ π} }}\Delta t}}{Q}f + \frac{1}{2}{{\left( {\frac{{{\rm{ \mathsf{ π} }}\Delta t}}{Q}} \right)}^2}{f^2}} \right]{\rm{d}}f}\\ {\;\;\;\;\;\; = \frac{{{\rm{ \mathsf{ π} }}\Delta t}}{Q}{\int _F}A\left( {t, f} \right)f{\rm{d}}f - \frac{1}{2}{{\left( {\frac{{{\rm{ \mathsf{ π} }}\Delta t}}{Q}} \right)}^2}{\int _F}A\left( {t, f} \right){f^2}{\rm{d}}f} \end{array}$ | (12) |
上式可简化为
| $\Delta G{Q^2} - B\left( t \right){\rm{ \mathsf{ π} }}\Delta tQ + \frac{1}{2}C\left( t \right){({\rm{ \mathsf{ π} }}\Delta t)^2} = 0$ | (13) |
其中
| $ B\left( t \right) = {\int _F}A\left( {t, f} \right)f{\rm{d}}f\;\;\;\;\;\;\;\;C\left( t \right) = {\int _F}A\left( {t, f} \right){f^2}{\rm{d}}f $ |
虽然式(13)存在两个解,但通过实验发现,其中一个解是一个非常小的数,即非Q值的真解,而Q值的有效解为
| $Q = \frac{{{\rm{ \mathsf{ π} }}\Delta t{\left[ {B\left( t \right) + \sqrt {{B^2}\left( t \right) - 2C\left( t \right)\Delta G} } \right]}}}{{2\Delta G}}$ | (14) |
该式为本文ASID算法Q值估计的基本公式,即是利用同层位不同旅行时间的地震子波振幅谱之差实现Q值估计,一般适用于叠前多道地震数据Q值估计。
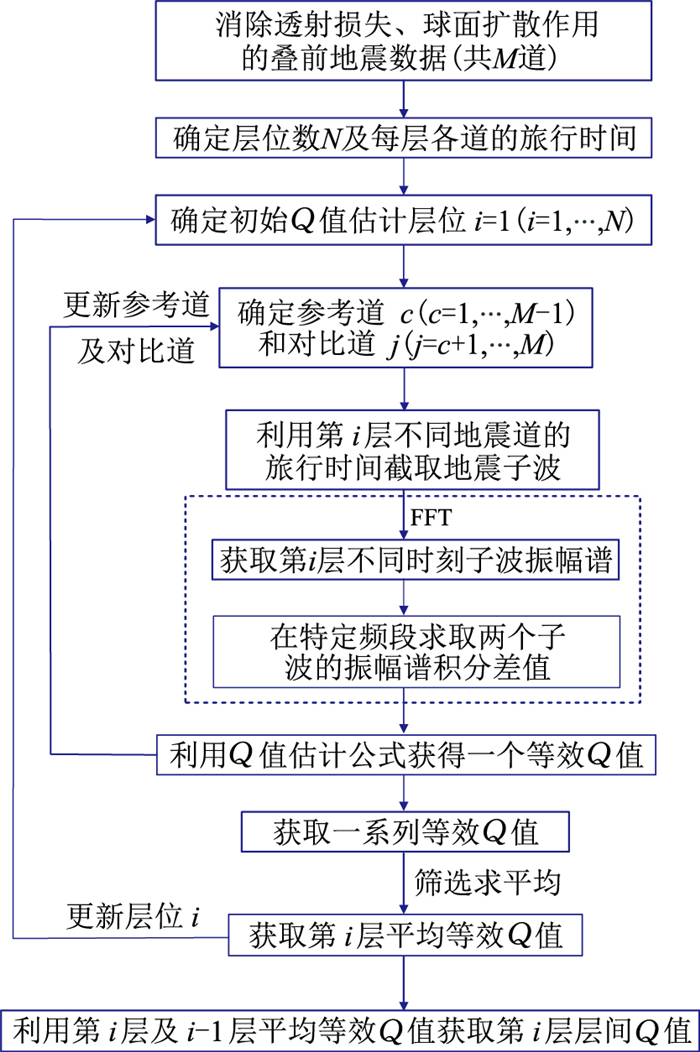
图 1为多层介质叠前地震数据ASID算法的流程图。对于同层地层来说,可通过改变参考道和对比道的位置,利用其子波振幅谱信息获取一系列Q值。但在实际资料Q值估计时,同层位上获取的一系列Q值中,可能会存在一些Q值小于零或数值过大,这些不合理结果须剔除。然后再将有效Q值估计结果进行平均,获得平均等效Q值,提高Q值估计的准确程度,弱化噪声等环境因素对Q值估计的影响。
|
图 1 多层介质叠前地震数据ASID法Q值估计流程 |
估算Q值时需选择频带宽度和时窗宽度。另外,随机干扰也会影响Q值估计。为此,对不同带宽、不同时窗和不同噪声环境进行了试验,并将本文方法与LSR、CFS和LSAD三种常用方法做对比分析。
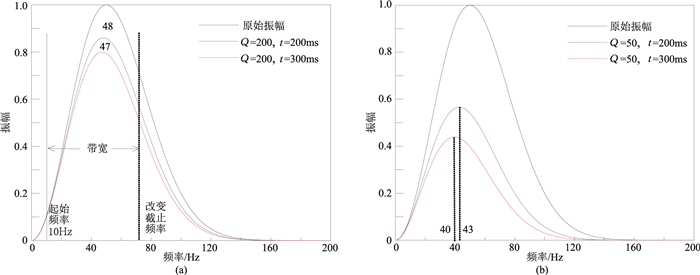
2.1.1 频带宽度试验为获取准确的Q值,许多频域Q值估计方法都需选取适当的频带宽度,过宽或过窄的频带都可能导致Q值估计效果不理想[18, 25]。为了测试带宽对ASID法的影响,选取主频为50Hz的Ricker子波,分别模拟了Q=200和50时不同旅行时的一维衰减地震记录(图 2)。相同Q值的地震子波旅行时分别为200ms和300ms。原始Ricker子波的宽度约为40ms,由于ASID算法是基于不同时刻地震子波振幅谱积分差值估算Q值的,这里给出了不同衰减程度的子波振幅谱(图 3)。可见随着旅行时间的增大及Q值的减小,振幅谱的主频向低频方向移动,且振幅谱有效频带宽度减小。

|
图 2 不同Q值的合成衰减地震记录 |
|
图 3 Q=200(a)和Q=50(b)的不同时刻地震子波的振幅谱 |
由于频率过低时振幅谱较小,因此选取起始频率为10Hz,截止频率从20Hz开始递增,获得了ASID法和其他三种常规方法的Q值估计结果随截止频率的变化(图 4)。Q值估计过程中,均使用60ms时窗拾取子波。从图 4可看出:截止频率较小时,LSR法和CFS法的Q值估计误差较大,随着截止频率增加,四种方法获得Q值均逐渐接近理论值;在一定的中频段内,Q值估计结果较稳定,即效果较好;但截止频率较大时,随着截止频率的增加,LSR法和LSAD法的估计效果明显变差,而ASID法基本不受截止频率的影响。由此可知:LSR法不适于截止频带较小和较大时的Q值估计,需选择合适的频段;CFS法不适于截止频率较小时的Q值估计,不过该方法在高频段时,其受频率影响程度弱于LSR法和LSAD法;LSAD法则不适于高频段的Q值估计;而ASID法受频率影响最小,尤其高频处频率变化基本不影响Q值估计。

|
图 4 Q=200(a)和Q=50(b)时不同方法估计的Q值随截止频率的变化(起始频率为10Hz) 波浪线表示该段的值已超出取值范围 |
为了探究ASID算法不易受频率影响的原因,并了解泰勒级数展开对Q值估计的影响,图 5给出不同截止频率下振幅谱积分差的理论值和泰勒级数展开近似、这两者的差值,以及Q估算值。从图 5a和图 5b可见,随着截止频率的增加(即带宽增大),振幅谱积分差先迅速增加,后趋于平缓,这主要缘于高频处不同时刻的地震子波振幅谱均趋于零(图 3);泰勒级数展开形式下的振幅谱积分差近似值与理论值基本一致,不存在明显差值。从图 5c和图 5d可见,理论值与近似值之差也随截止频率的增加先迅速递增,后平缓变化;两者虽存在一定差值,但幅度较小,且该差值也是Q值估算误差的主要来源。从图 5e、图 5f可见,Q估计值与频率关系不大,在截止频率为30Hz时误差最大,但相对误差仍小于5%;无论频率多高,Q估算值基本无变化,相对误差都在3%以内。上述分析表明,本文方法所用振幅谱积分差对高频不敏感,高频干扰对方法的影响不大;虽使用二阶泰勒级数展开,但它带来的误差较小;Q值估计与频率关系不大,无论截止频率设定得过高或过低,Q值估计误差均较小。

|
图 5 不同时刻子波振幅谱积分差理论值与泰勒级数展开下的近似值 (a)和(b)分别是Q=200和Q=50的振幅谱理论值与近似值;(c)和(d)分别是Q=200和Q=50的振幅谱理论值与近似值差值;(e)和(f)分别是Q=200和Q=50时ASID法的Q估算结果 |
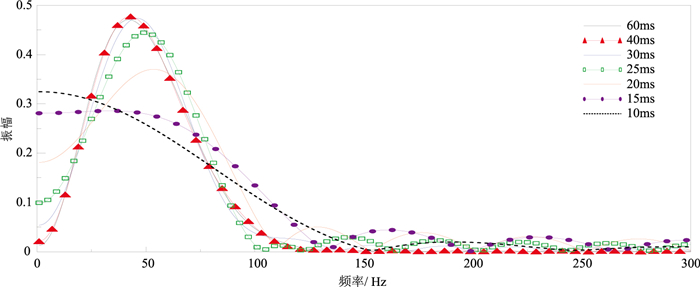
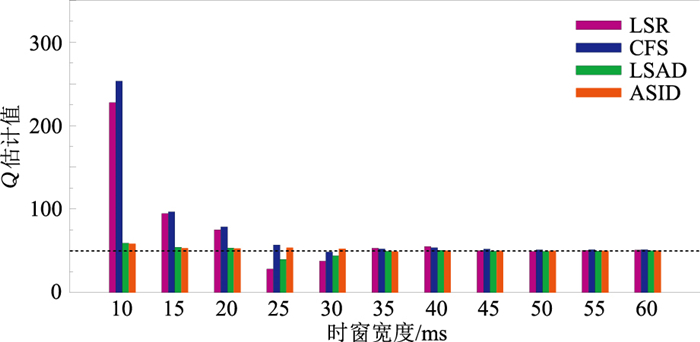
为了厘清ASID算法受时窗宽度的影响程度,仍基于图 2的一维合成衰减地震记录,选择不同时窗宽度进行试验。从不同时窗子波振幅谱(图 6)的整体上看,60ms与40ms的子波频谱几乎完全重合,即当选取完整子波时,其宽度对振幅谱影响较小。随着时窗宽度的减小,振幅谱之间差异变大,低频段能量不断增加,且频带有所拓宽;当时窗为10ms时,振幅谱峰值处于零频点附近。在不同时窗宽度下,分别利用本文方法及LSR、CFS、LSAD方法估算Q值,为了使其他三种方法的Q估算值最佳,选定频带范围均为10~100Hz,不同方法的Q估算值见图 7。可见当时窗宽度较小(10ms或20ms)时,LSR和CFS法估计的Q值远大于真实值,LSAD和ASID法则能估算出更接近真实的Q值,且ASID法更精确(25ms、30ms);随着时窗宽度的增加,四种方法均能较好地获取真实Q值,尤其时窗宽度大于子波宽度时。该试验表明,LSR法和CFS法并不适合小时窗(即非完整子波)下的Q值估计,而ASID法受时窗宽度影响最小。
|
图 6 不同时窗(10~60ms)的子波振幅谱(Q=50) |
|
图 7 不同时窗宽度下四种方法的Q值估计柱状图(Q=50) |
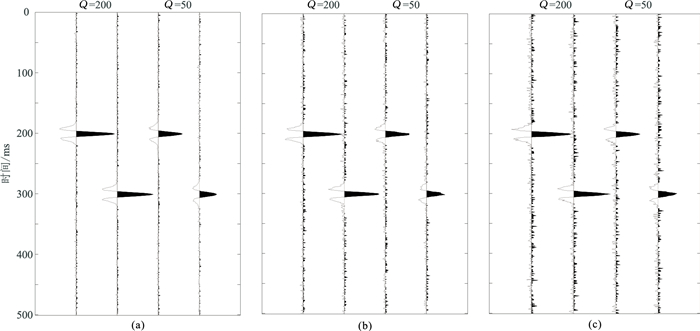
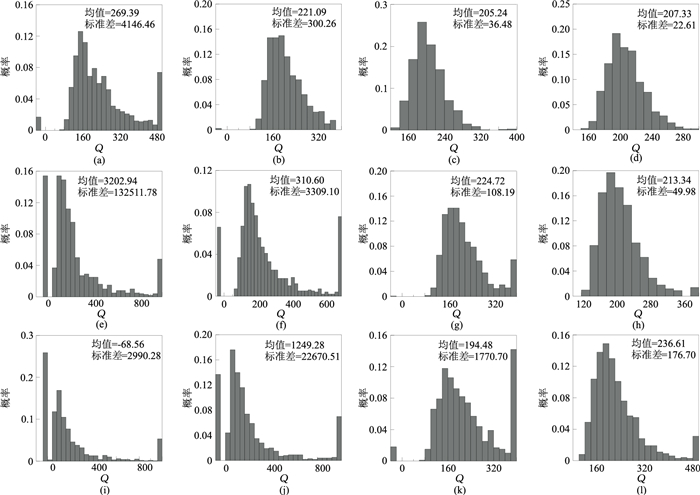
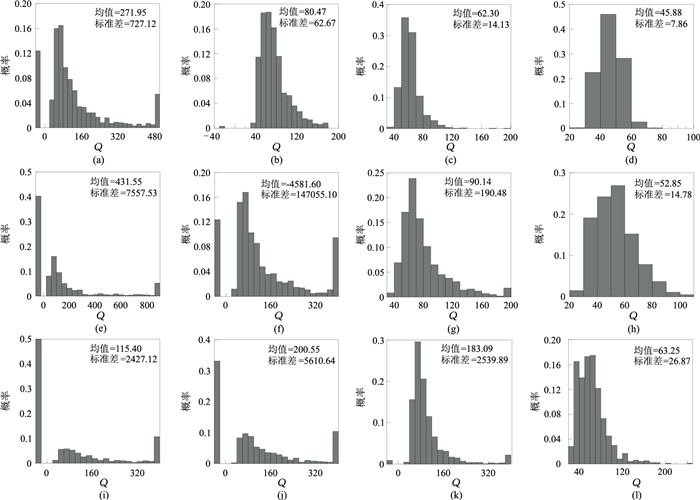
为了分析噪声对Q值估计的影响,对图 2一维合成衰减地震道分别加入5%、10%和15%的高斯随机噪声(图 8),对所得记录均随机运行1000次,得到三种噪声环境下Q值估计概率分布图(图 9和图 10)。在估算Q值过程中,选取的时窗宽度均为40ms,频带范围仍为10~100Hz。需指出的是,在图 9和图 10中,Q估算值超出横坐标取值范围的,均统计在坐标轴的两侧,即小于0的统计在-40~0之内,超出横坐标最大值的统计在最大值处,不过在计算平均值和均方差时使用的是实际Q估算值。
|
图 8 分别添加5%(a)、10%(b)、15%(c)噪声的一维地震记录 |
|
图 9 Q=200时三种噪声环境下四种方法Q值估计概率分布图 (a)~(d)5%噪声下LSR法、CFS法、LSAD法、ASID法;(e)~(h)10%噪声下LSR法、CFS法、LSAD法、ASID法;(i)~(l)15%噪声下LSR法、CFS法、LSAD法、ASID法 |
|
图 10 Q=50时三种噪声环境下四种方法Q值估计概率分布图 (a)~(d)5%噪声下LSR法、CFS法、LSAD法、ASID法;(e)~(h)10%噪声下LSR法、CFS法、LSAD法、ASID法;(i)~(l)15%噪声下LSR法、CFS法、LSAD法、ASID法 |
从该两图可看出:LSR法受噪声干扰影响最严重,Q估算值几乎完全失真,即使噪声含量较低(图 9a、图 10a,5%噪声)时,其Q值估计误差也很大;CFS法在噪声含量较低、Q值较大(图 9b)时,Q估算值较可靠,但随着噪声增加、Q值减小,其计算误差迅速增加,也难以有效估计Q值;LSAD法在Q值较大(图 9c、图 9g、图 9k)时,具有较强抗噪能力,能估算出较真实的Q值,在Q值较小(图 10c、图 10g、图 10k)时,其计算误差随噪声环境的恶化而增加,已不能有效进行强噪声、小Q值的估算(图 10k);相对于其他三种方法,ASID法抗干扰能力最强,能有效准确地估算Q值,且其概率分布更接近于正态分布,标准差也是最小,不过随着噪声含量的增加,误差会有所增大。
该试验表明,LSR法受噪声影响最严重,即使少量噪声也会导致较大Q值估算误差;CFS法仅适用于Q值较大、噪声含量较低时的Q值估计;LASD法不适用于强噪声、小Q值的估计;ASID法受噪声强度和Q值影响较小,能在不同噪声环境中准确估算Q值。
2.2 含薄层的共炮点道集测试为了验证ASID法在薄层Q值估计中的效果,设计一个水平三层介质模型,模型参数如表 1所示。
|
|
表 1 三层水平介质模型参数 |
在合成地震记录时,为了与实际相符,兼顾了反射系数和大地滤波作用的影响(图 11a),震源采用主频为50Hz的Ricker子波,道间距为20m,第一道检波器位置与震源重合,共80道地震数据。需说明的是,在利用ASID算法和常规Q值估算法预测Q值之前,首先要获得消除反射系数影响的地震记录(图 11b)。设薄层(第二层)厚度为10m,确保小于薄层定义的最大厚度(子波宽约40ms,则薄层最大厚度为λa/2=VTa/2=1400m/s×40ms×0.5=28m)。

|
图 11 合成衰减CSP道集 (a)兼顾反射系数、大地滤波作用;(b)消除反射系数影响 |
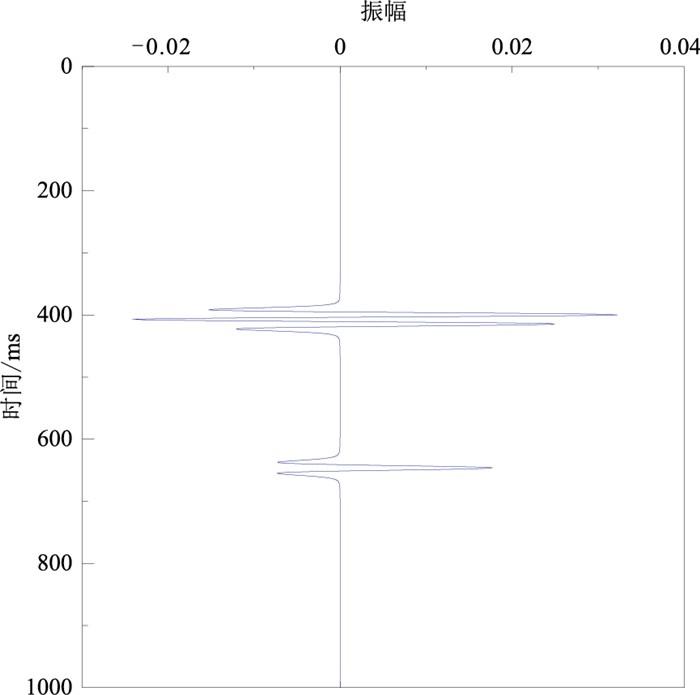
图 12是消除反射系数影响后的首道地震记录,可见接收到的第二层顶、底界面的反射子波发生了明显干涉,地震子波负边瓣幅值相互叠加,幅值明显增加,已与第二层地震子波的主峰幅值相当。实际地震记录中常遇此情形,尤其对于油气层。
|
图 12 图 11b的第一道地震数据 |
由于此模型为多层模型,可采用图 1的流程完成ASID算法的Q值估计,其他算法则只需将图 1虚线部分处理步骤换成对应算法的Q值估计流程,即可实现不同算法的Q值估计。
为进一步提高方法的合理性,首先删除LSR、CFS和LSAD法Q估算值中的负值和大于1000的数值,再将一系列Q值做平均化处理,得到等效Q值,最后利用常规层间Q值求取方法[11, 18]获取层间Q值(图 13)。与此同时,为避免子波干涉的影响,第一、第二层选取子波宽度为12ms,第三层选取整个子波宽度(40ms),频带范围仍选用10~100Hz。
|
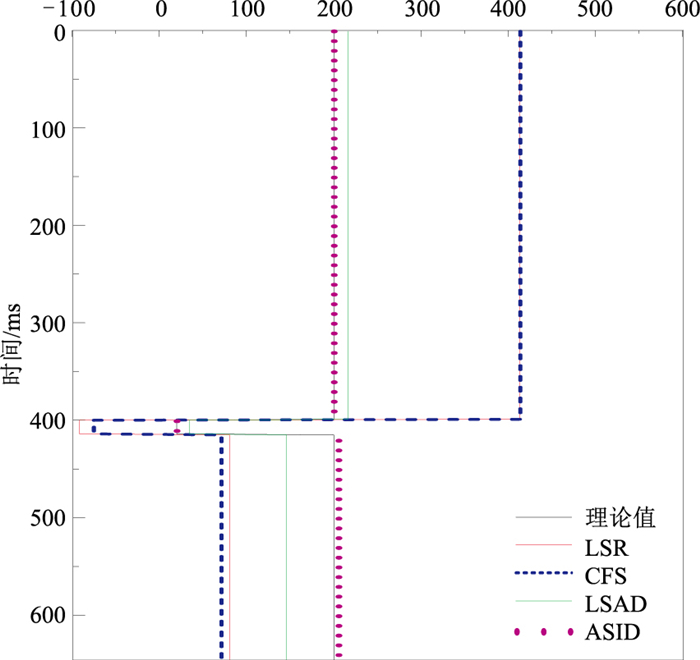
图 13 不同Q值估计方法计算结果 |
从图 13可见,由于第一层选取非完整子波,导致LSR和CFS法在第一层上估计的Q值(分别为413.4和414.0)远高于真实值,这与前述时窗宽度试验结果相一致;第二层同样选取非完整子波,且第二层层间Q值计算需使用第一层Q值,由于第一层Q估算值已严重失真,导致第二层Q值为负值(分别为-91.4和-74.9);第三层Q值估计受到上两层Q值估计不准确的影响,误差同样较大。LSAD法对含薄层的地震记录Q值估计效果较好(图 13),在三层介质上的Q估算值分别为216.1、34.3和145.9,相对误差分别为8.06%、71.50%和27.08%,远小于LSR和CFS法的估算结果。而ASID是受时窗宽度影响最小的方法(图 7),故对薄层Q值的估计则更准确,它在三层介质上的Q估算值分别为200.6、20.4和206.0,相对误差分别仅为0.28%、1.94%和2.98%,整体精度比LSAD法提高了近20倍。
3 实例应用选用M海域共中心点(CMP)地震道集(图 14),分别应用ASID和LSAD法进行Q值估计试验。时间采样间隔为4ms。需补充说明的是,该组数据是已消除球面扩散及透射损失作用影响的叠前地震数据。通过对比同相轴一致的不同地震道,发现基本所有地层对应的地震子波横向衰减均较快,表明地层Q值可能相对较小。

|
图 14 M海域CMP地震道集 |
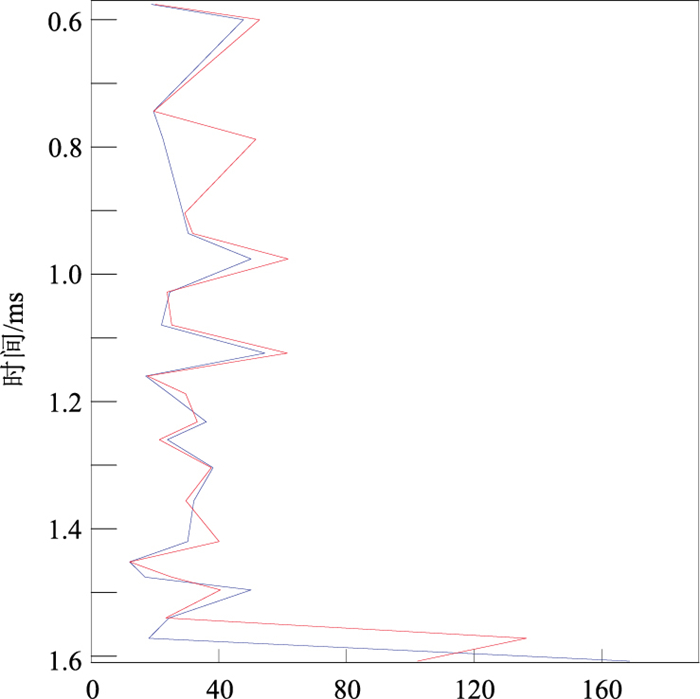
为了合理确定Q值估计时的频段,从第一道地震记录的振幅谱(图 15)可知,主频约为21Hz,带宽约为10~40Hz。在估算Q值时,选取时窗为28ms(包含完整子波)、频带处于10~40Hz。基于图 1的Q值估计流程,分别利用ASID和LSAD方法获取等效Q值(图 16),可见两种方法估计的等效Q值相似度较高,说明所得等效Q值具有一定的可信度。该等效Q值在30~60区间,整体上偏小,反映了沉积层可能具有一定的黏度。

|
图 15 第一道振幅谱 |
|
图 16 ASID(红线)与LSAD(蓝线)估算的等效Q值 |
品质因子Q是用于提高地震记录纵向分辨率和分析储层特征的关键参数。本文在地震波振幅衰减项的二阶泰勒级数展开基础上,利用不同时刻地震子波振幅谱积分差值与Q值的关系,构建了一种Q值估计(ASID)方法。针对频带宽度、时窗宽度及噪声干扰等的试验结果表明,相对于LSR、CFS和LSAD法,ASID法受频带宽度和时窗宽度影响更小、抗干扰能力更强。含薄层的三层介质模型试验表明ASID法具有更高的Q值估计精度,能更准确地估算薄层Q值。
还应说明,本文算法是一种基于叠前(CMP道集)数据Q值估计方法,在前期地震数据处理中,应预先做好振幅增益恢复、抽道集、透射损失和球面扩散补偿等预处理,且这些预处理的质量直接影响Q值估计的准确程度。如增益恢复处理得不好,会导致无效的Q值估计结果;未做透射损失和球面扩散补偿会导致Q估算值偏低。因此,在Q值估计之前,应充分做好数据处理的前期准备以获取更准确的Q值。
| [1] |
KOLSKY H. The propagation of stress pulses in viscoelastic solids[J]. The Philosophical Magazine, 1956, 1(8): 693-710. DOI:10.1080/14786435608238144 |
| [2] |
KNEIB G, SHAPIRO S A. Viscoacoustic wave pro-pagation in 2-D random media and separation of absorption and scattering attenuation[J]. Geophysics, 1995, 60(2): 459-467. DOI:10.1190/1.1443783 |
| [3] |
FUTTERMAN W I. Dispersive body waves[J]. Journal of Geophysical Research, 1962, 67(13): 5279-5291. DOI:10.1029/JZ067i013p05279 |
| [4] |
KJARTANSSON E. Constant Q -wave propagation and attenuation[J]. Journal of Geophysical Research, 1979, 84(B9): 4737-4748. DOI:10.1029/JB084iB09p04737 |
| [5] |
WANG Y H. Inverse Q -filter for seismic resolution enhancement[J]. Geophysics, 2006, 71(3): V51-V60. DOI:10.1190/1.2192912 |
| [6] |
ZHANG J, WANG Y G, NOBES D C, et al. Deep seismic reflection data interpretation using balanced filtering method[J]. Geophysics, 2017, 82(5): N43-N49. DOI:10.1190/geo2016-0061.1 |
| [7] |
KLIMENTOS T, MCCANN C. Relationships among compressional wave attenuation, porosity, clay content, and permeability in sandstones[J]. Geophysics, 1990, 55(8): 998-1014. DOI:10.1190/1.1442928 |
| [8] |
张壹, 王赟, 陈本池, 等. 强衰减介质中地震波场的频率—空间域特征[J]. 石油地球物理勘探, 2020, 55(5): 1016-1028, 1046. ZHANG Yi, WANG Yun, CHEN Benchi, et al. Cha-racteristics of seismic wave field in frequency-space domain in strong attenuation media[J]. Oil Geophy-sical Prospecting, 2020, 55(5): 1016-1028, 1046. |
| [9] |
GLADWIN M T, STACEY F D. Anelastic degradation of acoustic pulses in rock[J]. Physics of the Earth and Planetary Interiors, 1974, 8(4): 332-336. DOI:10.1016/0031-9201(74)90041-7 |
| [10] |
STAINSBY S D, WORTHINGTON M H. Q estimation from vertical seismic profile data and anomalous variations in the central North Sea[J]. Geophysics, 1985, 50(4): 615-626. DOI:10.1190/1.1441937 |
| [11] |
DASGUPTA R, CLARK R A. Estimation of Q from surface seismic reflection data[J]. Geophysics, 1998, 63(6): 2120-2128. DOI:10.1190/1.1444505 |
| [12] |
QUAN Y L, HARRIS J M. Seismic attenuation to-mography using the frequency shift method[J]. Geo-physics, 1997, 62(3): 895-905. |
| [13] |
高静怀, 杨森林, 王大兴. 利用VSP资料直达波的包络峰值处瞬时频率提取介质品质因子[J]. 地球物理学报, 2008, 51(3): 853-861. GAO Jinghuai, YANG Senlin, WANG Daxing. Quality factor extraction using instantaneous frequency at envelope peak of direct waves of VSP data[J]. Chinese Journal of Geophysics, 2008, 51(3): 853-861. DOI:10.3321/j.issn:0001-5733.2008.03.026 |
| [14] |
TONN R. The determination of the seismic quality factor Q from VSP data: a comparison of different computational methods[J]. Geophysical Prospecting, 1991, 39(1): 1-27. DOI:10.1111/j.1365-2478.1991.tb00298.x |
| [15] |
江雨濛, 曹思远, 陈思远, 等. 应用时变子波的盲反射系数反演[J]. 石油地球物理勘探, 2021, 56(5): 1001-1009. JIANG Yumeng, CAO Siyuan, CHEN Siyuan, et al. A blind deconvolution method based on the time-varying wavelet[J]. Oil Geophysical Prospecting, 2021, 56(5): 1001-1009. |
| [16] |
WANG Y H. Q analysis on reflection seismic data[J]. Geophysical Research Letters, 2004, 31(17): L17606. |
| [17] |
赵宁, 曹思远, 王宗俊, 等. 频域统计性属性组合提取品质因子Q[J]. 石油地球物理勘探, 2013, 48(4): 545-552. ZHAO Ning, CAO Siyuan, WANG Zongjun, et al. Seismic Q estimation by combinations of frequency statistics attributes[J]. Oil Geophysical Prospecting, 2013, 48(4): 545-552. |
| [18] |
WANG S D, YANG D F, LI J N, et al. Q factor estimation based on the method of logarithmic spectral area difference[J]. Geophysics, 2015, 80(6): V157-V171. DOI:10.1190/geo2014-0257.1 |
| [19] |
王静, 姚正新, 张彦斌, 等. VSP全井段Q值估计[J]. 石油地球物理勘探, 2018, 53(增刊2): 58-64. WANG Jing, YAO Zhengxin, ZHANG Yanbin, et al. Whole-well length VSP Q estimation[J]. Oil Geophysical Prospecting, 2018, 53(S2): 58-64. |
| [20] |
刘国昌, 李超. 基于多射线联合反演的速度无关叠前地震数据Q值估计[J]. 地球物理学报, 2020, 63(4): 1569-1584. LIU Guochang, LI Chao. Velocity-independent pre-stack seismic Q estimation based on multi-ray joint inversion[J]. Chinese Journal of Geophysics, 2020, 63(4): 1569-1584. |
| [21] |
苏勤, 曾华会, 田彦灿, 等. 表层Q值确定性求取与空变补偿方法[J]. 石油地球物理勘探, 2019, 54(5): 988-996. SU Qin, ZENG Huahui, TIAN Yancan, et al. Near-surface Q value estimation and quantitative amplitude compensation[J]. Oil Geophysical Prospecting, 2019, 54(5): 988-996. |
| [22] |
HARGREAVES N D, CALVERT A J. Inverse Q filtering by Fourier transform[J]. Geophysics, 1991, 56(4): 519-527. DOI:10.1190/1.1443067 |
| [23] |
WANG Y H. A stable and efficient approach of inverse Q filtering[J]. Geophysics, 2002, 67(2): 657-663. DOI:10.1190/1.1468627 |
| [24] |
YANG D F, LIU J, LI J N, et al. Q -factor estimation using bisection algorithm with power spectrum[J]. Geophysics, 2020, 85(3): V233-V248. DOI:10.1190/geo2018-0403.1 |
| [25] |
LI J N, WANG S X, YANG D F, et al. An improved Q estimation approach: the weighted centroid frequency shift method[J]. Journal of Geophysics and Engineering, 2016, 13(3): 399-411. DOI:10.1088/1742-2132/13/3/399 |



 王彦国,江西省南昌市昌北经济开发区广兰大道418号东华理工大学地球物理与测控技术学院,330013。Email:
王彦国,江西省南昌市昌北经济开发区广兰大道418号东华理工大学地球物理与测控技术学院,330013。Email: