随着地震各向异性理论的发展和应用,工业界基于VTI介质的地震建模和成像技术日趋成熟;TTI各向异性建模和成像技术在实际中得到较广泛的应用[1];学术界已开始研究如基于正交各向异性理论等的更复杂应用技术。
地震各向异性参数的获取一直是各向异性应用的关键。与地面地震相比,VSP测量作为各向异性参数获取的一种途径,具有较高的精度和准确的深度优势。前人研究表明,应用VTI模型可以更加精确地描述长排列上的地震波旅行时特性[2];基于VTI假设,给出了不同形式的时差关系:Byun等[3-4]应用一种双参数速度分析对VSP合成数据进行速度分析;Hake等[5]导出了VTI介质时差的3项泰勒展开式;Tsvankin等[6-7]对Hake的公式进行了改进,并引入渐近拟合使新公式在大炮检距上更逼近真值;Alkhalifah等[8-9]提出用两个参数表达的非双曲时差关系描述VTI介质的地震波旅行时,已在地面地震数据各向异性动校正等处理中得到了广泛的应用[10-12];白海军等[13]和陈沅忠等[14]将Alkhalifah的方法应用于VSP数据,均取得了较好的效果。
以上方法主要是基于VTI或TTI介质的纵波非双曲线时差进行速度分析和旅行时反演,难以获得更复杂的任意各向异性参数。VSP能够直接测量地震波的慢度和极化信息,且不受上覆地层影响。极化和慢度矢量是表征Christoffel方程的直接参数,理论上只要获得足够多的慢度和极化信息,就可以反演介质的所有各向异性参数。根据这一特点,Jech等[15]提出了各向异性介质的一阶扰动方法。Horne等[16]和Gomes等[17]基于扰动理论,提出了应用慢度和极化矢量求解介质弱各向异性参数的方法,并得到了一些成功的应用。
在前人研究的基础上,本文系统地介绍了基于慢度和极化信息反演各向异性参数的方法原理,并给出了Walkaway VSP慢度和极化数据的获取方法,提出了基于加权迭代的任意弱各向异性参数反演算法的详细实现过程,应用一组TTI模型合成数据和一口实际井资料进行处理试验,取得了理想的效果。
1 方法原理 1.1 Christoffel方程及扰动方法介质中传播的平面波遵循Christoffel方程[18]
| $ \left(\varGamma_{j k}-G_{m} \delta_{j k}\right) g_{j}^{(m)}=0 $ | (1) |
式中:Γjk=aijklninl为Christoffel矩阵,其中a是密度归一化弹性张量,n为波的传播方向矢量,i、j、k、l均取1~3,表示坐标方向;m=1、2、3,分别代表各向异性介质中传播的qS1、qS2、qP波;Gm是Christoffel矩阵的三个特征值;g(m)为三种波的极化矢量。式(1)中使用了爱因斯坦求和约定。
由于实际介质大多是弱各向异性[19-20],基于扰动理论,Christoffel传播方程可近似表述为[21]
| $ \begin{aligned} &\left(\widetilde{\varGamma}_{j k}-\widetilde{G}_{m} \delta_{j k}\right) \Delta g_{j}^{(m)}+\left(\Delta \varGamma_{j k}-\Delta G_{m} \delta_{j k}\right) \widetilde{g}_{j}^{(m)}+ \\ &\left(\Delta \varGamma_{j k}-\Delta G_{m} \delta_{j k}\right) \Delta g_{j}^{(m)}=0 \end{aligned} $ | (2) |
式中:线“~”表示在各向同性参考介质中的基本量;“Δ”表示在弱各向异性介质中的扰动量。
1.2 qP波慢度和极化矢量正反演公式只考虑式(2)中的qP波(m=3),忽略其中二阶项,并引入了三个相互垂直的单位矢量[22]
| $ \left\{\begin{array}{l} \boldsymbol{e}^{(1)}=D^{-1}\left(n_{1} n_{3}, n_{2} n_{3}, n_{3}^{2}-1\right) \\ \boldsymbol{e}^{(2)}=D^{-1}\left(-n_{2}, n_{1}, 0\right) \\ \boldsymbol{e}^{(3)}=\boldsymbol{n}=\left(n_{1}, n_{2}, n_{3}\right) \end{array}\right. $ | (3) |
式中
| $ p_{i}=\frac{n_{i}}{\sqrt{\alpha^{2}+B_{33}}} $ | (4) |
| $ g_{i}^{(3)}=n_{i}+\alpha\left[p_{j} e_{j}^{\left(K^{\prime}\right)}\right] e_{i}^{\left(K^{\prime}\right)}+\frac{B_{K^{\prime} 3}}{\alpha^{2}-\beta^{2}} e_{i}^{\left(K^{\prime}\right)} $ | (5) |
式中:p和g分别是qP波的慢度和极化矢量;α和β分别表示参考介质中qP波和qS波的相速度,K′=1、2;B为与弱各向异性参数相关的弱各向异性矩阵[25],可表示为
| $ B_{K L}=\Delta a_{i j k l} e_{i}^{(K)} n_{j} n_{k} e_{l}^{(L)} \quad K, L=1,2,3 $ | (6) |
其中Δa为密度归一化弹性张量的扰动量。
反过来,通过慢度矢量和极化矢量,可以求解弱各向异性介质的弹性参数[23-24]
| $ B_{K^{\prime} 3}=\left(\alpha^{2}-\beta^{2}\right)\left[g_{i}^{(3)} e_{i}^{\left(K^{\prime}\right)}-\alpha \Delta p_{i} e_{i}^{\left(K^{\prime}\right)}\right] $ | (7) |
| $ B_{33}=-2 \alpha^{4} p_{i} \Delta p_{i} $ | (8) |
式中Δp为弱各向异性介质中慢度矢量的扰动,与各向同性参考介质中的慢度矢量
| $ p_{i}=\tilde{p}_{i}+\Delta p_{i} $ | (9) |
式中
式(7)和式(8)是关于15个弱各向异性参数的线性公式。
1.3 qP波慢度矢量和极化矢量的计算 1.3.1 极化矢量在数学上,质点的运动轨迹可以认为是空间点的集合。对于三分量的VSP记录,这种离散采样点的质点运动轨迹具有相关性,可以通过三分量记录的协方差矩阵统计其空间运动规律。根据矩阵的特征值和特征向量可定量地确定极化椭球(长、中、短)各轴的大小和椭球的空间位置及其标准椭球方程,并能求出质点运动轨迹的极化参数。协方差矩阵定义为
| $ \boldsymbol{M}_{C}=\left(\begin{array}{ccc} \sum C_{1} C_{1} & \sum C_{1} C_{2} & \sum C_{1} C_{3} \\ \sum C_{2} C_{1} & \sum C_{2} C_{2} & \sum C_{2} C_{3} \\ \sum C_{3} C_{1} & \sum C_{3} C_{2} & \sum C_{3} C_{3} \end{array}\right) $ | (10) |
式中:C1=c1τ-c1;C2=c2τ-c2;C3=c3τ-c3。其中:c1τ、c2τ、c3τ是分析时窗内的三个分量的样点值,τ为分析时窗内的样点序号;c1、c2、c3为对应时窗内三个分量的数学期望。
求解协方差矩阵的特征值和对应的特征向量,可以确定极化方向,其中最大特征值对应的特征向量就是qP波的极化矢量。
1.3.2 慢度矢量一般情况下,可通过邻近两个检波器的时差dt和深度差dh求取慢度的垂向分量
| $ p_{z}=\frac{\mathrm{d} t}{\mathrm{~d} h} $ | (11) |
慢度p是一个局部量,不依赖于上覆地层速度结构。根据地震波走时的互易性,如果介质是横向均匀的,则炮点到接收点的走时等于接收点到炮点的走时。当介质横向非均匀性比较弱时可以将接收点与炮点互易,利用共接收点的旅行时计算慢度矢量的水平分量。
旅行时曲线一般情况下都不光滑,其一阶导数不连续甚至不存在。为了得到更稳定的慢度矢量,本文采用多点平滑和相邻五点三次多项式求导的方法计算慢度矢量。
1.4 Walkaway VSP反演弱各向异性参数方法通过将BKL代入式(7)和式(8),可以建立弱各向异性参数与慢度及极化矢量的关系式。如果慢度矢量的扰动Δp的三个分量和极化矢量g(3)的三个分量都已知,可以单独使用式(7)或式(8)建立一个关于未知数为弱各向异性参数的线性方程组,或者联合式(7)和式(8)建立方程组,求解该线性方程组即可得弱各向异性参数。
以Walkaway VSP为例,通过极化分析和慢度计算可以得到极化矢量g(3)和慢度矢量p,进而可得Δp。反演中还需要确定qP波的传播方向n。考虑到qP波极化方向和传播方向非常接近,用qP波的极化方向g(3)作为初始n,反演弱各向异性参数,再通过式(5)正演gcal(3),将正演值gcal(3)与测量值g(3)的差值作为n的修正量Δn,通过多次迭代,可反演弱各向异性参数。反演的目标函数定义为
| $ \varPhi=\sum\limits_{I=1}^{N} w_{I}\left(y_{I}-A_{I J} x_{J}\right)^{2} $ | (12) |
式中:N是数据点个数;y表示式(7)和式(8)的观测参数和已知量;w为观测参数的权系数;x为待反演的弱各向异性参数,其维数为Npar;J=1, 2, …, Npar;A为N×Npar阶系数矩阵。弱各向异性参数的估计可以通过奇异值分解求解,即
| $ \boldsymbol{x}=\boldsymbol{V} \boldsymbol{\varLambda}^{-1} \boldsymbol{U}^{\mathrm{T}} \boldsymbol{d} $ | (13) |
式中:U和V是系数矩阵ATwA两个正交的N×N奇异矩阵;Λ是由ATwA的奇异值构成N×N对角矩阵;d=ATwy。
权系数w由数据的初始权重wd和更新后的测量值与正演计算值残差的权重wr组成
| $ w_{I}=w_{I}^{\mathrm{d}} w_{I}^{\mathrm{r}} $ | (14) |
数据的初始权重wd由两部分构成,一部分是参与运算的数据类型的质量估计权系数wq,另一部分权系数由慢度或极化数据的可靠性决定,即
| $ w_{I}^{\mathrm{d}}=w_{I}^{\mathrm{q}} \exp \left[-\frac{\left(r_{I}^{\mathrm{obs}}-r_{I}^{\mathrm{inp}}\right)^{2}}{2 \sigma^{2}}\right] $ | (15) |
式中:rIobs为第I个观测的慢度或极化数据的任一分量值;rIinp为rIobs的多项式拟合值;σ为|rIinp|与|rIobs|的平均差值。
权系数wr为反演迭代时慢度或者极化矢量残差的再加权[26]
| $ w_{I}^{\mathrm{r}}=\max{}^{2}\left[0,1-\left(\frac{\mathrm{d} r_{I}}{\omega \frac{\mathrm{d} r_{\text {med }}}{\sigma_{\text {med }}}}\right)^{2}\right] $ | (16) |
式中:drI为第I个慢度或者极化矢量的观测值与正演计算值的残差;σmed=0.67449,为高斯噪声的中值;ω是dr的标准偏差截断因子,一般选择3~6间的数;drmed定义为
| $ \mathrm{d} r_{\mathrm{med}}=\operatorname{med}\left(\left|\mathrm{d} r_{I}-\operatorname{med}\left(\mathrm{d} r_{I}\right)\right|\right) $ | (17) |
其中med(·)表示取数列的中值。
求解式(13)后,每个模型参数的最小二乘估计误差EJ为[26]
| $ E_{J}^{2}=\varOmega T_{J J} $ | (18) |
式中:TJJ为奇异值和奇异矩阵构成的协方差矩阵T=VΛ-2VT的对角元素;Ω为加权剩余量的变化
| $ \varOmega=\frac{\sum\limits_{I=1}^{N}\left(\mathrm{~d} r_{I}-\overline{\mathrm{d} r}\right)^{2}-\frac{\sum\limits_{I=1}^{N}\left(\mathrm{~d} r_{I}-\overline{\mathrm{d} r}\right)^{2}}{N}}{N-N_{\mathrm{par}}} $ | (19) |
式中
独立的弱各向异性参数共有21个,其中与qP波相关的有15个:εx、εy、εz、δx、δy、δz、χx、χy、χz、ε15、ε16、ε24、ε26、ε34和ε35。若要反演15个参数,需要布设5条以上Walkaway VSP测线;如果对两个正交的测线进行联合反演,最多可得到9个参数:εx、εy、εz、δx、δy、ε15、ε24、ε34和ε35;如果仅使用一条测线,只能反演5个参数,即εx、εz、δx、ε15和ε35[25]。
2 模型资料测试模型是一个弹性参数随深度线性变化的TTI模型,相速度的各向异性程度(相速度的最大最小值之差与最大值的比值)为4%。地表处的TTI弹性参数(密度归一化的)矩阵Θ3和10km深处的弹性参数矩阵Θ4分别由相应的两个VTI弹性矩阵Θ1和Θ2经过绕y轴顺时针旋转40°、再绕z轴(向下为正)顺时针旋转30°后得到。四个弹性参数矩阵分别为
| $ \boldsymbol{\varTheta}_{1}=\left(\begin{array}{cccccc} 14.4826 & 3.7099 & 4.4600 & 0 & 0 & 0 \\ 3.7099 & 14.4826 & 4.4600 & 0 & 0 & 0 \\ 4.4600 & 4.4600 & 13.3900 & 0 & 0 & 0 \\ 0 & 0 & 0 & 4.9800 & 0 & 0 \\ 0 & 0 & 0 & 0 & 4.9800 & 0 \\ 0 & 0 & 0 & 0 & 0 & 5.3846 \end{array}\right) $ | (20) |
| $ \boldsymbol{\varTheta}_{2}=\left(\begin{array}{cccccc} 50.6892 & 12.9846 & 15.6100 & 0 & 0 & 0 \\ 12.9846 & 50.6892 & 15.6100 & 0 & 0 & 0 \\ 15.6100 & 15.6100 & 46.8650 & 0 & 0 & 0 \\ 0 & 0 & 0 & 17.4300 & 0 & 0 \\ 0 & 0 & 0 & 0 & 17.4300 & 0 \\ 0 & 0 & 0 & 0 & 0 & 18.8523 \end{array}\right) $ | (21) |
| $ \boldsymbol{\varTheta}_{3}=\left(\begin{array}{rrrrrr} 14.3509 & 3.9889 & 4.2066 & 0.1109 & -0.1545 & -0.0648 \\ 3.9889 & 14.4594 & 4.1689 & -0.0400 & 0.2773 & -0.0291 \\ 4.2066 & 4.1689 & 14.0760 & -0.1552 & -0.2688 & 0.0326 \\ 0.1109 & -0.0400 & -0.1552 & 5.0473 & -0.1743 & -0.2159 \\ -0.1545 & 0.2773 & -0.2688 & -0.1743 & 4.8461 & -0.1739 \\ -0.0648 & -0.0291 & 0.0326 & -0.2159 & -0.1739 & 5.1875 \end{array}\right) $ | (22) |
| $ \boldsymbol{\Theta}_{4}=\left(\begin{array}{rrrrrr} 50.2282 & 13.9610 & 14.7231 & 0.3881 & -0.5409 & -0.2269 \\ 13.9610 & 50.6078 & 14.5912 & -0.1401 & 0.9704 & -0.1018 \\ 14.7231 & 14.5912 & 49.2660 & -0.5431 & -0.9407 & 0.1142 \\ 0.3881 & -0.1401 & -0.5431 & 17.6655 & -0.6099 & -0.7557 \\ -0.5409 & 0.9704 & -0.9407 & -0.6099 & 16.9612 & -0.6085 \\ -0.2269 & -0.1018 & 0.1142 & -0.7557 & -0.6085 & 18.1563 \end{array}\right) $ | (23) |
观测系统由6条等方位间隔的Walkaway VSP测线组成。每条测线布设32个炮点,井孔两边各16个;井源距范围是100~3100m,炮间距为200m。井中1000~1550m深度等间距布设12个检波器,检波器间距为50m。
联合应用式(7)和式(8),通过6条Walkaway VSP的慢度矢量和极化矢量的3个分量,反演了模型的15个弱各向异性参数。
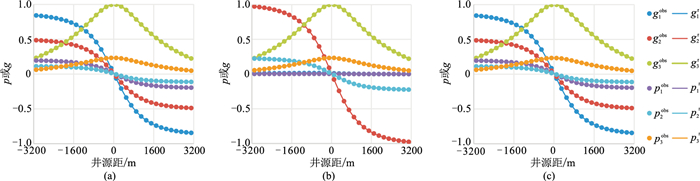
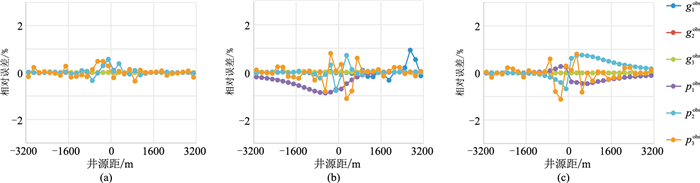
以深度1250m的检波点为例,其他深度结果类似。图 1展示了方位角为30°/210°、90°/270°和150°/330°测线测量的慢度和极化矢量随井源距的变化曲线,可见测量的慢度/极化矢量与真值完全吻合。图 2为测量的极化矢量和慢度矢量的相对误差,可见极化矢量的相对误差非常小,慢度矢量的水平分量误差稍大一些,但基本都小于1%。
|
图 1 3条Walkaway测线测量的慢度、极化矢量与真值对比 (a)30°/210°;(b)90°/270°;(c)150°/330°。上标“obs”表示测量值,“r”表示真值 |
|
图 2 3条Walkaway测线测量的慢度、极化矢量的相对误差 (a)30°/210°;(b)90°/270°;(c)150°/330° |
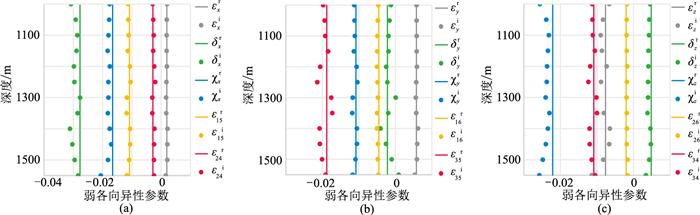
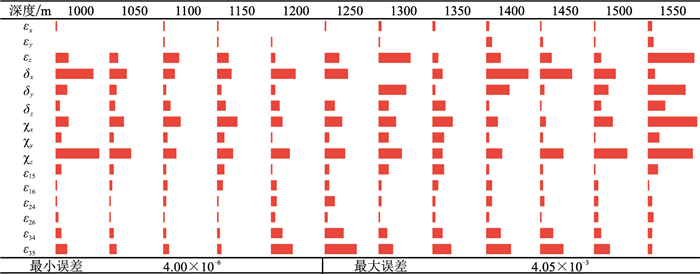
图 3为6条测线联合反演的不同深度15个弱各向异性参数结果。反演的弱各向异性参数(散点)在不同深度上有所不同,但基本都在真值(直线) 的附近,其绝对误差(图 4)最大为4.05×10-3,远小于最小的各向异性参数,说明模型的反演结果精度很高。
|
图 3 弱各向异性参数反演结果与真值的对比 (a)εx、δx、χx、ε15、ε24;(b)εy、δy、χy、ε16、ε35;(c)εz、δz、χz、ε26、ε34。上标“i”表示反演值,“r”表示真值 |
|
图 4 反演的弱各向异性参数的绝对误差条形图 |
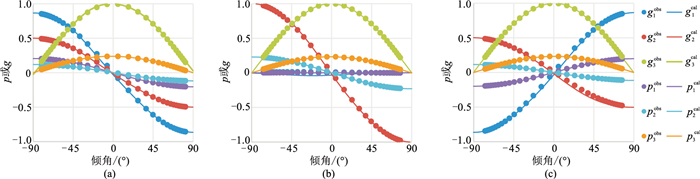
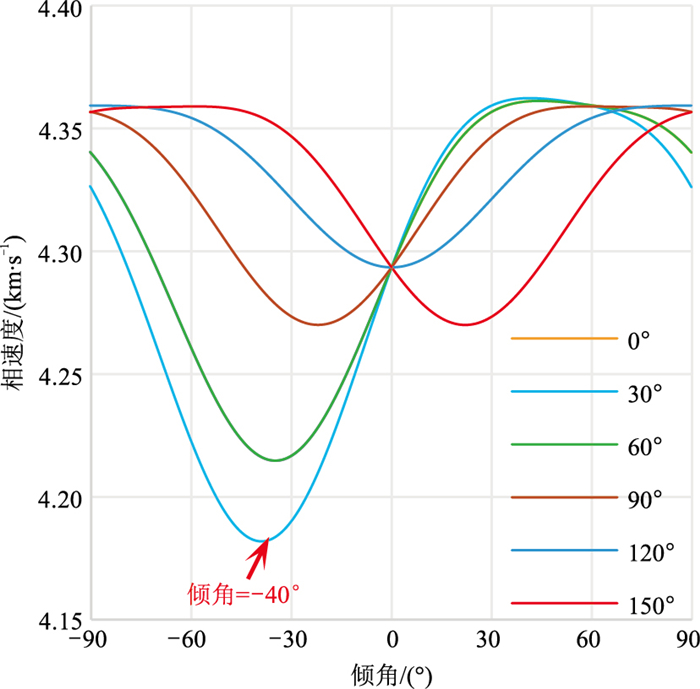
图 5是利用反演的弱各向异性参数通过式(4)和式(5)正演计算的不同方位测线(30°/210°、90°/270°和150°/330°)1250m深度的慢度和极化矢量与测量值的对比,可以看出二者高度吻合。图 6是利用式(4)正演的不同方位、不同倾角在1250m深度处接收点的相速度曲线,可见:120°/300°测线的相速度曲线对称,说明这个方位是TTI对称平面的垂直方向,那么对称平面方位角则为30°/210°;在对称平面上,-40°倾角时相速度最小,说明这是对称轴倾角,通过对称平面上的相速度两个极值计算的各向异性程度为4%,与TTI模型的设计值完全一致。表 1给出了所有深度点计算的各向异性程度和TTI对称轴方向,与模型设计值高度一致。
|
图 5 3条Walkaway测线正演计算的慢度、极化矢量与测量值的对比 (a)30°/210°;(b)90°/270°;(c)150°/330°。上标“obs”表示测量值,“cal”表示计算值,图 9、图 10同 |
|
图 6 不同方位测线速度随倾角的变化曲线 |
|
|
表 1 不同深度接收点处反演的各向异性程度和TTI对称轴方向 |
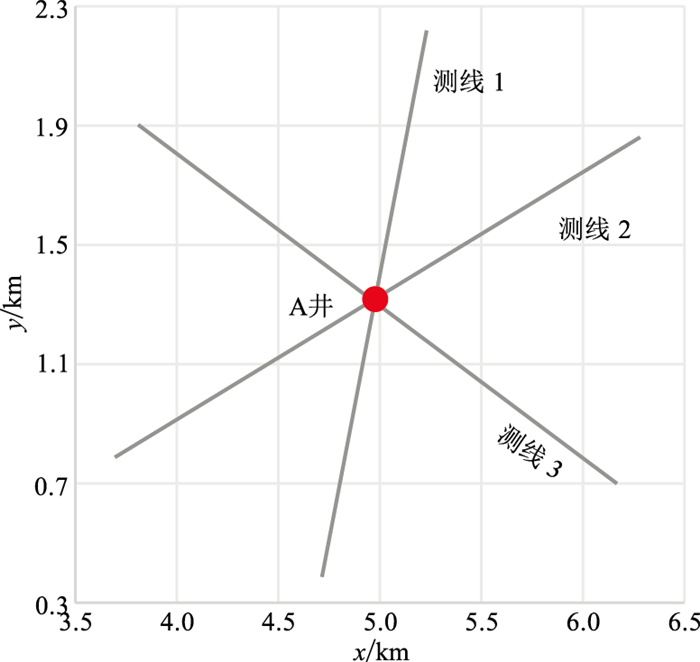
以A井3条Walkaway VSP采集数据为例。测线布置如图 7,其中测线1布设450炮、测线2布设460炮、测线3布设470炮。接收点深度范围为4560~5670m,共75级,间距为15m。
|
图 7 实际资料测线布置示意图 |
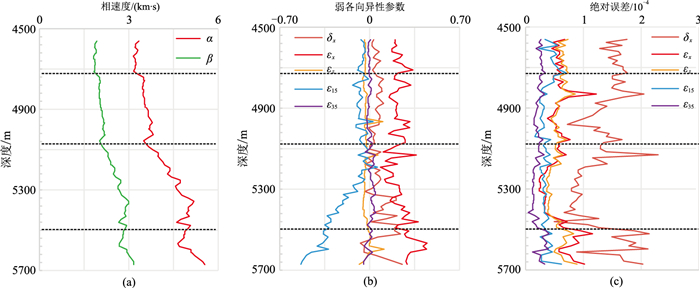
基于上述3条测线,可反演9个弱各向异性参数,其中5个参数(εx、εz、δx、ε15和ε35)结果比较稳定。图 8a和图 8b分别是反演的速度和5个弱各向异性参数随深度的变化曲线。在地层分界面附近,尤其是第二和第三界面处,相速度有较大的抖动(图 8a),反演估计的绝对误差也较大(图 8c),可能是由于在地层分界面上、下的接收点时差变化较大,造成垂直慢度的误差较大。在盐丘(第三条虚线以下)中各向异性参数有明显的变大趋势,说明盐丘各向异性很强。从图 8c可发现,几个ε参数的反演误差都比δx小,这是因为ε只与qP波各向异性有关,δ不仅与qP波有关,还与qS波有关,而本文反演只用到了qP波信息,但反演误差的最大值为2.296×10-4,仍远小于弱各向异性参数值。
|
图 8 反演的速度(a)、弱各向异性参数(b)及其误差(c)随深度的变化曲线 水平虚线表示地层界面 |
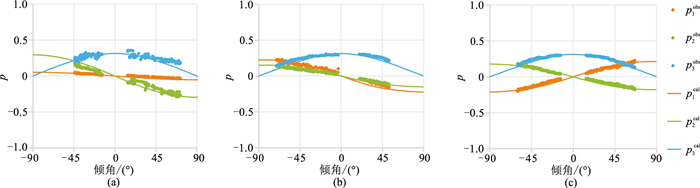
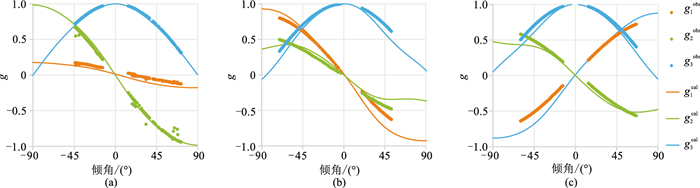
图 9和图 10分别是应用反演的弱各向异性参数正演计算的3条测线的第一个接收点的慢度和极化矢量与测量值的对比,可以看出,测线1的慢度和极化矢量的计算值与测量值都吻合的较好,测线2和测线3基本能吻合,说明反演的弱各向异性参数正确地反映了测量的慢度和极化矢量所携带的地层各向异性信息。
|
图 9 应用反演的弱各向异性参数计算的慢度矢量与测量值的对比 (a)测线1;(b)测线2;(c)测线3 |
|
图 10 应用反演的弱各向异性参数计算的极化矢量与测量值的对比 (a)测线1;(b)测线2;(c)测线3 |
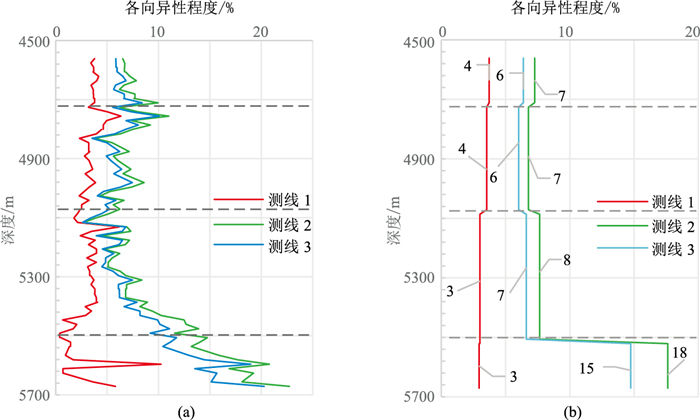
图 11是计算的不同深度的各向异性程度及其各层的平均各向异性程度。如图中所示,测线1的各向异性程度较弱,测线2、测线3较强,其中测线2最强。从深度上看,深度5500m以下盐丘各向异性明显增强,其中测线2最大,超过18%。
|
图 11 3条测线不同深度的各向异性程度曲线(a)与地层平均各向异性程度(b)的对比 |
本文系统地介绍了基于扰动理论的qP波的慢度和极化矢量正、反演方法,给出了精度高、稳定的慢度和极化矢量计算方法,提出了适用于慢度和极化矢量反演任意弱各向异性参数的加权迭代反演算法。
通过设计6条Walkaway VSP的TTI模型处理试验,反演的15个弱各向异性参数精度很高;应用反演的弱各向异性参数计算的慢度和极化矢量与测量值完全匹配;正演的相速度结果表明,模型各向异性程度和对称轴与理论值完全一致。
实际3条测线Walkaway VSP资料反演的5个弱各向异性参数取值范围和各向异性程度都符合地质认识,各向异性随深度变化趋势与地层分界面对应较好;应用弱各向异性参数计算的慢度和极化矢量与测量值吻合很好;反演误差远小于各向异性参数的数量级。
模型和实际应用表明,本文方法能够用于高精度的地震各向异性参数提取,具备较高的应用价值。
| [1] |
杨宗青, 李宏伟, 欧居刚, 等. TTI介质各向异性参数优化提取方法[J]. 石油地球物理勘探, 2020, 55(1): 111-116. YANG Zongqing, LI Hongwei, OU Jugang, et al. An optimized method for extracting anisotropic parameters in TTI media[J]. Oil Geophysical Prospecting, 2020, 55(1): 111-116. |
| [2] |
刘洋, 魏修成. 几种反射波时距方程的比较[J]. 地球物理学进展, 2005, 20(3): 645-653. LIU Yang, WEI Xiucheng. Comparison on several time distance equations of reflecion wave[J]. Progress in Geophysics, 2005, 20(3): 645-653. DOI:10.3969/j.issn.1004-2903.2005.03.011 |
| [3] |
BYUN B S. Seismic parameters for media with elliptical velocity dependencies[J]. Geophysics, 1982, 47(12): 1621-1626. DOI:10.1190/1.1441312 |
| [4] |
BYUN B S, CORRIGAN D, GAISER J E. Anisotropic velocity analysis for lithology discrimination[J]. Geophysics, 1989, 54(12): 1564-1574. DOI:10.1190/1.1442624 |
| [5] |
HAKE H, HELBIG K, MESDAG C S. Three-term Taylor series for t2-x2-curves of P-and S-waves over la-yered transversely isotropic ground[J]. Geophysical Prospecting, 1984, 32(5): 828-850. DOI:10.1111/j.1365-2478.1984.tb00742.x |
| [6] |
TSVANKIN I, Thomsen L. Nonhyperbolic reflection moveout in anisotropic media[J]. Geophysics, 1994, 59(8): 1290-1304. DOI:10.1190/1.1443686 |
| [7] |
TSVANKIN I. Normal moveout from dipping reflectors in anisotropic media[J]. Geophysics, 1995, 60(1): 268-284. DOI:10.1190/1.1443755 |
| [8] |
ALKHALIFAH T, TSVANKIN I. Velocity analysis for transversely isotropic media[J]. Geophysics, 1995, 60(5): 1550-1566. DOI:10.1190/1.1443888 |
| [9] |
ALKHALIFAH T. Velocity analysis using nonhyperbolic moveout in transversely isotropic media[J]. Geo-physics, 1997, 62(6): 1839-1854. |
| [10] |
王光杰, 张中杰, 滕吉文. TI介质双参数速度分析[J]. 地球物理学进展, 2004, 19(1): 113-118. WANG Guangjie, ZHANG Zhongjie, TENG Jiwen. Velocity analysis using nonhyperbolic moveout in transversely isotropic media[J]. Progress in Geophy-sics, 2004, 19(1): 113-118. DOI:10.3969/j.issn.1004-2903.2004.01.016 |
| [11] |
徐亦鸣, 黄中玉, 刘路佳. 各向异性介质纵波速度分析[J]. 石油物探, 2004, 43(5): 438-440. XU Yiming, HUANG Zhongyu, LIU Lujia. P-wave velocity analysis in anisotropy medium[J]. Geophysical Prospecting for Petroleum, 2004, 43(5): 438-440. DOI:10.3969/j.issn.1000-1441.2004.05.005 |
| [12] |
卢明辉, 唐建侯, 胡彬, 等. VTI介质P波非双曲时差分析[J]. 地球物理学进展, 2005, 20(2): 328-331. LU Minghui, TANG Jianhou, HU Bin, et al. Analysis of P wave nonhyperbolic reflection moveout in VTI media[J]. Progress in Geophysics, 2005, 20(2): 328-331. DOI:10.3969/j.issn.1004-2903.2005.02.012 |
| [13] |
白海军, 孙赞东, 李彦鹏. 3D VSP共检波点道集各向异性分析及参数提取[J]. 石油地球物理勘探, 2011, 46(增刊1): 53-59. BAI Haijun, SUN Zandong, LI Yanpeng. Anisotropy analysis and parameters extraction on 3D VSP common receiver gathers[J]. Oil Geophysical Prospecting, 2011, 46(S1): 53-59. |
| [14] |
陈沅忠, 张锐锋, 唐传章, 等. VSP井地联合地震勘探技术应用——以华北束鹿泥灰岩勘探为例[J]. 石油地球物理勘探, 2018, 53(增刊2): 50-57. CHEN Yuanzhong, ZHANG Ruifeng, TANG Chuan-zhang, et al. A joint VSP and surface seismic survey for marlstones in Shulu, Huabei Oilfield[J]. Oil Geophysical Prospecting, 2018, 53(S2): 50-57. |
| [15] |
JECH J, PŠENIK I. First-order perturbation method for anisotropic media[J]. Geophysical Journal International, 1989, 99(2): 369-376. DOI:10.1111/j.1365-246X.1989.tb01694.x |
| [16] |
HORNE S, LEANEY S. Short note: polarization and slowness component inversion for TI anisotropy[J]. Geophysical Prospecting, 2000, 48(4): 779-788. DOI:10.1046/j.1365-2478.2000.00205.x |
| [17] |
GOMES E, ZHENG X, PŠENÍK I, et al. Local determination of weak anisotropy parameters from walkaway VSP qP-wave data in the Java sea region[J]. Studia Geophysica et Geodaetica, 2004, 48(1): 215-231. DOI:10.1023/B:SGEG.0000015593.29477.88 |
| [18] |
CERVENY V. Seismic Ray Theory[M]. Cambridge: Cambridge University Press, 2001.
|
| [19] |
THOMSEN L. Weak elastic anisotropy[J]. Geophy-sics, 1986, 51(10): 1954-1966. |
| [20] |
谷一鹏, 印兴耀, 梁锴, 等. VTI介质弹性波相速度扩展各向异性线性近似[J]. 石油地球物理勘探, 2020, 55(3): 635-642. GU Yipeng, YIN Xingyao, LIANG Kai, et al. Extended anisotropic linear approximation for elastic phase velocity in VTI media[J]. Oil Geophysical Prospecting, 2020, 55(3): 635-642. |
| [21] |
ZHENG X Y. Inversion for elastic parameters in weakly anisotropic media[J]. Geophysical Journal International, 2004, 159(3): 1077-1089. DOI:10.1111/j.1365-246X.2004.02455.x |
| [22] |
PŠENÍK I, GAJEWSKI D. Polarization, phase velo-city, and NMO velocity of qP-waves in arbitrary weakly anisotropic media[J]. Geophysics, 1998, 63(5): 1754-1766. DOI:10.1190/1.1444470 |
| [23] |
PŠENÍK I, ZHENG X Y. Determination of weak ani-sotropy parameters from the qP wave particle motion measurements//Seismic Waves in Complex 3-D Structures[R]. Charles University, Prague, 1998, 299-306.
|
| [24] |
ZHENG X, PŠENÍK I. Local determination of weak anisotropy parameters from qP-wave slowness and particle motion measurements[J]. Pure and Applied Geophysics, 2002, 159(7): 1881-1905. |
| [25] |
田鑫, 洪启宇, 郑需要. 多测线变偏移距VSP地震各向异性反演[J]. 地震学报, 2015, 37(2): 266-277, 370. TIAN Xin, HONG Qiyu, ZHENG Xuyao. Seismic anisotropic inversion of multiple walkaway VSPs[J]. Acta Seismologica Sinica, 2015, 37(2): 266-277, 370. |
| [26] |
WALDHAUSER F, ELLSWORTH W L. A double-difference earthquake location algorithm: Method and application to the Northern Hayward Fault, California[J]. Bulletin of the Seismological Society of Ame-rica, 2000, 90(6): 1353-1368. DOI:10.1785/0120000006 |



 杨心超,江苏省南京市上高路219号中国石化石油物探技术研究院,211103。Email:
杨心超,江苏省南京市上高路219号中国石化石油物探技术研究院,211103。Email: