② 广州海洋地质调查局, 广东广州 510760;
③ 中山大学地球科学与工程学院, 广东珠海 519082
② Guangzhou Marine Geological Survey (Guangzhou), Guangzhou, Guangdong 510760, China;
③ School of Earth Sciences and Engineering, Sun Yat-Sen University, Zhuhai, Guangdong 519082, China
随着海洋油气勘探逐渐从常规油气藏向复杂油气藏转变,对海洋地震勘探方法、技术提出了更高的要求。为实现高精度、高分辨率成像,多年来国内、外学者提出了许多高分辨率处理方法,包括反褶积[1]、高频衰减补偿[2-3]等,主要聚焦于提升地震资料的低频和高频成分,拓宽频带,其理想目标是获得反射系数剖面[4]。近年来高分辨率处理技术的研究重点已转向如何拓展地震资料的低频成分[5]、同时保持高频的宽频处理阶段。在海洋地震勘探中则发展了以鬼波压制为主的宽频处理技术[6-13]。
虽然鬼波压制方法能够有效拓宽数据频带,但鬼波压制方法对水深和速度等参数比较敏感,其中鬼波延迟时间和海面反射系数是影响鬼波压制效果的两个重要参数,且这两个参数均无法直接获得[14]。由于地震波到达拖缆上不同水听器的入射角不同,波在地下介质中传播时的速度也不同,因此鬼波延迟时间很难准确估算;在大多数鬼波压制方法中,海面反射系数参数通常假设为-1,但这只是一个近似值,不同时刻海面各处的反射系数也不完全相同。参数的细微变化都会导致频谱形态的较大差异,鬼波压制后频谱中会出现低频能量过强的现象,处理结果往往不被地质解释人员认可。对于宽频处理后的频谱能量分布尚无统一的评价标准,为此需要构建可用于所有宽频地震数据的统一标准。
本文首先从优化频谱形态入手,分析了宽频地震频谱形态特点,提出在倍频视角下优化各频率成分与能量分布关系的宽频地震子波计算方法,进而通过宽频地震子波整形[15]的方式,消除海洋数据处理中鬼波压制时因参数控制引起的频谱形态上的差异,实现了宽频地震数据的优化;其次,对比了宽频地震子波、雷克子波、俞氏子波振幅谱形态差异,利用算例测试了频带宽度对子波波形的影响;最后,将宽频地震子波应用于压制鬼波后的宽频数据子波整形,从而优化频谱中各频率的能量分布,取得了显著效果。
1 宽频子波的构建在地震资料处理中,地震子波是一个非常重要的概念,它贯穿于许多重要环节[16],是地震资料反褶积、偏移、特征提取、波阻抗反演、地震资料解释和地震模型正演的基础。地震数据处理中,目标地震子波的选择与地震资料的分辨能力密切相关,合适的目标地震子波有助于提高信号的分辨率、保真度和信噪比。较为常规的目标子波有带限子波、雷克子波等。在地震宽频处理中,这些子波均有不足之处。带限子波旁瓣较多、吉布斯效应较强;雷克子波振幅谱频带较窄,不具有宽频特征;俞氏子波采用对雷克子波按照主频积分的办法丰富低频[17],作为一种宽频地震子波,已被广泛应用于地震数据处理[18-22]。
宽频地震数据处理是高精度地震勘探技术发展的主流方向,一般用倍频程定义频带宽度。在频谱两端的斜坡处,对于5Hz和10Hz频率而言,虽然只相差5Hz,但频率上却相差一个倍频程;而对于50Hz和55Hz频率而言,同样是相差5Hz,但却仅有10%的倍频程,两者没有可比性。考察倍频程均为1的5Hz和10Hz、50Hz和100Hz的能量则更具可比性。因而,在倍频视角下,考察频率与能量关系(频谱形态)显得更有意义。
1.1 倍频程坐标系建立横轴以2为底的频率的对数坐标系(以下称为倍频程坐标系),该坐标系下频率与普通坐标系下频率f的关系为
| $ \hat f = {\rm{lb}}\;f $ | (1) |
式中
取以2为底的频率的对数具有倍频程的物理意义,频率经过对数运算后,高频被压缩到较小范围内,方便从倍频程的角度去考察频率与能量的关系。
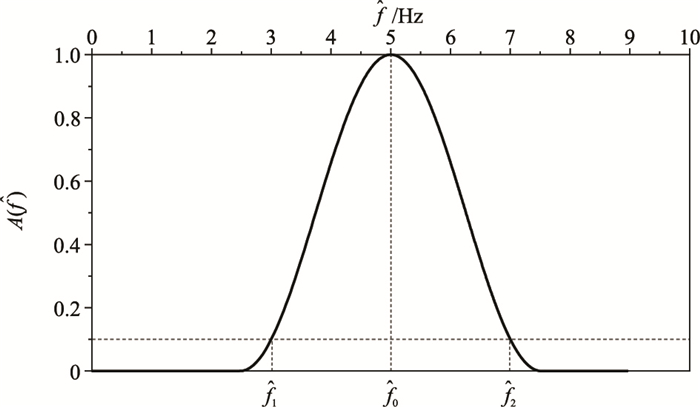
1.2 光滑振幅谱曲线频谱形态优化的思路是使其更光滑,频率和能量的关系更协调(即不同频率的能量对比合理)。这里构建倍频程坐标系下光滑的函数曲线作为地震子波优化的振幅谱曲线(图 1)。众所周知,单周期余弦函数曲线、高斯函数曲线均具备对称且光滑的性质。这里选取单周期余弦函数曲线作为倍频程域的子波频谱,其频率和能量的关系协调(不同频率范围的能量对比合理,从主频过渡到能量为0的频率比较自然)且处处光滑。
|
图 1 倍频程坐标系下的光滑振幅谱曲线 有效频带范围为8~128Hz,峰值频率为32Hz,n为4 |
根据工业界常用的“-20dB带宽”概念,振幅谱的幅度从最大幅度Emax降到0.1Emax之间的频率范围为有效频带范围。给定有效频带范围[f1, f2],则倍频程数n可表示为n=lb(f2/f1),选取[-π, π]范围内的余弦函数曲线,构建关于倍频程坐标系下的光滑振幅谱曲线。经归一化后,该曲线可表述为
| $ \begin{gathered} A(\hat{f})=\frac{1}{2}\left\{\cos \left[2 \pi a\left(\hat{f}-\hat{f}_{0}\right)\right]+1\right\} \\ \hat{f} \in\left[\hat{f}_{0}-\frac{1}{2 a}, \hat{f}_{0}+\frac{1}{2 a}\right] \end{gathered} $ | (2) |
式中
| $ {{\hat f}_0} = \frac{1}{2}\left( {{{\hat f}_1} + {{\hat f}_2}} \right) $ | (3) |
a与倍频程数n的关系为
| $ \frac{1}{a} = \frac{{n{\rm{ \mathsf{ π} }}}}{{\arccos \left( {2\beta - 1} \right)}} $ | (4) |
式中β为振幅谱的幅度衰减系数,用于控制有效频带宽度,本文取值为0.1。
1.3 坐标转换结合式(1)、式(2)将光滑函数曲线恢复到普通坐标系,则普通坐标系下的曲线可表述为
| $ \begin{array}{l} A(f) = \frac{1}{2}\left\{ {\cos \left[ {2{\rm{ \mathsf{ π} }}alb\left( {\frac{f}{{\sqrt {{f_1}{f_2}} }}} \right)} \right] + 1} \right\}\\ \;\;\;\;\;\;\;\;\;\;\;\;f \in \left[ {{2^{{{\hat f}_0} - \frac{1}{{2a}}}}, {2^{{{\hat f}_0} + \frac{1}{{2a}}}}} \right] \end{array} $ | (5) |
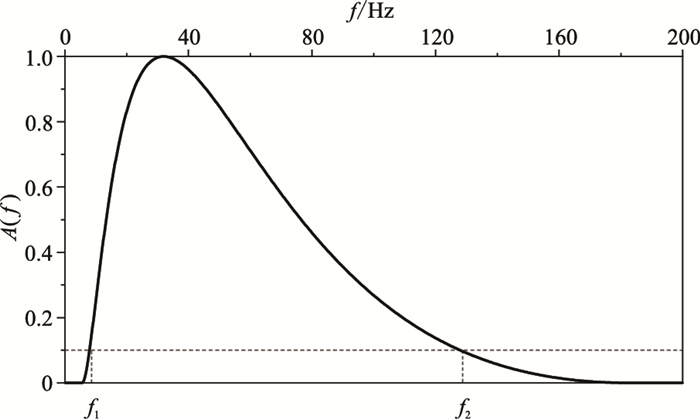
图 2是在普通坐标系下的光滑振幅谱曲线。对比图 1可知:低频部分相对压缩,能量得到显著提升;高频虽然能量不强,但高频的范围相对宽泛;所得曲线是光滑的单峰函数,且左支陡度较大,右支陡度较小,曲线形态与实际资料相符。
|
图 2 普通坐标系下的光滑振幅谱曲线 有效频带范围为8~128Hz,峰值频率为32Hz,n为4 |
频率域地震子波W(f)可表述为
| $ {W\left( f \right) = {W_{\rm{R}}}\left( f \right) + {\rm{i}}{W_{\rm{I}}}\left( f \right)} $ | (6) |
式中WR(f)、WI(f)分别为频率域子波的实部和虚部。
若子波为零相位,则虚部为零,将坐标转换后的光滑函数曲线作为频率域子波的振幅谱,则有
| $ {W\left( f \right) = A\left( f \right)} $ | (7) |
然后进行反傅里叶变换,得到时间域倍频子波
| $ w(t)=\int_{-\infty}^{+\infty} W(f) \mathrm{e}^{\mathrm{i} 2 \pi f t} \mathrm{~d} f $ | (8) |
根据上述方法,可以构建倍频程坐标系下的光滑函数曲线,经坐标转换和反傅里叶变换得到倍频子波。
基于上述方法原理,采用单周期余弦函数曲线计算子波。设定有效频带范围为6~96Hz,倍频程数n为4,采样率为1ms,得到的子波如图 3所示。

|
图 3 零相位的倍频子波 |
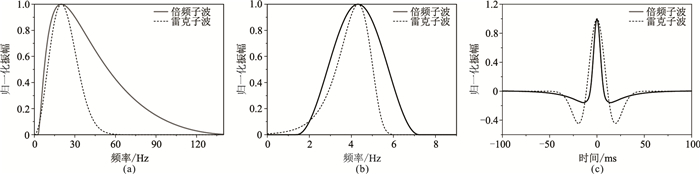
图 4为相同低截止频率(4Hz)及峰值频率(20Hz)的倍频子波与雷克子波的振幅谱和零相位子波波形的对比。由图可见,相较于雷克子波振幅谱,倍频子波的频带更宽,低、高频能量更丰富(图 4a、图 4b);相较于雷克子波波形,倍频子波主瓣更窄,旁瓣幅度为主瓣幅度的15.74%,远低于雷克子波的44.49%(图 4c)。
|
图 4 相同低频端截止频率(4Hz)及峰值频率(20Hz)的零相位倍频子波与雷克子波对比 (a)普通坐标系振幅谱;(b)倍频程坐标系振幅谱;(c)时间域子波波形 |
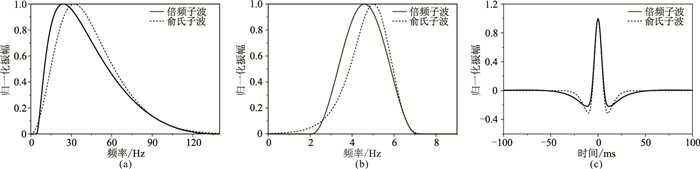
图 5为相同有效频带范围(6~96Hz)的倍频子波与俞氏子波的振幅谱和零相位子波波形对比。由图 5可见:相较于俞氏子波振幅谱,倍频子波的低频能量增强,同时能够保持高频能量(图 5a、图 5b);在倍频程坐标系下,倍频子波振幅谱形态趋向于正态分布,各频率成分能量分布更协调,而俞氏子波振幅谱整体能量往高频方向集中(图 5b);相较于俞氏子波波形,倍频子波旁瓣幅度更小,为主瓣幅度的21.67%,低于俞氏子波的31.33%(图 5c)。
|
图 5 相同有效频带范围(6~96Hz)的倍频子波与俞氏子波的对比 (a)普通坐标系振幅谱;(b)倍频程坐标系振幅谱;(c)时间域子波波形 |
关于倍频子波参数的选择,较适用的为低截止频率f1和倍频程数n的组合。图 6是一组低截止频率固定、倍频程数n取不同值时的子波及振幅谱。从图中可以看出,n越大,子波延续时间越短,主瓣宽度越窄,旁瓣幅度越小,趋向于脉冲信号(图 6a)。随着n的增大,振幅谱频带变宽,峰值频率增大;相较于普通坐标系(图 6b),在倍频程坐标系(图 6c)下的振幅谱曲线陡度变小,形态更光滑。实际地震资料处理时,可通过对分辨率和保真度的不同要求选择合适的n。

|
图 6 固定低截止频率(6Hz)时、不同倍频程数n的倍频子波对比 (a)时间域波形;(b)普通坐标系振幅谱;(c)倍频程坐标系振幅谱 |
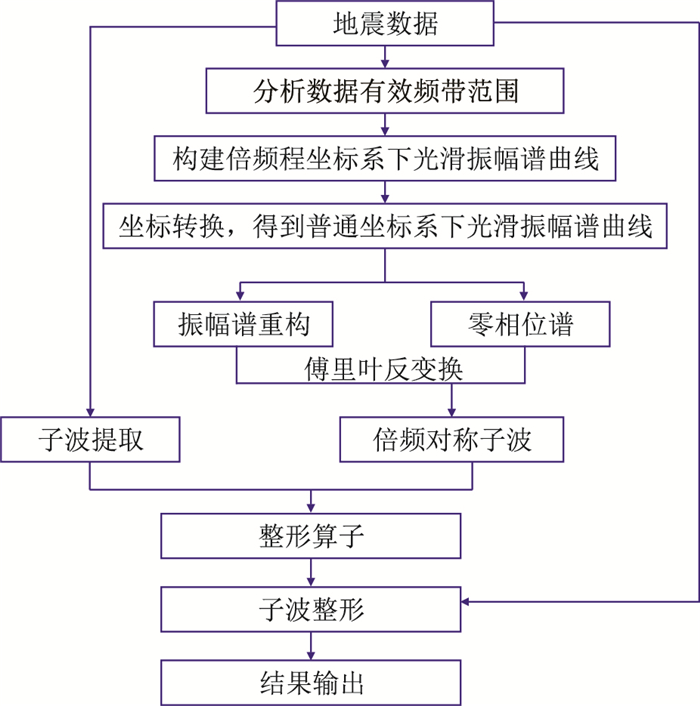
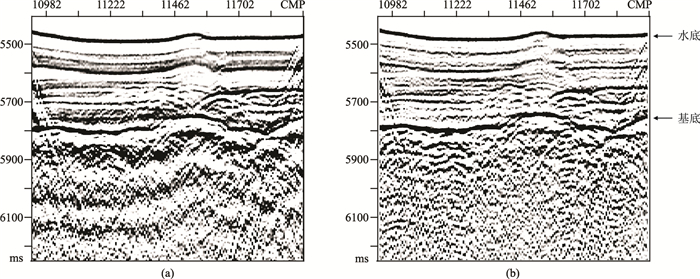
倍频子波可应用于宽频数据子波整形,其处理流程如图 7所示。本文选取经鬼波压制后的宽频地震数据进行子波整形处理。从高信噪比段数据提取的子波的有效频带范围为6~90Hz,将其设为目标子波的有效频带范围。图 8是南海深海盆区沉积层地震数据子波整形前、后的地震剖面对比。由图可见,经子波整形处理后(图 8b),水底、基底强反射界面能量更聚焦,波组特征更加清晰,气泡效应得到消除,分辨率也得到提升,有利于后续精细地震解释。
|
图 7 宽频数据子波整形流程 |
|
图 8 南海深海盆区沉积层地震数据应用子波整形前(a)、后(b)剖面对比 |
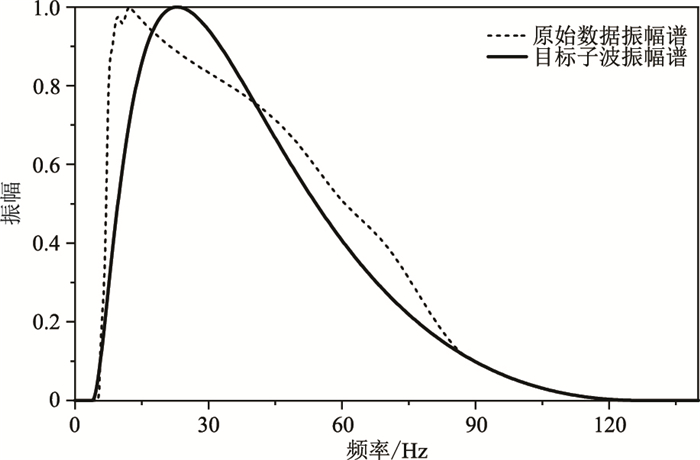
图 9是子波整形前、后的振幅谱对比,可以看出,子波整形处理后的主频得到提升,低频能量得到压制,振幅谱更光滑,高低频能量分布更协调。
|
图 9 原始数据与目标子波振幅谱对比 |
频谱中各频率成分的能量分布是反映宽频地震数据品质的一个重要因素。宽频处理结果频率成分丰富,但频谱形态往往差异较大。为更好地显示或表达具有较为丰富频率的宽频数据,在充分考虑数据中各频率成分的能量分布前提下,本文提出倍频视角的宽频地震子波优化方法,获得以下认识。
(1) 零相位地震子波优化的本质是对频谱形态进行优化,故在宽频处理时需关注目标子波频谱形态,在拓宽频带的同时需兼顾各频率成分的能量分布,而从倍频程的角度去考察这一关系更合理。
(2) 本文方法构建的“倍频子波”具有宽频特征。选用光滑函数曲线计算振幅谱,有效减弱了子波的吉布斯效应;在倍频程域通过有效频带范围及倍频程数构建目标子波,是一种新的宽频地震子波计算方式。
(3) 实际地震数据处理时,通过对鬼波压制后的宽频数据进行子波整形,消除了因参数敏感引起的频谱形态差异,可改善地震数据显示效果。
如果宽频子波为一个集合,则俞氏子波和倍频子波均是其中的一个子集。在俞氏子波的应用场景下,倍频子波可以作为替代。倍频子波实际上突出的是倍频视角,在实际使用时,也可以用三个参数(主频、有效低截频率、有效高截频率)设计倍频子波(不严格对称),突出主频,确保吉布斯效应较小。
| [1] |
MARGRAVE G F. Theory of nonstationary linear filtering in the Fourier domain with application to time-variant filtering[J]. Geophysics, 1998, 63(1): 244-259. DOI:10.1190/1.1444318 |
| [2] |
WANG Y H. A stable and efficient approach of inverse Q filtering[J]. Geophysics, 2002, 67(2): 657-663. DOI:10.1190/1.1468627 |
| [3] |
PINNEGAR C R, MANSINHA L. The S-transform with windows of arbitrary and varying shape[J]. Geo-physics, 2003, 68(1): 381-385. |
| [4] |
蔡希玲. 俞氏子波在地震数据处理中的应用研究[J]. 石油地球物理勘探, 2000, 35(4): 497-507. CAI Xiling. Application of Yu wavelet to seismic data processing[J]. Oil Geophysical Prospecting, 2000, 35(4): 497-507. DOI:10.3321/j.issn:1000-7210.2000.04.012 |
| [5] |
公亭, 王兆磊, 顾小弟, 等. 宽频地震资料处理配套技术[J]. 石油地球物理勘探, 2016, 51(3): 457-466. GONG Ting, WANG Zhaolei, GU Xiaodi, et al. Broadband seismic data matching processing[J]. Oil Geophysical Prospecting, 2016, 51(3): 457-466. |
| [6] |
LINDSEY J P. Elimination of seismic ghost reflections by means of a linear filter[J]. Geophysics, 1960, 25(1): 130-140. DOI:10.1190/1.1438679 |
| [7] |
JOVANOVICH D B, SUMNER R D, AKINS-EASTERLIN S L. Ghosting and marine signature deconvolution: a prerequisite for detailed seismic interpretation[J]. Geophysics, 1983, 48(11): 1468-1485. DOI:10.1190/1.1441431 |
| [8] |
WEGLEIN A B, GASPAROTTO F A, CARVALHO P M, et al. An inverse-scattering series method for attenuating multiples in seismic reflection data[J]. Geophysics, 1997, 62(6): 1975-1989. DOI:10.1190/1.1444298 |
| [9] |
WEGLEIN A B, SHAW S A, MATSON K H, et al. New approaches to deghosting towed-streamer and ocean-bottom pressure measurements[C]. SEG Technical Program Expanded Abstracts, 2002, 21: 2114-2117.
|
| [10] |
ZHANG J F, WEGLEIN A B. Application of extinction theorem deghosting method on ocean bottom data[C]. SEG Technical Program Expanded Abstracts, 2006, 25: 2674-2678.
|
| [11] |
管西竹, 陈宝书, 符力耘, 等. 基于波动方程的上下缆地震数据鬼波压制方法研究[J]. 地球物理学报, 2015, 58(10): 3746-3757. GUAN Xizhu, CHEN Baoshu, FU Liyun, et al. The study of a deghosting method of over/under streamer seismic data based on wave equation[J]. Chinese Journal of Geophysics, 2015, 58(10): 3746-3757. DOI:10.6038/cjg20151025 |
| [12] |
许自强, 方中于, 顾汉明, 等. 海上变深度缆数据最优化压制鬼波方法及其应用[J]. 石油物探, 2015, 54(4): 404-413. XU Ziqiang, FANG Zhongyu, GU Hanming, et al. The application of optimal deghosting algorithm on marine variable-depth streamer data[J]. Geophysical Prospecting for Petroleum, 2015, 54(4): 404-413. DOI:10.3969/j.issn.1000-1441.2015.04.006 |
| [13] |
王艳冬, 王小六, 桑淑云, 等. 渤海海域水平拖缆数据宽频处理关键技术[J]. 石油地球物理勘探, 2020, 55(1): 10-16. WANG Yandong, WANG Xiaoliu, SANG Shuyun, et al. Key techniques for broadband processing of plane streamer data in Bohaisea[J]. Oil Geophysical Prospecting, 2020, 55(1): 10-16. |
| [14] |
封强, 韩立国, 杨帆. 非高斯性最大化变深度缆鬼波压制方法[J]. 石油地球物理勘探, 2020, 55(1): 57-63. FENG Qiang, HAN Liguo, YANG Fan. A deghosting method for variable-depth streamer data based on non-Gaussian maximization[J]. Oil Geophysical Prospecting, 2020, 55(1): 57-63. |
| [15] |
程志国, 王克非, 张龙. 子波整形反褶积在提高分辨率处理中的作用[J]. 天然气技术与经济, 2012, 6(6): 15-18, 77. CHENG Zhiguo, WANG Kefei, ZHANG Long. Role of wavelet shaping deconvolution in high-resolution seismic processing[J]. Natural Gas Technology and Economy, 2012, 6(6): 15-18, 77. |
| [16] |
俞寿朋. 高分辨率地震勘探[M]. 北京: 石油工业出版社, 1993. YU Shoupeng. High Resolution Seismic Exploration[M]. Beijing: Petroleum Industry Press, 1993. |
| [17] |
俞寿朋. 宽带Ricker子波[J]. 石油地球物理勘探, 1996, 31(5): 605-615. YU Shoupeng. Wide-band Ricker wavelet[J]. Oil Geo-physical Prospecting, 1996, 31(5): 605-615. |
| [18] |
李英才, 王艳仓, 李旭, 等. 地表一致性俞氏子波反褶积[J]. 石油物探, 1997(S1): 56-62. |
| [19] |
曹思远, 杨东升. 基于俞氏子波的时频分解[C]. 中国地球物理学会第22届年会论文集, 成都, 2006, 178. CAO Siyuan, YANG Dongsheng. Time frequency decomposition based on Yu wavelet[C]. Proceedings of the 22nd Annual Meeting of China Geophysical Society, Chengdu, 2006, 178. |
| [20] |
栾颖. 约束稀疏脉冲波阻抗反演方法在煤层识别中的应用[D]. 吉林长春: 吉林大学, 2010. LUAN Ying. The Application of Constrained Sparse Spike Inversion in the Coal Bed Identification[D]. Jilin University, Changchun, Jilin, 2010. |
| [21] |
苏世龙, 贺振华, 戴晓云, 等. 岩性油气藏地震保幅处理技术及其应用——以东部某油田岩性气藏为例[J]. 物探与化探, 2015, 39(1): 54-59. SU Shilong, HE Zhenhua, DAI Xiaoyun, et al. The application of relative amplitude compensation technology to lithologic reservoir exploration: a case study of lithologic gas reservoir in an oilfield of eastern China[J]. Geophysical and Geochemical Exploration, 2015, 39(1): 54-59. |
| [22] |
HOU D J, ZHOU D H, ZHANG Z J, et al. The application of broadband Ricker wavelet in thin reservoir description[C]. Extended Abstracts of 79th EAGE Conference & Exhibition 2017, 1-5.
|



 成谷, 广东省珠海市唐家湾中山大学珠海校区海琴4号楼A412, 519082。Email:
成谷, 广东省珠海市唐家湾中山大学珠海校区海琴4号楼A412, 519082。Email: 