② 中国石油大学(华东)地球科学与技术学院, 山东青岛 266580;
③ 中国石油化工股份有限公司石油勘探开发研究院, 北京 100083
② School of Geosciences, China University of Petroleum (East China), Qingdao, Shandong 266580, China;
③ SINOPEC Petroleum Exploration and Production Research Institute, Beijing 100083, China
致密油气是一种非常重要的非常规资源,是接替常规油气资源、支撑油气革命不可或缺的力量[1]。中国拥有丰富的致密油气资源,储层普遍经历了复杂的成岩和构造作用,多以基质致密、储集空间类型多样、特低孔低渗的缝控型为主[2]。缝控型致密储层中的裂缝不仅控制有效储层的规模和油气储量,同时还是油气开采过程中重要的运输通道。由于储层含油气性和产能高度依赖裂缝,裂缝的有效性评价是分析储层质量以及油气勘探部署的重要依据[3-4]。裂缝开度(FVA)作为定量描述裂缝发育特征的参数,是评价裂缝有效性的基础,对于指导致密油气储层勘探开发具有重要的参考价值[5]。
目前,裂缝开度的计算方法主要包括实验测量、数值模拟及测井计算等三种。Ponziani等[6]利用实验装置准确测量岩心的裂缝开度,但受取心技术的限制,测量结果数量较少且在深度上不连续;Van Stappen等[7]依靠微CT成像和三维激光扫描设备获取了不同围压下的裂缝开度,但装备适用范围有限,无法真实还原地层条件;丁文龙等[8]基于数学模型,运用有限元方法对构造应力场进行数值模拟,得到了裂缝发育区的裂缝开度信息,但应力场有限元模拟需考虑地质体的岩石物理特征,所需参数较多,且参数的选取依赖研究者的主观经验;Boadu[9]通过数值模拟实验建立了地震信号特征与裂缝开度之间的关系,利用地震属性预测裂缝开度等储层特征参数,但预测结果存在垂向分辨率低、多解性强等问题;Aghli等[10]采用图像处理的方法对电成像测井资料进行处理、计算,得到了连续且垂向分辨率高的裂缝开度数据,但由于成像测井测量成本高昂,计算的开度数据受测量深度的限制。地球物理常规测井资料具有纵向分辨率高、连续性好、信息量大、成本低等优点,对大多数油气田而言,如何利用常规测井信息建立裂缝的测井响应机理模型,进而计算地层裂缝开度,是亟需解决的实际问题[11]。
在常规油气储层中,成岩作用差异往往导致岩石成分和结构发生变化,产生不同的测井响应,可以利用多元线性回归(MLR)等线性方法预测储层参数[12]。而缝控型致密油气储层的强非均质性导致常规测井数据与裂缝开度之间存在复杂的非线性关系,简单的线性模型并不能准确表征地下裂缝张开程度的变化趋势,因此需要建立一个非线性预测模型表示常规测井数据与裂缝开度之间的转换关系。机器学习可通过模拟人类、自然行为对历史数据进行学习,找出其中的规律,进而利用新的数据对目标进行预测[13-14]。国内外许多学者借助机器学习模型强大的非线性映射能力,对常规测井资料的数据特征进行深度挖掘,在储层参数预测方面取得了良好的应用效果[15-19],但单一机器学习模型仍存在泛化性差、易受噪声数据干扰等缺点[20]。
委员会机器(CM)采用集成的思想,模仿人类委员会的决策机制,将一个复杂的计算任务分给多个计算能力优异的专家,各个专家各自独立求解,然后利用某种组合机制组合这些专家的解,得到最终的全局最优解[21-23]。委员会机器可将训练好的学习模型全部利用起来,整合各个学习模型的优势,在储层参数预测方面得到了有效应用[24-25]。尽管委员会机器方法取得了成功,但各专家模型的组合权重一般是通过人工平均赋值或优化算法获得,这些组合策略易受到人为经验和模型各种参数调节的影响。如何得到合理、有效的组合策略,是模型面临的难题之一[26-27]。
为了提高组合权重的计算精度,增加模拟组合策略的可解释性,本文利用递阶层次结构模型和门神经网络模型对传统委员会机器进行改进,基于条件交替期望变换理论,综合考虑各个专家网络的预测性能,添加组合权重自适应生成的层次网络模块,形成了一个新的委员会机器模型——层次专家委员会机器模型(HECM)。运用该模型在研究工区实现了井中裂缝开度预测,并与单一机器模型和传统委员会机器模型的预测结果进行了对比。结果表明,HECM的预测结果与岩心测量结果更吻合。
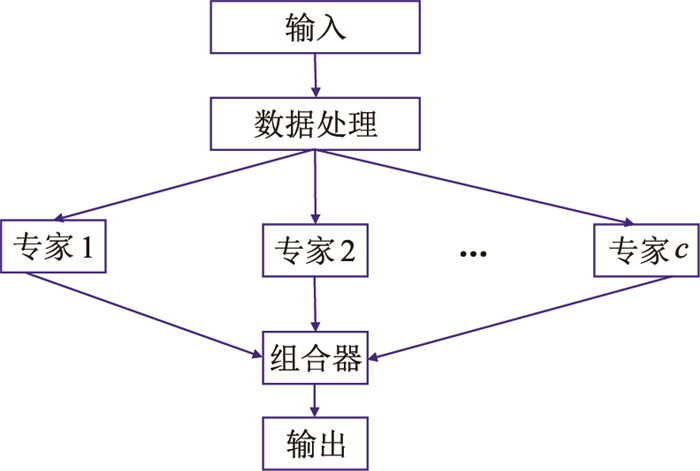
1 方法原理 1.1 委员会机器模型设计原则委员会机器网络由几个训练有素的专家机器组成,专家机器通常是由多种智能算法并行构建的机器学习模型。每个专家机器使用完全相同的输入,基于不同的初始网络条件独立完成训练,最后将各专家机器输出的结果进行线性加权平均并作为委员会机器的输出。委员会机器的网络结构如图 1所示。
|
图 1 委员会机器的网络结构 |
在使用单一机器学习模型预测裂缝开度时,通常会训练多种机器学习模型,最终选取预测效果最好的一个,其余的模型则被舍弃,从而造成学习资源的浪费。当各学习模型预测效果相当时,则会出现难以选择的情况。此外,模型的泛化性能很大程度上取决于数据本身,在某一样本集取得最佳预测效果的模型并不一定适用其他的独立样本集。而委员会机器能够充分利用这些训练好的模型,整合各模型的优势,有效提高自身的泛化性和预测性能[28]。
1.2 层次网络模块的构建原理类似于委员会机器的搭建思想,本文提出的HECM也要对各专家机器的输出进行加权组合,但不同的是,这些权重不再是人为指定或无条件求和平均,而是由一个额外的层次网络模块自适应生成。该模块主要由递阶层次结构模型和门神经网络模型构成,可对基础专家的输出结果进行评价、分析,决定各个基础专家在全局输出中的贡献。基于层次网络模块自适应计算权重的步骤如下[29]。
(1) 构建递阶层次结构。将影响预定目标的因素进行分组,并将每一组作为一个层次,按最高层(目标层)、多重中间层(准则层)以及最低层(方案层)的形式排列起来。层与层之间可以建立子层次,上、下层因素之间的联系可用连接线表示,形成具有自上而下主导关系的递阶层次结构。
(2) 构造判断矩阵。当确定好上、下层之间的主导关系后,需计算联系上层某因素(目标A或某个准则U)的下层各因素在上层因素之中所占的比重。
假定A层中的某一因素与下一层次B中的因素有联系,则可构造A、B层次之间的判断矩阵
| $ \boldsymbol{P}=\left[\begin{array}{cccc} b_{11} & b_{12} & \cdots & b_{1 n} \\ b_{21} & b_{22} & \cdots & b_{2 n} \\ & & \vdots & \\ b_{n 1} & b_{n 2} & \cdots & b_{n n} \end{array}\right] $ | (1) |
式中bij表示对于A层某一因素而言,因素bi对bj的相对重要性的判断值。一般取1、3、5、7、9等5个等级标度,其中1表示bi与bj同等重要,3表示bi较bj稍重要,5表示bi较bj明显重要。按照该准则,因素之间的相对重要性依次上升。当5个等级不够用时,可采取2、4、6、8表示相邻判断的中值。
(3) 层次单排序。层次单排序是为了确定同一层次因素对于上一层次某因素相对重要性的排序权值。通过求解判断矩阵的最大特征根λmax所对应的归一化后的特征向量W,其分量即为对应因素单排序的权重值
| $ \boldsymbol{P} \boldsymbol{W}=\lambda_{\max } \boldsymbol{W} $ | (2) |
为了检验层次单排序的合理性,需要对判断矩阵进行一致性检验。可用随机一致性比率(Random Conformance Rate,CR)对判断矩阵进行检验
| $ \mathrm{CI}=\frac{\lambda_{\max }-n}{n-1} $ | (3) |
| $ \mathrm{CR}=\frac{\mathrm{CI}}{\mathrm{RI}} $ | (4) |
式中:CI(Consistency Index)为矩阵一致性指标;RI(Mean Random Consistency Index)为平均随机一致性指标,其取值规则如表 1所示[30]。当CR<0.01时,判断矩阵具有令人满意的一致性,否则需要对判断矩阵进行调整,直到CR<0.01为止。
|
|
表 1 平均随机一致性指标的取值规则 |
(4) 层次总排序。层次总排序需要从上到下依次逐层进行,假设已算出第k-1层上n个因素相对于总目标的排序w(k-1)=[w1(k-1), …, wn(k-1)]T (k=1, 2, …, m),那么第k层m个因素对于k-1层上以第j个因素为准则的单排序向量为uj(k)=[u1j(k), u2j(k), …, umj(k)]T(j=1, 2, …, n),将不受第j个因素支配的因素权重值取零,于是可得到m×n阶矩阵
| $ \begin{aligned} \boldsymbol{U}^{(k)} &=\left[\begin{array}{llll} \boldsymbol{u}_{1}^{(k)}, \boldsymbol{u}_{2}^{(k)}, \cdots, \boldsymbol{u}_{n}^{(k)} \end{array}\right] \\ &=\left[\begin{array}{llll} u_{11}^{(k)} & u_{12}^{(k)} & & u_{1 n}^{(k)} \\ u_{21}^{(k)} & u_{22}^{(k)} & & u_{2 n}^{(k)} \\ & & \ddots & \\ u_{m 1}^{(k)} & u_{m 2}^{(k)} & & u_{m n}^{(k)} \end{array}\right] \end{aligned} $ | (5) |
其中U(k)中的第j列为第k层m个因素对于第k-1层上第j个因素为准则的单排序向量。
记第k层上各因素对总目标的总排序为w(k)=(w1(k), …, wn(k))T,则有
| $ \begin{aligned} \boldsymbol{w}^{(k)}=& \boldsymbol{U}^{(k)} \boldsymbol{w}^{(k-1)} \\ =& {\left[\begin{array}{llll} u_{11}^{(k)} & u_{12}^{(k)} & & u_{1 n}^{(k)} \\ u_{21}^{(k)} & u_{22}^{(k)} & & u_{2 n}^{(k)} \\ u_{m 1}^{(k)} & u_{m 2}^{(k)} & & u_{m n}^{(k)} \end{array}\right]\left[\begin{array}{c} w_{1}^{(k-1)} \\ w_{2}^{(k-1)} \\ \vdots \\ w_{n}^{(k-1)} \end{array}\right] }\\ =& \left[\begin{array}{c} \sum\limits_{j=1}^{n} u_{1 j}^{(k)} w_{j}^{(k-1)} \\ \sum\limits_{j=1}^{n} u_{2 j}^{(k)} w_{j}^{(k-1)} \\ \vdots \\ \sum\limits_{j=1}^{n} u_{m j}^{(k)} w_{j}^{(k-1)} \end{array}\right] \end{aligned} $ | (6) |
从而得到各基础方案对应的初始权重
| $ w_{i}^{(k)}=\sum\limits_{j=1}^{n} u_{i j}^{(k)} w_{j}^{(k-1)} \quad i=1,2, \cdots, m $ | (7) |
同样,为了评价层次总排序的计算结果的一致性,也需要计算与单排序类似的检验量。第k层的总排序的一致性比率计算公式为
| $ \mathrm{CR}^{(k)}=\frac{\sum\limits_{j=1}^{m} w_{j}^{(k-1)} \mathrm{CI}_{j}^{(k)}}{\sum\limits_{j=1}^{m} w_{j}^{(k-1)} \mathrm{RI}_{j}^{(k)}} $ | (8) |
式中CIj(k)和RIj(k)分别为第k层中某些因素对k-1层第j个因素单排序的一致性指标和平均随机一致性指标。
(5) 门网络模块更新权重。利用单层感知器(SLP),构建一个由多元非线性函数和交替条件期望变换(ACE)算法激活的门神经网络模块,即
| $ \theta(Y)=\sum\limits_{i=1}^{p} \varphi_{i}\left(X_{i}\right)+\varepsilon $ | (9) |
式中:θ是关于因变量Y的期望转化函数;φ是关于自变量X的期望转化函数;ε为回归误差;p为变量的个数。
按照ACE算法的理论[31],利用式(9)进行非线性回归得到的误差方差方程为
| $ e^{2}(\theta, \varphi)=\frac{E\left\{\left[\theta(Y)-\sum\limits_{i=1}^{p} \varphi_{i}\left(X_{i}\right)\right]^{2}\right\}}{E\left[\theta^{2}(Y)\right]} $ | (10) |
据此建立以误差方差最小为优化目标的优化方程
| $ \left\{\begin{array}{l} \min \left[e^{2}(\theta, \varphi)\right] \\ \text {s. t. }\ \ E\left[\theta^{2}(Y)\right]=1 \\ E[\theta(Y)]=E\left[\varphi_{1}\left(X_{1}\right)\right]=\cdots=E\left[\varphi_{p}\left(X_{p}\right)\right]=0 \end{array}\right. $ | (11) |
为了求解误差方差方程,每个变量建立如下的单一条件期望函数
| $ \varphi_{i}\left(X_{i}\right)=E\left\{\left[\theta(Y)-\sum\limits_{j=1, j \neq i}^{p} \varphi_{j}\left(X_{j}\right) \mid X_{i}\right]\right\} $ | (12) |
| $ \theta(Y)=\frac{E\left[\sum\limits_{i=1}^{p} \varphi_{i}\left(X_{i}\right) \mid Y\right]}{\left\|\sum\limits_{i=1}^{p} \varphi_{i}\left(X_{i}\right) \mid Y\right\|_{2}} $ | (13) |
通过反复交替条件期望,不断迭代计算,求得最小的误差方差,即能获得一组最佳的因变量和多个自变量(θ*, φ1*, φ2*, …, φp*)的变换关系。
那么,在变换空间中,最优的期望变换方程可表示为
| $ \theta^{*}(Y)=\sum\limits_{i=1}^{p} \varphi_{i}^{*}\left(X_{i}\right)+\varepsilon^{*} $ | (14) |
式中ε*遵循均值为零的正态分布。
因此,通过门神经网络模块更新权重后,可进一步提高基础方案的预测精度。
1.3 HECM的构建方案如图 2所示,为了获得最佳的预测性能,以目标预测精度作为总体评价目标,选取平均绝对误差(MAE)、均方根误差(RMSE)、总绝对误差(TAE)、决定系数(R2)等4个参数为目标评价准则因素;将每个准则因素作为基础专家网络单元的性能评价指标,构建相应的判断矩阵,两两比较每个基础专家网络单元的性能表现,以确定各自重要性;将核岭回归(KRR)、支持向量回归(SVR)、BP神经网络(BPN)等3个机器学习模型作为基础专家网络单元,把每个基础网络单元的输出结果选为待评价方案,送入性能评议模块进行评判打分。最后利用单层感知器和ACE算法构成一个门神经网络模块(主席决策层),对打分结果进行综合决策,从而得到最优的解决方案。

|
图 2 HECM的网络结构 |
研究区位于四川盆地川西坳陷孝泉—丰谷隆起带的新场气田。受龙门山造山带抬升的影响,目的层须家河组经历了由海相向陆相的变迁,经过印支期、燕山期和喜山期等多期次构造运动,形成了气水关系复杂的致密碎屑岩气藏。须二段(须家河组二段)为主要含气层段,储层岩性主要为浅灰色中粒岩屑石英砂岩,受构造、沉积以及差异成岩作用等多种因素的影响,不同深度的储集性能差异明显[32]。
统计、分析工区的高产气井S井4000~5400m段的105组岩心和井壁成像测井资料,发现该段裂缝以低角度斜缝为主,裂缝充填程度较低,裂缝开度最小值为0.018mm,最大值为1.950mm,平均值为0.410mm,裂缝开度主要集中在0.100~0.700mm。将裂缝开度与实际产能关联分析,发现主要产气层的裂缝开度与产气量存在明显的正相关。因此,本文以岩心和成像测井资料计算的裂缝开度作为预测对象,基于提出的HECM,选取常规测井数据当作模型驱动,研究适用于致密砂岩储层的裂缝开度预测方法。
2.2 学习样本优选与数据预处理在机器学习中,学习样本的有效性和代表性是决定预测效果的两个重要因素。储层裂缝张开程度受岩性的控制,而各类测井曲线又能够从不同角度反映地下岩石的物理特性,因此可结合不同测井资料的响应特征,筛选对裂缝开度敏感的测井参数作为预测模型的学习样本。
岩石矿物组成的差异对裂缝的形成和发育具有控制作用,因而能够揭示泥质含量的测井曲线会对开启裂缝较为敏感。对于裂缝开度较大的地层,泥浆滤液会在井壁渗透形成泥饼,导致井径(CAL)测量值变小。同时,泥浆和地层水的流动不仅使地层产生电动势,也使铀元素更易被裂缝或井壁吸附而发生沉淀,导致自然电位(SP)和自然伽马(GR)测量值变大。另外,致密砂岩孔隙结构的不同导致地层非均质性和流体压力产生差异,也能影响裂缝的形成与分布,因而揭示孔隙度的测井曲线也对裂缝较为敏感。由于裂缝开启,井壁内充填密度较小的流体造成声波能量衰减严重、地层中含氢指数增大、密度测井仪器极板不能较好地贴合井壁,导致密度(DEN)测量值降低,声波时差(AC)和中子孔隙度(CNL)测量值升高。与岩性和孔隙度系列测井相比,电阻率系列测井提供的信息能更好地反映裂缝的张开程度。致密砂岩作为高阻地层,其电阻率变化主要取决于地层岩性和流体性质,裂缝的存在会引起地层水和泥浆的入侵,导致深侧向(RD)和浅侧向(RS)电阻率明显降低,且裂缝的张开程度越大,深、浅侧向电阻率之间的差异越小[33]。
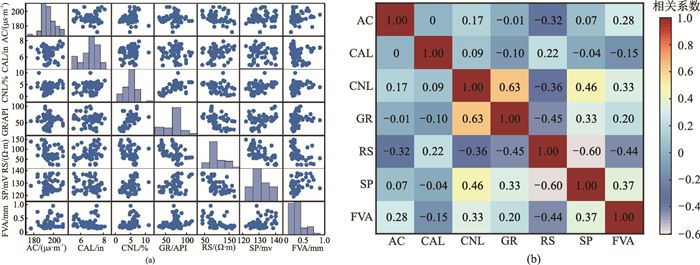
定性分析测井资料变化规律不足以获得实际工区敏感的测井参数,需要结合实际工区样本集的数据分布特征,进行相关系数定量计算,排序、筛选出敏感的测井参数,结果如图 3所示。从图中可以看出,各常规测井参数与裂缝开度虽具有一定的相关性,但整体的相关系数都较低。直接利用测井参数进行训练,预测难度较大,需要进一步的数据处理以提升样本集的质量。因此,基于计算结果,初步选择AC、CNL、RS、SP这4个参数构建预测模型的学习样本数据集。
|
图 3 不同测井参数与裂缝开度相关性分析 (a)测井参数与裂缝开度的散点交会图;(b)各变量间的相关系数热力图 |
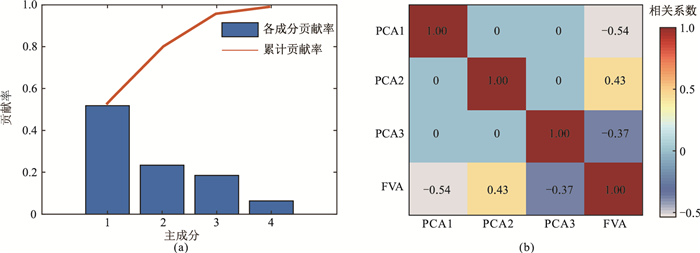
利用Z-Score标准化处理和主成分分析(PCA)构建数据预处理模块,可以消除数据间量纲不同和相关冗余性对模型预测精度的影响[34]。数据处理后的结果如图 4所示。从图 4a中可以看出,处理后的学习样本前三个主成分的累计贡献率就超过90%,能够较好地代替原有输入样本变量。从图 4b中可以看出,处理后的学习样本之间的伪相关性消失,各主成分之间的相关系数为0,各主成分变量与裂缝开度的整体相关性有所提升。因此,经数据预处理后的学习样本属性由4个减少到3个,不仅减轻了模型的学习负担,还进一步提高了学习样本的质量。
|
图 4 数据处理后的结果 (a)各主成分贡献率;(b)各变量间的相关系数热力图 |
工区的研究样本数量较少,裂缝开度的预测本质上属于极小样本的非线性回归问题。利用HECM预测裂缝开度主要包括两个阶段:第一阶段,通过KRR、SVR、BPN等不同的机器学习模型构建基础专家网络单元,每个网络单元接收相同的输入数据并给出独立的裂缝开度预测结果,评判专家以各性能评价指标表现作为评判标准,为各基础专家网络单元的预测结果进行打分,再由大会评议层讨论、确定各基础专家网络单元所占的初始权重;第二阶段,利用SLP模型和ACE算法构建主席决策层,对大会评议层讨论的结果进行迭代更新,从而得到模型的最终输出。
将经过预处理后的样本数据按2∶1的比例进行分区,随机选取70个样本数据作为训练集,剩余的35个样本数据作为测试集。先将带有标签的训练集输入到各基础专家网络单元中进行训练,再利用测试集进行结果的验证,各模型的超参数设置及预测的性能表现如表 2、图 5所示。
|
|
表 2 各基础网络单元超参数设置及模型性能评估指标 |
|
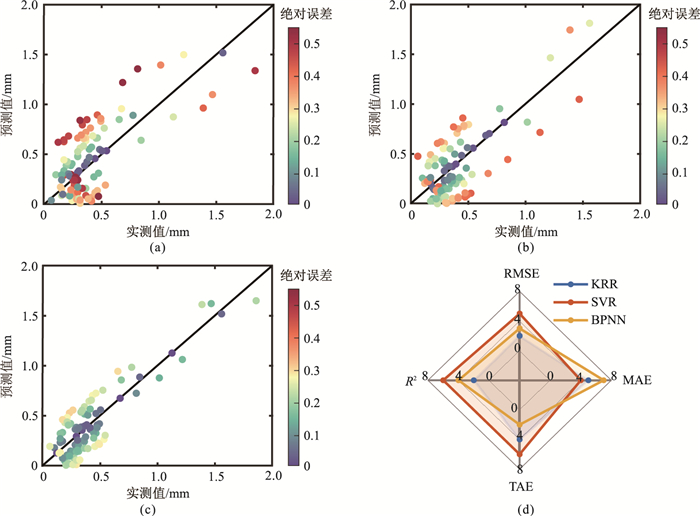
图 5 基础专家网络单元KRR(a)、BPN(b)、SVR(c)的裂缝开度预测结果及性能得分雷达图(d) |
从表 2中可以看出,KRR网络单元超参数设置少,网络复杂度低,训练集预测结果稳定,但容错能力较差,测试集预测效果不佳;BPN网络单元超参数调节简单,非线性映射能力强,训练集预测结果极为优秀,但在训练中过于追求经验风险最小,出现了过拟合的现象,面对小样本的测试集数据时泛化能力不足,预测效果一般;SVR网络单元虽超参数设置较多,但基于结构风险最小化原则,对噪声数据的容忍度高,训练集和预测集预测效果均较好。
从图 5可以看出,面对无规律的实际数据,单个网络单元在小样本训练中易受方差和偏差的影响,各基础专家网络单元输出误差波动性大,稳定性不足,预测结果与实际结果有差异,预测精度仍需提升。各基础网络单元之间的预测结果差异较大,因此需要通过专家评判层和大会评议层依据模型性能评价指标,从不同角度对各基础专家网络单元的性能进行综合评判、打分,并根据打分结果确定每个基础网络单元的初始权重。
将各基础专家网络单元的预测结果当成门神经网络的自变量,利用SLP模型将各自变量输入到ACE算法的变换空间,以回归误差方差最小为期望,通过反复交替条件期望,迭代更新各自变量的初始权重。最后将取得最优变换后的自变量总和作为HECM的输出,并将输出的结果与传统的CM和SVR回归模型进行对比(图 6)。
|
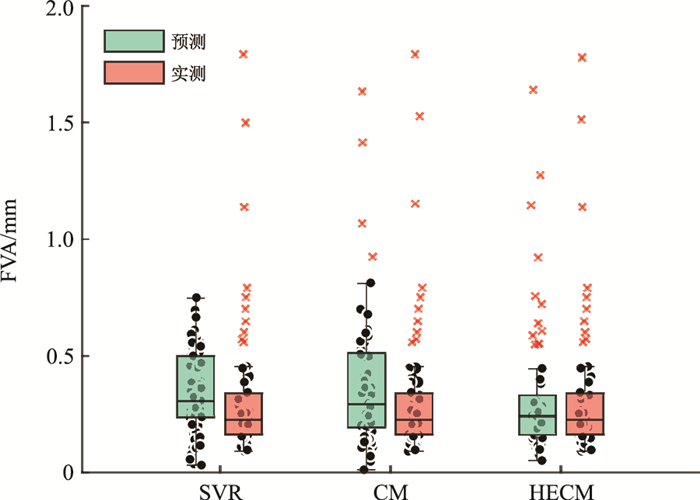
图 6 各模型的预测结果与实测结果的箱线图 |
从图 6可以看出,SVR回归模型作为基础网络单元中综合性能表现最好的学习模型,预测结果的箱线图与实测结果差异明显。SVR模型的上、下界限相对于中位数的跨度远高于实测结果,上、下四分位数和中位数也都大于实测结果,导致箱体之内的正常数据波动较大,对离群值的预测精度较低。CM模型虽然整体数据分布与实测结果类似,但箱体特征与实测结果差异较大,四分位间距远大于实测结果,箱体之内的正常数据分布不稳定,上、下界限波动范围较广,对离群值的预测能力有限。HECM模型无论是整体数据分布,还是箱体特征,都与实测结果吻合程度较高,对离群值尤其是特殊极端值仍有稳定的预测能力,具备较高的预测精度。
2.4 应用效果为了进一步验证HECM在实际资料中的应用效果,利用训练好的模型对工区的高产S探井的裂缝开度进行预测,并与常用的裂缝开度计算经验公式进行预测效果对比(图 7)。
|
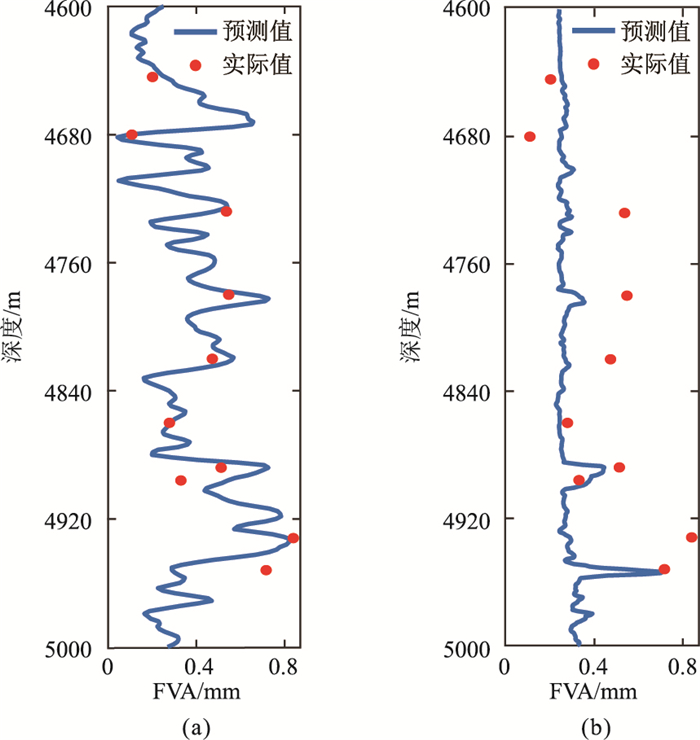
图 7 不同方法预测的裂缝开度结果对比 (a)HECM;(b)经验公式 |
由图可见,基于双侧向电阻率经验公式[35]计算的裂缝开度与实测结果吻合较差,受限于公式形式和经验参数的选取,在某些非裂缝因素引起的电阻率降低的深度段,得到的裂缝开度误差较大;另外在裂缝非常发育的深度段,由于双侧向的深、浅电阻率的差异较小,导致计算的裂缝开度过于稳定,从而无法准确表征实际地层裂缝张开程度的变化趋势。从整体上看,HECM预测的裂缝开度与实测结果更加吻合,预测的裂缝开度曲线变化趋势更符合地下的实际情况,可为后续利用地震数据进行三维裂缝开度反演提供可靠的井中裂缝开度信息。
3 结论(1) 致密油气储层岩性复杂、储集空间类型多样、纵向非均质性极强,常规裂缝开度预测方法难以准确估算井中裂缝开度。基于层次专家委员会机器模型有效地建立了常规测井数据、成像测井、岩心资料与岩石裂缝张开程度之间的非线性映射关系,可以很好地应用于致密油气储层的裂缝开度预测。
(2) 层次专家委员会机器模型在计算复杂度没有明显增加的情况下,能够发挥各个机器学习模型的优势,充分挖掘测井数据中蕴含的地质信息,克服了经验公式的岩性适用限制,为致密油气储层裂缝开度的定量预测提供了新的思路。
(3) 致密油气储层裂缝开度预测本质上属于含噪声的小样本复杂、无规律回归问题,数据质量的好坏直接关系到模型的预测精度。如果能增加实测样本的数量,丰富测井曲线的类型,选择相关性更好的测井数据参与训练,那么模型的预测精度能够得到提升。另外,如何剔除性能较差的基础网络单元,挑选性能更强、差异更大的基础网络单元进行组合,进一步提高模型的泛化能力,仍需要进行更深层次的研究。
| [1] |
孙龙德, 邹才能, 贾爱林, 等. 中国致密油气发展特征与方向[J]. 石油勘探与开发, 2019, 46(6): 1015-1026. SUN Longde, ZOU Caineng, JIA Ailin, et al. Development characteristics and orientation of tight oil and gas in China[J]. Petroleum Exploration and Development, 2019, 46(6): 1015-1026. |
| [2] |
贾承造, 邹才能, 杨智, 等. 陆相油气地质理论在中国中西部盆地的重大进展[J]. 石油勘探与开发, 2018, 45(4): 546-560. JIA Chengzao, ZOU Caineng, YANG Zhi, et al. Signi-ficant progress of continental petroleum geology theory in basins of Central and Western China[J]. Petroleum Exploration and Development, 2018, 45(4): 546-560. |
| [3] |
邹才能, 朱如凯, 吴松涛, 等. 常规与非常规油气聚集类型、特征、机理及展望——以中国致密油和致密气为例[J]. 石油学报, 2012, 33(2): 173-187. ZOU Caineng, ZHU Rukai, WU Songtao, et al. Types, characteristics, genesis and prospects of conventional and unconventional hydrocarbon accumulations: taking tight oil and tight gas in China as an instance[J]. Acta Petrolei Sinica, 2012, 33(2): 173-187. |
| [4] |
吕文雅, 曾联波, 刘静, 等. 致密低渗透储层裂缝研究进展[J]. 地质科技情报, 2016, 35(4): 74-83. LYU Wenya, ZENG Lianbo, LIU Jing, et al. Fracture research progress in low permeability tight reservoirs[J]. Geological Science and Technology Information, 2016, 35(4): 74-83. |
| [5] |
吕文雅, 苗凤彬, 张本键, 等. 四川盆地剑阁地区须家河组致密砾岩储层裂缝特征及对天然气产能的影响[J]. 石油与天然气地质, 2020, 41(3): 484-491. LYU Wenya, MIAO Fengbin, ZHANG Benjian, et al. Fracture characteristics and their influence on natural gas production: A case study of the tight conglome-rate reservoir in the Upper Triassic Xujiahe Formation in Jian'ge area, Sichuan Basin[J]. Oil & Gas Geo-logy, 2020, 41(3): 484-491. |
| [6] |
PONZIANI M, ESLOB E, LUTHI S, et al. Experimental validation of fracture aperture determination from borehole electric microresistivity measurements[J]. Geophysics, 2015, 80(3): D175-D181. DOI:10.1190/geo2014-0334.1 |
| [7] |
VAN STAPPEN J F, MEFTAH R, BOONE M A, et al. In situ triaxial testing to determine fracture permeability and aperture distribution for CO2 sequestration in Svalbard, Norway[J]. Environmental Science & Technology, 2018, 52(8): 4546-4554. |
| [8] |
丁文龙, 曾维特, 王濡岳, 等. 页岩储层构造应力场模拟与裂缝分布预测方法及应用[J]. 地学前缘, 2016, 23(2): 63-74. DING Wenlong, ZENG Weite, WANG Ruyue, et al. Method and application of tectonic stress field simulation and fracture distribution prediction in shale reservoir[J]. Earth Science Frontiers, 2016, 23(2): 63-74. |
| [9] |
BOADU F K. Relating the hydraulic properties of a fractured rock mass to seismic attributes: Theory and numerical experiments[J]. International Journal of Rock Mechanics and Mining Sciences, 1997, 34(6): 885-895. DOI:10.1016/S1365-1609(97)80002-0 |
| [10] |
AGHLI G, MOUSSAVI-HARAMI R, MOHAMMADIAN R. Reservoir heterogeneity and fracture parameter determination using electrical image logs and petrophysical data (a case study, carbonate Asmari Formation, Zagros Basin, SW Iran)[J]. Petroleum Science, 2020, 17(1): 51-69. DOI:10.1007/s12182-019-00413-0 |
| [11] |
孙致学, 姜宝胜, 肖康, 等. 基于新型集成学习算法的基岩潜山油藏储层裂缝开度预测算法[J]. 油气地质与采收率, 2020, 27(3): 32-38. SUN Zhixue, JIANG Baosheng, XIAO Kang, et al. Prediction of fracture aperture in bedrock buried hill oil reservoir based on novel ensemble learning algorithm[J]. Petroleum Geology and Recovery Efficiency, 2020, 27(3): 32-38. |
| [12] |
项云飞, 康志宏, 郝伟俊, 等. 基于线性回归与神经网络的储层参数预测复合方法[J]. 科学技术与工程, 2017, 17(31): 46-52. XIANG Yunfei, KANG Zhihong, HAO Weijun, et al. A composite method of reservoir parameter prediction based on linear regression and neural network[J]. Science Technology and Engineering, 2017, 17(31): 46-52. DOI:10.3969/j.issn.1671-1815.2017.31.008 |
| [13] |
闫星宇, 顾汉明, 肖逸飞, 等. XGBoost算法在致密砂岩气储层测井解释中的应用[J]. 石油地球物理勘探, 2019, 54(2): 447-455. YAN Xingyu, GU Hanming, XIAO Yifei, et al. XGBoost algorithm applied in the interpretation of tight-sand gas reservoir on well logging data[J]. Oil Geophysical Prospecting, 2019, 54(2): 447-455. |
| [14] |
王俊, 曹俊兴, 尤加春. 基于GRU神经网络的测井曲线重构[J]. 石油地球物理勘探, 2020, 55(3): 510-520. WANG Jun, CAI Junxing, YOU Jiachun. Reconstruction of logging traces based on GRU neural network[J]. Oil Geophysical Prospecting, 2020, 55(3): 510-520. |
| [15] |
何健, 文晓涛, 聂文亮, 等. 利用随机森林算法预测裂缝发育带[J]. 石油地球物理勘探, 2020, 55(1): 161-166. HE Jian, WEN Xiaotao, NIE Wenliang, et al. Fracture zone prediction based on random forest algorithm[J]. Oil Geophysical Prospecting, 2020, 55(1): 161-166. |
| [16] |
匡立春, 刘合, 任义丽, 等. 人工智能在石油勘探开发领域的应用现状与发展趋势[J]. 石油勘探与开发, 2021, 48(1): 1-11. KUANG Lichun, LIU He, REN Yili, et al. Application and development trend of artificial intelligence in petroleum exploration and development[J]. Petroleum Exploration and Development, 2021, 48(1): 1-11. |
| [17] |
ZERROUKI A A, AÏFA T, BADDARI K. Prediction of natural fracture porosity from well log data by means of fuzzy ranking and an artificial neural network in Hassi Messaoud oil field, Algeria[J]. Journal of Petroleum Science and Engineering, 2014, 115: 78-89. DOI:10.1016/j.petrol.2014.01.011 |
| [18] |
CRANGANU C, BREABAN M. Using support vector regression to estimate sonic log distributions: A case study from the Anadarko Basin, Oklahoma[J]. Journal of Petroleum Science and Engineering, 2013, 103: 1-13. DOI:10.1016/j.petrol.2013.02.011 |
| [19] |
谷宇峰, 张道勇, 鲍志东. 测井资料PSO-XGBoost渗透率预测[J]. 石油地球物理勘探, 2021, 56(1): 26-37. GU Yufeng, ZHANG Daoyong, BAO Zhidong. Permeability prediction using PSO-XGBoost based on logging data[J]. Oil Geophysical Prospecting, 2021, 56(1): 26-37. |
| [20] |
秦敏, 胡向阳, 梁玉楠, 等. 利用Stacking模型融合法识别高温、高压储层流体[J]. 石油地球物理勘探, 2021, 56(2): 364-371. QIN Min, HU Xiangyang, LIANG Yunan, et al. Using stacking model fusion to identify fluid in high tempe-rature and high-pressure reservoir[J]. Oil Geophysical Prospecting, 2021, 56(2): 364-371. |
| [21] |
ASOODEH M, BAGHERIPOUR P, GHOLAMI A. NMR parameters determination through ACE committee machine with genetic implanted fuzzy logic and genetic implanted neural network[J]. Acta Geophysica, 2015, 63(3): 735-760. DOI:10.1515/acgeo-2015-0003 |
| [22] |
ANSARI H R. Use seismic colored inversion and power law committee machine based on imperial competitive algorithm for improving porosity prediction in a he-terogeneous reservoir[J]. Journal of Applied Geophy-sics, 2014, 108(9): 61-68. |
| [23] |
ZHOU Z H, WU J X, TANG W. Ensembling neural networks: Many could be better than all[J]. Artificial Intelligence, 2002, 137(1/2): 239-263. |
| [24] |
GOLSANAMI N, KADKHODAIE-ILKHCHIA, SH-ARGHI Y, et al. Estimating NMR T2 distribution data from well log data with the use of a committee machine approach: A case study from the Asmari formation in the Zagros Basin, Iran[J]. Journal of Petroleum Science and Engineering, 2014, 114: 38-51. DOI:10.1016/j.petrol.2013.12.003 |
| [25] |
JAFARI K S A, MASHOHOR S. Robust committee machine for water saturation prediction[J]. Journal of Petroleum Science and Engineering, 2013, 104: 1-10. DOI:10.1016/j.petrol.2013.03.009 |
| [26] |
白洋, 谭茂金, 肖承文, 等. 致密砂岩气藏动态分类委员会机器测井流体识别方法[J]. 地球物理学报, 2021, 64(5): 1745-1758. BAI Yang, TAN Maojin, XIAO Chengwen, et al. Dynamic classification committee machine-based fluid typing method from wireline logs for tight sandstone gas reservoir[J]. Chinese Journal of Geophysics, 2021, 64(5): 1745-1758. |
| [27] |
TAN M J, BAI Y, ZHANG H T, et al. Fluid typing in tight sandstone from wireline logs using classification committee machine[J]. Fuel, 2020, 271: 117601. DOI:10.1016/j.fuel.2020.117601 |
| [28] |
金健, 黄国兴, 梁道雷, 等. 一种含两层专家网络的委员会机器模型[J]. 计算机科学, 2008, 35(1): 160-163. JIN Jian, HUANG Guoxing, LIANG Daolei, et al. A committee machine with two-layer expert nets[J]. Computer Science, 2008, 35(1): 160-163. DOI:10.3969/j.issn.1002-137X.2008.01.043 |
| [29] |
万方. 基于生命周期的产业集群综合竞争力研究[D]. 浙江金华: 浙江师范大学, 2014. WAN Fang. Study on the Comprehensive Competitiveness of Industrial Clusters Based on Life Cycle[D]. Zhejiang Normal University, Jinhua, Zhejiang, 2014. |
| [30] |
张小东, 张硕, 孙庆宇, 等. 基于AHP和模糊数学评价地质构造对煤层气产能的影响[J]. 煤炭学报, 2017, 42(9): 2385-2392. ZHANG Xiaodong, ZHANG Shuo, SUN Qingyu, et al. Evaluating the influence of geological structure to CBM productivity based on AHP and fuzzy mathematics[J]. Journal of China Coal Society, 2017, 42(9): 2385-2392. |
| [31] |
GHOLAMI A, MOHAMMADZADEH O, KORD S, et al. Improving the estimation accuracy of titration-based asphaltene precipitation through power-law committee machine (PLCM) model with alternating conditional expectation (ACE) and support vector regression (SVR) elements[J]. Journal of Petroleum Exploration and Production Technology, 2016, 6(2): 265-277. DOI:10.1007/s13202-015-0189-3 |
| [32] |
李蒙, 商晓飞, 赵华伟, 等. 基于likelihood地震属性的致密气藏断裂预测——以四川盆地川西坳陷新场地区须二段为例[J]. 石油与天然气地质, 2020, 41(6): 1299-1309. LI Meng, SHANG Xiaofei, ZHAO Huawei, et al. Prediction of fractures in tight gas reservoirs based on likelihood attribute: A case study of the 2nd member of Xujiahe Formation in Xinchang area, Western Sichuan Depression, Sichuan Basin[J]. Oil & Gas Geo-logy, 2020, 41(6): 1299-1309. |
| [33] |
刘冬冬, 杨东旭, 张子亚, 等. 基于常规测井和成像测井的致密储层裂缝识别方法——以准噶尔盆地吉木萨尔凹陷芦草沟组为例[J]. 岩性油气藏, 2019, 31(3): 76-85. LIU Dongdong, YANG Dongxu, ZHANG Ziya, et al. Fracture identification for tight reservoirs by conventional and imaging logging: a case study of Permian Lucaogou Formation in Jimsar Sag, Junggar Basin[J]. Lithologic Reservoirs, 2019, 31(3): 76-85. |
| [34] |
周游, 张广智, 高刚, 等. 核主成分分析法在测井浊积岩岩性识别中的应用[J]. 石油地球物理勘探, 2019, 54(3): 667-675. ZHOU You, ZHANG Guangzhi, GAO Gang, et al. Application of kernel principal component analysis in well logging turbidite lithology identification[J]. Oil Geophysical Prospecting, 2019, 54(3): 667-675. |
| [35] |
EZATI M, AZIZZADEH M, RIAHI M A, et al. Cha-racterization of micro-fractures in carbonate Sarvak reservoir, using petrophysical and geological data, SW Iran[J]. Journal of Petroleum Science and Engineering, 2018, 170: 675-695. DOI:10.1016/j.petrol.2018.06.058 |



 张广智, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email:
张广智, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email: 