② 东北电力大学通信工程系, 吉林吉林 132012;
③ 吉林大学仪器科学与电气工程学院, 吉林长春 130026;
④ 吉林大学通信工程学院, 吉林长春 130012;
⑤ 吉林大学地球探测科学与技术学院, 吉林长春 130026
② Department of Communication Engineering, Northeast Electric Power University, Jilin, Jilin 132012, China;
③ College of Instrumentation and Electrical Engineering, Jilin University, Changchun, Jilin 130026, China;
④ College of Communication Engineering, Jilin University, Changchun, Jilin 130012, China;
⑤ College of Geo-exploration Science and Technolo-gy, Jilin University, Changchun, Jilin 130026, China
受采集条件限制,地震记录中常常混有大量的随机噪声,这对地震资料后续处理带来了不利影响。沙漠地区通常地表地质条件复杂,噪声干扰严重。以塔里木盆地实际资料为例,沙粒介质的吸收作用造成随机噪声高频能量衰减,地震记录中噪声和实际信号之间存在严重的频谱混叠[1-2]。同时,沙漠环境相对空旷,风场强度大且作用复杂,导致地震资料表现出“强噪声、弱信号”的特征。传统方法在针对沙漠地区复杂噪声的衰减能力可能发生退化[3]。随着易探、易采资源枯竭,急需对复杂地质结构中的非常规油气资源进行开发利用[4],如何实现沙漠地区低信噪比记录中频带混叠噪声的有效衰减,成为业内亟待解决的技术瓶颈之一。
随着勘探技术的发展,一系列随机噪声衰减方法已经应用于地震资料处理领域,例如维纳滤波[5]、F-X预测滤波[6]、经验模态分解(Empirical Mode Decomposition, EMD)[7]和时频峰值滤波(Time-Frequency Peak Filtering, TFPF)[8]等方法。然而,上述传统方法通常是建立在某些先验假设的基础上,如F-X预测滤波要求随机噪声是平稳的。当实际资料不满足上述条件时,方法性能可能发生退化[6];此外,上述方法也存在一定局限性,如EMD方法的模态混叠问题[9]和TFPF方法的窗函数确定问题[10]。
为持续提升噪声衰减能力,多尺度方法也用于勘探随机噪声衰减处理,主要包括小波变换[11-12]、曲波变换[13-14]、Seislet变换和Shearlet变换[15-17]等。这些方法可以通过稀疏分解将有效信号和噪声在变换域中进行分离,进而选择合适的阈值函数实现不同尺度信息的提取与有效信号的恢复。尽管多尺度方法在性能上优于传统方法,但是阈值函数的选取问题制约着相关方法处理效果的提升。
近年来,基于卷积神经网络(Convolutional Neural Networks,CNN)的去噪理论得到了快速发展[18-19],以生成对抗网络(Generative Adversarial Network,GAN)、去噪卷积神经网络(Feed-forward Denoising Convolutional Neural Networks,DnCNN)及其改进的方法为代表的一系列智能衰减网络被提出并应用于地震数据处理中。基于CNN的衰减方法通过构建信号和噪声训练数据集,从大量标记数据中构建非线性映射关系[20-21],提取并分析地震数据集的潜在特征并自适应地实现有效信号的高保真恢复[22-23]。由于浅层提取的为边缘、空间的细节信息,并且特征图分辨率相对较高,而深层提取的是语义信息,特征图分辨率相对较低,会丢失一些空间信息,导致信息严重失衡[24]。同时,相关方法在整个网络几乎都是相同的卷积操作,网络结构单一,只是通过堆叠的方式扩大感受野提取不同的特征,随着网络深度的增加,这种方式容易造成过拟合。
为获得更好的噪声衰减性能,本文提出一种新型多分支去噪卷积神经网络(Diverse Branch Block Convolutional Neural Networks, DBBCNN),并将其应用于地震勘探随机噪声的衰减领域。与传统的去噪卷积神经网络DnCNN相比,DBBCNN引入空洞卷积获取多尺度信息,降低了网络的复杂度,用来提高去噪性能;引入多分支模块DBB((Diverse Branch Block,DBB),将不同尺度、不同复杂度的分支结合在一起,增强单个卷积的表示能力,丰富特征空间,使训练的微结构复杂化;引入了长路径操作融合全局特征和局部特征以增强去噪网络的表达能力。
模拟和实际数据结果表明,DBBCNN网络可有效提升地震数据信噪比,同时在有效信号幅度保持和地震勘探随机噪声压制方面也具有明显的优势。
1 DnCNN结构DnCNN是由Zhang等[25]提出的一种去噪卷积神经网络,其网络采用级联的结构(图 1),包括多个卷积层(Conv)、批标准化层(BN)和线性整流单元(ReLU)。卷积层是通过卷积运算对高维特征进行自动提取[1],每个卷积层需64个3×3的卷积核,步长为1,其基本作用为
| $ \mathit{\boldsymbol{c}} = \mathit{\boldsymbol{\omega }}*\mathit{\boldsymbol{a}} + \mathit{\boldsymbol{b}} $ | (1) |

|
图 1 DnCNN结构 |
式中:c表示卷积层的输出;a表示卷积层的输入;ω和b分别表示卷积滤波器的权重和偏置。该网络引入BN层有效地避免梯度消失问题,即通过一定的规范化手段,把输入到激活函数的数据强行拉回到均值为0、方差为1的标准正态分布,使每一层的输入有一个近似的分布[25-26],从而提高网络的收敛速度。BN层操作可表示为
| $ \left\{\begin{array}{l} n_{\gamma, \beta}\left(m_{i}\right)=\gamma * \frac{m_{i}-\hat{\mu}}{\hat{\sigma}}+\beta \\ \hat{\mu}=\frac{1}{B} \sum\limits_{i=1}^{B} m_{i} \\ \hat{\sigma}=\sqrt{\frac{\sum\limits_{i=1}^{B}\left(m_{i}-\hat{\mu}\right)^{2}}{B}}+\eta \end{array}\right. $ | (2) |
式中:mi和nγ, β(mi)分别为BN的输入和输出;B为批标准化尺寸;η为一个极小的常数,主要是为了防止分母为0;γ和β表示可学习的参数。ReLU代表修正线性单元,是一种常用的激活函数[25-26],其基本作用如下式所示
| $ {f_{{\rm{ReLU}}}} = {\rm{max}}\left[ {0, {n_{\gamma , \beta }}\left( {{m_i}} \right)} \right] $ | (3) |
式中:max表示最大值函数;fReLU表示激活函数。与其他激活函数相比,修正线性单元具有更好的效果。并且,该网络采用的是残差的思想恢复被破坏的图像,能够很好地解决深度神经网络的退化问题,提高去噪性能。
2 DBBCNN结构和去噪原理 2.1 DBBCNN络结构DBBCNN是一种DnCNN的改进网络,主要针对DnCNN在特征提取、特征融合和无法有效利用浅层信息等方面存在的不足而提出的一种多分支的特征增强网络,其网络结构如图 2所示。对比Dn-CNN,DBBCNN的主要改进可概括为以下四点。

|
图 2 DBBCNN结构 |
首先,针对DnCNN特征空间单一问题,DBB-CNN利用DBB模块部分替代传统DnCNN中的Conv+BN+ReLU模块。DBB模块结构如图 3所示,利用卷积核大小为1×1、填充为0、步长为1的卷积序列、多尺度的卷积(卷积核大小为3×3、填充为1、步长为1)以及平均池化Avg(池化核大小为3×3、填充为1、步长为1)增强单个卷积的表示能力,将不同尺度、不同复杂度的分支结合在一起,丰富特征空间,使训练的微结构复杂化,从而使训练模型达到更高的性能水平。

|
图 3 多分支模块(DBB)结构 |
其次,对于去噪网络而言,获取多尺度上、下文信息十分重要,一般通过扩大感受野获取上、下文信息,但利用下采样操作增大感受野会导致空间分辨率的丢失。为了不损失空间分辨率,还要扩大感受野,该去噪网络引入了空洞卷积(DilConv),空洞卷积可在不改变卷积核大小的同时增大感受野,在不损失图像信息的前提下,更好地保留图像的空间特征。因此本文在网络的第2、第5、第9和第12层引入了空洞卷积来扩大感受野。
再次,在此基础上,随着网络深度的增加,浅层信息越来越被忽视,导致一些关键特征丢失,故引入长路径操作(Cat)融合全局特征和局部特征,以增强去噪网络的表达能力。由于输入的噪声图像包含了强噪声信息,因此选择原始输入与深层互补增强去噪模型的表示能力,即用一种拼接操作融合全局特征和局部特征。
最后,由于BN就是在每一层的非线性处理之前加入标准化、缩放、移位操作减轻内部协变量的移位,给训练带来更快的速度、更好的表现,减轻协变量对网络初始化变量的影响,故本文从第1层开始就加入BN。
综上所述,与DnCNN相比,DBBCNN能够实现对特征更精细、更准确地提取,从而更好地从含噪数据中恢复有效信号。
2.2 去噪原理沙漠地区实际地震资料可表示为纯净信号与随机噪声在时空域的叠加[27-28]
| $ \mathit{\boldsymbol{y}} = \mathit{\boldsymbol{x}} + \mathit{\boldsymbol{n}} $ | (4) |
式中:y为含噪地震记录;x为有效信号;n为低频噪声。
DBBCNN去噪网络采用了残差思想,通过标签数据建立y与n之间的复杂的非线性映射关系
| $ \mathit{\boldsymbol{\hat n}} = R\left( {\mathit{\boldsymbol{y}}, \mathit{\boldsymbol{ \boldsymbol{\varTheta} }}} \right) $ | (5) |
式中:R表示一种非线性映射关系;
| $ \left\{\begin{array}{l} L(\boldsymbol{\varTheta})=\frac{1}{2 P} \sum\limits_{k=1}^{P}\left\|n-\boldsymbol{n}_{k}\right\|_{\mathrm{F}}^{2} \\ \boldsymbol{n}_{k}=\boldsymbol{y}_{k}-\boldsymbol{x}_{k} \end{array}\right. $ | (6) |
对网络参数Θ进行训练。其中:nk为第k个低频噪声片;||·||F为Frobe-nious范数;P表示训练样本数;xk、yk分别表示第k个有效信号片和含噪地震记录片。由于训练样本数巨大,利用整个训练集计算L(Θ)的梯度是不可行的,故本文采用Adam最小化L(Θ),参数更新的大小不会随梯度大小的缩放而变化。即在每次迭代过程中,只利用小部分训练样本计算梯度,这样不仅可降低网络的计算量,也可提高网络的效率。利用训练好的去噪网络,可得到去噪后的地震资料
| $ \mathit{\boldsymbol{\hat x}} = \mathit{\boldsymbol{y}} - \mathit{\boldsymbol{\hat n}} $ | (7) |
式中
DBBCNN是一种有监督的深度学习方法,其需要大量的高真实性训练数据优化网络参数,训练集的完备性对网络的学习效果和去噪的准确性影响很大。虽然已有去噪网络在地震资料去噪领域取得成效,但目前仍没有完备的、公开的地震资料的训练集,为更好地从实际地震资料特征出发,本文利用正演建模数据同实际勘探数据相结合,共同构建用于地震勘探随机噪声消减的训练集。
DBBCNN作为有监督的学习网络,其训练集包括有效信号集和含噪信号集。由于无法从实际记录中获取有效反射信号,本文通过正演建模方式构建有效信号训练集,即用雷克子波模拟地震资料中的有效信号,具体定义为
| $ s\left( t \right) = A\{ 1 - 2[{\rm{ \mathsf{ π} }}{f_0}{(t - {t_0})^2}]\} {{\rm{e}}^{ - \left[ {{\rm{ \mathsf{ π} }}{f_0}(t - {t_0})} \right]}}^{^2} $ | (8) |
式中:A为振幅;t为时间;t0为起始时间;f0为主频。具体建模参数范围如表 1所示,共生成100幅模拟记录。研究过程中,利用64×64的滑动窗截取模拟信号数据,共得到8500个信号片,这些正演数据通过幅值归一化后共同组成了有效信号训练集。
|
|
表 1 正演建模参数 |
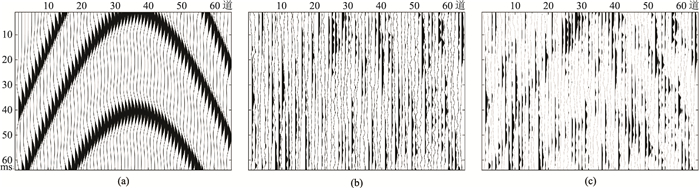
为保证衰减方法的处理精度,本文采用塔里木盆地沙漠地区被动源噪声数据构建噪声训练集。在无人工震源激发情况下,采集得到2000道、30000采样点的实际噪声数据,对数据进行随机截取后得到8750个噪声片,对其进行幅度归一化后,得到噪声训练集。此外,为提高DBBCNN的泛化能力,利用信号片和噪声片叠加生成随机信噪比含噪数据,具体而言,就是将实际噪声数据能量进行放缩后与信号训练集数据进行叠加,得到分布在[-10, 0]dB范围内随机信噪比含噪记录,组构含噪信号训练集,用以模拟不同条件下实际记录中的噪声水平。同时,以有效信号为标签将含噪数据与有效信号数据进行一一匹配,用以满足网络训练需求,不同训练数据范例如图 4所示。
|
图 4 训练数据示例 (a)纯净信号片;(b)噪声片;(c)含噪信号片 |
实验环境为Matlab2016,服务器配置为E5-2600 v4处理器、Windows 10(64位)操作系统、64GB内存、双NVIDA GeForce GTX 1080显卡。在训练过程中,基于服务器硬件条件,批标准化次数设置为64,训练块大小设置为64×64,并采用L2损失函数计算训练过程中的损失。此外,网络共17层,利用Adam算法实现损失函数优化,网络的初始学习率设置为[10-3,10-4]。为方便训练,对训练数据进行归一化处理,训练周期设置为50。具体训练参数如表 2所示。
|
|
表 2 雷克子波在不同相位旋转下的波峰时移量 |
DBBCNN的详细训练流程可概括为以下步骤。
(1) 从有效信号集和噪声集中随机选取一个有效信号片和一个噪声片,构造含噪信号片并使其作为去噪网络的输入;噪声片作为去噪网络的标签数据。
(2) 通过映射,去噪网络输出去噪后的结果。
(3) 计算误差(式(6)中损失函数的值),并将误差通过梯度下降法进行反向传播,通过Adam优化器调整网络参数。
(4) 重复步骤(1)~步骤(3),式(6)中的损失函数趋于稳定。
(5) 经过50个训练周期,可得到针对沙漠地区地震资料的去噪模型。利用该模型就可预测含噪地震资料中的有效信号,进而实现信噪分离。
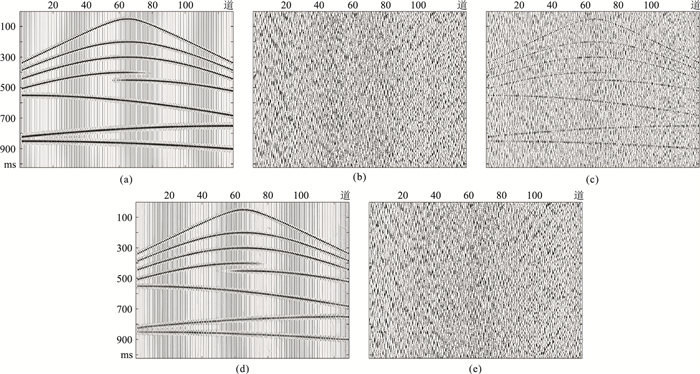
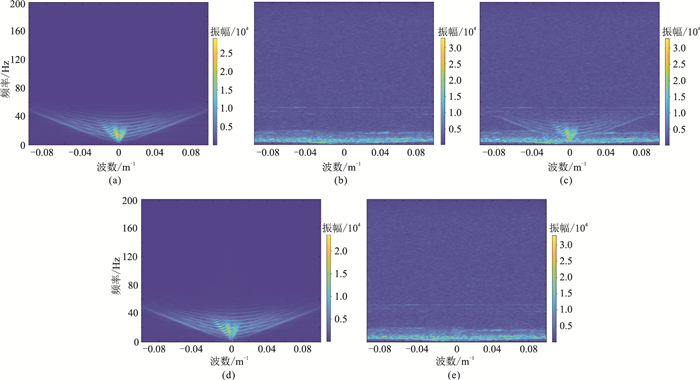
4 地震记录处理与分析 4.1 模拟数据去噪结果对比为验证DBBCNN的网络性能,本文采用正演建模方法构建模拟纯净记录。仿真记录共包含128道记录,记录由1024个采样点组成,采样频率为500Hz。此外,为模拟实际勘探记录特征,生成了具有不同形状和主频的反射同相轴,结果如图 5a所示;在此基础上,将实际噪声同仿真记录进行叠加,得到-6dB的含噪数据,实际噪声和含噪数据结果分别如图 5b和图 5c所示;应用DBBCNN对含噪记录进行处理,去噪结果和滤除噪声如图 5d和图 5e所示。由图可见,DBBCNN可有效抑制复杂噪声,较好地恢复受到强噪声影响的反射信息,恢复的同相轴在连续性和光滑性上都具有明显改善,同时处理后的信噪比达到了12.1dB,这也验证了本文方法的有效性。同时,对上述结果进行了F-K谱分析,结果如图 6所示。由图可见,信号和噪声成分在频率分布方面存在明显的混叠,例如纯净信号能量主要分布在0~40Hz频带内,而噪声能量主要集中在更低频段(0~20Hz)。信号和噪声的频带混叠对噪声衰减带来巨大影响,可能导致传统噪声衰减算法在处理性能方面出现退化。图 6c为含噪记录F-K谱,明显的混叠现象和噪声成分导致信号特征模糊,难以恢复。利用DBBCNN方法对上述含噪记录进行处理,恢复信号和滤除噪声的F-K谱分别如图 6d和图 6e所示。结果表明,所提方法可有效压制复杂低频噪声,恢复的有效信号同纯净信号在F-K域分布特征方面表现出极其相近的特征,充分验证了所提算法的有效性。同时滤除噪声与叠加的实际噪声也具有相近的F-K谱,并无明显有效信号特征残留,这也说明了噪声衰减算法对于信号幅度保持具有明显优势。
|
图 5 模拟数据DBBCNN去噪分析 (a)纯净信号;(b)实际沙漠噪声;(c)含噪数据;(d)去噪结果;(e)滤除噪声 |
|
图 6 模拟数据去噪结果F-K谱分析 (a)纯净信号;(b)实际沙漠噪声;(c)含噪数据;(d)去噪结果;(e)滤除噪声 |
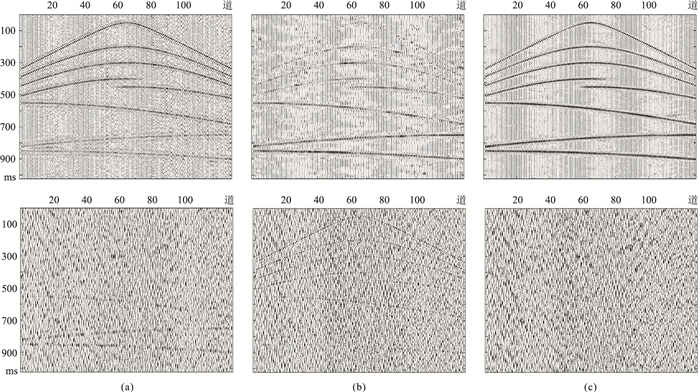
为进一步分析DBBCNN的去噪性能,分别选取带通滤波器、小波变换和DnCNN网络进行对比。其中带通滤波器通带频率设置为15~38Hz,以实现信号的有效恢复;小波基函数为db4小波,分解层数为15层,采用软阈值方法实现噪声压制。此外,为保证结果的客观性,DnCNN方法同本文所提方法使用相同的训练集和实验环境。三种方法对图 5c所示含噪记录进行处理,结果和滤除的噪声如图 7所示。结果表明:由于信号和噪声的频率混叠,带通滤波在恢复有效信号的同时,无法有效抑制同频噪声(图 7a);小波方法无法有效恢复有效信号(图 7b);传统DnCNN方法滤除噪声中存在明显信号成分残留(图 7c下),说明相关方法在面对沙漠地区复杂噪声时处理结果不甚理想;相比之下,DnCNN和DBBCNN对噪声压制效果较好,同相轴清晰、连贯,滤除的噪声特征与实际噪声相近,但是DnCNN结果中有少量假轴存在,而DBBCNN可准确恢复有效反射信息。
|
图 7 模拟数据三种方法去噪结果(上)及滤除噪声对比(下) (a)带通滤波器;(b)小波变换;(c)DnCNN |
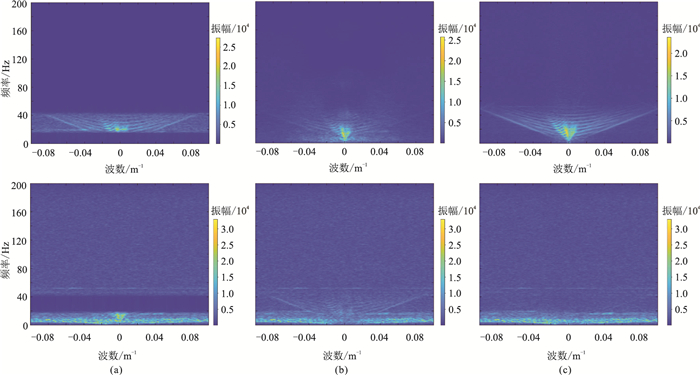
将图 5c中的含噪数据通过带通滤波器和小波变换分别将信噪比提高了8.3dB和8.4dB,说明传统方法处理能力有待提升;DnCNN和DBBCNN分别将信噪比提高了15.5dB和18.1dB,表明DBBCNN网络在复杂噪声衰减领域的有效性。同时,在F-K域比较、分析了去噪结果和滤除噪声的性质(图 8)。观察带通滤波器处理结果的F-K谱可见,带通滤波器只是简单滤除相关通带外的信息,导致通带外与噪声混叠在一起的有效信号也被滤除掉了,并且带通滤波器的去噪结果中可清晰观察到同频噪声成分的残留(图 8a);小波变换恢复信号同纯净信号在F-K谱方面存在较大差异,不仅噪声压制不彻底,而且在去除噪声的同时,有效信息明显也被压制了,在滤除噪声的F-K谱中可看到明显的残留信号(图 8b)。反观去噪网络处理结果,DnCNN和DBBCNN可有效去除噪声,并且有效信息恢复的很完整(图 6e),但仔细观察,DnCNN处理后滤除的噪声中有细微有效信号残留(图 8c)。因此,相较于带通滤波器、小波变换以及DnCNN算法,DBBCNN可以实现复杂沙漠随机噪声背景下有效反射信息的高质量恢复,具有更好的噪声衰减能力。
|
图 8 模拟数据三种方法去噪结果(上)和滤除噪声(下)的F-K谱图 (a)带通滤波;(b)小波变换;(c)DnCNN |
为定量分析不同方法在去噪能力方面的差异,定义去噪结果的信噪比和均方误差分别为
| $ \mathrm{SNR}=10 \lg \left\{\frac{\sum\limits_{i=1}^{N} \sum\limits_{j=1}^{M}[x(i, j)]^{2}}{\sum\limits_{i=1}^{N} \sum\limits_{j=1}^{M}[\hat{x}(i, j)-x(i, j)]^{2}}\right\} $ | (9) |
| $ \mathrm{MSE}=\frac{1}{N \times M} \sum\limits_{i=1}^{N} \sum\limits_{j=1}^{M}[\hat{x}(i, j)-x(i, j)]^{2} $ | (10) |
式中M和N分别表示道数和采样点数。不同方法去噪结果的SNR和MSE如表 3所示,DBBCNN方法在去噪能力方面明显优于带通滤波器、小波变换以及DnCNN方法,其SNR最大和MSE最小。与此同时,DBBCNN同样可以有效恢复低信噪比记录中的有效信息,例如-10dB含噪记录,经过DBBCNN处理后,信噪比提升了近20dB。以上对比分析表明,DBBCNN可在恢复信号的同时有效压制沙漠地区强随机噪声,在去噪能力方面明显优于传统方法。
|
|
表 3 四种方法去噪结果对应的SNR和MSE |
本文选取塔里木盆地三维沙漠地面地震数据对DBBCNN衰减方法性能进行验证。处理的共炮点记录共216道,采样频率为2ms,每道记录长度为3s,实际记录如图 9a所示,部分反射同相轴受到随机噪声的影响已无法有效辨识,如浅层反射信息(红框所示);同时由于面波等强干扰的影响(绿框所示),同相轴连续性被破坏且难以辨认。利用带通滤波器、小波变换、DnCNN和DBBCNN方法对实际资料进行处理,结果如图 9b~图 9e所示。

|
图 9 实际沙漠地震数据不同方法的处理结果(左)及滤除噪声(右)对比 (a)实际沙漠共炮点记录;(b)带通滤波器;(c)小波变换;(d)DnCNN;(e)DBBCNN |
对上述结果进行对比分析表明:①带通滤波器(图 9b)和小波变换(图 9c)无法取得较好的去噪效果,虽然部分噪声有所衰减,但去噪后的记录中仍然存在大量的低频噪声,有效信号仍然在随机噪声的淹没之中,同相轴连续性很差,不易识别;同时,对面波的去除也不够明显,依然有大量残留的面波导致同相轴不清晰和不连贯,在滤除的噪声中仍有明显的同相轴存在,即经带通滤波器和小波变换处理后,在压制噪声的同时有效信号的幅值也被削弱了。②经DnCNN(图 9d)和DBBCNN(图 9e)处理后,地震记录的背景较为干净,表明DnCNN和DBBCNN对于初至前随机噪声的压制非常彻底,且有效信号恢复较清晰,对面波的压制也很有效,同相轴的连续性明显增强。但DnCNN处理后,部分恢复的同相轴不清晰,部分区域同相轴出现间断的现象。为便于比较,对图 9b~图 9e中黄色方框处放大显示(图 10和图 11)。可见带通滤波(图 10b、图 11b)和小波变换(图 10c、图 11c)处理后,有效信号依然受大量噪声影响,滤除掉的噪声可见有明显的信号残留,DnCNN整体上对噪声压制效果良好(图 10d、图 11d),但一些浅层信息恢复不佳,在滤除的噪声中,能够看到残留的浅层信息。经DBBCNN处理后,恢复的有效信号更清晰、更连续,一些浅层的细节信息也被很好地恢复出来,即使是在严重频谱混叠噪声和低SNR条件下,也能有效地压制噪声并重构有效信号(图 10e、图 11e);在DBBCNN的残差结果中,几乎不存在有效信号残留,即DBBCNN处理几乎没有造成有效信号的能量损失。

|
图 10 图 9区域1局部放大的处理结果(左)及滤除噪声(右)效果对比 (a)实际地震数据;(b)带通滤波;(c)小波变换;(d)DnCNN;(e)DBBCNN |
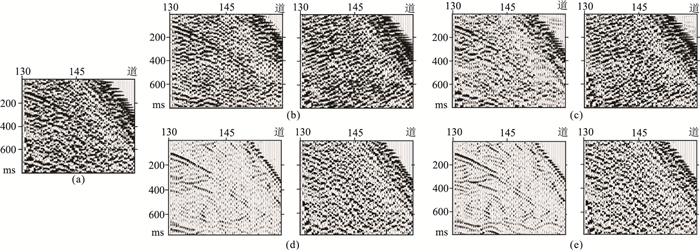
|
图 11 图 9区域2局部放大的处理结果(左)及滤除噪声(右)效果对比 (a)实际地震数据;(b)带通滤波;(c)小波变换;(d)DnCNN;(e)DBBCNN |
总之,经DBBCNN处理后,实际记录中大部分低频噪声、面波得到有效抑制,有效信号恢复较好。
5 结论本文搭建了一种新型DBBCNN去噪网络,采用“模拟建模加真实数据”的策略构建训练集,并将训练好的网络应用于地震资料随机噪声的衰减中,模拟数据和实际地震资料处理结果表明,DBBCNN对于复杂随机噪声的压制和有效信号的恢复是行之有效的。获得的认识和结论如下。
(1) 空洞卷积、DBB以及长路径操作可有效地丰富特征空间,使网络对特征的提取更加精细、准确,从而进一步增强网络的表达能力。
(2) DBBCNN作为一种有监督的深度学习方法,训练集中有效信号集通过正演模拟的方式构建,噪声集通过选取真实沙漠低频噪声片构建。实验结果表明,这种“模拟建模加真实数据”的策略使数据集更接近于真实地震勘探数据,从而使网络能够发挥更优的性能。
(3) 通过比较DBBCNN和带通滤波器、小波变换以及DnCNN等方法的处理结果发现,无论是模拟数据还是实际的数据,DBBCNN的去噪结果同相轴更清晰和连续,在压制噪声的同时有效信号得以保护,是一种更高效的去噪方法。
| [1] |
DONG X T, LI Y, YANG B J. Desert low-frequency noise suppression by using adaptive DnCNNs based on the determination of high-order statistic[J]. Geophysical Journal International, 2019, 219(2): 1281-1299. DOI:10.1093/gji/ggz363 |
| [2] |
李光辉, 李月. 沙漠地区地震勘探随机噪声建模及其在噪声压制中的应用[J]. 地球物理学报, 2016, 59(2): 682-692. LI Guanghui, LI Yue. Random noise of seismic exploration in desert modeling and its applying in noise attenuation[J]. Chinese Journal of Geophysics, 2016, 59(2): 682-692. |
| [3] |
林红波, 张丹丹. 自适应结构方向复扩散压制沙漠地震随机噪声[J]. 吉林大学学报(信息科学版), 2020, 37(5): 463-469. LIN Hongbo, ZHANG Dandan. Adaptive structure-oriented complex diffusion filtering for desert seismic random noise attenuation[J]. Journal of Jilin University(Information Science Edition), 2020, 37(5): 463-469. |
| [4] |
HARRIS P E, WHITE R E. Improving the perfor-mance of f-x prediction filtering at low signal-to-noise ratios[J]. Geophysical Prospecting, 1997, 45(2): 269-302. DOI:10.1046/j.1365-2478.1997.00347.x |
| [5] |
MENDEL J. White-noise estimators for seismic data processing in oil exploration[J]. IEEE Transactions on Automatic Control, 1977, 22(5): 694-706. DOI:10.1109/TAC.1977.1101597 |
| [6] |
CANALES L L. Random noise reduction[C]. SEG Te-chnical Program Expanded Abstracts, 1984: 525-527.
|
| [7] |
AMEZQUITA SANCHEZ J P, CHAVEZ ALEGRIA O, VALTIERRA RODRIGUEZ M, et al. Detection of ULF geomagnetic anomalies associated to seismic activity using EMD method and fractal dimension theory[J]. IEEE Latin America Transactions, 2017, 15(2): 197-205. DOI:10.1109/TLA.2017.7854612 |
| [8] |
TIAN Y A, LI Y, YANG B J. Variable-eccentricity hyperbolic-trace TFPF for seismic random noise atte-nuation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(10): 6449-6458. DOI:10.1109/TGRS.2013.2296603 |
| [9] |
MA H T, QIAN Z B, LI Y, et al. Noise reduction for desert seismic data using spectral kurtosis adaptive bandpass filter[J]. ActaGeophysica, 2019, 67(1): 123-131. |
| [10] |
XIONG M J, LI Y, WU N. Random-noise attenuation for seismic data by local parallel radial-trace TFPF[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(7): 4025-4031. DOI:10.1109/TGRS.2013.2278981 |
| [11] |
MOUSAVI S M, LANGSTON C A, HORTON S P. Automatic microseismic denoising and onset detection using the synchrosqueezed continuous wavelet transform[J]. Geophysics, 2016, 81(4): V341-V355. DOI:10.1190/geo2015-0598.1 |
| [12] |
YU Z, ABMA R, ETGEN J, et al. Attenuation of noise and simultaneous source interference using wavelet denoising[J]. Geophysics, 2017, 82(3): V179-V190. DOI:10.1190/geo2016-0240.1 |
| [13] |
SHAN H, MA J W, YANG H Z. Comparisons of wavelets, contourlets and curvelets in seismic denoising[J]. Journal of Applied Geophysics, 2009, 69(2): 103-115. DOI:10.1016/j.jappgeo.2009.08.002 |
| [14] |
ZHAO X, LI Y, ZHUANG G H, et al. 2-D TFPF based on Contourlet transform for seismic random noise attenuation[J]. Journal of Applied Geophysics, 2016, 129: 158-166. DOI:10.1016/j.jappgeo.2016.03.030 |
| [15] |
董新桐, 马海涛, 李月. 丘陵地带地震资料随机噪声压制新技术: 高阶加权阈值函数的Shearlet变换[J]. 地球物理学报, 2019, 62(10): 4039-4046. DONG Xintong, MA Haitao, LI Yue. The new technology for suppression of hilly land seismic random noise: Shearlet transform and the high order weighted threshold function[J]. Chinese Journal of Geophysics, 2019, 62(10): 4039-4046. DOI:10.6038/cjg2019M0582 |
| [16] |
ZHANG C, VAN DER BAAN M. Multicomponent microseismic data denoising by 3D shearlet transform[J]. Geophysics, 2018, 83(3): A45-A51. DOI:10.1190/geo2017-0788.1 |
| [17] |
DONG X T, JIANG H, ZHENG S, et al. Signal-to-noise ratio enhancement for 3C downhole microseismic data based on the 3D shearlet transform and improved back-propagation neural networks[J]. Geophysics, 2019, 84(4): V245-V254. DOI:10.1190/geo2018-0621.1 |
| [18] |
张建明, 詹智财, 成科扬, 等. 深度学习的研究与发展[J]. 江苏大学学报(自然科学版), 2015, 36(2): 191-200. ZHANG Jianming, ZHAN Zhicai, CHENG Keyang, et al. Review on development of deep learning[J]. Journal of Jiangsu University(Natural Science Edition), 2015, 36(2): 191-200. DOI:10.3969/j.issn.1671-7775.2015.02.013 |
| [19] |
张岩, 李新月, 王斌, 等. 基于联合深度学习的地震数据随机噪声压制[J]. 石油地球物理勘探, 2021, 56(1): 9-25, 56. ZHANG Yan, LI Xinyue, WANG Bin, et al. Random noise suppression of seismic data based on joint deep learning[J]. Oil Geophysical Prospecting, 2021, 56(1): 9-25, 56. |
| [20] |
宋辉, 高洋, 陈伟, 等. 基于卷积降噪自编码器的地震数据去噪[J]. 石油地球物理勘探, 2020, 55(6): 1210-1219. SONG Hui, GAO Yang, CHEN Wei, et al. Seismic noise suppression based on convolutional denoising autoencoders[J]. Oil Geophysical Prospecting, 2020, 55(6): 1210-1219. |
| [21] |
曲之琳, 胡晓飞. 基于改进激活函数的卷积神经网络研究[J]. 计算机技术与发展, 2017, 27(12): 77-80. QU Zhilin, HU Xiaofei. Research on convolutional neural network based on improved activation function[J]. Computer Technology and Development, 2017, 27(12): 77-80. |
| [22] |
孙俊, 何小飞, 谭文军, 等. 空洞卷积结合全局池化的卷积神经网络识别作物幼苗与杂草[J]. 农业工程学报, 2018, 34(11): 159-165. SUN Jun, HE Xiaofei, TAN Wenjun, et al. Recognition of crop seedling and weed recognition based on dilated convolution and global pooling in CNN[J]. Transactions of the Chinese Society of Agricultural Engineering, 2018, 34(11): 159-165. |
| [23] |
张利刚. 基于全空洞卷积神经网络的图像语义分割[D]. 吉林长春: 东北师范大学, 2018. ZHANG Ligang. Fully Dilated Convolutional Networks for Semantic Segmentation[D]. Northeast Normal University, Changchun, Jilin, 2018. |
| [24] |
LIU Z M, GAO G Y, SUN L, et al. IPG-Net: image pyramid guidance network for small object detection[C]. 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Seattle, WA, USA, 2020, 4422-4430.
|
| [25] |
ZHANG K, ZUO W M, CHEN Y J, et al. Beyond a Gaussian denoiser: residual learning of deep CNN for image denoising[J]. IEEE Transactions on Image Processing, 2017, 26(7): 3142-3155. DOI:10.1109/TIP.2017.2662206 |
| [26] |
李海山, 陈德武, 吴杰, 等. 叠前随机噪声深度残差网络压制方法[J]. 石油地球物理勘探, 2020, 55(3): 493-503. LI Haishan, CHEN Dewu, WU Jie, et al. Pre-stack random noise suppression with deep residual network[J]. Oil Geophysical Prospecting, 2020, 55(3): 493-503. |
| [27] |
王琪琪, 汤井田, 张良, 等. 利用多层感知机的地震数据去噪[J]. 石油地球物理勘探, 2020, 55(2): 272-281. WANG Qiqi, TANG Jingtian, ZHANG Liang, et al. Seismic data denoising based on multi-layer perceptron[J]. Oil Geophysical Prospecting, 2020, 55(2): 272-281. |
| [28] |
张恒磊, 胡哲, 胡祥云, 等. 基于反射波各向异性特征的保真去噪方法[J]. 石油地球物理勘探, 2017, 52(2): 233-241. ZHANG Henglei, HU Zhe, HU Xiangyun, et al. Seismic fidelity de-noising with reflection anisotropy[J]. Oil Geophysical Prospecting, 2017, 52(2): 233-241. |



 董新桐, 吉林省长春市朝阳区南湖大路5372号吉林大学南湖校区, 130012。Email:
董新桐, 吉林省长春市朝阳区南湖大路5372号吉林大学南湖校区, 130012。Email: 