② 东方地球物理公司物探技术研究中心, 河北涿州 072751
② Geophysical Research & Development Center, BGP Inc., CNPC, Zhuozhou, Hebei 072751, China
地震相分析是根据地震反射同相轴的外部形态、内部结构、顶底接触关系、动力学以及运动学特征,分析地层、岩性及油气分布情况,在油气田的勘探、评价、开发、生产等阶段都有着广泛的应用。
20世纪90年代以前,多以二维地震数据为主,解释人员通过视觉、逐个剖面定性描述同相轴的振幅、频率、相位等信息[1],并根据这些信息的差别,结合区域构造、沉积背景,依据钻井标定,进一步将地震相转化为沉积相,这是狭义上的地震相分析流程[2]。之后,三维地震勘探兴起,数据量大幅增加,解释人员逐个剖面地开展地震相分析已经变得不切实际。随着地震属性技术的发展,进入了以地震属性分析技术为中心的地震相分析阶段,这是广义上的地震相分析。
地震属性分析主要是通过对原始地震数据进行某种数学变换,提取或是放大原始地震信号的某种差异,如瞬时属性、几何结构等;后来又进一步提出如甜点、纹理[3]、地震倒谱特征[4]等属性。通常情况下,地质体特征需要借助不同地震属性进行多维度刻画。以机器学习视角而言,通过多维属性空间开展地震相分析是一个典型的模式识别问题。根据是否使用“标签”数据(如钻井、岩心、露头资料等)辅助地震相分析以及参与算法训练,地震相分析可分为有监督和无监督两种类型。
无监督地震相分析是一种纯数据驱动、不依赖于标签数据的方法,旨在将数据中呈现的自然模式通过算法表示出来。常用的无监督算法包括K-Means聚类[5-6]、自组织映射(SOM)[7-8]等。该类方法可以反映不同地震反射特征之间的差别,其存在的主要问题是如何将已有的地质认识、钻探成果与地震相相匹配。
有监督地震相分析是通过建立地震反射特征与标签数据对之间的映射关系,将已证实的地质认识与地震相关联。有监督地震相分析的算法种类繁多,常用的有贝叶斯分类、随机森林、支持向量机等。Wrona等[9]对比了20种机器学习算法,其中有监督类地震相分析技术预测精度最高可达0.983。
许多学者研究了有监督与无监督地震相分析方法的优劣及适用性[10-14]。其中,Ross等[14]认为无监督地震相分析技术适用于宏观尺度、介观尺度的沉积相描述,而有监督地震相分析技术比较适合于储层尺度的储层描述。但无论是有监督型还是无监督型,地震相分析结果对地震属性均具有极高的依赖性。
面对越来越多的地震属性种类,选择地震属性或是地震属性组合辅助地震相的研究变得越来越困难[15-16]。为了解决这个问题,Zhao等[17]和Qi等[18]研究了属性种类的筛选方法,以规避解释人员对于属性选择的主观性。
地震相分析主要包括地震属性提取和归类两个方面。以AlexNet网络[19]为代表的深度学习技术通过逐层堆叠非线性神经元,对大量原始数据进行多层级的变换,自动发现适用于聚类、分类、监测目标的数据表示[20]。因此,深度学习技术可以开展数据驱动下的地震相分析,避开人为属性选择的主观性。
利用合成数据或丰富的井数据作为地震相标签,建立端到端的卷积神经网络模型,可以直接输出地震相的分类结果[21-23]。通常情况下,丰富的地震相标签数据是一项稀缺资源[24],而无监督类的深度学习算法是一种对数据要求较低且具广泛应用前景的技术。Qian等[25]利用深度卷积自编码网络,对叠前地震道集进行数据特征的表示学习,然后利用K-Means算法对学习得到的特征空间进行聚类。Duan等[26-27]借鉴计算机视觉所发展的聚类网络架构[28],直接优化特征空间,计算聚类中心点,进行平面地震相成图工作。从网络的训练角度来看,Duan等[26-27]所提方法是对Qian等[25]的进一步发展,Qian等[25]提取的特征空间能够恢复原始输入地震信号,注重对地震数据的表示能力;Duan等[26-27]在特征空间上的进一步训练,更有利于特征空间的聚类,相对而言,忽略了特征空间的表示。
在前人研究基础上,本文提出基于深度嵌入网络的地震相聚类技术。以深度卷积自编码网络为架构,在网络训练中引入聚类损失函数和重建损失函数;同时,构建联合损失函数并加以优化,兼顾地震数据的表示能力和聚类能力。本文首先介绍深度嵌入网络技术的原理,然后将该方法应用于A致密气探区的地震相分析,最后讨论其应用效果。
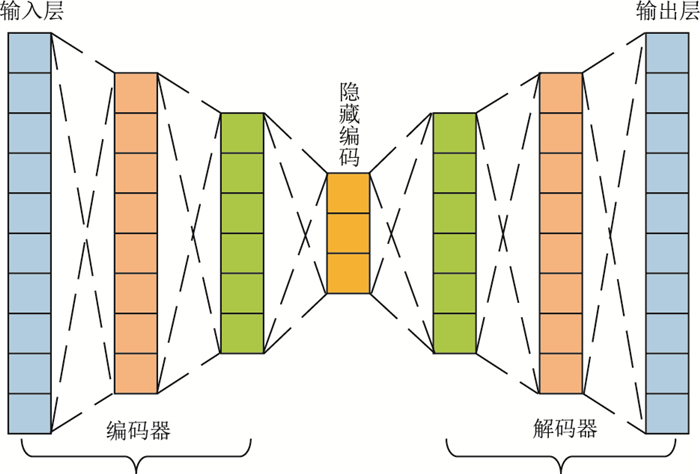
1 方法原理 1.1 自编码神经网络结构自编码神经网络是一种无监督神经网络架构[29],由编码器、隐藏编码(特征编码)和解码器三个部分构成(图 1)。其中,编码器通常由多神经网络层构成,解码器结构则为编码器结构的镜像。编码器的输入与解码器的输出维度一致,而隐藏编码的维度通常远远低于数据输入的维度,也就是所谓的“瓶颈层”[30]。“瓶颈层”可以避免出现网络仅复制输入层而将其作为输出层的这种简单的恒等映射(即
| $ \mathit{\boldsymbol{\tilde x}} = {g_\mathit{\boldsymbol{\varphi }}}[{f_\mathit{\boldsymbol{\theta }}}(\mathit{\boldsymbol{x}})] $ | (1) |
|
图 1 自编码网络结构示意图 |
式中:θ与φ是自编码网络参数;编码器表示为z=fθ(x),z是隐藏编码。
1.2 重建损失函数通过极小化输入x与输出
| $ \min\limits _{\boldsymbol{\theta}, \boldsymbol{\varphi}} L_{\mathrm{rec}}=\min \left\|\boldsymbol{x}-g_{\boldsymbol{\varphi}}\left[f_{\boldsymbol{\theta}}(\boldsymbol{x})\right]\right\|_{2}^{2} $ | (2) |
由于隐藏编码z维度远远低于输入数据x,通过优化重建损失函数,保证隐藏编码在捕捉输入数据重要“抽象”特征基础上,能够通过解码器恢复输入信号。直观地讲,重建损失函数控制网络的表示能力。
1.3 聚类损失函数通常是在数据变换后的空间实现数据的聚类,即隐藏编码z所属的空间。在隐藏空间Z上初始化k个聚类中心{μj}j=1k(k为聚类个数),采用学生T-分布(Student’s T-Distribution)定义隐藏空间任意一点zi与聚类中心μj的距离,即
| $ q_{i j}=\frac{\left(1+\frac{\left\|z_{i}-\boldsymbol{\mu}_{j}\right\|_{2}^{2}}{\alpha}\right)^{-\frac{\alpha+1}{2}}}{\sum_{j}\left(1+\frac{\left\|z_{i}-\boldsymbol{\mu}_{j}\right\|_{2}^{2}}{\alpha}\right)^{-\frac{\alpha+1}{2}}} $ | (3) |
式中:zi=fθ(xi)为第i个输入数据xi经过编码器编码之后的隐藏编码;α为学生T-分布的自由度,本文取值为1。
μj是待学习参数,利用qij的2次幂定义辅助目标概率分布,即
| $ p_{i j}=\frac{\frac{q_{i j}{ }^{2}}{\sum\limits_{i} q_{i j}}}{\sum\limits_{j} \frac{q_{i j}{ }^{2}}{\sum\limits_{i} q_{i j}}} $ | (4) |
式(4)表明:对于接近聚类中心的隐藏编码赋予高的概率;对于远离聚类中心的隐藏编码赋予低的概率。
对于隐藏编码的实际类别概率分布Q与目标概率分布P之间的接近程度,采用KL散度(Kullback-Leibler Divergence)度量。即
| $ L_{\mathrm{c}}=\mathrm{KL}(P \| Q)=\sum\limits_{i} \sum\limits_{j} p_{i j} \lg \frac{p_{i j}}{q_{i j}} $ | (5) |
式中KL(P||Q)表示两个概率P与Q之间的相对信息熵,又称为KL散度。通过对式(5)迭代优化,可实现聚类中心μj的更新,保证在隐藏空间上不同类别的“纯度”。对于Lc,本文称之为聚类损失函数。直观地讲,聚类损失函数负责的是网络对数据的聚类能力。μj迭代更新,是通过Lc对μj的求导运算实现。即
| $ \begin{gathered} \frac{\partial L_{c}}{\partial \boldsymbol{\mu}_{j}}=-\frac{\alpha+1}{\alpha} \sum\limits_{i}\left[\left(1+\frac{\left\|\boldsymbol{z}_{i}-\boldsymbol{\mu}_{j}\right\|_{2}^{2}}{\alpha}\right)^{-1} \times\right. \\ \left.\left(p_{i j}-q_{i j}\right)\left(\boldsymbol{z}_{i}-\boldsymbol{\mu}_{j}\right)\right] \end{gathered} $ | (6) |
重建损失函数Lrec负责隐藏编码对于输入数据的有意义表示;聚类损失函数Lc负责隐藏空间实现“物以类聚”的分布,使其类内距离更紧密,类间距离更疏远。同时考虑隐藏空间的表示能力与聚类能力,可建立如下联合损失函数
| $ L = \left( {1 - \lambda } \right){L_{{\rm{rec}}}} + \lambda {L_{\rm{c}}} $ | (7) |
式中λ∈[0, 1]为权重超参数,本文取值为0.1。过大的λ会破坏隐藏编码对于输入数据的表示能力,且造成损失函数梯度下降过于缓慢;而过小的λ则会降低在隐藏编码空间上的聚类程度。优化联合损失函数,使目标函数取得极小值
| $ \min\limits _{\boldsymbol{\theta}, \boldsymbol{\varphi}, \boldsymbol{\mu}} L=\min \left[(1-\lambda) L_{\mathrm{rec}}+\lambda L_{\mathrm{c}}\right] $ | (8) |
本文将以上网络架构以及损失函数构成称为地震相深度嵌入聚类网络(图 2)。
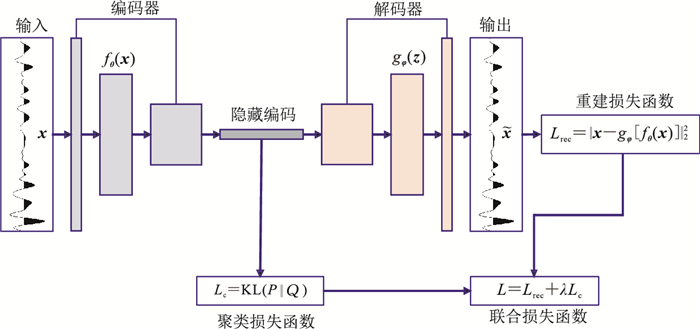
|
图 2 地震相深度嵌入聚类网络结构 |
通过四个阶段完成网络训练。第一阶段,训练自编码网络,这一阶段仅优化重建损失函数,确定自编码网络参数θ、φ的初始化估计θinit、φinit;第二阶段,利用编码器初始化参数θinit,对原始地震数据进行编码zinit=fθinit(xi);第三阶段,通过K-Means算法初始化隐藏编码的聚类中心{μjinit}j=1k;第四阶段,极小化联合损失函数(式(8)),同时更新、迭代自编码网络参数θ、φ、{μj}j=1k。
1.6 地震相成图如前述,可得到优化后的自编码网络参数θoptim、φoptim、{μjoptim}j=1k。对任意地震道xi,作为编码器输入,得到隐藏编码zioptim=fθoptim(xi)。计算该地震道隐藏编码与优化后聚类中心的欧氏距离
| $ d_{i j}=\left\|\boldsymbol{z}_{i}^{\text {optim }}-\boldsymbol{\mu}_{j}^{\text {optim }}\right\|_{2} $ | (9) |
取j*=
将本文方法应用于鄂尔多斯盆地A致密气探区,以验证其效果。
2.1 研究区概况研究区目的层为下二叠统太原组二段(本文简称太二段),埋深约2000m,厚度为45~60m,为浅水海陆过渡相三角洲沉积环境,河道近南北向展布,水下分流河道砂体发育。太二段呈低频、强振幅、连续反射的特征(图 3)。

|
图 3 研究区太二段地震反射特征黄色虚线为太二段底 |
自编码器网络结构采用卷积层和线性连接层共计9层(表 1)。输入地震数据维度为每个地震道32个时间采样点,其中编码器组成为Conv163→Conv323→Conv643→FC10(Convns表示卷积核个数为n、卷积核尺寸为s,滑动步长为2的卷积层,FC10表示输出维度为10的全连接层)。解码器结构为编码器的镜像,为FC256→Dconv323→Dconv163→Dconv13(Dconvns表示卷积核个数为n、卷积核尺寸为s、滑动步长为2的转置卷积层)。选用线性修正单元ReLU作为激活函数。采用卷积层和转置卷积层作为网络结构的主要组成单元,主要是利用卷积层的参数共享特性、对输入数据的下采样与上采样的方便特性。在保证网络的学习能力前提下,尽可能减少网络参数以减少计算量、降低网络的过拟合风险。
|
|
表 1 模型参数 |
根据钻探成果和区域沉积演化特征,选择6个类别对地震相聚类。优化算法采用Adam算法,学习率为0.001。
2.3 方法的聚类能力与表示能力利用T-SNE(T-Distributed Stochastic Neighbor Embedding)技术[31]对隐藏编码进行降维,将10维隐藏编码降为2维,并进行2维交会(图 4)。由图可见,随着迭代次数的增加,具有相似地震反射特征的地震道逐渐聚集,不同地震反射特征的地震道逐渐远离,证实了方法对于地震相的聚类能力。试验表明,500次迭代后,隐藏编码能够形成比较明显的聚类特征。

|
图 4 训练阶段隐藏编码T-SNE二维交会图 迭代次数:(a)0;(b)100;(c)200;(d)300;(e)400;(f)500。纵横坐标为降维后数据的聚集程度,无量纲。图 6同 |
通过解码器对取得的隐藏编码重建地震数据。由图 5可见,隐藏编码能完全恢复原始地震信号的特征,残差很小,相对误差小于5%,证实了隐藏编码对于地震数据的表示能力。

|
图 5 地震剖面对比 (a)输入地震剖面;(b)重建地震剖面;(c)输入剖面与重建剖面之差 |
式(7)有两种极端情况:①当λ=0时,即L=Lrec,本文方法退化为Qian等[25]提出的地震相聚类,即注重网络对于地震数据的表示能力,而不考虑隐藏编码的聚类能力(图 6a);②当λ=1时,即L=Lc,本文方法退化等价于Duan等[26-27]的地震相聚类方法,其在隐藏编码空间上有较好的聚类能力,但无法兼顾地震数据的重建(图 6b)。

|
图 6 不同条件下隐藏编码T-SNE二维交会图(左)与重建地震剖面(右) (a)L=Lrec;(b)L=Lc |
本研究区k=6,对应6个地震相类别,不同方法成图结果如图 7所示。相比于均方根振幅属性(图 7a),本文方法(图 7b)优势体现在:①对河道的刻画更为准确,均方根振幅属性比较清晰地刻画了工区中部的两条河道,而本文方法(图 7b)同样刻画了这两条河道(相4、相6),同时还清晰地展示了工区西部的另一条河道(相6),并已被钻井证实;②能展示河道间的差别,中部的西支河道(相6)不同于东支河道(相4),钻井证实相6所代表的河道平均气层厚度、平均孔隙度、平均含气饱和度分别为5.4m、8.1%、53.4%,而相4所代表的河道平均气层厚度、平均孔隙度、平均含气饱和度分别为4.1m、7.7%、47.6%;③细节更丰富,相3所代表的河道边界以及相2代表的河道沉积局部加厚区,可以反映河道内部的非均质性。
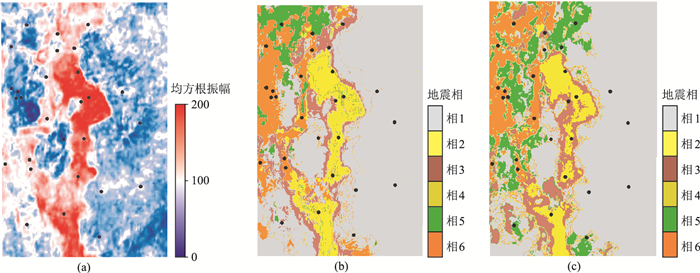
|
图 7 不同方法地震相分析结果对比 (a)均方根振幅属性;(b)本文方法;(c)K-Means方法。黑圆点为井位 |
相比K-Means聚类算法(图 7c),本文方法优势体现在:①信噪比更高, 对地震数据的噪声相对不敏感;②更符合沉积规律,如图 7b展示的河道边界(相3)仅仅围绕着河道主体,而图 7c河道边界与主体存在一定程度的混淆;③井震符合率更高。在28口实钻井的地震相标定中,本文方法符合率为89.3%,而K-Means聚类算法符合率为78.6%。
3 结束语地震相分析属于模式识别范畴,需要考虑对原始数据进行变换以及变换后的数据聚类特征,因此地震相聚类需要同时考虑数据变换的合理性以及数据变换后的聚类能力。
本文以兼顾数据变换的表示能力及数据的聚类能力为出发点,采用卷积自编码网络结构,引入聚类损失函数与重建损失函数,建立联合损失函数并优化,使网络结构兼顾两类能力。
卷积自编码网络的编码层和解码层,在理论上可以类比地球物理信号的正、反变换。引入两类损失函数,通过编码(正变换)后具有聚类的特征,再经过解码(反变换)后,也能逼近原始地震信号。
将本文方法应用到鄂尔多斯东缘A致密气探区,结果表明,本文方法比均方根振幅属性刻画河道更为准确,能揭示河道内部非均质性;比K-Means聚类算法预测结果井震符合率更高。
| [1] |
朱剑兵, 赵培坤. 国外地震相划分技术研究新进展[J]. 勘探地球物理进展, 2009, 32(3): 167-171. ZHU Jianbing, ZHAO Peikun. Advances in seismic facies classification technology abroad[J]. Progress in Exploration Geophysics, 2009, 32(3): 167-171. |
| [2] |
CHOPRA S, MARFURT K J. Unsupervised machine learning applications for seismic facies classification[C]. SPE/AAPG/SEG Unconventional Resources Technology Conference, Colorado, USA, 2019, URTEC-2019-557-MS.
|
| [3] |
蔡涵鹏, 胡浩炀, 吴庆平, 等. 基于叠前地震纹理特征的半监督地震相分析[J]. 石油地球物理勘探, 2020, 55(3): 504-509. CAI Hanpeng, HU Haoyang, WU Qingping, et al. Semi-supervised seismic facies analysis based on prestack seismic texture[J]. Oil Geophysical Prospecting, 2020, 55(3): 504-509. |
| [4] |
桑凯恒, 张繁昌, 李传辉. 地震倒谱特征参数谱聚类地震相分析方法[J]. 石油地球物理勘探, 2021, 56(1): 38-48. SANG Kaiheng, ZHANG Fanchang, LI Chuanhui. Seismic facies analysis based on cepstrum characteristic parameters and spectral clustering[J]. Oil Geophysical Prospecting, 2021, 56(1): 38-48. |
| [5] |
Galvis I S, Villa Y, Duarte C, et al. Seismic attribute selection and clustering to detect and classify surface waves in multicomponent seismic data by using K-means algorithm[J]. The Leading Edge, 2017, 36(3): 239-248. DOI:10.1190/tle36030239.1 |
| [6] |
解滔, 郑晓东, 张 . 基于线性预测倒谱系数的地震相分析[J]. 地球物理学报, 2016, 59(11): 4266-4277. XIE Tao, ZHENG Xiaodong, ZHANG Yan. Seismic facies analysis based on linear prediction cepstrum coefficients[J]. Chinese Journal of Geophysics, 2016, 59(11): 4266-4277. DOI:10.6038/cjg20161127 |
| [7] |
ZHAO T, LI F Y, MARFURT K J. Constraining self-organizing map facies analysis with stratigraphy: An approach to increase the credibility in automatic seismic facies classification[J]. Interpretation, 2017, 5(2): T163-T171. DOI:10.1190/INT-2016-0132.1 |
| [8] |
DE MATOS M C, OSORIO P L, JOHANN P R. Unsupervised seismic facies analysis using wavelet transform and self-organizing maps[J]. Geophysics, 2007, 72(1): P9-P21. DOI:10.1190/1.2392789 |
| [9] |
WRONA T, PAN I, GAWTHORPE R L, et al. Seismic facies analysis using machine learning[J]. Geophysics, 2018, 83(5): O83-O95. DOI:10.1190/geo2017-0595.1 |
| [10] |
LIU Z G, CAO J X, LU Y J, et al. A seismic facies classification method based on the convolutional neural network and the probabilistic framework for seismic attributes and spatial classification[J]. Interpretation, 2019, 7(3): SE225-SE236. DOI:10.1190/INT-2018-0238.1 |
| [11] |
MARROQUÍN I D, BRAULT J J, HART B S. A vi-sual data-mining methodology for seismic facies analy-sis: Part 1:testing and comparison with other unsupervised clustering methods[J]. Geophysics, 2009, 74(1): P1-P11. DOI:10.1190/1.3046455 |
| [12] |
MARROQUÍN I D, BRAULT J J, HART B S. A vi-sual data-mining methodology for seismic facies analy-sis: Part 2:application to 3D seismic data[J]. Geophysics, 2009, 74(1): P13-P23. DOI:10.1190/1.3046456 |
| [13] |
COLÉOU T, POUPON M, AZBEl K. Unsupervised seismic facies classification: A review and comparison of techniques and implementation[J]. The Leading Edge, 2003, 22(10): 942-953. DOI:10.1190/1.1623635 |
| [14] |
ROSS C P, COLE D M. A comparison of popular neural network facies-classification schemes[J]. The Leading Edge, 2017, 36(4): 340-349. DOI:10.1190/tle36040340.1 |
| [15] |
MARROQUÍN I D. A knowledge-integration framework for interpreting seismic facies[J]. Interpretation, 2014, 2(1): SA1-SA9. DOI:10.1190/INT2013-1218-SPSEINTRO.1 |
| [16] |
BARNES A E. Redundant and useless seismic attri-butes[J]. Geophysics, 2007, 72(3): P33-P38. DOI:10.1190/1.2716717 |
| [17] |
ZHAO T, LI F Y, MARFURT K J. Seismic attribute selection for unsupervised seismic facies analysis using user-guided data-adaptive weights[J]. Geophy-sics, 2018, 83(2): O31-O44. |
| [18] |
QI J, ZHANG B, LYU B, et al. Seismic attribute selection for machine-learning-based facies analysis[J]. Geophysics, 2019, 85(2): O17-O35. |
| [19] |
KRIZHEVSKY A, SUTSKEVER I, HINTON G E. Imagenet classification with deep convolutional neural networks[C]. Proceedings of the 25th International Conference on Neural Information Processing Systems, Granada, Spain, 2012, 1097-1105.
|
| [20] |
LECUN Y, BENGIO Y, HINTON G. Deep learning[J]. Nature, 2015, 521(7553): 436-444. DOI:10.1038/nature14539 |
| [21] |
闫星宇, 顾汉明, 罗红梅, 等. 基于改进深度学习方法的地震相智能识别[J]. 石油地球物理勘探, 2020, 55(6): 1169-1177. YAN Xingyu, GU Hanming, LUO Hongmei, et al. Intelligent seismic facies classification based on an improved deep learning method[J]. Oil Geophysical Prospecting, 2020, 55(6): 1169-1177. |
| [22] |
ZHAO T. Seismic facies classification using different deep convolutional neural networks[C]. SEG Technical Program Expanded Abstracts, 2018, 37: 2046-2050.
|
| [23] |
DRAMSCH J S, LVTHJE M. Deep-learning seismic facies on state-of-the-art CNN architectures[C]. SEG Technical Program Expanded Abstracts, 2018, 37: 2036-2040.
|
| [24] |
QI J, LIN T F, ZHAO T, et al. Semisupervised multiattribute seismic facies analysis[J]. Interpretation, 2016, 4(1): SB91-SB106. DOI:10.1190/INT-2015-0098.1 |
| [25] |
QIAN F, YIN M, LIU X Y, et al. Unsupervised seismic facies analysis via deep convolutional autoencoders[J]. Geophysics, 2018, 83(3): A39-A43. DOI:10.1190/geo2017-0524.1 |
| [26] |
DUAN Y T, ZHENG X D, HU L L, et al. Seismic facies analysis based on deep convolutional embedded clustering[J]. Geophysics, 2019, 84(6): IM87-IM97. DOI:10.1190/geo2018-0789.1 |
| [27] |
DUAN Y T, ZHENG X D, HU L L. Seismic-facies analysis based on deep-encoder clustering[C]. SEG Technical Program Expanded Abstracts, 2018, 37: 2152-2156.
|
| [28] |
XIE J Y, GIRSHICK R, FARHADI A. Unsupervised deep embedding for clustering analysis[C]. Procee-dings of the 33rd International Conference on Machine Learning, New York, USA, 2016, 478-487.
|
| [29] |
O'Shea T, Hoydis J. An introduction to deep learning for the physical layer[J]. IEEE Transactions on Cognitive Communications and Networking, 2017, 3(4): 563-575. DOI:10.1109/TCCN.2017.2758370 |
| [30] |
罗仁泽, 李阳阳. 一种基于RUnet卷积神经网络的地震资料随机噪声压制方法[J]. 石油物探, 2020, 59(1): 51-59. LUO Renze, LI Yangyang. Random seismic noise attenuation based on RUnet convolutional neural network[J]. Geophysical Prospecting for Petroleum, 2020, 59(1): 51-59. |
| [31] |
VAN DER MAATEN L, HINTON G. Visualizing data using T-SNE[J]. Journal of Machine Learning Research, 2008, 9(86): 2579-2605. |



 李祺鑫, 北京市朝阳区太阳宫南街6号院中海油研究总院, 100028。Email:
李祺鑫, 北京市朝阳区太阳宫南街6号院中海油研究总院, 100028。Email: 