② 中国石油大学(华东)地球科学与技术学院, 山东青岛 266580;
③ 中海石油海南分公司, 海南海口 570311;
④ 中国石化石油勘探开发研究院, 北京 100083;
⑤ 中国石油塔里木油田公司勘探开发研究院, 新疆库尔勒 841000
② School of Geosciences, China University of Petroleum(East China), Qingdao, Shandong 266580, China;
③ Hainan Company, China National Offshore Oil Corporation, Haikou, Hainan 570311, China;
④ Petroleum Exploration and Production Research Institute, SINOPEC, Beijing 100083, China;
⑤ Exploration and Production Research Institute, Tarim Oilfield Company, PetroChina, Korla, Xinjiang 841000, China
在海洋地震勘探中,因海水表面这一强反射界面的存在,检波器采集的地震数据会包含反射波和鬼波[1]。鬼波的存在会严重限制地震勘探的频带宽度、降低地震资料的信噪比。因此,为提高地震资料品质,必须研发能有效压制鬼波的适用技术。经过几十年的研发,已涌现出多种鬼波压制技术,这些技术主要分为两大类。
第一类是通过改变采集方式,采集更宽频带地震资料以限制鬼波。这些地震采集技术包括上下缆采集、双检采集、斜缆采集和海底电缆采集等[2]。上下缆采集技术最早由Parrack[3]提出,随后S nneland等[4]将波场分离方法应用于上下缆采集地震资料,并有效地压制了鬼波。但上下双缆必须在同一垂直剖面内,对电缆的定位精度要求较高,且双缆方式的施工成本也较高。随着科技的发展,双检采集技术被提出并应用于海上地震勘探,利用水检和陆检接收波场的极性特点,将水检与陆检资料能量匹配合并处理以压制鬼波[5-6],该技术在使用前需先对陆检资料进行标定,且合并压制效果受陆检资料信噪比影响。斜缆采集技术是将电缆倾斜布置于海水中,不同炮检距的检波器因沉放深度不同,其采集的地震资料波场也不同,即采集的波场更丰富,鬼波时差也具有多样性[7-8],有利于后续鬼波压制处理。近年来,海底电缆采集技术越来越受到重视,海底电缆将检波器布设在海底,位置相对固定,受海浪影响小,具有较大的炮检入射角,故在海洋地震勘探中具有明显优越性[9]。
第二类是鬼波压制处理技术,是指在资料处理阶段通过反演手段计算一次波或通过波场外推方式计算出鬼波,再通过匹配相减压制鬼波。Fokkema等[10]是最早通过频率—波数域波场外推法实现鬼波压制的。Zhang[11]提出一种基于格林函数理论的鬼波压制技术,该方法引入参考介质与扰动介质,通过选择不同的闭合曲面和格林函数压制经海面反射的下行波,即压制了鬼波。贺兆全等[12]论证了双检合并理论及处理技术,由于水检和陆检的自身结构和工作原理不同,二者对上行波响应极性相同,而对鸣震、鬼波等下行波极性相反,将水检与陆检合并可得到较满意的鬼波压制效果,但陆检资料的信噪比往往较低,这也成为制约该方法应用效果的主要因素。Soubaras[13]提出利用偏移和镜像偏移数据进行联合反褶积的鬼波压制方法,即首先生成相对海水表面对称的镜像数据,再对数据和镜像数据分别做叠前时间偏移,最后利用偏移后的两个数据道集进行联合反褶积,成功压制了鬼波。Wang等[14]基于Bootstrap方法,在f-x-y域实现了鬼波压制。
王芳芳等[15]详细论述了逆散射级数法鬼波压制原理,并实现了基于该理论的鬼波压制。Sun等[16]在MWD方法基础上提出EMWD(Enhanced model-based water-layer related demultiple)算法,与MWD相比该方法减少了对自适应减法的依赖性,降低了计算成本。Song等[17]提出频率域高分辨率Radon变换鬼波压制方法,并取得了较好的实际应用效果。王冲等[18]推导出频率—慢度域鬼波滤波算子及自适应迭代反演求解上行波的算法。张威等[19]基于平面波传播理论,导出τ-p域拖缆观测的总波场与海水表面观测的上行波波场之间的新关系式;通过建立线性τ-p方程,利用最小平方残差法反演得到海水表面观测的上行波波场;再通过延拓得到拖缆观测的上行波波场。马继涛等[20]提出一种基于波场外推和阈值截断的鬼波压制算法,该算法对含鬼波的地震数据进行两次波场外推,并对结果进行求和及阈值截断处理,得到海面位置的地震数据;然后利用该数据再次进行波场外推,分别得到鬼波和一次波,通过自适应相减得到不含鬼波的一次波波场。封强等[21]推导出包含海面反射系数和鬼波延迟时间的镜像记录生成公式和联合反褶积去鬼波公式,并基于非高斯性最大化,以负熵为非高斯性度量,采用滑动时空数据窗口解决鬼波参数变化问题,获得最优化的海面反射系数和鬼波延迟时间,进而通过联合反褶积压制鬼波。毕丽飞等[22]通过简化逆散射级数公式预测层间多次波,引入二维卷积盲分离方法实现层间多次波的自适应匹配相减,模型和实际资料测试均证明所提方法能在压制层间多次波的同时,更好地保护一次波。李钟晓等[23]引入伪地震数据算法,实现了一次波与预测多次波的分离。李继伟等[24]提出一种基于自适应相减滤波与Curvelet变换组合的压制面波方法。
基于格林函数理论的鬼波预测方法不需已知地层速度信息,就能准确预测鬼波;同时格林函数的构建灵活、便捷,适用于各种观测系统[25-26]。本文从克希霍夫衍射理论出发,根据地震波传播路径构建鬼波传播的格林函数,将其与原始地震记录褶积从而预测鬼波,再结合曲波域匹配相减技术实现对鬼波的压制。但格林函数与原始地震数据褶积时,一次波会预测出鬼波(一阶多次波),低阶多次波预测出高阶多次波,使预测处理后的波场更复杂;在曲波域匹配相减采用阈值处理方法时,很难设置合适阈值,即会削减一次波能量,造成一次波损伤和鬼波压制不彻底等问题。本文提出的多次迭代格林函数鬼波压制方法是先将原始波场与预测鬼波进行匹配相减得到一次波波场,利用该一次波波场与格林函数进行褶积计算新的鬼波波场,再从原始波场中将鬼波匹配相减得到更干净的一次波波场。模型和实际资料处理结果表明,该方法能在有效保护一次波的同时较好地压制鬼波,且显著拓宽地震资料频宽。
1 方法原理 1.1 基于格林函数的鬼波预测方法基于格林函数的鬼波预测方法具体过程为:根据已知海水深度和地震波在海水的传播速度等参数,构建鬼波传播的格林函数;将其与原始地震记录褶积得到预测波场,将原始波场与预测波场进行匹配相减得到一次波波场;将该一次波场与格林函数褶积计算新的预测波场,再从原始波场中减去预测波场得到新的一次波。通过上述迭代运算,逐渐实现对鬼波的准确预测及压制。具体表达式如下
| $ \left\{\begin{array}{l} \boldsymbol{M}_{1}=\boldsymbol{D} \otimes \boldsymbol{G} \\ \boldsymbol{P}_{1}=\boldsymbol{D} \varXi \boldsymbol{M}_{1} \\ \boldsymbol{M}_{i+1}=\boldsymbol{P}_{i} \otimes \boldsymbol{G} \end{array}\right. $ | (1) |
式中:M1表示预测波场;D表示原始地震记录;G表示格林函数;P1表示通过一次匹配相减得到的一次波波场;Mi+1表示第i次迭代计算的预测波场;
| $ \boldsymbol{G}=R \cdot \frac{\mathrm{e}^{-\mathrm{i} \omega t}}{\boldsymbol{r}} $ | (2) |
式中:R代表海水表面反射系数;ω为角频率;r为鬼波相对于一次波多传播的距离;t为对应的传播时间。但这样构建的格林函数仅考虑了地震波传播时能量的球面扩散和时移等运动学特征,并未考虑地震波的动力学特征,而动力学特征对于鬼波的精准预测也十分重要。
本文基于Kirchhoff衍射理论,闭合曲面SC外一个点源P0对曲面内一点P的波场值可由曲面边界上的波场值求出。即一个闭合曲面SC对曲面内某一点P的波场值总贡献u为
| $ \boldsymbol{u}=\int_{S_{\mathrm{C}}} A \mathrm{e}^{\mathrm{i} \omega t} \frac{\mathrm{e}^{-\mathrm{i} k \boldsymbol{r}_{0}}}{r_{P_{0}}-Q} \cdot \frac{\mathrm{e}^{-\mathrm{i} k r}}{r_{Q-P}} K(\theta) \mathrm{d} s $ | (3) |
式中:A表示曲面SC上的波场振幅;rP0-Q为点源P0到曲面SC上一点Q的距离;rQ-P为点Q到P之间的距离;k=ω/vw,为波数,其中vw为海水中波速;θ为rP0-Q与rQ-P之间夹角;K(θ)表示角度因子,其值如下
| $ k(\theta)= \begin{cases}\cos \theta & \theta<\frac{\pi}{2} \\ 0 & \theta \geqslant \frac{\pi}{2}\end{cases} $ | (4) |
在海底电缆勘探中,将电缆以上半空间看成闭合曲面SC的内部,其上半空间趋于无穷远处的曲面上波场为零,因此可由电缆上的波场值计算出SC曲面内某一点P的波场值,从而实现波场延拓。
鬼波的形成可看成是检波器记录的地震波波场延拓后的克希霍夫叠加[27]。对于拖缆观测系统,检波器鬼波传播路径如图 1a所示,可见其海底一阶多次波(图 1b)相对于检波器鬼波多经过了一次海底反射,且多传播了一段距离,这个多传播的距离会随电缆深度而变化。对于海底电缆观测系统,相当于将拖缆观测系统的电缆深度增大到海底。此时海底一阶多次波(图 1d)相对于鬼波(图 1c)多传播的路径很短,其传播时间可忽略不计,因此海底电缆的一阶多次波与检波器鬼波会混叠在一起,这两种波可在处理中同时进行压制。

|
图 1 海洋地震勘探地震波传播示意图 (a)拖缆观测系统鬼波传播路径;(b)拖缆观测系统一阶多次波传播路径;(c)海底电缆观测系统鬼波传播路径;(d)海底电缆观测系统一阶多次波传播路径 |
本文以海底电缆观测系统为例,置于海底的检波器在接收到海底反射波的同时也会作为一个新的球面波震源,产生二次元波向外扩散,二次源波经海面反射后产生下行波场,再次被检波器接收。按照该原理对海底电缆采集波场进行延拓,可实现对海底电缆鬼波和多次波的预测,但在延拓过程中只考虑海水表面的强反射,因此预测的只是与水层有关的多次波。经延拓后,海底地层一次反射波变为检波器鬼波或一阶多次波(图 2红色路径);海底一阶多次波经延拓后变为二阶多次波(图 2绿色路径),依此类推,低阶多次波延拓后变为更高阶多次波。
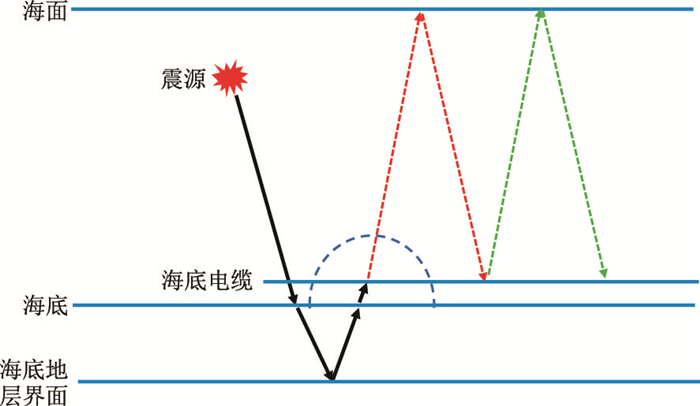
|
图 2 海底电缆波场延拓示意图 |
根据地震波的传播路径,进一步计算经海水表面反射后最终被检波器接收到的波场值
| $ \boldsymbol{u}=\frac{1}{2 {\rm{ \mathsf{ π}}} c} \iint_{S_{\mathrm{C}}} F\left(t-\frac{\boldsymbol{r}_{\mathrm{ex}}}{c}\right) \cdot \frac{\cos \theta}{\boldsymbol{r}_{\mathrm{ex}}^{2}} \mathrm{~d} s $ | (5) |
式中:F(t)=R·δ(t),表示海面反射波的理论脉冲;rex为波场延拓距离。由该式可将鬼波预测格林函数改写为新形式,即在式(2)中加入角度算子以控制不同入射角地震道的叠加权重,则格林函数变化为
| $ \boldsymbol{G}=R \cdot \frac{1}{\boldsymbol{r}} \mathrm{e}^{-\mathrm{i} \omega t} K(\theta) $ | (6) |
在三维情况下利用格林函数方法理论预测鬼波时,需对大量数据进行叠加求和,对计算机运算性能有一定要求。为了在不影响预测效果的前提下提高计算效率,采用限制预测孔径的方法,只使用设定孔径内的地震数据进行鬼波预测(图 3),这样可在保证鬼波预测精度的同时大幅度减少运算量。
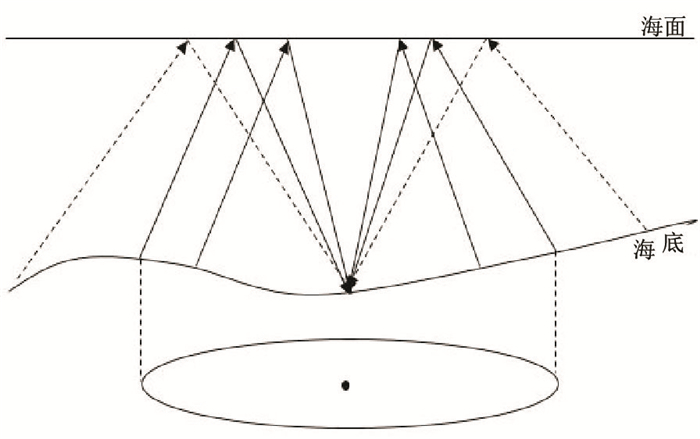
|
图 3 有限孔径鬼波预测示意图 |
传统的匹配相减技术是在最小平方理论基础上发展起来的,该方法在能量匹配过程中会干扰原始地震数据并引入新的噪声。因此,为了更好地适应各种复杂地震数据,在尽可能消除鬼波的同时保留有效信号,本文引入曲波变换法以实现匹配相减。曲波变换由于其多尺度和多方向等特性,在图像处理中可很好地对细节信息进行刻画和提取,在地球物理领域得到广泛应用[28]。另外,相比于小波变换等其他稀疏变换,曲波变换对二维分段光滑函数具有更好的非线性逼近性,同时其稀疏性也更强[29],可取得更好的匹配相减效果。
曲波变换是将原始信号在给定的函数或矢量集上进行分解,得到原始信号在曲波域的稀疏表示。曲波变换通过基函数与信号的内积形式实现信号的稀疏表示,连续的曲波变换的系数可表示为
| $ \begin{aligned} c(j, l, p) &=\left\langle f, \varphi_{j, l, p}\right\rangle=\int f(x) \bar{\varphi}_{j, l, p}(x) \mathrm{d} x \\ &=\frac{1}{(2 {\rm{ \mathsf{ π}}})^{2}} \int \hat{f}(\omega) U_{j}\left(R_{\theta_{l}} \omega\right) \mathrm{e}^{j\left\langle x_{p}^{(j, l)}, \omega\right\rangle} \mathrm{d} \omega \end{aligned} $ | (7) |
式中:c(j,l,p)为尺度j、方向l、位置p的曲波系数,它们分别控制伸缩量、旋转量和平移量;f为信号;φj,l,p为曲波基函数;Uj为频率域定义的窗函数;xp(j, l)=R-1θl(p1×2-j, p2×2-j/2);R-1θl为Rθl的逆矩阵;Rθl表示旋转矩阵,其具体表达式为
| $ \boldsymbol{R}_{\theta_{l}}=\left(\begin{array}{cc} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{array}\right) $ | (8) |
因Rθl为正交矩阵,故Rθl-1是Rθl的转置。
在得到曲波系数c(j,l,p)之后,采用阈值处理方法压制鬼波。常见的曲波阈值处理方法有两种,即硬阈值法和软阈值法[30]。
硬阈值法的准则是,设定一个阈值T,将大于T的曲波系数予以保留,小于T的曲波系数赋值为零,即
| $ C(j, l, p)= \begin{cases}c(j, l, p) & |c(j, l, p)| \geqslant T \\ 0 & |c(j, l, p)|<T\end{cases} $ | (9) |
软阈值法的准则是,同样设定一个阈值,将小于阈值的曲波系数赋值为零,大于阈值的系数减去给定阈值,即
| $ C(j, l, p)=\left\{\begin{array}{l} \operatorname{sgn}[c(j, l, p)] (|c|-T) \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ |c(j, l, p)| \geqslant T \\ \ \ \ \ \ \ \ \ 0 \ \ \ \ \ \ \ \ \ \ \ \ \ |c(j, l, p)|<T \end{array}\right. $ | (10) |
式中:sgn(·)为阶跃函数;c(j, l, p)、C(j,l,p)分别为阈值处理前、后的曲波系数。
硬阈值法和软阈值法都有各自优点和局限性。硬阈值法在保留有效波同相轴及弱小信号方面有较好效果,在曲率较大处去噪效果较好;软阈值法在压制噪声方面优势较明显,在相同阈值情况下,噪声压制比硬阈值法更彻底,但同时也会在一定程度上损害一次波。在曲波变换压制鬼波方法中,阈值的设定至关重要,因此本文在上述两种方法基础上,采用改进的相对强度阈值设定方法。
在预测的鬼波与原始地震数据匹配较好的情况下,将原始地震数据的曲波系数与预测的鬼波的曲波系数做对比,得到相对强度,即有
| $ q(j, l, p)=\left|\frac{c_{\mathrm{r}}(j, l, p)}{c_{\mathrm{m}}(j, l, p)}\right| $ | (11) |
式中:cr(j,l,p)为原始地震数据的曲波系数;cm(j,l,p)为匹配后预测的鬼波曲波系数。相对强度的阈值法准则为:若q(j,l,p) < T,则将其视为鬼波;若q(j,l,p)>T,则将其视为有效波。然后再采取硬阈值法计算曲波系数,即小于阈值的系数赋值为零,大于阈值的系数被保留。
在预测鬼波过程中,由于子波变化和能量差异等原因,造成地震资料在相位和振幅等信息上存在误差,所以可根据地震数据能量随时间的变化用不同的时窗截取地震数据。把每个时窗内的数据进行最小二乘匹配;再将原始数据与匹配后的鬼波数据进行曲波正变换,在曲波域采用阈值处理法压制鬼波;最后将处理后的数据反变换到时间域,便可得到压制鬼波后的地震数据。
2 模型试算为了验证本文论述方法的有效性,使用射线追踪法对海底电缆进行正演模拟,通过模型数据分析本文方法有效性。设计层状模型海底深度为50m,海水速度为1500m/s,海底以下地层速度依次增大,震源深度为5m,检波器放置于海底,共1201道,道间距为5m,震源采用主频为30Hz的雷克子波,采样间隔为1ms,接收5s的地震记录。正演模拟时,对模型上边界不做任何处理,以模拟海平面的自由界面;对左、右、下界面使用PML吸收边界条件,以模拟地震波在半无限介质中的传播。数值模拟采用的速度模型如图 4所示,图中横纵坐标(m)可转化为网格点数,网格单元尺寸为5m×5m。
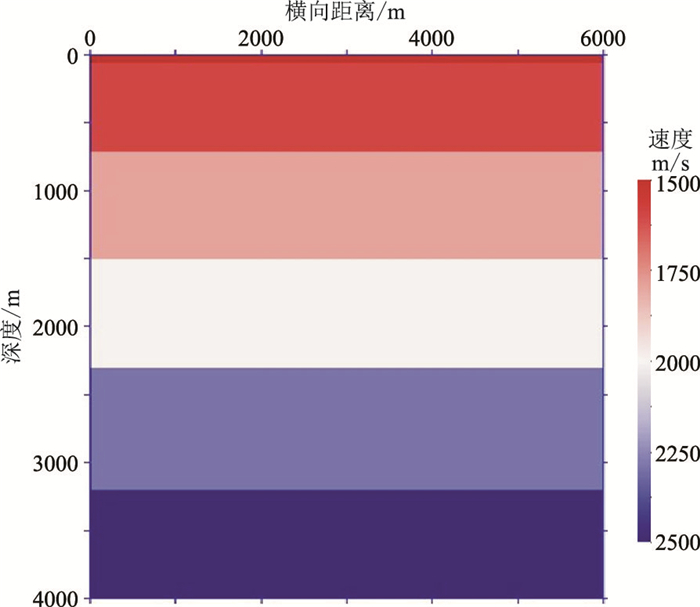
|
图 4 速度模型 |
从利用速度模型(图 4)正演模拟得到的单炮记录(图 5a)可见,在每一个地层界面的反射波之后都跟随一个与其波形相似的波,它们之间存在一定的时差,该“跟随”波即是鬼波。

|
图 5 模拟地震记录的一次、二次迭代结果 (a)正演炮集记录;(b)一次迭代压制鬼波后记录(匹配相减损害一次波);(c)一次迭代调整匹配阈值后记录(匹配相减残留鬼波);(d)二次迭代鬼波压制后炮集记录 |
图 5b为一次迭代鬼波压制后单炮记录,从中可见鬼波虽得到很好压制,但同时对一次波也造成了一定损伤。为此,调整曲波域匹配相减的阈值,所得结果如图 5c所示,可见调整匹配相减参数后一次波得到了很好保留,但其鬼波尚有一定程度的残留。于是利用本文多次迭代法对压制后单炮记录进行第二次迭代预测,将预测的多次波再从原始数据中匹配相减后得到图 5d所示结果。第二次迭代匹配相减所用阈值与第一次图 5b中设定阈值完全相同。对比这两次迭代结果,可见在图 5d中不仅一次波得到充分保留,而且在图 5c中残留的鬼波也得到了较彻底的压制。
通过单道数据分析展示鬼波压制效果。图 6a和图 6b分别为第800和第1000道的单道曲线鬼波压制前(红线)、后(蓝线)的结果,对比可见在鬼波压制后紧跟在一次反射波之后的鬼波已被消除。

|
图 6 第800道(a)和第1000道(b)鬼波压制前、后单道对比 |
进一步对鬼波压制前、后单炮记录做频谱分析,验证本文方法对陷频点的补偿作用。陷频点公式为
| $ f_{\text {notch }}=\frac{n v_{\mathrm{w}}}{2 h} $ | (12) |
式中:fnotch为陷频点处频率;n代表第n个陷频点;h为电缆沉放深度;模型数据的电缆深度为50m,可知陷频点的频率分别为15、30、45Hz。
图 7a和图 7b分别为鬼波压制前、后地震数据的f-k谱,可见鬼波压制后,陷波频率得到较好补偿。对鬼波压制前、后地震数据的频谱(图 8)进行分析,可见鬼波压制前(红线)位于15、30、45Hz等处的陷频点,在鬼波压制后(蓝线)都得到有效补偿。

|
图 7 鬼波压制前(a)、后(b)的f-k谱分析 |
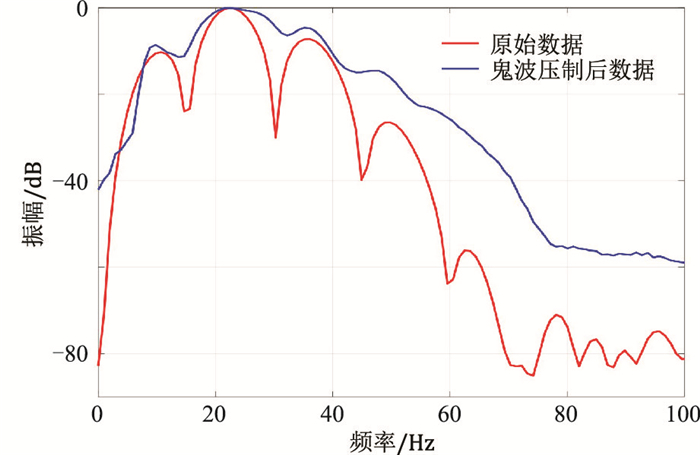
|
图 8 鬼波压制前、后模拟数据频谱分析 |
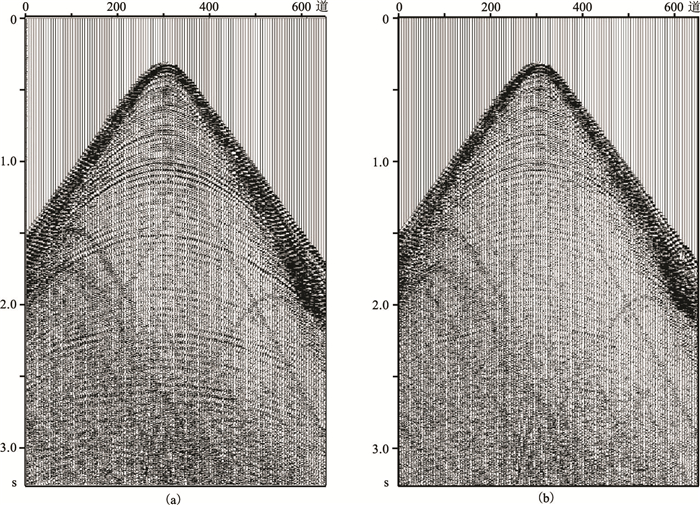
M工区水深约为18m,使用海底电缆进行采集,共部署5条测线,每炮650道,道间距为50m,采样点为3500个,采样间隔为2ms,震源深度为5m。对比鬼波压制前(图 9a)、后(图 9b)的炮集记录,可见处理后的单炮记录上鬼波得到较好压制,消除了一些假反射轴,提高了资料信噪比。
|
图 9 原始(a)和用本文方法压制鬼波后(b)的单炮记录 |
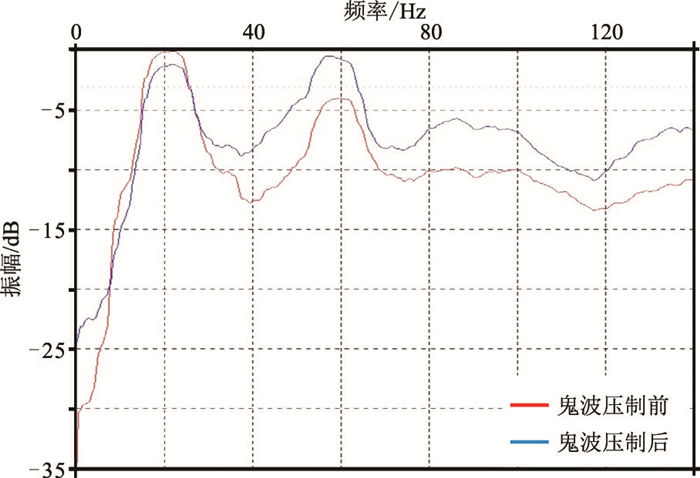
分析从该实际炮集记录得到的频谱(图 10),可见鬼波压制后陷频点振幅得到很好补偿,地震资料的高频成分增强,频带拓宽。
|
图 10 鬼波压制前、后实际地震数据频谱分析 |
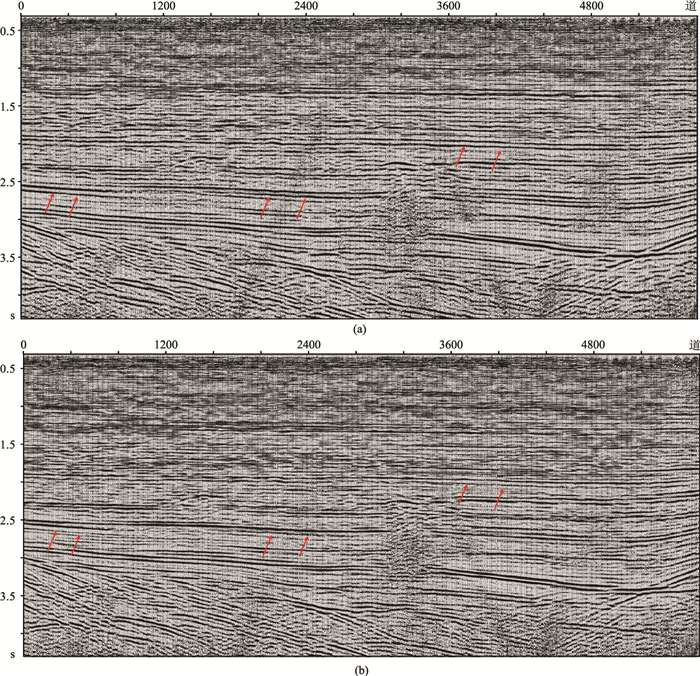
观察鬼波压制前(图 11a)、后(图 11b)该工区实际叠加剖面,可见鬼波压制后消除了(原始叠加剖面中的)一些虚假同相轴(红色箭头指示处),地震资料的信噪比得到提高。
|
图 11 鬼波压制前(a)、后(b)实际叠加剖面 |
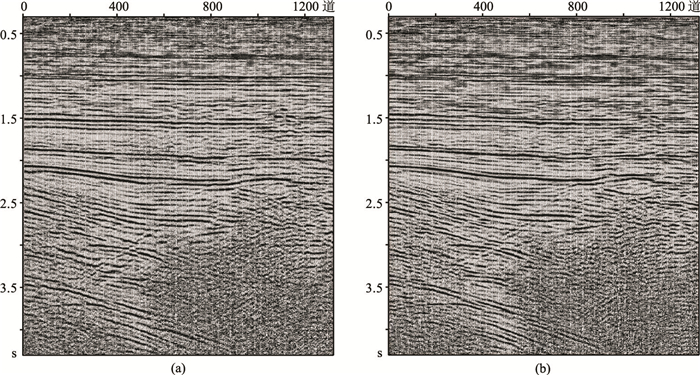
图 12为另一实际工区鬼波压制前、后的对比叠加剖面,可见鬼波压制前的一些虚假同相轴受到压制(图 12b),进一步证明了本文所提方法对鬼波的有效压制作用。
|
图 12 鬼波压制前(a)、后(b)局部叠加剖面对比 |
鬼波压制是海洋宽频地震勘探核心问题,采用基于格林函数的多次迭代鬼波预测与匹配相减鬼波压制方法,对模拟和实际海底电缆数据进行处理,有效提高了数据的信噪比,得出如下结论。
(1) 根据鬼波传播路径构建鬼波的格林函数,将其与原始地震数据褶积计算出鬼波,通过匹配相减得到一次波后,将该一次波再与格林函数褶积得到新的鬼波波场,通过如此迭代可逐步提高鬼波的预测精度。
(2) 曲波域匹配相减是采用相对强度的阈值处理实现鬼波压制,但在压制鬼波的同时,务必兼顾最大程度地保留一次波有效信息。
(3) 本文方法属于模型驱动方法,需用准确的检波器深度和海水速度计算准确的波场延拓距离,从而实现高精度的鬼波预测,且适用于拖缆和海底电缆等多种观测系统。
(4) 实际海上地震勘探中,海水界面反射系数常常不是严格的-1.0,因此需考虑粗糙海水表面对波场延拓的影响。海底沉积物的软硬对地震波反射振幅也有一定影响。下一步拟将这两个影响因素添加到算法中,从而进一步改进、完善算法。
| [1] |
吴志强. 海洋宽频带地震勘探技术新进展[J]. 石油地球物理勘探, 2014, 49(3): 421-430. WU Zhiqiang. New advances in marine broadband seismic exploration[J]. Oil Geophysical Prospecting, 2014, 49(3): 421-430. |
| [2] |
余本善, 孙乃达. 海上宽频地震采集技术新进展[J]. 石油科技论坛, 2015, 34(1): 41-45. YU Benshan, SUN Naida. Latest development of marine broadband seismic acquisition technology[J]. Oil Forum, 2015, 34(1): 41-45. DOI:10.3969/j.issn.1002-302x.2015.01.008 |
| [3] |
PARRACK A L. Method of marine reflection-type seismic exploration[P]. U S Patent, 3952281, 1976-4-20.
|
| [4] |
SØNNELAND L, BERG L E, EIDSVIG P, et al. 2-D deghosting using vertical receiver arrays[C]. SEG Technical Program Expanded Abstracts, 1986, 5: 516-519.
|
| [5] |
BARR F J, SANDERS J. Attenuation of water-column reverberations using pressure and velocity detectors in a water-bottom cable[C]. SEG Technical Program Expanded Abstracts, 1989, 8: 653-656.
|
| [6] |
CARLSON D, LONG A, SOLLNER W, et al. Increased resolution and penetration from a towed dual-sensor streamer[J]. First Break, 2007, 25(12): 71-77. |
| [7] |
RAY C H, MOORE N A. High resolution, marine seismic stratigraphic system[P]. U S Patent, 4353121, 1982-10-5.
|
| [8] |
BEARNTH R E, MOORE N A. Air gun-slant cable seismic results in the Gulf of Mexico[C]. SEG Technical Program Expanded Abstracts, 1989, 8: 649-652.
|
| [9] |
余本善, 孙乃达. 海底地震采集技术发展现状及建议[J]. 海洋石油, 2015, 35(2): 1-5. YU Benshan, SUN Naida. Current development si-tuations and suggestion on the techniques of ocean bottom seismic acquisition[J]. Offshore Oil, 2015, 35(2): 1-5. DOI:10.3969/j.issn.1008-2336.2015.02.001 |
| [10] |
FOKKEMA J T, VAN DEN BERG P M. Seismic Applications of Acoustic Reciprocity[M]. Elsevier, 1993.
|
| [11] |
ZHANG J. Wave Theory Based Data Preparation for Inverse Scattering Multiple Removal, Depth Imaging and Parameter Estimation: Analysis and Numerical Tests of Green's Theorem Deghosting Theory[D]. University of Houston, Houston, Texas, 2007.
|
| [12] |
贺兆全, 张保庆, 刘原英, 等. 双检理论研究及合成处理[J]. 石油地球物理勘探, 2011, 46(4): 522-528. HE Zhaoquan, ZHANG Baoqing, LIN Yuanying, et al. Response characteristics of dual-sensor and their application in OBC data Processing[J]. Oil Geophysical Prospecting, 2011, 46(4): 522-528. |
| [13] |
SOUBARAS R. Deghosting by joint deconvolution of a migration and a mirror migration[C]. SEG Technical Program Expanded Abstracts, 2010, 29: 3406-3410.
|
| [14] |
WANG P, PENG C. Premigration deghosting for marine towed streamer data using a bootstrap approach[C]. SEG Technical Program Expanded Abstracts, 2012, 31: 1-5.
|
| [15] |
王芳芳, 李景叶, 陈小宏. 基于逆散射级数法的鬼波压制方法[J]. 地球物理学报, 2013, 56(5): 1628-1636. WANG Fangfang, LI Jingye, CHEN Xiaohong. Deghosting method based on inversion scattering series[J]. Chinese Journal of Geophysics, 2013, 56(5): 1628-1636. |
| [16] |
SUN W Q, HU J T, WANG H Z, et al. Enhanced model-based water-layer related demultiple[C]. SEG Global Meeting Abstracts, 2014, 349-351.
|
| [17] |
SONG J G, GONG Y L, LI S. High resolution frequency domain Radon transform and variable-depth streamer data deghosting[J]. Applied Geophysics, 2015, 12(4): 564-572. DOI:10.1007/s11770-015-0525-x |
| [18] |
王冲, 顾汉明, 许自强, 等. 最小二乘反演迭代算法在压制海上变深度缆采集数据虚反射中的应用[J]. 地球物理学报, 2016, 59(5): 1790-1803. WANG Chong, GU Hanming, XU Ziqiang, et al. The application of least-squares inversion iteration algorithm to deghost for marine variable-depth streamer data[J]. Chinese Journal of Geophysics, 2016, 59(5): 1790-1803. |
| [19] |
张威, 韩立国, 李洪建, 等. 基于LSMR算法的斜缆数据鬼波压制方法[J]. 石油地球物理勘探, 2017, 52(3): 434-441. ZHANG Wei, HAN Liguo, LI Hongjian, et al. Deghosting of variable depth streamer data based on LSMR[J]. Oil Geophysical Prospecting, 2017, 52(3): 434-441. |
| [20] |
马继涛, 王艳冬, 陈小宏, 等. 基于波场外推和阈值截断的鬼波压制方法[J]. 石油地球物理勘探, 2018, 53(2): 227-235. MA Jitao, WANG Yandong, CHEN Xiaohong, et al. A ghost suppression method based on wavefield extrapolation and threshold truncation[J]. Oil Geophysical Prospecting, 2018, 53(2): 227-235. |
| [21] |
封强, 韩立国, 杨帆. 非高斯性最大化变深度缆鬼波压制方法[J]. 石油地球物理勘探, 2020, 55(1): 57-63. FENG Qiang, HAN Liguo, YANG Fan. A deghosting method for variable-depth streamer data based on non-Gaussian maximization[J]. Oil Geophysical Prospecting, 2020, 55(1): 57-63. |
| [22] |
毕丽飞, 秦宁, 李钟晓, 等. 应用逆散射级数波场预测和2D卷积盲分离压制层间多次波[J]. 石油地球物理勘探, 2020, 55(3): 521-529. BI Lifei, QIN Ning, LI Zhongxiao, et al. Wavefield prediction with inverse scattering series and 2D blind separation of convolved mixtures for suppressing internal multiples[J]. Oil Geophysical Prospecting, 2020, 55(3): 521-529. |
| [23] |
李钟晓, 高好天, 陈鑫泽, 等. 基于3D匹配滤波器和伪地震数据算法的多次波自适应相减方法[J]. 石油地球物理勘探, 2020, 55(3): 530-540. LI Zhongxiao, GAO Haotian, CHEN Xinze, et al. Adaptive multiple subtraction based on a 3D matching filter and pseudo seismic data algorithm[J]. Oil Geophysical Prospecting, 2020, 55(3): 530-540. |
| [24] |
李继伟, 臧殿光, 刁永波, 等. 自适应相减和Curvelet变换组合压制面波[J]. 石油地球物理勘探, 2020, 55(5): 1005-1015. LI Jiwei, ZANG Dianguang, DIAO Yongbo, et al. Combination of adaptive subtraction and Curvelet transform to suppress surface waves[J]. Oil Geophysical Prospecting, 2020, 55(5): 1005-1015. |
| [25] |
杨金龙, WEGLEIN A B. 基于格林理论的鬼波压制方法及其应用[J]. 石油物探, 2017, 56(4): 507-515. YANG Jinlong, WEGLEIN A B. A deghosting method based on Green's theorem and its application[J]. Geophysical Prospecting for Petroleum, 2017, 56(4): 507-515. DOI:10.3969/j.issn.1000-1441.2017.04.006 |
| [26] |
李洪建, 韩立国, 巩向博, 等. 基于格林函数理论的波场预测和鬼波压制方法[J]. 地球物理学报, 2016, 59(3): 1113-1124. LI Hongjian, HAN Liguo, GONG Xiangbo, et al. A wavefield prediction and ghost suppression method based on Green function theory[J]. Chinese Journal of Geophysics, 2016, 59(3): 1113-1124. |
| [27] |
宋建国, 姜梦奇, 杨宇. 基于克希霍夫衍射理论的水层多次波预测方法[J]. 地球物理学进展, 2016, 31(5): 2133-2138. SONG Jianguo, JIANG Mengqi, YANG Yu. Water-layer multiple prediction method based on Kirchhoff diffraction theory[J]. Progress in Geophysics, 2016, 31(5): 2133-2138. |
| [28] |
周含蕊. 基于逆散射级数的虚反射消除方法研究与应用[D]. 山东青岛: 中国石油大学(华东), 2016. ZHOU Hanrui. Research and Application of Deghosting Based on Inverse-scattering Series Theory[D]. China University of Petroleum(East China), Qingdao, Shandong, 2016. |
| [29] |
王通, 王德利, 冯飞, 等. 三维稀疏反演多次波预测及曲波域匹配相减技术[J]. 吉林大学学报(地球科学版), 2017, 47(6): 1865-1874. WANG Tong, WANG Deli, FENG Fei, et al. Multiple prediction with 3D sparse inversion and curvelet match[J]. Journal of Jilin University(Earth Science Edition), 2017, 47(6): 1865-1874. |
| [30] |
郝振江, 冯飞, 王德利, 等. Curvelet域海底电缆多次波压制方法研究[J]. 世界地质, 2013, 32(1): 130-136. HAO Zhenjiang, FENG Fei, WANG Deli, et al. Research on OBC multiple wave attenuation method in Curvelet domain[J]. Global Geology, 2013, 32(1): 130-136. DOI:10.3969/j.issn.1004-5589.2013.01.017 |



 宋建国, 山东省青岛市经济技术开发区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email:
宋建国, 山东省青岛市经济技术开发区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email: 