② 湖北文理学院数学与统计学院, 湖北襄阳 441053
② School of Mathematics and Statistics, Hubei University of Arts and Science, Xiangyang, Hubei 441053, China
地震波在地层传播过程中,会受到介质的吸收和散射效应,导致地震波的主频降低、频宽变窄,从而降低中、深层地震资料分辨率,给油气勘探带来诸多困难[1]。地震波在地下介质中传播时产生的衰减效应,可以用品质因子Q定量表示[2]。实验室测量表明,地层对地震波的吸收作用主要取决于岩石物性、孔隙度、孔隙流体成分及饱和度等[3], 因此,Q值估计是预测和直接寻找油气储层的有效途径之一[4]。准确的Q模型还可用于反Q滤波[5-6]以提高地震资料的分辨率,为后续精细解释和准确成像提供高分辨率的地震资料。
近年来,学者们已经提出了许多种Q估计方法。常见的Q估计方法一般可分为时间域、频率域和时频域三大类[7]。时间域方法包括脉冲上升时间法、子波模拟法等;频率域方法包括对数谱比法(Logarithmic Spectral Ratio,LSR)[8]、中心频率偏移法(Center Frequency Shift,CFS)[9]、峰值频率偏移法(Peak Frequency Shift, PFS)[9]等;时频域方法包括子波包络峰值频率偏移法[10]、基于Gabor谱的常Q估计方法(Constant-Q Estimation via Gabor Analysis, CVG)[11]等。其中,CVG方法是一种基于Gabor变换的Q值估计方法,它不需对地震子波进行假设,已广泛应用于提取地震数据的品质因子Q。但是,由于Gabor变换的窗函数固定,该方法对窗函数的参数比较敏感;同时,CVG方法对含噪地震数据的估计精度并不理想。
为了克服上述缺点,本文提出了一种新的基于S变换和变分法的Q估计方法(Q Estimation Based on the Calculus of Variations and S Transform, CVS)。与Gabor变换相比,S变换[12]具有多尺度分辨率和自适应调整窗长度等优点,可有效避免CVG方法对窗函数比较敏感的问题。首先,推导了非平稳地震数据在S变换域中的近似表示。然后,根据该近似表示构建品质因子Q和子波之间的优化函数,利用微分和变分法对该优化函数进行求解,进而得到品质因子Q的计算表达式;与CVG方法相比,提出的Q估计方法无需假设地震子波的类型,也不必人为调节窗函数的长度。最后,为提高CVS方法的准确性和抗噪性,设计了一种自适应参数选择的方案,对计算过程中的积分区间进行自动选取。
综上所述,CVS方法有效解决了CVG方法中存在的需要固定窗长和抗噪性较差的问题,显著提高了Q值计算的准确性和稳定性。模型数据和实际数据算例均验证了该方法的有效性。
1 基本原理 1.1 非平稳地震数据的S域近似表示常规的地震资料高分辨率处理一般建立在传统的平稳褶积模型[13]上。考虑到地震波在传播过程中存在衰减效应,需在平稳褶积模型中引入衰减,得到更符合实际地下情况的非平稳褶积模型[14]。令x(t)为非平稳反射地震数据,其频域形式在非平稳褶积模型中可表示为
| $ \hat{x}(f)=\hat{\omega}(f) \int_{-\infty}^{+\infty} \alpha(t, f) r(t) \mathrm{e}^{-\mathrm{i} 2 {\rm{ \mathsf{ π} }} f t} \mathrm{~d} t $ | (1) |
式中:(f)和(f)分别表示非平稳地震数据和震源子波的傅里叶变换,f表示频率;t表示时域地震数据中传播的时间;r(t)表示反射系数;α(t, f)为地震衰减函数。本文使用Kolsky-Futterman衰减模型[15-16]表示Q滤波效应,即
| $ \alpha(t, f)=\exp \left(\frac{-{\rm{ \mathsf{ π} }} f t}{Q}\right) \exp \left[\mathrm{i} 2 t f \ln \frac{\left(\frac{f}{f_{\mathrm{R}}}\right)}{Q}\right] $ | (2) |
式中fR表示参考频率。
对式(1)进行傅里叶逆变换,x(t)可表示为
| $ x(t)=\iint \hat{\omega}(f) \alpha(u, f) r(u) \mathrm{e}^{2 {\rm{ \mathsf{ π} }} \mathrm{i} f(t-u)} \mathrm{d} f \mathrm{d} u $ | (3) |
式中u表示与时间和频率相关的衰减模型中的时间变量。
由于S变换的窗函数随着频率变化,所以低频与高频的时频分辨率具有差异,这有利于刻画地震数据的非平稳性。引入S变换分析非平稳地震数据。地震数据x(t)的S变换[7]定义为
| $ \begin{aligned} S_{x}(\tau, \nu) &=\int_{-\infty}^{+\infty} x(t) g(t-\tau, \nu) \mathrm{e}^{-\mathrm{i} 2 {\rm{ \mathsf{ π} }} \nu t} \mathrm{~d} t \\ &=\int_{-\infty}^{+\infty} x(t) \frac{|\nu|}{\sqrt{2 {\rm{ \mathsf{ π} }}}} \mathrm{e}^{-\frac{(t-\tau)^{2} \nu^{2}}{2}} \mathrm{e}^{-\mathrm{i} 2 {\rm{ \mathsf{ π} }} \nu t} \mathrm{~d} t \end{aligned} $ | (4) |
式中:τ和ν分别是时间变量和频率变量;g是高斯窗函数。由式(4)能看出,与Gabor变换的固定高斯窗函数相比,S变换的窗函数可随频率进行调节,一定程度上解决了Gabor变换中固定窗的问题。
为更清楚说明地震信号的S变换多尺度分辨率的优势,选择主频为40Hz的Ricker子波分别进行Gabor变换和S变换(图 1)。由图可见,S变换中高频分量具有更好的时间分辨率,低频分量具有更好的频率分辨率,因此S变换比Gabor变换能够更好地描述非平稳地震数据。
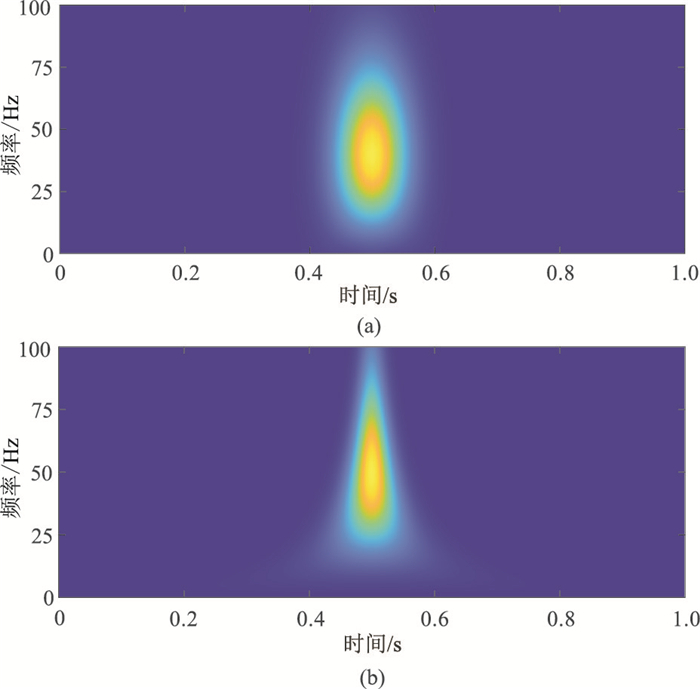
|
图 1 地震数据Gabor变换结果(a)和S变换结果(b) |
将式(3)代入式(4),式(4)可表示为
| $ \begin{aligned} S_{x}(\tau, \nu)=& \int_{-\infty}^{+\infty}\left[\iint \hat{\omega}(f) \alpha(u, f) r(u) \mathrm{e}^{2 {\rm{ \mathsf{ π} }} \mathrm{i} f(t-u)} \mathrm{d} f \mathrm{d} u\right] \times \\ & \frac{|\nu|}{\sqrt{2 {\rm{ \mathsf{ π} }}}} \mathrm{e}^{-\frac{(t-\tau)^{2} \nu^{2}}{2}} \mathrm{e}^{-\mathrm{i} 2 {\rm{ \mathsf{ π} }} \nu t} \mathrm{d} t \end{aligned} $ | (5) |
在式(5)中进行变量替换:t′=t-τ和f′=ν-f,并对
| $ \begin{aligned} S_{x}(\tau, \nu) &=\int_{-\infty}^{+\infty}\left[\iint \hat{w}(f) \alpha(u, f) r(u) \mathrm{e}^{2 {\rm{ \mathsf{ π} }} \mathrm{i} f(t-u)} \mathrm{d} f \mathrm{d} u\right] \cdot \frac{|\nu|}{\sqrt{2 {\rm{ \mathsf{ π} }}}} \mathrm{e}^{-\frac{(t-\tau)^{2} \nu^{2}}{2}} \mathrm{e}^{-\mathrm{i} 2 {\rm{ \mathsf{ π} }} u} \mathrm{d} t \\ &=\iint \hat{\omega}(f) \alpha(u, f) r(u) \mathrm{e}^{-2 {\rm{ \mathsf{ π} }} \mathrm{i} f u}\left[\int_{-\infty}^{+\infty} \frac{|\nu|}{\sqrt{2 {\rm{ \mathsf{ π} }}}} \mathrm{e}^{-\frac{(t-\tau)^{2} \nu^{2}}{2}} \mathrm{e}^{-\mathrm{i} 2 {\rm{ \mathsf{ π} }} t(\nu-f)} \mathrm{d} t\right] \mathrm{d} f \mathrm{d} \nu t \\ &=\iint \hat{w}(f) \alpha(u, f) r(u) \mathrm{e}^{-2 {\rm{ \mathsf{ π} }} \mathrm{i} f u-2 {\rm{ \mathsf{ π} }} \mathrm{i} \tau(\nu-f)}\left[\int_{-\infty}^{+\infty} \frac{|\nu|}{\sqrt{2 {\rm{ \mathsf{ π} }}}} \mathrm{e}^{-\frac{t^{\prime 2} \nu^{2}}{2}} \mathrm{e}^{-\mathrm{i} 2 {\rm{ \mathsf{ π} }} t^{\prime}(\nu-f)} \mathrm{d} t^{\prime}\right] \mathrm{d} f \mathrm{d} u \\ &=\iint \hat{\omega}(f) \alpha(u, f) r(u) \mathrm{e}^{-2 {\rm{ \mathsf{ π} }} \mathrm{i} f u} \mathrm{e}^{-2 {\rm{ \mathsf{ π} }} \mathrm{i} \tau(\nu-f)} g(\nu-f, \nu) \mathrm{d} f \mathrm{d} u\\ &=\iint \hat{\omega}\left(\nu-f^{\prime}\right) \alpha\left(u, \nu-f^{\prime}\right) r(u) \mathrm{e}^{-2 {\rm{ \mathsf{ π} }} \mathrm{i} u\left(\nu-f^{\prime}\right)} \mathrm{e}^{-2 {\rm{ \mathsf{ π} }} \mathrm{i} \tau f^{\prime}} g\left(f^{\prime}, \nu\right) \mathrm{d} f \mathrm{d} u \\ &\approx \iint \hat{\omega}(\nu) \alpha(u, \nu) r(u) \mathrm{e}^{-2 {\rm{ \mathsf{ π} }} \mathrm{i} u\left(\nu-f^{\prime}\right)} \mathrm{e}^{-2 {\rm{ \mathsf{ π} }} \mathrm{i} \tau f^{\prime}} g\left(f^{\prime}, \nu\right) \mathrm{d} f^{\prime} \mathrm{d} u \\ &\approx \int \hat{\omega}(\nu) \alpha(u, \nu) r(u) \mathrm{e}^{-2 {\rm{ \mathsf{ π} }} \mathrm{i} u \nu} g(u-\tau, \nu) \mathrm{d} u \\ &\approx \int \hat{\omega}(\nu) \alpha\left(\tau-u^{\prime}, \nu\right) r\left(\tau-u^{\prime}\right) \mathrm{e}^{-2 {\rm{ \mathsf{ π} }} \mathrm{i}\left(\tau-u^{\prime}\right) \nu} g\left(u^{\prime}, \nu\right) \mathrm{d} u \\ &\approx \hat{\omega}(\nu) \alpha(\tau, \nu) \int r(u) \mathrm{e}^{-2 {\rm{ \mathsf{ π} }} \mathrm{i} u\nu} g(\tau-u, \nu) \mathrm{d} u \end{aligned} $ | (6) |
因此,非平稳地震数据的S域可近似表示为
| $ S_{x}(\tau, \nu) \approx \hat{\omega}(\nu) \alpha(\tau, \nu) S_{r}(\tau, \nu) $ | (7) |
式中Sr(τ, ν)表示反射系数的S变换结果。
1.2 品质因子Q的计算公式在近似表示的基础上,仅考虑地震记录的振幅谱,式(7)可表示为
| $ \left|S_{x}(\tau, \nu)\right| \approx|\hat{\omega}(\nu)||\alpha(\tau, \nu)|\left|S_{r}(\tau, \nu)\right| $ | (8) |
假设反射系数序列的谱是白的,在非平稳地震数据变换到S域后,式(8)可以忽略|Sr(τ, ν)|项,进一步简化并两边取对数可得
| $ \ln \left|S_{x}(\tau, \nu)\right| \approx \ln |\hat{\omega}(\nu)|-{\rm{ \mathsf{ π} }} \tau\nu / Q $ | (9) |
式中Q是待求的参数。一个鲁棒的思路是优化关于Q的目标函数,从而得到一个稳定解。通过式(9),能够在最小二乘的意义下,基于S变换建立如下的目标函数
| $ L(\hat{\omega}, Q)=\iint\limits_{\varOmega}\left[\ln \left|S_{x}(\tau, \nu)\right|-\ln |\hat{\omega}(\nu)|+\frac{{\rm{ \mathsf{ π} }} \tau\nu}{Q}\right]^{2} \mathrm{~d} \tau \mathrm{d} \nu $ | (10) |
式中Ω表示有效能量的积分区间。由于地震数据是带限的,计算Q过程中的积分范围也是有限的,实际积分中只考虑S变换谱中显著的数值区域Ω,为此,定义一个加权函数作为被积函数的因子,即
| $ \begin{gathered} \iint\limits_{\varOmega} h(\tau, \nu) \mathrm{d} \tau \mathrm{d} \nu=\int_{\tau_{\min }}^{\tau_{\max }} \int_{\nu_{\min }}^{\nu_{\max }} h(\tau, \nu) F_{\varOmega}(\tau, \nu) \mathrm{d} \tau \mathrm{d} \nu \\ F_{\varOmega}(\tau, \nu)= \begin{cases}1 & (\tau, \nu) \in \varOmega \\ 0 & (\tau, \nu) \notin \varOmega\end{cases} \end{gathered} $ | (11) |
式中:h(τ, ν)为被积函数;FΩ(τ, ν)为加权函数;τmin和τmax分别表示地震信号的传播开始时间和结束时间;νmin和νmax分别表示积分区间的上、下频率边界。
积分区间确定后,通过最小化式(10)求解稳定的品质因子Q。观察式(10)可得,
| $ Q={\rm{ \mathsf{ π} }} \frac{\int_{\varOmega} \tau^{2} \nu^{2} \mathrm{~d} \tau \mathrm{d} \nu}{\int_{\varOmega} \tau \nu \ln \frac{|\hat{\omega}(\nu)|}{\left|S_{x}(\tau, \nu)\right|} \mathrm{d} \tau \mathrm{d} \nu} $ | (12) |
式(12)中包含
| $ \begin{aligned} \Delta L=& L(\ln |\hat{\omega}(\nu)|+\delta \ln |\hat{\omega}(\nu)|, Q)-L(\hat{\omega}, Q) \\ =& \int_{\varOmega}(\delta \ln |\hat{\omega}(\nu)|)^{2} \mathrm{~d} \tau \mathrm{d} \nu-\\ & 2 \iint\limits_{\varOmega}\left(\ln \left|S_{x}(\tau, \nu)\right|-\ln |\hat{\omega}(\nu)|+\right.\\ &{\rm{ \mathsf{ π} }} \tau \nu / Q) \delta \ln |\hat{\omega}(\nu)| \mathrm{d} \tau \mathrm{d} \nu \end{aligned} $ | (13) |
对于任意的
| $ \begin{aligned} \int_{\nu_{\min }}^{\nu_{\max }} &\left\{\int_{\tau_{\min }}^{\tau_{\max }} \ln \left|S_{x}(\tau, \nu)\right| F_{\varOmega}(\tau, \nu) \mathrm{d} \tau-\right.\\ & \ln \left|\hat{\omega}_{\tau}(\nu)\right| \int_{\tau_{\min }}^{\tau_{\max }} F_{\varOmega}(\tau, \nu) \mathrm{d} \tau+\\ &\left.\frac{{\rm{ \mathsf{ π} }} \nu}{Q} \int_{\tau_{\min }}^{\tau_{\max }} \tau F_{\varOmega}(\tau, \nu) \mathrm{d} \tau\right\} \delta \ln |\hat{\omega}(\nu)| \mathrm{d} \nu=0 \end{aligned} $ | (14) |
式(14)中,对于任意的δ
| $ |\hat{w}(\nu)|=\exp [p(\nu)+{\rm{ \mathsf{ π} }} \nu \bar{\tau}(\nu) / Q] $ | (15) |
式中
| $ p(\nu)=\frac{\int_{\tau_{\min }}^{\tau_{\max }} \ln \left|S_{x}(\tau, \nu)\right| F_{\varOmega}(\tau, \nu) \mathrm{d} \tau}{\int_{\tau_{\min }}^{\tau_{\max }} F_{\varOmega}(\tau, \nu) \mathrm{d} \tau} $ | (16) |
| $ \bar{\tau}(\nu)=\frac{\int_{\tau_{\min }}^{\tau_{\max }} \tau F_{\varOmega}(\tau, \nu) \mathrm{d} \tau}{\int_{\tau_{\min }}^{\tau_{\max }} F_{\varOmega}(\tau, \nu) \mathrm{d} \tau} $ | (17) |
将式(15)代入式(12),消除子波变量,得到最终的Q值计算公式
| $ Q={\rm{ \mathsf{ π} }} \frac{\int_{\varOmega} \tau \nu^{2}[\tau-\bar{\tau}(\nu)] \mathrm{d} \tau \mathrm{d} \nu}{\int_{\varOmega} \tau \nu\left[p(\nu)-\ln \left|S_{x}(\tau, \nu)\right|\right] \mathrm{d} \tau \mathrm{d} \nu} $ | (18) |
上述积分区域Ω对Q值计算精度起着重要的作用。对于含有强烈噪声的地震数据,传统的Q估计方法很难估计高精度的Q值,如CFS、CVG和LSR。为了解决这一问题,通常采用两步估计方法:第一步是应用某种去噪算法,对含噪地震数据进行去噪处理,提高地震数据的质量;第二步是从去噪后的地震数据中提取品质因子Q。显而易见,两步法需要较高的时间成本以及依赖去噪算法的效果。因此,本文提出了一个自适应的积分区间选择算法,这种方法可以在地震数据中出现较高噪声的情况下得到相对准确的Q值。
分析式(18),估计Q值时需要对时频谱的时间变量τ和频率变量ν进行二重积分,积分区间Ω可由τmin、τmax、νmin、νmax四个参数确定。显而易见,τmin和τmax能够被地震信号的先验信息确定。根据地震信号的传播时间,本文在合成数据算例中设置τmin=0和τmax=1s。这样就仅需要考虑频率参数νmin和νmax如何设置。
小波变换中常用VisuShrink算法[17]设置一个全局阈值[18],从而确定有效能量空间。全局阈值的计算公式为
| $ \lambda=\sigma \sqrt{2 \ln N} $ | (19) |
式中:σ为高斯噪声标准方差;N为地震信号采样点数。
受VisuShrink去噪算法的启发,本文提出一种时变阈值的自适应频率参数选择方案,其具体步骤如下:
(1) 利用S变换得到给定地震数据的时频谱|Sx(τ, ν)|。
(2) 由于地震资料的衰减是随波的传播而累积的,所以对每个时刻τi∈[τmin, τmax]计算当前的阈值ρτi,公式如下
| $ \rho_{\tau_{i}}=k M_{\tau_{i}} \sqrt{2 \ln N} $ | (20) |
式中:k是与信噪比相关的调整参数;Mτi表示时刻τi对应的S变换谱系数的均值。
(3) 对于每个时刻的τi,当满足|Sx(τi, νmin, τi)|=ρτi和|Sx(τi, νmax, τi)|=ρτi时,确定当前低频νmin, τi和高频νmax, τi。
(4) 所有时刻计算的上、下限频率构成了不规则的积分区间Ω。其中:νmin=min(νmin, τ1, νmin, τ2,…,νmin, τN);νmax=max(νmax, τ1, νmax, τ2, …, νmax, τN)。
CVS方法将上述方案确定的积分区间应用到式(18),并计算非平稳地震数据中的品质因子Q。
2 模型测试在上述自适应积分区间选择方法的基础上,首先研究不同参数k对CVS方法的Q值估计结果的影响,选择相对误差最小时对应的k值,并代入时变阈值计算公式,从而确定合适的积分区间;然后,通过合成的无噪地震数据和不同信噪比的含噪地震数据验证本文所提出的CVS方法,并与CVG、CFS和LSR三种方法进行对比。
2.1 自适应积分区间中参数k的选择在上述提出的自适应积分区间的确定方法中,参数k需要人为设置。为验证不同参数k对CVS方法所估计Q值的影响,实验采用主频为30Hz的Ricker子波、理论Q为50以及如图 2所示的反射系数合成无噪地震数据。向无噪地震数据中加入不同信噪比的高斯白噪声后,得到信噪比为5、12和20dB的含噪地震数据。针对无噪与含噪地震数据,分别选取不同范围的k进行Q值估计。
|
图 2 白的伪随机反射系数 |
根据实验结果可得,选择合理的k值有利于CVS方法最终估计出高精度的Q值。如图 3所示,对于无噪地震数据,应该设置k=0.07;对于信噪比为20、12和5dB的含噪地震数据,分别设置k的值为0.14、0.18、0.25。由图可见,参数k与信噪比相关。当k值设置合理时,k和Mτi的乘积能够作为高斯标准方差的近似。无噪地震数据应选择较小的k,以避免S变换中幅值过小的系数,从而避免Q值估计过程中不稳定的情况出现。而对于含噪地震数据还需在一定程度上抑制噪声,所以k值随着信噪比的增加而减小。
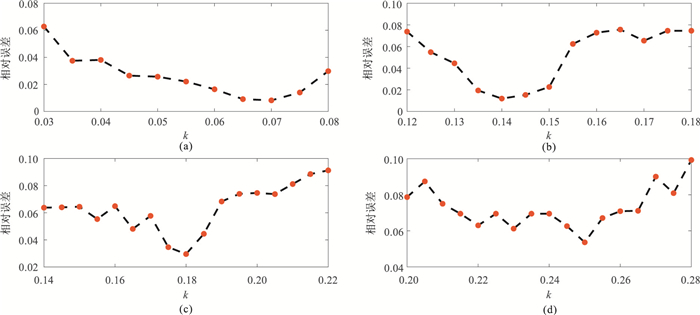
|
图 3 不同范围k对地震数据的Q估计精度的影响 (a)无噪数据;(b)信噪比为20dB的含噪数据;(c)信噪比为12dB的含噪数据;(d)信噪比为5dB的含噪数据 |
在本实验中,非平稳地震数据由图 2所示白的伪随机反射系数序列和主频为30Hz的Ricker子波生成。图 4分别为Q=25、50、75、100和125的5道非平稳地震信号。对于CVS方法,式(18)中的参数k设置为0.07。

|
图 4 5种理论Q合成的非平稳地震数据 |
上述四种方法的Q值估计结果如图 5所示,为了更明显地展示不同方法的估计精度,在每列柱状图上显示了相应实验条件下的估计结果。与理论Q值(红色)相比,CFS(绿色)的估计结果偏大,这是因为CFS需要假设源子波的谱是高斯谱[9],而实验中采用的Ricker子波并不满足这一假设。LSR方法(紫色)由于没有假设地震子波,所以其估计精度高于CFS,但是低于CVG(黄色)和CVS(蓝色)。CVG方法和所提出的CVS方法都有较高的精度。具体来说,当Q=25和50时,CVG和CVS方法的估计结果比较接近;但当Q高于75时,CVS方法估计结果更接近理论Q值。

|
图 5 地震子波为Ricker时,CVS、CVG、CFS和LSR方法Q值估计结果 |
为了进一步对比本文所提的方法和CVG方法,本实验测试了Gabor变换中选取不同长度的窗函数对CVG方法所估计Q值的影响。仍对图 4中的合成地震数据进行分析,其中Gabor变换中高斯窗的长度twin分别设置为20、40、80、120ms。图 6显示Q=25、50、75、100和125时,采用不同窗长度的CVG方法和CVS方法的估计结果。显然,与各种窗长的CVG方法相比,所提出的CVS方法在所有情况下都更接近理论Q值。与CVS方法相比,CVG方法对窗函数的长度很敏感。在四种时窗中,twin为80ms的窗长是最合适的,其对应的CVG估计精度最高。twin为40ms时,CVG的估计精度略低于80ms的估值精度。选择twin为20ms和120ms的窗函数时,CVG方法的估计误差较大。这是因为twin为80ms的时间窗与完整的震源子波的持续时间接近,过长或过短的时间窗都会影响时频分辨率,从而影响Q估计的精度。因此,所提CVS方法的一个重要优势为S变换的窗函数和频率相关,无需设置窗函数的长度。
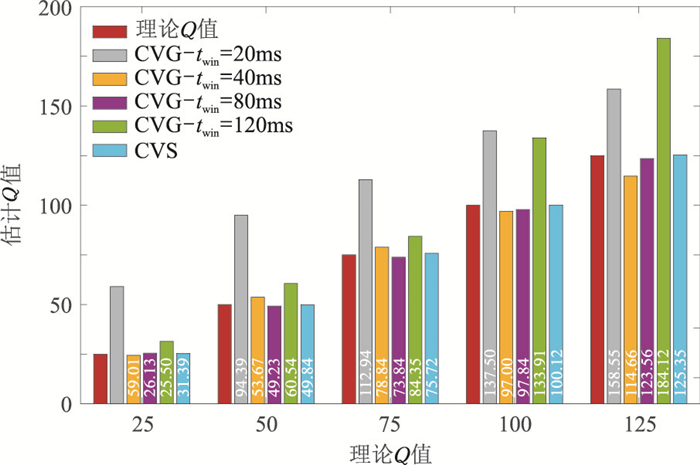
|
图 6 地震子波是Ricker时,四种窗函数长度的CVG和CVS的Q值估计结果 |
为了揭示四种Q值估计方法对地震子波类型的依赖性,实验选择不同类型的地震子波与图 2中的反射系数合成地震记录,包括Ricker子波、Gauss子波和广义地震子波(GSW)[19]。将这三个地震子波的主频均设置为30Hz。实验测试了三种子波类型下,CVS、CVG、CFS和LSR方法估计Q值的相对误差,结果如图 7所示。由图可见,CVG方法、CVS方法和LSR方法对子波的类型并不敏感,在三种子波情况下,LSR方法的估计结果在5%附近波动;而对于CVG和CVS方法,所有估计结果的相对误差均保持在5%以下。进一步比较这两种方法,所提出的CVS方法在大多数情况下具有更小的相对误差;对于CFS方法,该方法仅在Gauss子波中Q值估计的相对误差小于5%,在其他两种子波中Q值估计是不准确的。综上所述,无论地震子波的类型如何,所提CVS方法估计的Q值均与理论Q值最接近。
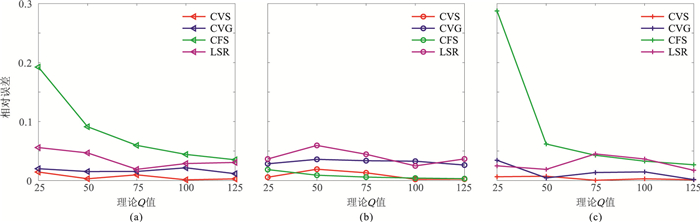
|
图 7 不同的地震子波,CVS、CVG、CFS和LSR方法Q值估计的相对误差 (a)Ricker子波;(b)Gauss子波;(c)GSW子波 |
为了更进一步研究CVS方法的抗噪性,本文估计了含噪情况下不同方法的Q值。含噪地震记录如图 8所示。由于加入了高斯白噪声,实验结果统计了重复估计100次Q值结果的平均值和标准差。模型数据理论Q值为40,地震子波采用Ricker子波,其他参数与上述实验相同。CVS、CVG、CFS和LSR方法对不同信噪比的含噪地震数据所估计Q值的统计结果如表 1所示。此外,通过CVS方法分别从信噪比为5、12和20dB的含噪地震数据中提取的Q值结果如图 9所示。可以看出,随着地震数据信噪比的增加,CVS方法计算结果均值的精度也在增加,且落在理论Q附近的估计值越来越多。由表 1可得,无论信噪比为5、12还是20dB,本文提出的CVS方法的估计结果均是最准确、稳定的,说明CVS能够通过自适应参数确定合理的积分区间,从而一定程度上抑制噪声,提高该方法抗噪能力,最终估计出稳定的Q值。
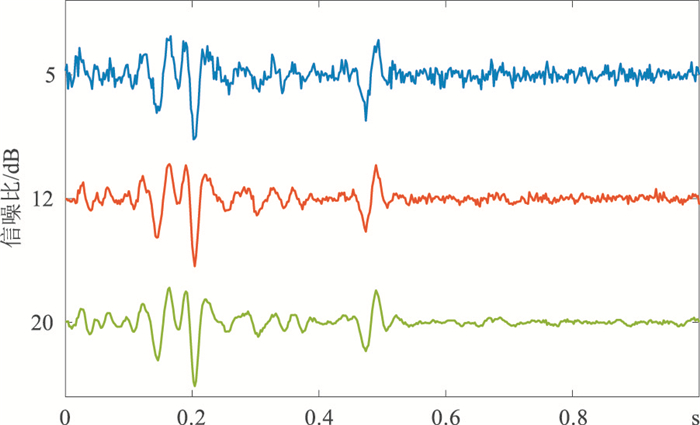
|
图 8 不同信噪比的含噪地震数据 |
|
|
表 1 不同信噪比下CVS、CVG、CFS和LSR的Q值估计统计结果(理论Q为40) |

|
图 9 不同信噪比的含噪地震数据CVS方法估计结果 (a)5dB;(b)12dB;(c)20dB |
将CVS、CFS和CVG方法应用于实际地震资料。图 10是来自中国某油田的叠后地震剖面,有2口井位于地震剖面。井1在目标层(1.3~1.4s)钻遇气砂岩,获得12.9815m3/d的工业气流。井2的储层不发育,证实为干井。
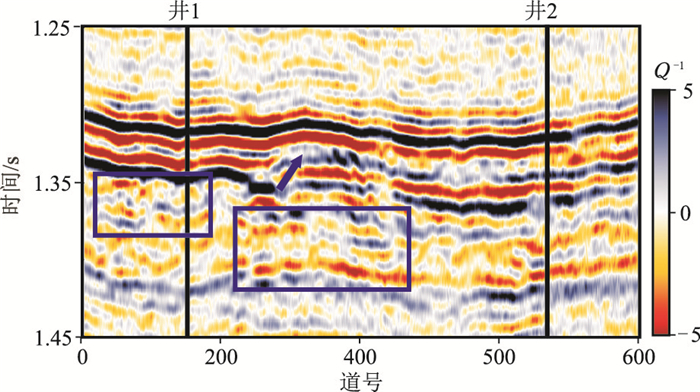
|
图 10 某油田叠后地震剖面 |
根据本文CVS方法,选择目标层附近(1.25~1.45s)的地震数据进行Q值估计。考虑实际资料的Q一般不是常Q,因此需要利用滑动窗多次计算Q值。针对实际数据,将非平稳的地震数据进行划分[20],然后在每段内计算层间Q。对于局部时窗内的地震数据,时频振幅谱的形状与较大幅值系数主要由时变子波确定[20],因此在式(8)中忽略反射系数序列的时频谱是成立的。实际地震资料受多种因素的影响,会出现异常的Q值结果。剔除异常结果后,采用样条拟合方法拟合各地震道的Q值,最终显示等效吸收剖面(Q-1),如图 11所示。从图 11可以清楚地看出,CVS、CFS和CVG方法的估计结果在总体趋势上是一致的。在井1位置,CVS方法估计的Q值最小;在井2位置,CVS方法估计的Q值最大。总体而言,相比于另外两种方法,CVS方法具有更好的有效性、地震子波适应性和稳定性。
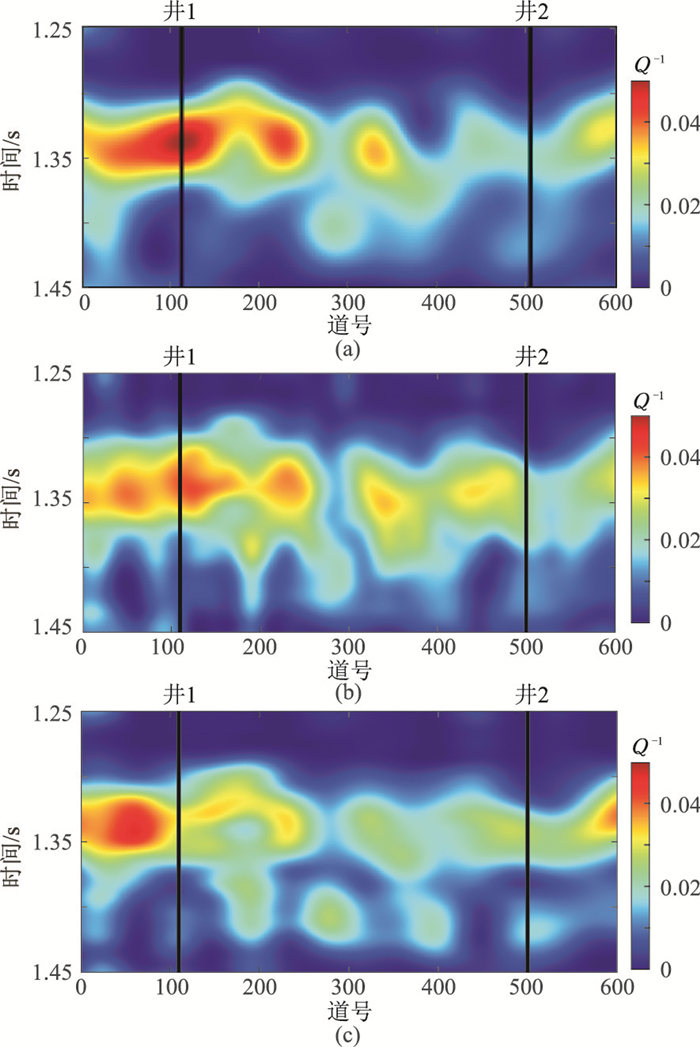
|
图 11 实际资料目标层附近的等效吸收(Q-1)剖面 (a)CVS方法;(b)CFS方法;(c)CVG方法 |
进一步利用CVS计算的Q值对实际资料进行反Q滤波[6],补偿后的结果如图 12所示。与图 10相比,蓝色矩形和箭头指示处的结果表明原始剖面经反Q滤波后,同相轴变地更细且更加连续,地震资料的分辨率得到提高。因此,实际资料验证了CVS方法能够估计有效的Q值,并且为后续反Q滤波提高地震资料的分辨率奠定了坚实的基础。
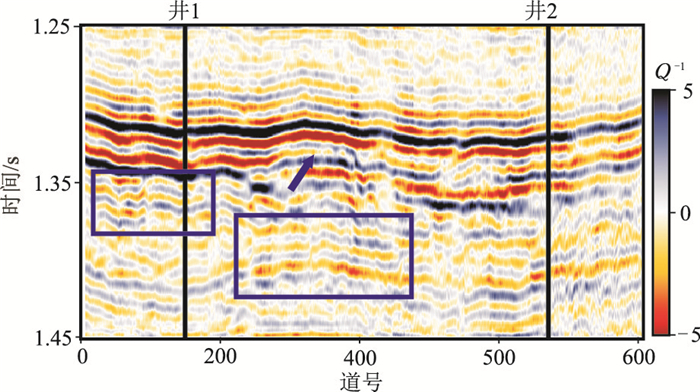
|
图 12 利用CVS方法得到的Q值对实际资料反Q滤波处理后的结果 |
本文提出了一种新的基于S变换和变分法的Q值估计方法(CVS方法)。模型数据和实际数据的计算结果表明,应用CVS方法能够从叠后反射地震数据中有效提取品质因子Q,实现储层识别和非平稳地震资料的衰减补偿。具体结论如下。
(1) 与CVG方法对比,将Gabor变换改为S变换,可以克服CVG方法对窗函数长度比较敏感的缺点。此外,利用S变换的多尺度分辨率的特点,可以更加精细地刻画地震数据的非平稳性,从而获得更准确的Q值。
(2) 与CVG方法和LSR方法对比,本文提出的CVS方法能够根据时频谱的能量自适应地选择合适的积分区间,具有更好的抗噪性能。
(3) 与传统的CFS方法对比,本文提出的方法不需要假设地震子波的类型,具有更好的子波适应性,并且在未知准确地震子波情况下,提供了准确估计Q值的理论基础。
| [1] |
RICKER N. The form and laws of propagation of seismic wavelets[J]. Geophysics, 1953, 18(1): 10-40. DOI:10.1190/1.1437843 |
| [2] |
马昭君, 刘洋. 地震波衰减反演研究综述[J]. 地球物理学进展, 2005, 20(4): 1074-1081. MA Zhaojun, LIU Yang. A summary of research on seismic attenuation[J]. Progress in Geophysics, 2005, 20(4): 1074-1081. DOI:10.3969/j.issn.1004-2903.2005.04.031 |
| [3] |
苑书金, 董宁, 于常青. 地震波衰减技术在鄂尔多斯盆地储层预测中的应用[J]. 石油物探, 2006, 45(2): 182-185. YUAN Shujin, DONG Ning, YU Changqing. Application of seismic wave attenuation technology in reservoir prediction in Ordos Basin[J]. Geophysical Prospecting for Petroleum, 2006, 45(2): 182-185. DOI:10.3969/j.issn.1000-1441.2006.02.012 |
| [4] |
苏勤, 曾华会, 田彦灿, 等. 表层Q值确定性求取与空变补偿方法[J]. 石油地球物理勘探, 2019, 54(5): 988-996. SU Qin, ZENG Huahui, TIAN Yancan, et al. Near-surface Q value estimation and quantitative amplitude compensation[J]. Oil Geophysical Prospecting, 2019, 54(5): 988-996. |
| [5] |
WANG Y H. A stable and efficient approach to inverse Q filtering[J]. Geophysics, 2002, 67(2): 657-663. DOI:10.1190/1.1468627 |
| [6] |
YANG Y, GAO J H, ZHANG G W, et al. An efficient attenuation correction method using the synchrosqueezing transform[C]. SEG Technical Program Expanded Abstracts, 2017, 3376-3380.
|
| [7] |
赵秋芳, 云美厚, 朱丽波, 等. 近地表Q值测试方法研究进展与展望[J]. 石油地球物理勘探, 2019, 54(6): 1397-1418. ZHAO Qiufang, YUN Meihou, ZHU Libo, et al. Progress and outlook of near-surface quality factor Q measurement and inversion[J]. Oil Geophysical Prospecting, 2019, 54(6): 1397-1418. |
| [8] |
LUO C, HUANG G T, LI X Y, et al. Q estimation by combining ISD with LSR method based on shaping-regularized inversion[J]. IEEE Geoscience and Remote Sensing Letters, 2019, 16(9): 1457-1461. DOI:10.1109/LGRS.2019.2900732 |
| [9] |
QUAN Y, HARRIS J M. Seismic attenuation tomography using the frequency shift method[J]. Geophysics, 1997, 62(3): 895-905. DOI:10.1190/1.1444197 |
| [10] |
高静怀, 杨森林, 王大兴. 利用VSP资料直达波的包络峰值处瞬时频率提取介质品质因子[J]. 地球物理学报, 2008, 51(3): 853-861. GAO Jinghuai, YANG Senlin, WANG Daxing. Quality factor extraction using instantaneous frequency at envelope peak of direct waves of VSP data[J]. Chinese Journal of Geophysics, 2008, 51(3): 853-861. DOI:10.3321/j.issn:0001-5733.2008.03.026 |
| [11] |
GROSSMAN J P, MARGRAVE G F, LAMOUREUX M P, et al. A robust algorithm for constant-Q wavelet estimation using Gabor analysis[C]. SEG Technical Program Expanded Abstracts, 2002, 21: 2210-2213.
|
| [12] |
STOCKWELL R G, MANSINHA L, LOWE R P. Localization of the complex spectrum: The S transform[J]. IEEE Transactions on Signal Processing, 1996, 44(4): 998-1001. DOI:10.1109/78.492555 |
| [13] |
高静怀, 张兵. 基于时频滤波的吸收衰减参数估算[J]. 石油地球物理勘探, 2012, 47(6): 931-936. GAO Jinghuai, ZHANG Bing. Seismic attenuation parameter estimation based on the time-frequency filtering[J]. Oil Geophysical Prospecting, 2012, 47(6): 931-936. |
| [14] |
MARGRAVE G F, LAMOUREUX M P, HENLEY D C. Gabor deconvolution: Estimating reflectivity by nonstationary deconvolution of seismic data[J]. Geophysics, 2011, 76(3): W15-W30. DOI:10.1190/1.3560167 |
| [15] |
KOLSKY H. The propagation of stress pulses in visco-elastic solids[J]. Philosophical Magazine, 1956, 1(8): 693-710. DOI:10.1080/14786435608238144 |
| [16] |
FUTTERMAN W. Dispersive body waves[J]. Journal of Geophysical Research, 1962, 67(4): 5279-5291. |
| [17] |
DONOHO D L. Ideal spatial adaptation by wavelet shrinkage[J]. Biometrika, 1994, 81(3): 425-455. DOI:10.1093/biomet/81.3.425 |
| [18] |
夏洪瑞, 葛川庆, 彭涛. 小波时空变阈值去噪方法在可控震源资料处理中的应用[J]. 石油地球物理勘探, 2010, 45(1): 23-27. XIA Hongrui, GE Chuanqing, PENG Tao. Application of wavelet time-space-varying threshold denoising method in vibroseis seismic data processing[J]. Oil Geophysical Prospecting, 2010, 45(1): 23-27. |
| [19] |
WANG Y H. Generalized seismic wavelets[J]. Geo-physical Journal International, 2015, 203(2): 1172-1178. DOI:10.1093/gji/ggv346 |
| [20] |
WANG L L, GAO J H, ZHANG W, et al. Enhancing resolution of nonstationary seismic data by molecular-Gabor transform[J]. Geophysics, 2013, 78(1): V31-V41. DOI:10.1190/geo2011-0450.1 |



 高静怀, 陕西省西安市咸宁西路28号西安交通大学信息与通信工程学院, 710049。Email:
高静怀, 陕西省西安市咸宁西路28号西安交通大学信息与通信工程学院, 710049。Email: 