② 油气资源与探测国家重点实验室, 北京 102249
② State Key Laboratory of Petroleum Resources and Prospecting, Beijing 102249, China
地震数据在采集过程中由于受到周围环境、采集设备和方法、人为因素等影响,常伴随噪声。地震数据中的噪声可分为随机噪声和相干噪声[1]。相干噪声具有一定的主频和视速度,如面波、多次波等。随机噪声没有固定的频率和传播方向。
噪声压制是地震数据处理中的一个经典问题,噪声压制效果影响数据处理和解释效果。针对地震数据噪声压制,人们提出了多种行之有效的方法。如:基于自回归技术的f-x域反褶积方法[2];基于变换和阈值的去噪方法,利用有效信号和噪声在变换域的特征差异压制噪声,包括傅里叶变换[3]、小波变换[4]、曲波变换[5]、Seislet变换[6-8]等。有人提出了数据驱动的模态分解方法,将地震信号分解为一系列模态函数,噪声通常分布在高频,通过压制高频噪声去噪,如经验模态分解[9-11]、变分模态分解[12-13]等。此外,还有基于矩阵低秩表示的去噪方法,假设构造低秩矩阵可表示无噪数据,通过选取合适的秩重构信号压制噪声,如基于奇异值分解[14-15]和过完备字典信号稀疏表示(K-SVD)核函数的方法[16]。
虽然常规去噪方法众多,但每种方法都受某种假设或条件的限制。如:基于阈值的去噪方法需要人为多次调试选取阈值;基于模态分解的方法需要根据输入信号的分解特征选取模态函数的数量;变分模态分解需要求解一系列优化问题分解信号,其中需要人为设定一系列参数。另外,上述方法中一些优化问题具有多个局部极值,导致算法可能收敛到局部最优解而非全局最优解。因此,寻找具有鲁棒性的地震数据去噪方法一直是人们关心的问题。
近年来,伴随着图形处理器(GPU)技术、云计算和人工智能的发展,深度卷积神经网络蓬勃发展。如在图像识别和分类领域相继出现了亚历克斯网络(AlexNet)、几何视觉小组网络(VGGNet)、谷歌网络(GoogleNet)、残差网络(ResNet)和U型网络(U-Net)等较典型的卷积网络模型[17]。在图像去噪领域人们提出了基于ResNet模型的降噪卷积神经网络(Denoising Convolutional Neural Network,DnCNN)方法[18]、基于自编码器(AutoEncoder)的深度卷积神经网络[19]和基于U-Net的卷积神经网络等方法[20]。与传统方法相比,基于深度学习的去噪方法是数据驱动的,无需人为设置参数。该类方法通过训练集训练自适应性的更新网络的权重与偏执,从数据集中提取有效信号的特征,或者学习信号中噪声的特征,具有较好的泛化能力[21-26]。近年来,人们将深度学习和常规去噪方法结合,取得了不错的去噪效果[27-30]。
通过总结前人去噪方法的特点,本文提出了一种基于平稳小波变换与深度ResNet的地震随机噪声压制方法,采用ResNet拓扑结构,结合平稳小波变换压制地震数据噪声。残差模块有效避免了网络过深引起的梯度消失或计算消耗但损失函数趋于饱和的问题。另外,小波变换是一种高效的特征提取方法,能够获得信号低频和不同方向高频特征信息,分区域学习信号或噪声的特征。传统离散小波变换具有平移不变性,阈值去噪方法具有一定的局限性,在非连续点易产生Gibbs振荡现象。平稳小波变换[31]是一种非抽样的小波变换,通过“隔点补零”操作,使每一层分解的近似系数和细节系数与原始信号长度相同。在信号重构时无需上采样操作,可有效避免由于下采样造成的Gibbs振荡现象,弥补了离散小波变换的不足。在训练数据集方面,本文利用了DnCNN算法中的Train400数据集[32]。所提方法的去噪思路为:
首先,对Train400数据集旋转不同角度以增加训练集数据量,经过旋转变换后再加入高斯噪声。
然后,对训练集中的每幅图片进行1级平稳Haar小波分解,得到训练数据集。训练数据集的标签为无噪图片旋转不同角度后的1级Haar平稳小波分解。另外,为了避免梯度消失,在每一个模块中采用批量归一化。所提方法通过训练提取信号中噪声的小波变换高、低频信息,在此基础上通过直连通道,从含噪数据的小波分解中减去学习到的噪声的小波分解,得到去噪信号的小波分解。
最后,通过逆平稳小波变换得到去噪信号。
模拟数据和实际地震数据去噪试验表明,所提方法有效压制了地震随机噪声,获得的去噪数据的信噪比高于传统方法。不足之处在于,该方法需要构造训练集进行训练,如果训练集过大会导致训练过程较费时。
1 相关理论首先介绍平稳小波变换和ResNet的基本原理,在此基础上,提出了基于平稳小波变换与深度ResNet的随机噪声压制方法。
1.1 平稳小波变换小波变换被称为信号处理领域的“显微镜”,能够在不同尺度下观察、分析信号。小波变换可以捕捉信号的低频信息和不同方向的高频信息。离散小波变换是对基小波的尺度和平移离散化,具有平移不变性,但在不连续点由于下采样易产生Gibbs振荡现象。平稳小波变换采用“隔点补零”方法,使每一层分解的近似系数和细节系数的长度与原信号相同,可有效避免下采样产生的Gibbs振荡现象。图 1、图 2分别为含噪模型数据的1级离散(DWT)、1级平稳Haar小波分解(SWT),可见后者的4个分解特征的连续性好于前者。

|
图 1 含噪模型数据(左)的1级离散Haar小波分解(右) L为低频分量; H为水平高频分量;V为垂直高频分量;D为对角高频分量。图 2同 |

|
图 2 含噪模型数据(左)的1级平稳Haar小波分解(右) |
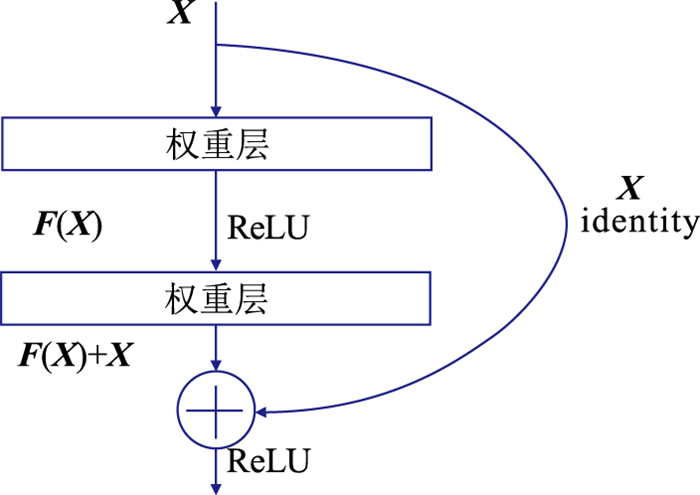
人们普遍认为深度神经网络随着网络深度加大而应该具有更强的表达能力,如从7层的AlexNet到19层的VGGNet。然而实际情况是,当网络达到一定深度后,若一味增加网络层数(或者简单地堆叠网络)不一定能提高精度,反而使算法收敛得更慢。基于此,人们提出了残差学习。原来的网络是通过训练集训练,使网络学习输入X到输出H(X)的映射表示。然而,随着网络深度增大,不容易使损失函数快速下降。残差学习通过在网络中增加快捷恒等映射(图 3),模块学习输入和输出的差(故名为残差)。残差学习使损失函数具有较快的收敛速度。另外,在网络中加入批量归一化模块可以克服梯度消失与梯度爆炸的问题。
|
图 3 ResNet示意图 X为网络输入,通过加入恒等映射(identity),网络学习输入和输出的残差F(X) |
基于残差学习发展的DnCNN方法,在网络结构中加入直连恒等映射,使网络学习信号的噪声,收敛速度较快。DnCNN结构(图 4)主要包括卷积加激活层(Conv+ReLU)、多个卷积与批量归一化加激活函数模块(Conv+BN+ReLU)、卷积层(Conv),批量归一化能够避免梯度消失问题,具有较快的收敛速度。

|
图 4 DnCNN结构 输入为含噪声图片;网络包含三个模块:①卷积加激活函数(Conv+ReLU),卷积核尺寸一般为3×3或者5×5,去掉了池化层;②卷积、批量归一化加激活函数(Conv+BN+ReLU);③卷积层(Conv)。输出为图片的噪声 |
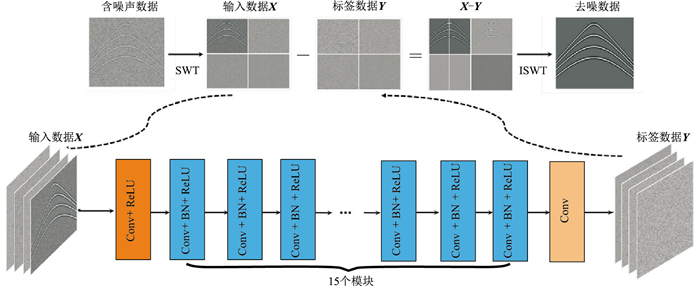
基于平稳小波变换与深度ResNet的随机噪声压制方法的网络结构与DnCNN相同(图 5)。在输入和输出之间添加恒等映射直连通道,使模型学习噪声。模型参数共560705个,可训练参数为558785个。算法的训练数据集为DnCNN模型中的Train400数据集(图 6)。
|
图 5 小波变换与深度ResNet结构 对含噪数据进行1级平稳Haar小波变换,得到高、低频信息作为ResNet的输入。网络包含三个模块:①卷积加激活函数(Conv+ReLU),卷积核尺寸为3×3,卷积层厚度为64,激活函数为ReLU;②15个卷积、批量归一化加激活函数(Conv+BN+ReLU),每一个卷积核的尺寸为3×3,卷积层厚度为64,激活函数为ReLU;③卷积层(Conv),厚度为4,卷积核尺寸为3×3。输出为噪声的1级Haar小波变换的四个分量。用输入减去输出得到去噪信号的1级Haar平稳小波变换的四个分量,最后通过逆平稳小波变换(ISWT)得到去噪信号 |

|
图 6 DnCNN模型中Train400部分训练数据集快照 每幅图片为尺寸为180×180的灰度图,共400张 |
首先对该数据集中的每幅图片进行不同角度的旋转变换,之后分割为40×40的图片库。
然后加入标准方差σ为0.15的高斯随机噪声,对含噪数据进行1级Haar平稳小波变换得到每幅图片的4个分量(低频、水平高频、垂直高频、对角高频),并得到90000张图片形成的训练集。将不含噪图片旋转、分割为40×40图片的1级平稳Haar小波分解作为标签。通过加入直连通道,使网络学习噪声的平稳小波变换信息。用含噪信号的小波变换信息减去噪声的小波分解信息,得到去噪信号的1级平稳小波变换的4个分量。
最后通过逆小波变换得到去噪信号。
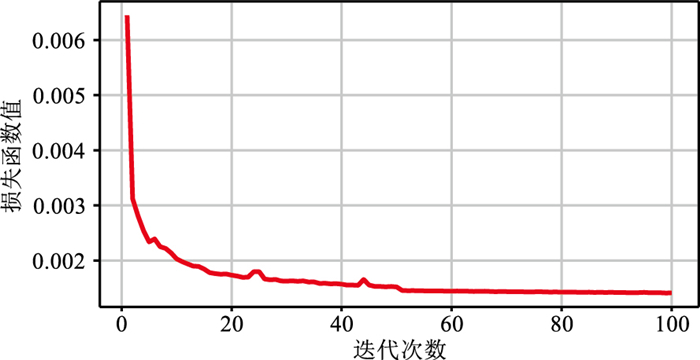
在训练过程中,采用批量梯度下降法,训练集被分割为大小为128的小块(patch size=128),优化算法采用亚当(Adam)方法,学习速率为0.002。为了加快算法的速度,将数据存储为python中的npy格式。本文所提模型的损失函数为均方误差函数
| $ L=\sum\limits_{j=1}^{4}\left\|\boldsymbol{W}_{j}(\widetilde{\boldsymbol{X}})-\boldsymbol{W}_{j}(\boldsymbol{X})\right\|_{2}^{2} $ | (1) |
式中:Wj(j=1, 2, 3, 4)表示信号的Haar小波分解的4个分量;
|
图 7 模型损失函数随迭代次数的变化 |
通常由人为观测法和数学指标定量对比法衡量去噪效果。峰值信噪比为常用的数学指标,其表达式为
| $ \mathrm{PSNR}=10 \lg \frac{\mathrm{MAX}_{\mathrm{I}}^{2}}{\mathrm{MSE}} $ | (2) |
这里MSE表示均方误差,其表达式为
| $ \mathrm{MSE}=\frac{1}{m n} \sum\limits_{p, q=0}^{m-1, n-1}[I(p, q)-K(p, q)]^{2} $ | (3) |
式中:I、K分别为不含噪信号和去噪信号;MAXI为输入像素点的最大分量;m、n分别为像素点的最大行、列数。除了PSNR外,信噪比(SNR)也是定量分析信号去噪效果的一个指标,其表达式为
| $ \mathrm{SNR}=10 \lg \frac{A_{\mathrm{s}}^{2}}{A_{\mathrm{n}}^{2}} $ | (4) |
式中:As为信号能量;An为噪声能量。
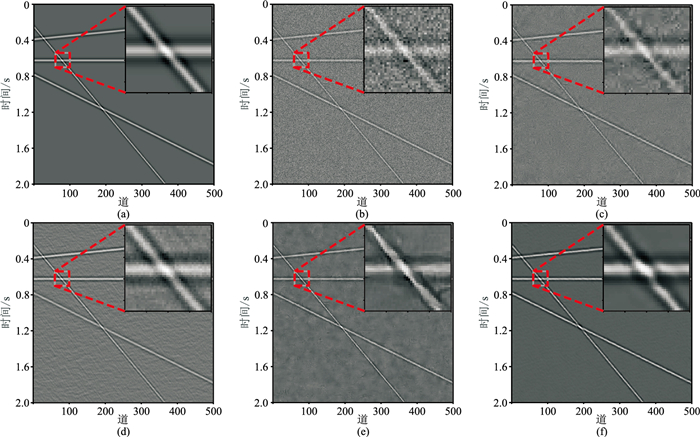
2 数值试验 2.1 模拟数据图 8为含有4个不同斜率的线性同相轴的模拟数据去噪效果对比。由图可见:f-x域反褶积法(图 8d)的去噪效果好于小波阈值法(图 8c),但均不如DnCNN法(图 8e);本文方法的去噪效果最好,去噪结果(图 8f)与不含噪数据(图 8a)几乎相同(放大区域)。
|
图 8 含有4个不同斜率的线性同相轴的模拟数据去噪效果对比
(a)不含噪数据;(b)含噪数据(σ=0.15);(c)小波阈值法;(d)f-x域反褶积法;(e)DnCNN法;(f)本文方法 红色方框区域被放大显示于右上角,图 9、图 10同 |
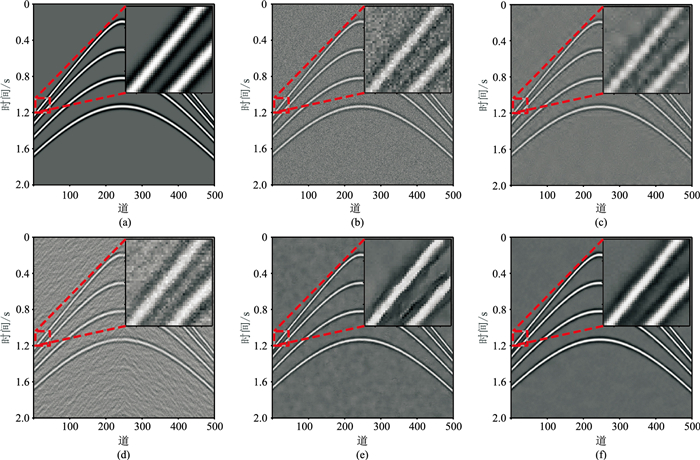
图 9为含有4个不同抛物线形状同相轴的模拟数据去噪效果对比。由图可见:小波阈值法(图 9c)的去噪效果优于f-x域反褶积法(图 9d),这是由f-x域反褶积法的特点决定的,但这两种方法的去噪效果均不如DnCNN法(图 9e);本文方法(图 9f)的去噪效果很好(放大区域)。
|
图 9 含有4个不同抛物线形状同相轴的模拟数据去噪效果对比 (a)不含噪数据;(b)含噪数据(σ=0.15);(c)小波阈值法;(d)f-x域反褶积法;(e)DnCNN法;(f)本文方法 |
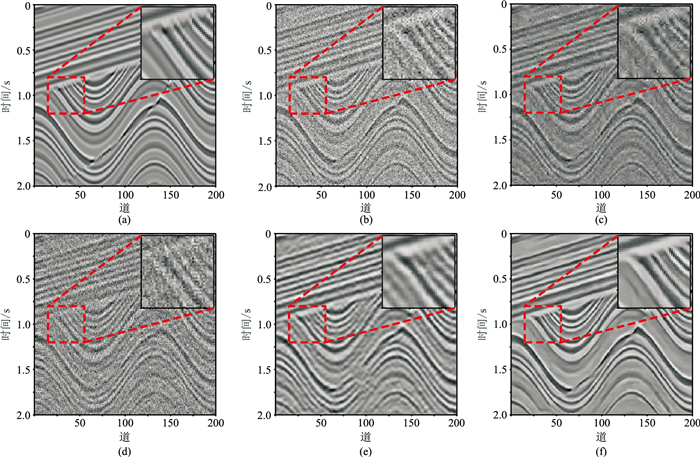
图 10为复杂模拟数据去噪效果对比。由图可见,本文方法(图 10e)的去噪效果最好,小波阈值法(图 10c)的去噪效果优于f-x域反褶积法(图 10d),但不如DnCNN法(图 10e)。
|
图 10 复杂模拟数据去噪效果对比 (a)不含噪数据;(b)含噪数据(σ=0.15);(c)小波阈值法;(d)f-x域反褶积法;(e)DnCNN法;(f)本文方法 |
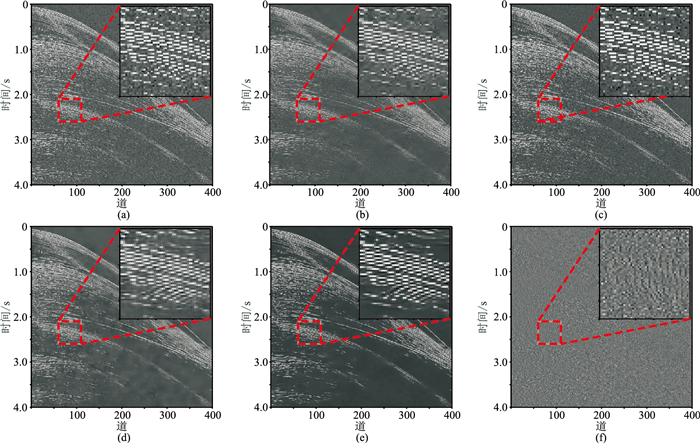
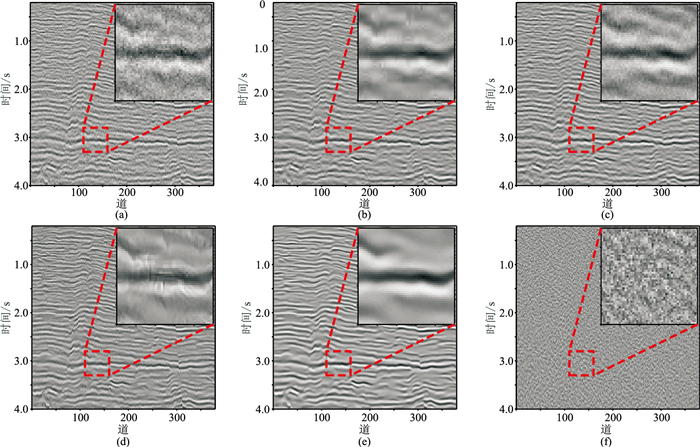
调用前期训练好的模型对实际地震数据去噪。图 11为海上叠前地震数据去噪效果对比。由图可见,小波阈值法(图 11b)和f-x域反褶积法(图 11c)的去噪效果不明显,DnCNN法(图 11d)的去噪效果较好,但不如本文方法(图 11e、图 11f)突出。图 12为实际叠后地震数据去噪效果对比。由图可见:小波阈值法(图 12b)和DnCNN法(图 12d)的去噪效果好于f-x域反褶积法(图 12c);本文方法(图 12e、图 12f)的去噪效果最好,在约3s处的同相轴更清楚。表 1、表 2分别为模拟数据和实际地震数据的PSNR、SNR,可见本文方法去噪结果的PSNR、SNR均较高。
|
图 11 海上叠前地震数据去噪效果对比
(a)海上叠前地震数据;(b)小波阈值法;(c)f-x域反褶积法;(d)DnCNN法;(e)本文方法;(f)本文方法滤除的噪声 红色方框区域被放大显示于右上角,图 12同 |
|
图 12 实际叠后地震数据去噪效果对比 (a)实际叠后地震数据;(b)小波阈值法;(c)f-x域反褶积法;(d)DnCNN法;(e)本文方法;(f)本文方法滤除的噪声 |
|
|
表 1 模拟数据和实际地震数据的PSNR |
|
|
表 2 模拟数据和实际地震数据的SNR |
本文提出的去噪方法结合了平稳小波变换和残差网络的优点,通过平稳小波变换分频带提取信号的噪声,实现多渠道联合去噪。残差网络通过学习噪声,克服了网络过深导致的网络学习效率退化现象,能够有效捕捉噪声。与传统去噪方法相比,本文方法具有较好的泛化能力。本文方法的不足之处在于需要构造大数据集进行训练,训练过程较耗时。另外,设计合理的网络拓扑结构以更好地去噪,以及如何构造地震数据训练集(目前基于深度学习的地震数据去噪方法的训练集一般采用自然图像)是今后的研究方向。
| [1] |
张军华, 吕宁, 田连玉, 等. 地震资料去噪方法综合评述[J]. 石油地球物理勘探, 2005, 40(增刊1): 121-127. |
| [2] |
康冶, 于承业, 贾卧, 等. f-x域去噪方法研究[J]. 石油地球物理勘探, 2003, 38(2): 136-138. KANG Ye, YU Chengye, JIA Wo, et al. A study on noise-suppression method in f-x domain[J]. Oil Geophysical Prospecting, 2003, 38(2): 136-138. DOI:10.3321/j.issn:1000-7210.2003.02.007 |
| [3] |
孔庆丰, 李心友. 傅立叶相关系数滤波的实践[J]. 石油物探, 2001, 40(4): 89-93. KONG Qingfeng, LI Xinyou. An application of Fourier correlation coefficient filtering[J]. Geophysical Prospecting for Petroleum, 2001, 40(4): 89-93. DOI:10.3969/j.issn.1000-1441.2001.04.014 |
| [4] |
蔡剑华, 熊锐. 基于频率切片小波变换的时频分析与MT信号去噪[J]. 石油物探, 2016, 55(6): 904-912. CAI Jianhua, XIONG Rui. Magnetotelluric data denosing based on time-frequency analysis of the frequency slice wavelet transform[J]. Geophysical Prospecting for Petroleum, 2016, 55(6): 904-912. DOI:10.3969/j.issn.1000-1441.2016.06.016 |
| [5] |
曹静杰, 杨志权, 杨勇, 等. 一种基于曲波变换的自适应地震随机噪声消除方法[J]. 石油物探, 2018, 57(1): 72-78. CAO Jingjie, YANG Zhiquan, YANG Yong, et al. An adaptive seismic random noise elimination method based on Curvelet transform[J]. Geophysical Prospecting for Petroleum, 2018, 57(1): 72-78. DOI:10.3969/j.issn.1000-1441.2018.01.010 |
| [6] |
张之涵, 孙成禹, 姚永强, 等. 三维曲波变换在地震资料去噪处理中的应用研究[J]. 石油物探, 2014, 53(4): 421-430. ZHANG Zhihan, SUN Chengyu, YAO Yongqiang, et al. Research on the application of 3D Curvelet transform to seismic data denoising[J]. Geophysical Prospecting for Petroleum, 2014, 53(4): 421-430. DOI:10.3969/j.issn.1000-1441.2014.04.007 |
| [7] |
张入化, 黄建平, 国运东, 等. 基于Seislet域分数阶阈值去噪算法的地震资料去噪[J]. 石油物探, 2020, 59(1): 40-50. ZHANG Ruhua, HUANG Jianping, GUO Yundong, et al. Fractional threshold denoising algorithm in Seislet domain for seismic data denoising[J]. Geophysical Prospecting for Petroleum, 2020, 59(1): 40-50. DOI:10.3969/j.issn.1000-1441.2020.01.005 |
| [8] |
FOMEL S and LIU Y. Seislet transform and seislet frame[J]. Geophysics, 2010, 75(3): V25-V38. DOI:10.1190/1.3380591 |
| [9] |
尚平萍, 李鹏, 杨安琪, 等. 基于CEEMDAN的地震信号高分辨率时频分析方法[J]. 石油物探, 2019, 58(4): 547-554. SHANG Pingping, LI Peng, YANG Anqi, et al. Seismic high-resolution time-frequency analysis based on CEEMDAN[J]. Geophysical Prospecting for Petroleum, 2019, 58(4): 547-554. DOI:10.3969/j.issn.1000-1441.2019.04.009 |
| [10] |
HUANG N E, SHEN Z, LONG S R, et al. The empi-rical mode decomposition and the Hilbert spectrum for nonlinear non-stationary time series analysis[J]. Proceeding of the Royal Society of A: Mathematical, Physical and Engineering Sciences, 1998, 454(1971): 903-995. DOI:10.1098/rspa.1998.0193 |
| [11] |
乐友喜, 杨涛, 曾贤德. CEEMD与KSVD字典训练相结合的去噪方法[J]. 石油地球物理勘探, 2019, 54(4): 729-736. YUE Youxi, YANG Tao, ZENG Xiande. Seismic denoising with CEEMD and KSVD dictionary combined training[J]. Oil Geophysical Prospecting, 2019, 54(4): 729-736. |
| [12] |
DRAGOMIRETSKIY K, ZOSSO D. Variational mode decomposition[J]. IEEE Transactions on Signal Processing, 2014, 62(3): 531-544. DOI:10.1109/TSP.2013.2288675 |
| [13] |
方江雄, 温志平, 顾华奇, 等. 基于变分模态分解的地震随机噪声压制方法[J]. 石油地球物理勘探, 2019, 54(4): 757-767. FANG Jiangxiong, WEN Zhiping, GU Huaqi, et al. Seismic random noise attenuation based on variational mode decomposition[J]. Oil Geophysical Prospecting, 2019, 54(4): 757-767. |
| [14] |
李江. 基于奇异值分解的角度域去噪方法[J]. 石油物探, 2019, 58(3): 427-432. LI Jiang. Seismic denoising in the angle domain based on singular value decomposition[J]. Geophysical Prospecting for Petroleum, 2019, 58(3): 427-432. DOI:10.3969/j.issn.1000-1441.2019.03.012 |
| [15] |
胡永泉, 黄建波, 田志华, 等. 基于单道SVD和振幅比的地面微地震资料去噪方法[J]. 石油物探, 2019, 58(1): 43-52. HU Yongquan, HUANG Jianbo, TIAN Zhihua, et al. Ground microseismic data denoising based on single-channel singular value decomposition and amplitude ratio[J]. Geophysical Prospecting for Petroleum, 2019, 58(1): 43-52. DOI:10.3969/j.issn.1000-1441.2019.01.006 |
| [16] |
毛海波, 马俊彦, 王晓涛, 等. 基于自适应字典学习的可控震源数据谐波噪声压制方法[J]. 石油物探, 2020, 59(5): 725-735. MAO Haibo, MA Junyan, WANG Xiaotao, et al. Harmonic noise suppression of vibroseis data based on adaptive dictionary learning[J]. Geophysical Prospecting for Petroleum, 2020, 59(5): 725-735. DOI:10.3969/j.issn.1000-1441.2020.05.006 |
| [17] |
HE K M, ZHANG X Y, REN S Q, et al. Deep residual learning for image recognition[C]. 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2016, doi: 10.1109/CVPR.2016.90.
|
| [18] |
ZHANG K, ZUO W M, CHEN Y J, et al. Beyond a Gaussian denoiser: residual learning of deep CNN for image denoising[J]. IEEE Transactions on Image Processing, 2017, 26(7): 3142-3155. DOI:10.1109/TIP.2017.2662206 |
| [19] |
SAAD O M, CHEN Y K. Deep denoising autoencoder for seismic random noise attenuation[J]. Geophysics, 2020, 85(4): V367-V376. DOI:10.1190/geo2019-0468.1 |
| [20] |
韩卫雪, 周亚同, 池越. 基于深度学习卷积神经网络的地震数据随机噪声去除[J]. 石油物探, 2018, 57(6): 862-869. HAN Weixue, ZHOU Yatong, CHI Yue. Deep learning convolutional neural networks for random noise attenuation in seismic data[J]. Geophysical Prospecting for Petroleum, 2018, 57(6): 862-869. DOI:10.3969/j.issn.1000-1441.2018.06.008 |
| [21] |
罗仁泽, 李阳阳. 一种基于RUnet卷积神经网络的地震资料随机噪声压制方法[J]. 石油物探, 2020, 59(1): 51-59. LUO Renze, LI Yangyang. Random seismic noise attenuation based on RUnet convolutional neural network[J]. Geophysical Prospecting for Petroleum, 2020, 59(1): 51-59. DOI:10.3969/j.issn.1000-1441.2020.01.006 |
| [22] |
YU S W, MA J W, and WANG W L. Deep learning for denoising[J]. Geophysics, 2019, 84(6): V333-V350. DOI:10.1190/geo2018-0668.1 |
| [23] |
ZHOU Y Y and WU G N. Unsupervised machine lear-ning for waveform extraction in microseismic denoising[J]. Journal of Applied Geophysics, 2020. DOI:10.1016/j.jappgeo.2019.103879 |
| [24] |
张岩, 李新月, 王斌, 等. 基于联合深度学习的地震数据随机噪声压制[J]. 石油地球物理勘探, 2021, 56(1): 9-25, 56. ZHANG Yan, LI Xinyue, WANG Bin, et al. Random noise suppression of seismic data based on joint deep learning[J]. Oil Geophysical Prospecting, 2021, 56(1): 9-25, 56. |
| [25] |
唐杰, 孟涛, 张文征, 等. 利用基于深度学习的过完备字典信号稀疏表示算法压制地震随机噪声[J]. 石油地球物理勘探, 2020, 55(6): 1202-1209. TANG Jie, MENG Tao, ZHANG Wenzheng, et al. Suppressing seismic random noise based on Deep-KSVD[J]. Oil Geophysical Prospecting, 2020, 55(6): 1202-1209. |
| [26] |
李海山, 陈德武, 吴杰, 等. 叠前随机噪声深度残差网络压制方法[J]. 石油地球物理勘探, 2020, 55(3): 493-503. LI Haishan, CHEN Dewu, WU Jie, et al. Pre-stack random noise suppression with deep residual network[J]. Oil Geophysical Prospecting, 2020, 55(3): 493-503. |
| [27] |
KANG E, MIN J H, YE J C. Wavelet domain residual network(WaveResNet) for low-dose X-ray CT reconstruction[EB/OL]. [2018-03-28]. https://arxiv.org/abs/1707.09938v2.
|
| [28] |
GU J and YE J C. Multi-scale wavelet domain residual learning for limited-angle CT reconstruction[EB/OL]. [2017-03-04]. https://arxiv.org/abs/1703.01382v1.
|
| [29] |
ZHANG F, XU Z C, CHEN W, et al. An image compression method for video surveillance system in underground mines based on residual networks and discrete wavelet transform[J]. Electronics, 2019. DOI:10.3390/electronics8121559 |
| [30] |
LIU Pengju, ZHANG H Z, ZHANG K, et al. Multi-level wavelet-CNN for image restoration[C]. 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops(CVPRW), 2018, doi: 10.1109/CVPRW.2018.00121.
|
| [31] |
FOWLER J E. The redundant discrete wavelet transform and additive noise[J]. IEEE Signal Processing Letters, 2005, 12(9): 629-632. DOI:10.1109/LSP.2005.853048 |
| [32] |
HE K M, ZHANG X Y, REN S Q, et al. Deep resi-dual learning for image recognition[C]. 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2016, doi: 10.1109/CVPR.2016.90.
|



 刘国昌, 北京市昌平区府学路18号中国石油大学(北京)油气资源与探测国家重点实验室, 102249。Email:
刘国昌, 北京市昌平区府学路18号中国石油大学(北京)油气资源与探测国家重点实验室, 102249。Email: 