由于地形等因素的影响,实测重磁数据的点位呈不规则离散分布。为了提高重磁数据的反演效率,需将数据进行规则网格化处理,目前常用方法有多元二次函数法[1]、最小曲率网格化方法[2-6]、克里金法[7-8]、等效源法[9]、离散光滑插值法[10-13]、样条函数法[14]、分形分析方法[15]、基于凸集投影的全局网格化方法[16]、最近邻方法[17]等。其中,等效源方法虽然可以使数据满足拉普拉斯方程,但计算量大、精度低;最近邻方法的关键问题是网格化点位受距离最近的已知点异常值的控制,对于异常极大值点的估计可能偏小;克里金法假设异常值满足概率分布,即待网格化点位的异常值由已知点的分布决定,这种方法计算效率低,且如果待网格化点位与已知点位概率分布不同时,无法很好地网格化;最小曲率法在数据稀疏的区域存在振荡现象。
位场滤波主要包括频率域方法和空间域方法。频率域方法主要有余弦镶边滤波、补偿圆滑滤波[18]、匹配滤波[19]、小波变换[20];空间域方法主要有多项式拟合、滑动平均、非线性曲率滤波及延拓法[21]等。
近些年来,深度学习逐渐应用于地球物理领域。自适应学习广泛应用于三维重力物性反演[22];卷积神经网络用于去除地震数据噪声[23];优化的卷积神经网络应用于地震数据道编辑[24];生成对抗神经网络是一种生成式模型,通过提取待插值数据的高维空间的特征,再将其变换至已插值的数据,可在一定程度上解决数据量少导致的判别模型过拟合的问题,可应用于地震数据的插值[25];机器学习和深度学习可应用于重磁数据的插值[26];卷积神经网络可实现地震数据的插值、重构[27-28];卷积神经网络可用于位场数据的去噪处理[29];改进深度学习算法可用于地震相的识别[30];残差网络的思想可用于叠前随机噪声的压制[31];数据增强用于波阻抗反演[32];联合深度学习应用于地震数据噪声压制[33]。其中,深度学习与机器学习在测井领域还被应用于岩性识别[34],区别于其他地球物理数据、测井数据及岩石样本数据具有数据量大、标签识别性好的特点,在此类任务中机器学习可以替代人工识别,这方面的应用取得了一定效果。机器学习方法中的贝叶斯优化被用于建立不规则物体的重力场模型[35]。
注意力机制的思想产生于二十世纪九十年代的图像处理,源于人类视觉作用机理的启发。人们认为,机器学习模型应该也像人脑一样在处理数据时根据需要关注特定的部分而无需关注全局。谷歌将其运用于图像分类工作[36],旨在选出图片中最值得注意的地方。之后,注意力机制开始应用于序列预测任务[37-38],这是该思想第一次应用于序列模型。自注意力机制始于谷歌对序列模型的注意力机制的改进[39],其放弃了循环神经网络方式而使用多头自注意力机制方式,其作用是把序列化的数据表示为向量,把位置信息融入元素,得到综合全局考虑的表示向量。
本文提出一种基于自注意力机制的深度学习模型进行重磁数据网格化。对模型设计一种新的位置编码方式,使用自注意力方式将此位置编码转换为一个高维位置隐表示,再将高维异常向量与高维位置向量相乘,可保留与网格化节点相关性更高的位置处的异常向量,无关处得到减弱,相乘得到的向量经过全连接层,最后输出该网格化节点的异常。相对于最近邻网格化方法(使用单一最近邻点),自注意力机制使用的是全局已知点的信息;相对于克里金网格化方法(假设网格化节点遵循与已知点相同的概率分布),自注意力机制深度学习模型无需对数据的先验做出任何假设,模型会自动学习重磁数据已知点与待网格化节点间的关系;最小曲率网格化方法假设异常曲面为一个长方形弹性薄片,实际上实测重磁数据并不能很好吻合这一假设,而自注意力模型在训练过程中逐步确定与待网格化点的关联性较大的已知点位,并将其异常映射至网格化异常,无须做任何先验假设。
本文提出采用深度学习自注意力机制神经网络实现网格化,为了实现自动识别数据干扰类型并进行相应滤波,采用卷积神经网络、卷积自编码器和自注意力机制神经网络完成整套流程,实现数据的网格化和滤波。利用本文方法可自动识别数据干扰类型,并针对不同干扰类型使用不同的模型去除干扰,一定程度上可以减少手动去除干扰的工作量。
1 基于深度学习的网格化方法与滤波处理流程网格化要求将采集的数据投影至规则网格,即通过非网格化的原始数据推断其附近规则点位的异常值,距离原始点位越近的网格化点与其关系越强。但如果直接通过固定表达式建立这种投影关系,例如传统的近邻方法、最小曲率法、克里金法等,其精度和效率不尽如人意,因为这些方法对数据的分布做了统计特征一致、最小弯曲量薄片等假设,而真实数据并不一定符合这些假设,即便是模型数据也无法严格服从这些假设。深度学习并不做统计假设,而是从大量数据中学习待网格化点位与已知点位之间的关系,再将自注意力机制融入深度学习模型,不仅考虑待网格化点位与已知点位之间的相对位置关系,还考虑已知道点位之间的相对位置关系。将模型位置关系融入表示式,最终通过全连接层生成待网格化点位。对于含有条带状干扰的数据,本质也是通过干扰区附近数据推断干扰区的数据,所以也可使用自注意力机制深度学习模型解决这个问题。
基于深度学习的重磁数据处理流程包括网格化和滤波两部分。通过深度学习对重磁数据网格化是基于这样的假设:数据具有局部相关性,即待网格化点的数据与其周围实测点的异常值存在相关性,深度学习网格化方法研究的就是这种相关性。滤波时,由于数据含有的干扰类型不止一种,例如高斯随机噪声、条带状干扰等,有时也可能是二者的叠加,所以需先使用深度学习判断干扰类型,再根据干扰类型选择相应的滤波方法。
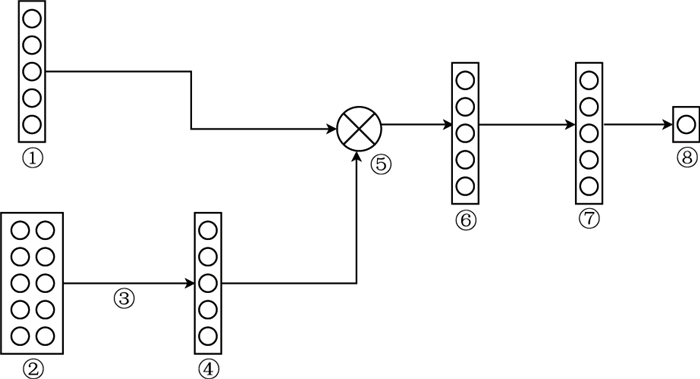
1.1 基于深度学习自注意力机制的网格化方法基于自注意力机制的网格化模型框架如图 1所示,对于训练这种模型,数据预处理阶段需计算出待网格化点与已知点位的相对位置编码。相对位置编码的设计方式为[38]
| $ \left\{\begin{array}{l} E\left(0, j_{1}\right)= \begin{cases}\sin \left(j_{1} / 10000^{2 i_{1} / 764}\right) & j_{1}=2 i_{1} \\ \cos \left(j_{1} / 10000^{2 i_{1} / 764}\right) & j_{1}=2 i_{1}+1\end{cases} \\ E\left(1, j_{2}\right)= \begin{cases}\sin \left(j_{2} / 10000^{2 i_{2} / 764}\right) & j_{2}=2 i_{2} \\ \cos \left(j_{2} / 10000^{2 i_{2} / 764}\right) & j_{2}=2 i_{2}+1\end{cases} \end{array}\right. $ | (1) |
|
图 1 基于自主注意力机制深度学习的网格化方法 ①已知点位的重磁异常向量;②待网格化点位与已知点之间的位置向量;③自注意力机制层;④已知点重磁异常位置隐表示;⑤相乘操作;⑥融合表示;⑦隐藏层;⑧待网格化点位异常值 |
式中:j1、j2为当前网格化点的x或y坐标;i1、i2分别由j1、j2对2取整得到。
假设已知点坐标为(x,y),其位置编码转换为(2,764)的矩阵E,再将E变换为(1,764×2)的一维向量,即该点的位置编码,得到的位置隐表示具有这样的特征:①已知点位与待网格化点位越接近,已知点位与待网格化点位向量的内积越大,反之则越小;②考虑了全局点位分布,已知点位与其他已知点位距离越远,代表该点所在区域较稀疏,则该点对待网格化点位的贡献越小。
对处理好的相对位置编码层使用自注意力机制方式变换为位置隐表示,即
| $ (\boldsymbol{q}, \boldsymbol{k}, \boldsymbol{v})=[\boldsymbol{Q}(\boldsymbol{P}), \boldsymbol{K}(\boldsymbol{P}), \boldsymbol{V}(\boldsymbol{P})] $ | (2) |
| $ \text { attention }(\boldsymbol{q}, \boldsymbol{k}, \boldsymbol{v})=\boldsymbol{v} \times \operatorname{softmax}\left(\frac{\boldsymbol{q} \boldsymbol{k}^{\mathrm{T}}}{\sqrt{d_\boldsymbol{k}}}\right) $ | (3) |
式中:P为已知点位或待网格化点位的位置向量;Q、K、V为可学习矩阵,与位置向量P相乘即得到向量q、k、v;softmax为概率归一化函数;attention是自注意力机制函数;dk是向量k的维度,其作用是避免注意力过度集中于附近点位。
深度学习滤波处理流程详见图 2。自注意力机制首先通过式(2)将位置编码P通过可训练的矩阵参数Q、K、V变换至当前位置向量q、k、v,自注意力层对q和k进行相似度计算,再经过softmax得出点位与其他已知点位之间的权重,再将此权重与v进行加权求和,得到融合了全局信息的位置表示attention(q、k、v)。图 1中重磁异常向量(标注为①)与attention(q、k、v)进行乘法操作,相当于遗忘门的作用,即如果该点处的位置隐表示的权重太低,相乘操作可确保融合表示中该点对待网格化点不再重要,只保留对待网格化点位重要的点的信息。
|
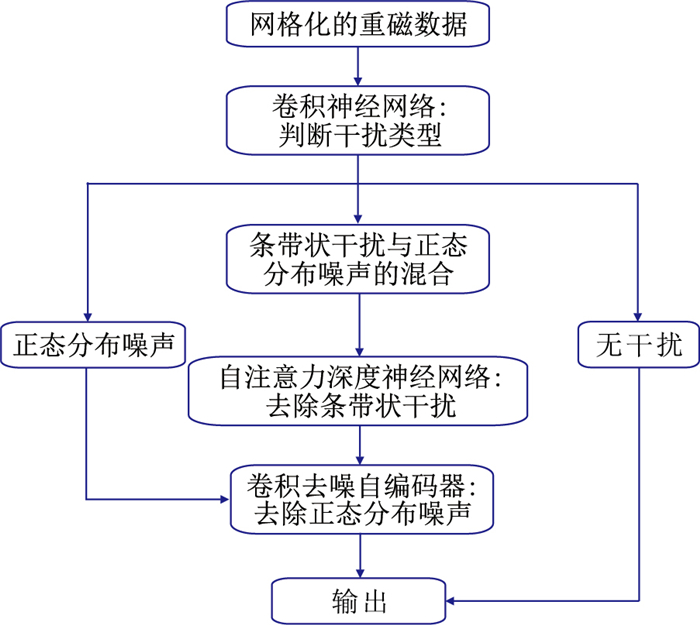
图 2 深度学习滤波处理流程 |
重磁数据中经常会出现条带状干扰和随机噪声,需要对干扰区域的数据通过重建方式进行滤波,并去除数据整体的随机噪声。本文提出基于深度学习的滤波处理流程,实现干扰区数据重构并去除随机噪声,如图 2所示。该流程首先判断数据所受干扰的类型,对于不同的噪声类型,使用不同的神经网络去噪滤波方法。
由于图像的初始维度较高,所以传统机器学习是直接对图像数据进行分类,其计算复杂度较高,故首先需要对数据进行降维,再使用分类方法进行训练。所以传统机器学习方法并没有利用图像具有局部相关性这一重要特征。卷积神经网络通过卷积层结构提取数据特征,很好地利用了局部相关性这一特征,同时具有平移不变性,即条带状干扰可平移到图像的其他地方,仍可以判别其干扰类型。
针对判断干扰类型的卷积神经网络需要对其进行超参数优化,调节卷积神经网络的参数(通道数,卷积层数,全连接层的层数),通过模型试验对比深度学习方法与传统机器学习方法的效果,模型训练收敛之后,打印模型在测试集中的准确率,如表 1所示(以表中准确率最高的编号为4的模型作为判别模型)。针对去除高斯随机噪声的卷积去噪自编码器进行超参数优化,对比不同网络结构下同一测试集的计算准确率,结果见表 2。选择测试集误差最小的网络结构1作为卷积去噪自编码器的结构。将表 1与表 2选出的网络结构进行可视化,这两个结构在训练过程中的损失函数下降曲线见图 3。
|
|
表 1 不同卷积神经网络对测试集判断噪声类型准确率统计 |
|
|
表 2 不同卷积去噪自编码器测试集误差对比 |

|
图 3 深度学习滤波方案模型及训练损失曲线 (a)卷积神经网络判别干扰类型模型;(b)图a模型训练过程损失函数曲线; (c)卷积自编码器恢复干扰区数据模型;(d)图c模型训练过程损失函数曲线 |
如果判断噪声类型为随机噪声,则使用卷积去噪自编码器对数据去噪;如果噪声类型为条带状干扰与高斯随机噪声的混合,则首先使用网格化方法自注意力机制神经网络对干扰区滤波,之后使用卷积去噪自编码器去除随机噪声。具体步骤如下。
(1) 根据条带状干扰区的异常值一般与周围点异常值的均值有明显差异这一特点,设定规则遍历异常整个点位,再选取这些异常值点位中呈条带状分布的点位作为条带状干扰区域;
(2) 从原始异常中选取与步骤(1)中相关区域的范围,分别将对应的未被掩盖区域的数据、被掩盖区域的数据作为模型的输入与输出,从而训练数据,训练数据的数量与异常点位数据量成正比;
(3) 使用深度学习框架、随机梯度下降法对自注意力神经网络进行训练;
(4) 使用训练好的模型预测干扰区数据所含噪声类型;
(5) 根据噪声类型选择相应方法进行滤波。
2 模型试验 2.1 深度学习网格化方法与传统网格化方法对比建立图 4所示模型,对比深度学习方法与常规网格化方法在已知点位均匀分布和不均匀分布情况下的效果。球体中心点坐标为(9m, 9m, -5m),半径为2m。背景密度为0,球体密度为3.0g/cm3。在地面坐标范围为[0, 20m](x方向)×[0, 20m](y方向)的区域中随机均匀采样64个点作为已知点位。

|
图 4 球体模型示意图 |
首先针对已知点分布不均匀的情况。分别利用深度学习方法和常规网格化方法对上述模拟的待网格化数据进行网格化,结果见图 5和表 3。

|
图 5 深度学习方法和传统网格化方法对球体模型测点不均匀分布条件下的网格化结果对比 (a)重力异常等值线图和随机测点分布;(b)自注意力机制神经网络训练集损失函数下降曲线; (c)深度学习网格化重力异常分布;(d)深度学习网格化结果与原始重力异常的差;(e)克里金网格化重力异常图;(f)克里金网格化结果与原始重力异常的差;(g)最小曲率网格化重力异常图;(h)最小曲率网格化结果与原始重力异常的差 |
|
|
表 3 点位不均匀情况下深度学习与传统网格化方法的计算误差及耗时统计 |
根据图 5可知:深度学习的网格化重力异常最大误差为0.002mGal;克里金网格化数据最大误差为0.006mGal,比前者误差稍大;最小曲率网格化数据的误差最大,为0.074mGal。这是因为最小曲率网格化方法本身在稀疏区域存在振荡现象,在网格化区域的边缘出现了误差较大的点。从图 5d、图 5f和图 5h的误差分布特征来看,深度学习的误差空间分布与坐标没有明显的关系,呈现出了近似高斯白噪声的特征;克里金方法的误差分布相对比较均匀,但在异常体附近出现了局部低值区,偏差的均值约为0.006mGal,这会对后续的反演解释造成干扰;最小曲率方法由于在稀疏区域存在振荡现象,所以在边缘区域出现了较低值,但偏差的整体均值也超过了克里金法误差的均值。根据表 3,上述几种方法计算速度从快至慢依次为深度学习方法、最小曲率网格化法和克里金法。
沿x与y方向每隔1.5m采集重力场数据,共计196个点。然后,针对球体模型且已知点分布均匀的情况,分别利用深度学习方法和常规网格化方法对待网格化数据进行网格化操作,结果见图 6。
|
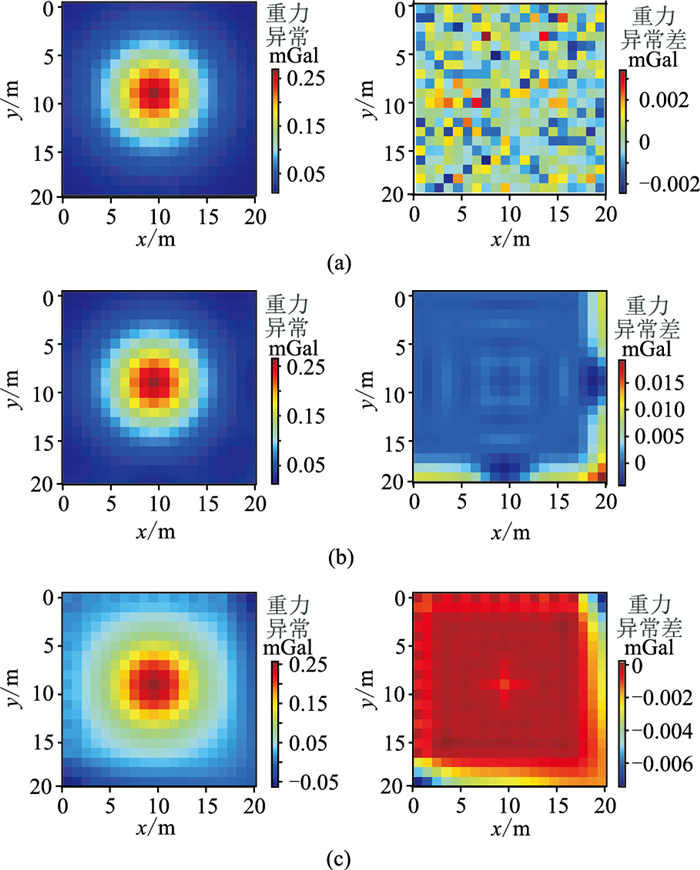
图 6 深度学习方法(a)、克里金网格化方法(b)和最小曲率网格化(c)重力异常图(左)及其与理论重力异常的差(右) |
从图 6可以看出,针对均匀点位数据网格化,克里金网格化方法和最小曲率网格化方法的误差极大值都出现在无网格化点位分布的边缘区域,且存在有规律的震荡现象,但是深度学习的网格化结果仍然呈现较标准的高斯零均值分布,这是因为模型在训练的过程中学习到了数据在边界位置处的先验分布,即由于训练数据在边界上呈现一定的分布特征,所以注意力机制模型在推理过程中,当发现边界处的位置编码与已知均匀点位位置编码没有太大关联度时,会自动使用学习到的经验,从而外推出了数据的边界,这也是深度学习方法较传统基于插值方式网格化方法不同之处。自注意力机制在这种情况下起到的作用是判断出了待网格化点位的值无法通过已知点位得出,所以深度学习模型也可以很好地适用于均匀点位网格化的情况。
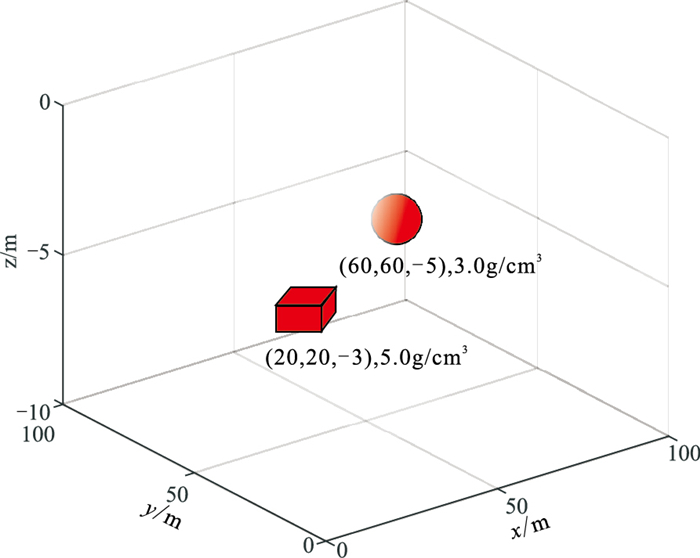
2.2 深度学习滤波方法与传统滤波方法对比建立图 7所示模型,模型包括一个球体和一个棱柱体重力异常体。图 8b为图 8a(原始不含干扰重力异常)加入均值为0、方差为0.1mGal2的高斯分布白噪声及穿切模型异常的条带状干扰的重力异常图。使用训练好的自注意力机制深度学习模型处理图 8b,得到去除干扰之后的结果,再将其输入卷积去噪自编码器,得到的最终处理结果见图 8c。用中值滤波方法处理条带状干扰、均值滤波处理高斯随机噪声的结果见图 8d。图 8c、图 8d与图 8a的差值分别见图 8e和图 8f。
|
图 7 球体和棱柱体模型示意图 |

|
图 8 条带状区域重力异常深度学习与传统滤波方法滤波结果对比 (a)原始重力异常;(b)含条带状干扰、高斯随机噪声的重力异常;(c)用自注意力神经网络处理条带状干扰、卷积自编码器去除高斯随机噪声的滤波结果;(d)用中值滤波方法处理条带状干扰、均值滤波处理高斯随机噪声的结果;(e)图c与图a的差;(f)图d与图a的差 |
由图 8可见,中值滤波方法并不能彻底去除高斯随机噪声,而深度学习方法处理结果则显示了卷积神经网络可以正确识别干扰类型为条带状干扰,并有效去除高斯分布噪声与条带状干扰;卷积去噪自编码器的处理结果较好地保留了原始棱柱体的重力异常特征,在空白区域也可以计算出缺失值(图 8c),根据每个点的误差统计结果,其分布特征与高斯随机噪声相符;传统方法对条带状干扰的滤波效果并不好,对空白区的数值计算结果误差较大,残差统计结果也较原始噪声值差别更大,而且,处理结果在地质体上方区域的误差较大,这会导致异常区数据反演结果出现较大偏差。
3 实际应用工区位于内蒙古自治区达尔汗茂明安联合旗,对此区域的实测磁场数据进行处理,以检验本文方法的处理效果。
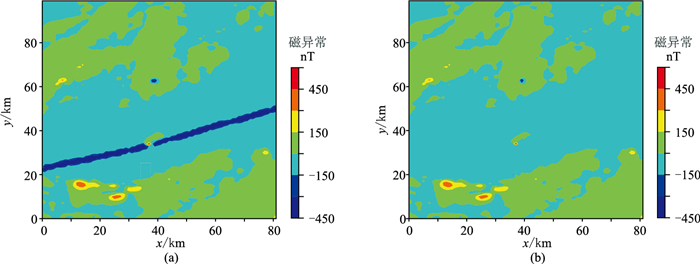
工区地面上有线缆,所以观测到的磁场数据中可见明显的线缆产生的磁异常干扰(图 9a中蓝色的条带状负值区域)。使用基于自注意力机制的深度学习模型,通过干扰区域的其他已知点数据对干扰区域进行滤波,结果见图 9b。由图可见,条带状干扰被有效去除,而条带状干扰区域由于地质体产生的异常值被有效保留了下来,该异常的极大值点也得到恢复。这表明模型有效地捕捉了条带状干扰区域内异常点之间的关系,证明深度学习方法可以有效应用于实际数据的滤波,效果良好。
|
图 9 工区实测磁场分布图(a)及深度学习方法的恢复结果(b) |
本文针对重磁数据网格化任务,设计了基于自注意力机制的深度学习网络结构;针对重力数据含有不同类型干扰的情况,采用卷积神经网络以及自注意力机制的方法可判断干扰类型;对来自内蒙古自治区的实测磁场数据应用本文方法进行恢复,结果较好。得到以下两点结论。
(1) 基于自注意力机制的网格化点位与已知点位之间的空间关联,将关联信息与异常信息进行融合,通过神经网络的方式输出点位异常,可以更好地表达重磁数据的已观测部分与未观测部分之间的局部相关性,兼顾了全局性与局部相关性。模型试验表明,传统的空间域方法计算结果的误差分布与原始异常的分布之间有相关性,而基于自注意力机制的深度学习方法由于学习到了待网格化点位与已知点位之间的位置上的关联,其误差相对较小。
(2) 卷积神经网络可以很好地判断数据是否含有随机噪声和条带状干扰。本文针对这两种噪声类型分别使用自注意力机制神经网络与卷积自编码器进行去除。模型试验表明这套方法具有良好效果;实际磁场数据处理结果表明该方法具有一定的实用性。
| [1] |
HARDY R L. Multiquadric equations of topography and other irregular surfaces[J]. Journal of Geophysical Research, 1971, 76(8): 1905-1915. DOI:10.1029/JB076i008p01905 |
| [2] |
BRIGGS I. Machine contouring using minimum curvature[J]. Geophysics, 1974, 39(1): 39-48. DOI:10.1190/1.1440410 |
| [3] |
SWAIN C J. A FORTRAN Ⅳ program for interpolating irregular spaced data using the difference equations for minimum curvature[J]. Computers & Geosciences, 1976, 1(4): 231-240. |
| [4] |
SMITH W H F, WESSEL P. Gridding with continues curvature splines in tension[J]. Geophysics, 1990, 55(3): 293-305. DOI:10.1190/1.1442837 |
| [5] |
王万银, 邱之云, 刘金兰, 等. 位场数据处理中的最小曲率扩边和补空方法研究[J]. 地球物理学进展, 2009, 24(4): 1327-1338. WANG Wanyin, QIU Zhiyun, LIU Jinlan, et al. Research on the method of minimum curvature expanding edge and filling gap in potential field data processing[J]. Progress in Geophysics, 2009, 24(4): 1327-1338. DOI:10.3969/j.issn.1004-2903.2009.04.022 |
| [6] |
刘兆平, 杨进, 武炜. 地球物理数据网格化方法的选取[J]. 物探与化探, 2010, 34(1): 93-97. LIU Zhaoping, YANG Jin, WU Wei. Selection of geophysics data grid method[J]. Geophysical and Geochemical Exploration, 2010, 34(1): 93-97. |
| [7] |
HANSEN R O. Interpretive gridding by anisotropic Krigging[J]. Geophysics, 1993, 58(10): 1491-1497. DOI:10.1190/1.1443363 |
| [8] |
孙洪泉. 地质统计学及其应用[M]. 北京: 中国矿业大学出版社, 1990.
|
| [9] |
CORDELL L. A scattered equivalent soured method for interpolation and gridding of potential field data in three dimensions[J]. Geophysics, 2012, 77(4): P629-P636. |
| [10] |
MALLET J L. Discrete smooth and interpolation in geometric modelling[J]. Computer Aided Design, 1992, 24(4): 178-191. DOI:10.1016/0010-4485(92)90054-E |
| [11] |
孟小红, 侯建全, 梁宏英, 等. 离散光滑插值方法在地球物理位场中的快速实现[J]. 物探与化探, 2002, 26(4): 302-306. MENG Xiaohong, HOU Jianquan, LIANG Hongying, et al. The fast realization of discrete smooth interpolation in the interpolation of potential data[J]. Geophysical and Geochemical Exploration, 2002, 26(4): 302-306. DOI:10.3969/j.issn.1000-8918.2002.04.015 |
| [12] |
CLAERBOUT J F. Image Estimation by Example[D]. Stanford University, California, 2002.
|
| [13] |
李冰, 刘洪, 李幼铭. 三维地震数据离散光滑插值的共轭梯度法[J]. 地球物理学报, 2002, 45(5): 691-699. LI Bing, LIU Hong, LI Youming. 3-D seismic data discrete smooth interpolation using conjugate gradient[J]. Chinese Journal of Geophysics, 2002, 45(5): 691-699. DOI:10.3321/j.issn:0001-5733.2002.05.011 |
| [14] |
郭志宏. 双三次样条内插网格化方法软件的研制开发及其应用[M]. 北京: 地质出版社, 1999.
|
| [15] |
刘沈衡, 李爱勇. 分形分析在重磁不规则网网格化中的应用[J]. 石油物探, 1999, 38(3): 108-111. LIU Shenheng, LI Aiyong. Application of fractal ana-lysis to gridding of irregular-grid gravity and magnetic data[J]. Geophysical Prospecting for Petroleum, 1999, 38(3): 108-111. |
| [16] |
闫浩飞, 刘国峰, 薛典军, 等. 基于凸集投影方法的重磁数据规则缺失重建[J]. 地球物理学进展, 2016, 31(5): 2192-2197. YAN Haofei, LIU Guofeng, XUE Dianjun, et al. Reconstruction of gravity/magnetic data with the projection-onto-convex-sets methods[J]. Progress in Geophysics, 2016, 31(5): 2192-2197. |
| [17] |
SAMBRIDGE M, Braun J, Mcqueen H. Geophysical parametrization and interpolation of irregular data using natural neighbours[J]. Geophysical Journal International, 2010, 122(3): 837-857. |
| [18] |
穆石敏. 区域地球物理数据处理方法及其应用[M]. 吉林长春: 吉林科学出版社, 1980.
|
| [19] |
董焕成, 李宗杰. 重力异常匹配滤波的原理与应用[J]. 物探与化探, 1993, 17(5): 331-340. DONG Huancheng, LI Zongjie. The principle and application of the matchfiltering method for gravitational anomalies[J]. Geophysical and Geochemical Exploration, 1993, 17(5): 331-340. |
| [20] |
杨文采, 施志群, 侯遵泽, 等. 离散小波变换与重力异常多重分解[J]. 地球物理学报, 2001, 44(4): 534-541, 582. YANG Wencai, SHI Zhiqun, HOU Zunze, et al. Discrete wavelet transform for multiple decomposition of gravity anomalies[J]. Chinese Journal of Geophysics, 2001, 44(4): 534-541, 582. DOI:10.3321/j.issn:0001-5733.2001.04.012 |
| [21] |
郭志宏, 徐昆. 中国航磁异常管理信息系统开发与建设[J]. 地球物理学进展, 2002, 17(4): 703-710. GUO Zhihong, XU Kun. The development and construction of China aeromagnetic anomaly management information system of China[J]. Progress in Geophy-sics, 2002, 17(4): 703-710. |
| [22] |
FERNANDO J S, SILVA D, VALÉRIA C F, et al. Adaptive learning 3D gravity inversion for salt-body imaging[J]. Geophysics, 2011, 76(3): A49-A52. |
| [23] |
韩卫雪, 周亚同, 池越. 基于深度学习卷积神经网络的地震数据随机噪声去除[J]. 石油物探, 2018, 57(6): 862-869, 877. HAN Weixue, ZHOU Yatong, CHI Yue. Deep learning convolutional neural networks for random noise attenuation in seismic data[J]. Geophysical Prospecting for Petroleum, 2018, 57(6): 862-869, 877. |
| [24] |
王文强, 孟凡顺, 孙文亮. 优化卷积神经网络在道编辑中的应用[J]. 地球物理学展, 2019, 34(1): 214-220. WANG Wenqiang, MENG Fanshun, SUN Wenliang. Trace editing based on optimized convolutional neural network[J]. Progress in Geophysics, 2019, 34(1): 214-220. |
| [25] |
王静. 基于生成对抗网络的地震数据插值[D]. 黑龙江哈尔滨: 哈尔滨工业大学, 2019.
|
| [26] |
WANG F, CHEN S C, and LIU Y N. Deep learning for gravity and magnetic data interpolation[C]. SEG Technical Program Expanded Abstracts, 2019, 38: 2533-2537.
|
| [27] |
郑浩, 张兵. 基于卷积神经网络的智能化地震数据插值技术[J]. 地球物理学进展, 2020, 35(2): 721-727. ZHENG Hao, ZHANG Bing. Intelligent seismic data interpolation via convolutional neural network[J]. Progress in Geophysics, 2020, 35(2): 721-727. |
| [28] |
毛博. 基于卷积神经网络的地震数据重构与模型构建研究[D]. 吉林长春: 吉林大学, 2020.
|
| [29] |
陈贝. 基于深度卷积神经网络的位场数据去噪研究[D]. 北京: 中国地质大学(北京), 2020.
|
| [30] |
闫星宇, 顾汉明, 罗红梅, 等. 基于改进深度学习方法的地震相智能识别[J]. 石油地球物理勘探, 2020, 55(6): 1169-1177. YAN Xingyu, GU Hanming, LUO Hongmei, et al. Intelligent seismic facies classification based on an improved deep learning method[J]. Oil Geophysical Prospecting, 2020, 55(6): 1169-1177. |
| [31] |
李海山, 陈德武, 吴杰, 等. 叠前随机噪声深度残差网络压制方法[J]. 石油地球物理勘探, 2020, 55(3): 493-503. LI Haishan, CHEN Dewu, and WU Jie, et al. Pre-stack random noise suppression with deep residual network[J]. Oil Geophysical Prospecting, 2020, 55(3): 493-503. |
| [32] |
伊小蝶, 吴帮玉, 孟德林, 等. 数据增广和主动学习在波阻抗反演中的应用[J]. 石油地球物理勘探, 2021, 56(4): 707-715. YI Xiaodie, WU Bangyu, MENG Delin, et al. Application of data augumentation and active learning to seismic wave impendence inversion[J]. Oil Geophysical Prospecting, 2021, 56(4): 707-715. |
| [33] |
张岩, 李新月, 王斌, 等. 基于联合深度学习的地震数据随机噪声压制[J]. 石油地球物理勘探, 2021, 56(1): 9-25. ZHANG Yan, LI Xinyue, WANG Bin, et al. Random noise suppression of seismic based on joint deep lear-ning[J]. Oil Geophysical Prospecting, 2021, 56(1): 9-25. |
| [34] |
安鹏, 曹丹平. 基于深度学习的测井岩性识别方法研究与应用[J]. 地球物理学进展, 2018, 33(3): 1029-1034. AN Peng, CAO Danping. Research and application of logging lithology identification based on deep learning[J]. Progress in Geophysics, 2018, 33(3): 1029-1034. |
| [35] |
ROBERTO F, RICCARDO B, RICHARD L. Mode-ling irregular small bodies gravity field via extreme learning machines and Bayesian optimization[J]. Advances in Space Research, 2021, 67(1): 617-638. |
| [36] |
MNIH V, HEESS N, GRAVES A, et al. Recurrent models of visual attention[J]. Advances in Neural Information Processing Systems, 2014, 3(1): 121-128. |
| [37] |
BAHDANAU D, CHO K, BENGIO Y. Neural Machine Translated by Jointly Learning to Align and Translate[OL]. http://pdfs.semanticscholar.org/071b/16f25117fb6133480c6259227d54fc2a5ea0.pdf.
|
| [38] |
LUONG M T, PHAM H, MACHING C D. Effective Approaches to Attention Based Neural Machine Translation[OL]. http://aclweb.org/anthology/D15-1166.
|
| [39] |
VASWANI A, SHAZEER N, PARMAR N, et al. Attention Is All You Need[M]. arXiv, 2017.
|



 李丽丽, 吉林省长春市西民主大街938号吉林大学地球探测科学与技术学院, 130026。Email:
李丽丽, 吉林省长春市西民主大街938号吉林大学地球探测科学与技术学院, 130026。Email: 