② 中海油研究总院, 北京 100027
② CNOOC Research Institute Co., Ltd., Beijing 100027, China
横波速度是开展叠前地震反演特别是蜗牛道集反演所必须的基础数据,是重要的储层岩性信息。但常规测井通常只能得到纵波速度数据,横波速度需要利用各种复杂的方法进行估算[1-2]。Greenberg等[3]、Castagna等[4]提出利用纵、横波速度的经验关系式估计横波速度,这类方法受实际地质条件影响较大,容易产生较大误差。目前常用的方法是基于岩石物理模型估算横波速度。Xu-White模型[5-6]把岩石的纵、横波速度与其孔隙度和孔隙纵横比联系起来,以此为基础预测横波速度;Xu等[7]和Payne等[8]通过分析不同孔隙结构对弹性参数的影响,建立了Xu-Payne模型进而预测碳酸盐岩的横波速度;张秉铭等[9]在纵波速度约束下,将刚性孔隙与柔性裂缝的体积分数引入原始Xu-Payne模型,取得了更好的预测效果;张元中等[10]分析了基于Greenberg-Castagna公式、近似Gassmann方程和Xu-White模型三种方法预测砂泥岩地层横波速度的基本思路,给出了对比结果及应用效果;罗水亮等[11]利用变型P-L模型及矩阵方程迭代在精细横波预测中取得较好的效果;唐杰等[12]、林凯等[13]均通过改进各种岩石物理模型预测横波速度。
基于岩石物理模型的横波速度预测方法需要依次建立岩石基质弹性模量模型、填充孔隙后得到的干岩石骨架弹性模量模型,以及填充流体得到的饱和流体模型等物理模型,再以弹性参数为中间变量,最后估算出横波速度。建模过程需要大量的中间参数,比如岩石矿物组分、孔隙结构特征等,这些参数是建模过程必需的,但都不易获得。此外,基质模量是通过矿物几何平均、算数平均等方法估算,加之多种岩石物理模型各自具有不同的假设条件、建模过程复杂等,诸多因素都对岩石物理模型的实际应用产生影响。
随着深度学习技术的发展,神经网络被广泛应用于油气地球物理勘探领域,以解决实际应用中的非线性数学问题[14-18]。其中,BP网络[19-20]、循环神经网络[21]等传统网络模型已成功应用于横波速度预测。这些网络以实际测井资料为输入、横波速度为期望输出,采用端到端的网络结构,由已知测井数据直接预测横波速度,摒弃构建复杂岩石物理模型的诸多环节,简化了复杂的运算过程,同时取得了很好的效果。
本文构建了一种横波速度预测的二次型寻优网络。尽可能简化网络结构,在全连接网络的基础上,使用二次型寻优算法进行误差反传(从输出层传至隐藏层和输入层)。通过与Adam[22]算法对比,验证了该优化算法预测效果更好、效率更高。此外,采用正交试验法[23]选取最显著影响横波速度预测效果的网络参数及训练策略,以达到提高预测精度的目的。网络训练选用横波速度的敏感参数(自然伽马、孔隙度和纵波速度)作为输入,真实横波速度作为输出,训练网络模型实现横波速度预测。最后应用实际测井数据进行测试,结果表明该方法能够高效、高精度地预测横波速度。
1 方法原理 1.1 二次型寻优网络结构二次型寻优网络是在全连接网络的基础上构建而成,其结构与全连接网络结构相似。全连接网络是根据多层感知机结构构建的神经网络,它在输入与输出之间加入一个或多个隐藏层,上、下两层之间的神经元相互连接,且下层神经元需要与上层所有神经元相连接,层内的神经元互不相连,其结构如图 1所示。

|
图 1 全连接网络结构 |
全连接神经网络具有端到端的特性,仅对输入与输出敏感,只需给定一组储层参数作为输入即可直接映射到横波速度上。全连接网络的学习过程是根据误差反传算法,调整神经元之间的权值和阈值的过程:样本数据输入到网络中经历正向传播(从输入层经隐藏层传至输出层)计算输出数据与期望数据的误差;然后将误差反传计算误差梯度,根据梯度调整连接权和阈值;最后经过反复迭代,直至训练出稳健的神经网络。
1.2 二次型寻优算法根据梯度调整连接权和阈值的方法称为神经网络的优化算法。优化算法是训练神经网络的核心,在提高网络训练效率的同时,可以提高网络的预测精度。二次型寻优算法即为一种优秀的优化算法,其衍生于牛顿迭代算法,并结合了二次型优化问题[24]。在神经网络训练中,使用均方误差(MSE)作为准则,则网络的代价函数定义为
| $ S(\boldsymbol{\beta})=\frac{1}{2} \sum\limits_{q=1}^{m}\left[f\left(\boldsymbol{x}_{q} ; \boldsymbol{\beta}\right)-y_{q}\right]^{2} $ | (1) |
式中:m为样本个数;f表示网络输出;x表示输入特征,含有3个分量,分别为自然伽马、纵波速度和孔隙度;β为n维向量,表示网络连接权值和阈值,即网络参数;y表示横波速度的真实值。
网络的优化目标为最小化S(β)。令r=f(x; β)-y,进而求得
| $ \left\{\begin{array}{l} \nabla S(\boldsymbol{\beta})=\boldsymbol{J}^{\mathrm{T}} \boldsymbol{r} \\ \nabla^{2} S(\boldsymbol{\beta})=\boldsymbol{H}=\boldsymbol{J}^{\mathrm{T}} \boldsymbol{J}+\boldsymbol{o} \end{array}\right. $ | (2) |
式中:J表示Jacobi矩阵;H表示Hessian矩阵;o是近似为零的向量。
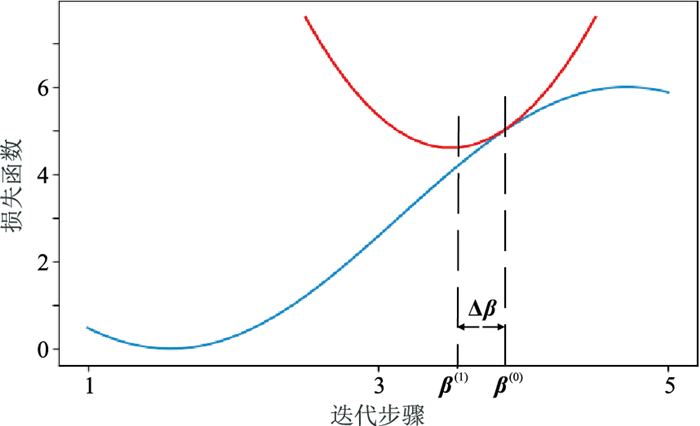
二次型寻优算法结合了牛顿迭代法的思想。如图 2所示,首先在初始点β(0)附近将目标函数展开为二阶泰勒公式,通过求此二阶泰勒公式的最优解得到步长Δβ,进而解出第二个迭代点β(1)。第二步迭代用β(1)处的二阶泰勒公式近似目标函数求解β(2)。经过反复迭代,即可求得目标函数的最优解。
|
图 2 泰勒展开示意图 |
在第t次迭代中,用S(β)在点β(t)处的二阶泰勒展开式近似S(β),可将式(1)转化为二次型问题
| $ \begin{aligned} F(\boldsymbol{\beta})=& S\left[\boldsymbol{\beta}^{(t)}\right]+\left\{\nabla S\left[\boldsymbol{\beta}^{(t)}\right]\right\}^{\mathrm{T}}\left[\boldsymbol{\beta}-\boldsymbol{\beta}^{(t)}\right]+\\ & \frac{1}{2}\left[\boldsymbol{\beta}-\boldsymbol{\beta}^{(t)}\right]^{\mathrm{T}} \nabla^{2} S\left[\boldsymbol{\beta}^{(t)}\right]\left[\boldsymbol{\beta}-\boldsymbol{\beta}^{(t)}\right] \end{aligned} $ | (3) |
通过求此二次型问题的最优解,可得到下一个迭代点β(t+1)。近似二次型的三维曲面如图 3所示。

|
图 3 近似二次型三维曲面 |
令A=▽2S[β(t)],b=▽S[β(t)],γ=-▽F(Δβ),同时Hessian矩阵是对称矩阵,对F(β)求导后得到简化公式
| $ \boldsymbol{\gamma}=A \Delta \boldsymbol{\beta}-\boldsymbol{b} $ | (4) |
在迭代中,梯度的反方向为目标函数下降最快的方向,即-▽F(Δβp)方向。根据一维搜索确定步长α,同时利用如下迭代公式找到二次型问题的最优解
| $ \boldsymbol{\gamma}_{p}=-\nabla F\left(\Delta \boldsymbol{\beta}_{p}\right)=\boldsymbol{A} \Delta \boldsymbol{\beta}_{p}-\boldsymbol{b} $ | (5) |
| $ \Delta \boldsymbol{\beta}_{(p+1)}=\Delta \boldsymbol{\beta}_{(p)}+\alpha \boldsymbol{\gamma}_{(p)} $ | (6) |
根据一维线搜索的链式法则可求得
| $ \alpha=\frac{\boldsymbol{\gamma}_{p}^{\mathrm{T}} \boldsymbol{\gamma}_{p}}{\boldsymbol{\gamma}_{p}^{\mathrm{T}} \boldsymbol{A} \boldsymbol{\gamma}_{p}} $ | (7) |
利用式(5)~式(7),即可得到式(3)所示二次型问题解的扰动量Δβ,进而求出β(t+1)=β(t)-Δβ。再经过嵌套循环、最小化代价函数等步骤,完成神经网络的训练过程。
此外,由式(4)可以看出,若矩阵A为非正定矩阵,则算法可能陷入局部最优,导致预测精度降低。此时可加入Levenberg-Marquardt[20]修正项,即G=A+ηI(I为单位矩阵,η为修正系数,η≥0),使其代替A。只要η足够大,就可以保证G为正定矩阵。
1.3 正交试验网络结构优选方法影响神经网络预测效果的因素有优化算法、每层神经元个数等,选择其最优组合能够提高神经网络的预测精度及效率,本文采用正交试验法进行筛选。统计学上,将试验所考虑的因素(如优化算法)称为因子,因子包含的所有情况(如Adam算法和二次型寻优算法)称为因子水平。正交试验法根据因子数和因子水平数选择相应的正交表,再依托正交表的正交性,从中挑选少数典型数据进行试验,即可实现通过最少的试验次数达到与全部试验相同的效果,进而分析出最优组合方案。
正交表是正交试验法的重要工具,它列举了一次试验所用的全部因子水平组合。其表达形式有L4(23)、L8(27)、L12(31×24)等,其中L表示正交表,每个数字各有不同含义。以L4(23)为例,它表示最多可安排3个因子(A、B、C),每个因子均有2个水平(1、2),共需做4次实验。L4(23)正交表如表 1所示。
|
|
表 1 L4(23)表 |
以上述正交表为基础的正交试验共需进行4次即可分析出较优方案。根据方差分析模型[23]及L4(23)表可知
| $ \left\{\begin{array}{l} z_{1}=\mu+a_{1}+b_{1}+c_{1}+\varepsilon_{1} \\ z_{2}=\mu+a_{1}+b_{2}+c_{2}+\varepsilon_{2} \\ z_{3}=\mu+a_{2}+b_{1}+c_{2}+\varepsilon_{3} \\ z_{4}=\mu+a_{2}+b_{2}+c_{1}+\varepsilon_{4} \end{array}\right. $ | (8) |
式中:zj(j=1,2,3,4)表示每次试验的结果,j为试验号;μ为试验结果的真实值;i为因子水平的编号(i=1, 2);ai、bi、ci分别表示因子A、B、C的主效应,反映某个因子的某个水平对试验结果的影响,且
将因子A中水平1的两次试验结果相加,有
| $ z_{1}+z_{2}=2 \mu+2 a_{1}+\varepsilon_{1}+\varepsilon_{2} $ | (9) |
类似地,将因子A中水平2的两次试验结果相加,并记为
| $ \left\{\begin{array}{l} k_{1}^{\mathrm{A}} \widehat = \frac{1}{2}\left(z_{1}+z_{2}\right)=\mu+a_{1}+\frac{1}{2}\left(\varepsilon_{1}+\varepsilon_{2}\right) \\ k_{2}^{\mathrm{A}} \widehat = \frac{1}{2}\left(z_{3}+z_{4}\right)=\mu+a_{2}+\frac{1}{2}\left(\varepsilon_{3}+\varepsilon_{4}\right) \end{array}\right. $ | (10) |
上式中随机误差的平均值可近似为零,因此可将因子A的主效应估计为
| $ \left\{\begin{array}{l} a_{1}=k_{1}^{\rm{A}}-\mu \\ a_{2}=k_{2}^{\rm{A}}-\mu \end{array}\right. $ | (11) |
正交试验将不参与比较的因子B和C置于同等条件并消除其影响,达到只比较因子A的目的。
由式(11)可知,若要比较因子A主效应的大小,只需比较k1A和k2A的大小即可。水平主效应越大,表示因子A的该水平对试验结果的影响越大,应当作为主要考虑因素。具有最大主效应的水平称为较优水平。
若将式(11)中两式相减,可得
| $ R_{\mathrm{A}}=a_{1}-a_{2}=k_{1}^{\mathrm{A}}-k_{2}^{\mathrm{A}} $ | (12) |
式中RA称为因子A的极差,反映因子水平变化对试验结果的影响,即因子的重要程度,值越大表示因子越重要。类似地可以计算出RB、RC。将RA、RB、RC由大到小依次排列,即可知因子主次。位于首位的因子,其水平变化对试验结果贡献最大,因此应当优先考虑;位于末位的因子,其水平变化对试验结果贡献较小,其影响可最后考虑。
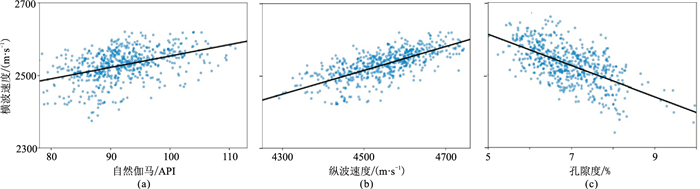
2 参数试验及预测结果分析 2.1 数据准备自然伽马、纵波速度和孔隙度是测井数据中较易获得的曲线。在典型砂泥岩地层中,这些数据均能反映地下介质的具体特征,是评价储层物性的重要参数,且与横波速度存在密切联系。自然伽马值能够反映地层骨架的泥质含量,在曲线上砂、泥岩呈现不同特征,由自然伽马与横波速度交会图(图 4a)可知,两者呈正相关。纵波速度和横波速度均与岩石骨架性质密切相关,由纵波速度与横波速度交会图(图 4b)可见,纵波速度与横波速度也存在较强的正相关性。孔隙度作为影响地震波速度的重要因素之一,同样可以反映地下介质的结构特征,与横波速度存在必然联系。由孔隙度与横波速度交会图(图 4c)可见,两者存在负相关性。
|
图 4 储层参数与横波速度交会图 (a)自然伽马与横波速度;(b)纵波速度与横波速度;(c)孔隙度与横波速度 |
选用8口井的实际测井数据进行横波速度预测,其中a1~a6井作为训练集,b1、b2井分别做为验证集和测试集。井数据包括自然伽马、孔隙度、纵波速度以及横波速度,训练集样本共2094组,验证集和测试集均为561组数据。图 5为a2井各参数曲线,其中输入数据为自然伽马、纵波速度和孔隙度,输出数据为横波速度。对输入数据进行特征缩放处理,对标准输出数据取对数处理,并设MSE为损失函数。

|
图 5 a2井各参数曲线 |
正交试验中,参与试验的网络参数及训练策略包括每层网络的神经元个数、隐藏层数、激活函数、优化算法以及训练集井数,表 2列出各因子的水平。
|
|
表 2 正交试验因子水平表 |
以表 2所列的因子水平为依据,试验选择了L16(43×22)正交表。表中安排5个因子,因子A、B、C有4个因子水平,因子D、E有2个因子水平,需进行16次试验筛选出最优的因子水平组合。将所有16种情况的因子水平组合安排在正交表上,并译成试验方案表(表 3)。
|
|
表 3 L16(43×22)正交试验方案表 |
以第5次试验为例,它表示在A、B、C、D、E五个因子上分别取第2、第1、第2、第2和第2个水平,具体解释为该次试验中每层网络的神经元个数为8个,构建1层隐藏层,激活函数为ReLU函数,采用二次型优化算法,合并a1、a2、a3和a4共四口井的数据作为训练集,试验结果得到其相关性评分为13.49。表 3中的相关性评分由相关系数经简单计算得来,它与相关系数类似,均反映预测结果与真实结果的相关性。使用相关性评分的目的是运算简便,在一定程度上放大了相关系数的数值,削弱了因数值过小引起的误差。
由表 3中16次试验得到的相关性评分结果计算出因子极差(R),得出较优因子水平并按因子主次排序。统计结果见表 4。
|
|
表 4 试验结果表 |
表 4中ki等于某一个因子的第i个水平在16次试验中得到的相关性评分之和再除以该水平的重复次数。例如:表 4中A因子的k1为13.29=(12.34+13.69+13.17+13.96)/4。表中多水平因子的极差R取某一个因子中任意两个ki间差值的最大值。例如:表 4中A因子的极差R计算方法为2.42=max(|k1-k2|, |k1-k3|, |k2-k3|)。
分析表 4可知,D2位于因子主次序列的首位,说明优化算法对横波速度预测的影响最大,使用二次型寻优算法能够提升预测结果的准确性。因子C位于第2位,激活函数对网络预测效果的影响较大,选择合适的激活函数能够对预测准确性起到积极的作用。每层神经元个数(因子A)与网络层数(因子B)对网络预测有一定的影响,选择更大的网络模型效果不一定更优,例如第16次试验中,构建4个隐藏层,每层15个神经元,最终得到相关性评分仅为1.37,远低于其他网络,这是由网络模型过于复杂导致过拟合造成。最终,采用的二次型寻优网络的参数及训练策略为:每层10个神经元、2个隐藏层、ReLU激活函数、二次型寻优算法、合并6口井的数据作为训练集。
训练时间也是评判网络模型优劣的重要标准,表 3展示了每次试验的训练时间。由于试验设置了损失函数阈值,达到阈值的几组试验会提前终止训练,训练时间明显减少。过于复杂的网络模型及过于简单的模型在训练时均不能达到阈值,故训练时间较长。此外,Adam算法与Tanh激活函数搭配使用时,同样不能达到阈值,训练提前结束,且预测效果欠佳;但当二次型算法与Tanh激活函数搭配时,结果恰恰相反,网络收敛速度快且评分更高,其效果与ReLU激活函数相当。说明激活函数与算法相互影响,Tanh和ReLU激活函数更适用于二次型算法。最终网络选用ReLU函数进行横波速度预测。
2.3 二次型寻优网络预测效果分析 2.3.1 算法预测效果对比选取二次型算法和Adam算法分别用验证井b1进行对比试验。分析过程中利用根均方误差(RMSE)作为网络评判标准
| $ \xi=\sqrt{\frac{1}{n} \sum\limits_{i=1}^{n}\left[y_{i}^{\text {pre }}-y_{i}^{\text {true }}\right]^{2}} $ | (13) |
式中:n为验证样本个数;yipre和yitrue分别为横波速度预测输出值和真实值。
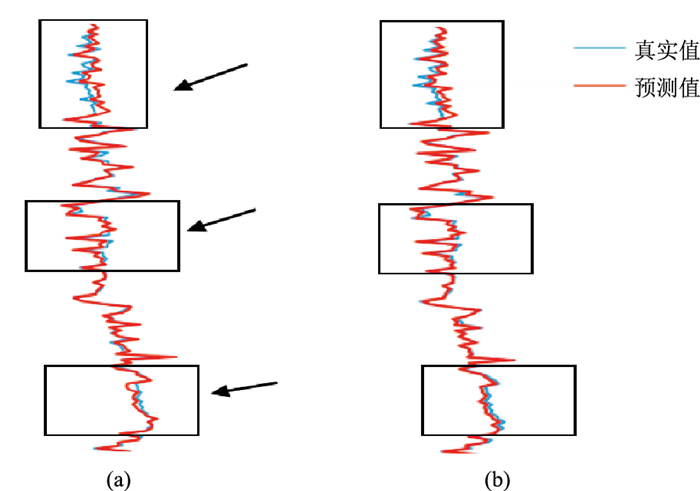
表 5统计了两种优化算法预测结果的ξ、MSE和训练时间,图 6显示两种优化算法得到的预测曲线对比。数据显示Adam算法和二次型算法的ξ分别为19.67和14.97,二次型算法的ξ明显降低近24%,说明二次型寻优算法预测精度更高。从图 6方框中可直观地看出,使用二次型寻优算法训练模型得到的横波速度预测曲线与真实值曲线拟合程度更高,说明该方法在横波速度预测中适用性更强。
|
|
表 5 两种优化算法预测结果对比 |
|
图 6 两种优化算法预测曲线对比 (a)Adam优化算法;(b)二次型算法 |
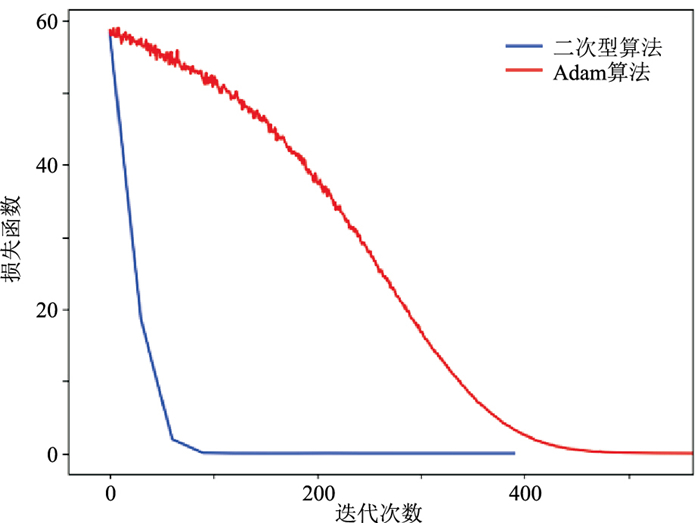
在训练效率方面,由表 5训练时间统计结果可知,二次型寻优算法训练时间只有Adam算法的十分之一,显然效率更高。从图 7损失函数下降曲线对比可见,二次型算法经过近100次迭代即可将损失函数值降低至接近零值,而Adam算法则需要近500次迭代才能达到相同效果。因此,于牛顿迭代算法基础上衍生而来的二次型寻优算法,同样具备收敛迅速的优点。
|
图 7 损失函数下降曲线对比 |
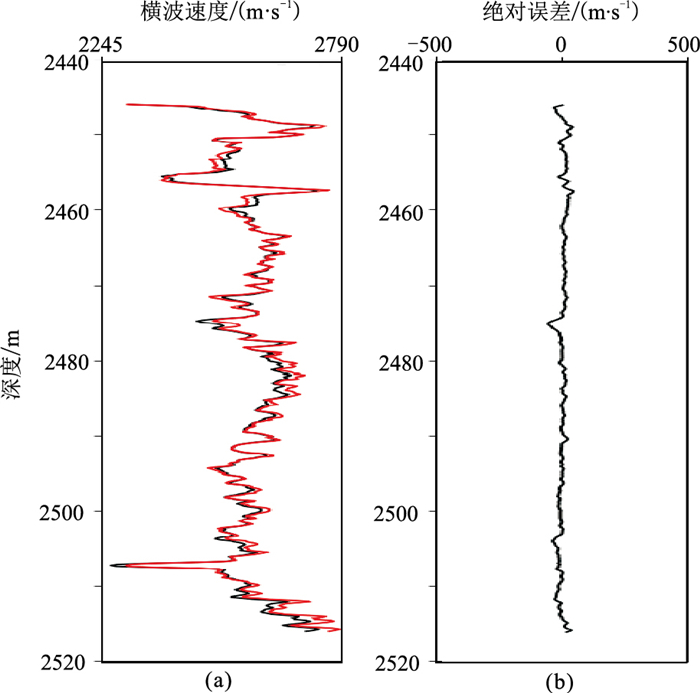
用测试井b2进行预测效果分析,使用正交试验优选后的网络进行横波速度预测。图 8a显示二次型寻优网络的横波速度预测曲线与实际曲线吻合程度较高,图中两曲线几乎重合,RMSE为15.56;同时,图 8b的绝对误差曲线显示误差的绝对值小于50m/s,表明两条曲线具有较高的匹配度。预测成果表明二次型寻优网络在横波速度预测中精度高、结果稳定。
|
图 8 二次型寻优网络的横波速度预测成果图 (a)真实(红)与预测(黑)值曲线对比;(b)真实与预测值绝对误差曲线 |
本文构建了一种端到端二次型寻优网络进行横波速度预测,同时,为了提高预测精度,利用正交试验法优选出网络参数及训练策略的最优组合,提高了网络的训练速度及预测效果。通过实际测井数据的训练和预测结果得出以下结论。
(1) 采用正交试验法进行横波速度预测的网络结构优选效果良好。只需进行16次正交试验,就能筛选出最优的网络参数及训练策略。最终确定最优网络参数及训练策略为:每层10个神经元、二次型寻优算法、ReLU激活函数、合并6口井的数据作为训练集、2个隐藏层。使用优选网络预测的横波速度精度高,预测结果稳定。
(2) 相对于Adam算法,二次型寻优算法不仅预测效果好,且训练效率高。从两种算法的RMSE对比结果可知,二次型算法比Adam算法降低近24%,说明基于二次型寻优算法的横波速度预测精度高。从训练过程的误差曲线及两种算法结果对比表可看出,二次型寻优算法的迭代次数和训练时间远小于Adam算法,说明二次型寻优算法具有更高的训练效率。
需要说明的是,二次型寻优算法在靠近极小值时收敛速度会变得缓慢,此时单纯增加训练次数只会降低计算效率,并不能明显提高预测精度,根据训练误差合理地设置阈值可以缓解这个问题。
| [1] |
郭栋, 印兴耀, 吴国忱. 横波速度计算方法与应用[J]. 石油地球物理勘探, 2007, 42(5): 535-538. GUO Dong, YIN Xingyao, WU Guochen. Computational approach of S-wave velocity and application[J]. Oil Geophysical Prospecting, 2007, 42(5): 535-538. DOI:10.3321/j.issn:1000-7210.2007.05.009 |
| [2] |
孙福利, 杨长春, 麻三怀, 等. 横波速度预测方法[J]. 地球物理学进展, 2008, 23(2): 470-474. SUN Fuli, YANG Changchun, MA Sanhuai, et al. An S-wave velocity predicted method[J]. Progress in Geophysics, 2008, 23(2): 470-474. |
| [3] |
GREENBERG M L, CASTAGNA J P. Shear-wave velocity estimation in porous rocks: theoretical formulation, preliminary verification, and applications[J]. Geophysical Prospecting, 1992, 40(2): 195-209. DOI:10.1111/j.1365-2478.1992.tb00371.x |
| [4] |
CASTAGNA J P, BATALE M L, EASTWOOD R L. Relationships between compressional-wave and shear-wave velocities in clastic silicate rocks[J]. Geophy-sics, 1985, 50(4): 571-581. |
| [5] |
XU S Y, WHITE R E. A new velocity model for clay-sand mixtures[J]. Geophysical Prospecting, 1995, 43(1): 91-118. DOI:10.1111/j.1365-2478.1995.tb00126.x |
| [6] |
XU S Y, WHITE R E. A physical model for shear-wave velocity prediction[J]. Geophysical Prospecting, 1996, 44(4): 687-717. DOI:10.1111/j.1365-2478.1996.tb00170.x |
| [7] |
XU S Y, PAYNE M A. Modeling elastic properties in carbonate rocks[J]. The Leading Edge, 2009, 28(1): 66-74. DOI:10.1190/1.3064148 |
| [8] |
PAYNE S S, WILD P, LUBBE R. An integrated solution to rock physics modeling in fractured carbonate reservoirs[C]. SEG Technical Program Expanded Abstracts, 2010, 29: 358-362.
|
| [9] |
张秉铭, 刘致水, 刘俊州, 等. 鄂尔多斯盆地北部复杂碳酸盐岩横波速度预测研究[J]. 石油物探, 2017, 56(3): 328-337. ZHANG Bingming, LIU Zhishui, LIU Junzhou, et al. An improved S-wave velocity prediction method for complex carbonate reservoir in North Ordos Basin, China[J]. Geophysical Prospecting for Petroleum, 2017, 56(3): 328-337. DOI:10.3969/j.issn.1000-1441.2017.03.003 |
| [10] |
张元中, 周开金, 赵建斌, 等. 砂泥岩地层横波测井曲线预测方法研究[J]. 石油物探, 2012, 51(5): 508-514. ZHANG Yuanzhong, ZHOU Kaijin, ZHAO Jianbin, et al. Shear-wave logging curve prediction method for shaly sand formation[J]. Geophysical Prospecting for Petroleum, 2012, 51(5): 508-514. DOI:10.3969/j.issn.1000-1441.2012.05.013 |
| [11] |
罗水亮, 杨培杰, 胡光明, 等. 基于变形P-L模型的矩阵方程迭代精细横波预测[J]. 地球物理学报, 2016, 59(5): 1839-1848. LUO Shuiliang, YANG Peijie, HU Guangming, et al. S-wave velocity prediction based on the modified P-L model and matrix equation iteration[J]. Chinese Journal of Geophysics, 2016, 59(5): 1839-1848. |
| [12] |
唐杰, 王浩, 姚振岸, 等. 基于岩石物理诊断的横波速度估算方法[J]. 石油地球物理勘探, 2016, 51(3): 537-543. TANG Jie, WANG Hao, YAO Zhen'an, et al. Shear wave velocity estimation based on rock physics diagnosis[J]. Oil Geophysical Prospecting, 2016, 51(3): 537-543. |
| [13] |
林凯, 贺振华, 熊晓军, 等. 基于基质矿物模量自适应提取横波速度反演方法[J]. 石油地球物理勘探, 2013, 48(2): 262-267. LIN Kai, HE Zhenhua, XIONG Xiaojun, et al. S-wave velocity inversion based on adaptive extraction of matrix mineral modulus[J]. Oil Geophysical Prospecting, 2013, 48(2): 262-267. |
| [14] |
张繁昌, 刘汉卿, 钮学民, 等. 褶积神经网络高分辨率地震反演[J]. 石油地球物理勘探, 2014, 49(6): 1165-1169. ZHANG Fanchang, LIU Hanqing, NIU Xuemin, et al. High resolution seismic inversion by convolutional neural network[J]. Oil Geophysical Prospecting, 2014, 49(6): 1165-1169. |
| [15] |
桑凯恒, 张繁昌. 基于模糊粗糙集的机器学习储层参数预测[J]. CT理论与应用研究, 2018, 27(4): 455-464. SANG Kaiheng, ZHANG Fanchang. Prediction of re-servoir parameters of machine learning based on fuzzy rough set[J]. CT Theory and Applications, 2018, 27(4): 455-464. |
| [16] |
徐旺林, 张繁昌, 郭彦如, 等. 贝叶斯全频信息同时反演在鄂尔多斯盆地碳酸盐岩储层预测中的应用[J]. 石油地球物理勘探, 2014, 49(4): 723-728. XU Wanglin, ZHANG Fanchang, GUO Yanru, et al. Bayesian full frequency simultaneous inversion for carbonate reservoir in Erdos Basin[J]. Oil Geophysical Prospecting, 2014, 49(4): 723-728. |
| [17] |
ZHANG Z D, ALKHALIFAH T. Regularized elastic full-waveform inversion using deep learning[J]. Geo-physics, 2019, 84(5): 741-751. |
| [18] |
YANG F S, MA J W. Deep-learning inversion: A next-generation seismic velocity model building me-thod[J]. Geophysics, 2019, 84(4): 583-599. DOI:10.1190/geo2018-0249.1 |
| [19] |
RUMELHART D, HINTON G, WILLIAMS R. Lear-ning representations by back-propagating errors[J]. Nature, 1986, 323(9): 533-536. |
| [20] |
吕晶, 谢润成, 周文, 等. LM-BP神经网络在泥页岩地层横波波速拟合中的应用[J]. 中国石油大学学报(自然科学版), 2017, 41(3): 75-83. LYU Jing, XIE Runcheng, ZHOU Wen, et al. Application of LM-BP neural network in simulation of shear wave velocity of shale formation[J]. Journal of China University of Petroleum (Edition of Natural Science), 2017, 41(3): 75-83. DOI:10.3969/j.issn.1673-5005.2017.03.009 |
| [21] |
孙宇航, 刘洋. 利用GRU神经网络预测横波速度[J]. 石油地球物理勘探, 2020, 55(3): 484-492. SUN Yuhang, LIU Yang. Prediction of S-wave velo-city based on GRU neural network[J]. Oil Geophysical Prospecting, 2020, 55(3): 484-492. |
| [22] |
KINGMA D P, BA J L. Adam: A method for stochastic optimization[C]. International Conference on Learning Representations, 2015, 1-13.
|
| [23] |
常兆光, 王清河, 杜彩凤. 应用统计方法[M]. 北京: 石油工业出版社, 2009. CHANG Zhaoguang, WANG Qinghe, DU Caifeng. Applied Statistical Methods[M]. Beijing: Petroleum Industry Press, 2009. |
| [24] |
SHEWCHUK J R. An Introduction to the Conjugate Gradient Method Without the Agonizing Pain[R]. School of Computer Science, Carnegie Mellon University, PA United States, 1994.
|



 张繁昌, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email:
张繁昌, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email: 