② 中国海洋大学海洋地球科学学院, 山东青岛 266100;
③ 海底科学与探测技术教育部重点实验室, 山东青岛 266100
② College of Marine Geosciences, Ocean University of China, Qingdao, Shandong 266100, China;
③ Key Lab of Submarine Geosciences and Prospecting Techniques of Ministry of Education, Qing-dao, Shandong 266100, China
海洋可控源电磁法是探测海底天然气水合物和油气资源等矿产资源的一种海洋地球物理勘探方法[1]。与围岩相比,石油和天然气水合物储层通常表现为高阻体,其电阻率是海底地层电阻率的数倍甚至几十倍,这为海洋可控源电磁探测提供了良好的物性基础[2-4]。与陆上油气勘探相比,海洋油气勘探风险较大,开采成本较高,因此,需要综合多种地质和地球物理方法进行海洋油气资源的探测[5]。利用海洋地震勘探方法可以获得海底地质构造信息,但难以确定构造内部流体的性质。利用海洋可控源电磁法,可以有效判断地震勘探方法圈定的异常体内的流体性质,有利于提高海洋油气资源勘探的成功率。
随着油田进入高含水率的开发晚期,开展油、气、水的识别、剩余油分布预测和油藏动态监测技术研究具有重大应用需求和实际意义[6-7]。近年来,时移地震方法得到了较大发展,该方法对油气藏开采过程的监测具有重要的应用价值。但是,时移地震技术对油田的储层条件和注采方式要求较高,时移重力法、时移电磁法等地球物理方法随之逐渐发展起来[8]。在时移电磁技术发展方面,目前的研究大多集中于数值模拟和可行性分析阶段。Lien等[9]通过数值模拟分析了海洋可控源电磁法用于监测油藏注水前缘的可行性;Orange等[10]基于经典二维油气模型分析了海洋可控源电磁法用于油气储层开采过程监测的可行性;Schamper等[11]通过建立陆地模型讨论了利用可控源电磁法确定油水界面(OWC)横向变化的可行性;Kong等[12]在传统海洋可控源电磁法的基础上,将电磁采集装置置于油气井中,验证了该方法用于油气开发监测的有效性;Wirianto等[13]通过复杂三维电阻率模型的数值模拟,研究了利用陆地可控源电磁法监测油气储层变化的可行性;Berre等[14]提出了一套适用于时移可控源电磁数据的三维反演算法;Black等[15]通过模型研究证明了通过时移海洋可控源电磁数据的三维反演可以确定油—水和气—水接触面;Black等[16]模拟了北海哈丁油田从试生产到停止开采期间的海洋可控源电磁数据,并通过三维反演确定了油—水和气—水界面,研究结果表明利用聚焦正则化反演结果能够成功监测油—水和气—水之间电阻率的剧烈变化,而平滑正则化反演则不能。除可行性分析外,一些学者还开展了井间电磁探测方法用于油藏开采监测的分析和监测试验等工作。沈金松等[17]分析了井间电磁探测方法在油气储层监测中的应用状况和存在的问题,并指出了井间电磁探测技术未来的发展方向;谢兴兵等[18]开展了时移长偏移距瞬变电磁法剩余油监测试验,初步验证了该方法对剩余油边界探测的有效性;王显祥等[19]探讨了多通道瞬变电磁法对油气动态监测的优势,研究结果表明多通道瞬变电磁法在合适偏移距下可有效圈定油气藏边界,并揭示了油气藏中油、气、水的分布变化;Li等[20]提出了多场源、多方位地—井垂直电磁剖面法,采用积分方程法模拟了油气藏注水开采进程中油气储层电阻率和含油饱和度动态变化时的电磁响应特征;Liu等[21]对页岩气田水力压裂过程进行了数值模拟和现场试验,结果验证了可控源电磁法对页岩气生产监测具有良好效果。
前人研究表明,将海洋可控源电磁法用于油气储层开采过程的监测是可行的,但这些研究未对影响监测效果的因素进行详细分析,且大多是基于海洋一维地电模型。因此,本文基于二维海洋地电模型,对不同发射频率、储层埋深、储层厚度、海水深度及不同工作方式下的海洋电磁场进行仿真模拟,详细分析了影响海洋可控源电磁法监测油气储层开采过程的因素。此外,本文还对比分析了“海底发射,海底接收”、“海底发射,井中接收”和“井中发射,井中接收”三种观测方式的监测效果。
1 二维正演理论 1.1 控制方程假定时谐因子为e-iωt,在似稳态情形下,电场E和磁场H满足控制方程
| $ \left\{\begin{array}{l} \nabla \times \boldsymbol{E}={\rm{i}} \omega \mu_{0} \boldsymbol{H} \\ \nabla \times \boldsymbol{H}-\sigma \boldsymbol{E}=\boldsymbol{J}_{\mathrm{s}} \end{array}\right. $ | (1) |
式中:μ0为真空中的磁导率;ω为角频率;σ为电导率;Js为电源电流分布。
对于一个二维海洋地电模型,假设构造走向为x,水平电偶源置于海底上方一定深度的海水中。对电场或者磁场沿x方向做傅里叶变换,即
| $ \hat{F}\left(k_{x}, y, z\right)=\int_{-\infty}^{\infty} f(x, y, z) \mathrm{e}^{-\mathrm{i} k_{x} x} \mathrm{~d} x $ | (2) |
式中:f代表电场E或磁场H的某个分量;kx为x方向的波数。
根据傅里叶变换的性质,可将式(1)转化为
| $ \begin{aligned} \nabla \cdot\left(\frac{{\rm{i}} \omega \mu_{0}}{\gamma^{2}} \nabla \hat{H}_{x}\right) &-{\rm{i}} \omega \mu_{0} \hat{H}_{x}-\frac{\partial}{\partial y}\left(\frac{{\rm{i}} k_{x}}{\gamma^{2}} \frac{\partial \hat{E}_{x}}{\partial z}\right)+\\ \frac{\partial}{\partial z}\left(\frac{{\rm{i}} k_{x}}{\gamma^{2}} \frac{\partial \hat{E}_{x}}{\partial y}\right) &=-\frac{\partial}{\partial y} \frac{{\rm{i}} \omega \mu_{0} J_{z} \delta_{\mathrm{A}}}{\gamma^{2}}+\frac{\partial}{\partial z} \frac{{\rm{i}} \omega \mu_{0} J_{y} \delta_{\mathrm{A}}}{\gamma^{2}} \end{aligned} $ | (3) |
| $ \begin{aligned} \nabla \cdot&\left(\frac{\sigma}{\gamma^{2}} \nabla \hat{E}_{x}\right)-\sigma \hat{E}_{x}-\frac{\partial}{\partial y}\left(\frac{\mathrm{i} k_{x}}{\gamma^{2}} \frac{\partial \hat{H}_{x}}{\partial z}\right)+\frac{\partial}{\partial z}\left(\frac{\mathrm{i} k_{x}}{\gamma^{2}} \frac{\partial \hat{H}_{x}}{\partial y}\right)= \\ &-\frac{\partial}{\partial y} \frac{\mathrm{i} k_{x} J_{y} \delta_{\mathrm{A}}}{\gamma^{2}}-\frac{\partial}{\partial z} \frac{\mathrm{i} k_{x} J_{z} \delta_{\mathrm{A}}}{\gamma^{2}}+J_{x} \delta_{\mathrm{A}} \end{aligned} $ | (4) |
式中:上标“^”表示波数域变量;δA=δ(ys)δ(zs)为模拟源分布的Delta函数,ys和zs表示发射源在y、z方向上的坐标;Jx、Jy、Jz分别代表电偶源x、y、z方向的偶极矩;γ2=kx2-iωμ0σ。
1.2 有限元方程利用加权余量法,由式(3)和式(4)出发可导出积分方程。将式(4)乘以电场的任意变分
| $ \begin{aligned} &\int_{\boldsymbol{\varOmega}} \frac{\sigma}{\gamma^{2}} \nabla \hat{E}_{x} \cdot \nabla \delta \hat{E}_{x} \mathrm{~d} \boldsymbol{\varOmega}+\int_{\boldsymbol{\varOmega}} \sigma \hat{E}_{x} \delta \hat{E}_{x} \mathrm{~d} \boldsymbol{\varOmega}- \\ &\ \ \ \ \int_{\boldsymbol{\varOmega}}\left(\frac{\partial \delta \hat{E}_{x}}{\partial y} \frac{{\rm{i}} k_{x}}{\gamma^{2}} \frac{\partial \hat{H}_{x}}{\partial z}-\frac{\partial \delta \hat{E}_{x}}{\partial z} \frac{{\rm{i}} k_{x}}{\gamma^{2}} \frac{\partial \hat{H}_{x}}{\partial y}\right) \mathrm{d} \boldsymbol{\varOmega} \\ &\ \ \ \ \ \ \ \ =-\oint_{\boldsymbol{\varGamma}} \delta \hat{E}_{x} \hat{H}_{\mathrm{t}} \mathrm{d} \boldsymbol{\varGamma}-\int_{\boldsymbol{\varOmega}} \frac{{\rm{i}} k_{x}}{\gamma^{2}}\left(\frac{\partial \delta \hat{E}_{x}}{\partial y} J_{y} \boldsymbol{\delta}_{\mathrm{A}}+\right. \\ &\ \ \ \ \ \ \ \ \left.\frac{\partial \delta \hat{E}_{x}}{\partial z} J_{z} \delta_{\mathrm{A}}\right) \mathrm{d} \boldsymbol{\varOmega}-\int_{\boldsymbol{\varOmega}} \delta \hat{E}_{x} J_{x} \delta_{\mathrm{A}} \mathrm{d} \boldsymbol{\varOmega} \end{aligned} $ | (5) |
式中:Γ表示模拟区域的边界;
类似地,将式(3)乘以磁场的任意变分
| $ \begin{aligned} &-\int_{\boldsymbol{\varOmega}} \frac{\mathrm{i} \omega \mu_{0}}{\gamma^{2}} \nabla \hat{H}_{x} \cdot \nabla \delta \hat{H}_{x} \mathrm{~d} \boldsymbol{\varOmega}-\int_{\boldsymbol{\varOmega}} \mathrm{i} \omega \mu_{0} \hat{H}_{x} \delta \hat{H}_{x} \mathrm{~d} \boldsymbol{\varOmega}+ \\ &\ \ \ \ \int_{\boldsymbol{\varOmega}}\left(\frac{\partial \delta \hat{H}_{x}}{\partial y} \frac{\mathrm{i} k_{x}}{\gamma^{2}} \frac{\partial \hat{E}_{x}}{\partial z}-\frac{\partial \delta \hat{H}_{x}}{\partial z} \frac{\mathrm{i} k_{x}}{\gamma^{2}} \frac{\partial \hat{E}_{x}}{\partial y}\right) \mathrm{d} \boldsymbol{\varOmega} \\ &\ \ \ \ \ \ \ \ =\int_{\boldsymbol{\varOmega}} \frac{\mathrm{i} \omega \mu_{0}}{\gamma^{2}}\left(J_{z} \delta_{\mathrm{A}} \frac{\partial \delta \hat{H}_{x}}{\partial y}-J_{y} \delta_{\mathrm{A}} \frac{\partial \delta \hat{H}_{x}}{\partial z}\right) \mathrm{d} \boldsymbol{\varOmega}+ \\ &\ \ \ \ \ \ \ \ \ \ \ \ \oint_{\boldsymbol{\varGamma}} \delta \hat{H}_{x} \hat{E}_{\mathrm{t}} \mathrm{d} \boldsymbol{\varGamma} \end{aligned} $ | (6) |
式中
将求解区域Ω分解成n个三角单元,单元编号记为e=1, 2, …, n。式(5)和式(6)的积分可分解为各个单元积分之和
| $ \begin{aligned} &\sum\limits_{e=1}^{n} \int_{\boldsymbol{\varOmega} e} \frac{\sigma}{\gamma^{2}} \nabla \hat{E}_{x} \cdot \nabla \delta \hat{E}_{x} \mathrm{~d} \boldsymbol{\varOmega}+\sum\limits_{e=1}^{n} \int_{\boldsymbol{\varOmega} e} \sigma \hat{E}_{x} \delta \hat{E}_{x} \mathrm{~d} \boldsymbol{\varOmega}- \\ &\ \ \ \ \sum\limits_{e=1}^{n} \int_{\boldsymbol{\varOmega}{e}}\left(\frac{\partial \delta \hat{E}_{x}}{\partial y} \frac{\mathrm{i} k_{x}}{\gamma^{2}} \frac{\partial \hat{H}_{x}}{\partial z}-\frac{\partial \delta \hat{E}_{x}}{\partial z} \frac{\mathrm{i} k_{x}}{\gamma^{2}} \frac{\partial \hat{H}_{x}}{\partial y}\right) \mathrm{d} \boldsymbol{\varOmega} \\ &\ \ \ \ \ \ \ \ =-\sum\limits_{e=1}^{n} \oint_{\boldsymbol\varGamma_{e}} \delta \hat{E}_{x} \hat{H}_{\mathrm{t}} \mathrm{d} \boldsymbol{\varGamma}-\sum\limits_{e=1}^{n} \int_{\boldsymbol{\varOmega} e} \delta \hat{E}_{x} J_{x} \delta_{\mathrm{A}} \mathrm{d} \boldsymbol{\varOmega}- \\ &\ \ \ \ \ \ \ \ \ \ \ \ \sum\limits_{e=1}^{n} \int_{\boldsymbol{\varOmega} e} \frac{\mathrm{i} k_{x}}{\gamma^{2}}\left(\frac{\partial \delta \hat{E}_{x}}{\partial y} J_{y} \delta_{\mathrm{A}}+\frac{\partial \delta \hat{E}_{x}}{\partial z} J_{z} \delta_{\mathrm{A}}\right) \mathrm{d} \boldsymbol{\varOmega} \end{aligned} $ | (7) |
| $ \begin{aligned} -& \sum\limits_{e=1}^{n} \int_{\boldsymbol{\varOmega} e} \frac{\mathrm{i} \omega \mu_{0}}{\gamma^{2}} \nabla \hat{H}_{x} \cdot \nabla \delta \hat{H}_{x} \mathrm{~d} \boldsymbol{\varOmega}-\sum\limits_{e=1}^{n} \int_{\boldsymbol{\varOmega} e} \mathrm{i} \omega \mu_{0} \hat{H}_{x} \delta \hat{H}_{x} \mathrm{~d} \boldsymbol{\varOmega}+\\ & \sum\limits_{e=1}^{n} \int_{\boldsymbol{\varOmega} e}\left(\frac{\partial \delta \hat{H}_{x}}{\partial y} \frac{\mathrm{i} k_{x}}{\gamma^{2}} \frac{\partial \hat{E}_{x}}{\partial z}-\frac{\partial \delta \hat{H}_{x}}{\partial z} \frac{\mathrm{i} k_{x}}{\gamma^{2}} \frac{\partial \hat{E}_{x}}{\partial y}\right) \mathrm{d} \boldsymbol{\varOmega} \\ &=\sum\limits_{e=1}^{n} \int_{\boldsymbol{\varOmega} e} \frac{\mathrm{i} \omega \mu_{0}}{\gamma^{2}}\left(J_{z} \delta_{\mathrm{A}} \frac{\partial \delta \hat{H}_{x}}{\partial y}-J_{y} \delta_{\mathrm{A}} \frac{\partial \delta \hat{H}_{x}}{\partial z}\right) \mathrm{d} \boldsymbol{\varOmega}+\\ &\ \ \ \ \ \sum\limits_{e=1}^{n} \oint_{\boldsymbol{\varGamma}_{e}} \delta \hat{H}_{x} \hat{E}_{\mathrm{t}} \mathrm{d} \boldsymbol{\varGamma} \end{aligned} $ | (8) |
由于切向分量
| $ \boldsymbol{K} \boldsymbol{U}=\boldsymbol{P} $ | (9) |
式中:K为复稀疏系数矩阵; U为电磁场分量; P为式(7)或式(8)的右端项。
本文采用直接求解方法(MUMPS)求解式(9),采用自适应网格细化策略获得高精度的数值解,详细推导过程见文献[5, 22]。
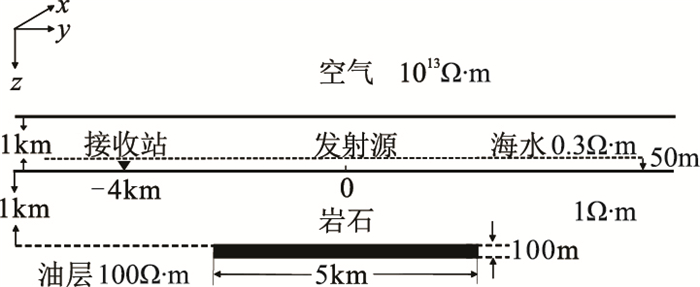
2 二维油气模型为了开展深海油藏开采过程监测仿真研究,建立图 1所示的二维海洋地电模型进行数值模拟。在距离海底上方50m的测线上沿y轴在-10~10km范围内匀速拖曳一个水平电偶极源。发射源长度为1m,发射电流为1A。拖曳过程中,假定发射源每移动200m发射一次电流。电磁信号采集站位于海底y=-4km处。本文采用海洋可控源电磁法二维正演程序[5]进行电磁信号数值模拟,该程序采用自适应有限元法分别求解关于总场和异常场的边值问题,有限元求解过程中采用非结构化三角单元网格剖分模型,利用后验误差估计方法指导网格加密细化。在图 1所示的二维海洋电磁地电模型下建立初始网格,网格单元数为485,采用自适应有限元方法[5]对网格逐步细化,每次增加大约5%的单元数,最终得到满足精度要求的细网格。由于采用分组并行计算,每组包含不同数量的发射和接收位置点,因此最终得到的网格大小及数量会有所不同。本文所有模拟均假设沿y轴正方向开采油气储层,开采后油气层的电阻率为1Ω·m。
|
图 1 二维海洋电磁地电模型 |
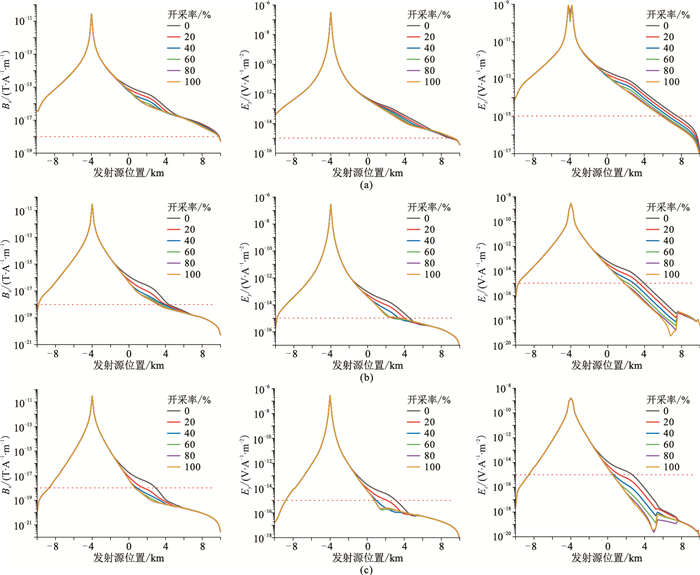
为研究发射频率对油气储层开采过程监测效果的影响,发射频率设为0.1、0.5、1.0Hz,依次计算油气储层不同开采程度下的电磁响应,结果见图 2。图中红色虚线表示海底电磁采集站的本底噪声,本文假设磁场本底噪声Babs=1×10-18T·A-1·m-1,电场本底噪声Eabs=1×10-15V·A-1·m-2。
|
图 2 不同发射频率下电磁分量Bx(左)、Ey(中)、Ez(右)响应曲线 (a)0.1Hz;(b)0.5Hz;(c)1.0Hz |
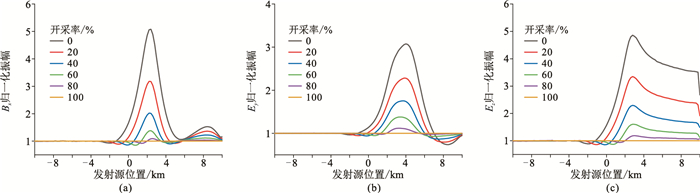
由图 2可知,随着发射频率增大,电磁响应的衰减速度增大。与分量Ey相比,分量Ez幅值较小,且衰减速度较大。需要注意的是,当发射源位于采集站正上方时,分量Ez的值应为零,但由于插值精度的原因,无法正确获得精确值,误差较大。为了进一步分析油气开采过程中电磁响应的变化特征,计算了归一化振幅(模型电磁响应与一维均匀半空间模型电磁响应的比值),发射频率为0.1Hz时的电磁场归一化振幅如图 3所示。由图 3可知,随着油气储层开采率的增大,归一化振幅逐渐减小。因此,油气储层开采过程的监测应选用较低的发射频率激发电磁场信号,电磁场的分析应以分量Bx和Ey为主。不同的电磁场分量归一化振幅最大值出现的位置是不同的,分量Bx、Ey和Ez的归一化振幅最大值分别出现在发射源位于2.4、4.0、2.8km的情况。为达到最佳的监测效果,应根据实际油气储层位置决定电磁信号采集站和发射源的位置。
|
图 3 发射频率为0.1Hz时电磁场分量Bx(a)、Ey(b)、Ez(c)归一化振幅 |
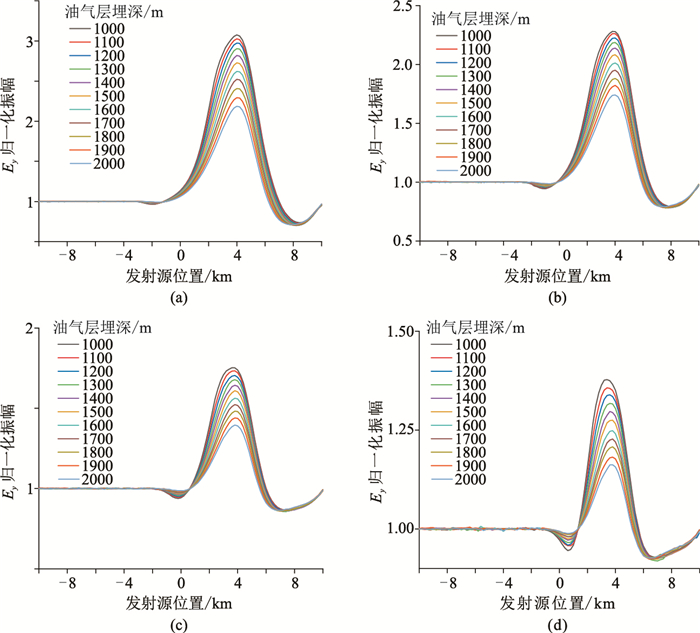
为了研究油气储层埋深对油气开采过程监测效果的影响,设计一个包含一组不同埋深油气储层的模型。油气储层厚度为100m,顶面埋深为1000~2000m,每隔100m取一个值。发射频率为0.1Hz,分别计算不同油气储层埋深、不同开采率下的Ey分量的归一化振幅,模拟结果见图 4。由图可知,即使油气储层埋深逐渐增大,归一化振幅最大值对应的发射源位置是不变的,但其幅值越来越小。这说明油气储层越深,其电磁响应越弱,不利于对其开采过程进行监测。
|
图 4 开采率为0(a)、20%(b)、40%(c)、60%(d)时不同油气储层埋深的Ey分量归一化振幅 |
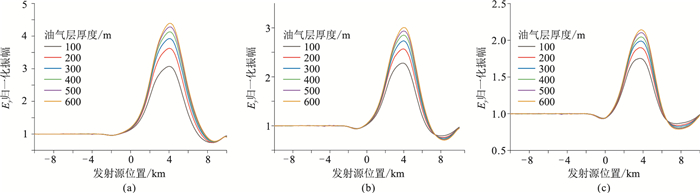
为了研究油气储层厚度对油气开采过程监测效果的影响,建立一组不同厚度的油气储层模型。储层厚度为100~600m,每隔100m取一个值,储层顶面埋深为1000m。设定发射频率为0.1Hz,分别计算不同油气储层厚度、不同开采率情况下Ey分量的归一化振幅,结果见图 5。由图可知,随着油气储层厚度增大,归一化振幅逐渐增大,这是由于随着油气储层规模的增大,其电磁响应增大。
|
图 5 开采率为0(a)、20%(b)、40%(c)时不同油气储层厚度的Ey分量归一化振幅 |
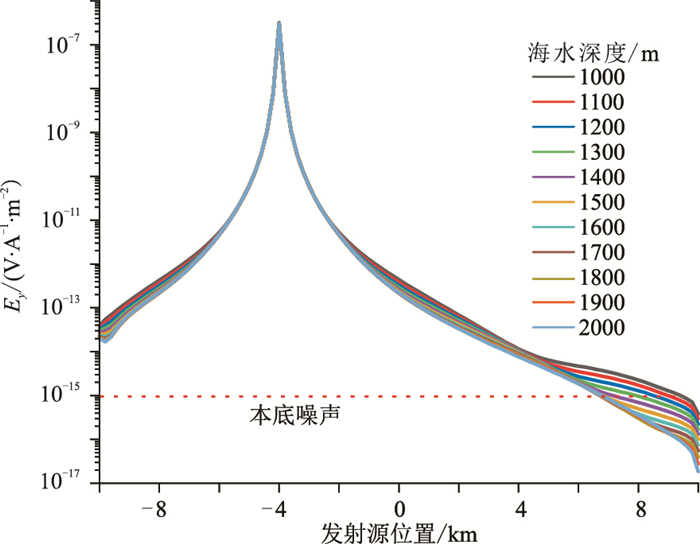
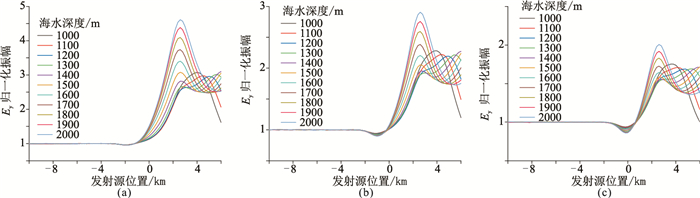
为了研究海水深度对油气开采过程监测效果的影响,选择一组海水深度1000~2000m,每隔100m取一个值,分别计算不同海水深度、不同开采率情况下的Ey分量归一化振幅(不含高阻油气层),结果见图 6。由图可知,当发射源靠近电磁采集站时,不同海水深度情况下的电磁场响应幅值相差不大;当收发距较大时,随着海水深度增大,电磁响应随收发距增大的衰减速度增大。当海水深度为2000m、发射源位置为7km时,Ey分量振幅小于海底电磁采集站的本底噪声。不同油气储层开采率下Ey分量归一化振幅结果见图 7。为了避免低于本底噪声的电磁响应对归一化振幅计算结果的影响,在计算归一化振幅时只保留了大于本底噪声的值。由图可知:当海水深度为1000、1100、1200和1300m时,同一开采率下Ey分量归一化振幅的极大值相差不大,只是对应的发射源位置不同;当海水深度大于1400m时,Ey分量归一化振幅的极大值随海水深度增大而增大,且对应的发射源位置不变,均位于油气储层的右边界处。这说明在1400~2000m海水深度范围内,海水深度越大,高阻油气储层的电磁响应越明显,越有利于油气储层开采过程的监测。
|
图 6 不同海水深度时均匀半空间模型Ey分量振幅 |
|
图 7 开采率为0(a)、20%(b)、40%(c)时不同海水深度下Ey分量归一化振幅 |
上述仿真算例中,电磁信号采集站均放置于海底,发射源在距离海底上方50m沿测线方向匀速拖曳,这种观测方式称为“海底发射,海底接收”。下面将讨论“海底发射、井中接收”和“井中发射、井中接收”两种观测方式对油气储层开采过程监测的影响。
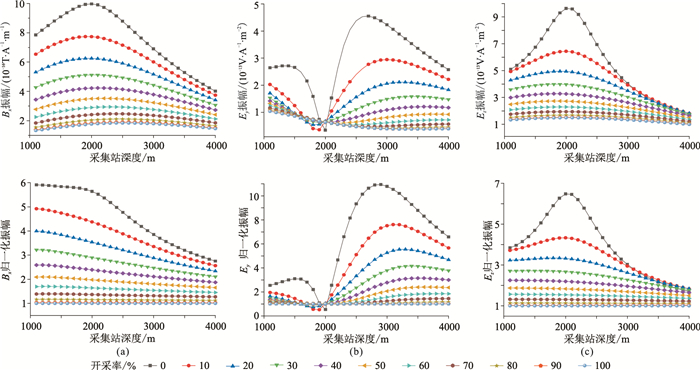
3.5.1 海底发射、井中接收为探讨海底发射、油气井中接收方式是否适宜油气储层开采过程的监测,将发射源置于海底上方50m、y=2.5km处,观测井位于油气储层左侧y=-3km处,将采集站均匀放置于井中1100~4000m深度范围,间隔为100m,发射频率为0.1Hz。设定11种不同的油气层开采率,分别为0、10%、20%、30%、40%、50%、60%、70%、80%、90%和100%。采集站位于井中不同深度、不同开采率下的电磁响应模拟结果见图 8。由图 8上可知,当采用井中观测方式时,电磁响应随采集站深度增大衰减较慢,1100~4000m深度范围内的电磁响应幅值保持相同的数量级。从Bx、Ey和Ez三个电磁分量幅值均能观测到由于油气开采引起的电磁响应变化。从归一化振幅(图 8下)来看,在油气层开采前,Ey分量归一化振幅的最大值约为11,明显大于“海底发射,海底接收”观测方式下的归一化振幅的最大值(图 3),说明井中观测方式更有利于油气储层开采过程的监测。
|
图 8 海底发射、井中接收方式下电磁分量Bx(a)、Ey(b)、Ez(c)振幅(上)及归一化振幅(下) |
假设发射源(垂直电偶极源)位于油气储层右侧y=3km处的垂直井中,深度范围为1100~4000m,间距为100m,发射频率为0.1Hz。观测井位于y=-3km处,采集站深度分别为1000、1500、2000、2500m。模拟“井中发射、井中接收”方式下油藏开采过程的监测效果,设定6种不同的油气层开采率,分别为0、20%、40%、60%、80%和100%。
不同开采程度情况下、电磁采集站在不同深度的Ez分量归一化振幅模拟结果如图 9所示。由图可知,从电磁采集站位于不同深度时接收的电磁数据均能看出由油气开采导致的电磁响应的变化。发射源越靠近高阻油气储层时,Ez分量的归一化幅值越大,幅值最大点出现的位置与采集站所处深度无关;采集站越靠近高阻油气储层时,Ez归一化振幅越大。这说明若采用“井中发射,井中接收”的方式,应将采集站置于与高阻油气储层相同的深度,以实现较好的监测效果。

|
图 9 井中发射、井中接收方式下采集站深度为1000m(a)、1500m(b)、2000m(c)、2500m(d)时Ez分量归一化振幅 |
本文基于二维海洋地电模型,假设不同环境、不同工作方式,对海洋电磁法监测油藏开采过程进行仿真,详细探讨了利用海洋可控源电磁法监测油气储层开采过程的影响因素,得出以下几点认识。
(1) 发射频率、油气储层厚度、油气储层埋深、海水深度均对油气储层开采过程监测效果有影响。数值模拟结果表明:发射频率越低,电磁信号衰减越慢,因此油气储层开采过程监测应选用尽量低的发射频率;油气储层埋深越小、储层厚度越大,高阻油气储层产生的电磁响应越明显,越有利于开采过程的监测;海水深度大于1400m时,海水深度越大,Ey分量归一化振幅的最大值越大,越有利于开采过程的监测。
(2) 本文对比了“海底发射,海底接收”、“海底发射,井中接收”和“井中发射,井中接收”三种观测方式对油气储层开采过程监测效果的影响。数值模拟结果表明:“井中接收”方式下电磁响应的归一化振幅的极值最大,且电磁响应随采集站深度的增大衰减较慢,这种观测模式更有利于油气储层开采过程的监测,不足之处是这种观测方式施工难度较大。
| [1] |
CONSTABLE S. Ten years of marine CSEM for hydrocarbon exploration[J]. Geophysics, 2010, 75(5): A67-A75. |
| [2] |
CONSTABLE S, SRNKA L J. An introduction to marine controlled-source electromagnetic methods for hydrocarbon exploration[J]. Geophysics, 2007, 72(2): WA3-WA12. DOI:10.1190/1.2432483 |
| [3] |
RUST W M. A historical review of electrical prospecting methods[J]. Geophysics, 1938, 3(1): 1-6. DOI:10.1190/1.1439461 |
| [4] |
何展翔, 孙卫斌, 孔繁恕, 等. 海洋电磁法[J]. 石油地球物理勘探, 2006, 41(4): 451-457. HE Zhanxiang, SUN Weibin, KONG Fanshu, et al. Marine electromagnetic approach[J]. Oil Geophysical Prospecting, 2006, 41(4): 451-457. DOI:10.3321/j.issn:1000-7210.2006.04.019 |
| [5] |
刘颖. 海洋可控源电磁法二维有限元正演及反演[D]. 山东青岛: 中国海洋大学, 2014.
|
| [6] |
胡祖志, 何展翔, 李德春, 等. 涩北气藏时移大地电磁监测技术可行性研究[J]. 石油地球物理勘探, 2014, 49(5): 997-1005. HU Zuzhi, HE Zhanxiang, LI Dechun, et al. Reservoir monitoring feasibility study with time lapse magnetotelluric survey in Sebei Gas Field[J]. Oil Geophysical Prospecting, 2014, 49(5): 997-1005. |
| [7] |
赵平起, 郝会民, 倪天禄, 等. 油藏渗流地球物理新方法探索[J]. 石油地球物理勘探, 2019, 54(3): 719-728. ZHAO Pingqi, HAO Huimin, NI Tianlu, et al. A novel technology: reservoir seepage geophysics[J]. Oil Geophysical Prospecting, 2019, 54(3): 719-728. |
| [8] |
彭荣华, 胡祥云, 刘云祥, 等. 时移二维大地电磁法用于油藏监测的可行性研究[C]. 北京: 中国地球物理学会第二十八届年会, 2012. PENG Ronghua, HU Xiangyun, LIU Yunxiang, et al. The feasibility study of time-lapse two dimensional magnetotelluric for reservoir monitoring[C]. Exten-ded Abstracts of the Chinese Geophysics Annual Mee-ting 2012, Beijing, 2012. |
| [9] |
LIEN M, MANNSETH T. Sensitivity study of marine CSEM data for reservoir production monitoring[J]. Geophysics, 2008, 73(4): F151-F163. DOI:10.1190/1.2938512 |
| [10] |
ORANGE A, KEY K, CONSTABLE S. The feasibility of reservoir monitoring using time-lapse marine CSEM[J]. Geophysics, 2009, 74(2): F21-F29. DOI:10.1190/1.3059600 |
| [11] |
SCHAMPER C, SPITZ S, REJIBA F. 4D CSEM feasibility study: a land example[C]. SEG Technical Program Expanded Abstracts, 2009, 28: 3850-3854.
|
| [12] |
KONG F N, ROTH F, OLSEN P A, et al. Casing effects in the sea-to-borehole electromagnetic method[J]. Geophysics, 2009, 74(5): F77-F87. DOI:10.1190/1.3173807 |
| [13] |
WIRIANTO M, MULDER W A, SLOB E C. A feasibility study of land CSEM reservoir monitoring in a complex 3-D model[J]. Geophysical Journal International, 2010, 181: 741-755. |
| [14] |
BERRE I, LIEN M, MANNSETH T. Robust inversion of controlled source electromagnetic data for production monitoring[C]. SEG Technical Program Expanded Abstracts, 2010, 29: 726-731.
|
| [15] |
BLACK N, WILSON G A, GRIBENKO A V, et al. 3D inversion of time-lapse CSEM data for reservoir surveillance[C]. SEG Technical Program Expanded Abstracts, 2010, 29: 716-720.
|
| [16] |
BLACK N, WILSON G A, GRIBENKO A V, et al. 3D inversion of time-lapse CSEM data based on dynamic reservoir simulations of the Harding field, North Sea[C]. SEG Technical Program Expanded Abstracts, 2011, 30: 666-670.
|
| [17] |
沈金松, 王志刚, 马超, 等. 井间电磁油气储层监测技术的发展和应用[J]. 石油地球物理勘探, 2014, 49(1): 213-224. SHEN Jinsong, WANG Zhigang, MA Chao, et al. Application of the cross-hole electromagnetic method (CHEM) in hydrocarbon reservoir monitoring[J]. Oil Geophysical Prospecting, 2014, 49(1): 213-224. |
| [18] |
谢兴兵, 周磊, 严良俊, 等. 时移长偏移距瞬变电磁法剩余油监测方法及应用[J]. 石油地球物理勘探, 2016, 51(3): 605-612. XIE Xingbing, ZHOU Lei, YAN Liangjun, et al. Remaining oil detection with time-lapse long offset & window transient electromagnetic sounding[J]. Oil Geophysical Prospecting, 2016, 51(3): 605-612. |
| [19] |
王显祥, 底青云, 邓居智. 多通道瞬变电磁法油气藏动态检测[J]. 石油地球物理勘探, 2016, 51(5): 1021-1030. WANG Xianxiang, DI Qingyun, DENG Juzhi. Reservoir dynamic detection based on multi-channel transient electromagnetic[J]. Oil Geophysical Prospecting, 2016, 51(5): 1021-1030. |
| [20] |
LI J H, HE Z X, XU Y X. Three-dimensional numerical modeling of surface-to-borehole electromagnetic method for monitoring reservoir[J]. Applied Geophysics, 2017, 14(4): 101-111. |
| [21] |
LIU R, LIU J, WANG J, et al. A time-lapse CSEM monitoring study for hydraulic fracturing in shale gas reservoir[J]. Marine and Petroleum Geology, 2020, 120: 104545. DOI:10.1016/j.marpetgeo.2020.104545 |
| [22] |
韦艳刚, 郭荣文, 刘颖, 等. 海洋可控源电磁法2.5维有限元正演模拟研究[J]. 物探化探计算技术, 2017, 39(5): 579-586. WEI Yan'gang, GUO Rongwen, LIU Ying, et al. 2.5D finite element modeling of marine controlled-source electromagnetic fields[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2017, 39(5): 579-586. DOI:10.3969/j.issn.1001-1749.2017.05.01 |



 丁学振, 山东省青岛市崂山区松岭路238号中国海洋大学海洋地球科学学院, 266100。Email:
丁学振, 山东省青岛市崂山区松岭路238号中国海洋大学海洋地球科学学院, 266100。Email: 