② 中国石化胜利石油管理局有限公司博士后科研工作站, 山东东营 257000;
③ 中国石油大港油田公司勘探开发研究院, 天津 300280
② Working Station for Postdoctoral Scientific Research, Shengli Oilfield Company, SINOPEC, Dongying, Shandong 257000, China;
③ Exploration and Development Research Institute, Dagang Oilfield Company, PetroChina, Tianjin 300280, China
油藏进入高含水开发期后,对储层物性的精细识别是剩余油挖潜的关键。现场通常由测井资料解释得到沿井的渗透率模型,然而不同学者的研究[1-5]证明,受注水冲刷影响,储层渗透率在开发后期会发生很大变化,在高度水淹层投产的新井,其测井解释结果已不能反映油藏开发初期的物性情况。
针对注水冲刷造成的储层渗透率时变问题,很多学者从不同角度进行了研究。孙国[6]、徐守余等[7]通过岩心测井资料研究了储层宏观参数变化规律,并利用神经网络方法建立储层参数的四维地质模型。彭仕宓等[8]通过建立注水开发前、后储层参数数学演化模型,综合岩心、测井和实验测试资料对注水过程中储层参数的变化规律进行了研究。束青林等[9]、李红南等[10]充分利用岩心资料,通过神经网络方法建立了宏观和微观储层参数的动态模型,并对剩余油分布模式做出了评价。张枫等[11]利用不同开发时期的测井资料,建立了储层参数随开发时间变化的数学模型,形成了不同开发时间四维动态演化模型,并对研究区剩余油分布进行了预测。么忠文等[12]、郭敬民[13]利用不同含水时期的水淹测井资料建立了水淹四维地质模型,以表征注水开发过程中储层流体动态变化。上述研究大多是通过实验或理论模型推导得到储层参数时变情况,然而地下流—固耦合的变化是复杂的,单一岩心实验或理论模型并不能够真实反映储层渗透率的变化情况。
地震属性反映地震波的几何特征与物理特征,这些特征在不同程度上反映了储层的岩性、渗透率以及孔隙流体的性质。由于对采集、处理因素所导致的时间、振幅、频率等方面的差异进行了处理,因此时移地震资料地震响应差异能够连续反映开发过程中的动态变化。本文充分利用三期时移地震资料预测研究区储层参数,在降低非油气藏因素影响的同时,提高油气藏内部渗透率参数预测精度,能够更好地突显油气藏储层渗透率参数在长期注水开发过程中的变化情况。
1 研究区概况研究区位于黄骅凹陷中区北大港二级断裂构造带的东南部,是油田的主要开发区之一。其北以港东主断层为界,南邻歧口凹陷,西至联盟地区,东到滩海区的港深64—港63-2井区,面积约50km2。研究区是河流相沉积的复合式砂岩油藏,在开发中油藏出现剩余油高度分散、注水冲刷储层渗透率变化等问题。
目前研究区内有1993年、2003年、2015年采集的三期全区覆盖地震数据,分别对应中低、高和特高含水三个开发阶段。针对资料因采集、处理因素导致的时间、振幅、频率等方面的差异进行了处理,提高了三期地震数据各项参数的一致性。通过偏最小二乘回归方法对多期地震属性进行分析,评价建立模型的拟合度,预测得到三个含水阶段的渗透率数据场,并通过示踪剂资料对预测结果进行验证,形成了一套储层参数时变性研究计算方法。
2 时移地震属性优选地震属性优化是地震属性分析技术的关键步骤,属性优化的质量直接影响预测结果的准确度和可靠性。地震属性携带有大量储层信息,并且与预测对象之间的关系复杂,预测对象对不同类型的地震属性具有不同的敏感度,因此需要优选出对预测对象最为敏感的地震属性。
优选地震属性的原则一般包括:①针对具体研究目标,选择对其相关性最高、最敏感、能够反映其本质特征的地震属性或属性组合;②选择相互独立、尽可能低维的属性集,减少冗余信息,达到最优属性集结构;③优选属性个数,使有效信息最大化,剔除干扰属性,减少因属性种类增加带来的不利影响。
通过文献调研各类地震属性物理意义发现,振幅类和频率类地震属性被较多应用在预测储层渗透率参数响应特征。在此基础上,对目的层段不受断层影响且地震属性数值正常的214口井数据提取了10种地震属性,并对沿井地震属性值与实际渗透率数值进行了相关性分析。由表 1统计数据可见,其中某些地震属性与渗透率的相关性较差。单一属性与渗透率的相关系数均小于0.50,说明单一属性的预测效果相对较差,需要通过属性组合更好地反映储层参数。本次研究从10个属性中优选出5个相关性较强的地震属性,分别是均方根振幅、反射强度、瞬时频率、振幅包络和主频,为下一步开展时移地震多属性预测渗透率变化奠定基础。
|
|
表 1 单一地震属性与渗透率相关性统计表 |
多属性预测分析是将优选出的敏感地震属性集或经降维处理的地震属性集作为输入,以预测测井数据为输出,利用线性、非线性方法,将地震属性与已知井的岩性、物性、含油气性等储层信息相结合,对储层参数进行定量预测[14];同时综合地质、测井、和实际生产等资料对预测结果的可靠性进行评价和分析。目前常用的多属性预测方法有多元逐步回归方法[15-16]、神经网络方法[17-18]、协克里金方法、支持向量机方法[19]、非参数回归分析方法等[20-22]。本次研究选用偏最小二乘回归方法建立不同期次时移地震属性与测井渗透率的相关性。偏最小二乘回归算法集成了主成分分析、典型相关分析、非线性回归分析的优点,通过建立多自变量与因变量间的回归关系对模型进行预测。相较于普通的多元回归方法,该方法可以更好地处理各自变量之间存在的多重相关性以及数据量小、样本较少的问题[23]。
偏最小二乘基本原理如下:
(1) 设有p个自变量的集合X和m个因变量的集合Y,且每个变量都有n个样本数据:
| $ \boldsymbol{X}=\left[\begin{array}{cccc} x_{11} & x_{12} & \cdots & x_{1 p} \\ x_{21} & x_{22} & \cdots & x_{2 p} \\ & & \vdots & \\ x_{n 1} & x_{n 2} & \cdots & x_{n p} \end{array}\right] $ | (1) |
| $ \boldsymbol{Y}=\left[\begin{array}{llll} y_{11} & y_{12} & \cdots & y_{1 m} \\ y_{21} & y_{22} & \cdots & y_{2 m} \\ & & \vdots & \\ y_{n 1} & y_{n 2} & \cdots & y_{m n} \end{array}\right] $ | (2) |
对原始数据X进行标准化处理
| $ x_{i j}^{*}=\frac{x_{i j}-\bar{x}_{j}}{\sqrt{\operatorname{var}\left(x_{j}\right)}} $ | (3) |
式中
(2) 求取主成分
从A0、B0中提取第一主成分t1和u1(t1、u1分别是A0与B0线性组合)
| $ \left\{\begin{array}{l} \boldsymbol{t}_{1}=\boldsymbol{A}_{0} \boldsymbol{\alpha}_{1}^{\mathrm{T}}=\alpha_{11} x_{1}, \alpha_{12} x_{2}, \cdots, \alpha_{1 p} x_{p} \\ \boldsymbol{u}_{1}=\boldsymbol{B}_{0} \boldsymbol{\beta}_{1}^{\mathrm{T}}=\beta_{11} y_{1}, \beta_{12} y_{2}, \cdots, \beta_{1 m} y_{m} \end{array}\right. $ | (4) |
| $ \max {\mathop{\rm cov}} \left( {{\mathit{\boldsymbol{t}}_1}, {\mathit{\boldsymbol{u}}_1}} \right)\;\;\;\;\;\;\;\;{\rm{s}}{\rm{. t}}{\rm{. }}\left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{\alpha }}_1^{\rm{T}}{\mathit{\boldsymbol{\alpha }}_1} = 1}\\ {\mathit{\boldsymbol{\beta }}_1^{\rm{T}}{\mathit{\boldsymbol{\beta }}_1} = 1} \end{array}} \right. $ | (5) |
式中:α1和β1为权重系数,可通过拉格朗日乘数法求得;cov(·,·)表示协方差。
根据主成分分析原理要求,t1、u1尽可能多地携带了各自数据集中的原始信息,并且自变量的主成分t1与因变量的主成分u1相关度达到最大,即求取t1、u1最大协方差。
(3) 建立原自变量、因变量与主成分之间的回归关系
| $ \left\{\begin{array}{l} \boldsymbol{A}_{0}=\boldsymbol{t}_{1} \boldsymbol{c}_{1}^{\mathrm{T}}+\boldsymbol{A}_{1} \\ \boldsymbol{B}_{0}=\boldsymbol{t}_{1} \boldsymbol{r}_{1}^{\mathrm{T}}+\boldsymbol{B}_{1}=\boldsymbol{u}_{1} \boldsymbol{w}_{1}^{\mathrm{T}}+\boldsymbol{B}_{1} \end{array}\right. $ | (6) |
式中:回归系数向量
用残差矩阵A1、B1取代A0和B0后,求第二主成分t2和u2并建立回归关系,如果残差矩阵B1中元素绝对值接近0,可认为回归方程达到预期精度并中止算法,否则继续重复步骤(2)~步骤(3)。
(4) 建立因变量与自变量间回归方程
若A0的秩为a,则有a个成分t1,t2,…, ta使
| $ \left\{\begin{array}{l} \boldsymbol{A}_{0}=\boldsymbol{t}_{1} \boldsymbol{t}_{1}^{\mathrm{T}}+\boldsymbol{\cdots}+\boldsymbol{t}_{a} \boldsymbol{c}_{a}^{\mathrm{T}}+\boldsymbol{A}_{a} \\ \boldsymbol{B}_{0}=\boldsymbol{t}_{1} \boldsymbol{r}_{1}^{\mathrm{T}}+\cdots+\boldsymbol{t}_{a} \boldsymbol{r}_{a}^{\mathrm{T}}+\boldsymbol{B}_{a} \end{array}\right. $ | (7) |
| $ t_{k}=\alpha_{k 1} x_{11}, \alpha_{k 2} x_{12}, \cdots, \alpha_{k p} x_{1 p} \quad(k=1, 2, \cdots, a) $ | (8) |
将式(8)代入Y=t1r1+t2r2+…+tara则得到m个因变量的回归方程
| $ \begin{gathered} y_{i l}=\alpha_{l 1} x_{11}+\alpha_{l 2} x_{12}+\cdots+\alpha_{l p} x_{m p} \\ (l=1, 2, \cdots, m) \end{gathered} $ | (9) |
(5) 交叉有效性检验
偏最小二乘回归法一般采用交叉有效性检验方法确定主成分提取个数,即通过增加一个新的成分,判断其能否提高回归方程的预测精度。具体实现如下。
首先将所有样本点分为训练集和验证集两部分,训练集为去掉样本点i的n-1个样本点集;然后对训练集用h个主成分拟合回归方程,并带入样本点i,得到对应拟合值
| $ \begin{gathered} \operatorname{PRESS}_{h l}=\sum\limits_{i=1}^{n}\left[y_{i l}-\hat{y}_{hl(-i)}\right]^{2} \\ i=1, 2, \cdots, n \quad l=1, 2, \cdots, m \end{gathered} $ | (10) |
则Y的预测误差平方和为
| $ \operatorname{PRESS}_{h}=\sum\limits_{l=1}^{m} \operatorname{PRESS}_{h l} $ | (11) |
同时用所有样本点拟合含h个主成分的回归方程,记第i个样本点预测值为
| $ \left\{\begin{array}{l} \mathrm{SS}_{h J}=\sum\limits_{l=1}^{m} \mathrm{SS}_{h l} \\ \mathrm{SS}_{h l}=\sum\limits_{i=1}^{n}\left[y_{i l}-\hat{y}_{hl(i)}\right]^{2} \end{array}\right. $ | (12) |
定义交叉有效性
| $ Q_{h}^{2}=1-\frac{\sum\limits_{i=1}^{n} \operatorname{PRESS}_{h i}}{\sum\limits_{i=1}^{n} \operatorname{SS}_{(h-1) i}}=1-\frac{\operatorname{PRESS}_{h}}{\operatorname{SS}_{(h-1)}} $ | (13) |
当Qh2 < 0.0975或
基于上述原理,利用偏最小二乘回归模型建立研究区资料样本集之间的联系。分别对研究区的三期地震资料进行地震属性提取,并将优选出的地震属性体转换为沿井地震属性曲线;以测井渗透率数据作为因变量,并将其对应期次的沿井地震数据作为自变量,采用偏最小二乘回归算法建立预测模型,通过预测模型对不同期次渗透率进行全区预测,得到三个含水时期渗透率曲线;最后利用验证数据集中的不同含水期样本井的原始渗透率数据与预测渗透率数据进行误差分析,并结合研究区示踪剂资料验证渗透率时变预测结果。
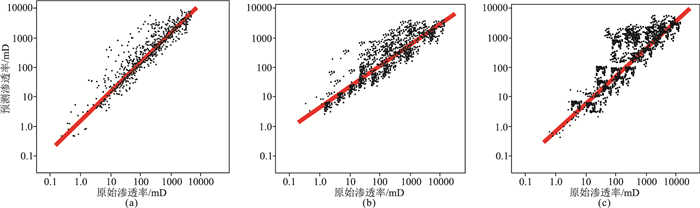
4 基于时移地震资料的储层渗透率时变性研究样本数量的不对等会造成预测结果的偏差,经统计,区内上世纪90年代前、2000年左右和2010年左右的投产井数分别为71、96和78口,数目相差不大。测井解释成果与三期时移地震资料相匹配,分别代表中低、高和特高含水阶段,能够为储层参数预测提供较好的数据基础。通过编制相应的软件,对研究区内不同含水阶段测井序列数据进行回归计算,以测井曲线中0.125m采样点为精度,建立包含三期沿井时移地震属性数据和各井投产时期测井解释的渗透率数据共104983个数据集。随机选取数据集中80%的数据构建训练集,通过偏最小二乘回归法建立当期沿井时移地震属性与当期测井解释渗透率之间的关系及预测模型;选取20%的数据构建验证集,将已知测井解释的原始渗透率与通过预测模型得到的同期次预测渗透率进行对比,用来验证结果的准确性。在模型训练完成后,分别绘制验证集中不同含水阶段通过测井解释得到的原始渗透率与通过偏最小二乘法得到的对应期次井的预测渗透率交会图(图 1)。对于验证集中的数据,原始测井解释渗透率和当期次预测渗透率数据间的相关性越高代表预测模型越准确,计算得到图 1中低、高、特高含水阶段层段内原始渗透率与预测渗透率交会的相关系数值分别为0.91、0.87、0.89,说明建立的偏最小二乘回归模型能够很好地进行渗透率预测,其验证结果与实际值相符。
|
图 1 不同含水时期原始渗透率和预测渗透率交会图 (a)中低含水时期;(b)高含水时期;(c)特高含水时期 |
为了细化研究区内渗透率变化规律,选取G2-62-1井区进行对比分析。该井区范围内主力开发小层包括NgⅠ1-1和NmⅣ3-1,两主力层均无明显断层分布,且构造较为平缓。从物性上看,NgⅠ1-1小层为中孔、中渗储层,井区范围内原始渗透率平均值为132mD;而NmⅣ3-1小层在该井控制区域内平均原始渗透率为7293mD,属于高孔、高渗储层。G2-62-1井区范围内两个主力层渗透率分布图显示(图 2),在同一小层内渗透率差异较小,NgⅠ1-1和NmⅣ3-1层的渗透率变异系数分别为0.14和0.23,按照渗透率变异系数分类[24],两小层在该井区范围内均属于弱非均质储层。

|
图 2 G2-62-1井区范围内NmⅣ3-1(左)、NgⅠ1-1(右)小层原始渗透率分布 |
将G2-62-1井两期预测渗透率曲线和一期测井原始渗透率曲线成果进行粗化,构建形成中低、高和特高含水期渗透率剖面图(图 3),对比不同含水阶段渗透率的变化。由图可见,两套储层受注水冲刷后,其渗透率变化并非简单的单调增加或减小,而是与岩石胶结程度和泥质含量等因素有关[25-28]。从图 3预测结果判断,该井控制范围内明化镇组和馆陶组的储层渗透率变化存在差异,其中NgⅠ1-1小层经注水冲刷后,渗透率变化表现为缓慢减小的趋势,由中低含水期的154mD变为特高含水期的120mD;而NmⅣ3-1小层经注水冲刷后渗透率变化表现为增加的趋势,由中低含水期的7211mD变为特高含水期的7903mD。

|
图 3 G2-62-1井三期渗透率剖面图 |
郭莉等[24]对油田注水开发过程中储层参数的变化规律按类别进行了分析,研究表明对于高孔、高渗储层,其黏土矿物和胶结物含量随注水冲刷而减少,溶蚀孔隙增多,整体表现为储层孔喉增大、物性变好的趋势。对于中孔、中渗油藏则出现注水冲刷导致喉道堵塞、孔喉减小、物性变差的趋势,注入水进入油层后,由于水对黏土矿物的聚散和水化膨胀作用,大孔道中的黏土矿物随水流带出被冲散、迁移,使孔道变得畅通,扩大了喉道直径;另一方面,一些被剥落或冲散的黏土在小孔隙中重新聚集,使小孔隙变得更小,增强了储层微观非均质性。采用常规岩心驱替实验分析单井三期渗透率变化差异的原因,得到的储层参数变化受到岩心尺度、实验条件、实验样本数等因素的影响,只能反映单一岩心储层参数变化规律。然而实际油藏储层物性分布复杂,时移地震作为一种能够反映全区参数场分布的资料,在储层参数预测方面能够发挥重要作用。图 3结果与高孔、高渗及中孔、中渗油藏驱替实验结果相符,进一步说明通过时移地震资料进行储层参数预测比单一岩心驱替实验结果更具可靠性。
5 成果验证利用示踪剂资料对比一个井组内不同方向注水窜流速度,进一步验证渗透率预测精度和准确性。在G2-62-1井明化镇组注入示踪剂检测资料,表 2记录了三口监测井水驱速度数据,G1-62井水驱速度为1.76m/d,速度较慢;G2-61-1井未见示踪剂;而监测井G1-61-2在短时间内检测出示踪剂,计算水驱速度达到7.49m/d。
|
|
表 2 G2-62-1注采井组水驱速度监测 |
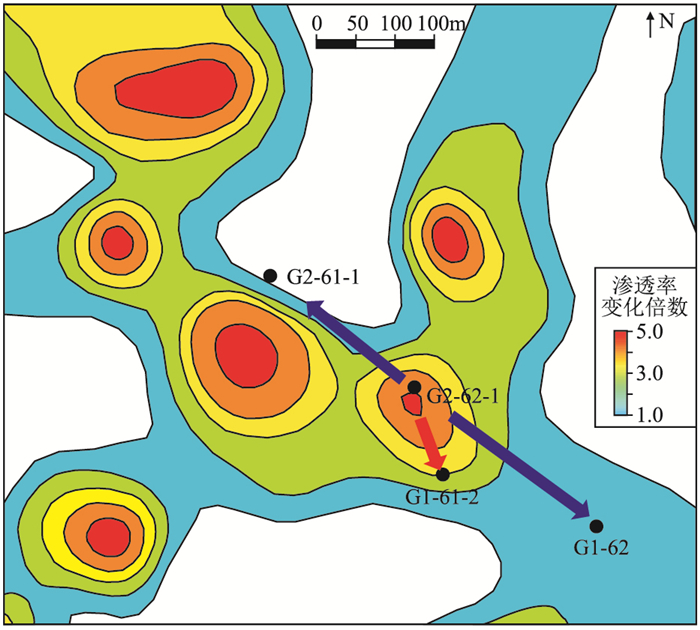
选取G2-62-1注采井组范围内各井1993年和2015年渗透率曲线,用NmⅣ3-1小层2015年单井渗透率数值除以1993年渗透率数值,得到各井点处渗透率变化倍数。以砂体分布作为约束条件对井点数据进行平面插值,得到NmⅣ3-1小层中低含水期—特高含水期的渗透率变化倍数分布图(图 4)。其中数值小于1表示经过注水冲刷后储层物性变差,从中低含水期到特高含水期渗透率数值变小;数值大于1表示从中低含水期到特高含水期储层渗透率数值变大。
|
图 4 G2-62-1井区NmⅣ3-1层渗透率变化倍数分布 |
由图 2已知NmⅣ3-1小层整体原始渗透率分布差异较小,砂体内部无大的断层分布,渗透率变化与注水冲刷量有直接关系,而物性的变化又影响了储层渗流特征。由于G2-61-1井处于NmⅣ3-1小层有效砂体外部,与G2-62-1注水井无直接连通关系,因此未见示踪剂响应。G1-62井有示踪剂显示,该井与G2-62-1注水井间水驱速度为1.76m/d,满足达西定律,同时从图 4可以看出,G1-62井位于渗透率变化明显区域的外部,未与注水井形成直接连通的渗流通道。G1-61-2井特高含水时期渗透率较中低含水时期增大近三倍,受G2-62-1注水井影响,G2-62-1与G1-61-2两井之间的储层渗透率发生变化,形成高渗通道,导致水驱速度为7.49m/d,远高于达西流的渗流速度,两井间渗透率变化已呈现高速非达西流的特征。
表 3对比了井组内各单井控制范围内的水驱速度与渗透率变化倍数之间的关系,直接对预测结果进行验证。通过时移地震资料预测,G1-62井控制区域内渗透率并未见明显变化,其水驱速度符合达西定律;G1-61-2井与G2-62-1井控区域内预测渗透率变化倍数分别为2.7和3.4,井间储层呈现孔喉增大、物性变好的趋势,其水驱速度明显高于G1-62井,呈现高速非达西流的趋势,说明基于多期时移地震属性预测的渗透率变化结果与水驱开发特征相一致。
|
|
表 3 G2-62-1注采井组预测渗透率变化倍数与水驱速度对比 |
(1) 地震属性参数的合理优选直接影响预测结果的准确度和可靠性。本文提取研究区时移地震资料的10种地震属性进行了相关性分析,优选其中均方根振幅、反射强度、瞬时频率、振幅包络和主频5种与渗透率相关性较高的属性,为下一步时移地震多属性预测渗透率时变规律提供了数据基础。
(2) 研究选用的偏最小二乘回归算法较普通多元回归法能够更好地处理自变量之间存在的多重相关性以及数据量小、样本较少的问题,应用回归模型建立多自变量和因变量间的回归关系并对模型进行预测,确定了研究区低、高、特高含水阶段原始渗透率和预测渗透率的相关系数值分别达到0.91、0.87、0.89,建立的回归模型能够很好地对渗透率进行预测。
(3) 不同类型储层渗透率时变规律存在差异,将建立的偏最小二乘回归预测模型应用于研究区NgⅠ1-1中孔、中渗储层,其渗透率变化表现为缓慢减小的趋势,由中低含水期的154mD变为特高含水期的120mD;而NmⅣ3-1高孔、高渗储层渗透率变化表现为增加的趋势,由中低含水期的7211mD变为特高含水期的7903mD。通过示踪剂资料进一步证明,建立的多期沿井渗透率预测模型在高含水油藏储层精细描述过程中具有可借鉴作用,该方法为指导高含水开发后期剩余油定量挖潜提供了依据。
| [1] |
ABBASZADEH-DEHGHANI M, BRIGHAM W E. Analysis of Unit Mobility Ration Well-to-well Tracer Flow to Determine Reservoir Heterogeneity[D]. Stanford University, California, USA, 1983.
|
| [2] |
李中超, 陈洪德, 余成林, 等. 严重非均质油藏注水开发流体动力地质作用[J]. 石油勘探与开发, 2013, 40(2): 209-214. LI Zhongchao, CHEN Hongde, YU Chenglin, et al. Hydrodynamic geological process of water injection development of severely heterogeneous reservoirs[J]. Petroleum Exploration and Development, 2013, 40(2): 209-214. |
| [3] |
BUTLER R M. Thermal Recovery of Oil and Bitumen[M]. Prentice Hall Inc., Englewood Cliffs, 1991.
|
| [4] |
HEARN C L, EBANKS W J, TYE R S, et al. Geolo-gical factors influencing reservoir performance of the Hartzog Draw Field, Wyoming[J]. Journal of Petro-leum Technology, 1984, 36(8): 1335-1344. DOI:10.2118/12016-PA |
| [5] |
辛治国, 贾俊山, 孙波. 优势流场发育阶段定量确定方法研究[J]. 西南石油大学学报(自然科学版), 2012, 34(2): 119-124. XIN Zhiguo, JIA Junshan, SUN Bo. Research on the quantitative determination of the dominant flow field development stages[J]. Journal of Southwest Petro-leum University(Science & Technology Edition), 2012, 34(2): 119-124. DOI:10.3863/j.issn.1674-5086.2012.02.017 |
| [6] |
孙国. 利用人工神经网络系统建立储层四维地质模型[J]. 油气地质与采收率, 2004, 11(3): 4-6. SUN Guo. 4D geological modeling using artificial neural network system[J]. Petroleum Geology and Recovery Efficiency, 2004, 11(3): 4-6. DOI:10.3969/j.issn.1009-9603.2004.03.002 |
| [7] |
徐守余, 王艳红. 利用神经网络建立储层宏观参数动态模型——以胜坨油田二区为例[J]. 油气地质与采收率, 2005, 12(6): 10-12. XU Shouyu, WANG Yanhong. Dynamic model of re-servoir macro-parameters built by neural net-work: taking the second block of Shengtuo Oilfield as an example[J]. Petroleum Geology and Recovery Efficiency, 2005, 12(6): 10-12. DOI:10.3969/j.issn.1009-9603.2005.06.003 |
| [8] |
彭仕宓, 尹志军, 李海燕. 建立储层四维地质模型的新尝试——以冀东高尚堡沙三段储层模型的建立为例[J]. 地质论评, 2004, 50(6): 662-667. PENG Shimi, YIN Zhijun, LI Haiyan. A new trial to build a 4-dimensional reservoir model: A case study of the reservoir model of member 3 of the Shahejie formation in Eastern Hebei province[J]. Geological Review, 2004, 50(6): 662-667. DOI:10.3321/j.issn:0371-5736.2004.06.018 |
| [9] |
束青林, 张本华, 徐守余. 孤岛油田河道砂储集层油藏动态模型及剩余油研究[J]. 石油学报, 2005, 26(3): 64-67, 73. SHU Qinglin, ZHANG Benhua, XU Shouyu. Dyna-mic model and remaining oil distribution of fluvial reservoir in Gudao Oilfield[J]. Acta Petrolei Sinica, 2005, 26(3): 64-67, 73. |
| [10] |
李红南, 王德军. 油藏动态模型和剩余油仿真模型[J]. 石油学报, 2006, 27(5): 83-87. LI Hongnan, WANG Dejun. Dynamic model of oil reservoir and simulation model of remaining oil[J]. Acta Petrolei Sinica, 2006, 27(5): 83-87. |
| [11] |
张枫, 李治平, 凌宗发, 等. 黄骅坳陷唐家河油田四维地质建模研究[J]. 天然气地球科学, 2007, 18(6): 897-902. ZHANG Feng, LI Zhiping, LING Zongfa, et al. Study on four-dimensional geological modeling of Tangjiahe oil-field in Huanghua depression[J]. Natural Gas Geo-science, 2007, 18(6): 897-902. DOI:10.3969/j.issn.1672-1926.2007.06.024 |
| [12] |
么忠文, 李忠权. 大庆杏树岗油田杏六中区储层四维地质建模[J]. 断块油气田, 2013, 20(6): 744-747. YAO Zhongwen, LI Zhongquan. Four dimensional geological modeling of reservoir in Xingliuzhong District, Xingshugang oilfield, Daqing[J]. Fault Block Oil and Gas Field, 2013, 20(6): 744-747. |
| [13] |
郭敬民. 大庆油田杏六中区萨二段高水淹期地质建模研究[J]. 长江大学学报(自科版), 2013, 10(10): 123-125. |
| [14] |
卢宝坤, 史謌. 测井资料与地震属性关系研究综述[J]. 北京大学学报(自然科学版), 2005, 41(1): 154-160. LU Baokun, SHI Ge. A review of study on relation between well logging data and seismic attributes[J]. Acta Scientiarum Naturalium Universitatis Pekinesis, 2005, 41(1): 154-160. DOI:10.3321/j.issn:0479-8023.2005.01.022 |
| [15] |
何周, 陈永军, 郭文建. 根据地震属性预测乌尔禾油田储集层孔隙度[J]. 新疆石油地质, 2007, 28(4): 500-503. HE Zhou, CHEN Yongjun, GUO Wenjian. Prediction of reservoir porosity in Wuerhe Field of Junggar Basin using seismic attributes[J]. Xinjiang Petroleum Geolo-gy, 2007, 28(4): 500-503. DOI:10.3969/j.issn.1001-3873.2007.04.033 |
| [16] |
杜波, 于正军, 韩建军. 多元线性回归法在DX北带砂砾岩储层孔隙度定量预测中的应用[J]. 天然气勘探与开发, 2012, 35(4): 36-40. DU Bo, YU Zhengjun, HAN Jianjun. Application of multiple linear regression to porosity quantitative prediction of sandy conglomerate bodies in northern DX[J]. Natrural Gas Exploration & Development, 2012, 35(4): 36-40. DOI:10.3969/j.issn.1673-3177.2012.04.008 |
| [17] |
凌云, 郭向宇, 蔡银涛, 等. 无基础地震观测的时移地震油藏监测技术[J]. 石油地球物理勘探, 2013, 48(6): 938-947. LING Yun, GUO Xiangyu, CAI Yintao, et al. 3.5D+4D seismic reservoir surveillance without baseline survey[J]. Oil Geophysical Prospecting, 2013, 48(6): 938-947. |
| [18] |
吴俊, 于兴河, 李胜利, 等. 地震多属性变换法及其在孔隙度预测——以束鹿凹陷西斜坡台家庄区块为例[J]. 石油物探, 2011, 50(4): 393-397. WU Jun, YU Xinghe, LI Shengli, et al. Seismic multi-attributes transformation method and its application on reservoir porosity prediction: Case study of Shulu Sag[J]. Geophysical Prospecting for Petroleum, 2011, 50(4): 393-397. DOI:10.3969/j.issn.1000-1441.2011.04.013 |
| [19] |
宫健, 许淑梅, 马云, 等. 基于地震属性的储层预测方法——以永安地区永3区块沙河街组二段为例[J]. 海洋地质与第四纪地质, 2009, 29(6): 95-102. GONG Jian, XU Shumei, MA Yun, et al. Reservoir prediciing method based on seismic attribute analyses: A case study of Es2x in Yong 3 Block of Yong'an Area[J]. Marine Geology & Quaternary Geology, 2009, 29(6): 95-102. |
| [20] |
赵改善. 油藏动态监测技术的发展现状与展望: 时延地震[J]. 勘探地球物理进展, 2005, 28(3): 157-168. ZHAO Gaishan. The status and outlook of dynamic reservoir monitoring: Time-lapse seismic[J]. Progress in Exploration Geophysics, 2005, 28(3): 157-168. |
| [21] |
韩大匡. 关于高含水油田二次开发理念、对策和技术路线的探讨[J]. 石油勘探与开发, 2010, 37(5): 583-591. HAN Dakuang. Discussions on concepts, counter-measures and technical routes for the redevelopment of high water-cut oilfields[J]. Petroleum Exploration and Development, 2010, 37(5): 583-591. |
| [22] |
李绪宣, 胡光义, 范廷恩, 等. 基于地震驱动的海上油气田储层地质建模方法[J]. 中国海上油气, 2011, 23(3): 143-147. LI Xuxuan, HU Guangyi, FAN Ting'en, et al. A me-thod of geological reservoir modeling based on seismic drive for offshore fields[J]. China Offshore Oil and Gas, 2011, 23(3): 143-147. DOI:10.3969/j.issn.1673-1506.2011.03.001 |
| [23] |
王治国, 尹成, 雷小兰, 等. 预测砂岩孔隙度的地震多属性优化模式对比[J]. 石油地球物理勘探, 2011, 46(3): 442-448. WANG Zhiguo, YIN Cheng, LEI Xiaolan, et al. Multi-attribute optimization analysis for sandstone porosity prediction[J]. Oil Geophysical Prospecting, 2011, 46(3): 442-448. |
| [24] |
郭莉, 王延斌, 刘伟新, 等. 大港油田注水开发过程中油藏参数变化规律分析[J]. 石油实验地质, 2006, 28(1): 85-90. GUO Li, WANG Yanbin, LIU Weixin, et al. Variation law of reservoir parameters during water flooding in Dagang oil field[J]. Petroleum Geology & Experiment, 2006, 28(1): 85-90. DOI:10.3969/j.issn.1001-6112.2006.01.017 |
| [25] |
郭向宇, 凌云, 高军, 等. 井地联合地震勘探技术研究[J]. 石油物探, 2010, 49(5): 438-450. GUO Xiangyu, LING Yun, GAO Jun, et al. Study of seismic-logging joint seismic exploration technology[J]. Geophysical Prospecting for Petroleum, 2010, 49(5): 438-450. DOI:10.3969/j.issn.1000-1441.2010.05.003 |
| [26] |
李熙盛, 梁卫, 宋强功, 等. 海上3.5维地震技术在南海惠州A油田"双特高"开发期的应用[J]. 石油地球物理勘探, 2020, 55(增刊): 92-97. LI Xisheng, LIANG Wei, SONG Qianggong, et al. Application of offshore 3.5D seismic survey for oil field development at high water cut and high recovery stage[J]. Oil Geophysical Prospecting, 2020, 55(S1): 92-97. |
| [27] |
撒利明, 甘利灯, 黄旭日, 等. 中国石油集团油藏地球物理技术现状与发展方向[J]. 石油地球物理勘探, 2014, 49(3): 611-626. SA Liming, GAN Lideng, HUANG Xuri, et al. The status and development direction of reservoir geophysics in CNPC[J]. Oil Geophysical Prospecting, 2014, 49(3): 611-626. |
| [28] |
丁伟. 互均衡处理技术的分析与应用[J]. 石油地球物理勘探, 2007, 42(1): 17-23. DING Wei. Analysis and application of cross equalization processing technique[J]. Oil Geophysical Prospecting, 2007, 42(1): 17-23. |



 郭奇, 山东省东营市东营区聊城路2号胜利石油管理局有限公司博士后科研工作站, 257000。Email:
郭奇, 山东省东营市东营区聊城路2号胜利石油管理局有限公司博士后科研工作站, 257000。Email: 