随着勘探开发程度的不断深化,具有圈闭规模小、储层薄、烃源丰富却分布零散等特点的深层微型油气藏已成为研究热点[1-2]。然而,受制于油气藏埋深大、地震信号的分辨能力不足等不利因素,加大了对微型河道、薄砂体等油气目标的识别难度。时频分析技术能提供时间域和频率域的联合分布信息,故被广泛应用于地震波等复杂非平稳信号的处理[3],进而在油气目标识别中发挥重要作用。
时频分析技术现已成为研究沉积微相、薄储层等地质目标的重要手段[4]。马见青等[5]根据S变换提供的有效地震信息,成功识别了复杂沉积环境;武迪等[6]结合变分模态分解与包络导数算子预测碳酸盐岩溶洞储层的油气分布;朱秋影等[7]利用时频分析技术预测依拉克构造有利河道砂体的空间展布;蒋炼等[8]利用分频技术预测砂体储层厚度和分布范围;张付瑷等[9]通过改进窗参数优化S变换从而精细刻画沉积微相及相应构造;杨道庆等[10]利用时频分析及地层切片技术精确描述地下分流河道的空间流向、水平延展、厚度变化等特征。
时频分析最常用的方法主要包括两种:一种是以短时傅里叶变换(STFT)[11]、小波变换[12-14]、Gabor变换[15]、广义S变换[16]为代表的线性时频分布;另一种则是以Wigner-Vile分布(WVD)、平滑伪Wigner-Ville分布(SPWVD)为代表的Cohen类广义双线性时频分布[17]。线性时频分析方法虽然计算速度较快,但存在时频聚焦性欠佳且分辨率低等不足。WVD具有较高分辨率和较突出的能量集中性,但因其非线性特征,在处理多分量数据时必然会产生大量交叉项从而干扰有效信号,很大程度上限制了其应用范围[18]。SPWVD属于Cohen类二次型时频分布的核函数方法,即基于WVD对信号瞬时自相关函数的时域和频域方向同时施加窗函数,改变核函数以抑制交叉项的产生。这种核函数法出色地抑制了交叉干扰项的生成,且仍保留了WVD的众多数学特性,适用于处理复杂地震数据[19]。
地震信号通常具有主频低、频带窄等特点[20],其时频分布在有效频带内的划分点数往往较少,难以保证理想的分辨率,使STFT、Gabor变换、广义S变换、WVD和SPWVD等时频分析技术在识别埋藏深、厚度小的微型地质目标时的精度不够高,必然会对油气藏地下空间分布的认识、储量估算、钻井勘探开发过程产生不利影响。
本文在SPWVD基础上,以线性调频Z变换(CZT)[21]替代SPWVD中的快速傅里叶变换(FFT),提出一种提高地震信号时频分辨率的计算方法(SPWVD-CZT)。利用CZT在三维空间内螺旋采样的特性,通过调整采样间隔和采样点数实现数据插值计算;在SPWVD基础上进一步完善地震数据时频谱的局部细节信息,为地下微型河道、薄储层等小幅度复杂油气目标的识别提供方法支撑。
1 SPWVD-CZT方法原理 1.1 SPWVD的定义定义信号x(t)的Wigner-Ville分布[22]为
| $ W_{x}(t, \sigma)=\int_{-\infty}^{+\infty} x\left(t+\frac{\tau}{2}\right) x^{*}\left(t-\frac{\tau}{2}\right) \mathrm{e}^{-\mathrm{j} \sigma \tau} \mathrm{d} \tau $ | (1) |
式中:Wx(t,σ)为信号x(t)的WVD,t为时间变量;σ为频率变量;τ为时间延迟;e-jστ为傅里叶变换的参数因子;x*为x的共轭。定义
| $ R_{x}(t, \tau)=x\left(t+\frac{\tau}{2}\right) x^{*}\left(t-\frac{\tau}{2}\right) $ | (2) |
式中Rx(t,τ)为x(t)的瞬时自相关函数。
在时域和频域同时对WVD进行加窗处理可抑制交叉项的产生,得到SPWVD分布[23]
| $ \begin{aligned} S_{\mathrm{pw}}(t, \sigma)=& \int_{-\infty}^{+\infty} h(\tau)\left[\int_{-\infty}^{+\infty} g(u-\tau) x\left(t+\frac{\tau}{2}\right) \times\right.\\ &\left.x^{*}\left(t-\frac{\tau}{2}\right) \mathrm{e}^{-\mathrm{j} \sigma\tau} \mathrm{d} u\right] \mathrm{d} \tau \end{aligned} $ | (3) |
式中:Spw(t,σ)为信号x(t)的SPWVD;h(τ)、g(u-τ)分别为时间和频率方向的窗函数,其中u为频率延迟。
总之,SPWVD能更清晰地反映信号能量的时频分布,同时极大程度地抑制了交叉项的产生,被广泛应用于地震数据的处理。
1.2 CZT的定义CZT是对FFT改进得到的,其原理是在Z平面内用一条螺旋线进行等间隔采样,采样点在螺旋线上呈现等角分布[24]。该方法计算功率谱和时频分布十分有效,且具有计算快速、不受数据序列长度限制、灵活性强等优点。
长度为N的离散信号序列x(n)的Z变换为
| $ X(z)=\sum\limits_{n=0}^{N-1} x(n) z^{-n} $ | (4) |
式中:n为离散时间变量;z为Z变换采样因子。
令zr=AW-r,A=A0ejθ0,W=W0ejφ0,则有
| $ z_{r}=A_{0} \mathrm{e}^{\mathrm{j} \theta_{0}} W_{0} \mathrm{e}^{-\mathrm{j} \varphi_{0} r} $ | (5) |
式中:zr为Z变换的采样因子,代替式(4)中的z, 其中r为空间步长;ejθ0为步长因子;e-jφ0r为幅角因子;A0、W0均为任意正实数。给定A0、W0、θ0、φ0,当r=0,1,…,∞时,可得到Z平面上的一系列点z0、z1、…、z∞,再对其做Z变换
| $ X\left(z_{r}\right)=\sum\limits_{n=0}^{\infty} x(n) z_{r}^{-n}=\sum\limits_{n=0}^{\infty} x(n) A^{-n} W^{n r} $ | (6) |
式中:A-n为采样步长;Wnr为采样幅角。
对信号做频谱分析时,应在单位圆上实现CZT[25]。A0和W0都应取为1,设离散信号X(n)的长度为n=0,1,…,N-1,变换的长度r=0,1,…,M-1,式(6)就变为
| $ X\left(z_{r}\right)=\sum\limits_{n=0}^{N-1} x(n) A^{-n} W^{n r} $ | (7) |
由Bluestein公式
| $ n r=\frac{r^{2}+n^{2}-(r-n)^{2}}{2} $ | (8) |
式(7)又可写为
| $ X\left(z_{r}\right)=\sum\limits_{n=0}^{N-1} x(n) A^{-n} W^{\frac{r^{2}}{2}} W^{\frac{n^{2}}{2}} W^{-\frac{(r-n)^{2}}{2}} $ | (9) |
令
| $ \begin{aligned} X\left(z_{r}\right) &=W^{\frac{r^{2}}{2}} \sum\limits_{n=0}^{N-1}[f(n) p(r-n)] \\ &=\sum\limits_{n=0}^{N-1} f(n) W^{-\frac{(r-n)^{2}}{2}} \\ &=W^{\frac{r^{2}}{2}}[f(r) * p(r)] \end{aligned} $ | (10) |
式中:
将CZT与SPWVD结合,利用CZT的特性,通过在Z平面上对信号采样重构增加频带内的划分点数,从而改善信号的局部细节,有效提升信号的时频分辨率。实现过程如下:
将连续信号离散化x(t)
| $ z(n)=x(n)+\mathrm{j} H[x(n)] $ | (11) |
式中:解析信号z(n)的实部是x(n),虚部H[x(n)]为x(n)的Hilbert变换。z(n)的WVD定义为
| $ W_{z}(n, \sigma)=2 \sum\limits_{-\infty}^{\infty} z(n+l) z^{*}(n-l) \mathrm{e}^{-\mathrm{j} 2 l{\sigma}} $ | (12) |
式中:Wz(n,σ)为z(n)的WVD;l为步长;z*为z的共轭;e-j2lσ为傅里叶变换因子。
在频域方向加上长度为N/4的矩形窗g(l),当|l|>N/8时,g(l)=0。可得频域方向加窗后的离散瞬时自相关函数为
| $ R(n, l)=z(n+l) z^{*}(n-l) g(l) g^{*}(-l) $ | (13) |
式中g*为g的共轭。
再对R(n,l)的时域方向加上长度为N/2的矩形窗h(l),当|l|>N/4时,h(l)=0。可得时域方向加窗后的离散瞬时自相关函数为
| $ \begin{aligned} K(n, l)=& h(n-2 l) \sum\limits_{-l}^{l} z(n+l) \times \\ & z^{*}(n-l) g(l) g^{*}(-l) \end{aligned} $ | (14) |
此时,K(n,l)也被称为SPWVD的核函数。
由于CZT和FFT的计算域为非负数(l=0,1,…,N-1),还需对核函数K(n,l)做循环位移,使得l位于0~(N-1)内,得到重新排序后的核函数
| $ K_{N}(n, l)= \begin{cases}K(n, l) &\ 0 \leqslant l \leqslant \frac{N}{2}-1 \\ K(n,-l) & \frac{N}{2} \leqslant l \leqslant N-1\end{cases} $ | (15) |
式中:K(n,l)为排序前正频率方向的核函数;K(n,-l)为排序前负频率方向的核函数。
设待分析频段的点数为M,根据FFT的快速计算原理,取最接近N+M-1的二次幂Q作为计算时的序列长度。由于WVD的周期为π,还应将CZT中的相角θ0和幅角φ0扩展为原来的两倍,即A=A0ej2θ0,W=W0ej2φ0。构造序列
| $ \delta(l)= \begin{cases}W^{\frac{l^{2}}{2}} & 0 \leqslant l \leqslant M-1 \\ 0 & M \leqslant l \leqslant Q-N \\ W^{-\frac{\left(\frac{N}{2}-l\right)^{2}}{2}} & Q-N+1 \leqslant l \leqslant Q-1\end{cases} $ | (16) |
式中:δ(l)为单位响应序列;
单位响应序列δ(l)的长度为Q,对SPWVD的序列补0,使得两个卷积的序列长度相同。再构造序列
| $ f(l)= \begin{cases}f^{*}(l) & 0 \leqslant l \leqslant \frac{N}{2}-1 \\ 0 & \frac{N}{2} \leqslant l \leqslant Q-\frac{N}{2} \\ f^{*}(l-Q+N) & Q-\frac{N}{2}+1 \leqslant l \leqslant Q-1\end{cases} $ | (17) |
式中:f(l)为重排的序列;f*(l)=KN(n, l)A-l×Wl2/2,0≤l≤N-1;KN(n,l)为式(15)中SPWVD循环位移后得到的核函数。
然后分别对δ(l)、f(l)做傅里叶变换
| $ \left\{\begin{array}{l} \varDelta(r)=\operatorname{FFT}[\delta(l)] \\ F(r)=\operatorname{FFT}[f(l)] \end{array}\right. $ | (18) |
再将Δ(r)与F(r)相乘,得到
| $ Y(r)=F(r) \varDelta(r) $ | (19) |
进一步作逆变换
| $ y(l)=\operatorname{IFFT}[Y(r)] $ | (20) |
将y(l)乘上加权系数
| $ S_{\mathrm{PWVD}-\mathrm{CZT}}\left(z_{l}\right)=W^{\frac{l^{2}}{2}} y(l) \quad 0 \leqslant l \leqslant M $ | (21) |
式中SPWVD-CZT(zl)为信号的SPWVD-CZT分布结果。
2 方法测试 2.1 模拟信号时频分析利用雷克子波可合成与实际地震信号近似的模拟信号,以验证SPWVD-CZT的时频分析能力。采用主频分别为40、20、10Hz的雷克子波,由下式
| $ x(n)=\left\{\begin{array}{l} 1.5 \times\left[1-2 \times(40 {\rm{ \mathsf{ π} }} n)^{2}\right] \mathrm{e}^{-(40 {\rm{ \mathsf{ π} }} n)^{2}} \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ n \in[0,0.2] \\ -0.8 \times\left[1-2 \times(20 {\rm{ \mathsf{ π} }} n)^{2}\right] \mathrm{e}^{-(20 {\rm{ \mathsf{ π} }} n)^{2}} \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ n \in(0.2,0.4] \\ 0.4 \times\left[1-2 \times(10 {\rm{ \mathsf{ π} }} n)^{2}\right] \mathrm{e}^{-(10 {\rm{ \mathsf{ π} }} n)^{2}} \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ n \in(0.4,0.6] \end{array}\right. $ | (22) |
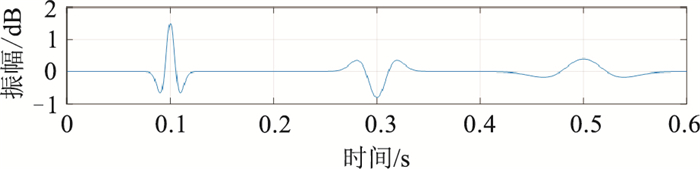
合成如图 1所示的模拟地震信号,可见其振幅峰值分别出现在0.1、0.3、0.5s位置。
|
图 1 模拟地震信号波形 |
将模拟地震信号做Hilbert变换,对加窗后的核函数做FFT获得SPWVD结果。与实际地震信号一样,模拟地震信号也具有主频低、频段窄的特点。选择频段0~100Hz,观察信号完整的时频分布。
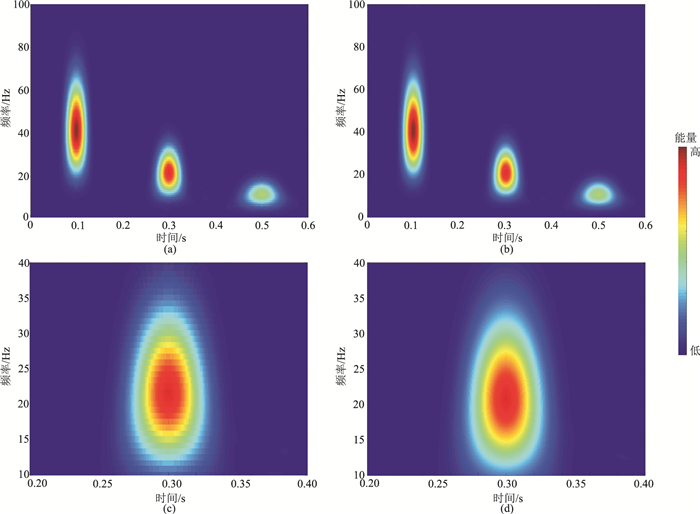
对比模拟信号的SPWVD(图 2a)和SPWVD- CZT(图 2b)处理结果,可见模拟地震信号在0.1、0.3、0.5s处的能量分布分别集中于40、20、10Hz处;SPWVD-CZT保留了SPWVD完整的时频分布和数学特性。由于模拟地震信号较平滑且时频域范围较大,难以直观地看到信号分辨率的提升,因此选取0.2~0.4s时段、10~40Hz频段做局部细节放大显示(图 2c和图 2d),对比可见SPWVD-CZT算法利用采样插值特性增加细化点数方式平滑了选定频段的时频分布(图 2d),进一步增强了模拟信号时频聚焦能力,同时完善了局部边缘细节,提升了信号的时频分辨率。
|
图 2 模拟地震信号的时频分析效果对比 (a)SPWVD;(b)SPWVD-CZT;(c)图a局部放大显示;(d)图b局部放大显示 |
相较于模拟地震信号,实际地震信号的频率、相位、振幅等信息更复杂。通过对实际单道地震记录进行SPWVD-CZT分析,进一步验证该时频分析方法的有效性。
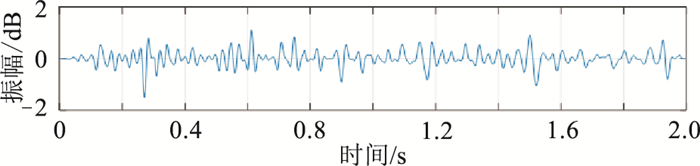
图 3为实际单道地震信号,采样率为2ms,时间采样点数(N)为1001。对其分别于0、100Hz频段做SPWVD-CZT处理(图 4b),细化点数(M)为600。
|
图 3 实际单道地震信号波形 |
|
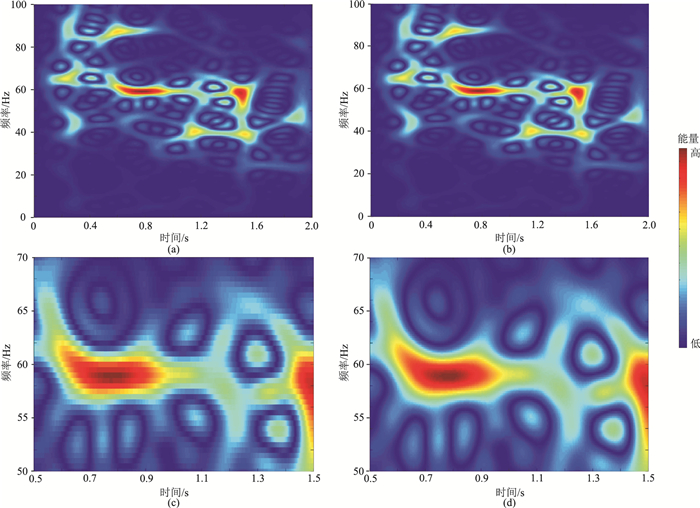
图 4 实际单道地震信号的时频分析对比 (a)SPWVD;(b)SPWVD-CZT;(c)图a局部放大显示;(d)图b局部放大显示 |
与实际单道地震信号的SPWVD处理结果(图 4a)对比,可见SPWVD-CZT算法(图 4b)对复杂实际单道地震信号仍具有完整的时频分析能力,不仅准确刻画出能量在时域和频域内的分布,而且保留了SPWVD优良的数学特性。选取0.5~1.5s时段、50~70Hz频段,同样对上述处理结果做局部细节放大显示(图 4c、图 4d),对比可知SPWVD-CZT算法(图 4d)通过在各采样点之间进行插值,增加有效频段内的划分点数,在保持高度时频聚焦性的同时平滑了地震信号的能量分布,更精确地刻画出功率谱随时间和频率的变化。
3 应用案例川西中侏罗统沙溪庙组属于浅水三角洲沉积体系,油气资源丰富,是目前四川盆地天然气产能建设的重要层系之一。依据沉积特征和地层厚度,沙溪庙组被划分为上沙溪庙组和下沙溪庙组,其中上沙溪庙组又进一步细分为沙溪一段和沙溪二段,下沙溪庙组为沙溪三段。上沙溪庙组厚度为450~700m,是由棕(褐)色泥岩、粉砂质泥岩与褐灰、浅绿灰色细砂岩组成的厚互层;下沙溪庙组厚度为134~250m,是由暗(褐)紫色含粉砂质泥岩为主、夹浅(绿)灰色细粒灰质岩屑长石砂岩组成的薄互层。
工区位于川西中江地区。根据埋藏深度、地层厚度和沉积特征等差异,该区沙溪三段J2s33被进一步细分为J2s33-1、J2s33-2和J2s33-3三套地层。J2s33河道砂体蕴含丰富的天然气资源,是该区陆相油气资源的主要赋存场所,当然也成为主要勘探目标。这些河道砂体的单层厚度大多处于5~20m,被泥岩地层包围,地震反射频率主要集中在20~50Hz,与其他岩性地层在空间分布上呈纵横交错叠置状态,识别难度大,严重影响该区井位部署、水平井迹设计等。因此,基于J2s33实际地震数据和地质层位等资料,采用SPWVD-CZT方法对J2s33-1、J2s33-2和J2s33-3三套地层的河道微相开展储层分布空间识别,对区内天然气高效勘探和经济开发具有重要意义。
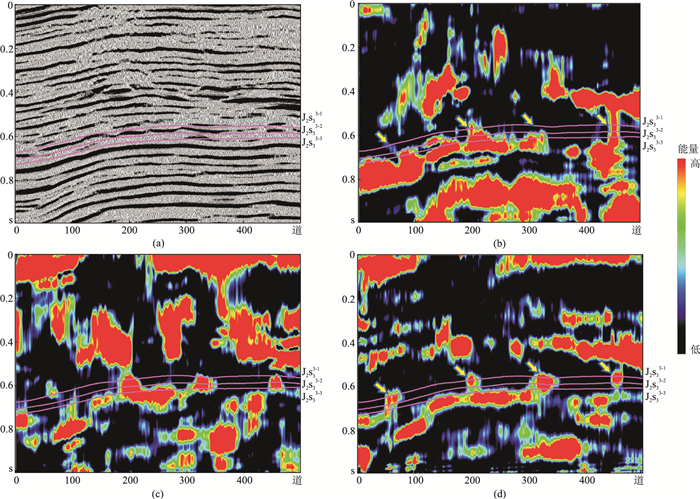
原始地震剖面(图 5a)显示了J2s33-1、J2s33-2和J2s33-3三套地层中河道微相反射能量强弱各异的“透镜体”响应特征。利用SPWVD-CZT算法分别得到20、35、50Hz单频地震剖面(图 5b~图 5d)。由于不同地下介质对频率具有不同的响应特征,在单频剖面中表现为能量随频率变化;J2s33河道砂体地震反射的频率主要集中于20~50Hz。以J2s33-1层为例,随着频率由20Hz增至50Hz,四条河道(黄色箭头)的能量越来越集中,功率谱响应更清晰,时频分辨率提升,可清晰地展现分流河道的分布。同时,对比J2s33内三套地层50Hz频率对应的两种算法的功率谱图,可见SPWVD-CZT算法结果(图 6b、图 6d、图 6f)具有更高分辨率,能更清晰地刻画J2s33-1、J2s33-2和J2s33-3三套地层中不同宽度的分流河道(红色线框)的沿层流向。同时,SPWVD-CZT算法还在SPWVD算法(图 6a、图 6c、图 6e)基础上进一步识别出一些较窄、更隐蔽的小河道(蓝色部分)。与较大分流河道相比,这些小河道的能量分散,识别难度更大。另外,SPWVD-CZT算法不仅能识别出分流河道的走势,并且对河流的宽度变化、空间展布等特征也能更好地展示。
|
图 5 原始剖面(a)与20(b)、35(c)、50Hz(d)的SPWVD-CZT单频剖面 |

|
图 6 J2s33三小层的两种算法的50Hz功率谱 (a)J2s33-1层的SPWVD;(b)J2s33-1层的SPWVD-CZT;(c)J2s33-2层的SPWVD;(d)J2s33-2层的SPWVD-CZT;(e)J2s33-3层的SPWVD;(f)J2s33-3层的SPWVD-CZT |
总之,SPWVD-CZT算法不仅保留了SPWVD优良的时频聚焦性和抑制交叉项产生的能力;同时利用CZT的空间采样特性,增加有效频段内划分点数,提升了信号的时频分辨率。川西地区J2s33河道储层研究实例结果表明,SPWVD- CZT在纵向和横向均能清晰地呈现河道微相的复杂结构,更精确地刻画分流河道的厚度、宽度、流向等特征及其变化,可为该区油气勘探开发提供技术支撑。
4 结论通过SPWVD-CZT方法研究,利用模拟地震信号、实际单道地震信号验证该算法对信号时频分辨率的提升效果,并将其应用于川西中江地区分流河道的识别。获得以下认识和结论。
(1) SPWVD-CZT具有优良的时频聚焦性,能完整地反映信号能量在时频域内的变化,它利用采样插值提升特性,增加有效频段划分点数,在SPWVD基础上进一步提升了信号时频分辨率。
(2) 利用SPWVD-CZT提取的模拟地震信号和实际单道记录的瞬时功率谱的能量分布更平滑、更均匀,时频谱图的边缘细节也更清晰。
(3) 针对埋藏深、隐蔽性强的分流河道储层,SPWVD-CZT能在一定程度上克服地震信号主频低、频带窄导致的分辨率不足问题,突出地下河道的横向宽度、纵向厚度、沿层走向等空间分布特征,提升油气资源勘探精度。该方法也为微型地质体识别提供了一种新思路,且拓展了传统时频分析理论。
| [1] |
梁狄刚, 冉隆辉, 戴弹申, 等. 四川盆地中北部侏罗系大面积非常规石油勘探潜力的再认识[J]. 石油学报, 2011, 32(1): 8-17. LIANG Digang, RAN Longhui, DAI Tanshen, et al. A re-recognition of the prospecting potential of Jurassic large-area and non-conventional oils in the central-northern Sichuan Basin[J]. Acta Petrolei Sinica, 2011, 32(1): 8-17. |
| [2] |
廖群山, 胡华, 林建平, 等. 四川盆地川中侏罗系致密储层石油勘探前景[J]. 石油与天然气地质, 2011, 32(6): 815-822. LIAO Qunshan, HU Hua, LIN Jianping, et al. Petroleum exploration prospects of Jurassic tight reservoirs in Central Sichuan Basin[J]. Oil & Gas Geology, 2011, 32(6): 815-822. |
| [3] |
邹红星, 周小波, 李衍达. 时频分析: 回溯与前瞻[J]. 电子学报, 2000, 28(9): 78-84. ZHOU Hongxing, ZHOU Xiaobo, LI Yanda. Which time-frequency analysis-A survey[J]. Acta Electronica Sinica, 2000, 28(9): 78-84. DOI:10.3321/j.issn:0372-2112.2000.09.022 |
| [4] |
庞锐, 刘百红, 孙成龙. 时频分析技术在地震勘探中的应用综述[J]. 岩性油气藏, 2013, 25(3): 92-96. PANG Rui, LIU Baihong, SUN Chenglong. Review on time-frequency analysis technique and its application in seismic exploration[J]. Lithologic Reservoirs, 2013, 25(3): 92-96. DOI:10.3969/j.issn.1673-8926.2013.03.016 |
| [5] |
马见青, 李庆春, 王美丁. 广义S变换在地震勘探中的研究进展[J]. 物探与化探, 2011, 35(2): 265-269. MA Jianqing, LI Qingchun, WANG Meiding. Some advances of general S transform in seismic exploration[J]. Geophysical & Geochemical Exploration, 2011, 35(2): 265-269. |
| [6] |
武迪, 宋维琪, 刘军, 等. 变分模态分解与包络导数算子结合的时频分析方法及溶洞储层预测[J]. 石油地球物理勘探, 2021, 56(2): 346-355. WU Di, SONG Weiqi, LIU Jun, et al. Seismic time-frequency analysis based on VMD and envelope deriva-tive operator for fractured-vuggy reservoir prediction[J]. Oil Geophysical Prospecting, 2021, 56(2): 346-355. |
| [7] |
朱秋影, 魏国齐, 杨威, 等. 利用时频分析技术预测依拉克构造有利砂体分布[J]. 石油地球物理勘探, 2017, 52(3): 538-547. ZHU Qiuying, WEI Guoqi, YANG Wei, et al. Favorable sand body prediction based on the time-frequency analysis in Iraqi Structure[J]. Oil Geophysical Prospecting, 2017, 52(3): 538-547. |
| [8] |
蒋炼, 曾驿, 文晓涛, 等. 基于地震相分析的砂体储层厚度描述[J]. 断块油气田, 2011, 18(3): 273-276. JIANG Lian, ZENG Yi, WEN Xiaotao, et al. Description of sand thickness based on seismic facies analysis[J]. Fault-Block Oil & Gas Field, 2011, 18(3): 273-276. |
| [9] |
张付瑷, 陈学华, 罗鑫, 等. 改进的窗参数优化S变换及其在河道检测中的应用[J]. 石油地球物理勘探, 2021, 56(4): 809-814, 881. ZHANG Fuai, CHEN Xuehua, LUO Xin, et al. Improved window parameter optimized S-transform and its application in channel detection[J]. Oil Geophysical Prospecting, 2021, 56(4): 809-814, 881. |
| [10] |
杨道庆, 张永华, 罗家群, 等. 时频分析技术识别泌阳凹陷毕店地区河道砂体[J]. 特种油气藏, 2014, 22(1): 12-15. YANG Daoqing, ZHANG Yonghua, LUO Jiaqun, et al. Channel sandbodys identification by time-frequency analysis in Bidian of Biyang Sag[J]. Special Oil & Gas Reservoirs, 2014, 22(1): 12-15. DOI:10.3969/j.issn.1006-6535.2014.01.003 |
| [11] |
DURAK L, ARIKAN O. Short-time Fourier transform: two fundamental properties and an optimal implementation[J]. IEEE Transactions Signal Process, 2003, 51(5): 1231-1242. DOI:10.1109/TSP.2003.810293 |
| [12] |
SINHA S, ROUTH P S, ANNO P D, et al. Spectral decomposition of seismic data with continuous-wavelet transform[J]. Geophysics, 2005, 70(6): P19-P25. DOI:10.1190/1.2127113 |
| [13] |
SINHA S, ROUTH P, ANNO P. Instantaneous spectral attributes using scales in continuous-wavelet transform[J]. Geophysics, 2009, 74(2): WA137-WA142. DOI:10.1190/1.3054145 |
| [14] |
WANG Y H. Seismic time-frequency spectral decomposition by matching pursuit[J]. Geophysics, 2007, 72(1): V13-V20. DOI:10.1190/1.2387109 |
| [15] |
QIAN S, CHEN D. Discrete Gabor transform[J]. IEEE Transactions on Signal Processing, 1993, 41(7): 2429-2438. DOI:10.1109/78.224251 |
| [16] |
PINNEGAR C R, MANSINHA L. Time-local spectral analysis for non-stationary time series: The S-transform for noisy signals[J]. Fluctuation and Noise Letters, 2003, 3(3): L357-L364. DOI:10.1142/S0219477503001439 |
| [17] |
COHEN L. Time-frequency Analysis[M]. Englewood Cliffs, N J, USA, 1995.
|
| [18] |
张晓燕, 彭真明, 张萍, 等. 基于分数阶Wigner-Ville分布的地震信号谱分解[J]. 石油地球物理勘探, 2014, 49(5): 839-845. ZHANG Xiaoyan, PENG Zhenming, ZHANG Ping, et al. Spectral decomposition of seismic signals based on fractional Wigner-Ville distribution[J]. Oil Geophysical Prospecting, 2014, 49(5): 839-845. |
| [19] |
赵培洪, 平殿发, 邓兵, 等. 魏格纳-维尔分布交叉项抑制方法综述[J]. 探测与控制学报, 2010, 32(1): 23-29. ZHAO Peihong, PING Dianfa, DENG Bing, et al. Review of cross-term suppression methods for Wigner-Ville distribution[J]. Journal of Detection & Control, 2010, 32(1): 23-29. DOI:10.3969/j.issn.1008-1194.2010.01.006 |
| [20] |
侯伯刚, 杨池银, 武站国, 等. 地震属性及其在储层预测中的影响因素[J]. 石油地球物理勘探, 2004, 39(5): 553-558, 574. HOU Bogang, YANG Chiyin, WU Zhanguo. Seismic attributes and its influencing factors in reservoir prediction[J]. Oil Geophysical Prospecting, 2004, 39(5): 553-558, 574. DOI:10.3321/j.issn:1000-7210.2004.05.011 |
| [21] |
马可, 张远安, 张开生. CZT和ZFFT频谱细化性能分析及FPGA实现[J]. 计算机测量与控制, 2016, 24(2): 288-289, 303. MA Ke, ZHANG Yuanan, ZHANG Kaisheng. Performance analysis for CZT and ZFFT spectrum zoom and its FPGA realization[J]. Computer Measurement & Control, 2016, 24(2): 288-289, 303. |
| [22] |
WIGNER E P. On the quantum correction for thermodynamic equilibrium[J]. Physical Review Journals, 1932, 40(5): 749-759. DOI:10.1103/PhysRev.40.749 |
| [23] |
赵俊, 张朝阳, 赖利峰, 等. 一种基于时频分析的跳频信号参数盲估计方法[J]. 电路与系统学报, 2003, 8(3): 46-50. ZHAO Jun, ZHANG Chaoyang, LAI Lifeng, et al. Blind parameter estimation of frequency-hopping signal based on time-frequency analysis[J]. Journal of Circuits and Systems, 2003, 8(3): 46-50. DOI:10.3969/j.issn.1007-0249.2003.03.011 |
| [24] |
李华, 李尚柏, 周维, 等. 线性调频Z变换在电力谐波分析中的应用[J]. 电测与仪表, 2005, 42(3): 1-5. LI Hua, LI Shangbo, ZHOU Wei, et al. Chrip-Z transform and its applications in power system harmonic analysis[J]. Electrical Measurement & Instrumentation, 2005, 42(3): 1-5. DOI:10.3969/j.issn.1001-1390.2005.03.001 |
| [25] |
罗国安, 高少武, 魏庚雨, 等. Chirp-Z变换谱分析压制地震记录单频干扰[J]. 石油地球物理勘探, 2009, 44(2): 166-172. LUO Guoan, GAO Shaowu, WEI Gengyu, et al. Suppression of mono-frequency interference on seismic record by Chrip-Z transform spectrum analysis[J]. Oil Geophysical Prospecting, 2009, 44(2): 166-172. DOI:10.3321/j.issn:1000-7210.2009.02.008 |



 徐天吉, 四川省成都市高新西区西源大道2006号电子科技大学清水河校区资源与环境学院, 611731。Email:
徐天吉, 四川省成都市高新西区西源大道2006号电子科技大学清水河校区资源与环境学院, 611731。Email: 