② 长江大学地球物理与石油资源学院, 湖北武汉 430110
② College of Geophysics and Petroleum Resources, Yangtze University, Wuhan, Hubei 430110, China
纵、横波速度在储层物性(孔隙度、饱和度等)参数预测和岩性及孔隙流体识别等方面扮演着不可替代的角色。准确的纵波和横波速度信息对精确描述储层特征、消除流体识别假象以及提高叠前地震反演和AVO属性分析精度等方面具有重要意义。然而,在实际油气勘探中,由于偶极声波测井测量施工成本较高,造成大多数测井数据中缺少横波速度资料。为此,人们广泛尝试利用岩石物理理论预测横波速度[1-4]。
Castagna等[5]给出了水饱和状态下碎屑硅质岩横波速度与纵波速度的经验关系的泥岩基线公式。Han等[6]针对75块砂岩样品开展了不同压力下的超声实验测量,拟合出横波速度与纵波速度的线性经验关系式。Nur等[7]假设岩石孔隙度小于临界孔隙度时,干岩石模量与岩石孔隙度线性相关,构建了临界孔隙度模型。
虽然上述经验模型使用方便,但其物理含义欠明确且需结合大量实际工区的测井和岩心数据进行校正。Kuster等[8]利用长波一阶散射理论推导出弹性模量与孔隙度和孔隙形状之间的定量关系式。Xu等[9]将岩石孔隙分成砂岩孔隙和泥岩孔隙,引入砂泥岩孔隙纵横比表征孔隙形状,综合应用Wyllie时间方程[10]、KT模型[8]和Gassmann方程[11]建立了砂泥岩岩石物理模型。该模型考虑了孔隙结构及孔隙形状对岩石弹性模量的影响,具有明确物理意义,在横波速度预测及岩石物理分析中得到广泛应用[12-13]。张广智等[14]提出了改进的Xu-White模型并应用于碳酸盐岩横波速度预测。
除了孔隙结构和孔隙类型外,岩石颗粒之间固结作用的强弱对岩石纵、横波速度也有重要影响。Pride等[15]通过引入固结参数表征岩石颗粒之间固结程度,建立了干岩石模量与基质模量的关系式。Lee[16]修正了Pride模型计算剪切模量的表达式,并将其应用于横波速度预测。张佳佳等[17]和侯波等[18]都将Pride模型成功地应用于横波速度预测。
上述经验公式和理论模型虽可较好地预测岩石纵、横波速度,但大多数模型仅考虑了成岩固结作用或聚焦于单一孔隙结构,缺少能同时兼顾多重孔隙结构与成岩作用的有效理论与方法,导致现有模型在复杂孔隙介质储层预测中呈现出适用性较差、稳定性不足和精度较低等特征。
为了兼顾成岩固结作用与双重孔隙结构对岩石骨架弹性模量的影响,本文提出一种考虑成岩固结作用的双重孔隙介质岩石物理模型。首先,基于微分等效介质(DEM)理论[19]推导出含有(软、硬)双重孔隙DEM解析模型;再从双重孔隙DEM模型出发,借鉴Pride模型思想,建立了考虑成岩固结作用的双重孔隙介质岩石物理模型;然后,结合Gass-mann方程建立饱和岩石纵、横波速度计算模型;最后,将该模型分别应用于实验数据和测井数据的速度预测,并对其预测结果进行对比分析,验证了本文所提考虑成岩固结作用的双重孔隙介质岩石物理模型的适用性和有效性。
1 方法原理 1.1 单孔隙DEM模型及其近似解经典DEM理论是通过将等体积增量的填充物逐渐添加到背景固体矿物中模拟双相等效介质,直至添加的填充物体积为真实孔隙度[20-21]。Berryman[22]给出DEM模型的微分方程组耦合形式
| $ (1-y) \frac{\mathrm{d}}{\mathrm{d} y}\left[K^{*}(y)\right]=\left[K_{i}-K^{*}(y)\right] P^{*} $ | (1) |
| $ (1-y) \frac{\mathrm{d}}{\mathrm{d} y}\left[\mu^{*}(y)\right]=\left[\mu_{i}-\mu^{*}(y)\right] Q^{*} $ | (2) |
式中:Ki和μi分别为第i种填充物的体积模量和剪切模量;K*和μ*对应为加入填充物后的体积模量和剪切模量;y为填充物含量;P*和Q*为填充物孔隙形状几何因子。
对于干岩石骨架,填充物的体积模量和剪切模量分别为Ki=0和μi=0,则式(1)、式(2)可简化为
| $ (1-y) \frac{\mathrm{d} K^{*}(y)}{\mathrm{d} y}=-K^{*} P^{*} $ | (3) |
| $ (1-y) \frac{\mathrm{d} \mu^{*}(y)}{\mathrm{d} y}=-\mu{ }^{*} Q^{*} $ | (4) |
对式(3)、式(4)从y=0到y=ϕ进行积分,并满足初始条件K*(0)=Kma、μ*(0)=μma,令Kdry=K*、μdry=μ*,得到单孔隙结构干岩石骨架模量
| $ K_{\mathrm{dry}} =K_{\mathrm{ma}}(1-\phi)^{P} $ | (5) |
| $ \mu_{\mathrm{dry}} =\mu_{\mathrm{ma}}(1-\phi)^{Q} $ | (6) |
式中:Kdry、μdry分别为干岩石骨架的体积模量和剪切模量;Kma、μma对应为岩石基质的体积模量和剪切模量;P和Q为与孔隙形状有关的几何因子;ϕ为岩石的总孔隙度。
1.2 双重孔隙DEM模型碎屑岩储层中通常发育两种孔隙类型,即微裂缝和孔隙[23]。本文利用DEM理论模拟双孔岩石的弹性性质,即是将单孔隙DEM理论拓展到双重孔隙DEM模型。为此,将上述孔隙对应定义为软孔和硬孔两种类型,分别用αso、αst表示软孔和硬孔的孔隙纵横比。考虑孔隙添加顺序,首先向岩石基质中加入软孔,按式(5)和式(6)可得岩石骨架模量
| $ K_{\mathrm{dry}}^{\mathrm{so}} =K_{\mathrm{ma}}\left(1-\phi_{\mathrm{so}}\right)^{P_{\mathrm{so}}} $ | (7) |
| $ \mu_{\mathrm{dry}}^{\mathrm{so}} =\mu_{\mathrm{ma}}\left(1-\phi_{\mathrm{so}}\right)^{Q_{\mathrm{so}}} $ | (8) |
式中:Kdryso、μdryso分别表示加入软孔隙后的体积模量和剪切模量;ϕso为软孔的孔隙度;Pso和Qso为软孔对应的几何因子,表征孔隙形状对干岩石体积模量和剪切模量的影响,是关于孔隙纵横比αso的函数,计算方法见附录A。
然后,将已引入软孔的基质视作新岩石基质,并向其中加入硬孔,可得最终干岩石骨架的模量
| $ K_{\mathrm{dry}} =K_{\mathrm{dry}}^{\mathrm{so}}\left(1-\phi_{\mathrm{st}}\right)^{P_{\mathrm{st}}} $ | (9) |
| $ \mu_{\mathrm{dry}} =\mu_{\mathrm{dry}}^{\mathrm{so}}\left(1-\phi_{\mathrm{st}}\right)^{Q_{\mathrm{st}}} $ | (10) |
式中:ϕst为硬孔的孔隙度,且有ϕ=ϕso+ϕst;Pst和Qst为硬孔对应的几何因子,是关于孔隙纵横比αst的函数,计算方法同上。将式(7)、式(8)代入式(9)和式(10),可得含有双重孔隙的干岩石骨架的模量
| $ K_{\mathrm{dry}} =K_{\mathrm{ma}}\left(1-\phi_{\mathrm{so}}\right)^{P_{\mathrm{so}}}\left(1-\phi_{\mathrm{st}}\right)^{P_{\mathrm{st}}} $ | (11) |
| $ \mu_{\mathrm{dry}} =\mu_{\mathrm{ma}}\left(1-\phi_{\mathrm{so}}\right)^{Q_{\mathrm{so}}}\left(1-\phi_{\mathrm{st}}\right)^{Q_{\mathrm{st}}} $ | (12) |
若先向岩石基质中加入硬孔,按照式(5)和式(6)可得到此时干岩石骨架的模量
| $ K_{\mathrm{dry}}^{\mathrm{st}} =K_{\mathrm{ma}}\left(1-\phi_{\mathrm{st}}\right)^{P_{\mathrm{st}}} $ | (13) |
| $ \mu_{\mathrm{dry}}^{\mathrm{st}} =\mu_{\mathrm{ma}}\left(1-\phi_{\mathrm{st}}\right)^{Q_{\mathrm{st}}} $ | (14) |
式中:Kdryst、μdryst分别表示加入硬孔后的体积模量和剪切模量,计算方法同上。
然后,将已引入硬孔的基质视作新的岩石基质,并向其中加入软孔,可得最终干岩石骨架的模量
| $ K_{\mathrm{dry}} =K_{\mathrm{dry}}^{\mathrm{st}}\left(1-\phi_{\mathrm{so}}\right)^{P_{\mathrm{so}}} $ | (15) |
| $ \mu_{\mathrm{dry}} =\mu_{\mathrm{dry}}^{\mathrm{st}}\left(1-\phi_{\mathrm{so}}\right)^{Q_{\mathrm{so}}} $ | (16) |
将式(13)、式(14)代入式(15)和式(16)中,可得含双重孔隙的干岩石骨架模量
| $ K_{\mathrm{dry}} =K_{\mathrm{ma}}\left(1-\phi_{\mathrm{st}}\right)^{P_{\mathrm{st}}}\left(1-\phi_{\mathrm{so}}\right)^{P_{\mathrm{so}}} $ | (17) |
| $ \mu_{\mathrm{dry}} =\mu_{\mathrm{ma}}\left(1-\phi_{\mathrm{st}}\right)^{Q_{\mathrm{st}}}\left(1-\phi_{\mathrm{so}}\right)^{Q_{\mathrm{so}}} $ | (18) |
与式(11)、式(12)对比可知,由双重孔隙DEM模型计算的弹性模量与两种孔隙的加入顺序无关。
1.3 考虑成岩固结作用的双重孔隙模型双重孔隙DEM模型可直接求解、计算简便且考虑了孔隙结构特征对弹性波速度的影响,但该模型忽略了岩石颗粒之间的固结压实作用对岩石弹性模量的影响。Pride等[15]通过引入固结参数表征岩石颗粒之间的固结程度,提出固结岩石的体积模量和剪切模量的简单表达式
| $ K_{\text {dry }} =\frac{K_{\mathrm{ma}}(1-\phi)}{W_{K}(c)} $ | (19) |
| $ \mu_{\text {dry }} =\frac{\mu_{\mathrm{ma}}(1-\phi)}{W_{\mu}(c)} $ | (20) |
式中:WK(c)、Wμ(c)为反映岩石骨架固结程度的函数,且有WK(c)=1+cϕ、Wμ(c)=1+1.5cϕ;c为固结参数,对于砂岩,通常取2 < c < 20。
Pride模型是一个经验模型,它揭示了岩石颗粒之间的固结压实作用对岩石弹性模量的影响。当c接近于2时,表明岩石颗粒之间固结程度较大,岩石骨架表现为更坚硬,弹性模量较高;当c接近于20时,表明岩石颗粒之间固结程度较小,岩石骨架表现为更疏松,弹性模量较低。
侯波等[24]将Pride模型思路应用于Keys-Xu模型,提出综合成岩作用和孔隙形状的岩石物理模型
| $ K_{\mathrm{dry}} =\frac{K_{\mathrm{dry}}^{\mathrm{Keys}-\mathrm{Xu}}}{W_{K}(c)} $ | (21) |
| $ \mu_{\mathrm{dry}} =\frac{\mu_{\mathrm{dry}}^{\mathrm{Key}-\mathrm{Xu}}}{W_{\mu}(c)} $ | (22) |
式中
| $ K_{\mathrm{dry}}^{\mathrm{Keys}-\mathrm{Xu}} =K_{\mathrm{ma}}(1-\phi)^{p} $ |
| $ \mu_{\mathrm{dry}}^{\mathrm{Keys}-\mathrm{Xu}} =\mu_{\mathrm{ma}}(1-\phi)^{Q} $ |
由式(19)、式(20)可知,Pride模型对岩石弹性模量的影响主要表现在分母上增加了一个固结参数的函数。本文采用相同做法,将Pride模型思路应用于新导出的双重孔隙DEM模型,提出考虑成岩固结作用的双重孔隙岩石物理模型
| $ K_{\mathrm{dry}} =\frac{K_{\mathrm{dry}}^{\mathrm{dp}}}{W_{K}(c)} $ | (23) |
| $ \mu_{\mathrm{dry}} =\frac{\mu_{\mathrm{dry}}^{\mathrm{dp}}}{W_{\mu}(c)} $ | (24) |
式中Kdrydp、μdrydp为“1.2节”(式(11)、式(12))推导的双重孔隙DEM模型,且有
| $ K_{\mathrm{dry}}^{\mathrm{dp}} =K_{\mathrm{ma}}\left(1-\phi_{\mathrm{so}}\right)^{P_{\mathrm{so}}}\left(1-\phi_{\mathrm{st}}\right)^{P_{\mathrm{st}}} $ |
| $ \mu_{\mathrm{dry}}^{\mathrm{dp}} =\mu_{\mathrm{ma}}\left(1-\phi_{\mathrm{so}}\right)^{Q_{\mathrm{so}}}\left(1-\phi_{\mathrm{st}}\right)^{Q_{\mathrm{st}}} $ |
代入式(23)和式(24),可得
| $ K_{\mathrm{dry}} =\frac{K_{\mathrm{ma}}\left(1-\phi_{\mathrm{so}}\right)^{P_{\mathrm{so}}}\left(1-\phi_{\mathrm{st}}\right)^{P_{\mathrm{st}}}}{1+c \phi} $ | (25) |
| $ \mu_{\mathrm{dry}} =\frac{\mu_{\mathrm{ma}}\left(1-\phi_{\mathrm{so}}\right)^{Q_{\mathrm{so}}}\left(1-\phi_{\mathrm{st}}\right)^{Q_{\mathrm{st}}}}{1+1.5 c \phi} $ | (26) |
当c逐渐减少并接近于0,即岩石完全固结时,式(25)和式(26)就变成式(11)和式(12),即DEM模型的近似模型。式中ϕ=ϕso+ϕst=ϕ(fso+ fst),其中fso、fst分别为软孔、硬孔孔隙所占总孔隙的比例。
为了探究孔隙度、固结参数、孔隙纵横比和软孔体积比对干岩石骨架模量和速度的影响,首先对本文模型、Xu-White模型和Pride模型进行数值模拟并对比其结果。以石英作为主介质,其体积模量和剪切模量分别取为38、44GPa。岩石中含有两种不同形状的孔隙,其孔隙纵横比分别为0.12和0.03,其孔隙体积占比分别取为98%和2%。
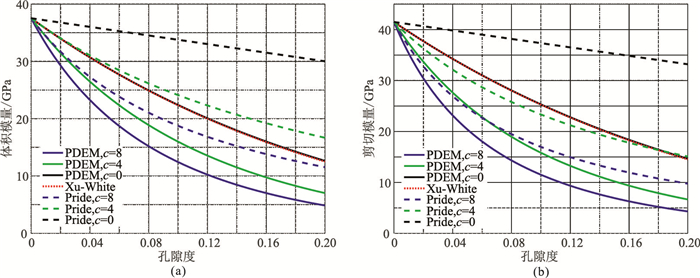
图 1、图 2分别是干岩石骨架模量、速度随孔隙度的变化特征。其中蓝色、绿色、黑色实线代表本文模型(PDEM)在固结参数分别取c=8,4,0时计算结果;红色虚线代表Xu-White模型计算结果;蓝色、绿色、黑色虚线代表Pride模型在固结参数分别取c=8,4,0时计算结果。从这两图可看出:干岩石骨架弹性模量和速度随总孔隙度的增加而减小;随固结参数增加(固结程度降低)而降低。当固结参数c为0时,本文模型计算结果与Xu-White模型计算结果相同;当c>0时,本文模型预测结果均低于Xu-White模型。这主要是因为在DEM理论推导中,Xu-White模型假设岩石骨架是由一个整体构成,而实际上岩石骨架是由岩石颗粒胶结而成的。胶结程度会影响岩石骨架模量和速度。而Pride模型计算结果均大于另两种模型,主要因为计算干岩石骨架模量时,Pride模型输入参数仅有孔隙度和固结参数,却未考虑孔隙结构的影响。
|
图 1 干岩石体积模量(a)和剪切模量(b)随孔隙度的变化特征 |

|
图 2 纵(a)、横(b)波速度随孔隙度的变化特征 |
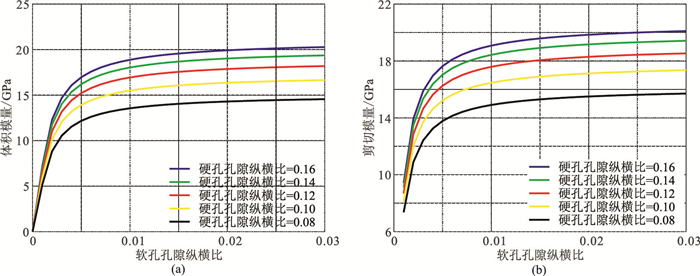
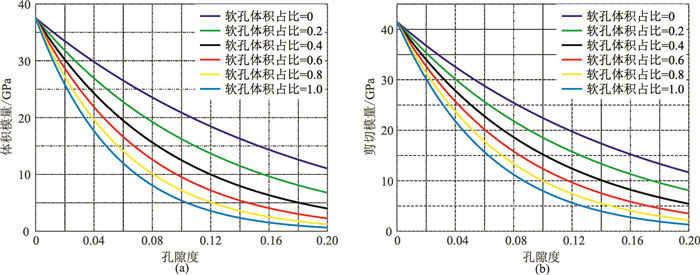
图 3和图 4展示孔隙度为0.2、固结参数为2时,干燥岩石弹性模量随孔隙纵横比和软孔体积比的变化特征。从图 3可看出,干岩石骨架弹性模量随孔隙纵横比的增加而增加,当软孔纵横比增加到0.008时,其增长率变缓。从图 4可见,随着软孔体积比的增加,干岩石骨架模量总体呈下降趋势。
|
图 3 干岩石体积模量(a)和剪切模量(b)随软孔隙纵横比的变化特征 |
|
图 4 干岩石体积模量(a)和剪切模量(b)随软孔体积比的变化特征 |
由式(25)、式(26)求得干岩石骨架的体积模量和剪切模量后,可通过Gassmann方程计算流体饱和岩石的体积模量和剪切模量
| $ K_{\mathrm{sat}}=K_{\mathrm{dry}}+\frac{\left(1-\frac{K_{\mathrm{dry}}}{K_{\mathrm{ma}}}\right)^{2}}{\frac{1-\phi}{K_{\mathrm{ma}}}+\frac{\phi}{K_{\mathrm{fl}}}+\frac{K_{\mathrm{dry}}}{K_{\mathrm{ma}}^{2}}} $ | (27) |
| $ \mu_{\mathrm{sat}}=\mu_{\mathrm{dry}} $ | (28) |
式中:Ksat、μsat分别为流体饱和岩石的体积模量和剪切模量;Kfl为孔隙流体的体积模量,可由Brie模型[25]中的计算公式Kfl=(Kw-Kg)Swe+Kg求取,其中Kw、Kg为水和气的体积模量,Sw为含水饱和度。一般地,指数e反映流体分布特征,在1~42区间取值,其中e取低值代表斑状饱和分布,e取高值代表均匀饱和分布。
最后,由纵、横波速度与流体饱和岩石的弹性模量和体密度之间的关系,可得到纵、横波速度
| $ V_{\mathrm{P}} =\sqrt{\frac{K_{\mathrm{sat}}+\frac{4}{3} \mu_{\mathrm{sat}}}{\rho_{\mathrm{sat}}}} $ | (29) |
| $ V_{\mathrm{S}} =\sqrt{\frac{\mu_{\mathrm{sat}}}{\rho_{\mathrm{sat}}}} $ | (30) |
式中:VP、VS分别为纵波和横波速度;ρsat为饱和岩石的体密度,其计算公式为
| $ \rho_{\mathrm{sat}}=\rho_{\mathrm{ma}}(1-\phi)+\left[\rho_{\mathrm{w}} S_{\mathrm{w}}+\rho_{\mathrm{g}}\left(1-S_{\mathrm{w}}\right)\right] \phi $ | (31) |
式中ρma、ρw、ρg分别为岩石基质、地层水、天然气的密度。
2 横波速度预测 2.1 技术流程利用本文模型预测横波速度,需提供两个关键参数:固结参数和软孔体积比。这两参数可利用本文优化计算流程(图 5)求得。其主要步骤为:

|
图 5 固结参数和软孔体积比反演流程图 |
(1) 利用式(25)和式(26)推导的岩石物理模型计算干岩石骨架模量,通过Gassmann方程进行流体替代得到饱和岩石弹性模量,进而计算纵波速度;
(2) 基于模拟退火算法不断调整输入参数,优化固结参数c和软孔隙体积比fso,使预测纵波速度与测量纵波速度的误差达到最小,进而得到优化后的固结参数和软孔体积比。
得到优化的固结参数和软孔体积比后,即可用“1.4节”饱和流体岩石物理模型(式(30))计算横波速度。
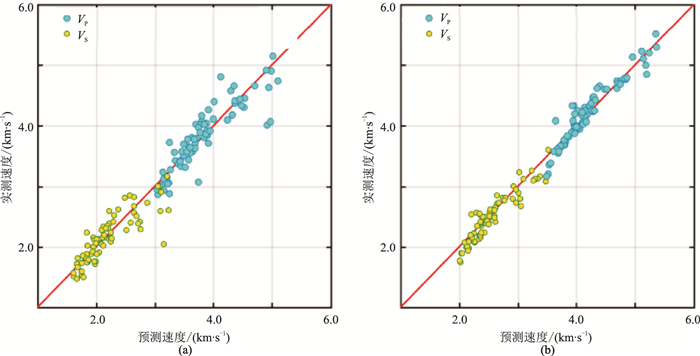
2.2 实验数据为了检验方法的适用性,将本文模型分别应用于压力为5和40MPa条件下的实验测量数据[6]和苏里格地区压力为29MPa条件下的实验测量数据[26]。通过反演流程(图 5),确定压力为5MPa时固结参数c为2.9,软孔体积占比fso为6%;压力为40MPa时固结参数c为2.0,软孔体积占比fso为1.5%;压力为29MPa时固结参数c为2.0,软孔体积占比fso为2.5%。从图 6和图 7可看出,在不同压力条件下,模型预测结果与实验数据绝大多数均吻合较好,均在拟合直线附近。需指出的是,由于苏里格实验数据中缺少泥质含量数据,本文对所有岩石样品采用统一的体积模量和剪切模量,这会对横波速度的预测精度造成影响。模型预测结果与实验数据对比表明,该模型对常规碎屑岩和致密砂岩储层均有较好的适应性。
|
图 6 压力为5(a)、40(b)MPa时预测的与实测的横波速度[6] |
|
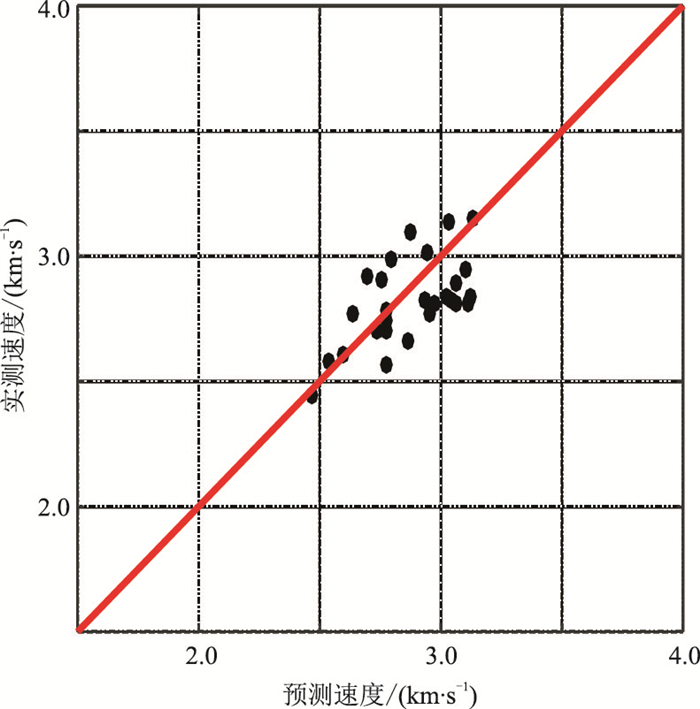
图 7 压力为29MPa时预测的与实测的的横波速度 |
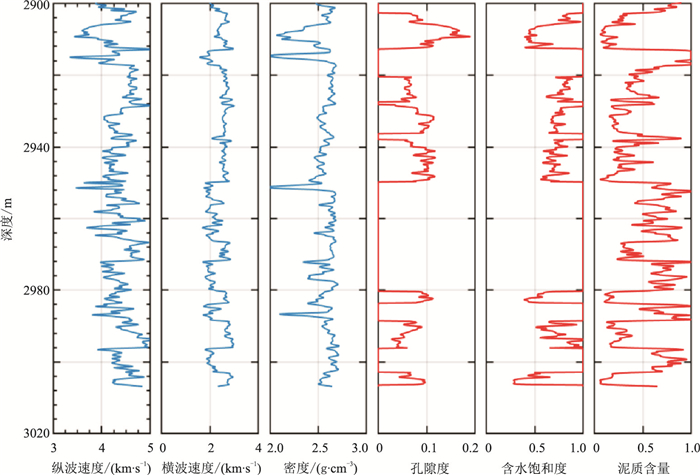
图 8显示苏里格地区M井测井数据,包括纵波速度、横波速度、密度及解释的孔隙度、含水饱和度和泥质含量。该工区目的层处于2900~3007m,为低孔、低渗致密砂岩储层,非储层段孔隙度几乎为零。此外,由于孔隙之间连通性差,气、水关系复杂,使流体在致密砂岩气藏中通常呈不均匀分布。本次建模所涉各种矿物的弹性模量和密度值参考表 1,将分别采用不同的岩石物理模型预测横波速度并做误差对比分析。
|
图 8 苏里格M井的测井数据及解释的物性参数 |
|
|
表 1 各种矿物弹性模量及密度 |
通过不断调整所选用岩石物理模型的自由参数,使其预测的横波速度与实测值之间误差最小。如临界孔隙度模型(CMP)[7]的临界孔隙度为0.39,Pride模型[15]的固结参数为2,本文模型(PDEM)的固结参数和软孔体积比分别为2和0.05,Xu-White(XW)[9]模型中砂岩孔隙纵横比为0.09、泥岩孔隙纵横比为0.056,KT[8]、SC[27]和DEM[19]模型的等效孔隙纵横比为0.13。
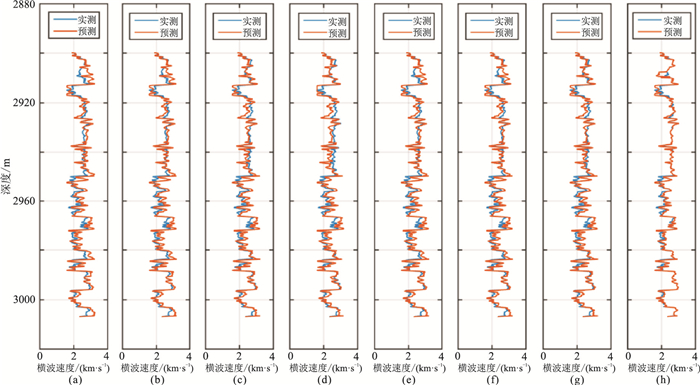
将本文模型和其他七种模型(Krief模型[28]、临界孔隙度模型、Pride模型、Xu-White模型、KT模型、DEM模型、SC模型)应用于图 8测井数据,分别得到图 9所示的横波速度预测结果(红线),并与实测横波速度(蓝线)进行对比。可见在2920~2950m、2960~2974m及2980~3007m三个层段,本文模型预测结果与实际横波测井数据的吻合程度好于其他模型。这是因为本文模型引入了可变固结参数(不同沉积环境及不同岩性的岩石的固结参数通常有差异)和两种孔隙类型。而非储层段的微小差异,可能是由含水饱和度和孔隙度解释的不准确造成的。
|
图 9 压力为29MPa时预测与实测的横波速度 (a)Krief模型;(b)临界孔隙度模型;(c)Pride模型;(d)Xu-White模型;(e)KT模型;(f)DEM模型;(g)SC模型;(h)PDEM模型 |
图 10为基于八种岩石物理模型预测的横波速度与实际横波测井数据之间的均方根误差直方图。可见基于本文模型的横波速度预测结果的均方根误差(143.8m/s)远小于其他模型预测结果的均方根误差(平均为220.0m/s),其中Krief模型的均方根误差更是高达278.0m/s。因此,本文模型对致密砂岩储层的横波速度具有更高预测精度。

|
图 10 八种岩石物理模型预测的横波速度的均方根误差 |
本文推导出双重孔隙DEM模型以表征复杂孔隙储层的孔隙结构,并研究储层弹性参数与孔隙结构和孔隙度的定量关系。孔隙结构的基本元素包括孔隙类型、孔隙形状、孔隙连通性等,现阶段可通过铸体薄片、SEM观测、微纳米CT扫描成像和数字岩心分析技术等微观结构成像手段做直接表征。如何应用地球物理方法间接定量表征储层复杂孔隙结构,一些学者曾开展了探索性研究。李红兵等[29]应用DEM模型和Gassmann方程由纵横波速度反演孔隙结构,并将其应用于横波速度预测。Zhang等[30]利用Sun氏模型从叠前地震数据中反演表征孔隙类型的孔隙结构因子。Li等[31]利用Xu-Payne模型从叠前地震数据定量预测了碳酸盐岩储层软孔、硬孔和参考孔的孔隙度大小。这些理论和方法的成功应用为利用本文模型实现微观孔隙结构量化表征提供了理论借鉴和技术支撑。
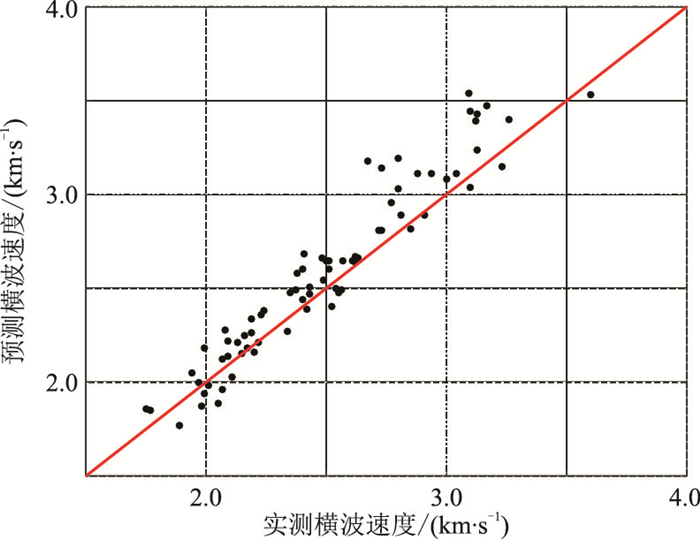
成岩固结作用和孔隙结构及类型是影响岩石弹性性质的两类重要因素,在构建岩石物理模型时应兼顾考虑。经典Xu-White模型只考虑了孔隙结构,图 11是针对同样的砂岩样品预测的横波速度与实测横波速度的交会图[8]。与本文模型预测结果(图 6)对比,可见Xu-White模型预测的横波速度(图 11)整体偏高。这可能是因为Xu-White模型未考虑成岩固结作用的影响。图 12是基于同样砂岩样品采用Pride模型预测的横波速度与实测横波速度的交会图。再与本文模型预测结果(图 6)对比,可见本文模型预测结果更靠近于拟合直线,即误差更小。从测井数据横波速度均方根误差(图 10)也可看出,本文模型预测结果的均方根误差均小于Xu-White模型和Pride模型。干岩石骨架弹性模量不仅与孔隙度和孔隙形状有关,且与矿物颗粒之间固结程度关联。本文模型同时考虑孔隙度、孔隙形状和固结参数,可从成岩固结作用和孔隙结构两方面解释干岩石弹性模量的影响机制,显著减少了仅考虑单一因素导致的计算误差,能更全面、精确地描述岩石骨架弹性模量随孔隙度的变化特征,具有更广阔应用前景。
|
图 11 Xu-White模型预测的与实测的横波速度交会[9] |

|
图 12 Pride模型预测的与实测的横波速度交会 |
本文基于DEM理论导出双重孔隙DEM模型,并与考虑成岩固结作用的Pride模型相结合,提出一种兼顾成岩固结作用和孔隙结构影响的岩石物理模型。通过引入固结参数、软孔和硬孔纵横比、体积占比,实现对岩石成岩作用和微观孔隙结构的联合表征。不同压力下的岩石物理实验数据的测试结果表明,该模型对常规碎屑岩储层和致密砂岩储层具有较强适用性。与其他岩石物理模型预测结果相比,本文模型预测的横波速度精度更高。
需指出的是,应用本文模型预测横波速度过程中,需优化多个参数,因此会增加一定计算量。
附录A 孔隙纵横比表达式岩石填充物的几何因子P和Q的计算公式为
| $ P=\frac{1}{3} T_{i i j j}(\alpha) $ |
| $ Q=\frac{1}{5}\left[T_{i j i j}(\alpha)-\frac{1}{3} T_{ii j j}(\alpha)\right] $ |
式中i、j均取1、2、3,对应x、y、z坐标。且有
| $ T_{i i j j}(\alpha)=\frac{3 F_{1}}{F_{2}} $ |
| $ T_{i j i j}-\frac{1}{3} T_{i i j j}=\frac{2}{F_{3}}+\frac{1}{F_{4}}+\frac{F_{4} F_{5}+F_{6} F_{7}-F_{8} F_{9}}{F_{2} F_{4}} $ |
其中
| $ F_{1}=1+A\left[\frac{3}{2}(f+\theta)-R\left(\frac{3}{2} f+\frac{5}{2} \theta-\frac{4}{3}\right)\right] $ |
| $ \begin{aligned} F_{2}=& 1+A\left[1+\frac{3}{2}(f+\theta)-R\left(\frac{3}{2} f+\frac{5}{2} \theta\right)\right]+\\ & B(3-4 R)+\frac{A}{2}(A+3 B)(3-4 R) \times \\ &\left[f+\theta-R\left(f-\theta+2 \theta^{2}\right)\right] \end{aligned} $ |
| $ F_{3}=1+A\left[1-\left(f+\frac{3}{2} \theta\right)+R(f+\theta)\right] $ |
| $ F_{4}=1+\frac{A}{4}[f+3 \theta-R(f-\theta)] $ |
| $ F_{5}=A\left[-f+R\left(f+\theta-\frac{4}{3}\right)\right]+B \theta(3-4 R) $ |
| $ \begin{aligned} F_{6}=& 1+A[1+f-R(f+\theta)]+\\ & B(1-\theta)(3-4 R) \end{aligned} $ |
| $ F_{7}=2+\frac{A}{4}[3 f+9 \theta-R(3 f+5 \theta)]+B \theta(3-4 R) $ |
| $ \begin{aligned} F_{8}=& A\left[1-2 R+\frac{f}{2}(R-1)+\frac{\theta}{2}(5 R-3)\right]+\\ & B(1-\theta)(3-4 R) \end{aligned} $ |
| $ F_{9}=A[(R-1) f-R \theta]+B \theta(3-4 R) $ |
上列各式中
| $ A =\mu_{i} / \mu_{\mathrm{ma}}-1 $ |
| $ B =\frac{1}{3}\left(\frac{K_{i}}{K_{\mathrm{ma}}}-\frac{\mu_{i}}{\mu_{\mathrm{ma}}}\right) $ |
| $ R=\left(1-2 \sigma_{\mathrm{ma}}\right) /\left[2\left(1-\sigma_{\mathrm{ma}}\right)\right] \quad(\sigma \text { 为泊松比 }) $ |
| $ \theta=\left\{\begin{array}{l} \frac{\alpha}{\left(\alpha^{2}-1\right)^{3 / 2}}\left[\alpha\left(\alpha^{2}-1\right)^{1 / 2}-\operatorname{arccosh} \alpha\right] \\ \frac{\alpha}{\left(\alpha^{2}-1\right)^{3 / 2}}\left[\cos ^{-1} \alpha-\alpha\left(\alpha^{2}-1\right)^{1 / 2}\right] \end{array}\right. $ |
该式中第一、第二行分别对应扁长、扁圆球体。
| $ f=\frac{\alpha^{2}}{1-\alpha^{2}}(3 \theta-2) $ |
对于扁圆球体,α < 1;对于扁长球体,α>1。
| [1] |
印兴耀, 李龙. 基于岩石物理模型的纵、横波速度反演方法[J]. 石油物探, 2015, 54(3): 249-253. YIN Xingyao, LI Long. P-wave and S-wave velocities inversion based on petrophysical model[J]. Geophy-sical Prospecting for Petroleum, 2015, 54(3): 249-253. |
| [2] |
孟大江, 文鹏飞, 张如伟, 等. 天然气水合物横波速度等效介质模型预测方法[J]. 石油地球物理勘探, 2020, 55(1): 117-125. MENG Dajiang, WEN Pengfei, ZHANG Ruwei, et al. Gas hydrate S-wave velocity prediction method based on effective medium model[J]. Oil Geophysical Prospecting, 2020, 55(1): 117-125. |
| [3] |
刘致水, 刘俊州, 董宁, 等. 富有机质岩石横波速度预测方法[J]. 石油地球物理勘探, 2021, 56(1): 127-136, 154. LIU Zhishui, LIU Junzhou, DONG Ning, et al. Investigation to S-wave velocity prediction method for organic-rich rock[J]. Oil Geophysical Prospecting, 2021, 56(1): 127-136, 154. |
| [4] |
刘致水, 孙赞东, 董宁, 等. 一种修正的Kuster-Toksöz岩石物理模型及应用[J]. 石油地球物理勘探, 2018, 53(1): 113-121. LIU Zhishui, SUN Zandong, DONG Ning, et al. A modified Kuster-Toksöz rock physics model and its application[J]. Oil Geophysical Prospecting, 2018, 53(1): 113-121. |
| [5] |
CASTAGNA J P, BATZLE M L, EASTWOOD R L. Relationships between compressional-wave and shear-wave velocities in clastic silicate rocks[J]. Geophy-sics, 1985, 50(4): 571-581. |
| [6] |
HAN D H, NUR A, MORGAN D. Effects of porosity and clay content on wave velocities in sandstones[J]. Geophysics, 1986, 51(11): 2093-2107. DOI:10.1190/1.1442062 |
| [7] |
NUR A, MAVKO G, DVORKIN J, et al. The key to relating physical properties to porosity in rocks[J]. The Leading Edge, 1995, 14(3): 878-881. |
| [8] |
KUSTER G T, TOKSÖZ M N. Velocity and attenuation of seismic waves in two-phase media: Part Ⅰ, Theoretical formulations[J]. Geophysics, 1974, 39(5): 587-606. DOI:10.1190/1.1440450 |
| [9] |
XU S, WHITE R E. A new velocity model for clay-sand mixtures[J]. Geophysical Prospecting, 1995, 43(1): 91-118. DOI:10.1111/j.1365-2478.1995.tb00126.x |
| [10] |
WYLLIE M R J, GREGORY A R, GARDNER L W. Elastic wave velocities in heterogeneous and porous media[J]. Geophysics, 1956, 21(1): 41-70. DOI:10.1190/1.1438217 |
| [11] |
GASSMANN F. Elastic waves through a packing of spheres[J]. Geophysics, 1951, 16(4): 673-685. DOI:10.1190/1.1437718 |
| [12] |
郭栋, 印兴耀, 吴国忱. 横波速度计算方法与应用[J]. 石油地球物理勘探, 2007, 42(5): 535-538. GUO Dong, YIN Xingyao, WU Guochen. Computational approach of S-velocity and application[J]. Oil Geophysical Prospecting, 2007, 42(5): 535-538. |
| [13] |
郑旭桢, 王涛, 刘钊, 等. 泥岩基质弹性参数对Xu-White模型横波速度估算的影响[J]. 石油地球物理勘探, 2017, 52(5): 990-998. ZHENG Xuzhen, WANG Tao, LIU Zhao, et al. In-fluence of clay elastic parameters on S-wave velocity estimation based on Xu-White model[J]. Oil Geophysical Prospecting, 2017, 52(5): 990-998. |
| [14] |
张广智, 李呈呈, 印兴耀, 等. 基于修正Xu-White模型的碳酸盐岩横波速度估算方法[J]. 石油地球物理勘探, 2012, 47(5): 717-722. ZHANG Guangzhi, LI Chengcheng, YIN Xingyao, et al. A shear velocity estimation method for carbonate rocks based on the improved Xu-White model[J]. Oil Geophysical Prospecting, 2012, 47(5): 717-722. |
| [15] |
PRIDE S R, BERRYMAN J G, HARRIS J M. Seismic attenuation due to wave-induced flow[J]. Journal of Geophysical Research, 2004, 109(B1): B01201. |
| [16] |
LEE M W. A simple method of predicting S-wave velocity[J]. Geophysics, 2006, 69(5): 161-164. |
| [17] |
张佳佳, 李宏兵, 刘怀山, 等. 几种岩石骨架模型的适用性研究[J]. 地球物理学进展, 2010, 25(5): 1697-1702. ZHANG Jiajia, LI Hongbing, LIU Huaishan, et al. Accuracy of dry frame modes in the study of rock physics[J]. Progress in Geophysics, 2010, 25(5): 1697-1702. |
| [18] |
侯波, 陈小宏, 张孝珍. 临界孔隙度Pride模型及其应用[J]. 石油地球物理勘探, 2012, 47(2): 277-281. HOU Bo, CHEN Xiaohong, ZHANG Xiaozhen. Critical porosity pride model and its application[J]. Oil Geophysical Prospecting, 2012, 47(2): 277-281. |
| [19] |
NISHIZAWA O. Seismic velocity anisotropy in a medium containing oriented cracks transversely isotropic case[J]. Journal of the Physical Earth, 1982, 30(4): 331-347. DOI:10.4294/jpe1952.30.331 |
| [20] |
NORRIS A. A differential scheme for the effective moduli of composites[J]. Mechanics of Materials, 1985, 4(3): 1-16. |
| [21] |
ZIMMERMAN R W. The effect of microcracks on the elastic moduli of brittlematerials[J]. Journal of Material Science Letters, 1985, 4(2): 1457-1460. |
| [22] |
BERRYMAN J G. Single-scattering approximations for coefficients in Biot's equations of poroelasticity[J]. Journal of the Acoustical Society of America, 1992, 91(2): 551-571. DOI:10.1121/1.402518 |
| [23] |
李宏兵, 张佳佳. 多重孔岩石微分等效介质模型及其干燥情形下的解析近似式[J]. 地球物理学报, 2014, 57(10): 3422-3430. LI Hongbing, ZHANG Jiajia. A different effective medium model of multiple-porosity rock and its analytical approximations for dry rock[J]. Chinese Journal of Geophysics, 2014, 57(10): 3422-3430. |
| [24] |
侯波, 康洪全, 程涛. 综合成岩作用和孔隙形状的岩石物理模型及其应用[J]. 物探与化探, 2019, 43(1): 161-167. HOU Bo, KANG Hongquan, CHENG Tao. A new rock physics model integrating diagenesis and pore shape and its application[J]. Geophysical & Geochemical Exploration, 2019, 43(1): 161-167. |
| [25] |
BRIE A, PAMPURI F, MARSALA A F, et al. Shear sonic interpretation in gas-bearing sands[J]. SPE Journal, 1995, 305(95): 701-710. |
| [26] |
王大兴. 致密砂岩气储层的岩石物理模型研究[J]. 地球物理学报, 2016, 59(12): 4603-4622. WANG Daxing. Study on the physics model of gas reservoirs in tight sandstone[J]. Chinese Journal of Geophysics, 2016, 59(12): 4603-4622. |
| [27] |
WU T T. The effective of inclusion shape on the elastic moduli of a two-phase material[J]. International Journal of Solids and Structures, 1966, 2(1): 1-8. DOI:10.1016/0020-7683(66)90002-3 |
| [28] |
KRIEF M, GARAT J, STELLINGWERFF J, et al. A petrophysical interpretation using the velocities of P and S waves[J]. Log Analyst, 1990, 31(3): 355-369. |
| [29] |
李宏兵, 张佳佳, 姚逢昌. 岩石的等效孔隙纵横比反演及其应用[J]. 地球物理学报, 2013, 56(2): 608-615. LI Hongbing, ZHANG Jiajia, YAO Fengchang. Inversion of effective pore aspect rations for porous rocks and its application[J]. Chinese Journal of Geophysics, 2013, 56(2): 608-615. |
| [30] |
ZHANG T, ZHANG R, TIAN J, et al. Two-parameter prestack seismic inversion of porosity and pore-structure parameter of fractured carbonate reservoirs[J]. Interpretation, 2018, 6(4): 1-36. |
| [31] |
LI H B, ZHANG J J, CAI S J, et al. A two-step method to apply Xu-Payne multi-porosity model to estimate pore type from seismic data for carbonate reservoirs[J]. Petroleum Science, 2020, 17(3): 51-63. |



 李红兵, 北京市海淀区学院路20号中国石油勘探开发研究院油气地球物理研究所, 10083。Email:
李红兵, 北京市海淀区学院路20号中国石油勘探开发研究院油气地球物理研究所, 10083。Email: 