② 中国石化石油勘探开发研究院, 北京 100083
② Research Institute of Petroleum Exploration and Development, SINOPEC, Beijing 100083, China
岩石物理模型是描述储层特征与弹性参数之间关系的数学函数。针对不同地质目标,基于等效介质理论,人们提出多种岩石物理模型以描述岩石中矿物颗粒与一定形状岩石孔隙之间的关系[1-4]。
目前,考虑孔隙结构对岩石弹性参数影响的岩石物理模型主要有2D孔隙和3D孔隙模型两种:2D孔隙形状包括椭圆形、裂缝形、多边形;3D孔隙形状有球形、椭球形、针形和裂缝形。
在2D孔隙研究中,Kuster等[2]推导了含多种椭圆形孔隙岩石的弹性参数公式。Zimmerman[5]系统研究了多种2D孔隙形状对岩石弹性参数的影响。Mauge等[6]研究了各向同性与各向异性情况下裂缝孔隙对岩石弹性参数的影响。Thorpe等[7]在自适应岩石物理模型框架下推算了岩石中含方向随机的椭圆形孔隙的弹性模量公式。Jasiuk等[8-9]导出了含多边形孔隙介质的弹性模量公式。Kachanov等[4]推导了含2D规则多边形孔隙岩石的岩石物理模型公式,使用3个参数描述规则形状孔隙对岩石弹性参数的影响;且利用Savin方法[10]求得三角形、正方形等几种2D规则多边形孔隙的孔隙形状因子。
在3D孔隙研究中,Mackenzie[11]构建了含3D球形孔隙的岩石物理模型。Zimmerman[12]推算出含椭球体孔隙岩石的刚度张量。Eshelby[13]求得含低孔隙度球形孔隙岩石的弹性张量。Berryman利用自适应岩石物理模型分析了含随机分布的椭球体包含物岩石的弹性张量[1];又在自适应岩石物理模型基础上给定了多种3D孔隙的形状因子,最常用的包括球形、针形及裂缝形[14]。
这些经典模型基本都只适用于矿物简单、孔隙类型单一的情况,且都仅适用于高频条件。Xu等[15]将微分Kuster-Toksöz模型[2]、Gassmann方程[16]、Wyllie时间平均公式[17]组合起来,得到一种兼顾两种矿物、两种2D椭圆形孔隙、适用于低频条件的岩石物理模型。其后众多学者基于不同需求,利用不同的基础岩石物理模型进行组合,获得多个在业界应用效果良好的岩石物理模型。这些模型使用的基础岩石物理模型主要为自适应模型和微分等效介质(DEM)理论,所考虑的孔隙形状也基本是2D椭圆形孔隙[15, 18-22]和3D椭球体孔隙[23-25],且鲜见其他孔隙类型的岩石物理模型的研究与应用。
2D椭圆形模型和3D椭球体模型应用较多的原因在于其描述孔隙形状变化的参数只有孔隙纵横比,研究者可反演该参数[21, 25],并赋予其具体地质意义。虽然Kachanov等[4]推导出2D规则多边形孔隙岩石物理模型,但该模型的孔隙形状参数有三个,不同多边形孔隙的形状因子具体数值不同,应用时需根据Savin方法[10]求取孔隙形状参数具体数值;且岩石孔隙形状极为复杂,这几种规则多边形孔隙未能囊括岩石所有复杂孔隙形状;当每次使用时,研究者尚不能预知岩石孔隙形状并确定孔隙形状因子;三种参数不利于岩石物理研究中经常使用的数学方法的应用。因此,限制了该模型的推广和应用。
为此,引入一个等效孔隙形状因子g,替代Kachanove 2D模型中的多个形状因子参数,得到简化的2D规则多边形孔隙岩石物理模型。文中厘定了等效孔隙形状因子的理论参数范围,并通过数值模拟、实验室测试及实际测井资料应用,证实了本文方法对砂岩储层的适用性。
1 基本原理 1.1 Kachanove岩石物理模型经典Mori-Tanaka岩石物理模型是基于平均应力场近似理论推导的含孔隙干岩石模型。在此基础上Kachanove等[4]给出含2D规则多边形孔隙干岩石的杨氏模量Edry和泊松比σdry计算公式
| $ E_{\mathrm{dry}} =E_{\mathrm{m}}\left[1+\frac{2\left(h_{3}-h_{2}\right) \phi}{1-\phi}\right]^{-1} $ | (1) |
| $ \sigma_{\mathrm{dry}} =\frac{\sigma_{\mathrm{m}}+\phi(1-\phi)^{-1}}{1+2\left(h_{3}-h_{2}\right) \phi(1-\phi)^{-1}} $ | (2) |
式中:Em和σm是岩石基质的杨氏模量和泊松比;ϕ是孔隙度;h2和h3是孔隙形状因子,部分情况下h3与另一因子h1有关系,具体细节见表 1。
|
|
表 1 多种规则孔隙形状及其等效孔隙形状因子h1、h2、h3和g(据文献[4]) |
表 1是三角形、四边形、五边形的孔隙形状示意图及其对应的形状因子h1、h2和h3。利用Savin方法[10]求取2D规则多边形孔隙形状因子。在应用该模型时,需先由岩石镜下薄片观察岩石的孔隙形状,确定孔隙形状因子,再计算岩石弹性模量。此外,该模型只能应用于表 1所列几种2D规则多边形孔隙,其他形状孔隙则据Savin方法[10]推导,且此模型中孔隙形状因子参数较多,难以与自适应算法等数学方法结合,限制了该模型的可应用性。
1.2 简化的多边形孔隙岩石物理模型引入一个等效孔隙形状因子
| $ g=2\left(h_{3}-h_{2}\right)-1 $ | (3) |
替代式(1)和式(2)中多个孔隙形状因子,即简化Kachanove模型。表 1列举了几种多边形孔隙的g值。
将式(3)代入式(1)和式(2),可得
| $ E_{\mathrm{dry}}=E_{\mathrm{m}} \frac{1-\phi}{1+g \phi} $ | (4) |
| $ \sigma_{\mathrm{dry}}=\frac{\sigma_{\mathrm{m}}(1-\phi)+\phi}{1+g_{\phi}} $ | (5) |
由杨氏模量E、泊松比σ与体积模量K、剪切模量G之间的关系[26]
| $ E=\frac{9 K G}{3 K+G} \qquad \sigma=\frac{3 K-2 G}{2(3 K+G)} $ |
经过数学运算,得到
| $ K_{\mathrm{dry}} =\frac{3 K_{\mathrm{m}} G_{\mathrm{m}}(1-\phi)}{3 G_{\mathrm{m}}+\left[\left(3 K_{\mathrm{m}}+G_{\mathrm{m}}\right) g-3 K_{\mathrm{m}}-4 G_{\mathrm{m}}\right] \phi} $ | (6) |
| $ G_{\mathrm{dry}} =\frac{9 K_{\mathrm{m}} G_{\mathrm{m}}(1-\phi)}{9 K_{\mathrm{m}}+\left[2\left(3 K_{\mathrm{m}}+G_{\mathrm{m}}\right) g+3 K_{\mathrm{m}}+4 G_{\mathrm{m}}\right] \phi} $ | (7) |
式中:Kdry、Gdry分别是干岩石体积模量和剪切模量;Km和Gm分别是岩石基质的体积模量和剪切模量。
为明确g的取值范围,对上两式取g的导数
| $ \begin{aligned} \frac{\mathrm{d} K_{\mathrm{dry}}}{\mathrm{d} g}=&\frac{2 E_{\mathrm{m}} \phi\left[\phi-\sigma_{\mathrm{m}}(\phi-1)\right](\phi-1)}{3\left[2 \frac{\phi-\sigma_{\mathrm{m}}(\phi-1)}{g \phi+1}-1\right]^{2}(g \phi+1)^{3}}-\\ &\frac{E_{\mathrm{m}} \phi(\phi-1)}{3\left[2 \frac{\phi-\sigma_{\mathrm{m}}(\phi-1)}{g \phi+1}-1\right](g \phi+1)^{2}} \end{aligned} $ | (8) |
| $ \begin{aligned} \frac{\mathrm{d} G_{\mathrm{dry}}}{\mathrm{d} g}=& \frac{E_{\mathrm{m}} \phi(\phi-1)}{2\left[\frac{\phi-\sigma_{\mathrm{m}}(\phi-1)}{g_{\phi}+1}+1\right]\left(g_{\phi}+1\right)^{2}}-\\ & \frac{E_{\mathrm{m}} \phi\left[\phi-\sigma_{\mathrm{m}}(\phi-1)\right](\phi-1)}{2\left[\frac{\phi-\sigma_{\mathrm{m}}(\phi-1)}{g_{\phi}+1}+1\right]^{2}\left(g_{\phi}+1\right)^{3}} \end{aligned} $ | (9) |
若式(8)和式(9)有意义,则式中分母部分不为0。即要使式(8)有意义,则g的取值需满足
| $ 2 \frac{\phi-\sigma_{\mathrm{m}}(\phi-1)}{g{\phi}+1}-1 \neq 0 $ | (10) |
| $ g \phi+1 \neq 0 $ | (11) |
要使式(9)有意义,则g取值需满足式(11)和下式
| $ \frac{\phi-\sigma_{m}(\phi-1)}{g \phi+1}+1 \neq 0 $ | (12) |
因为ϕ∈[0, 1],岩石基质泊松比σm∈(0,0.5),经推导可知:g∈(1, +∞)为式(6)定义域,g∈(-1, +∞)为式(7)定义域。在计算纵波速度时需同时使用式(6)和式(7),此时形状因子g∈(1, +∞)。
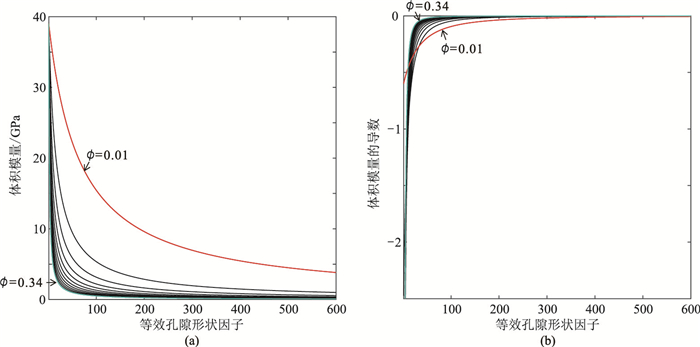
图 1为不同孔隙度的砂泥岩体积模量(式(6),图 1a)及其对g的导数(式(8),图 1b)随g变化的正演曲线。图中不同的曲线表示孔隙度在0.01~0.34区间以0.03的步长变化。其中砂泥岩基质的体积和剪切模量分别为39.0、32.8GPa;孔隙含水,水的体积模量为2.2GPa,g在1~600区间变化。
|
图 1 体积模量(a)和体积模量的导函数(b)随等效孔隙形状因子的变化曲线 |
从该图可见:①形状因子g越接近1,体积模量越大;随着g增大,岩石体积模量降低。②g较小时,模量降低速率快;随着g增大,模量降低速率变慢;当g大于某个数时,弹性模量的变化率基本可忽略,因此实际应用中g的取值并非无限大,而是一个有限的数,图中当g大于约500时,弹性模量的变化率即可忽略,故本文设定取值范围是g∈(1, 500]。③弹性模量随g的变化率与孔隙度有关,当孔隙度较小时,模量随g的变化率较小。进一步研究得知,剪切模量变化规律与体积模量一致。
2 模型测试与应用在改进的多边形孔隙模型中,弹性模量只与一个参数(等效孔隙形状因子g)有关。因此,在已知孔隙度、岩石基质弹性模量和g时,结合2D-Kachanove模型和Gassmann方程[16],可求取饱和流体岩石的纵、横波速度[26]
| $ V_{\mathrm{Pc}}=\sqrt{\frac{K_{\mathrm{sat}}+\frac{4}{3} G_{\mathrm{sat}}}{\rho_{\mathrm{sat}}}} $ | (13) |
| $ V_{\mathrm{Sc}}=\sqrt{\frac{G_{\mathrm{sat}}}{\rho_{\mathrm{sat}}}} $ | (14) |
式中:VPc、VSc分别是饱和流体岩石的纵、横波速度;Ksat、Gsat和ρsat分别是饱和流体岩石的体积模量、剪切模量和密度,且有ρsat=ρm(1-ϕ)+ρfϕ,其中ρm、ρf分别为岩石基质、孔隙流体的密度,对于干岩石,ρf取0。需要说明的是,若岩石基质矿物较复杂,可通过VRH平均公式[26]计算多种矿物混合情形下的岩石基质体积模量和剪切模量。
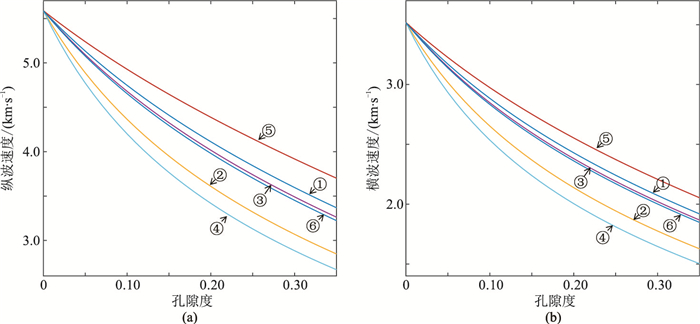
2.1 初始和简化的Kachanove 2D模型对比假设岩石基质是含黏土的石英,其体积模量和剪切模量分别为39.0、32.8GPa,密度为2.65g/cm3;孔隙含水,其体积模量和密度分别为2.2GPa和0.99g/cm3。利用式(1)和式(2)可计算含几种规则形状孔隙岩石的速度—孔隙度关系曲线(图 2)。由该图可见:
|
图 2 含表 1中几种孔隙的岩石纵波速度(a)、横波速度(b)随孔隙度变化曲线 |
(1) 相同孔隙度下含不同形状孔隙岩石的速度随孔隙度的变化规律不同,具有圆角的凸边孔隙速度大于具有尖角的凹边孔隙。如在三角形孔隙中,速度大小排序为①>②;四边形孔隙中,速度排序为③>④;五边形孔隙中,速度排序为⑤>⑥。
(2) 分别针对凸边和凹边孔隙,对比三角形、四边形、五边形孔隙,可见五边形孔隙>三边形孔隙>四边形孔隙,其中三边形孔隙与四边形孔隙近似。
结合表 1、图 2可见,对于不同形状的孔隙,当g增大时岩石速度降低,g降低时岩石速度增高,通过g的变化,可达到代替原始模型中多个孔隙形状因子的目的。
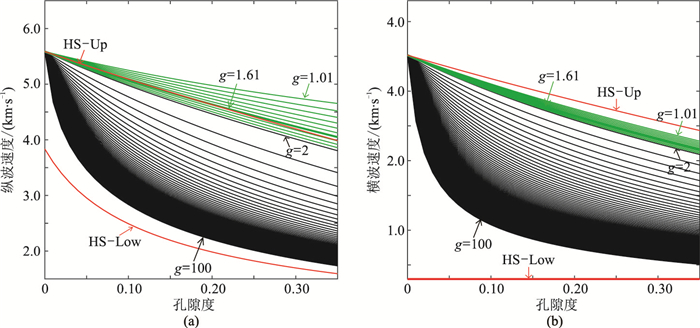
图 3为由改进模型计算的岩石速度随孔隙度、等效孔隙形状因子变化的曲线图。图中岩石基质、孔隙流体参数与图 2一致,绿色曲线部分是g在1.01~1.91之间以0.10为步长进行变化,黑色曲线部分是g在2~100之间以1为步长进行变化。对比图 2和图 3可知,改进模型除能表达图 2中几种孔隙类型外,g在理论定义域内的其他取值提供了描述更多孔隙形状的可能性,从而极大地扩大了原始模型描述孔隙类型的可能性。
|
图 3 由改进模型计算的岩石纵波速度(a)、横波速度(b)随孔隙度、等效孔隙形状因子的变化曲线 HS-Up和HS-Low分别指Hashin-Shtrikman上、下限 |
图 3中还给出了Hashin-Shtrikman上、下限[26],可见g=1.61时计算的纵波速度随孔隙度的变化曲线与Hashin-Shtrikman上限基本一致,g=100时计算的纵波速度随孔隙度的变化曲线接近Hashin-Shtrikman下限且在其上方。当g在1.01~100取值时,横波速度曲线总在Hashin-Shtrikman上、下限之间。数值实验还发现,g取较大数值范围(如1~10000)时,所得结果也基本一致。需强调的是,本文改进模型与经典DEM模型呈现的规律类似。
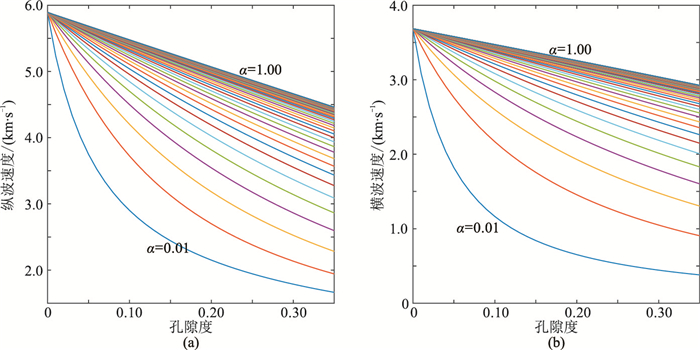
图 4为2D椭圆形孔隙的DEM模型计算的纵、横波速度[25]与孔隙度关系图。对比图 4与图 3可知,改进模型通过g的变化描述孔隙结构对速度的影响,而DEM模型则通过椭圆形孔隙的孔隙纵横比(椭圆短轴与长轴之比)α描述孔隙结构对速度的影响,两者效果基本一致。
|
图 4 通过2D椭圆形孔隙的DEM模型计算的纵波速度(a)和横波速度(b)与孔隙度关系 图中曲线是椭圆形孔隙的孔隙纵横比α从1.00到0.01之间按照步长0.01进行变化 |
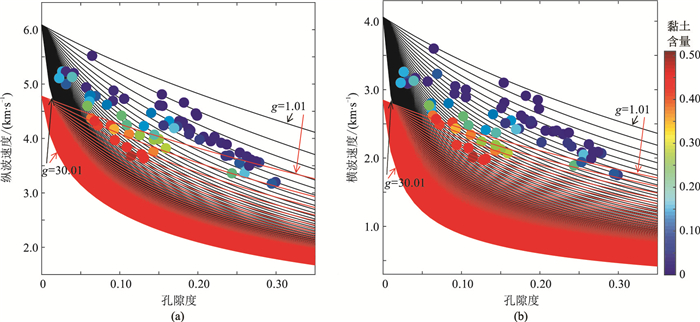
利用Han等[27]在超声实验室40MPa条件下针对砂泥岩测量的75个数据点测试本文方法。Han数据的孔隙度范围是0.02~0.31,黏土含量为0~0.5。将本文方法数值正演结果与实测数据进行叠合(图 5)。所用参数如表 2所示。该图显示,随着孔隙度增加,岩石速度降低;孔隙度不变时,随着g变大,岩石速度降低;孔隙度及形状因子g相同时,泥岩速度低于砂岩。通过孔隙度、黏土含量、g的变化,可包括所有数据点,即改进模型可解释测量数据的孔隙度—黏土含量—速度三者之间关系。
|
图 5 基于改进模型的纵波速度(a)和横波速度(b)正演结果 黑线代表往纯石英基质加入0~0.35孔隙度(干孔隙空腔)的变化;红线代表以50%石英+50%黏土混合物作为基质(用VRH平均公式计算混合矿物体积模量和剪切模量),往其中加入0~0.35孔隙度(干孔隙空腔)的变化;从上到下的黑线和红线均代表等效孔隙形状因子g在1.01~30.01区间以步长1变化。样点为一组砂岩岩心测试数据[27],其颜色对应不同的黏土含量 |
在岩石物理研究过程中,理想情况是通过岩心等实物观测岩石的孔隙结构,并将实际观测参数代入岩石物理模型。然而,实际应用中很难精确确定待研究岩石的真实孔隙形态,因此需将岩石物理模型与数学工具结合,采取迭代或自适应方法求取等效孔隙结构参数。从图 5可知,当以较小步长变化孔隙形状因子,总能找到一条曲线穿过图 5a中每个实测样点,即将该样点的孔隙形状等效为该曲线所对应的孔隙形状,再以此孔隙形状因子求算横波速度。还可看出,穿过图 5a中每个样点的曲线不一定与图 5b中曲线吻合,但差距不太大,其原因是在测量纵、横波速度时,人、仪器因素必然导致针对同一目标的测量数据有误差。
本文利用速度预测效果验证模型的可应用性。现实中的岩石都是非常复杂的混合物,影响岩石弹性模量的因素包括岩石的组成矿物及其弹性模量、孔隙度、孔隙流体、等效孔隙形状因子等,而本文改进的岩石物理模型是考虑纯粹的理想情况。因此,参考Xu-White砂泥岩速度预测流程[15]的思路,采取多个模型结合以构建等效介质模型的速度计算流程可简述为:①使用VRH平均公式[26]计算岩石基质体积模量和剪切模量;②利用式(6)和式(7)计算含干孔隙岩石的弹性模量;③利用Wood方程[26]计算混合流体的体积模量,并用Gassmann方程[16]计算饱和流体岩石的弹性模量;④利用式(13)计算饱和流体岩石纵波速度;⑤利用计算的纵波速度VPc与实测纵波速度VPm构建目标函数ε=|VPm-VPc(g)|/VPm,并使ε取极小值,以求取等效孔隙形状因子g;⑥利用g最终求得横波速度。
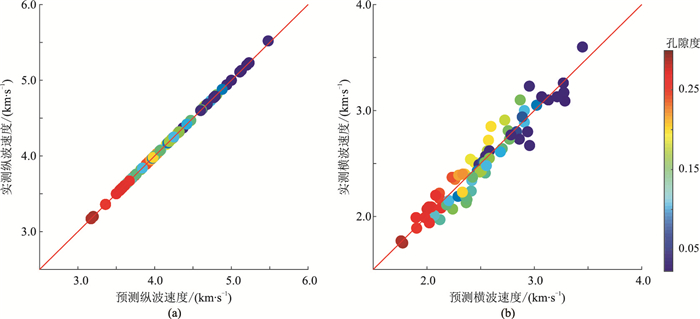
图 6为利用文献[27]数据在纵波速度约束下得到的计算速度与实测速度的对比图。从图 6a可知计算纵波速度与实测纵波速度一致,这是由于等效孔隙形状因子是由纵波速度计算得到的,基于此孔隙形状因子计算的纵波速度与实测纵波速度吻合度较高(基本是相等的)。图 6b中数据点均匀分布于对角线(红线)附近,说明预测横波速度与实测数据吻合度较高。
|
图 6 预测纵波(a)、横波(b)速度与实测速度交会图 |
选取计算与实测速度之间相对误差的平均值AE、均方根误差RMSE、相关系数R2等参数[28]定量评价预测结果。由表 3可见,计算结果与实测数据之间误差较小,即利用改进模型能获得较准确的砂岩储层横波速度,这说明本文改进模型适用于砂泥岩储层。
|
|
表 3 实测数据与预测数据之间的的误差统计表 |
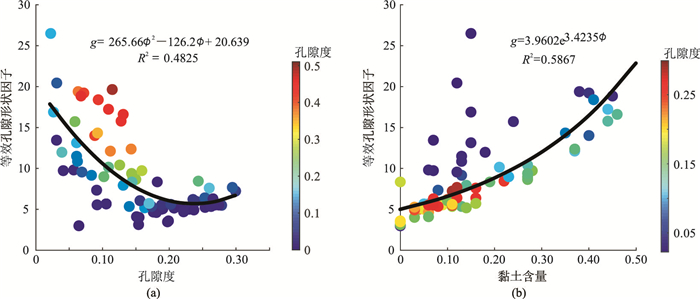
由纵波速度求得的孔隙形状因子如图 7所示。可见等效孔隙形状因子随孔隙度增大呈“先降后略增”趋势,且随黏土含量的增大而增大。需要说明的是,由纵波速度虽可求取每个样点的孔隙形状因子,但由于测量、测井解释过程中的误差,以及孔隙流体、矿物等参数影响,所求得的孔隙形状因子并不一定能精确表征孔隙的具体形状,其中包含了由其他因素造成的误差,但通过该参数的自适应可帮助研究者获得接近实测数据的横波速度。
|
图 7 等效孔隙形状因子与孔隙度(a)和黏土含量(b)的交会图 |
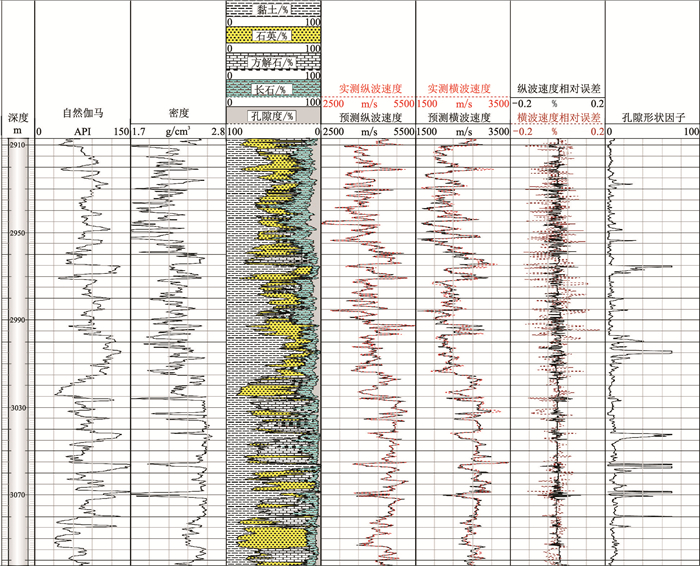
将本文方法应用于四川盆地西部地区三叠系沙河街组砂岩储层段。图 8展示了该区A井目的层段的测井解释、速度预测及孔隙形状因子计算等综合结果。利用多矿物测井解释方法[29]估算孔隙度、矿物体积含量,解释的矿物包括黏土、石英、方解石、长石。经过测试、标定,计算过程中使用的矿物体积模量和剪切模量如表 2所示。将矿物的体积分数、孔隙度数据引入岩石物理模型,在纵波速度数据约束下预测横波速度。由图 8可见,本文方法预测结果与实测数据吻合度较高,纵、横波速度的相对误差基本控制在8%以内。表 3为实测数据与预测数据之间的误差统计,可见测井数据预测的横波速度的误差平均值为0.008、均方根误差为0.137、相关系数为0.853。图 8和表 3均说明新方法在砂泥岩测井资料中的应用效果良好。
|
图 8 四川盆地西部地区A井三叠系沙河街组砂岩储层段速度预测与实测数据对比图 |
(1) 针对规则形状孔隙的2D-Kachanove模型孔隙形状因子的参数多、仅能表示几种孔隙形状、难以与自适应等数学算法结合等问题,本文引入新等效孔隙形状因子以替换原始模型的多个孔隙形状因子,得到一个简化的2D-Kachanove岩石物理模型。等效孔隙形状因子的理论取值范围是(1, +∞)。
(2) 数值算例表明:随着g增大,岩石弹性模量降低,且降低速率逐渐变小;当g大于某个数时,弹性模量的变化率基本可忽略,因此实际应用中g的取值并非无限大,而是一个有限的数。相对于原始模型仅能考虑几种孔隙形状,改进模型可考虑g在理论取值范围内的任意值,从而扩大了原始2D-Kachanove模型的应用范围并使其更易于推广。
(3) 利用简化岩石物理模型对实验室测试数据及测井资料进行横波速度预测,结果证明简化模型在砂(泥)岩储层中有较好应用效果。
| [1] |
BERRYMAN J G. Long-wavelength propagation in composite elastic media (Ⅰ.Spherical inclusions and Ⅱ.Ellipsoidal inclusions)[J]. Journal of the Acoustical Society of America, 1980, 68(6): 1809-1831. DOI:10.1121/1.385171 |
| [2] |
KUSTER G T, Toksöz M N. Velocity and attenua-tion of seismic waves in two-phase media: Part Ⅰ, Theoretical formulations[J]. Geophysics, 1974, 39(5): 587-606. DOI:10.1190/1.1440450 |
| [3] |
MORI T, TANAKA K. Average stress in matrix and average elastic energy of materials with misfitting inclusions[J]. Acta Metallurgica, 1973, 21(5): 571-574. DOI:10.1016/0001-6160(73)90064-3 |
| [4] |
KACHANOV M, TSUKROV I, SHAFIRO B. Effective moduli of solids with cavities of various shapes[J]. Applied Mechanics Reviews, 1994, 47(1S): S151-S174. DOI:10.1115/1.3122810 |
| [5] |
ZIMMERMAN R W. Compressibility of two-dimensional cavities of various shapes[J]. Journal of Applied Mechanics, 1986, 53(3): 500-504. DOI:10.1115/1.3171802 |
| [6] |
MAUGE C, KACHANOV M. Interacting arbitrarily oriented cracks in anisotropic matrix, Stress intensity factors and effective moduli[J]. International Journal of Fracture, 1992, 58(4): R69-R74. DOI:10.1007/BF00048960 |
| [7] |
THORPE M F, SEN P N. Elastic moduli of two-dimensional composite continua with elliptical inclusions[J]. Journal of the Acoustical Society of America, 1985, 77(5): 1674-1680. DOI:10.1121/1.391966 |
| [8] |
JASIUK I, CHEN J, THORPE M F. Effective elastic properties of two-dimensional composites: material with polygonal holes[C]. In Processing, Fabrication and Manufacturing of Composite Materials, Winter Annual Meetings of the American Society of Mechanical Engineers, Materials Division MD, 1992, 35(11): 61-73.
|
| [9] |
JASIUK I, CHEN J, THORPE M F. Elastic moduli of two dimensional materials with polygonal and elliptical holes[J]. Applied Mechanics Reviews, 1994, 47(1): S18-S28. |
| [10] |
Savin G N. Stress Distribution Around Holes[M]. NASA Technical Translation TT F-607, Washington D C, 1970.
|
| [11] |
MACKENZIE J K. The elastic constants of a solid containing spherical holes[J]. Proceedings of the Physical Society, Section B, 1950, 63(1): 2-11. DOI:10.1088/0370-1301/63/1/302 |
| [12] |
ZIMMERMAN R W. Compressibility of an isolated spheroidal cavity in an isotropic elastic medium[J]. Journal of Applied Mechanics, 1985, 52(3): 606-608. DOI:10.1115/1.3169108 |
| [13] |
ESHELBY J D. The determination of the elastic field of an ellipsoidal inclusion, and related problem[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1957, 241(1226): 376-396. |
| [14] |
BERRYMAN J G. Mixture theories for rock properties//Rock Physics and Phase Relations: A Handbook of physical constants[M]. American Geophysical Union, Ahrens T J ed, Washington DC, 1995, 205-228.
|
| [15] |
XU S Y, WHITE R E. A new velocity model for clay-sand mixtures[J]. Geophysical Prospecting, 1995, 43(1): 91-118. DOI:10.1111/j.1365-2478.1995.tb00126.x |
| [16] |
GASSMANN F. Elastic waves through a packing of spheres[J]. Geophysics, 1951, 16(4): 673-685. DOI:10.1190/1.1437718 |
| [17] |
WYLLIE M R, GREGORY A R, GARDNER L W. Elastic wave velocities in heterogeneous and porous media[J]. Geophysics, 1956, 21(1): 41-70. DOI:10.1190/1.1438217 |
| [18] |
张广智, 李呈呈, 印兴耀, 等. 基于修正Xu-White模型的碳酸盐岩横波速度估算方法[J]. 石油地球物理勘探, 2012, 47(5): 717-722. ZHANG Guangzhi, LI Chengcheng, YIN Xingyao, et al. A shear velocity estimation method for carbonate rocks based on the improved Xu-White model[J]. Oil Geophy-sical Prospecting, 2012, 47(5): 717-722. |
| [19] |
GUO Z Q, LI X Y, LIU C, et al. A shale rock physics model for analysis of brittleness index, mineralogy and porosity in the Barnett shale[J]. Journal of Geophy-sics and Engineering, 2013, 10(2): 1742-2132. |
| [20] |
刘致水, 刘俊州, 董宁, 等. 富有机质岩石横波速度预测方法[J]. 石油地球物理勘探, 2021, 56(1): 127-136, 154. LIU Zhishui, LIU Junzhou, DONG Ning, et al. An investigation of a shear-wave velocity prediction method for organic-enriched rock[J]. Oil Geophysical Prospecting, 2021, 56(1): 127-136, 154. |
| [21] |
YANG F Y, YIN X Y, LIU B. S-wave velocity self-adaptive prediction based on a variable dry rock frame equivalent model[J]. Journal of Geophysics and Engineering, 2014, 11(4): 045015. DOI:10.1088/1742-2132/11/4/045015 |
| [22] |
杨文强, 宗兆云, 姜曼, 等. 基于等效介质理论的天然气水合物岩石物理建模方法[J]. 石油地球物理勘探, 2021, 56(3): 528-535. YANG Wenqiang, ZONG Zhaoyun, JIANG Man, et al. Rock physics modeling method of natural gas hydrate based on equivalent medium theory[J]. Oil Geophysical Prospecting, 2021, 56(3): 528-535. |
| [23] |
董宁, 霍志周, 孙赞东, 等. 泥页岩岩石物理建模研究[J]. 地球物理学报, 2014, 57(6): 1990-1998. DONG Ning, HUO Zhizhou, SUN Zandong, et al. An investigation of a new rock physics model for shale[J]. Chinese Journal of Geophysics, 2014, 57(6): 1990-1998. |
| [24] |
LIU Z S, SUN Z D. New brittleness indexes and their application in shale/clay gas reservoir prediction[J]. Petroleum Exploration and Development, 2015, 42(1): 117-124. |
| [25] |
LIU Z S, SUN Z D. The differential Kuster-Toksöz rock physics model for predicting S-wave velocity[J]. Journal of Geophysics and Engineering, 2015, 12(5): 839-848. DOI:10.1088/1742-2132/12/5/839 |
| [26] |
MAVKO G, MUKERJI T and DVORIKIN J. The Rock Physics Handbook: Tools for Seismic Analysis in Po-rous Media[M]. Cambridge University Press, 1998.
|
| [27] |
HAN D H, NUR A, MORGAN D. Effects of porosity and clay content on wave velocities in sandstones[J]. Geophysics, 1986, 51(11): 2093-2107. DOI:10.1190/1.1442062 |
| [28] |
刘致水, 孙赞东, 董宁, 等. 一种修正的Kuster-Toksöz岩石物理模型及应用[J]. 石油地球物理勘探, 2018, 53(1): 113-121. LIU Zhishui, SUN Zandong, DONG Ning, et al. A modified Kuster-Toksöz rock physics model and its application[J]. Oil Geophysical Prospecting, 2018, 53(1): 113-121. |
| [29] |
雍世和, 张超谟. 测井数据处理与综合解释[M]. 山东东营: 中国石油大学出版社, 2002: 313-320. YONG Shihe, ZHANG Chaomo. Logging Data Processing and Comprehensive Interpretation[M]. Dongying, Shandong: China University of Petroleum Press, 2002: 313-320. |



 刘致水, 陕西省西安市雁塔区南二环126号长安大学地质工程与测绘学院地球物理系, 710054。Email:
刘致水, 陕西省西安市雁塔区南二环126号长安大学地质工程与测绘学院地球物理系, 710054。Email: