精确的速度模型是复杂介质叠前深度偏移准确成像的前提。传统的旅行时层析和偏移速度分析等方法已无法满足当前高精度成像的需求。相比传统方法,全波形反演能够充分利用地震数据中的信息,理论上可以实现更高精度的速度建模[1-4]。早在二十世纪八十年代,Tarantola[5-6]就给出了时间域全波形反演的理论框架,但受制于当时计算机水平,该理论未得到充分发展。随后,Pratt[7]实现了频率域全波形反演,并提出多尺度反演的概念。二维情况下,频率域方法计算效率更高,单一频率波场模拟仅需一次矩阵分解,即可通过替换震源项实现多炮并行。同时,在多尺度反演框架下,只需由低到高几个频率成分即可实现反演过程,不仅降低了计算成本,而且降低了反演的非线性。由此,全波形反演开始得以迅速发展,并逐步应用于实际数据。
全波形反演是高度非线性和不适定的反问题。当初始模型远离真实模型时,会存在周波跳跃现象,极易陷入局部极值。虽然全局优化方法在理论上可以得到全局最优解,但高昂的计算成本使其难以应用于实际。在目标函数中添加正则化项约束反演过程,是缓解全波形反演非线性和不适定性的一种处理方式,如在模型域中通过将先验信息应用于模型空间等[8-10]。典型的Tikhonov正则化方法是基于L2范数[11],能缓解反问题的不适定性,但通常会使反演结果变得光滑,不利于刻画地层边界。相较于L2范数正则化,L1范数能使反演结果具有稀疏表征的效果,更符合实际地质情况。
全变分(Total variation,TV)正则化方法[12]通过求解全变分约束的非线性最小化问题实现噪声压制,同时保留图像原本的结构特征。Askan[13]将TV正则化应用于各向异性介质的全波形反演,以同时反演速度和黏弹性参数,在压制反演结果高振荡现象的同时,保留了结果的不连续变化。Burs-tedde等[14]以一维全波形反演为例,证明了TV正则化的反演结果比Tikhonov正则化方法更符合实际层状介质。Anagaw[15]将TV正则化应用于地震成像,详细给出了TV正则化的构造公式。随后,TV正则化得到了进一步发展,出现了TV正则化的初对偶实现方法、L2范数+加权L2范数正则化的两步法[16]等。Anagaw等[17]给出基于TV正则化的全波形反演方法,提高了反演结果分辨地层边界的能力。
近年来,人们开始将Tikhonov正则化和TV正则化相结合,以期同时具备两者的优势。Lin等[18]提出了改进的TV正则化方法,将其解耦为基于L2范数的Tikhonov正则化和标准L2范数问题;Sun等[19]融合Tikhonov正则化和TV正则化,提出了双参数整形正则化全波形反演方案,提高了边界精度和收敛速度[20];Aghamiry等[21]构建两类基于Tikhonov和TV正则化的混合正则项:第一类为二者的凸组合(CC),第二类则是二者的卷积下确界(IC),认为基于IC的复合正则化反演的误差最小。
Hu等[22]基于L2范数和加权L2范数正则化方法,提出了一种结合高斯—牛顿方法和乘法正则化的同时多频反演算法。Guitton等[23]提出了一种L2范数预处理全波形反演,利用倾角估计,通过定向Laplacian滤波器对梯度施加具有地质意义的约束。随后,Guitton[24]又提出了一种块状正则化方法,并比较了L1范数和Cauchy函数正则化项的差异。Ma等[25]研究了图像引导梯度,在稀疏模型空间中计算梯度,用一种改进的图像引导共轭梯度方法求解稀疏全波形反演,通过约束梯度与地下倾角补充低频成分。Asnaashari等[26]提出了一种全波形反演方案,其中有两个模型惩罚项,Tikhonov项和从声波测井、钻井数据或野外地质信息中导出的先验模型项。Van Leeuwen等[27]提出通过扩展搜索空间减少全波形反演中的局部极小值。Yu等[28]建立了基于L2范数和非光滑L1范数组合的混合双参数正则化,该方法可以快速收敛到真实模型,反演精度较高。Yan等[29]提出了一种基于Lp-Lq范数的最小化模型,突出了模型结构的边缘信息。Xue等[30]通过使用Seislet正则化实现全波形反演,Seislet正则化可以在多震源同时激发导致的强串扰伪像和数据存在强随机噪声的情况下,恢复高精度速度模型,极大地提高全波形反演的稳健性。利用条件Lipschitz稳定性估计,Shi等[31]设计了迭代正则化的全波形反演,通过将缩放后梯度投影到与参数化相关的子空间实现,保证了Lipschitz稳定性。
在目标函数中添加正则化项是约束全波形反演结果的一种重要途径,而对比分析不同正则化项对反演结果的影响有助于理解不同正则化的特点。因此,本文首先分别简要介绍了Tikhonov、TV、双参数整形、混合双参数、稀疏结构约束正则化的基本原理,而后通过对背斜—超覆模型、Marmousi模型测试,分析五种正则化方法的特点,为正则化方法的应用提供参考。
1 不同正则化方法的基本原理基于L2范数的全波形反演目标函数[29]为
| $ E=\|\delta \boldsymbol{d}\|_{2}^{2}+r(\boldsymbol{m})=\left\|\boldsymbol{d}_{\mathrm{obs}}-\boldsymbol{d}_{\mathrm{cal}}\right\|_{2}^{2}+r(\boldsymbol{m}) $ | (1) |
式中:m是速度模型;dcal为模拟数据;dobs为观测数据;δd为模拟数据与观测数据的残差;r(m)为正则化项。
本文在频域中实现全波形反演,采用伴随状态法求取梯度,应用L-BFGS优化算法(Limited-memory Broyden-Fletcher-Goldfarb-Shanno Algorithm)更新模型。
1.1 Tikhonov正则化Tikhonov正则化使用模型的二次函数作为惩罚项,以获得具有平滑效果的稳定近似解,其形式为[11, 32-33]
| $ r(\boldsymbol{m})=\alpha\left\|\boldsymbol{m}-\boldsymbol{m}_{0}\right\|_{2}^{2} $ | (2) |
式中:m0是初始速度模型;α是正则化项权重。正则化项权重α保证正则化项占目标函数的5%~10%。α增大会使反演结果更平滑,并降低反演精度。
r(m)的梯度可写为
| $ \nabla r(\boldsymbol{m})=2 \alpha\left(\boldsymbol{m}-\boldsymbol{m}_{0}\right) $ | (3) |
TV正则化是稀疏约束全波形反演方法的一种,该方法能够突出并保留反演结果的边界信息,其形式[34-35]为
| $ r(\boldsymbol{m})=\alpha \int_{\varOmega} \sqrt{|\nabla \boldsymbol{m}|^{2}+\varepsilon_{1}} \mathrm{~d} \varOmega $ | (4) |
式中:ε1通常被选择为一个极小的正数;Ω为模型空间范围。正则化项权重α可以通过实验获得,以保证正则化项占目标函数的5%~10%。α越大,边界越清晰,但会降低反演精度。
r(m)的梯度为
| $ \nabla r(\boldsymbol{m})=\nabla \cdot \frac{\nabla \boldsymbol{m}}{\sqrt{|\nabla \boldsymbol{m}|^{2}+\varepsilon_{1}}} $ | (5) |
其离散形式为
| $ \frac{\partial r(\boldsymbol{m})}{\partial m_{i, j}}=\nabla \cdot \frac{\nabla m_{i, j}}{\sqrt{\left|\nabla m_{i, j}\right|^{2}+\varepsilon_{1}}} $ | (6) |
式中:i=1,2,…,Nx;j=1,2,…,Nz。其中Nx、Nz分别为模型在水平和垂直方向的坐标点总个数。
1.3 双参数整形正则化基于Tikhonov和TV正则化的双参数整形正则化项为[19]
| $ \begin{aligned} r(\boldsymbol{m})=& \alpha\left[\gamma_{1}\left\|\boldsymbol{m}-\boldsymbol{m}_{0}\right\|_{2}^{2}+\right.\\ &\left.\left(1-\gamma_{1}\right) \int_{\varOmega} \sqrt{|\nabla \boldsymbol{m}|^{2}+\varepsilon_{1}} \mathrm{~d} \varOmega\right] \end{aligned} $ | (7) |
r(m)的梯度为
| $ \begin{aligned} \nabla r(\boldsymbol{m})=& \alpha\left[\gamma_{1}\left(\boldsymbol{m}-\boldsymbol{m}_{0}\right)+\right.\\ &\left.\left(1-\gamma_{1}\right) \nabla \cdot \frac{\nabla \boldsymbol{m}}{\sqrt{|\nabla \boldsymbol{m}|^{2}+\varepsilon_{1}}}\right] \end{aligned} $ | (8) |
式中:γ1为0到1之间的常数。当γ1趋近于0时,反演结果趋向于TV正则化;当γ1等于1时,接近Tikhonov正则化结果,本文取γ1=0.4。α增大会降低反演精度。
1.4 混合双参数正则化混合双参数正则化反演方法结合了L2范数和L1范数的优势,使用L2范数拟合实际数据,并通过L1范数约束减少了非唯一性和离散值,形式为[28]
| $ r(\boldsymbol{m})=\alpha\left\|\boldsymbol{m}-\boldsymbol{m}_{0}\right\|_{2}^{2}+\gamma_{2}\|\boldsymbol{m}\|_{1}=r_{1}(\boldsymbol{m})+r_{2}(\boldsymbol{m}) $ | (9) |
式中:r1(m)是L2范数正则化项;r2(m)是L1范数正则化项;参数γ2调控反演精度。
r1(m)的梯度与式(3)相同。r2(m)中的L1范数用Huber范数fHuber近似,即
| $ r_{2}(\boldsymbol{m})=\gamma_{2} f_{\text {Huber }}(\boldsymbol{m})=\gamma_{2} \sum\limits_{i, j} h_{\varepsilon_{2}}\left(m_{i, j}\right) $ | (10) |
式中hε2(·)定义为非线性分段函数
| $ h_{\varepsilon_{2}}(x)=\left\{\begin{array}{l} -x-\frac{\varepsilon_{2}}{2} \quad x<-\varepsilon_{2} \\ \frac{x^{2}}{2 \varepsilon_{2}} \quad|x| \leqslant \varepsilon_{2} \\ x-\frac{\varepsilon_{2}}{2} \quad x>\varepsilon_{2} \end{array}\right. $ | (11) |
其中ε2通常选择为一个极小的正数。
r2(m)的梯度可用Huber函数的导数近似
| $ \frac{\partial r_{2}(\boldsymbol{m})}{\partial m_{i, j}}=\gamma_{2} \frac{\partial f_{\text {Huber }}(\boldsymbol{m})}{\partial m_{i, j}}=\gamma_{2} \sum\limits_{i, j} h_{\varepsilon_{2}}^{\prime}\left(m_{i, j}\right) $ | (12) |
h′ε2(·)可以写为
| $ h_{\varepsilon_{2}}^{\prime}(x)= \begin{cases}-1 \quad x<-\varepsilon_{2} \\ \frac{x}{\varepsilon_{2}} \quad |x| \leqslant \varepsilon_{2} \\ 1 \quad x>\varepsilon_{2}\end{cases} $ | (13) |
地下模型结构具有隐含的稀疏特征,因此可以用L1范数来描述。通过差分算子提取结构信息,利用不同的p和q参数进行Lp-Lq范数约束。
定义由三部分组成的结构化正则化项[29]为
| $ \begin{aligned} r(\boldsymbol{m}) &=\frac{\lambda_{1}}{2}\left\|\boldsymbol{D}_{x} \boldsymbol{m}\right\|_{p}+\frac{\lambda_{2}}{2}\left\|\boldsymbol{D}_{z} \boldsymbol{m}\right\|_{q}+\gamma_{3}\|\boldsymbol{m}\|_{1} \\ &=r_{1}(\boldsymbol{m})+r_{2}(\boldsymbol{m}) \end{aligned} $ | (14) |
式中:λ1、λ2和γ3是正则化项权重;r1(m)为差分算子正则化项;r2(m)为L1范数正则化项。
对于p=q=2,r1(m)的梯度可写为
| $ \nabla r_{1}(\boldsymbol{m})=\left(\lambda_{1} \boldsymbol{D}_{x}^{\mathrm{T}} \boldsymbol{D}_{x}+\lambda_{2} \boldsymbol{D}_{z}^{\mathrm{T}} \boldsymbol{D}_{z}\right) \boldsymbol{m} $ | (15) |
当p=q=1时,L1范数用Huber范数近似,L1范数正则化项的梯度可用Huber函数的导数近似。
在不同的反演阶段,权重的选择不相同。r1和r2的最大值不应超过E(m)的百分之十。本文不同方向的正则化项权重取相同值,即λ1=λ2,也可根据实际需求或地下构造选取不同的参数组合。λ1和λ2在增强反演结果的连续性、去噪方面效果明显。
2 不同正则化反演结果分析本文采用背斜—超覆模型和Marmousi模型对比不同正则化方法对反演结果的影响。
2.1 背斜—超覆模型背斜—超覆模型(图 1a)横向有386个网格点,纵向有200个网格点,空间采样间隔为10m。共设置42炮,均匀分布于地表水平方向0.4~3.6km范围内。每炮126道接收,检波点均匀分布于地表水平方向0.4~3.6km范围内,检波器固定。四周均采用完全匹配层吸收边界条件。采用真实模型平滑后的结果(图 1b)作为初始模型。

|
图 1 背斜—超覆速度(v)模型 (a)真实;(b)初始 |
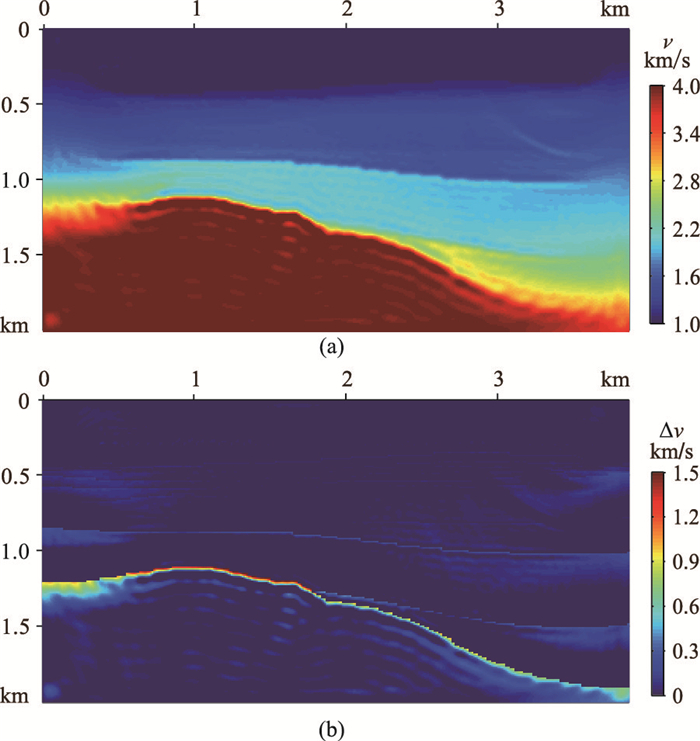
图 2a为背斜—超覆模型未加正则化的反演结果,速度分界面不清晰,底层高速体(最底层红色的高速体)存在层状假象,深层(深度1~2km范围)均衡性差。图 2b为背斜—超覆模型未加正则化的反演结果与真实模型的残差(Δv),可见深层反演精度较低,速度分界面残差较大。
|
图 2 背斜—超覆速度模型未加正则化的反演结果(a)及其残差(b) |
Tikhonov正则化反演结果(图 3a)有一定的平滑效果,底层高速体层状假象相对于未正则化反演结果有所减弱,箭头所指的速度分界面在箭头右侧清晰度明显降低。TV正则化反演结果(图 3b)底层高速体速度反演精度大幅提高,层状假象相对于其他反演结果最弱,深层反演均衡性最好,边界刻画最清晰,但不能清晰反演出箭头位置右侧的速度分界面。

|
图 3 背斜—超覆模型不同正则化方法反演结果对比 (a)Tikhonov;(b)TV;(c)双参数整形;(d)混合双参数;(e)稀疏结构约束(p=q=2);(f)稀疏结构约束(p=q=1) |
图 3c为双参数整形正则化反演结果,边界刻画清晰,层位清晰,底层高速体层状假象比TV正则化反演结果略强,深层反演均衡性好,可较清晰分辨速度分界面至箭头位置。相比未正则化反演,混合双参数正则化反演(图 3d)结果底层高速体层状假象变弱,深层反演均衡性有所提高。
当p=q=2时,稀疏结构约束正则化反演结果(图 3e)速度连续性最强,层位清晰,底层高速体层状假象比未正则反演结果弱,深层反演均衡性好。当p=q=1时,稀疏结构约束正则化反演结果(图 3f)底层高速体层状假象比未正则反演结果弱。
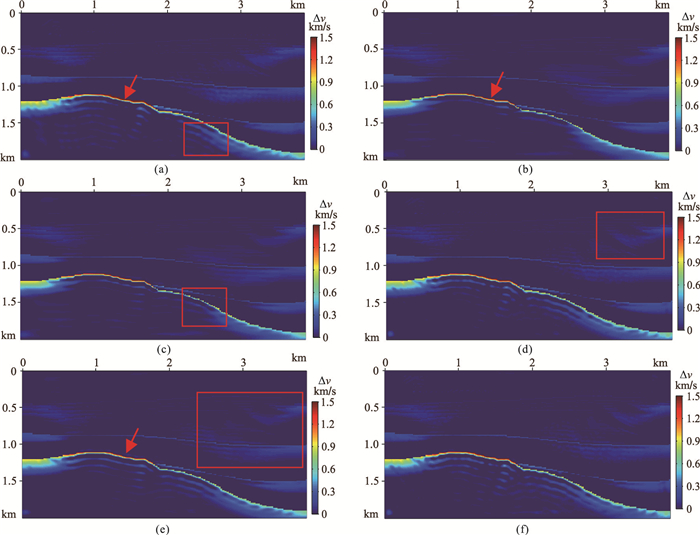
图 4为背斜—超覆模型不同正则化方法反演结果与真实模型残差。Tikhonov正则化反演结果残差(图 4a)在矩形框内残差值小于未正则化,箭头所指的速度分界面处残差也小于未正则化反演结果。TV正则化(图 4b)底层高速体与真实模型残差最小;箭头所指的速度分界面残差值最小(与其他反演结果相比)。双参数整形正则化(图 4c)在矩形框内与真实模型的残差小于TV正则化。混合双参数正则化(图 4d)在矩形框内和底层高速体残差比未正则化残差小。当p=q=2时,稀疏结构约束正则化(图 4e)在浅层矩形框内残差小于未正则化,整体上相比其他反演结果更接近真实模型速度。当p=q=1时,稀疏结构约束正则化(图 4f),底层高速体与真实模型残差小于未正则化。
|
图 4 背斜—超覆模型不同正则化方法反演结果与真实模型的残差 (a)Tikhonov;(b)TV;(c)双参数整形;(d)混合双参数;(e)稀疏结构约束(p=q=2);(f)稀疏结构约束(p=q=1) |
图 5为背斜—超覆模型不同正则化方法反演目标目标函数的下降曲线,可以发现:Tikhonov正则化、TV正则化、双参数整形正则化目标函数收敛更快;混合双参数正则化、稀疏结构约束正则化反演目标函数前30次下降速度快,后30次迭代目标函数下降趋势变缓。

|
图 5 背斜—超覆模型不同正则化反演目标函数下降曲线 |
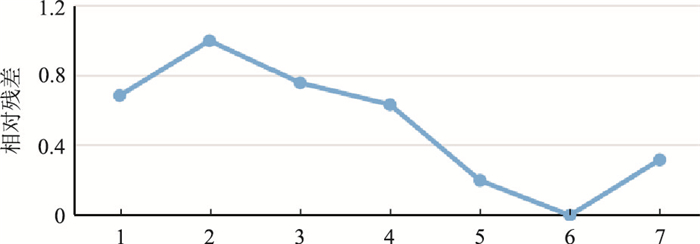
图 6为背斜—超覆模型不同正则化方法反演结果的模拟数据与观测数据的相对残差曲线,可以看出,Tikhonov正则化、TV正则化残差值会略大于未正则化,因为两侧的反演精度降低;双参数整形、混合双参数、稀疏结构约束正则化(p=q=2、p=q=1)的反演结果,残差值均小于未加正则化反演结果的残差值,说明这三种方法整体上的反演精度高于未加正则化,稀疏结构约束(p=q=2)正则化的反演精度最高。
|
图 6 背斜—超覆模型不同正则化反演的数据相对残差 横坐标1~7分别代表:未加正则化、Tikhonov正则化、TV正则化、双参数整形正则化、混合双参数正则化、稀疏结构约束正则化(p=q=2)、稀疏结构约束正则化(p=q=1) |
图 7为背斜—超覆模型不同正则化方法反演结果在x=1.78km处的单道对比,可见:Tikhonov正则化和混合双参数正则化速度反演结果略大于未正则反演结果;TV正则化和双参数整形正则化能更准确地反映分界面的速度突变;稀疏结构约束正则化(p=q=2)反演速度整体上更接近真值。

|
图 7 背斜—超覆模型反演结果的单道对比 |
Marmousi模型(图 8a)横向有630个网格,纵向有200个网格,空间采样间隔为10m。共设置60炮,均匀分布于地表水平方向0.4~5.8km范围内。每炮180道接收,均匀分布于地表水平方向0.4~5.8km范围内,四周均采用完全匹配层吸收边界条件。采用真实模型的平滑结果作为反演的初始模型(图 8b)。

|
图 8 Marmousi模型 (a)真实速度;(b)初始速度;图a中三个方框为重点分析区 |
由于本文采用较为理想的初始模型及多尺度反演方法,因此,在未加正则化的情况下即可较真实反演出与真实速度相匹配的速度场(图 9),但整体反演结果都有噪声分布,底部高速体和速度分界面反演精度较低,速度分界面细节刻画不清晰。Tikhonov正则化反演结果(图 10a)较未正则的反演结果更平滑,速度分界面精度有所提高,箭头所示的深部高速体形态反映较为真实。TV正则化反演结果(图 10b)层位清晰,界面刻画、去噪效果很好,在箭头所示处,速度分界面刻画更精确,几乎完全消除了噪声,但深层(纵向1.6~2km)反演精度有所下降。

|
图 9 Marmousi模型未加正则化反演结果 |

|
图 10 Marmousi模型不同正则化方法反演结果对比 (a)Tikhonov;(b)TV;(c)双参数整形;(d)混合双参数;(e)稀疏结构约束(p=q=2);(f)稀疏结构约束(p=q=1) |
图 10c为双参数整形正则化反演结果,融合了Tikhonov正则化和TV正则化的优势,不但精确刻画了界面、压制了噪声,而且提高了深层的反演精度。与TV正则化相比,双参数整形正则化反演的深层高速体形态更真实(箭头所示)。混合双参数正则化反演结果(图 10d)压制了部分噪声,速度分界面细节刻画相对清晰,浅层(纵向0~1km)低速体保真度较高,深层反演精度略有下降(与未加正则反演相比)。
稀疏结构约束正则化(p=q=2)反演结果(图 10e)能有效地增强地层的连续性,去噪效果明显,提高了反演精度;与本文的其他正则化方法相比,图中箭头所指的深层高速体,速度连续性最强,速度分界面细节刻画最清晰。稀疏结构约束正则化(p=q=1)的反演结果(图 10f)浅层低速体保真度较高,与其他正则化方法相比,深层反演精度最高(箭头所示)。
图 11为Marmousi模型不同正则化方法反演结果的模拟数据与观测数据的相对残差曲线,可以发现:Tikhonov、TV、双参数整形、混合的双参数、稀疏结构约束(p=q=2)正则化的反演残差均小于未加正则化,说明这五种方法的反演精度要高于未加正则化;仅稀疏结构约束正则化(p=q=1)反演残差大于未加正则化;稀疏结构约束正则化(p=q=2)反演残差最小,反演精度最高。

|
图 11 Marmousi模型不同正则化反演的数据相对残差 横坐标1~7分别代表:未加正则化、Tikhonov正则化、TV正则化、双参数整形正则化、混合双参数正则化、稀疏结构约束正则化(p=q=2)、稀疏结构约束正则化(p=q=1) |
图 12为Marmousi模型不同正则化反演目标函数下降曲线。TV、混合双参数正则化目标函数趋于稳定的速度更快。所有正则化反演方法,在前20次时目标函数值下降快,后20次迭代目标函数趋于平稳。

|
图 12 Marmousi模型不同正则化反演目标函数下降曲线 |
将图 8方框1处Marmousi模型不同正则化反演结果进行局部放大,如图 13和图 14所示。未正则化的反演结果(图 13)的深层高速体地层连续性较差,速度分界面刻画不够清晰;Tikhonov正则化反演结果(图 14a)中深层高速体地层连续性有所增强但精度略有降低;TV正则化反演结果(图 14b)的速度分界面刻画清晰,去噪效果明显,深层反演精度明显降低;双参数整形正则化反演结果(图 14c)在TV正则化反演凸显速度分界面和去噪的基础上,提高了深层反演精度;混合双参数正则化反演结果(图 14d)增强了深层高速体地层的连续性,深层反演精度降低较小。

|
图 13 Marmousi模型未加正则化反演结果的局部放大(图 8a方框1处) |

|
图 14 Marmousi模型不同正则化反演结果的局部放大(图 8a方框1处) (a)Tikhonov;(b)TV;(c)双参数整形;(d)混合双参数;(e)稀疏结构约束(p=q=2);(f)稀疏结构约束(p=q=1) |
稀疏结构约束正则化(p=q=2)反演结果(图 14e),相比于前几种方法,深层高速体地层连续性最好,保真度最高,速度分界面细节刻画最清晰,去噪效果明显,几乎没有降低深层反演精度。稀疏结构约束正则化(p=q=1)反演结果(图 14f)提高了深层的反演精度,与未加正则化的反演结果相比速度分界面更清晰。
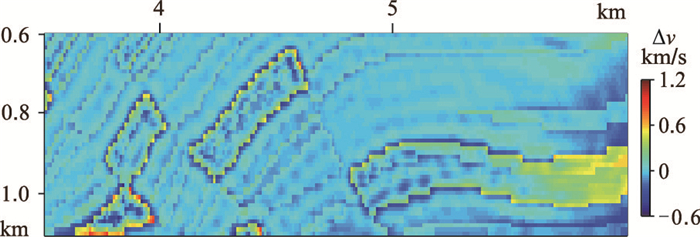
将图 8方框2处Marmousi模型不同正则化反演结果的残差进行局部放大,如图 15和图 16所示,可以直观地显示反演结果在不同位置处的失配程度。Tikhonov正则化反演结果(图 16a)比未正则化(图 15)在横向3.5~5.0km处残差变小,在横向5.0~6.0km处残差略有增大。与其他方法相比在速度分界面处TV正则化反演结果的残差(图 16b)最小。与TV正则化相比,双参数整形正则化反演结果的残差(图 16c)比TV正则化在横向5.0~5.5km处明显减小。混合双参数正则化反演结果的残差(图 16d)小于未正则化。稀疏结构约束正则化(p=q=2)反演结果的残差(图 16e)最小,增强了速度的连续性,使反演结果保真度有所提高。稀疏结构约束正则化(p=q=1)反演结果的残差(图 16f)小于未正则化。
|
图 15 Marmousi模型未加正则化反演结果残差的局部放大(图 8a方框2处) |

|
图 16 Marmousi模型不同正则化反演结果残差的局部放大(图 8a方框2处) (a)Tikhonov;(b)TV;(c)双参数整形;(d)混合双参数;(e)稀疏结构约束(p=q=2);(f)稀疏结构约束(p=q=1) |
图 17a是Marmousi模型不同正则化反演结果在x=3km处的单道(图 8a方框3处)对比,可明显看出,在第一个峰值两侧的速度界面,TV和双参数整形正则化反演结果更接近真值,其次是稀疏结构约束正则化(p=q=2)的反演结果较接近真实值。图 17b是Marmousi模型不同正则化反演结果残差在x=3km处的单道(图 8a方框3处)对比,TV正则化和双参数整形正则化的残差更小。

|
图 17 Marmousi模型不同正则化反演结果(a)及其残差(b)在x=3km处的单道对比 |
本文详细对比分析了Tikhonov正则化等五种正则化方法在全波形反演中的作用。背斜—超覆模型和Marmousi模型测试表明:
(1) Tikhonov正则化增强反演结果的连续性,使反演结果更平滑;TV正则化在刻画边界的同时,去噪效果明显,但这两种典型的正则化方法的深层反演精度都有所降低;
(2) 双参数整形正则化方法融合了Tikhonov正则化和TV正则化的优点,并提高了深层的反演精度;
(3) 混合双参数正则化增强了反演结果的地层连续性,对浅层低速体的反演精度有一定程度的提高;
(4) 稀疏结构约束正则化(p=q=2)有效增强了反演结果的地层连续性,速度分界面细节刻画更清晰,去噪效果良好,且深层反演精度降低较小;
(5) 稀疏结构约束正则化(p=q=1),对深层反演精度有所提高。
总之,稀疏结构约束正则化(p=q=2)的反演结果兼顾了各方法在去噪、增强地层连续性以及保留边缘结构等方面的优势。
| [1] |
辛天亮, 黄建平, 解飞, 等. 基于数据相似性的不依赖子波的频率域全波形反演[J]. 石油地球物理勘探, 2020, 55(2): 341-350. XIN Tianliang, HUANG Jianping, XIE Fei, et al. Source-independent frequency-domain full waveform inversion based on data similarity[J]. Oil Geophysical Prospecting, 2020, 55(2): 341-350. |
| [2] |
韩如冰, 郎超. 频率域八阶NAD有限差分模拟及全波形反演[J]. 石油地球物理勘探, 2019, 54(6): 1254-1266. HAN Rubing, LANG Chao. The eighth-order frequency-domain NAD method and full waveform inversion[J]. Oil Geophysical Prospecting, 2019, 54(6): 1254-1266. |
| [3] |
徐夷鹏, 任志明, 李振春, 等. 一阶近似瞬时频率时间域声波全波形反演[J]. 石油地球物理勘探, 2020, 55(5): 1029-1038. XU Yipeng, REN Zhiming, LI Zhenchun, et al. First-order approximate instantaneous frequency and time domain acoustic full waveform inversion[J]. Oil Geophysical Prospecting, 2020, 55(5): 1029-1038. |
| [4] |
刘张聚, 童思友, 方云峰, 等. 基于时域加权的拉普拉斯-频率域弹性波全波形反演[J]. 石油地球物理勘探, 2021, 56(2): 302-312. LIU Zhangju, TONG Siyou, FANG Yunfeng, et al. Laplace-frequency domain elastic wave full waveform inversion based on time-domain weighting[J]. Oil Geophysical Prospecting, 2021, 56(2): 302-312. |
| [5] |
TARANTOLA A. Linearized inversion of seismic reflection data[J]. Geophysical Prospecting, 1984, 32(6): 998-1015. DOI:10.1111/j.1365-2478.1984.tb00751.x |
| [6] |
TARANTOLA A. Inversion of seismic reflection data in the acoustic approximation[J]. Geophysics, 1984, 49(8): 1259-1266. DOI:10.1190/1.1441754 |
| [7] |
PRATT R G. Inverse theory applied to multi-source cross-hole tomography, Part Ⅱ: Elastic wave-equation method[J]. Geophysical Prospecting, 1990, 38(3): 287-310. DOI:10.1111/j.1365-2478.1990.tb01846.x |
| [8] |
李振春, 李闯, 黄建平, 等. 基于先验模型约束的最小二乘逆时偏移方法[J]. 石油地球物理勘探, 2016, 51(4): 738-744. LI Zhenchun, LI Chuang, HUANG Jianping, et al. Least squares reverse time migration method based on prior model constraints[J]. Oil Geophysical Prospecting, 2016, 51(4): 738-744. |
| [9] |
杨国权, 丁鹏程, 李振春, 等. 应用线性程函方程和整形正则化的三维初至波旅行时层析[J]. 石油地球物理勘探, 2017, 52(2): 264-272. YANG Guoquan, DING Pengcheng, LI Zhenchun, et al. Three-dimensional first-arrival travel time tomography using linear equations and shaping regularization[J]. Oil Geophysical Prospecting, 2017, 52(2): 264-272. |
| [10] |
王彦飞, 斯捷潘诺娃 I E, 提塔连科 V N, 等. 地球物理数值反演问题[M]. 北京: 高等教育出版社, 2011.
|
| [11] |
TIKHONOV A N and ARSENIN V A. Solution of Ill Posed Problems[M]. Winston & Sons, Washington, 1977.
|
| [12] |
RUDIN L I, OSHER S, FATEMI E. Nonlinear total variation based noise removal algorithms[J]. Physica D Nonlinear Phenomena, 1992, 60(1-4): 259-268. DOI:10.1016/0167-2789(92)90242-F |
| [13] |
ASKAN A. Full Waveform Inversion for Seismic Velocity and an Elastic Losses in Heterogeneous Structures[D]. Carnegie Mellon University, Pennsylvania, USA, 2006.
|
| [14] |
BURSTEDDE C, GHATTAS O. Algorithmic strategies for full waveform inversion: 1D experiments[J]. Geophysics, 2009, 74(6): WCC37-WCC46. DOI:10.1190/1.3237116 |
| [15] |
ANAGAW A Y. Total Variation and Adjoint State Methods for Seismic Wavefield Imaging[D]. Alberta University, Edmonton, Alberta, Canada, 2009.
|
| [16] |
RAMIREZ A C, LEWIS W R. Regularization and full-waveform inversion: A two-step approach[C]. SEG Technical Program Expanded Abstracts, 2010, 29: 2773-2778.
|
| [17] |
ANAGAW A Y, SACCHI M D. Full waveform inversion with total variation regularization[C]. The 2011 CSPG CSEG CWLS Joint Annual Convention, Calgary, Canada, 2011, 1-4.
|
| [18] |
LIN Y, HUANG L. Acoustic-and elastic-waveform inversion using a modified total-variation regularization scheme[J]. Geophysical Journal International, 2015, 200(1): 489-502. |
| [19] |
SUN R X, HAN L G, SUN E Y. Dual-parameter shaping regularized full waveform inversion in frequency domain[J]. Global Geology, 2015, 18(4): 258-262. |
| [20] |
LEWANDOWSKI M. Geophysical Inverse Theory and Regularization Problems[M]. Elsevier, Netherlands, 2002.
|
| [21] |
AGHAMIRY H S, GHOLAMI A, OPERTO S. Compound regularization of full-waveform inversion for imaging piecewise media[J]. IEEE Transactions on Geosciences and Remote Sensing, 2020, 58(2): 1192-1204. DOI:10.1109/TGRS.2019.2944464 |
| [22] |
HU W, ABUBAKAR A, HABASHY T M. Simultaneous multifrequency inversion of full-waveform seismic data[J]. Geophysics, 2009, 74(2): R1-R14. DOI:10.1190/1.3073002 |
| [23] |
GUITTON A, AYENI G, DIAZ E. Constrained full-waveform inversion by model reparameterization[J]. Geophysics, 2012, 77(2): R117-R127. DOI:10.1190/geo2011-0196.1 |
| [24] |
GUITTON A. Blocky regularization schemes for full-waveform inversion[J]. Geophysical Prospecting, 2012, 60(5): 870-884. DOI:10.1111/j.1365-2478.2012.01025.x |
| [25] |
MA Y, HALE D, GONG B, et al. Image-guided sparse-model full waveform inversion[J]. Geophysics, 2012, 77(4): R189-R198. DOI:10.1190/geo2011-0395.1 |
| [26] |
ASNAASHARI A, BROSSIER R, GARAMBOIS S, et al. Regularized seismic full waveform inversion with prior model information[J]. Geophysics, 2013, 78(2): R25-R36. DOI:10.1190/geo2012-0104.1 |
| [27] |
VAN LEEUWEN T, HERRMANN F J. Mitigating local minima in full-waveform inversion by expanding the search space[J]. Geophysical Journal International, 2013, 195(1): 661-667. DOI:10.1093/gji/ggt258 |
| [28] |
YU C X, WANG Y F, ZHAO J T, et al. Double parameterized regularization inversion method for migration velocity analysis in transversely isotropic media with a vertical symmetry axis[J]. Geophysical Prospecting, 2014, 62(5): 1040-1053. DOI:10.1111/1365-2478.12117 |
| [29] |
YAN Z, WANG Y. Full waveform inversion with sparse structure constrained regularization[J]. Journal of Inverse and Ill-Posed Problems, 2017, 26(2): 243-257. |
| [30] |
XUE Z, ZHU H, FOMEL S. Full-waveform inversion using seislet regularization[J]. Geophysics, 2017, 82(5): A43-A49. DOI:10.1190/geo2016-0699.1 |
| [31] |
SHI J, BERETTA E, HOOP M D, et al. A numerical study of multi-parameter full waveform inversion with iterative regularization using multi-frequency vibroseis data[J]. Computational Geosciences, 2020, 24(1): 89-107. DOI:10.1007/s10596-019-09897-6 |
| [32] |
何清龙. 基于有限差分-对比源方法的波动方程全波形反演研究[D]. 黑龙江哈尔滨: 哈尔滨工业大学, 2016.
|
| [33] |
TIKHONOV A N, GONCHARSKY A, STEPANOV V V, et al. Numerical Methods for the Solution of Ill-posed Problems[M]. Springer, Berlin, 2013.
|
| [34] |
OVCHARENKO O, KAZEI V, PETER D, et al. Variance-based model interpolation for improved full-waveform inversion in the presence of salt bodies[J]. Geophysics, 2018, 83(5): R541-R551. DOI:10.1190/geo2017-0575.1 |
| [35] |
刘亚飞. 全变分约束全波形反演方法研究[D]. 北京: 中国石油大学(北京), 2016.
|



 王维红, 黑龙江省大庆市高新技术产业开发区学府街99号东北石油大学地球科学学院, 163318。Email:
王维红, 黑龙江省大庆市高新技术产业开发区学府街99号东北石油大学地球科学学院, 163318。Email: 