② 青岛海洋科学与技术试点国家实验室, 山东青岛 266071;
③ 中国石油塔里木油田公司, 新疆库尔勒 841000
② Pilot National Laboratory for Marine Science and Technology(Qingdao), Qingdao, Shandong 266071, China;
③ Tarim Oilfield Company, PetroChina, Korla, Xinjiang 841000, China
确定地下构造及地下介质物性一直都是油气勘探的重要内容。相较于传统的偏移成像方法,全波形反演方法(FWI)利用了全部的波场信息,具有精细刻画地下构造和物性的潜力[1-3]。相比于声波近似的全波形反演,弹性波全波形反演(EFWI)既可以反演出更精准的纵横波速度信息,同时还可以反演出更丰富的弹性参数信息[4-6]。
EFWI以最小化观测数据和模拟数据的残差为目标函数,通过梯度类的优化算法不断地更新模型,以此提高观测数据与模拟数据之间的匹配程度。在全波形反演中,常用的最优化方法有最速下降法、共轭梯度(Conjugate Gradient,CG)法,牛顿法、拟牛顿法以及高斯—牛顿法等牛顿类算法[7]。其中最速下降法是最简便的优化算法,其计算量最小,但在极小点附近收敛较慢[8]。Tarantola[9]将最速下降法应用于时间域声波近似的地震反射数据反演。CG法是利用目标函数在当前迭代点处的负梯度方向与上一步的搜索方向的线性组合,作为下一步的搜索方向。Wang等[10]将CG法应用于实际资料的时域参数反演,获得了较好的成像剖面。牛顿类算法至少具有二阶收敛性,在反演过程中有较快的收敛速度,但Hessian矩阵计算很困难[11]。拟牛顿法则是通过求取近似Heesian矩阵的方式大大降低了计算量与存储量。Brossier将[12]拟牛顿法中的L-BFGS算法(Limited-memory Broyden-Fletcher-Goldfarb-Shanno Algorithm)应用于全波形反演,并通过模型数据验证了L-BFGS算法的有效性;Malinowski等[13]将L-BFGS算法应用于实际资料的黏滞声波介质的参数反演。
地震波在地下介质传播过程中,其能量会随着深度的增加而衰减。因此在常规EFWI中,常存在深部照明不足、收敛速度不稳定的问题[14]。针对这一问题,采用预条件算子对梯度进行修正是一种较为常用的方式。Gauthier等[15]通过给深层的梯度赋于更大的权重补偿深部能量;Pratt等[16]用对角近似的Hessian矩阵对梯度进行预处理;Shin等[17]提出了伪Hessian矩阵的概念,并证明了伪Hessian矩阵可提高逆时偏移的成像精度;李闯等[18]结合Hessian算子的近似及一种快速高通滤波方法发展了一种预条件最小二乘逆时偏移算法;Chen等[19]将伪Hessian算子应用于弹性波最小二乘逆时偏移中,加快了偏移成像的收敛速度。
将对角近似的伪Hessian矩阵作为梯度预条件算子,与CG法、L-BFGS法结合,可实现预条件共轭梯度(P-CG)法、预条件L-BFGS(P-L-BFGS)法反演。本文使用绕射体模型和Marmousi Ⅱ模型进行试算,从多个角度对比了CG法、P-CG法、L-BFGS法以及P-L-BFGS法反演的优劣。
1 方法原理 1.1 EFWI基础理论二维情况下,非均匀各向同性弹性介质时间域一阶速度—应力波动方程为
| $ \left\{\begin{array}{l} \frac{\partial v_{x}}{\partial t}=\frac{1}{\rho}\left(\frac{\partial \tau_{x x}}{\partial x}+\frac{\partial \tau_{x z}}{\partial z}\right) \\ \frac{\partial v_{z}}{\partial t}=\frac{1}{\rho}\left(\frac{\partial \tau_{x z}}{\partial x}+\frac{\partial \tau_{z z}}{\partial z}\right) \\ \frac{\partial \tau_{x x}}{\partial t}=(\lambda+2 \mu) \frac{\partial v_{x}}{\partial x}+\lambda \frac{\partial v_{z}}{\partial z} \\ \frac{\partial \tau_{z z}}{\partial t}=\lambda \frac{\partial v_{x}}{\partial x}+(\lambda+2 \mu) \frac{\partial v_{z}}{\partial z} \\ \frac{\partial \tau_{x z}}{\partial t}=\mu\left(\frac{\partial v_{z}}{\partial x}+\frac{\partial v_{x}}{\partial z}\right) \end{array}\right. $ | (1) |
式中:vx和vz分别为x、z方向的振动速度;τxx、τxz和τzz为应力;λ和μ为拉梅常数;ρ为密度。求解该方程即为弹性波正演过程。
全波形反演是在正演的基础上通过最小化数据残差δu=uobs-umod求解模型参数m,其中uobs为观测数据,umod为模拟数据。基于L2范数的目标函数定义为
| $ E=\frac{1}{2}(\delta \boldsymbol{u})^{\mathrm{T}} \delta \boldsymbol{u} $ | (2) |
基于伴随状态法可求得目标函数对于λ、μ和ρ的一阶导数为[20]
| $ \left\{\begin{array}{l} \frac{\partial E}{\partial \lambda}=\int_{G} \int_{T} \frac{1}{4(\lambda+\mu)^{2}}\left(\tau_{x x}^{\mathrm{w}}+\tau_{z z}^{\mathrm{w}}\right)\left(\frac{\partial \tau_{x x}}{\partial t}+\frac{\partial \tau_{z z}}{\partial t}\right) \mathrm{d} t \mathrm{d} \boldsymbol{x} \\ \frac{\partial E}{\partial \mu}=\int_{G} \int_{T}\left[\frac{1}{4(\lambda+\mu)^{2}}\left(\tau_{x x}^{\mathrm{w}}+\tau_{z z}^{\mathrm{w}}\right)\left(\frac{\partial \tau_{x x}}{\partial t}+\frac{\partial \tau_{z z}}{\partial t}\right)+\right. \\ \ \ \ \ \ \ \ \ \ \ \left.\frac{1}{4 \mu^{2}}\left(\tau_{x x}^{\mathrm{w}}-\tau_{z z}^{\mathrm{w}}\right)\ \ \left(\frac{\partial \tau_{x x}}{\partial t}-\frac{\partial \tau_{z z}}{\partial t}\right)+\frac{1}{\mu^{2}} \tau_{x z}^{\mathrm{w}} \frac{\partial \tau_{x z}}{\partial t}\right] \mathrm{d} t \mathrm{d} \boldsymbol{x} \\ \frac{\partial E}{\partial \rho}=-\int_{G} \int_{T}\left(v_{x}^{\mathrm{w}} \frac{\partial v_{x}}{\partial t}+v_{z}^{\mathrm{w}} \frac{\partial v_{z}}{\partial t}\right) \mathrm{d} t \mathrm{d} \boldsymbol{x} \end{array}\right. $ | (3) |
式中:x=(x,z);G为反演模型的空间范围;T为记录长度;上标“w”表示伴随波场。
在弹性波多参数全波形反演中,模型参数的选择对于反演的收敛速度及反演精度都有影响[14]。针对各向同性弹性介质,主要有三种参数化方式:拉梅常数及密度(λ,μ,ρ)、纵横波速度及密度(VP,VS,ρ)以及纵横波阻抗及密度(IP,IS,ρ)[21-22]。(λ,μ,ρ)参数化方式的参数耦合效应较强,(VP,VS,ρ)与(IP,IS,ρ)参数化方式的反演精度相当,优于(λ,μ,ρ)[23]。由于密度主要影响反射波场的强弱,对波场的运动学信息影响不大,因此无论采用何种参数化方式,密度都是最难反演的参数[24]。由于(VP,VS,ρ)参数化反演结果更为稳定,本文选择该参数化方式。
纵横波速度与拉梅常数关系为
| $ \left\{\begin{array}{l} \lambda=\rho\left(V_{\mathrm{P}}^{2}-2 V_{\mathrm{S}}^{2}\right) \\ \mu=\rho V_{\mathrm{S}}^{2} \end{array}\right. $ | (4) |
使用链式求导法则可将目标函数对于拉梅常数及密度的梯度转化为纵、横波速度及密度的梯度
| $ \left\{\begin{array}{l} \frac{\partial E}{\partial V_{\mathrm{P}}}=2 \rho V_{\mathrm{P}} \frac{\partial E}{\partial \lambda} \\ \frac{\partial E}{\partial V_{\mathrm{S}}}=-4 \rho V_{\mathrm{S}} \frac{\partial E}{\partial \lambda}+2 \rho V_{\mathrm{P}} \frac{\partial E}{\partial \mu} \\ \frac{\partial E}{\partial \rho}=\left(V_{\mathrm{P}}^{2}-2 V_{\mathrm{S}}^{2}\right) \frac{\partial E}{\partial \lambda}+V_{\mathrm{S}}^{2} \frac{\partial E}{\partial \mu}+\frac{\partial E}{\partial \rho} \end{array}\right. $ | (5) |
在时间域EFWI中,由于地震波在传播过程中受到几何扩散效应、观测系统和复杂地表等因素的影响,会出现梯度能量分布不均衡的现象[25]。针对这一问题,可以通过构造梯度预条件算子对梯度项进行修正,从而改善深部成像质量,提高反演的收敛速度。
本文采用对角近似的伪Hessian矩阵作为梯度预条件算子
| $ \left\{\begin{array}{l} H_{\mathrm{pseudo }}^{V_{\mathrm{P}}}=\sum\limits_{N_{\mathrm{s}}} \int 2 V_{\mathrm{P}}^{4} \frac{\left(\frac{\partial \sigma_{x x}}{\partial t}+\frac{\partial \sigma_{z z}}{\partial t}\right)^{2}}{\left(V_{\mathrm{P}}^{2}-V_{\mathrm{S}}^{2}\right)^{2}} \mathrm{d} t \\ H_{\mathrm{pseudo}}^{V_{\mathrm{S}}}=\sum\limits_{N_{\mathrm{s}}} \int 4 V_{\mathrm{S}}^{4}\left[\frac{\left(\frac{\partial \sigma_{x x}}{\partial t}+\frac{\partial \sigma_{z z}}{\partial t}\right)^{2}}{2\left(V_{\mathrm{P}}^{2}-V_{\mathrm{S}}^{2}\right)^{2}}+\frac{\left(\frac{\partial \sigma_{x x}}{\partial t}-\frac{\partial \sigma_{z z}}{\partial t}\right)^{2}}{2 V_{\mathrm{S}}^{4}}+\frac{\left(\frac{\partial \sigma_{x z}}{\partial t}\right)^{2}}{V_{\mathrm{S}}^{4}}\right] \mathrm{d} t \\ H_{\mathrm{pseudo}}^{\rho}=\sum\limits_{N_{\mathrm{s}}} \int \frac{\left(\frac{\partial v_{x}}{\partial t}\right)^{2}+\left(\frac{\partial v_{z}}{\partial t}\right)^{2}+\left(\frac{\partial \sigma_{x z}}{\partial t}\right)^{2}+\left(\frac{\partial \sigma_{x x}}{\partial t}\right)^{2}+\left(\frac{\partial \sigma_{z z}}{\partial t}\right)^{2}}{\rho^{2}} \mathrm{d} t \end{array}\right. $ | (6) |
式中Ns为总炮数。使用预条件算子后的梯度项为
| $ \left\{\begin{array}{l} \left.\frac{\partial E}{\partial V_{\mathrm{P}}}\right|_{\text {prec }}=\frac{\partial E / \partial V_{\mathrm{P}}}{H_{\text {pseudo }}^{V_{\mathrm{P}}}} \\ \left.\frac{\partial E}{\partial V_{\mathrm{S}}}\right|_{\text {prec }}=\frac{\partial E / \partial V_{\mathrm{S}}}{H_{\mathrm{pseudo}}^{V_{\mathrm{S}}}} \\ \left.\frac{\partial E}{\partial \rho}\right|_{\text {prec }}=\frac{\partial E / \partial \rho}{H_{\text {pseudo }}^{\rho}} \end{array}\right. $ | (7) |
反演由初始模型m1出发,通过不断地更新迭代使目标函数E(m)达到最小值。在梯度类优化方法中,模型迭代更新的公式为
| $ \boldsymbol{m}_{k+1}=\boldsymbol{m}_{k}+\alpha_{k} \boldsymbol{d}_{k} $ | (8) |
式中:mk+1和mk分别为第k+1次和第k次迭代的模型参数;dk为第k次迭代的下降方向;αk为步长。本文通过抛物线插值法求取步长,使用局部优化方法求解下降方向。
1.3.1 CG法对于最简单的最速下降法,其基本思想是:函数在某一点沿其负梯度方向下降最快,在该点的下降方向dk为
| $ \boldsymbol{d}_{k}=-\nabla_{\boldsymbol{m}} E\left(\boldsymbol{m}_{k}\right) $ | (9) |
最速下降法的方法较为简单,每一次迭代的计算量较少,所需要的存储量也较少。但因为梯度是函数的局部性质,从局部看在某一点的附近下降快,但是整体上可能走了很多弯路,因此最速下降法收敛速度较慢[8, 11]。为了提高收敛速度,有学者提出了CG优化算法。
CG法最早是由Hestenes等[26]为求解线性方程组提出。在此基础上,Fletcher等[27]提出了求解非线性最优化问题的CG法。CG法利用在当前迭代的负梯度方向与上次的下降方向进行适当的线性组合作为最新的下降方向,其表达式为
| $ \boldsymbol{d}_{k+1}=-\nabla_{\boldsymbol{m}} E\left(\boldsymbol{m}_{k}\right)+\gamma_{k} \boldsymbol{d}_{k-1} $ | (10) |
式中γk为组合系数,有以下三种求法:
(1) Fletcher-Reeves公式
| $ \gamma_{k}=\frac{\left\|\nabla_{\boldsymbol{m}} E\left(\boldsymbol{m}_{k}\right)\right\|^{2}}{\left\|\nabla_{\boldsymbol{m}} E\left(\boldsymbol{m}_{k-1}\right)\right\|^{2}} $ | (11) |
(2) Dixon-Myers公式
| $ \gamma_{k}=-\frac{\left\|\nabla_{\boldsymbol{m}} E\left(\boldsymbol{m}_{k}\right)\right\|^{2}}{\boldsymbol{d}_{k}^{\mathrm{T}} \nabla_{\boldsymbol{m}} E\left(\boldsymbol{m}_{k-1}\right)} $ | (12) |
(3) Polak-Ribiere-Polyak公式
| $ \gamma_{k}=-\frac{\left[\nabla_{\boldsymbol{m}} E\left(\boldsymbol{m}_{k}\right)\right]^{\mathrm{T}}\left[\nabla_{\boldsymbol{m}} E\left(\boldsymbol{m}_{k}\right)-\nabla_{\boldsymbol{m}} E\left(\boldsymbol{m}_{k-1}\right)\right]}{\left\|\nabla_{\boldsymbol{m}} E\left(\boldsymbol{m}_{k-1}\right)\right\|^{2}} $ | (13) |
本文组合系数采用Fletcher-Reeves公式,简称F-R公式。
CG法在EFWI中的具体实现步骤如下:
(1) 输入初始模型m1、观测记录uobs、地震子波;
(2) 通过有限差分法正演得到当前模型的模拟记录ukmod;
(3) 计算炮记录残差δuk=uobs-ukmod和波场残差;
(4) 基于波场残差反传波场和正演波场,计算得到梯度
(5) 若k=1,则下降方向为dk=-
(6) 计算最优化步长αk;
(7) 更新模型mk+1=mk+αkdk;
(8) 如果达到最大迭代次数或反演结果达到精度要求,结束;否则返回步骤(2)。
1.3.2 P-CG法在CG法的基础上,使用对角近似的Hessian矩阵作为梯度预处理算子,可以提高反演的收敛速度,提升模型深部的成像质量。
P-CG法的EFWI实现很简单,仅需在CG法的反演步骤(4)中使用梯度预条件算子对梯度进行校正即可。预处理后的梯度为
| $ \nabla _\mathit{\boldsymbol{m}}^{{\rm{prec }}}E\left( {{\mathit{\boldsymbol{m}}_k}} \right) = {\nabla _\mathit{\boldsymbol{m}}}E\left( {{\mathit{\boldsymbol{m}}_k}} \right)/H_{{\rm{pseudo }}}^\mathit{\boldsymbol{m}} $ | (14) |
CG法具有一阶线性收敛的性质,但其收敛速度不及牛顿类算法。牛顿类算法的基本原理如下。
在初始模型m1处,将目标函数E(m1+δm1)在初始点处使用Taylor展开,可得[28]
| $ E\left(\boldsymbol{m}_{1}+\delta \boldsymbol{m}_{1}\right) \approx E\left(\boldsymbol{m}_{1}\right)+\delta \boldsymbol{m}_{1} \frac{\partial E}{\partial \boldsymbol{m}}+\frac{1}{2} \delta \boldsymbol{m}_{1} \frac{\partial^{2} E}{\partial \boldsymbol{m}^{2}} \delta \boldsymbol{m}_{1}^{\mathrm{T}} $ | (15) |
对上式两边同时求取δm1的导数,并令其为零,可得
| $ \frac{\partial E\left(\boldsymbol{m}_{1}+\delta \boldsymbol{m}_{1}\right)}{\partial \delta \boldsymbol{m}_{1}}=\frac{\partial E}{\partial \boldsymbol{m}}+\delta \boldsymbol{m}_{1} \frac{\partial^{2} E}{\partial \boldsymbol{m}^{2}}=0 $ | (16) |
则有
| $ \delta \boldsymbol{m}_{1}=-\left(\frac{\partial^{2} E}{\partial \boldsymbol{m}^{2}}\right)^{-1} \frac{\partial E}{\partial \boldsymbol{m}} $ | (17) |
式中
| $ \boldsymbol{m}_{k+1}=\boldsymbol{m}_{k}-\alpha_{k} \boldsymbol{H}_{k}^{-1} \nabla_{\boldsymbol{m}} E(\boldsymbol{m}) $ | (18) |
牛顿法具有二阶收敛速度,但计算Hessian矩阵的逆需要巨大的计算量和存储量。为此,前人提出了多种近似计算Hessian矩阵的拟牛顿算法,其中BFGS算法具有最高的数值稳定性[29],被认为是最好的优化方法之一[8, 11, 30]。
BFGS算法通过迭代求取近似Hessian矩阵,以减小计算量。近似的Hessian矩阵的求取方式为
| $ \boldsymbol{H}_{k}=\boldsymbol{\eta}_{k-1}^{\mathrm{T}} \boldsymbol{H}_{k-1} \boldsymbol{\eta}_{k-1}+\varepsilon_{k-1} \boldsymbol{s}_{k-1} \boldsymbol{s}_{k-1}^{\mathrm{T}} $ | (19) |
式中:Hk为第k次求得的近似Hessian矩阵;sk-1=mk-mk-1,为模型参数的更新量;
由式(18)可以看出,BFGS算法每一次迭代都需要计算并存储相应的近似矩阵。而L-BFGS算法在迭代过程中,仅保存部分梯度算子和模型修正量的信息求取近似Hessian矩阵,避免了存储近似Hessian矩阵[31]。L-BFGS算法求取近似的Hessian矩阵的公式为
| $ \begin{aligned} &\boldsymbol{H}_{k}=\left(\prod\limits_{i=0}^{M-1} \boldsymbol{\eta}_{k-1-i}^{\mathrm{T}}\right) \boldsymbol{H}_{0}\left(\prod\limits_{i=0}^{M-1} \boldsymbol{\eta}_{k-1-i}\right)+ \\ &\sum\limits_{j=1}^{M}\left[\varepsilon_{k-1-M+j}\left(\prod\limits_{l=0}^{M-j} \boldsymbol{\eta}_{k-1-l}^{\mathrm{T}}\right) \boldsymbol{s}_{k-1-M+j} \boldsymbol{s}_{k-1-M+j}^{\mathrm{T}}\left(\prod\limits_{l=0}^{M-j} \boldsymbol{\eta}_{k-1-l}\right)\right] \end{aligned} $ | (20) |
式中:H0为初始近似Hessian矩阵;M为L-BFGS算法内部迭代次数。由上式可以看出,L-BFGS算法仅需要存储M个sk和yk即可完成对于近似矩阵的求取。
Brossier[12]将L-BFGS算法引入到二维频率域黏弹介质全波形反演,其实现流程如下:
(1) 输入初始模型m1、观测记录uobs、地震子波;
(2) 通过有限差分法正演得到当前模型模拟记录ukmod;
(3) 计算炮记录残差δuk=uobs-ukmod和波场残差;
(4) 基于波场残差反传波场与正演波场,计算得到梯度
(5) 如果k=1,则下降方向为dk=-
(6) 令q=
(7) 计算
(8) 若i= k-M循环结束;否则,
(9) 计算
(10) 令i=k-M;
(11) 计算
(12) 若i=k-1循环结束,输出下降方向dk=-χ,否则,
(13) 计算最优化步长αk;
(14) 更新模型mk+1=mk+αkdk;
(15) 若达到最大迭代次数或反演结果达到精度要求,结束;否则返回步骤(2)。
1.3.4 P-L-BFGS法L-BFGS算法已经有了较快的收敛速度,可以进一步使用预条件算子对梯度进行修正,提高反演精度。
P-L-BFGS法在L-BFGS基础上实现,即在L-BFGS法反演步骤(4)中使用梯度预条件算子对梯度进行校正(式(14))。相应地,步骤(6)、步骤(7)中的q和yi则变为
| $ \boldsymbol{q}=\nabla_{\boldsymbol{m}}^{\text {prec }} E\left(\boldsymbol{m}_{k}\right) $ | (21) |
| $ \boldsymbol{y}_{i}=\nabla_{\boldsymbol{m}}^{\text {prec }} E\left(\boldsymbol{m}_{i+1}\right)-\nabla_{\boldsymbol{m}}^{\text {prec }} E\left(\boldsymbol{m}_{i}\right) $ | (22) |
本文对绕射体模型和MarmousiⅡ模型在相同初始模型、相同观测系统、相同主频子波的条件下,使用四种优化方法分别进行反演,并从多个角度对比各优化方法的优劣。
2.1 绕射体模型绕射体模型如图 1所示,在模型深度460~500m、横向不同的位置处,分布了纵波速度、横波速度和密度三个绕射体。该模型虽不能代表实际地下介质情况,但可直观地看出各参数间的耦合效应。同时也可以更方便讨论不同优化方法对于参数耦合效应的压制效果。

|
图 1 绕射体真实模型 (a)纵波速度;(b)横波速度;(c)密度模型 |
模型的横向与纵向的网格数为200×100,网格间距为10m,共放20炮,炮间距为100m,地表全孔径接收,检波点距为10m,炮点与检波点的埋深均为10m,采样间隔为1.5ms,样点数为1500。正演和反演均使用主频为15Hz的雷克子波作为震源,将绕射体去除后的背景场作为初始模型,反演总迭代次数为100。为了进一步提高反演的稳定性,引入了多尺度反演策略,即通过维纳滤波器对地震数据进行低通滤波(截止频率分别为8和15Hz),降低地震数据主频[32]。然后对8Hz低通滤波后的数据进行反演,在此基础上再对15Hz低通滤波后的数据进行反演,两次反演皆迭代50次。CG法、P-CG法、L-BFGS法和P-L-BFGS法的反演结果如图 2~图 5所示。

|
图 2 CG法反演结果 (a)纵波速度;(b)横波速度;(c)密度 |

|
图 3 P-CG法反演结果 (a)纵波速度;(b)横波速度;(c)密度 |

|
图 4 L-BFGS法反演结果 (a)纵波速度;(b)横波速度;(c)密度 |

|
图 5 P-L-BFGS法反演结果 (a)纵波速度;(b)横波速度;(c)密度 |
由图 2和图 3可见,三参数的反演结果都存在很强的参数耦合效应,而图 4和图 5的参数耦合效应则得到了明显的压制。这说明L-BFGS法在对于参数耦合效应的压制方面明显优于CG法。同时由图 2~图 5可以看出,密度的反演精度比纵、横波速度低。
为了更加明显地对比不同优化方法下的参数耦合效应,抽取深度500m处四种方法的反演结果与真实、初始模型的曲线对比如图 6所示。
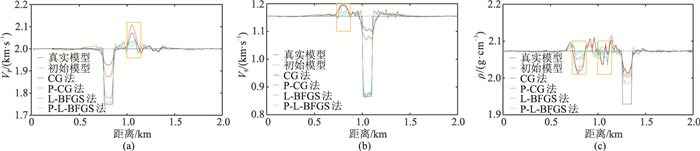
|
图 6 z=500m四种方法的反演结果与真实、初始模型曲线对比 (a)纵波速度;(b)横波速度;(c)密度 |
由图 6a可以看出,在横向1.0~1.1km处有明显的纵波速度异常,与横波速度绕射体模型的位置重合,为横波绕射体在纵波模型上留下的“反演脚印”,说明纵、横波速度耦合效应较强,与密度的耦合效应很弱。同理,由图 6b和图 6c可知:横波速度与纵波速度的耦合效应较强,与密度的耦合效应很弱;而密度曲线最复杂,与纵、横波速度均存在较强的耦合效应。
引入相关系数的概念,定量反映反演效果。相关系数定义[33]为
| $ r=\frac{\sum\limits_{l}\left(m_{l}^{\text {true }}-\overline{m}^{\text {true }}\right)\left(m_{l}^{\text {inv }}-\overline{m}^{\text {inv }}\right)}{\sqrt{\left[\sum\limits_{l}\left(m_{l}^{\text {inv }}-\overline{m}^{\text {inv }}\right)^{2}\right]\left[\sum\limits_{l}\left(m_{l}^{\text {true }}-\overline{m}^{\text {true }}\right)^{2}\right]}} $ | (23) |
式中:mltrue为模型第l个参数的真值;mlinv为第l个参数的反演结果;上划线表示求均值。式(23)表明,相关系数越高则反演模型与真实数值越接近,即反演精度越高。绕射体模型四种优化算法反演结果的相关系数曲线如图 7所示。
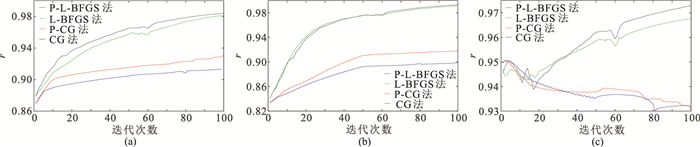
|
图 7 绕射体模型四种优化算法反演结果的相关系数曲线对比 (a)纵波速度;(b)横波速度;(c)密度 |
由于参数之间的耦合效应,CG法与P-CG法反演结果的三参数相关系数数值均较小,甚至密度的相关系数随迭代次数的增加而不断减小。L-BFGS法和P-L-BFGS法反演结果的三个参数相关系数均大于0.96,后者略大。
由以上分析可知,对于绕射体模型,P-L-BFGS法反演精度最高,L-BFGS法次之,CG法最低。
应用残差收敛曲线(图 8)分析四种优化方法在反演过程中的收敛速度和稳定性。由图 8可见,CG法在反演过程中极不稳定,很容易陷入局部极值,且残差的波动较大;在使用了梯度预处理算子后情况得到了改善,但在第74~第76次迭代中由于算法本身的局限性出现了梯度计算错误,导致残差能量异常;L-BFGS法和P-L-BFGS法在整个反演过程中则更稳健,且收敛速度也要比CG法和P-CG法更快,数据残差也更小。图 9为P-CG法和P-L-BFGS法第75次迭代下的纵波速度下降方向,P-CG法的下降方向出现了明显的数值异常。
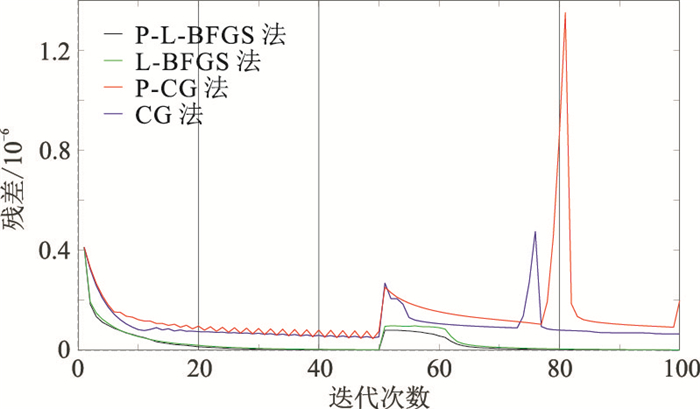
|
图 8 绕射体模型四种优化算法反演的残差曲线对比 |
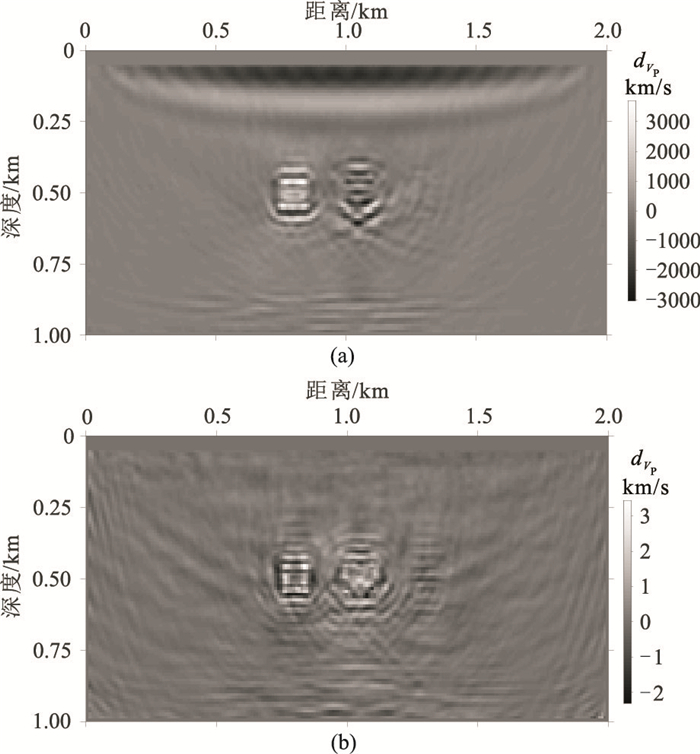
|
图 9 绕射体模型P-CG法(a)与P-L-BFGS法(b)第75次迭代计算的纵波速度下降方向对比 |
Marmousi Ⅱ模型是勘探地球物理学中常用的标准模型,其真实的纵、横波速度、密度分布如图 10所示。模型的横网格数为450×150,网格间距为10m;共60炮,炮间距为70m,地表全孔径接收,检波点间距10m,炮点和检波点的埋深均为10m,采样间隔为0.5ms,样点数为4000。正演与反演均使用主频为15Hz的雷克子波作为震源,真实模型平滑结果作为初始模型(图 11),反演最大迭代次数为60。为了获得更好的反演效果,引入了基于维纳滤波器的多尺度反演策略,8Hz和15Hz低通滤波数据分别迭代30次。CG法、P-CG法、L-BFGS法和P-L-BFGS法的反演结果如图 12~图 15所示。

|
图 10 真实Marmousi Ⅱ模型 (a)纵波模型;(b)横波模型;(c)密度模型 |

|
图 11 Marmousi Ⅱ初始模型 (a)纵波;(b)横波;(c)密度 |

|
图 12 Marmousi Ⅱ模型CG法反演结果 (a)纵波模型;(b)横波模型;(c)密度模型 |

|
图 13 Marmousi Ⅱ模型P-CG法反演结果 (a)纵波模型;(b)横波模型;(c)密度模型 |

|
图 14 Marmousi Ⅱ模型L-BFGS法反演结果 (a)纵波模型;(b)横波模型;(c)密度模型 |

|
图 15 Marmousi Ⅱ模型P-L-BFGS法反演结果 (a)纵波模型;(b)横波模型;(c)密度模型 |
对比图 13与图 14、图 15与图 16可见,使用预条件算子后深部照明得到了明显增强,说明梯度预处理算子在应用于复杂模型时效果较为明显;对于纵、横波速度反演效果最好的是P-L-BFGS法,但在反演密度时发生了明显的过拟合现象。
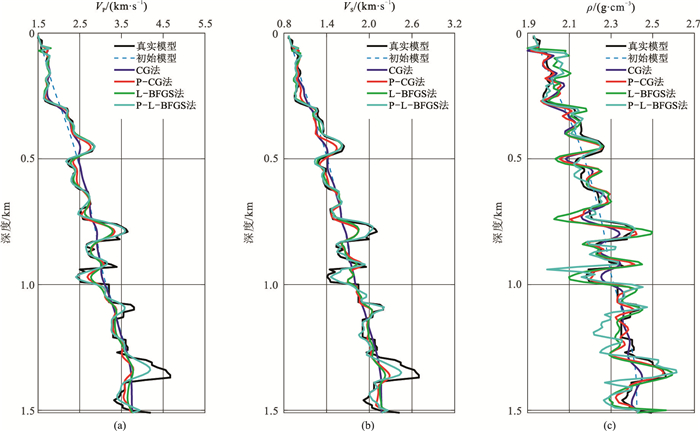
|
图 16 Marmousi Ⅱ模型四种方法反演结果与真实、初始模型的单道对比 (a)纵波模型;(b)横波模型;(c)密度模型 |
抽取横向2250m处四种方法的反演结果,与真实、初始模型的曲线对比如图 16所示。由图可见,P-L-BFGS法反演的纵横波速度与真值最接近,CG法偏离程度最大,P-CG法与L-BFGS法结果相近;对于密度反演,L-BFGS法与P-L-BFGS法在部分深度段出现了明显的偏差,是过拟合现象造成。图 17为四种方法反演结果的相关系数曲线,可以看出:P-L-BFGS法纵、横波速度反演结果与真实模型最接近;比较出乎意料的是四种方法的密度反演相关系数均呈下降趋势,其中CG法下降幅度最小,P-L-BFGS法下降幅度最大,这也再次体现了密度反演的复杂性。
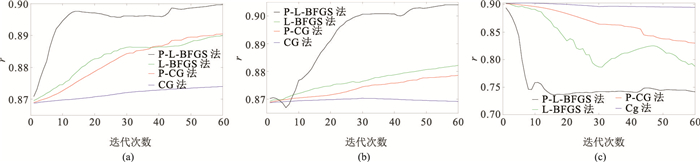
|
图 17 Marmousi Ⅱ模型四种方法反演结果的相关系数曲线对比 (a)纵波模型;(b)横波模型;(c)密度模型 |
在收敛速度方面,P-L-BFGS法收敛速度最快,L-BFGS法次之,P-CG法略逊于L-BFGS法,CG法最次(图 18)。
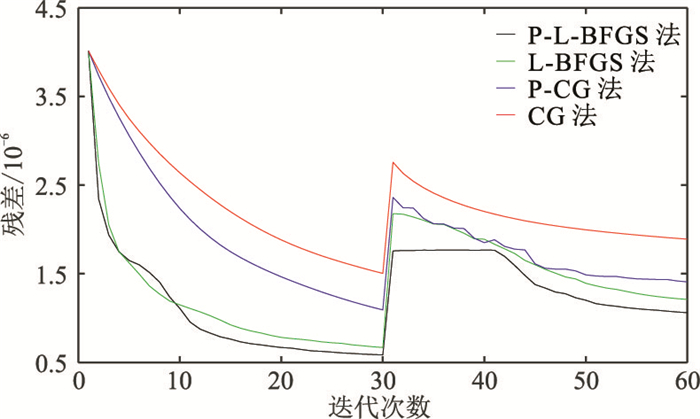
|
图 18 Marmousi Ⅱ模型四种反演方法的残差曲线对比 |
本文通过对比绕射体模型和MarmousiⅡ模型的CG法、P-CG法、L-BFGS法和P-L-BFGS法反演结果,获得如下结论:
(1) 将不同参数的绕射体布置在相同深度的不同位置,通过横向抽取单道曲线的方式直观地展示了参数之间的耦合效应,可为反演策略的选择提供参考;
(2) 对于研究参数耦合效应的绕射体模型,L-BFGS算法在反演过程中求解了近似Hessian矩阵,相比于CG法具有天然的优势;
(3) 对于复杂的MamousiⅡ模型,P-L-BFGS法和L-BFGS法的纵波速度反演结果明显优于P-CG法和CG法,但密度反演效果明显较差。因此在优化方法的选择上需慎重,并不是算法越复杂精度越高;
(4) 梯度预条件算子可以提高深部照明效果,提高反演精度,并加快反演的收敛速度。在对Mar-mousiⅡ模型的密度进行反演时,预条件L-BFGS法的过拟合现象更加明显,这与预条件算子的选取密切相关,因此在选择梯度预条件算子时需谨慎。
以上结论均是在数值算例的基础上得到的,四种优化算法在实际数据中的应用效果还需要进一步分析。
| [1] |
JEONG W, LEE H Y, MIN D J. Full waveform inversion strategy for density in the frequency domain[J]. Geophysical Journal International, 2012, 188(3): 1221-1242. DOI:10.1111/j.1365-246X.2011.05314.x |
| [2] |
刘张聚, 童思友, 方云峰, 等. 基于时域加权的拉普拉斯-频率域弹性波全波形反演[J]. 石油地球物理勘探, 2021, 56(2): 302-312, 331. LIU Zhangju, TONG Siyou, FANG Yunfeng, et al. Full elastic waveform inversion in Laplacian-Fourier domain based on time-domain weighting[J]. Oil Geophysical Prospecting, 2021, 56(2): 302-312, 331. |
| [3] |
王华忠, 盛燊. 走向精确地震勘探的道路[J]. 石油物探, 2021, 60(5): 693-708. WANG Huazhong, SHENG Shen. Pathway toward accurate seismic exploration[J]. Geophysical Prospecting for Petroleum, 2021, 60(5): 693-708. |
| [4] |
VIGH D, SUN D, WATTS D, et al. Elastic full-waveform inversion application using multicomponent measurements of seismic data collection[J]. Geophysics, 2014, 79(2): R63-R77. DOI:10.1190/geo2013-0055.1 |
| [5] |
邵祥奇, 何兵寿, 史才旺. 基于分频编码的弹性波全波形反演[J]. 石油地球物理勘探, 2020, 55(6): 1321-1329. SHAO Xiangqi, HE Bingshou, SHI Caiwang. Elastic full waveform inversion based on frequency-division encoding[J]. Oil Geophysical Prospecting, 2020, 55(6): 1321-1329. |
| [6] |
王毓玮, 董良国, 黄超, 等. 降低弹性波全波形反演强烈非线性的分步反演策略[J]. 石油地球物理勘探, 2016, 51(2): 288-294. WANG Yuwei, DONG Liangguo, HUANG Chao, et al. Stepwise inversion strategy for reducing strong nonlinearity in full waveform inversion of elastic wave[J]. Oil Geophysical Prospecting, 2016, 51(2): 288-294. |
| [7] |
VIRIEUX J, OPERTO S. An overview of full-waveform inversion in exploration geophysics[J]. Geophysics, 2009, 74(6): WCC1-WCC26. DOI:10.1190/1.3238367 |
| [8] |
唐焕文. 实用最优化方法[M]. 辽宁大连: 大连理工大学出版社, 2004.
|
| [9] |
TARANTOLA A. Inversion of seismic reflection data in the acoustic approximation[J]. Geophysics, 1984, 49(8): 1259-1266. DOI:10.1190/1.1441754 |
| [10] |
WANG Z Y, ZHANG Y N, CAI H M, et al. Nonli-near process control of wave-equation inversion and its application in the detection of gas[J]. Journal of Computer Applications, 2008, 28(3): 3-13. |
| [11] |
马昌凤. 最优化方法及其Matlab程序设计[M]. 北京: 科学出版社, 2010.
|
| [12] |
BROSSIER R. Two-dimensional frequency-domain vi-sco-elastic full waveform inversion: Parallel algorithms, optimization and performance[J]. Computers and Geosciences, 2010, 37(4): 444-455. |
| [13] |
MALINOWSKI M, OPERTO S, RIBODETTI A. High-resolution seismic attenuation imaging from wide-aperture onshore data by visco-acoustic frequency-domain full-waveform inversion[J]. Geophysical Journal International, 2011, 186(3): 1179-1204. DOI:10.1111/j.1365-246X.2011.05098.x |
| [14] |
张凯, 李振春, 陈永芮, 等. 一种新的用于全波形反演的能量加权梯度方法[J]. 石油物探, 2015, 54(1): 77-82. ZHANG Kai, LI Zhenchun, CHEN Yongrui, et al. A new energy weighted gradient method for full waveform inversion[J]. Geophysical Prospecting for Petroleum, 2015, 54(1): 77-82. |
| [15] |
GAUTHIER O, VIRIEUX J, TARANTOLA A. Two-dimensional nonlinear inversion of seismic waveforms: Numerical results[J]. Geophysics, 1986, 51(7): 1387-1403. DOI:10.1190/1.1442188 |
| [16] |
PRATT R G, SHIN C, HICK G J. Gauss-Newton and full Newton methods in frequency-space seismic waveform inversion[J]. Geophysical Journal International, 1998, 133(2): 341-362. DOI:10.1046/j.1365-246X.1998.00498.x |
| [17] |
SHIN C S, JANG S H, MIN D J. Improved amplitude preservation for prestack depth migration by inverse scattering theory[J]. Geophysical Prospecting, 2001, 49(5): 592-606. DOI:10.1046/j.1365-2478.2001.00279.x |
| [18] |
李闯, 黄建平, 李振春, 等. 预条件最小二乘逆时偏移方法[J]. 石油地球物理勘探, 2016, 51(3): 513-520. LI Chuang, HUANG Jianping, LI Zhenchun, et al. Preconditioned least squares reverse-time migration method[J]. Oil Geophysical Prospecting, 2016, 51(3): 513-520. |
| [19] |
CHEN K, SACCHI M D. Elastic least-squares reverse time migration via linearized elastic full-waveform inversion with pseudo-Hessian preconditioning[J]. Geophysics, 2017, 82(5): S341-S358. DOI:10.1190/geo2016-0613.1 |
| [20] |
PLESSIX R E. A review of the adjoint-state method for computing the gradient of a functional with geophysical applications[J]. Geophysical Journal International, 2006, 167(2): 495-503. DOI:10.1111/j.1365-246X.2006.02978.x |
| [21] |
TARANTOLA A. A strategy for nonlinear elastic inversion of seismic reflection data[J]. Geophysics, 1986, 51(10): 1893-1903. DOI:10.1190/1.1442046 |
| [22] |
FORGUES E, LAMBARE G. Parameterization study for acoustic and elastic ray+Born inversion[J]. Journal of Seismic Exploration, 1997, 6(2): 253-278. |
| [23] |
KÖHN D, DE NIL D, KURZMANN A, et al. On the influence of model parametrization in elastic full waveform tomography[J]. Geophysical Journal International, 2012, 191(1): 325-345. DOI:10.1111/j.1365-246X.2012.05633.x |
| [24] |
郭振波. 弹性介质波形反演方法研究[D]. 山东青岛: 中国石油大学(华东), 2014.
|
| [25] |
张广智, 姜岚杰, 孙昌路, 等. 基于照明预处理的分步多参数时间域声波全波形反演方法研究[J]. 石油物探, 2017, 56(1): 31-37. ZHANG Guangzhi, JIANG Lanjie, SUN Changlu, et al. The stepped multi-parameter FWI of acoustic media in time-domain by L-BFGS method with illumination analysis[J]. Geophysical Prospecting for Petroleum, 2017, 56(1): 31-37. |
| [26] |
HESTENES M R, STIEFEL E L. Methods of conjugate gradients for solving linear systems[J]. Journal of Research of the National Bureau of Standards(United States), 1952, 49(6): 409-436. DOI:10.6028/jres.049.044 |
| [27] |
FLETCHER R, REEVES C M. Function minimization by conjugate gradients[J]. The Computer Journal, 1964, 7(2): 149-154. DOI:10.1093/comjnl/7.2.149 |
| [28] |
KÖHN D. Time Domain 2D Elastic Full Waveform Tomography[D]. Kiel University, Schleswig-Holstein, Germany, 2011.
|
| [29] |
DAVIDON W C. Variable metric method for minimi-zation[J]. Siam Journal on Optimization, 1991, 1(1): 1-17. DOI:10.1137/0801001 |
| [30] |
NOCEDA J, WRIGHT S J. Numerical Optimization(2nd Edition)[M]. Springer Science & Business Media, New York, USA, 2006.
|
| [31] |
苗永康. 基于L-BFGS算法的时间域全波形反演[J]. 石油地球物理勘探, 2015, 50(3): 469-474. MIAO Yongkang. Full waveform inversion in time domain based on L-BFGS algorithm[J]. Oil Geophy-sical Prospecting, 2015, 50(3): 469-474. |
| [32] |
FU L, GUO B W, SCHUSTER G T. Multiscale phase inversion of seismic data[J]. Geophysics, 2018, 83(2): R159-R171. DOI:10.1190/geo2017-0353.1 |
| [33] |
NGUYEN B D, MCMECHAN G A. Five ways to avoid storing source wavefield snapshots in 2D elastic prestack reverse time migration[J]. Geophysics, 2015, 80(1): S1-S18. DOI:10.1190/geo2014-0014.1 |



 黄建平, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email:
黄建平, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email: 