② 东方地球物理公司新兴物探开发处, 河北涿州 072751
② New Resources Geophysical Exploration Division, BGP Inc., CNPC, Zhuozhou, Hebei 072751, China
地球内部广泛存在各向异性介质[1-5]。TI介质是目前地震勘探理论研究和资料处理中经常使用的各向异性介质模型[6-9]。在反射波地震勘探中,非均匀各向异性介质反射旅行时一般由多方位、多炮检距的射线追踪计算。尽管已有的各向异性射线追踪正演模拟足够快,但当用于反射波反演时,因需反复计算多方位、多炮检距旅行时,使反演过程非常费时[10-13]。对于最大排列长度与反射深度比接近1(简称常规排列),介质具有不太复杂结构的CMP(Common Middle Point)反射时距关系可由测线方位上的NMO(Normal Moveout)速度描述[13-16],因而可通过该反射时距关系计算反射波旅行时。这样,NMO速度的计算则成为反射波旅行时快速计算的基础。
在各向异性介质中,随射线传播角度而变化的速度使NMO速度方法的求解变得异常复杂。已有的计算各向异性NMO速度多数对应于简单的TI模型,如:Thomsen[17]给出了水平界面VTI介质中同类波(非转换波)的NMO速度解;Tsvankin[15, 18]导出了水平界面HTI和TI介质对称轴方位与界面走向一致时同类波的NMO速度解;Grechka等[19]推导了三维倾斜界面VTI介质同类波的NMO速度解;姚陈[20]导出了三维倾斜界面对称轴任意取向的TI介质同类波NMO速度解。这些已有的NMO速度解都是针对单层介质,而由地面观测得到的NMO速度一般是地下多层介质速度的等效结果。如果界面倾斜,无法再利用Dix公式[21]或广义Dix方程[13]建立地表观测的等效NMO速度和层速度的联系。为此,Grechka等[22]提出了NMO速度面的概念,通过对沿零炮检距射线路径上不同层的速度面的Dix型平均化(Dix型平均算法),得到水平地表上的等效NMO速度,该算法需要数值求解由介质弹性常数表示的Christoffel方程。
本文在现有的单层三维倾斜界面对称轴任意取向TI介质NMO速度面解析解[23-24]的基础上,运用Dix型平均算法[22]求解多层介质水平地表的等效NMO速度,进而运用由NMO速度描述的CMP反射时距关系实现反射波旅行时快速算法。与Grechka等[22]的数值计算NMO速度面不同,上述NMO速度面解析解完全由介质的各向异性参数和界面参数描述。
本文所述快速算法在探究NMO速度与地层各向异性参数及界面特征的关系、垂向非均匀TI介质反射波旅行时反演等方面有实际应用价值。
1 等效NMO速度的计算方法 1.1 NMO速度面解析解简述考虑多层倾斜界面对称轴任意空间取向的TI介质,其常规排列同类波反射时距关系可由随测线方位变化的NMO速度描述[13-16](假设每一炮检对的反射波旅行时是单值)
| $ t^{2}=t_{0}^{2}+\frac{X^{2}}{v_{\mathrm{nmo}}^{2}(\varphi)} $ | (1) |
式中:t是测线方位角为φ、炮检距为X时同类反射波旅行时;t0为零炮检距双程反射旅行时;vnmo(φ)是测线方位角为φ时的NMO速度。
对于单层TI介质,利用姚陈[20]导出的NMO速度解,可由式(1)快速计算反射旅行时。对于多层倾斜TI介质,因来自地下不同层反射波旅行时t是其传播路径上多层介质的综合反映,与t相对应的vnmo(φ)也是多层介质的综合反映,因此需要先求得vnmo(φ),再由式(1)快速计算来自不同界面的反射波旅行时。由于倾斜界面的存在,使等效NMO速度和层速度无法再通过Dix公式[21]或广义Dix方程[13]建立联系,因此本文运用由Grechka等[22]提出的NMO速度面概念,即把NMO速度做为三维空间方向单位矢量的函数,得到单层倾斜界面TI介质的NMO速度面,再运用Dix型平均算法计算水平地表上的等效NMO速度。
图 1给出的观测系统示意图中,设S为激发点,R为接收点,其中心点CMP即为坐标系原点O, 测线SR在三维空间中的方向单位矢量为L,可将NMO速度vnmo(L)表示为[22]
| $ v_{\mathrm{nmo}}^{-2}(\boldsymbol{L})=\boldsymbol{L} \boldsymbol{U} \boldsymbol{L}^{\mathrm{T}} $ | (2) |

|
图 1 观测系统示意图 S′、R′为S、R在水平地表的投影,P为界面上相反射点,G为界面上群反射点;γ为OP与c的夹角,φ为OS′与x1轴夹角,θ为OS与x3轴夹角;当炮检距X=0时,零炮检距射线OP与r方向一致,OG表示零炮检距群反射路径,与c的夹角为γg |
式中:L=(sinθcosφ,sinθsinφ,cosθ)是单位矢量,其中θ和φ为L的倾角和方位角;U是一个3×3对称矩阵
| $ \boldsymbol{U}=\left[\begin{array}{lll} U_{1,1} & U_{1,2} & U_{1,3} \\ U_{1,2} & U_{2,2} & U_{2,3} \\ U_{1,3} & U_{2,3} & U_{3,3} \end{array}\right] $ | (3) |
显然,式(2)表示了vnmo(L)在三维空间中所有可能方向的矢径,所有矢径端点构成了NMO速度面;当θ=90°,式(2)表示的则是水平面上仅随φ变化的vnmo(φ)。对于单层倾斜界面、对称轴任意空间取向、任意各向异性强度的TI介质,文献[23-24]将U的各元素显式地表示为零炮检距射线的相速度v及其对相角γ的导数dv/dγ、群角γg以及介质对称轴方向c和反射界面法线方向r的解析函数。其中相速度v是对称轴方向的qP(qS)波速度vP0(vS0)、各向异性参数(如ε、δ等)和相角γ的函数。c和r可表示为
| $ \left\{\begin{array}{l} \boldsymbol{c}=\left(\sin \theta_{c} \cos \varphi_{c}, \sin \theta_{c} \sin \varphi_{c}, \cos \theta_{c}\right) \\ \boldsymbol{r}=\left(\sin \theta_{r} \cos \varphi_{r}, \sin \theta_{r} \sin \varphi_{r}, \cos \theta_{r}\right) \end{array}\right. $ | (4) |
式中:θc、φc分别为对称轴的倾角和方位角;θr、φr分别为倾斜界面法线的倾角和方位角。
显然,零炮检距射线相角γ与c、r关系为
| $ \cos \gamma=\boldsymbol{c} \cdot \boldsymbol{r}=\sin \theta_{c} \sin \theta_{r} \cos \left(\varphi_{c}-\varphi_{r}\right)+\cos \theta_{c} \cos \theta_{r} $ | (5) |
而γ与γg满足[17]
| $ \sin \gamma_{\mathrm{g}} =\frac{v \sin \gamma+\frac{\mathrm{d} v}{\mathrm{~d} \gamma} \cos \gamma}{v_{\mathrm{g}}} $ | (6) |
| $ \cos \gamma_{\mathrm{g}} =\frac{v \cos \gamma-\frac{\mathrm{d} v}{\mathrm{~d} \gamma} \sin \gamma}{v_{\mathrm{g}}} $ | (7) |
式中vg为群传播速度,有
| $ v_{\mathrm{g}}=\sqrt{v^{2}+\left(\frac{\mathrm{d} v}{\mathrm{~d} \gamma}\right)^{2}} $ | (8) |
在得到零炮检距射线相角γ后,将相速度v及式(5)~式(8)代入U的解析解,可求得群反射点G及零炮检距双程反射旅行时t0。
此外,U的元素满足[24]
| $ \left\{\begin{array}{l} U_{1,3}=q_{1} U_{1,1}+q_{2} U_{1,2} \\ U_{2,3}=q_{1} U_{1,2}+q_{2} U_{2,2} \\ U_{3,3}=q_{1}^{2} U_{1,1}+2 q_{1} q_{2} U_{1,2}+q_{2}^{2} U_{2,2} \end{array}\right. $ | (9) |
式中
| $ \left\{\begin{array}{l} q_{1}=-\frac{\sin \theta_{r} \cos \varphi_{r} \sin \gamma_{\mathrm{g}}-\sin \theta_{c} \cos \varphi_{c} \sin \left(\gamma_{\mathrm{g}}-\gamma\right)}{\cos \theta_{r} \sin \gamma_{\mathrm{g}}-\cos \theta_{c} \sin \left(\gamma_{\mathrm{g}}-\gamma\right)} \\ q_{2}=-\frac{\sin \theta_{r} \sin \varphi_{r} \sin \gamma_{\mathrm{g}}-\sin \theta_{c} \sin \varphi_{c} \sin \left(\gamma_{\mathrm{g}}-\gamma\right)}{\cos \theta_{r} \sin \gamma_{\mathrm{g}}-\cos \theta_{c} \sin \left(\gamma_{\mathrm{g}}-\gamma\right)} \end{array}\right. $ | (10) |
根据文献[22],U满足
| $ U_{k, m}=\tau_{0} \frac{\mathrm{d} p_{k}}{\mathrm{~d} x_{m}} \quad k, m=1,2,3 $ | (11) |
式中:τ0是从零炮检距射线反射点到CMP的单程旅行时;p=(p1,p2,p3)为在零炮检距反射点激发、CMP位置的慢度矢量。对单一均匀层,Uk, m可由给定零炮检距射线慢度矢量求解Christoffel方程获得[22]。与此相比较,由给定的单层倾斜界面对称轴任意空间取向TI介质参数,应用U解析解直接计算NMO速度面更为简洁、快速。
特别指出的是,Grechka在理论上证实了均匀任意各向异性介质中同类反射波的NMO速度面为一椭圆柱面,其轴线平行于零炮检距射线方向[22, 24]。从几何意义上理解,NMO速度面与三维空间内任一平面(与NMO速度面轴线平行的平面除外)的交线都为椭圆。由单层TI介质NMO速度面解析解[23-24]计算多层介质中来自反射界面同类波的水平地表上等效NMO速度,涉及到沿零炮检距射线路径上计算每一单层的层间Uint(l)(l为层序号,目标层为第1层向地面算起),以及计算从第1层到第l层的等效U(l)。
1.2 单层Uint的计算若l=1,零炮检距射线方向矢量直接取反射界面法线空间取向(正入射原理),从而计算单层的Uint(1)以及零炮检距群反射点到CMP的单程旅行时τ0, 1,此时Uint(1)亦是等效U(1)。若l>1,除目标层下界面(反射界面)外,零炮检距射线与其路径上的其他界面一般并不垂直,此时需要该层中零炮检距射线方向参数代替式(5)中的界面法线参数θr和φr,然后再计算层l的Uint(l)。每层中的射线方向参数可由零炮检距射线追踪确定,同时获得射线在每层中的单程旅行时τ0, l。
1.3 U与空间任一平面的交线W的计算[22]NMO速度面与空间任一平面D的交线为该平面内的椭圆。平面D的法线单位矢量z由倾角θD和方位角φD表示为
| $ \mathit{\boldsymbol{z}} = \left( {\sin {\theta _D}\cos {\theta _D},\sin {\theta _D}\sin {\varphi _D},\cos {\theta _D}} \right) $ | (12) |
由该矢量,在平面D内可以找到两个相互垂直单位矢量b(1)和b(2)
| $ \boldsymbol{b}^{(1)}=\left(\cos \theta_{D} \cos \varphi_{D}, \cos \theta_{D} \sin \varphi_{D},-\sin \theta_{D}\right) $ | (13) |
| $ \boldsymbol{b}^{(2)}=\left(-\sin \theta_{D}, \cos \theta_{D}, 0\right) $ | (14) |
平面D内的任一单位矢量b可表示为
| $ \boldsymbol{b}=\boldsymbol{b}^{(1)} \cos \varphi_{\boldsymbol{b}}+\boldsymbol{b}^{(2)} \sin \varphi_{\boldsymbol{b}} $ | (15) |
式中φb为b相对b(1)的方位角。将b视作L,则φb=φ,将式(13)~式(15)代入式(2),可得
| $ v_{\mathrm{nmo}}^{-2}(\varphi)=W_{1,1} \cos ^{2} \varphi+2 W_{1,2} \sin \varphi \cos \varphi+W_{2,2} \sin ^{2} \varphi $ | (16) |
式中
| $ W_{i, j}=\sum\limits_{k=1}^{3} \sum\limits_{m=1}^{3} B_{k, m, i, j} U_{k, m} \quad i, j=1,2 $ | (17) |
| $ B_{k, m, i, j}=\frac{1}{2}\left[b_{k}^{(i)} b_{m}^{(j)}+b_{k}^{(j)} b_{m}^{(i)}\right] $ | (18) |
式(16)表示,平面D内随方位角φ变化的NMO速度为椭圆,说明在已知等效U或Uint后,可以计算其与任一确定平面D的交线,即该平面上的等效W或层间Wint(元素Wi, j=Wj, i)。
1.4 任一平面上等效W的计算在求得每层的Uint后,因Uint(1)等于U(1),用式(17)可求界面l(l层上界面)与U(l)的交线W(l),及界面l与Uint(l+1)的交线Wint(l+1),然后由零炮检距射线位移连续性及在界面上满足Snell定律的Dix型平均算法[22],获得关于界面l+1的等效W(l+1)
| $ \boldsymbol{W}^{-1}(l+1)=\frac{\tau_{0}(l) \boldsymbol{W}^{-1}(l)+\tau_{0, l+1} \boldsymbol{W}_{\text {int }}^{-1}(l+1)}{\tau_{0}(l+1)} $ | (19) |
式中
因NMO速度面轴线平行于零炮检距射线[22-23],因此,在得到W(l+1)后,可以通过式(9)求得相应的Uk, 3(k=1, 2, 3),从而实现对等效U(l+1)的重构。但在这个过程中,式(5)及式(10)中要用零炮检距射线方向参数代替界面法线参数θr、φr。
重复1.3~1.5节的计算,可求得全部层位的等效U。最后,运用式(16)求得水平地面上的等效NMO速度椭圆vnmo(φ),此时,式(12)中z=(0, 0, 1)。
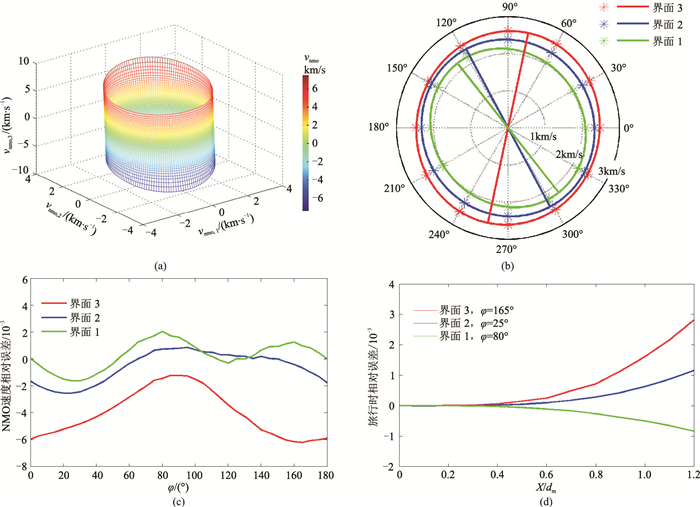
2 计算实例对于三层倾斜界面、对称轴任意取向的TI介质模型(表 1),本文方法计算的的等效NMO速度面、等效NMO速度椭圆、CMP道集反射旅行时误差如图 2所示,计算中P波相速度v使用了简明的Thomsen弱各向异性近似[17]。由水平地表上第3界面P波反射等效NMO速度面(图 2a)可以看出,等效NMO速度面为一椭圆柱面(第1、第2界面P波反射等效NMO速度面亦为椭圆柱面)。图 2b为水平地表与三个界面P波反射等效NMO速度面的交线,即水平地表上获取的三个界面反射的等效NMO速度椭圆,与常规排列下最优拟合射线追踪计算旅行时得到的NMO速度(星号)在所有方位(间隔30°)都相符;第1、2及3界面的等效NMO速度椭圆长轴(粗直线)方位取向不同,分别为129°、118°和78°。图 2c计算了图 2b中3个椭圆上的等效NMO速度与最优拟合射线追踪计算旅行时得到的NMO速度的相对误差随方位角的变化,可以看出:对应三个界面的等效NMO速度的最大相对误差分别位于80°、25°、165°;随着深度的增加,相对误差也整体增大,但仍在10-3数量级内。在每一界面等效NMO速度相对误差最大的方位上,计算了由本文方法及射线追踪法得到的旅行时的相对误差(图 2d),可以看出:每层的反射旅行时相对误差都很小(10-4~10-3数量级),但随炮检距与界面深度比(X/dm)的增大,相对误差以似指数形式增大;比较不同界面旅行时相对误差发现,随着界面深度增大,同一X/dm值对应的相对误差也有所增大。
|
|
表 1 三层倾斜界面的TI介质模型参数 |
|
图 2 等效NMO速度面、等效NMO速度椭圆及CMP道集旅行时精度分析 (a)第3界面的等效NMO速度面;(b)水平面上三个界面的本文方法计算NMO速度椭圆与常规排列最优拟合射线追踪计算的NMO速度(星号)对比;(c)NMO速度相对误差随方位角的变化曲线;(d)旅行时相对误差随方位角、炮检距的变化曲线 |
可用本文方法计算共炮点(CSP)道集反射旅行时。设炮点处界面的深度为ds,它与测线方位角φ、炮检距X及中心点深度dm关系为
| $ d_{\mathrm{m}}(\varphi, X)=d_{\mathrm{s}}-0.5 X \cos \theta_{r} \cos \left(\varphi-\varphi_{r}\right) $ | (20) |
先根据式(20)计算出激发点与接收点的中心点距各层底界面的深度dm(φ, X),再计算该中心点不同界面反射波的水平地表等效NMO速度和零炮检距反射时间,然后按照式(1)计算出对应层的CSP道集反射旅行时。
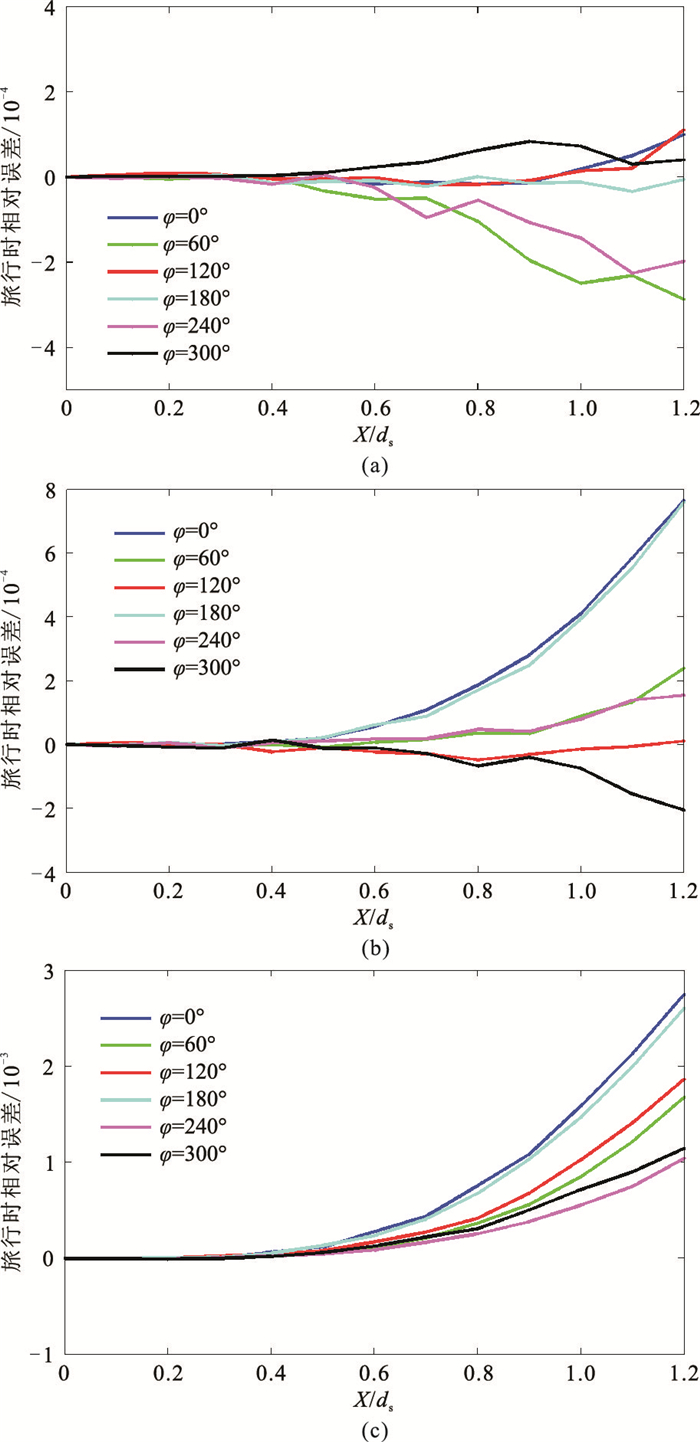
图 3为本文方法计算的三层倾斜界面TI模型CSP集反射旅行时与射线追踪计算旅行时之间相对误差随X/ds的变化曲线,可以看出:X/ds < 0.5时,三个界面的反射旅行时相对误差在所有方位上都非常小;随X/ds增大,旅行时相对误差也在增大;第1界面的相对误差总体上小于第2层,所有方位上相对误差在X/ds < 1.2时亦处于10-4数量级;第1界面较大相对误差出现在60°和240°方位,第2、第3界面较大相对误差都出现在0°和180°方位;第3界面相对误差明显大于第1、第2界面,在X/ds < 1.2时处于10-3数量级。由图 3可知,各层全方位反射旅行时相对误差处于10-4~10-3数量级,但随X/ds增大,以似指数形式增大;随着反射深度增大,相同X/ds对应的各方位旅行时相对误差也增大。
|
图 3 CSP道集反射旅行时相对误差随X/ds的变化曲线 (a)第1界面;(b)第2界面;(c)第3界面 |
表 1所示的三层倾斜界面TI模型具有一定的代表性。由图 2、图 3的计算结果可知,由单层倾斜TI介质NMO速度面解析解,运用Grechka给出的Dix型平均算法计算等效NMO速度,利用常规排列CMP时距关系实现了CMP及CSP集反射波旅行时的快速计算,且计算得到的旅行时具有较高的精度。但随着炮检距与界面深度比(X/ds或X/dm)的增大,各层界面反射波旅行时相对误差以指数形式增大,且随着反射深度增大,相同X/ds或X/dm对应的旅行时相对误差也增大。这些现象可由与各向异性及垂向非均匀相关的非双曲时距特性予以解释,同时对本文提出的快速计算反射波旅行时方法给出约束条件。
对于炮检距与反射深度比接近1(常规排列),介质具有不太复杂结构的反射波CMP时距关系,可由双曲方程式(1)较好地描述[13-16],但当这一比值大于1后,受各向异性及垂向非均匀的影响,反射波时距曲线逐渐表现出明显的非双曲特性[13],此时通过双曲方程(式(1))计算的旅行时则是不可靠的,因而旅行时相对误差必然增大。与此相类似的原因,在相同炮检距与界面深度比的情况下,随着反射深度增大,反射波时距也逐渐表现出了一定程度的非双曲性,尽管从图 2d及图 3结果认识到,这种非双曲性在炮检距与界面深度比不大于1时还是很小的。有鉴于此,作为依据CMP时距的快速模拟计算反射波旅行时方法,在最大排列长度与反射深度比接近1,即在常规排列下,本文方法计算结果合理、可靠[14, 24]。
3 结论本文以单层倾斜TI介质NMO速度面解析解计算等效NMO速度为基础,利用常规排列下CMP时距关系实现了倾斜层状TI介质模型CMP及CSP集反射波旅行时的快速计算。数值实验表明,等效NMO速度的计算结果与常规排列下最优拟合射线追踪计算旅行时得到的NMO速度相比,其相对误差为10-3数量级,而由等效NMO速度运用CMP时距计算的理论旅行时与射线追踪计算旅行时相比,其相对误差为10-4~10-3数量级。本文的快速计算反射波旅行时方法具有较高的计算精度,适用于介质结构不太复杂、最大排列长度与反射深度比接近1的常规排列。
本文的反射波旅行时的快速计算方法,因等效NMO速度椭圆(全方位上的等效NMO速度)的计算仅需通过正入射原理追踪一条零炮检距射线并由单层倾斜TI介质NMO速度面解析解运用Dix平均算法求得,因此,由反射时距关系快速计算反射波旅行时要比通常多方位角、多炮检距的射线追踪方法效率高得多,一般情况下可能快几个数量级,适应用于TI介质旅行时反演[10-13]。
本文TI介质反射波旅行时快速计算方法可推广到具有光滑弯曲界面的层状各向异性模型。
| [1] |
腾吉文, 张中杰, 王光杰, 等. 地球内部各圈层介质的地震各向异性与地球动力学[J]. 地球物理学进展, 2000, 15(1): 1-34. TEN Jiwen, ZHANG Zhongjie, WANG Guangjie, et al. Seismic anisotropy and geodynamics of layer structures inside the earth[J]. Progress in Geophy-sics, 2000, 15(1): 1-34. DOI:10.3969/j.issn.1004-2903.2000.01.001 |
| [2] |
常利军, 王春镛, 丁志峰. 鄂尔多斯块体及周缘上地幔各向异性研究[J]. 中国科学: 地球科学, 2011, 41(5): 686-699. CHANG Lijun, WANG Chunyong, DING Zhifeng. Upper mantle anisotropy in the Ordos Block and its margins[J]. Science China: Earth Sciences, 2011, 41(5): 686-699. |
| [3] |
太龄雪, 高原, 刘庚, 等. 利用中国地震科学台阵研究青藏高原东南缘地壳各向异性: 第一期观测资料的剪切波分裂特征[J]. 地球物理学报, 2015, 58(11): 4079-4091. TAI Lingxue, GAO Yuan, LIU Geng, et al. Crustal seismic anisotropy in the southeastern margin of Tibetan Plateau by China Array data: shear-wave splitting from temporary observations of the first phase[J]. Chinese Journal of Geophysics, 2015, 58(11): 4079-4091. |
| [4] |
张中杰. 地震各向异性研究进展[J]. 地球物理学进展, 2002, 17(2): 281-293. ZHANG Zhongjie. Research progress in seismic anisotropy[J]. Progress in Geophysics, 2002, 17(2): 281-293. DOI:10.3969/j.issn.1004-2903.2002.02.014 |
| [5] |
姜晓宇, 张研, 甘利灯, 等. 花岗岩潜山裂缝地震预测技术[J]. 石油地球物理勘探, 2020, 55(3): 694-704. JIANG Xiaoyu, ZHANG Yan, GAN Lideng, et al. Seismic techniques for predicting fractures in granitic buried hills[J]. Oil Geophysical Prospecting, 2020, 55(3): 694-704. |
| [6] |
王洪求, 杨午阳, 谢春辉, 等. 不同地震属性的方位各向异性分析及裂缝预测[J]. 石油地球物理勘探, 2014, 49(5): 925-931. WANG Hongqiu, YANG Wuyang, XIE Chunhui, et al. Azimuthal anisotropy analysis of different seismic attributes and fractures prediction[J]. Oil Geophysical Prospecting, 2014, 49(5): 925-931. |
| [7] |
刘依谋, 印兴耀, 张三元, 等. 宽方位地震勘探技术新进展[J]. 石油地球物理勘探, 2014, 49(3): 596-610. LIU Yimou, YIN Xingyao, ZHANG Sanyuan, et al. Recent advance in wide-azimuth seismic exploration[J]. Oil Geophysical Prospecting, 2014, 49(3): 596-610. |
| [8] |
王赟, 文鹏飞, 李宗杰, 等. 多分量油气地震勘探技术急需解决的几个问题[J]. 石油地球物理勘探, 2020, 55(6): 1395-1406. WANG Yun, WEN Pengfei, LI Zongjie, et al. Several urgent problems faced multi-component seismic in oil and gas exploration[J]. Oil Geophysical Prospecting, 2020, 55(6): 1395-1406. |
| [9] |
王赟, 杨顶辉, 殷长春, 等. 各向异性地球物理与矢量场[J]. 科学通报, 2017, 62(23): 2595-2605. WANG Yun, YANG Dinghui, YIN Changchun, et al. Anisotropic geophysics and vector field[J]. Chinese Science Bulletin, 2017, 62(23): 2595-2605. |
| [10] |
黄光南, ZHOU Bing, 邓居智, 等. 各向异性TI介质qP反射波旅行时层析成像[J]. 地球物理学报, 2015, 58(6): 2035-2045. HUANG Guangnan, ZHOU Bing, DENG Juzhi, et al. Reflection travel time chromatographic imaging of qP wave in anisotropic TI media[J]. Chinese Journal of Geophysics, 2015, 58(6): 2035-2045. |
| [11] |
卢明辉, 唐建侯, 杨慧珠, 等. 正交各向异性介质中P波旅行时分析及Thomsen参数反演[J]. 地球物理学报, 2005, 48(5): 1167-1171. LU Minghui, TANG Jianhou, YANG Huizhu, et al. P wave travel time analysis and inversion for Thomsen's parameters in orthogonal anisotropy media[J]. Chinese Journal of Geophysics, 2005, 48(5): 1167-1171. DOI:10.3321/j.issn:0001-5733.2005.05.026 |
| [12] |
王潇, 杨锴. 基于二维VTI拟声波程函方程的椭圆各向异性立体层析反演[J]. 地球物理学报, 2018, 61(12): 4954-4964. WANG Xiao, YANG Kai. Three dimensional chro-matographic inversion for elliptic anisotropy based on 2-D VTI quasisound-wave eikonal equation[J]. Chinese Journal of Geophysics, 2018, 61(12): 4954-4964. DOI:10.6038/cjg2018M0212 |
| [13] |
GRECHKA V, TSVANKIN I, COHEN J K. Gene-ralized Dix equation and analytic treatment of normal-moveout velocity for anisotropic media[J]. Geophysi-cal Prospecting, 1999, 47(2): 117-148. DOI:10.1046/j.1365-2478.1999.00120.x |
| [14] |
TSVANKIN I, THMOSEN L. Nonhyperbolic reflection move out in anisotropic media[J]. Geophysics, 1994, 59(8): 1290-1304. DOI:10.1190/1.1443686 |
| [15] |
TSVANKIN I. Reflection moveout and parameter estimation for horizontal transverse isotropy[J]. Geophysics, 1997, 62(2): 614-629. DOI:10.1190/1.1444170 |
| [16] |
TSVANKIN I. P-wave signatures and notation for transversely isotropic media: An overview[J]. Geophysics, 1996, 61(2): 467-483. DOI:10.1190/1.1443974 |
| [17] |
THOMSEN L. Weak elastic anisotropy[J]. Geophy-sics, 1986, 51(10): 1954-1966. |
| [18] |
TSVANKIN I. Normal moveout from dipping reflector in anisotropic media[J]. Geophysics, 1995, 60(1): 268-284. DOI:10.1190/1.1443755 |
| [19] |
GRECHKA V, TSVANKIN I. 3-D description of normal move out in anisotropic inhomogeneous media[J]. Geophysics, 1998, 63(3): 1079-1092. DOI:10.1190/1.1444386 |
| [20] |
姚陈. 任意空间取向TI和三维倾斜界面P波NMO速度[C]. 中国地球物理学会年会文集, 2004, 493-493.
|
| [21] |
DIX C H. Seismic velocities from surface measurements[J]. Geophysics, 1955, 20(1): 68-86. DOI:10.1190/1.1438126 |
| [22] |
GRECHKA V, TSVANKIN I. NMO-velocity surfaces and Dix-type formulas in anisotropic heterogeneous media[J]. Geophysics, 2002, 67(3): 939-951. DOI:10.1190/1.1484536 |
| [23] |
ZHANG J Z, YAO C, HAO C T, et al. Analytic solution to NMO-velocity surface in TI media with an arbitrary symmetry axis[C]. 4th Congress of Balkan Geophysical Society, Bucharest, Romania, 2005, 385-388.
|
| [24] |
张建中. 三维TI介质中P波NMO速度及VSP走时联合反演[D]. 北京: 中国地震局地质研究所, 2005. ZHANG Jianzhong. Joint Inversion of P Wave Velo-cities and VSP Traveltimes in 3-D TI Media[D]. Institute of Geology, China Earthquake Administration, Beijing, 2005. |



 安全, 内蒙古自治区呼和浩特市新城区哲里木路80号内蒙古地震局, 010080。Email:
安全, 内蒙古自治区呼和浩特市新城区哲里木路80号内蒙古地震局, 010080。Email: 