地震波场正演模拟是研究地震波在地下传播规律的重要手段,在地震成像、反演中起至关重要的作用[1]。有限元法[2]、有限差分法[3-5]、伪谱法[6]等多种数值模拟方法,在地震波场正演模拟中得到了成功应用。其中有限差分法因计算效率快、精度高、实施过程便捷而被广泛地应用于波动方程正演模拟。
然而,常规有限差分法对复杂地形的处理存在诸多问题,其中最主要的是界面的网格化离散。通常对模拟区域做网格离散时网格步长都是固定的,这种离散方式会带来两个问题:一是固定网格步长可能导致真实速度界面与模型界面不重合,造成一次反射波旅行时不准确;二是当地下界面较复杂或地表起伏(起伏界面在海洋环境更常见)时,使用规则网格对模型做离散时会出现阶梯状边界,进而产生虚假绕射波[7-9],破坏地震波场数值模拟结果。为了消除虚假反射,许多学者对传统有限差分法(FD)。进行了大量研究,包括对起伏界面加密的变网格算法[10]、基于坐标变换的垂向网格映射法[11]、贴体网格法[12-13]等,这些方法在一定程度上有效压制了阶梯状绕射,但各自也存在问题。例如,变网格算法本质上是采用更小网格步长离散起伏界面,因而不能从根本上消除阶梯状绕射;基于坐标变换的差分方法需对波动方程做相应变换,实施过程较为复杂。
针对以上问题,本文将目光转向近年兴起的无网格算法。无网格算法是一种基于散点近似、用于求解偏微分方程问题的数值计算方法,剖分点随速度模型灵活变化,能有效避免虚假反射[14-15]。不同于基于网格的传统数值计算方法,无网格法的计算框架是基于散点,即无网格法使用的基本单元是离散的场节点,场变量的近似函数是通过预定义的散点信息进行描述的[16]。
近年来,无网格法在地球物理正演模拟中应用广泛,从电磁到地震勘探领域均能见到无网格正演模拟相关文献[15, 17-20]。苏洲等[17]使用移动最小二乘近似法进行二维大地电磁正演模拟。李俊杰等[18]详细讨论了无网格点插值法在大地电磁中的应用,并将其与无单元Galerkin法、有限元法正演结果进行对比分析。何兵红[15]研究了基于无网格的波动方程地震正反演方法,并提出了速度自适应无网格场节点建立方法,以此提高计算效率。刘鑫[19]讨论了无网格有限差分法边界条件,并将其用于频率域正演模拟。Duan等[20]将径向基函数无网格法用于声波方程正演模拟,并对频散、稳定性进行了详细地讨论。
广义有限差分法(Generalized finite difference method,GFDM)是众多无网格法的一种。初期的广义有限差分法是20世纪70年代由Jesen[21]、Perrone[22]和Liszka[23]等在有限差分计算框架下发展而来的,此类方法是基于网格应用距离函数抓取必要的节点实施运算,是早期无网格法的一种典型形式。本文应用的广义有限差分法是由Benito等[24]在经典广义有限差分法基础上发展而来的,使用加权最小二乘法求取残差函数极小值,引入权重函数以表征不同距离的节点对中心节点的影响程度。
广义有限差分法基于泰勒函数展开和加权最小二乘拟合,将微分方程中未知参数的偏导数表示为相邻节点函数值的线性组合,克服了传统方法对网格的依赖性。该方法能根据不同地质模型构建适用的场节点分布形式,生成的节点与起伏地表或边界贴合,适用于处理不规则边界或起伏界面问题。目前,该方法已被广泛应用于求解多种数学和工程问题。Ureña等[25]将广义有限差分法用于弹性波方程正演模拟,并讨论了规则及不规则节点下的频散及稳定性条件。Benito等[26]进一步研究了地震波在各向异性介质中的传播。Wei等[27]将其用于声介质研究。Gu等[28]使用广义有限差分求解工程反问题。陈剑等[29]将广义有限差分法应用于静态电磁场模拟。大量研究结果表明广义有限差分法在处理复杂问题上具有独特优势及广阔应用前景[30-31]。
本文将广义有限差分法应用于标量波方程正演模拟中,基于速度模型采用合适的布点方式,从而在常规有限差分处理起伏界面时,消除因阶梯状网格剖分带来的虚假反射及反射波旅行时不准确等问题;对不同模型进行试算,验证了广义有限差分法的有效性和稳定性。
1 基本原理二维标量波方程表达式为
| $ \frac{\partial^{2} u}{\partial t^{2}}=v^{2}\left(\frac{\partial^{2} u}{\partial x^{2}}+\frac{\partial^{2} u}{\partial z^{2}}\right) $ | (1) |
时间上采用中心差分
| $ \frac{\partial^{2} u_{0}^{n}}{\partial t^{2}}=\frac{1}{(\Delta t)^{2}}\left(u_{0}^{n+1}-2 u_{0}^{n}+u_{0}^{n-1}\right) $ | (2) |
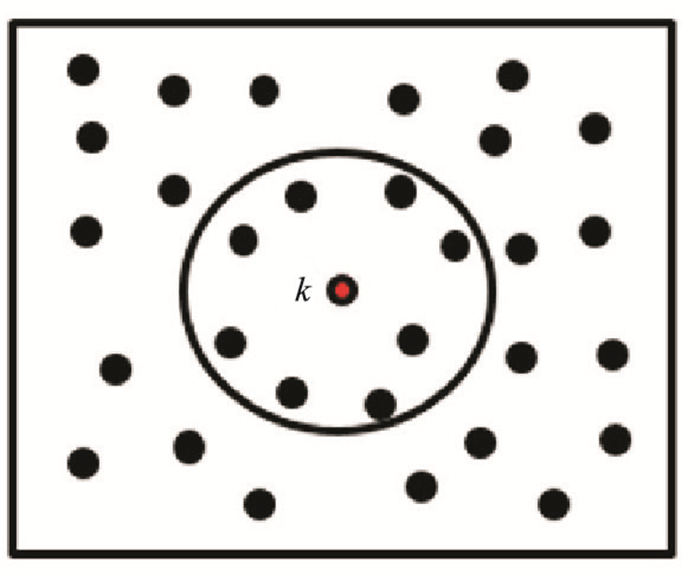
本文使用广义有限差分法求取空间偏导数。该方法基于泰勒函数展开及加权最小二乘法,首先对求解区域进行节点离散(图 1)。对于求解域内的某一点k(记作u0),选择其邻近的S个点构成子区域(图 1圆形区域),将k点作为中心点,子区域内的任一点i在中心点k处的泰勒展开式表示为
| $ \begin{aligned} u_{i}=& u_{0}+h_{i} \frac{\partial u_{0}}{\partial x}+l_{i} \frac{\partial u_{0}}{\partial z}+\frac{h_{i}^{2}}{2} \frac{\partial^{2} u_{0}}{\partial x^{2}}+\\ & \frac{l_{i}{ }^{2}}{2} \frac{\partial^{2} u_{0}}{\partial z^{2}}+h_{i} l_{i} \frac{\partial^{2} u_{0}}{\partial x \partial z}+o\left(x^{3}, z^{3}\right) \\ & i=1,2, \cdots, S \end{aligned} $ | (3) |
|
图 1 广义有限差分法示意图 |
式中hi=xi-x0,li=zi-z0,分别表示子区域内节点i到中心节点的x方向和z方向距离。
此处将泰勒展开式保留到二阶项,即二阶精度;若要提高差分精度,可将泰勒展开式保留到更高阶。
定义残差函数
| $ \begin{aligned} B_{u}=& \sum\limits_{i=1}^{S}\left(u_{0}-u_{i}+h_{i} \frac{\partial u_{0}}{\partial x}+l_{i} \frac{\partial u_{0}}{\partial z}+\frac{h_{i}^{2}}{2} \frac{\partial^{2} u_{0}}{\partial x^{2}}+\right.\\ &\left.\frac{l_{i}^{2}}{2} \frac{\partial^{2} u_{0}}{\partial z^{2}}+h_{i} l_{i} \frac{\partial^{2} u_{0}}{\partial x \partial z}\right)^{2} \omega_{i}^{2}\left(h_{i}, l_{i}\right) \end{aligned} $ | (4) |
式中ωi为第i点的权重函数[24]。
设Du为中心点处可能出现的所有偏导数向量
| $ \boldsymbol{D}_{u}=\left(\frac{\partial u_{0}}{\partial x}, \frac{\partial u_{0}}{\partial z}, \frac{\partial^{2} u_{0}}{\partial x^{2}}, \frac{\partial^{2} u_{0}}{\partial z^{2}}, \frac{\partial^{2} u_{0}}{\partial x \partial z}\right)^{\mathrm{T}} $ | (5) |
根据最小二乘原理,残差函数Bu0对Du求偏导
数,并令偏导数值为零
| $ \frac{\partial B_{u_{0}}}{\partial \boldsymbol{D}_{u}}=0 $ | (6) |
可得如下矩阵方程
| $ \boldsymbol{A}_{u} \cdot \boldsymbol{D}_{u}=\boldsymbol{b}_{u} $ | (7) |
其中
| $ \boldsymbol{A}_{u}=\left(\begin{array}{ccccc} \sum\limits_{i=1}^{S} h_{i}^{2} \omega_{i}^{2} & \sum\limits_{i=1}^{S} h_{i} l_{i} \omega_{i}^{2} & \sum\limits_{i=1}^{S} \frac{h_{i}^{3}}{2} \omega_{i}^{2} & \sum\limits_{i=1}^{S} \frac{h_{i} l_{i}^{2}}{2} \omega_{i}^{2} & \sum\limits_{i=1}^{S} h_{i}^{2} l_{i} \omega_{i}^{2} \\ \sum\limits_{i=1}^{S} h_{i} l_{i} \omega_{i}^{2} & \sum\limits_{i=1}^{S} l_{i}^{2} \omega_{i}^{2} & \sum\limits_{i=1}^{S} \frac{h_{i}^{2} l_{i}}{2} \omega_{i}^{2} & \sum\limits_{i=1}^{S} \frac{l_{i}^{3}}{2} \omega_{i}^{2} & \sum\limits_{i=1}^{S} h_{i} l_{i}^{2} \omega_{i}^{2} \\ \sum\limits_{i=1}^{S} \frac{h_{i}^{3}}{2} \omega_{i}^{2} & \sum\limits_{i=1}^{S} \frac{h_{i}^{2} l_{i}}{2} \omega_{i}^{2} & \sum\limits_{i=1}^{S} \frac{h_{i}^{4}}{4} \omega_{i}^{2} & \sum\limits_{i=1}^{S} \frac{h_{i}^{2} l_{i}^{2}}{4} \omega_{i}^{2} & \sum\limits_{i=1}^{S} \frac{h_{i}^{3} l_{i}}{2} \omega_{i}^{2} \\ \sum\limits_{i=1}^{S} \frac{h_{i} l_{i}^{2}}{2} \omega_{i}^{2} & \sum\limits_{i=1}^{S} \frac{l_{i}^{3}}{2} \omega_{i}^{2} & \sum\limits_{i=1}^{S} \frac{h_{i}^{2} l_{i}^{2}}{4} \omega_{i}^{2} & \sum\limits_{i=1}^{S} \frac{l_{i}^{4}}{4} \omega_{i}^{2} & \sum\limits_{i=1}^{S} \frac{h_{i} l_{i}^{3}}{2} \omega_{i}^{2} \\ \sum\limits_{i=1}^{S} h_{i}^{2} l_{i} \omega_{i}^{2} & \sum\limits_{i=1}^{S} h_{i} l_{i}^{2} \omega_{i}^{2} & \sum\limits_{i=1}^{S} \frac{h_{i}^{3} l_{i}}{2} \omega_{i}^{2} & \sum\limits_{i=1}^{S} \frac{h_{i} l_{i}^{3}}{2} \omega_{i}^{2} & \sum\limits_{i=1}^{S} h_{i}^{2} l_{i}^{2} \omega_{i}^{2} \end{array}\right)\ \ \ \ \ \ \boldsymbol{b}_{u}=\left(\begin{array}{c} \sum\limits_{i=1}^{S} h_{i}\left(u_{i}-u_{0}\right) \omega_{i}^{2} \\ \sum\limits_{i=1}^{S} l_{i}\left(u_{i}-u_{0}\right) \omega_{i}^{2} \\ \sum\limits_{i=1}^{S} \frac{h_{i}^{2}}{2}\left(u_{i}-u_{0}\right) \omega_{i}^{2} \\ \sum\limits_{i=1}^{S} \frac{l_{i}^{2}}{2}\left(u_{i}-u_{0}\right) \omega_{i}^{2} \\ \sum\limits_{i=1}^{S} h_{i} l_{i}\left(u_{i}-u_{0}\right) \omega_{i}^{2} \end{array}\right) $ |
至此可求得空间各处偏导数的值
| $ \left\{\begin{array}{l} \boldsymbol{D}_{u}=\boldsymbol{A}_{u}^{-1} \boldsymbol{b}_{u}=-\boldsymbol{M}_{0} u_{0}+\sum\limits_{i=1}^{S} \boldsymbol{M}_{i} u_{i} \\ \boldsymbol{M}_{0}=\sum\limits_{i=1}^{S} \boldsymbol{M}_{i} \end{array}\right. $ | (8) |
Mi表示相邻节点的广义有限差分系数。
将式(8)代入标量波方程中,可得标量波方程的广义有限差分格式
| $ \begin{aligned} u_{0}^{n+1}=& 2 u_{0}^{n}-u_{0}^{n-1}+(v \cdot \Delta t)^{2}\left(-m_{0} u_{0}^{n}+\right.\\ &\left.\sum\limits_{i=1}^{S} m_{i} u_{i}^{n}-\eta_{0} u_{0}^{n}+\sum\limits_{i=1}^{S} \eta_{i} u_{i}^{n}\right) \end{aligned} $ | (9) |
式中mi、ηi为广义有限差分系数,与节点间距、差分阶数、权重函数等有关。
使用广义有限差分法求解标量波方程的过程中,只需使用离散节点的坐标信息,对空间节点的连接信息无要求,使得该方法灵活多变,对复杂模型的适应性更强。
2 频散分析 2.1 理论分析使用广义有限差分做地震波场正演模拟,由于采用离散方程逼近连续方程,不可避免会出现数值频散现象,严重干扰地震波场数值模拟结果[32-34]。对标量波方程广义有限差分频散关系做理论研究,需就节点间距、差分阶数、权重函数等因素对频散进行计算,得出这些因素与频散的关系。
空间导数广义有限差分为
| $ \left\{\begin{array}{l} \frac{\partial^{2} u_{0}^{n}}{\partial x^{2}}=-m_{0} u_{0}^{n}+\sum\limits_{i=1}^{S} m_{i} u_{i}^{n} \\ \frac{\partial^{2} u_{0}^{n}}{\partial z^{2}}=-\eta_{0} u_{0}^{n}+\sum\limits_{i=1}^{S} \eta_{i} u_{i}^{n} \end{array}\right. $ | (10) |
将式(10)代入标量波方程中,可得离散介质标量波方程
| $ \frac{1}{v^{2}} \frac{\partial^{2} u_{0}}{\partial t^{2}}=-m_{0} u_{0}^{n}+\sum\limits_{i=1}^{S} m_{i} u_{i}^{n}-\eta_{0} u_{0}^{n}+\sum\limits_{i=1}^{S} \eta_{i} u_{i}^{n} $ | (11) |
假设有一频率为f的平面简谐波,其传播方向与z轴夹角为α,波数为k,则其波函数可写成
| $ \begin{aligned} u(x, z, t)=& \exp [\mathrm{j}(2 {\rm{ \mathsf{ π} }} f t-2 {\rm{ \mathsf{ π} }} k x \sin \alpha-\\ &2 {\rm{ \mathsf{ π} }} k z \cos \alpha)] \end{aligned} $ | (12) |
将波函数代入离散介质标量波方程(式(11)),可得
| $ \begin{aligned} -(2 {\rm{ \mathsf{ π} }} f)^{2} &=v^{2} \sum\limits_{i=1}^{s}\left(m_{i}+\eta_{i}\right) \times \\ & {\left[\cos \left(2 {\rm{ \mathsf{ π} }} k \Delta x_{i} \sin \alpha+2 {\rm{ \mathsf{ π} }} k \Delta z_{i} \cos \alpha\right)-1\right.} \\ &\left.- \operatorname{jsin}\left(2 {\rm{ \mathsf{ π} }} k \Delta x_{i} \sin \alpha+2 {\rm{ \mathsf{ π} }} k \Delta z_{i} \cos \alpha\right)\right] \end{aligned} $ | (13) |
将k=f/v(f)代入式(13),可得
| $ \begin{aligned} \frac{v^{2}(f)}{v^{2}} &=\frac{1}{(2 {\rm{ \mathsf{ π} }} k)^{2}} \sum\limits_{i=1}^{s}\left(m_{i}+\eta_{i}\right) \times \\ & {\left[1-\cos \left(2 {\rm{ \mathsf{ π} }} k \Delta x_{i} \sin \alpha+2 {\rm{ \mathsf{ π} }} k \Delta z_{i} \cos \alpha\right)+\right.} \\ &\left.{\rm{j}} \sin \left(2 {\rm{ \mathsf{ π} }} k \Delta x_{i} \sin \alpha+2 {\rm{ \mathsf{ π} }} k \Delta z_{i} \cos \alpha\right)\right] \end{aligned} $ | (14) |
式中:v(f)为各频率对应的相速度;Δxi、Δzi分别表示周围节点到中心节点的x方向和z方向距离。
无网格差分模板中节点不一定对称,因此频散关系式(14)中的虚数部分不为零。频散关系式(14)中的实部和虚部分别记作
| $ \begin{aligned} E_{\mathrm{R}}=& \frac{1}{(2 {\rm{ \mathsf{ π} }} k)^{2}} \sum\limits_{i=1}^{S}\left(m_{i}+\eta_{i}\right) \times \\ & {\left[1-\cos \left(2 {\rm{ \mathsf{ π} }} k \Delta x_{i} \sin \alpha+2 {\rm{ \mathsf{ π} }} k \Delta z_{i} \cos \alpha\right)\right] } \end{aligned} $ | (15) |
| $ \begin{aligned} E_{\mathrm{I}}=& \frac{1}{(2 {\rm{ \mathsf{ π} }} k)^{2}} \sum\limits_{i=1}^{S}\left(m_{i}+\eta_{i}\right) \times \\ & \sin \left(2 {\rm{ \mathsf{ π} }} k \Delta x_{i} \sin \alpha+2 {\rm{ \mathsf{ π} }} k \Delta z_{i} \cos \alpha\right) \end{aligned} $ | (16) |
取频散关系的模
| $ E_{\mathrm{m}}=\sqrt{E_{\mathrm{R}}^{2}+E_{\mathrm{I}}^{2}} $ | (17) |
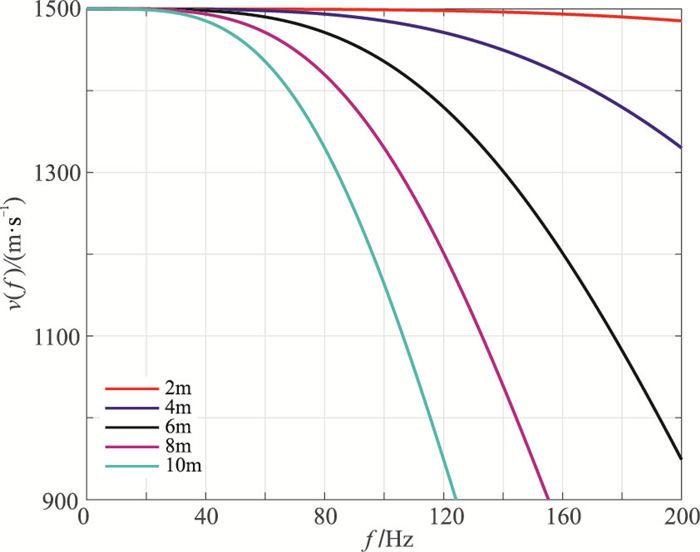
设地层速度为1500m/s,使用四阶精度计算空间导数,分别采用2、4、6、8、10m的节点间隔,计算得到图 2所示的地震波传播速度与频率的关系。从该图可见,随着节点间距的增大,频散程度逐渐增强,尤其是高频成分,这与规则网格有限差分法所得结果相一致。
|
图 2 不同节点间距的频散关系曲线 |
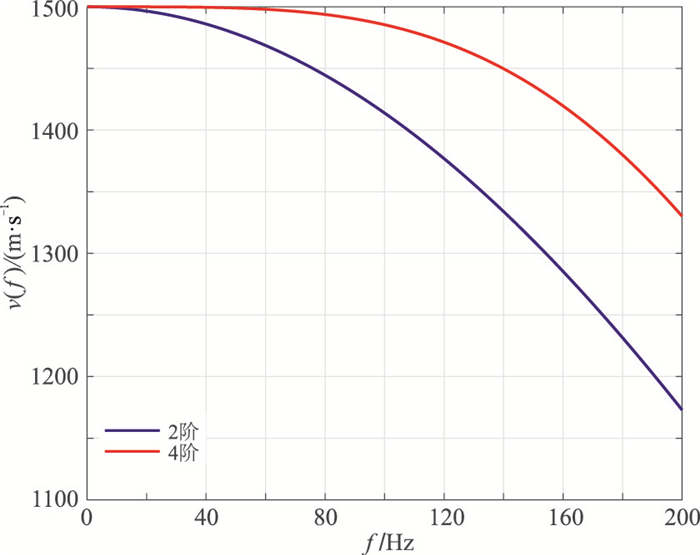
设地层速度仍为1500m/s,节点间距为4m,分别使用二阶和四阶精度计算空间导数,得到地震波传播速度与频率的关系(图 3)。可见提高差分阶数可显著降低频散程度。同为4m节点间距情况下,四阶差分精度可保证60Hz以下频率分量基本无频散,而二阶精度只能确保极低频率成分无明显频散。
|
图 3 两种差分阶数的频散关系曲线 |
前已述及,广义有限差分法基于泰勒函数展开和加权最小二乘法,计算域内任一点的空间偏导数值可表示为相邻一组节点函数值的加权和,且距离中心节点越近,权值越大。如式(14)中的系数m和η的取值受权函数影响。
设置相同的地层速度和节点间距,以四阶精度计算空间导数,使用下列不同的权函数
| $ \begin{cases}w_{\mathrm{I}}=1 / d_{i}^{3} & \\ w_{\mathrm{II}}=1 / d_{i}^{2} & \\ w_{\mathrm{III}}=\exp \left[-1 /\left(D_{x} \times D_{z}\right) d_{i}^{2}\right] & \\ w_{\mathrm{IV}}= \begin{cases}1-6\left(\frac{d_{i}}{d_{\mathrm{m}}}\right)^{2}+8\left(\frac{d_{i}}{d_{\mathrm{m}}}\right)^{3}-3\left(\frac{d_{i}}{d_{\mathrm{m}}}\right)^{4} & d_{i} \leqslant d_{\mathrm{m}} \\ 0 & d_{i}>d_{\mathrm{m}}\end{cases} \end{cases} $ | (18) |
求解系数矩阵,得到地震波传播速度与频率的关系(图 4)。式中:di为子区域内其他节点到中心节点的距离;dm为di的最大值:Dx、Dz分别为横向和纵向单位节点间距。可见使用不同的权重函数得到的频散曲线在中高频部分的频散程度是不同的,通常指数函数得到的结果最佳。

|
图 4 不同权函数的频散关系曲线 |
广义有限差分法是一种无网格方法,计算过程中需用到节点的坐标信息,因此整个计算区域节点生成的质量对模拟结果的精度有重要影响。尽管作为一种无网格类方法,广义有限差分法具有节点布置的任意性,可在求解区域内随机撒点进行计算,但大量的数值计算结果表明,在节点个数相同的情况下,整个计算区域内的节点布置越均匀,所获得的模拟结果精度越高[35]。为了使整体的数值计算结果达到最佳,应尽可能地使数据点均匀地充满计算空间,在均匀介质模型下,节点可完全规则分布。需说明的是,虽然数据点呈网格状规则分布,但彼此之间并无关联,这也正是广义有限差分法同有限差分法的区别。
当模拟区域较复杂时,如崎岖海底界面、起伏地表等,规则分布的节点无法准确描述界面位置,会造成一次反射波旅行时不准确,且产生阶梯状绕射。因此,需根据实际地形情况调整节点位置,使生成的节点贴合起伏地形形态。但从整体上看节点是类似均匀分布的,从而避免了由于节点的不规则带来的计算误差,获得最佳正演模拟效果。
基于以上考虑,本文采用一种沿层位布置节点的方案[11],即根据界面形态确定节点位置,使生成的节点与界面贴合(图 5)。该方法生成的节点可很好地描绘界面,同时避免了“阶梯状网格”的出现,有效压制了阶梯状绕射。
|
图 5 节点离散示意图 |
该方法总共分为三个步骤:
(1) 通过速度模型拾取界面位置,并获取界面高程(若高程直接由函数给出,则直接进行步骤(3);
(2) 对高程做平滑处理;
(3) 根据每一层界面的位置进行布点,求取节点坐标的公式为
| $ \left\{\begin{array}{l} X(x, z)=x \Delta x \\ Z(x, z)=\frac{G(x)-P(x)}{g(1)-p(1)}[z-h(1)]+H(x) \end{array}\right. $ | (19) |
式中:G(x)、P(x)分别表示两个界面的高程函数;g(1)、p(1)表示计算域两个界面的位置,决定了两个界面之间的节点数量。
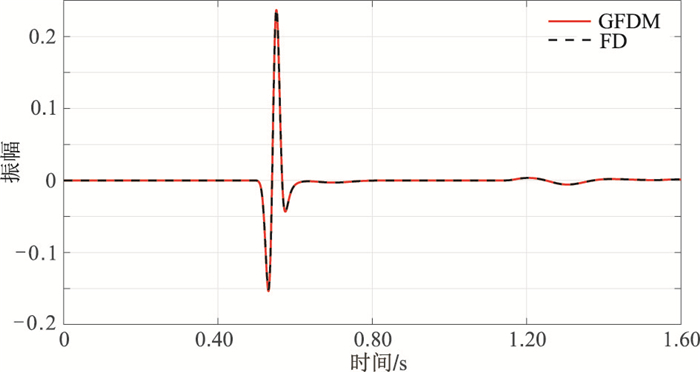
3.2 模型验证 3.2.1 均匀介质模型为了验证广义有限差分的正确性,首先选取一个2000m×2000m的二维均匀介质模型做正演模拟,节点间距为5m,时间步长为0.8ms,地震波速度为2000m/s,采用主频为20Hz的雷克子波,震源位于模型中心。分别采用广义有限差分法(图 6a)和常规有限差分法(图 6b)做正演模拟,得到400ms时刻的地震波场,可见两种方法都能得到较好结果,对比抽取的中心道地震记录(图 7),二者基本相符。

|
图 6 广义有限差分法(a)和规则网格有限差分法(b)的400ms时刻波场快照 |
|
图 7 均匀介质模型的两种算法模拟的中心道记录 |
常规有限差分正演模拟采用的网格步长是固定的,会造成一次反射波旅行时不准确,下面通过一个简单的两层模型验证广义有限差分法对于旅行时模拟的准确性。模型上、下层速度分别为2500、4000m/s,模型尺寸为1000m×1000m,节点间距(网格步长)为5m,时间步长为0.4ms,采用主频为30Hz的雷克子波,震源位于(500m,5m)处。
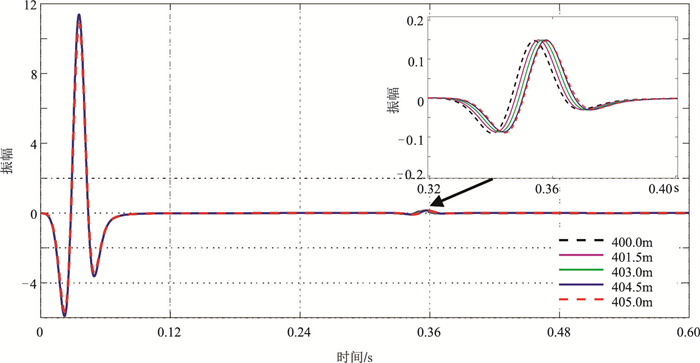
对该模型离散时,常规有限差分采用5m固定网格步长,故只有当界面处于5的整数倍位置(如界面位于400m)时,网格点才能准确地描述界面。但当界面处于400.0~405.0m时,采用常规有限差分所得剖分结果都是相同的,正演得到的反射波旅行时也不会发生任何变化。而采用广义有限差分法离散模型时,可对节点位置进行调整,节点坐标随真实界面位置而变化,因此可得到更准确的反射波旅行时信息。分别选取界面位于401.5、403.0、404.5m三处做广义有限差分正演,以说明真实界面与模型界面不一致时,采用常规有限差分与广义有限差分正演模拟得到的反射波旅行时信息的差异。图 8中黑色和红色虚线分别表示界面深度为400.0、405.0m时使用常规有限差分法正演模拟得到的地震记录,品红色、绿色和蓝色实线对应表示界面深度为401.5、403.0、404.5m时使用广义有限差分法正演模拟得到的地震记录。对比两种算法情况下反射波信息可知,在400.0~405.0m深度区间内,广义有限差分法与常规有限差分法的振幅值基本不随深度变化。但从旅行时信息可见,当界面深度为401.5、403.0、404.5m时,由于界面不在整网格点上,常规有限差分法只能得到400.0m和405.0m的整网格记录,而使用广义有限差分法的三条记录时间偏移量随深度增加而增加,与实际情况相符。
|
图 8 不同界面深度地震记录 |
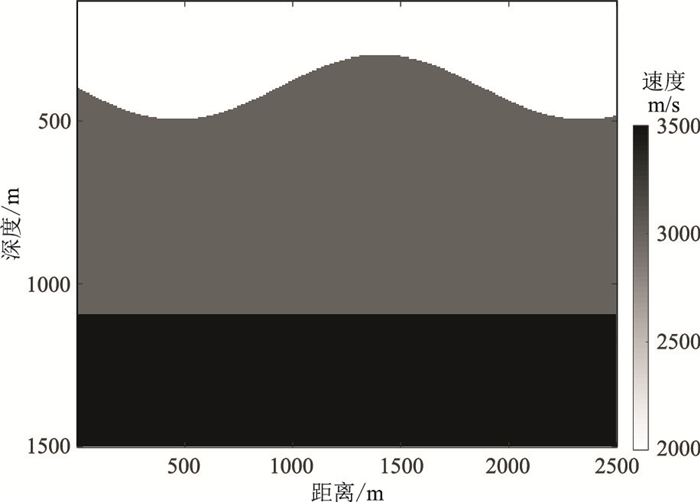
常规有限差分法处理起伏界面时存在阶梯状散射问题,这些散射波严重影响了正演模拟的精度,给后续反演带来很大误差。使用广义有限差分法做正演模拟可通过建立合适的场节点离散形式压制散射波。图 9所示的含起伏界面的三层速度模型中,上、中、下层的速度分别为2000、3000、3500m/s,模型尺寸为2500m×1500m,节点间距为5m,时间采样间隔为0.4ms,震源采用主频为30Hz的雷克子波,位于(1250m,5m)处。
|
图 9 起伏界面速度模型 |
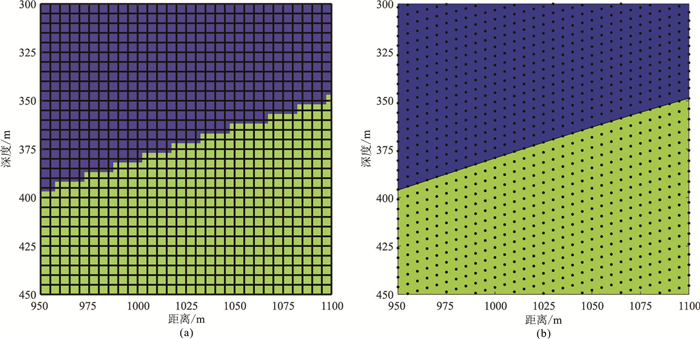
规则网格有限差分法的网格与广义有限差分法的局部节点划分如图 10所示。
|
图 10 规则网格有限差分法(a)和广义有限差分法(b)的局部网格(节点)分布 |
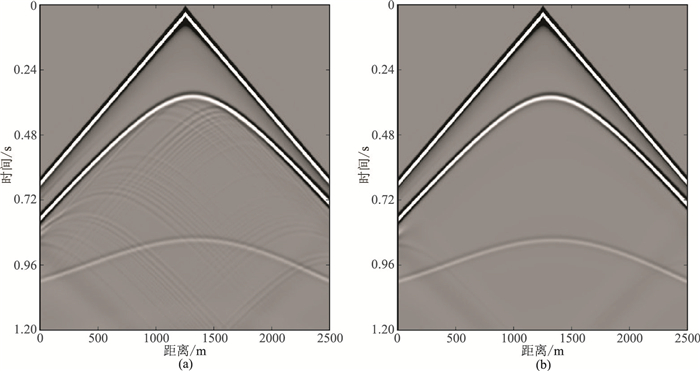
分别采用常规有限差分法和广义有限差分法进行正演模拟,其中广义有限差分法采用3.1节所述布点方式。从所得相应地震记录可见,常规有限差分正演记录(图 11a)中一次反射波后面存在大量散射波,而广义有限差分正演记录(图 11b)上则基本看不到散射波。
|
图 11 规则网格有限差分法(a)和广义有限差分法(b)模拟的地震记录 |
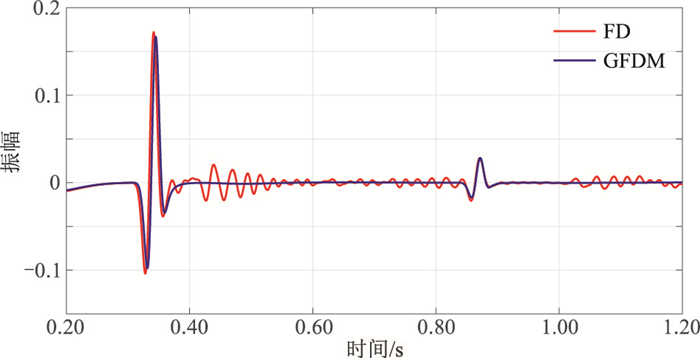
抽取两种方法模拟记录的中心道(图 12)进行对比,可见常规有限差分记录(红线)的一次反射波后跟随着强烈震荡,而广义有限差分模拟记录(蓝线)则没有震荡现象。该处理结果表明广义有限差分法正演模拟对阶梯状绕射具有显著压制作用,适用于含起伏界面地层的正演模拟。
|
图 12 起伏界面模型两种算法模拟的中心道记录对比 |
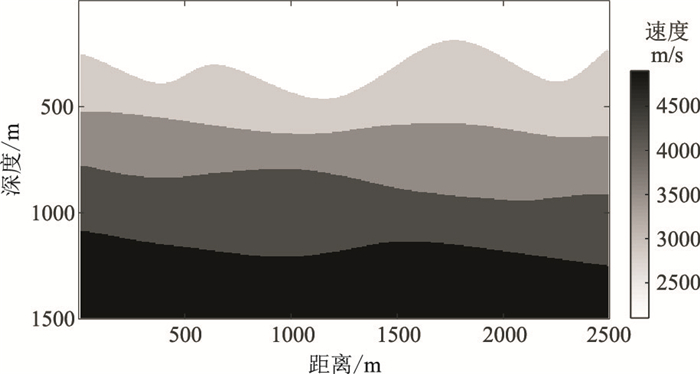
最后,设计剧烈起伏模型以验证本文算法对复杂模型的适应性。图 13所示模型共有五层,尺寸为2500m×1500m,平均节点间距约为5m,时间采样间隔为0.4ms,震源采用主频为20Hz的雷克子波,位于(1250m,5m)处。应用本文算法正演模拟,得到400ms(图 14a)和600ms(图 14b)时刻的波场快照。从应用本文算法正演模拟得到的地震记录(图 15),可清晰看到来自地下不同界面的反射波,且在起伏界面处未产生阶梯状反射,表明本文算法对复杂模型具有一定适应性。
|
图 13 具有剧烈起伏界面的复杂模型 |

|
图 14 400ms(a)和600ms(b)时刻的波场快照 |
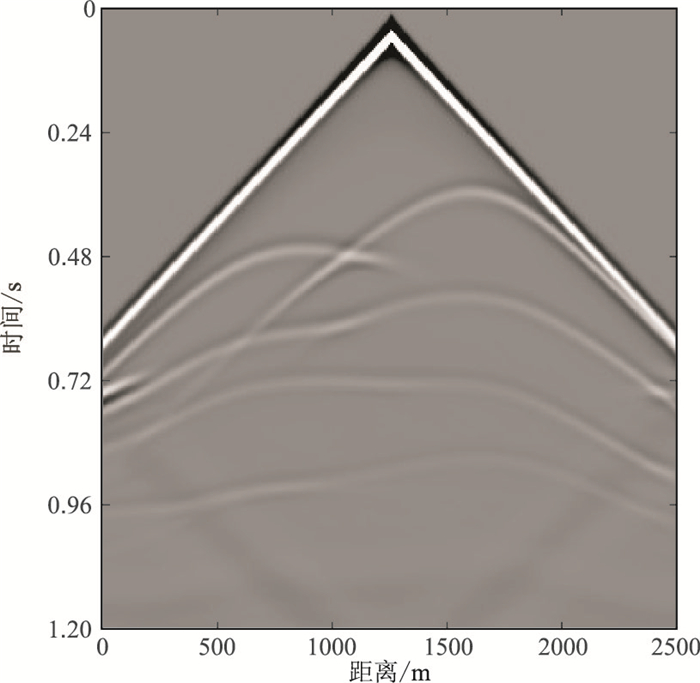
|
图 15 本文复杂模型的正演模拟地震记录 |
本文将广义有限差分法应用于标量波方程正演模拟,通过理论分析与数值计算,取得了如下认识与结论:
(1) 广义有限差分法是一种无网格数值计算方法,它基于散点近似,克服了传统方法对网格的依赖,可在模拟区域灵活布设节点,适用于高维复杂模型的正演模拟。
(2) 使用广义有限差分法进行正演模拟时,通过建立合适的场节点分布形式,使模型节点与真实速度界面相一致,可准确地描绘速度界面,避免了常规有限差分正演中网格与速度界面无法对齐的情形,从而消除了阶梯状绕射,且能得到更准确的旅行时信息。
(3) 广义有限差分正演模拟中的一个主要问题是如何进行节点离散,本文使用的节点离散方案适用于含起伏界面的层状模型,有效地压制了阶梯状反射,能获得很好的正演效果。对于横向速度变化剧烈,或含有断层之类的模型,其模拟效果较差,因此还需探寻更稳定、更适用的节点离散方案。
| [1] |
裴正林, 牟永光. 地震波传播数值模拟[J]. 地球物理学进展, 2004, 19(4): 933-941. PEI Zhenglin, MU Yongguang. Numerical simulation of seismic wave propagation[J]. Progress in Geophy-sics, 2004, 19(4): 933-941. DOI:10.3969/j.issn.1004-2903.2004.04.038 |
| [2] |
张剑锋. 一种高精度有限元弹性波场正演方法[J]. 石油地球物理勘探, 1994, 29(1): 29-36. ZHANG Jianfeng. An accurate method for finite-element elastic wave field modeling[J]. Oil Geophy-sical Prospecting, 1994, 29(1): 29-36. |
| [3] |
ALTERMAN Z S, KARAL F C J. Propagation of elastic waves in layered media by finite difference methods[J]. Bulletin of the Seismological Society of America, 1968, 58(1): 367-398. |
| [4] |
刘洋, 李承楚, 牟永光. 任意偶数阶精度有限差分法数值模拟[J]. 石油地球物理勘探, 1998, 33(1): 1-10. LIU Yang, LI Chengchu, MOU Yongguang. Finite-difference numerical modeling of any even-order accuracy[J]. Oil Geophysical Prospecting, 1998, 33(1): 1-10. DOI:10.3321/j.issn:1000-7210.1998.01.001 |
| [5] |
李青阳, 吴国忱, 段沛然. 准规则网格高阶有限差分法非均质弹性波波场模拟[J]. 石油地球物理勘探, 2019, 54(3): 539-550. LI Qingyang, WU Guochen, DUAN Peiran. Elastic wavefield forward modeling in heterogeneous media based on the quasi-regular grid high-order finite difference[J]. Oil Geophysical Prospecting, 2019, 54(3): 539-550. |
| [6] |
谭文卓, 吴帮玉, 李博, 等. 梯形网格伪谱法地震波场模拟[J]. 石油地球物理勘探, 2020, 55(6): 1282-1291. TAN Wenzhuo, WU Bangyu, LI Bo, et al. Seismic wave simulation using a trapezoid grid pseudo-spectral method[J]. Oil Geophysical Prospecting, 2020, 55(6): 1282-1291. |
| [7] |
李振春, 肖建恩, 曲英铭, 等. 时间域起伏自由地表正演模拟综述[J]. 地球物理学进展, 2016, 31(1): 300-309. LI Zhenchun, XIAO Jianen, QU Yingming, et al. The review of irregular free-surface forward modeling in time domain[J]. Progress in Geophysics, 2016, 31(1): 300-309. |
| [8] |
YAO G, DA SILVA N V, DEBENS H A, et al. Accurate seabed modeling using finite difference methods[J]. Computational Geosciences, 2018, 22(2): 469-484. DOI:10.1007/s10596-017-9705-5 |
| [9] |
LI Q, WU G, WU J, et al. Finite difference seismic forward modeling method for fluid-solid coupled media with irregular seabed interface[J]. Journal of Geophysics and Engineer, 2019, 16(1): 198-214. DOI:10.1093/jge/gxy017 |
| [10] |
曲英铭, 李振春, 黄建平, 等. 基于多尺度双变网格的时间域全波形反演[J]. 石油物探, 2016, 55(2): 241-250. QU Yingming, LI Zhenchun, HUANG Jianping, et al. Full waveform inversion based on multi-scale dual-variable grid in time domain[J]. Geophysical Prospecting for Petroleum, 2016, 55(2): 241-250. DOI:10.3969/j.issn.1000-1441.2016.02.010 |
| [11] |
曲英铭, 黄建平, 李振春, 等. 分层映射法起伏自由地表弹性波正演模拟与波场分离[J]. 石油地球物理勘探, 2016, 51(2): 261-271. QU Yingming, HUANG Jianping, LI Zhenchun, et al. Elastic wave forward modeling and wave-filed separation of irregular free-surface based on the layered mapping method[J]. Oil Geophysical Prospecting, 2016, 51(2): 261-271. |
| [12] |
蒋丽丽. 面向地质条件的贴体网格生成技术[D]. 吉林长春: 吉林大学, 2010.
|
| [13] |
李庆洋, 李振春, 黄建平, 等. 基于贴体全交错网格的起伏地表正演模拟影响因素[J]. 吉林大学学报(地球科学版), 2016, 46(3): 920-929. LI Qingyang, LI Zhenchun, HUANG Jianping, et al. Factors analysis of seismic modeling with topography based on a fully staggered body-fitted grids[J]. Journal of Jilin University(Earth Science Edition), 2016, 46(3): 920-929. |
| [14] |
刘立彬, 段沛然, 张云银, 等. 基于无网格的地震波场数值模拟方法综述[J]. 地球物理学进展, 2020, 35(5): 1815-1825. LIU Libin, DUAN Peiran, ZHANG Yunyin, et al. An overview of mesh-free method of seismic forward numerical simulation[J]. Progress in Geophysics, 2020, 35(5): 1815-1825. |
| [15] |
何兵红. 基于无网格的波动方程地震正反演方法研究[D]. 山东青岛: 中国石油大学(华东), 2016.
|
| [16] |
杨建军. 无网格法: 理论与算法[M]. 北京: 科学出版社, 2018: 12.
|
| [17] |
苏洲, 胡文宝. 二维大地电磁正演中的无网格算法[J]. 物探与化探, 2012, 36(6): 1024-1028. SU Zhou, HU Wenbao. Meshless algorithm in two-dimensional electromagnetic forward calculation[J]. Geophysical & Geochemical Exploration, 2012, 36(6): 1024-1028. |
| [18] |
李俊杰, 严家斌. 无网格点插值法大地电磁二维正演数值模拟[J]. 石油物探, 2014, 53(5): 617-626. LI Junjie, YAN Jiabin. Magnetotelluric two-dimensional forward numerical modeling by meshfree point interpolation method[J]. Geophysical Prospecting for Petroleum, 2014, 53(5): 617-626. DOI:10.3969/j.issn.1000-1441.2014.05.016 |
| [19] |
刘鑫. 波动方程交错网格和无网格有限差分数值模拟中的吸收边界条件[D]. 北京: 中国石油大学(北京), 2018.
|
| [20] |
DUAN P, GU B, LI Z, et al. An adaptive node-distribution method for radial basis function finite difference modelling with optimal shape parameter[J]. Geophysics, 2021, 86(1): T1-T18. DOI:10.1190/geo2019-0670.1 |
| [21] |
JENSEN P S. Finite difference technique for variable grids[J]. Computer& Structures, 1972, 2(1-2): 17-29. |
| [22] |
PERRONE N, KAO R. A general finite difference me-thod for arbitrary meshes[J]. Computer& Structures, 1975, 5(1): 45-57. |
| [23] |
LISZKA T, ORKISZ J. The finite difference method at arbitrary irregular grids and its application in applied mechanics[J]. Computer & Structures, 1980, 11(1-2): 83-95. |
| [24] |
BENITO J J, UREÑA F and GAVETE L. Influence of several factors in the generalized finite difference method[J]. Applied Mathematical Modelling, 2001, 25(12): 1039-1053. DOI:10.1016/S0307-904X(01)00029-4 |
| [25] |
UREÑA F, BENITO J J, SALETE E, et al. A note on the application of the generalized finite difference method to seismic wave propagation in 2D[J]. Journal of Computational and Applied Mathematics, 2012, 236(12): 3016-3025. DOI:10.1016/j.cam.2011.04.005 |
| [26] |
BENITO J J, UREÑA F, GAVETE L, et al. A GFDM with PML for seismic wave equations in heterogeneous media[J]. Journal of Computational and Applied Mathematics, 2013, 252(Nov): 40-51. |
| [27] |
WEI J, WANG S, HOU Q, et al. Generalized finite difference time domain method and its application to acoustics[J]. Mathematical Problems in Engineering, 2015, ID640305, 13. |
| [28] |
GU Y, WANG L, CHEN W, et al. Application of the meshless generalized finite difference method to inverse heat source problems[J]. International Journal of Heat and Mass Transfer, 2017, 108(May): 721-729. |
| [29] |
陈剑, 刘春明, 王茂海, 等. 广义有限差分法在静态电磁场计算中的应用[J]. 电工技术学报, 2018, 33(7): 1579-1587. CHEN Jian, LIU Chunming, WANG Maohai, et al. Application of the generalized finite difference method to static electromagnetic problems[J]. Transaction of China Electrotechnological Society, 2018, 33(7): 1579-1587. |
| [30] |
HUANG J, CHU C, FAN C, et al. On the propagation of nonlinear water waves in a three-dimensional numerical wave flume using the generalized finite difference method[J]. Engineering Analysis with Boundary Elements, 2020, 119(Oct): 225-234. |
| [31] |
UREÑA F, GAVETE L, BENITO J J, et al. Solving the telegraph equation in 2-D and 3-D using genera-lized finite difference method(GFDM)[J]. Enginee-ring Analysis with Boundary Elements, 2020, 112(Mar): 13-24. |
| [32] |
吴国忱, 王华忠. 波场模拟中的数值频散分析与校正策略[J]. 地球物理学进展, 2005, 20(1): 58-65. WU Guochen, WANG Huazhong. Analysis of numerical dispersion in wave-field simulation[J]. Progress in Geophysics, 2005, 20(1): 58-65. DOI:10.3969/j.issn.1004-2903.2005.01.012 |
| [33] |
董良国, 李培明. 地震波传播数值模拟中的频散问题[J]. 天然气工业, 2004, 24(6): 53-56. DONG Liangguo, LI Peiming. Dispersive problem in seismic wave propagation numerical modeling[J]. Natural Gas Industry, 2004, 24(6): 53-56. DOI:10.3321/j.issn:1000-0976.2004.06.016 |
| [34] |
孙成禹, 宫同举, 张玉亮, 等. 波动方程有限差分法中的频散与假频分析[J]. 石油地球物理勘探, 2009, 44(1): 43-48. SUN Chengyu, GONG Tongju, ZHANG Yuliang, et al. Analysis on dispersion and alias in finite-difference solution of wave equation[J]. Oil Geophysical Prospecting, 2009, 44(1): 43-48. DOI:10.3321/j.issn:1000-7210.2009.01.009 |
| [35] |
BENITO J J, UREÑA F, GAVETE L, et al. Implementations with generalized finite differences of the displacements and velocity-stress formulations of seismic wave propagation problem[J]. Applied Mathe-matical Modelling, 2017, 52(Dec): 1-14. |



 吴国忱, 山东省青岛市经济技术开发区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email:
吴国忱, 山东省青岛市经济技术开发区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email: 