地震波速度是地震勘探的重要参数之一,它贯穿于地震勘探的全过程。地震波速度信息是利用地震资料实施地质勘探和地质目标体预测的重要载体或评价指标。不论是构造解释[1-4]、岩性预测[5-6]、储层含油气检测[7-8],还是储层参数(包括孔隙度、饱和度、压力等)定量估算[9-13],均离不开速度信息。迄今为止,关于地震波速度影响因素的理论研究、实验测试等已非常全面深入,相关文献汗牛充栋。不论是在理论研究还是应用实践中,研究者出于不同考虑将各种与地震波速度有关联的现象均视为速度影响因素,从而造成了不同层级、不同类别地震波速度影响因素的堆叠和分类的混乱,既不利于地震波速度变化内在机理的研究,也不利于现实问题内在本质的分析与认识。Tatham等[14]将影响地震波速度的各种参数初步总结为:岩性、孔隙度、孔隙流体类型、孔隙形状、埋深与压力、温度和各向异性。在2008年出版的《岩石物理手册:孔隙介质中地震分析工具》[15]一书的中译本序言中,王之敬教授对影响岩石地震特性的因素进行了全面总结,并将其概括为岩石本身特性、饱和流体特性、所处环境等三大类,几乎囊括了迄今为止所提出的各种影响因素,详见表 1。
|
|
表 1 影响岩石地震特性的因素[15] |
众所周知,岩石地震特性的变化实际上是岩石速度变化的外在反映,因此岩石地震特性影响因素通常也被视为地震波速度影响因素。由表 1可见,饱和度作为描述岩石孔隙中流体含量的物理量,应属于孔隙流体特性的描述范畴,将它归类到所处环境显然不是很合适。其次,诸如紧密度(压实)、埋深、地质年代、各向异性等因素仅仅是地震波速度变化的外在表现,并不能反映地震波速度变化的内在本质。紧密度(压实)、埋深与地质年代对地震波速度的影响,本质上主要是由上覆地层压力变化引起的;而地震波速度各向异性变化则是由于岩石介质内部非均质性,如矿物颗粒或孔隙、裂隙结构的形状以及排列方式的差异等引起的[16-18]。由此可见,将埋深、地质年代、各向异性等视为地震波速度的影响因素显然是不合适的,无法反映速度变化的内在本质。这些至少从一个侧面说明,现有的地震波速度影响因素描述以及分类是欠科学严谨的。
表 2给出了从20世纪80年代到现今国内、外部分代表性教材中有关地震波速度影响因素的相关内容。不难看出,不同的教材关于地震波速度影响因素的阐述大同小异,其中以岩性、密度、孔隙度、埋深、地质年代几项因素在各教材中出现频度最高。中国国内教材中关于地震波速度影响因素的内容鲜有更新,大多呈现新教材照搬或沿用过往老教材的内容。这并不意味着地震波速度影响因素分析成果的成熟与完善,恰恰反映出教材编写过程中习惯于照搬照抄,缺乏相关研究和创新。当然,目前业内关于地震波速度影响因素分析尚未形成统一的认识可能也是造成现有教材无法更新的原因之一。综上所述,笔者认为进一步厘清地震波速度的影响因素及其分类是很有必要的,不仅有助于科学研究机理分析,而且有助于教材的更新。本文抛砖引玉,以唯物辩证法内外因理论为指导,尝试对地震波速度影响因素进行系统梳理,以期为研究者深入理解地震波速度的变化提供参考和借鉴。
|
|
表 2 部分代表性教材中地震波速度影响因素列表 |
为了更好地说明地震波与地震波速度之间的关系,下面从物理学之波动学理论相关概念出发,分析说明波速与波的关系。
众所周知,波是能量传播的一种形式。具体来说,振动在空间介质中的传播就是波。机械振动在弹性介质中的传播称为弹性波或机械波,如水波、声波和地震波等;电磁振动在空间电磁介质中的传播称为电磁波,如无线电波、光波以及地质雷达勘探中所用的雷达波等。很显然,机械波和电磁波是两种不同性质的波,二者产生的条件和方法不同。但是机械波和电磁波均可以用统一的数学方程表达,用相同的数学方法研究,也可以用波长、频率、波速等物理量描述其特征。通常波速定义为单位时间内波形(或振动状态)在空间介质中传播的距离,一般用质点位移对时间的微分来表达。由于振动状态一般以相位为标志,所以通常所说波速主要是指相速度。由于机械波是在弹性介质中传播的波,所以其波速主要由空间介质的弹性模量和密度所决定。而电磁波速度则由空间介质的介电常数和磁导率所决定。显然,不同性质的波,波速各不相同。如在空气中,室温条件下声波速度约为340m/s;而电磁波在真空中的速度等于光速,约为3×108m/s。尽管空气中电磁波传播速度比真空中小,但二者相差极小,一般认为电磁波在空气中的传播速度也是3×108m/s。这是为什么雷雨天往往先看到闪电(电磁波)后听到雷声(声波)的原因所在。从上述波速概念不难发现,波速实际上包含了波与空间介质一体两面双重内容。换言之,波速大小取决于波的性质和空间介质特性。对于相同的介质,波的性质或种类不同,相应的速度也各不相同。对于确定的某一种波,相应波速主要决定于介质特性,可视为反映介质内在本质特性的物理量。
除了机械波与电磁波的分类外,基于波的偏振特点不同,可以将波分为纵波和横波。依据弹性波传播理论,在均匀各向同性弹性介质假设条件下,通过求解弹性波传播波动方程,可获得纵、横波速度表达式如下[21, 24]
| $ V_{\mathrm{P}}=\sqrt{\frac{K+\frac{4}{3} \mu}{\rho}}=\sqrt{\frac{(1-\sigma) E}{(1+\sigma)(1-2 \sigma) \rho}} $ | (1) |
| $ V_{\mathrm{S}}=\sqrt{\frac{\mu}{\rho}}=\sqrt{\frac{E}{2 \rho(1+\sigma)}} $ | (2) |
式中:VP为纵波速度;VS为横波速度;K为体积模量;μ为剪切模量;ρ为密度;E为杨氏模量;σ为泊松比。后面四个弹性常数中只有两个是独立的,已知其中任意两个量,均可换算出另外两个量。
从式(1)和式(2)可见,尽管纵波和横波均为机械波,但由于两种波偏振方式的差异,导致二者在相同介质中呈现出不同的传播速度,再次说明抛开具体的波来谈论波速是不可取的,波速因波而存在,波速与波之间具有内在的一致性。正是由于弹性介质中可以传播纵波和横波两类波,因而介质具有纵波和横波两种波速。由此可见,波的分类决定了波速的分类。
在反射波地震勘探中,地震波速度是指地震波在岩层中的传播速度,简称地震速度或岩石速度,如砂岩速度、页岩速度等。由于早期反射波地震勘探主要利用纵波,因此在谈到地震波速度或岩石速度时,除非特别说明,一般均指纵波速度。这一点从表 2所列出的大多数教材中关于岩石速度的列表和分析几乎均为纵波速度可以证明。然而,随着多波多分量以及横波地震勘探技术的发展,关于横波速度的研究和应用日益增多,因此地震波速度概念不再是纵波速度的代名词。地震波速度实际上同时包含了纵波速度和横波速度两方面内容,或者说,地震波速度可分为纵波速度和横波速度两类。不过,在实际应用中,人们潜意识中依然习惯性地将地震波速度视为纵波速度。当涉及横波速度时,则加以特别标明。此外,按照波传播所能到达的空间范围或者说极化方式不同,地震波可分为体波与面波或线性极化波与面极化波。地震纵、横波均为线性极化波,Rayleigh面波为面极化波。不论是体波还是面波,不同的波型传播速度各不相同。考虑到面波是两种体波相互干涉而产生的,并非独立存在的,如P波与SV波彼此干涉产生Rayleigh波,与SH波干涉产生Love波,因此下面仅就传统意义上的地震纵、横波速度的影响因素加以讨论。为了避免后续阐述中概念的混乱,讨论中将不区分纵波速度和横波速度,对于确实存在明显差异的地方将特别加以分析说明。换言之,后续关于地震波速度影响因素的论述对于纵、横波速度均适用。
1.2 地震波速度频散在地震勘探中,通常将地震波速度随地震波频率变化的现象称为地震波速度频散[29]。对于单频简谐地震波而言,波速与频率之间的关系表达式可写为
| $ V=\frac{\lambda}{T}=\lambda f $ | (3) |
式中:V为波速;λ为波长;T为周期;f为频率。
式(3)是关于波速与频率关系的最简单的描述。在均匀各向同性介质中,地震波以恒速传播,波速大小仅与介质特性有关,见式(1)和式(2),与波的频率、周期等无关,因而不会出现速度频散现象。
大量研究结果表明,饱和流体岩石的地震纵、横波速度通常与地震波的频率有关,这使得在勘探地震波频率(< 200Hz)、声波测井频率(≈104Hz)和超声实验测试频率(105~106Hz)之间进行波速对比变得非常复杂。在Boit双相介质假设条件下[30-31],通过求解有损耗情形下的双相介质波动方程,可求得纵、横波速度频散表达式如下[32]
| $ V_{\mathrm{P}}^{2} \approx \frac{V_{\mathrm{P} \infty}^{4}+V_{\mathrm{P} 0}^{4}\left(\frac{\omega_{\mathrm{b}}}{A \omega}\right)^{2}}{V_{\mathrm{P} \infty}^{2}+V_{\mathrm{P} 0}^{2}\left(\frac{\omega_{\mathrm{b}}}{A \omega}\right)^{2}} $ | (4) |
| $ V_{\mathrm{P} 0}^{2}=\frac{1}{\rho}\left(K_{\mathrm{b}}+\frac{4}{3} \mu+\frac{(1-\beta)^{2}}{\frac{1-\varphi-\beta}{K_{\mathrm{m}}}+\frac{\varphi}{K_{\mathrm{f}}}}\right) $ | (5) |
| $ V_{\mathrm{P} \infty}^{2}=\frac{1}{\rho\left(1-\frac{\rho_{\mathrm{f}} \varphi}{c{\rho}}\right)}\left(K_{\mathrm{b}}+\frac{4}{3} \mu+\frac{\frac{\rho \varphi}{c \rho_{\mathrm{f}}}+(1-\beta)\left(1-\beta-\frac{2 \varphi}{c}\right)}{\frac{1-\varphi-\beta}{K_{m}}+\frac{\varphi}{K_{f}}}\right) $ | (6) |
| $ V_{\mathrm{S}}^{2} \approx \frac{V_{\mathrm{S} \infty}^{4}+V_{\mathrm{S} 0}^{4}\left(\frac{\omega_{\mathrm{b}}}{A \omega}\right)^{2}}{V_{\mathrm{S} \infty}^{2}+V_{\mathrm{S} 0}^{2}\left(\frac{\omega_{\mathrm{b}}}{A \omega}\right)^{2}} $ | (7) |
| $ V_{\mathrm{S} 0}=\sqrt{\frac{\mu}{\rho}} $ | (8) |
| $ V_{\mathrm{S} \infty}^{2}=\frac{\mu}{\rho-\frac{\rho_{\mathrm{f}} \varphi}{c}} $ | (9) |
| $ A=c-\frac{\varphi \rho_{\mathrm{f}}}{\rho} $ | (10) |
| $ \omega_{\mathrm{b}}=\frac{\eta \varphi}{k{\rho_{\mathrm{f}}}} $ | (11) |
| $ \beta=\frac{K_{\mathrm{b}}}{K_{\mathrm{m}}} $ | (12) |
式中:VP0、VP∞和VS0、VS∞分别为零频率和无穷大频率饱和流体岩石的纵、横波速度;ωb称为Biot特征频率,也是由“低”频域跃迁到“高”频域的“临界频率”;ω为角频率;c为质量耦合系数;k为渗透率;η为流体黏度;φ为孔隙度;ρf为孔隙流体密度;Kb为干岩石体积模量;Km岩石骨架体积模量;Kf为孔隙流体体积模量。式(5)与著名的Gassmann公式是一致的。该式为流体饱和双相介质波动方程第一类波的零频率近似。式(6)与Boit-Geerstma公式完全一致[33],称为Biot高频方程解。
迄今为止,关于地震波速度频散力学机制的阐述主要有两种:一是认为速度频散源于流体相与固体相之间的大尺度相对平均运动[30],常称之为Biot流动机制,见式(4);二是认为速度频散主要源于颗粒尺度的相对运动,也称为局部流动或喷射流(Squirt-flow)机制[34]。Dvorkin等[35]提出并建立了同时包含这两种机制的统一的理论模型,即BISQ(Biot-Squirt)模型。该模型目前已成为分析研究地震波速度频散效应的重要理论基石。
2 地震波速度影响因素为了更好地揭示地震波速度变化的内在本质和变化机理,关于速度影响因素的诠释最合理的分析方法应该是单因素归纳和分类。为此,依据唯物辩证法内外因辩证原理,可将地震波传播速度影响因素分为内在地质因素和外在环境因素或场作用两大类,详见表 3。前者主要是指组成岩石的矿物成分、孔隙及孔隙充填物等各种因素;后者则主要是指影响岩石特性的外部环境因素或统一称之为外在场作用,主要包括压力场、温度场,以及其他与岩石成岩、变质作用等有关的物理和化学场等。
|
|
表 3 地震波速度影响因素及分类 |
需要指出的是,对于不同的岩石,关于地震波速度影响因素的分析基本上不会超出表 3所列出的各种因素。但是,就各影响因素而言,对于不同岩石的影响力是存在差异的,或者说影响的权重不尽相同。以自然界广泛分布的三大类岩石——沉积岩、变质岩和火成岩为例,孔隙度可以说是影响各类岩石速度的关键因素。也就是说,孔隙度的变化对于三大类岩石各自速度的变化均具有较大的权重。若关注三大类岩石速度分布的一般规律,通常表现为火成岩速度最高,变质岩次之,沉积岩最低。之所以会呈现如此规律性,主要是由于沉积岩孔隙度一般较高,变质岩次之,火成岩最低。对于沉积岩而言,因孔隙度变化范围宽,所以速度变化范围最大;对于火成岩而言,因孔隙度变化范围较窄,所以速度变化范围较小。从这一角度来看,孔隙度对沉积岩速度变化影响的权重要远高于变质岩和火成岩。
此外,对于同一岩石而言,表 3所列出的各种因素对速度影响的权重也不是一成不变的,通常会随着勘探开发条件和环境的变化而变化。以温度为例,在常规油藏开采的地温梯度条件下,温度对岩石速度的影响一般较小,甚至可以忽略。然而,对于稠油热采而言,由于火烧稠油或向地下注入高温热蒸汽使得地层温度变化巨大,此时温度将成为速度变化的重要因素之一。
2.1 密度是地震波速度变化的桥梁众所周知,密度与岩石弹性参数(体积模量、剪切模量、泊松比、杨氏模量等)均为描述岩石物性的基本物理量。从式(1)和式(2)不难看出,地震波速度不仅与岩石弹性参数有关,也与岩石密度有关,主要表现为地震波速度与岩石弹性参数呈正相关,与岩石密度呈负相关。由此可见,地震波速度实际上是一个派生物理量,并非基本物理量。
在反射波地震勘探,用地震波速度代替岩石弹性参数来表征岩石的弹性特性已成为一种习惯。这主要是由于在大多数情形下,地震波速度与密度之间的负相关关系是隐性的,仅具有理论意义。现实中,绝大多数情况下这种负相关关系是无法凸显出来的。常见的情形是地震波速度与密度之间大多表现为正相关关系,即岩石密度越高,相应地震波速度也越大。究其原因,当岩石因内在地质特性或外在环境因素发生变化时,弹性参数(如K, μ)与密度的变化一般具有内在一致性,不过因弹性参数的变化一般均大于密度的变化,进而导致密度对地震波速度的影响无法凸显,几乎总是表现为地震波速度与弹性参数的变化相一致。正因如此,实际应用中,密度对地震波速度影响常常被忽略,地震波速度也因此几乎成为了表征岩石弹性特性的“代名词”。
但是,必须要清楚,地震波速度与密度之间变化规律的一致性(即正相关特性)仅仅是一种外在表现,并非密度对速度影响的内在本质反映。在孔隙流体变化导致岩石密度变化这种特殊情形下,地震波横波速度随密度的变化关系通常会显示出与理论负相关特征相一致的变化规律,即岩石密度增大,横波速度减小。
从上述分析可见,密度是影响地震波速度的重要因素之一,这也是业内共识。但是在表 3中笔者并未将密度作为地震波速度影响因素列出。原因在于,如果将密度作为地震波速度的影响因素,那么从式(1)和式(2)可知,地震波速度影响因素实际上只有密度和弹性参数两种。
因此,笔者承认密度是地震波速度的影响因素之一,但是不赞成将密度与岩石成分、孔隙度、孔隙充填物等并列作为影响地震波速度的同一层级因素。因为这样有可能造成认识上的误导,更不利于揭示速度变化的内在本质。应当以岩石成分、孔隙度、孔隙充填物等内在本质因素以及温度、压力等外在环境因素作为地震波速度影响因素,而密度和弹性参数仅仅是沟通地震波速度与各因素之间变化关系的桥梁和纽带。
2.2 岩性与速度关系的内在本质地震波速度通常被称为岩石速度。基于地震波速度反演资料进行岩性识别和储层横向预测司空见惯[4-6],基本依据在于不同岩性一般具有不同的地震波速度。因此人们习惯性认为岩性是影响地震波速度的因素。事实上,即使是对于同一岩性,地震波速度变化的范围也很宽。造成地震波速度变化的根本原因在于岩石矿物成分、结构、颗粒大小、含量、孔隙度等的差异性。换言之,岩性本身实际上是岩石成分、孔隙度、孔隙充填物等不同因素的综合反映,非单一因素。因此,将岩性作为地震波速度影响因素太过笼统,无法反映地震波速度变化的内在本质特征。至于将岩性与矿物成分两个不同层级的量并列作为地震波速度影响因素则更不合适,不仅不利于揭示地震波速度变化的本质,而且会造成分析和研究问题的混乱。
2.3 埋深、地质年代与速度关系的内在本质地震波速度随埋深与地质年代变化是无法否认的客观事实。但是,若因此就认为埋深与地质年代是影响地震波速度的因素是不严谨的。在煤、油、气地震勘探中,主要研究对象为沉积岩。众所周知,沉积岩速度一般随深度和地质年代的增加而增大,其本质是地质年代越老的地层埋深越大,遭受上覆地层压力也增大,正是由于地层压实作用随深度增加而增强,进而使得岩石孔隙度减小,地层速度增大。显然,造成沉积岩速度增大的根本原因主要在于地层压力的变化。因此,影响地震波速度的因素实际上是压力,并非埋深和地质年代。需指出的是,压力这一外在环境因素主要是通过改变岩石内在因素(如孔隙度等)达到影响地震波速度的结果。以超压层为例,一般表现出与某一浅部地层同等的速度大小,并未呈现出埋深越大速度越大的特点。根本原因在于该深度地层压力远高于地层正常压力,使地层孔隙度并未随埋深增加或压实作用而减小,相反与浅层某一等效深度地层具有相同孔隙度,因此速度也相同。这恰恰说明埋深并非影响地震波速度的内在本质因素。当然,地震波速度随埋深的变化,除了与压力作用有关的地层压实效应外,成岩作用过程中的胶结作用、重结晶作用等同样会对岩石速度造成一定程度的影响。事实上,成岩作用本身离不开地层压力场和温度场的影响。地震波速度随埋深、地质年代的变化,本质上是温度、压力以及成岩作用过程中物理化学场综合影响的结果。应当注意的是,地震波速度随地温梯度增加一般是减小的,其变化规律与压力的影响恰恰相反,只是由于在地层温压条件下,温度较压力对地震波速度的影响幅度要小得多。综上所述,埋深、地质年代对地震波速度的影响实际上是压力、温度、物理化学作用等多种环境因素综合作用下的外在表现。将埋深或地质年代作为影响地震波速度的因素是不恰当的,无法从根本上反映或揭示地震波速度变化的特征。
2.4 速度各向异性关系的内在本质众所周知,各向同性和各向异性指的是介质物理性质与方向的关系。若介质物理性质不依方向而变化,则称为各向同性介质;反之,若介质物理性质依方向而变化,称为各向异性介质。显然,不论是各向同性还是各向异性,均为介质物性特征的外在表现。因此,将各向异性作为地震波速度影响因素同样是不恰当的。研究[17, 36-37]表明,介质呈现各向异性的主要原因在于岩石构造的顺序性不均匀。这种顺序性在沉积岩中表现最为明显。通常有三种不同类型的顺序性。①与沉积过程的周期性循环或沉积旋回有关,如平行层理构造。②与岩石裂缝走向有关。受区域大地构造走向和构造应力作用影响,岩石裂缝往往沿一定方向发育,如平行层理方向、垂直层理方向,或与之斜交的方向等,岩石裂缝空间分布密度及发育方向的不同,造就了地震波速度与方向有关的异常分布。③岩石中具有晶体结构的矿物颗粒定向排列。对于具有后两种顺序性的岩石介质,因各向异性单元体的尺度远小于地震波波长,常将此类岩石介质称为理想各向异性介质。由此可见,真正决定地震波速度表现为各向同性或各向异性的内在本质取决于岩石自身内部构造(矿物排列方式、空间分布等)以及岩石内部孔隙、裂隙系统是否存在顺序性。在地震勘探中,大多数岩石介质,如火成岩、变质岩、碳酸盐岩、砂泥岩等,其弹性性质或地震波速度一般都没有表现出明显的方向性或方向性很弱,一般均可视为各向同性介质。但是,对于大多数沉积岩,特别是具有明显层理构造的页岩、煤,或岩石裂缝系统具有固定发育方向的裂缝灰岩,以及其他具有晶体结构的矿物颗粒规律排列的岩石等,均会呈现出较为明显的弹性或地震波速度各向异性。由此可见,直接将各向异性作为地震波速度的影响因素是不恰当的。真正导致地震波速度变化呈现各向异性或各向同性的本质因素是岩石内部的层理构造(矿物颗粒排列方式、空间分布等)以及孔隙、裂缝系统的空间分布。如果笼统地将影响因素看作是各向异性,那么将无法明确反映这种各向异性主要是由于岩石内部层理构造(矿物颗粒排列方式、空间分布等)引起的,还是由于孔隙、裂缝系统的空间分布引起的,或者二者兼而有之。
2.5 生产史、构造史、压力史、成藏过程等与地震波速度的关系地震波速度通常会随着生产史、构造史、压力史、成藏过程等变化,这种变化均为岩石内部特征变化的外在表现,并非地震波速度变化的内在本质。以油藏注水强化开采为例[32],在开采初期由于原油开采使得地层中含油饱和度减小,地层压力下降,进而可能导致地层孔隙闭合、孔隙度减小,这些均会对地震波速度变化产生影响;此后,随着注水强化开采工艺实施,地层压力趋于稳定,但是油藏内流体性质、油水饱和度的变化是必然的,而且地表冷水注入地下地层中会使得地层温度有所降低,这些同样会对地震波速度变化造成影响。不同的开发阶段由于储层变化特点不同,导致影响地震波速度变化的因素也不同,进而表现出地震波速度随生产史的不同变化规律。再者,对于不同的开采方式,地震波速度随生产史的变化也不尽相同,但究其本质不外乎地层温度、地层压力以及饱和度、孔隙度等变化。因此,笼统地将生产史作为地震波速度的影响因素是不恰当的。因为生产史本身是一个包含多因素的复杂系统,所以,将生产史作为地震波速度变化影响因素难以明确地震波速度变化本质,也难以构建普适变化规律。无独有偶,诸如构造史、压力史以及成藏过程等对地震波速度的影响均可能包含了岩石孔隙、孔隙流体、压力、温度等多种因素的综合影响,并非单因素变化。因此,将生产史、构造史、压力史、成藏过程等作为地震波速度变化的影响因素也是不恰当的,不利于地震波速度变化机理研究,无法揭示地震波速度变化的内在本质和普遍规律。
2.6 物理化学场对地震波速度的影响在岩石成岩作用过程中,单纯的压实作用主要是通过改变地层孔隙度进而影响地震波速度。但是在特定地层温度、压力条件下,岩石内部可能发生变质、相变、脱水、重结晶以及塑性变形等物理化学作用。变质作用可使得岩石性质由酸性变为基性或超基性,相应地震波速度会增大;相变是岩石在一定温度、压力条件下岩石结构的改变,如晶格改变,一般会使得地震波速度减小;当然岩石内部孔隙流体的相变,如地层水高温汽化和低温结冰固化等相态变化同样会改变地震波速度。岩石脱水是指在一定温度条件下失去结晶水,所排出的水或水蒸气储存于周围孔隙中,由此导致地震波速度变化;重结晶作用使得非结晶物质变成结晶物质或使细粒结晶物质变成粗粒结晶物质,进而使得地震波速度有所增大。岩石塑性化一般会使得地震波速度减小,而塑性硬化又会使得地震波速度增大[5]。由此可见,在特定温度、压力条件下,岩石遭受不同物理、化学场的作用,对地震波速度的影响同样是不可忽视的重要影响因素。
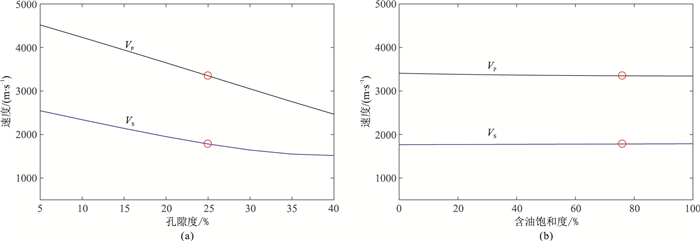
2.7 理论计算分析以大庆油田的一个油水饱和砂岩样实测纵、横波速度参数作为约束和控制,云美厚等[38]基于纵横波速度低频方程式(5)和式(8),计算了地震波速度随孔隙度、含油饱和度、地层孔隙压力、温度以及泥质含量的变化规律,结果见图 1~图 3。
|
图 1 地震波速度随孔隙度(a)和含油饱和度(b)的变化 |
|
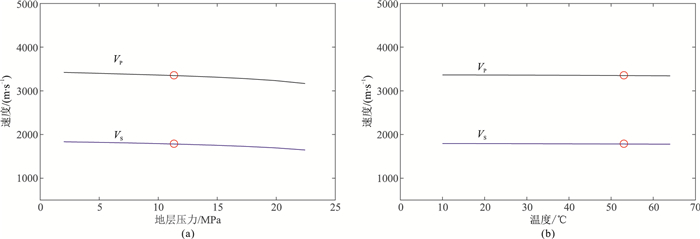
图 2 地震波速度随地层压力(a)和温度(b)的变化 |
|
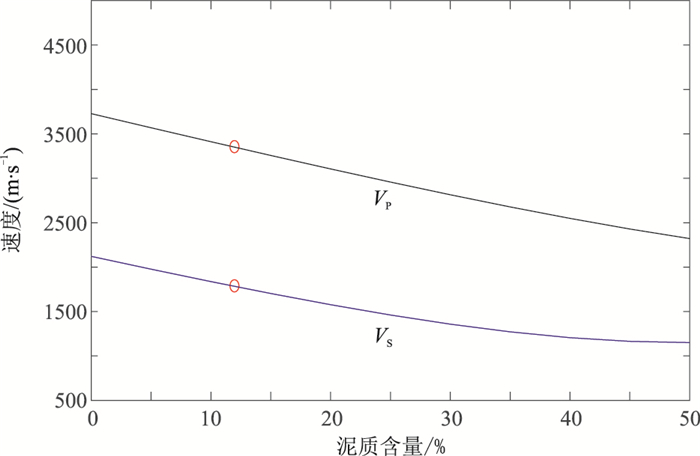
图 3 地震波速度随泥质含量的变化 |
图 1为储层油—水饱和情形下速度随孔隙度、含油饱和度的变化曲线。图中空心圆点为地震波速度控制点。显然,纵、横波速度随孔隙度的增加单调递减,且纵波速度的变化梯度比横波大。随含油饱和度的增加,纵波速度减小的幅度要远远小于地震波速度随孔隙度的变化。这至少可以从一个侧面说明孔隙度是影响地震波速度变化的关键因素。相比之下,横波速度随含油饱和度的变化更小,除高含油饱和度时略有增大外,地震波速度变化几乎可以忽略不计。这与前述结论认为孔隙流体类型和饱和度变化主要是通过密度的变化对横波速度产生微弱的影响完全一致。横波速度之所以会随含油饱和度增大略有增大,是因为随含油饱和度增加油水饱和岩石的密度降低。对于纵波而言,因含油饱和度增加引起密度降低的幅度远远低于岩石体积模量降低的幅度,所以纵波速度随含油饱和度增加总体上是减小的,但是减小的幅度很小。这说明对于固结岩石,地震波速度随含油饱和度的变化幅度远远低于孔隙度造成的地震波速度变化。
图 2a是当上覆地层压力为26MPa时,计算所得地震波速度随地层压力(即孔隙流体压力)的变化曲线。显然,随孔隙流体压力的增加地震波速度是减小的。这是因为上覆地层压力一定时,孔隙流体压力的增加意味着有效压力的减小,因而弹性模量减小,地震波速度降低。图 2b是当有效压力一定时,计算得到的地震波速度随温度的变化曲线。不难看出,地震波速度随温度的增加近似线性减小。这是因为温度增加通常会使得岩石基质软化,弹性模量减小,进而表现为地震波速度降低。
图 3为地震波速度随泥质含量变化曲线。可以看出,地震波速度随泥质含量的增加而减小。砂岩中泥质含量的高低在一定程度可以近似反映岩性的变化或砂岩矿物组成的变化。对比图 1a和图 3不难看出,泥质含量对地震波速度的影响与孔隙度影响基本相当,这至少可以从一个侧面说明岩石矿物组成是影响地震波速度的关键因素之一。
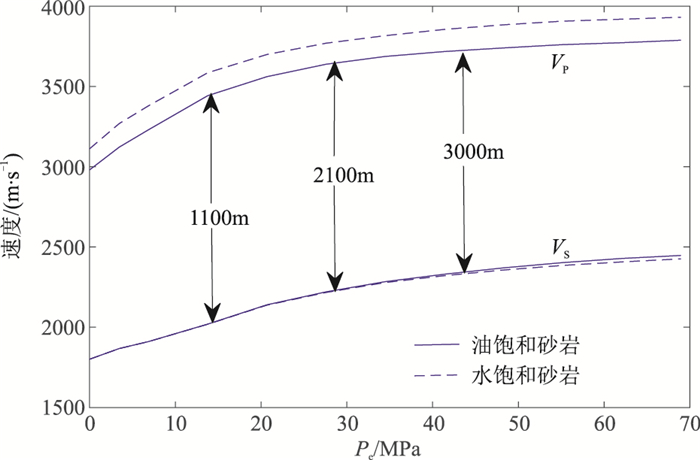
图 4显示了上覆地层压力一定时,砂岩储层埋深分别为1100m、2100m、3000m,且分别为油水饱和时的纵、横波速度随有效压力变化曲线[39]。由图可见,不论储层埋深如何,水饱和砂岩的纵波速度均高于轻质油饱和砂岩的纵波速度,但油水饱和岩石的横波速度之间变化很小,几乎是一致的。图中箭头所指的位置分别为相应深度正常压实情形下储层岩石的有效压力及速度值。这恰恰说明了纵、横波速度随深度增加而增大的内在本质在于地层有效压力的变化。
|
图 4 不同深度油水饱和砂岩纵横波速度随有效压力的变化 |
关于成岩作用对地震波速度的影响目前尚没有相关理论公式可以清楚揭示二者之间的关系。但是Murphy等[40]通过对气饱和纯石英砂(未固结成岩)和砂岩样品的超声波测量数据(测量有效压力为50MPa)的统计分析发现,干岩石骨架模量表现出对孔隙度的明显正相关关系,而且未固结成岩的气饱和纯石英砂样与固结成岩的砂岩样本干岩石骨架模量随孔隙度的变化关系并不一致。对于φ≤0.35的固结砂岩样本,最佳经验拟合公式为
| $ \left\{\begin{array}{l} K_{\mathrm{d}}=38.18\left(1-3.39 \varphi+1.95 \varphi^{2}\right) \\ \mu_{\mathrm{d}}=42.65\left(1-3.48 \varphi+2.19 \varphi^{2}\right) \end{array}\right. $ | (13) |
对于φ>0.35的未固结砂样,最佳经验拟合公式为
| $ \left\{\begin{array}{l} K_{\mathrm{d}}=\exp (-62.60 \varphi+22.58) \\ \mu_{\mathrm{d}}=\exp (-62.69 \varphi+22.73) \end{array}\right. $ | (14) |
利用上述二式简单计算后不难发现,固结砂岩样本干岩石体积模量和剪切模量均比未固结松散石英砂样高。这在一定程度上可以说明,成岩作用使岩石硬化,骨架模量增大,进而使得固结岩石纵横波速度增大。
云美厚等[41]曾就油藏注水开发过程中储层岩石地震波速度和密度的变化进行了较为细致的分析计算,揭示了油藏注水开发过程中储层地震波速度和密度的变化是注水开发引起的孔隙流体饱和度、储层温度及压力、孔隙度、渗透率和孔隙流体性质等共同作用的结果。在一定程度上说明了油藏生产史或成藏过程对地震速度影响的内在本质,同时也说明将油藏生产史或成藏过程等作为地震波速度影响因素是不恰当的。
3 结论(1) 地震波分类决定了地震波速度分类。对于确定的地震纵波或横波,相应波速主要决定于介质性质。
(2) 地震波速度是否表现出频散效应与介质特性有关。在均匀各向同性介质中地震波速度不存在频散,饱和流体岩石的地震波速度存在频散。造成频散的主要力学机制包括Biot流动机制和喷射流机制两种。
(3) 地震波速度影响因素可分为内在地质因素和外在环境因素两大类。前者主要包括岩石矿物成分、含量、结构、孔隙类型、孔隙度以及孔隙充填物类型、含量(饱和度)等岩石基本物性;后者主要指各种外在场作用,包括压力场、温度场、各种物理化学场等。
(4) 地震波速度是描述地震波传播特性的重要参数之一,但其并非描述岩石弹性特性的基本物理量,而是一个衍生物理量。它不仅与岩石弹性参数变化有关,而且与岩石密度变化有关,密度和弹性参数是链接地震波速度与岩石基本物性参数的纽带和桥梁,将密度作为地震波速度影响因素无法揭示速度变化的内在本质。
(5) 岩性是岩石矿物成分、结构、含量、孔隙等多种岩石基本地质特性的综合反映,笼统地将岩性作为影响地震波速度的因素同样无法反映速度变化的本质特征。
(6) 埋深、地质年代对地震波速度的影响实际上是地层压力、温度、物理化学作用等多因素综合作用下的外在表现,尤以压力影响最显著。将埋深、地质年代视为地震波速度影响因素无法从根本上反映或揭示地震波速度变化本质特征。
(7) 地震速度各向异性特征源于岩石内部矿物颗粒定向排列形成的层理构造、以及孔隙结构等空间分布的差异性。将各向异性作为地震波速度影响因素不足以全面准确反映岩石内在本质特征对速度的影响。
(8) 地震波速度随生产史、构造史、压力史、成藏过程等的变化一般为岩石孔隙、孔隙流体、压力、温度等各种因素综合作用下的外在表现,将其作为地震波速度变化的影响因素无法揭示速度变化内在本质和普遍规律,不利于地震波速度变化机理研究。
(9) 在特定条件下,岩石内部物理化学场对地震波速度的影响是不可忽视的。
| [1] |
杨茜娜, 张伟. 复频移完全匹配层在复杂速度模型中的应用[J]. 石油地球物理勘探, 2020, 55(6): 1271-1281. YANG Xin, ZHANG Wei. Application of CFS-PML in complex velocity models[J]. Oil Geophysical Prospecting, 2020, 55(6): 1271-1281. |
| [2] |
王鹏, 王小卫, 雍运动, 等. 马头营地区低幅度构造速度建模方法[J]. 石油地球物理勘探, 2020, 55(4): 766-773. WANG Peng, WANG Xiaowei, YONG Yundong, et al. Velocity modeling of the low-relief structure in the Matouying area of Jidong Oilfield[J]. Oil Geophysical Prospecting, 2020, 55(4): 766-773. |
| [3] |
姜岩, 程顺国, 王元波, 等. 大庆长垣油田断层阴影地震正演模拟及校正方法[J]. 石油地球物理勘探, 2019, 54(2): 320-329. JIANG Yan, CHENG Shunguo, WANG Yuanbo, et al. Seismic forward modeling for correction of fault shadow zones in Changyuan Oilfield, Daqing[J]. Oil Geophysical Prospecting, 2019, 54(2): 320-329. |
| [4] |
梁卫, 宋强功, 汪瑞良, 等. 构造+岩性油气藏地震处理、解释一体化实例研究[J]. 石油地球物理勘探, 2015, 50(2): 327-340. LIANG Wei, SONG Qianggong, WANG Ruiliang, et al. Integrated seismic processing and interpretation for a structural+stratigraphic reservoir: a case study[J]. Oil Geophysical Prospecting, 2015, 50(2): 327-340. |
| [5] |
张宪国, 林承焰, 张涛, 等. 井、震多尺度信息融合预测老油田浅层岩性气藏[J]. 石油地球物理勘探, 2009, 44(5): 609-612. ZHANG Xianguo, LIN Chengyan, ZHANG Tao, et al. Using well and seismic multi-scale information integration to predict shallow lithology gas reservoir in mature oilfield[J]. Oil Geophysical Prospecting, 2009, 44(5): 609-612. DOI:10.3321/j.issn:1000-7210.2009.05.017 |
| [6] |
付国强, 张国栋, 郭银菊. 庙北地区馆陶组砂岩百分含量预测[J]. 石油地球物理勘探, 2000, 35(4): 532-535, 542. FU Guoqiang, ZHANG Guodong, GUO Yinju. Sand content prediction for the Guantao formation in Miaobei area[J]. Oil Geophysical Prospecting, 2000, 35(4): 532-535, 542. DOI:10.3321/j.issn:1000-7210.2000.04.016 |
| [7] |
王九拴, 王绪本, 杨静, 等. 多波地震资料在三湖地区油气预测中的应用[J]. 石油地球物理勘探, 2012, 47(4): 605-609. WANG Jiushuan, WANG Xuben, YANG Jing, et al. Hydrocarbon prediction based on multi-wave data in Sanhu area[J]. Oil Geophysical Prospecting, 2012, 47(4): 605-609. |
| [8] |
向鼎璞, 张小平, 吴大奎. 拟层速度剖面在川中一川南过渡带油气勘探中的应用[J]. 石油地球物理勘探, 1990, 25(2): 177-190. XIANG Dingpu, ZHANG Xiaoping, WU Dakui. The application of pseudo interval velocity section to hydrocarbon exploration in the transitional zone between mid Sichuan and south Sichuan[J]. Oil Geophysical Prospecting, 1990, 25(2): 177-190. |
| [9] |
马如辉, 张平. 利用波阻抗反演预测地层孔隙率[J]. 石油地球物理勘探, 2002, 37(5): 537-540. MA Ruhui, ZHANG Ping. Study of method for prediction of formation porosity by wave impedance inversion[J]. Oil Geophysical Prospecting, 2002, 37(5): 537-540. DOI:10.3321/j.issn:1000-7210.2002.05.019 |
| [10] |
秦海旭, 吴国忱. 裂缝储层孔隙度、饱和度计算方法[J]. 石油地球物理勘探, 2015, 50(1): 103-110. QIN Haixu, WU Guochen. A method to calculate porosity and saturation in fractured reservoirs[J]. Oil Geophysical Prospecting, 2015, 50(1): 103-110. |
| [11] |
王峣钧, 陈双全, 王磊, 等. 基于斑块饱和模型利用地震波频散特征分析含气饱和度[J]. 石油地球物理勘探, 2014, 49(4): 715-722. WANG Yaojun, CHEN Shuangquan, WANG Lei, et al. Gas saturation analysis with seismic dispersion attribute based on patchy-saturation model[J]. Oil Geophysical Prospecting, 2014, 49(4): 715-722. |
| [12] |
周东红, 熊晓军. 一种高精度地层压力预测方法[J]. 石油地球物理勘探, 2014, 49(2): 344-348. ZHOU Donghong, XIONG Xiaojun. A method for high-precision prediction of formation pressure[J]. Oil Geophysical Prospecting, 2014, 49(2): 344-348. |
| [13] |
罗胜元, 何生, 宋国奇, 等. 渤南洼陷钻前地层压力地震预测[J]. 石油地球物理勘探, 2014, 49(2): 349-359. LUO Shengyuan, HE Sheng, SONG Guoqi, et al. Formation pressure prediction in Bonan Sag[J]. Oil Geophysical Prospecting, 2014, 49(2): 349-359. |
| [14] |
Tatham R H, McCormark M D. Multicomponent Seismology in Petroleum Exploration[M]. Tulsa: SEG, 1991.
|
| [15] |
(美)葛瑞·马沃可, 塔潘·木克基, 杰克·德沃金编著; 徐海滨, 戴建春译; 王之敬校. 岩石物理手册: 孔隙介质中地震分析工具[M]. 安徽合肥: 中国科学技术大学出版社, 2008.
|
| [16] |
周晓越, 甘利灯, 杨昊, 等. 利用叠前振幅和速度各向异性的联合反演方法[J]. 石油地球物理勘探, 2020, 55(5): 1084-1091. ZHOU Xiaoyue, GAN Lideng, YANG Hao, et al. A joint inversion method using amplitude and velocity anisotropy[J]. Oil Geophysical Prospecting, 2020, 55(5): 1084-1091. |
| [17] |
段茜, 刘向君, 梁利喜, 等. 裂缝参数对纵波各向异性影响的数值模拟[J]. 石油地球物理勘探, 2020, 55(3): 575-583, 590. DUAN Xi, LIU Xiangjun, LIANG Lixi, et al. Nume-rical simulation to the influence of fracture parameters on P-wave anisotropy[J]. Oil Geophysical Prospecting, 2020, 55(3): 575-583, 590. |
| [18] |
赵宇, 张玉贵, 于弘奕. 煤岩吸水率对声波速度各向异性影响的实验研究[J]. 石油地球物理勘探, 2017, 52(5): 999-1004. ZHAO Yu, ZHANG Yugui, YU Hongyi. Experimental research on effects of water absorption on acoustic velocity anisotropy in coal rock[J]. Oil Geophysical Prospecting, 2017, 52(5): 999-1004. |
| [19] |
长春地质学院编. 地震勘探——原理和方法[M]. 北京: 地质出版社, 1980: 67-73.
|
| [20] |
陆基孟. 地震勘探原理[M]. 北京: 石油工业出版社, 1982: 212-219, 378-337.
|
| [21] |
恽玲舲, 胡德昭, 朱慧娟, 等. 地球物理学原理及应用[M]. 江苏南京: 南京大学出版社, 1987: 10-12.
|
| [22] |
陆基孟. 地震勘探原理(上)[M]. 山东东营: 石油大学出版社, 1993: 189-194.
|
| [23] |
Sheriff R E, Geldart L P. Exploration Seismology (2nd Edition.)[M]. Cambridge: Cambridge University Press, 1995: 107-122.
|
| [24] |
张胜业, 潘玉玲. 应用地球物理学原理[M]. 湖北武汉: 中国地质大学出版社, 2004: 35-40.
|
| [25] |
朱广生, 陈传仁, 桂志先. 勘探地震学教程[M]. 湖北武汉: 武汉大学出版社, 2005: 262-271.
|
| [26] |
张玉芬. 反射波地震勘探原理和资料解释[M]. 北京: 地质出版社, 2007: 14-15.
|
| [27] |
熊章强. 地震勘探[M]. 湖南长沙: 中南大学出版社, 2010: 54-56.
|
| [28] |
吴建生, 王家林, 赵永辉, 等. 地球物理学入门[M]. 上海: 同济大学出版社, 2017: 53-54.
|
| [29] |
李民龙, 刘浩杰, 杨宏伟, 等. 跨频段岩石波速及频散的实验研究[J]. 石油地球物理勘探, 2020, 55(2): 373-378. LI Minlong, LIU Haojie, YANG Hongwei, et al. Experimental study on cross-frequency wave velocity and dispersion in rocks[J]. Oil Geophysical Prospecting, 2020, 55(2): 373-378. |
| [30] |
Biot M A. Theory of propagation of elastic waves in a fluid-saturated porous solid, I. Low frequency range[J]. The Journal of the Acoustical Society America, 1956, 28(2): 168-178. DOI:10.1121/1.1908239 |
| [31] |
Biot M A. Theory of propagation of elastic waves in a fluid-saturated porous solid, Ⅱ.High frequeney range[J]. The Journal of the Acoustical Society America, 1956, 28(2): 179-191. DOI:10.1121/1.1908241 |
| [32] |
云美厚. 油藏注水强化开采地震监测技术的研究与应用[D]. 北京: 中国地质大学, 2001, 11-17. YUN Meihou. A Study and Application of Seismic Monitoring for Reservoir Waterflood Enhanced Recovery[D]. China University of Geosciences, Beijing, 2001, 11-17. |
| [33] |
Geerstma J. Some aspects of elastic wave propagation in fluid saturation porous solids[J]. Geophysics, 1961, 26(2): 169-181. DOI:10.1190/1.1438855 |
| [34] |
Mavko G, Nur A. Wave attenuation in partially saturated rocks[J]. Geophysics, 1979, 44(2): 16l-178. |
| [35] |
Dvorkin J, Nur A. Dynamic poroelasticity: A unified model with the squirt and the Biot mechanisms[J]. Geophysics, 1993, 58(4): 524-533. DOI:10.1190/1.1443435 |
| [36] |
孙成禹. 地震波理论与方法[M]. 山东东营: 中国石油大学出版社, 2007: 129-136. SUN Chengyu. Theory and Methods of Seismic Wave[M]. Dongying, Shandong: China University of Petroleum Press, 2007: 129-136. |
| [37] |
郝奇. VTI介质速度和各向异性参数建模研究[D]. 吉林长春: 吉林大学, 2010, 15-17. HAO Qi. Study on the Model-building of Velocity and Anisotropic Parameters for VTI Media[D]. Jilin University, Changchun, Jilin, 2010, 15-17. |
| [38] |
云美厚, 管志宁. 储层条件下砂岩纵波和横波速度的理论计算[J]. 石油物探, 2002, 41(3): 289-292. YUN Meihou, GUAN Zhining. The estimation of P and S-wave velocities in sandstone under in-situ conditions[J]. Geophysical Prospecting for Petroleum, 2002, 41(3): 289-292. DOI:10.3969/j.issn.1000-1441.2002.03.008 |
| [39] |
云美厚, 管志宁. 储层温压变化与油藏地震监测[J]. 地球物理学进展, 2003, 18(1): 156-159. YUN Meihou, GUAN Zhining. Variation of temperature and pressure in reservoir and seismic monitoring[J]. Progress in Geophysics, 2003, 18(1): 156-159. DOI:10.3969/j.issn.1004-2903.2003.01.027 |
| [40] |
Murphy W, Reischer A, Hsu K. Modulus decomposition of compressional and shear velocities in sand bodies[J]. Geophysics, 1993, 58(2): 227-239. DOI:10.1190/1.1443408 |
| [41] |
云美厚, 管志宁. 油藏注水开发对储层岩石速度和密度的影响[J]. 石油地球物理勘探, 2002, 37(3): 280-286. YUN Meihou, GUAN Zhining. Effect of waterflood development on velocity and density of reservoir rock[J]. Oil Geophysical Prospecting, 2002, 37(3): 280-286. DOI:10.3321/j.issn:1000-7210.2002.03.015 |



 李晓斌, 河南省焦作市高新区世纪大道2001号河南理工大学资源与环境学院, 454000。Email:
李晓斌, 河南省焦作市高新区世纪大道2001号河南理工大学资源与环境学院, 454000。Email: 