海洋油气资源占全球油气资源的34%;中国海洋石油和天然气分别占中国石油和天然气资源量的22.9%和29.0%,探明率仅为12.1%,远低于世界平均水平的30%,勘探开发潜力巨大。海洋地震勘探中,水检数据是由位于海水拖缆或者海底电缆中的压力检波器接收的地震压力波场数据,能够很好地展现出地下地质构造和反射界面信息。可是,来自海面的虚反射噪声干扰总是如影随行,成为单一水检数据地震勘探一个难以克服的难题。
海洋地震勘探中,海洋震源子波是一个远场子波,包括震源虚反射。Loewenthal等[1]最早认识到速度波场可用于地震勘探,提出使用压力检波器和速度检波器进行海上和陆上地震勘探。Barr等[2]首先在海底电缆(Ocean Bottom Cable,OBC)勘探中使用压力和速度检波器记录水、陆检数据,压制海水鸣震多次波,开启了海洋双检数据地震勘探。Loewenthal[3]通过波动方程建立了水平均匀层状介质压力波场与速度波场之间的关系。
OBC双检地震勘探开始时仅仅在浅水区域进行,提供了同一位置水检和陆检两种数据,这两种数据分别使用水中(压力)检波器和陆地(垂直速度)检波器记录。其中,水中检波器记录的是压力波场;陆地检波器记录的是质点垂直速度波场。由于这两种检波器制做工艺和记录机理不同,对于同一位置处海面多次波干扰的表现特征也不同。垂直质点速度检波器的虚反射特征,总能准确地补偿压力检波器虚反射对有效信号的影响,且与检波器深度无关。利用两种检波器记录数据的上、下行波的差异,可以有效实现检波点端虚反射的压制并克服陷波效应,克服了单一压力波场数据处理技术的缺陷,从地震波场理论上解决了去除接收点虚反射问题[3-6]。Dragoset等[4]和Paffenholz等[7]建立了斯伦贝谢公司双检数据处理技术;Soubaras[8]建立了CGG公司双检数据处理技术。
海底电缆自1997年引入中国以来,双检数据处理技术得到了一定的发展。全海燕等[9]选择渤海湾地区采集的海底电缆双检数据说明做好频率匹配的一套处理思路;王振华等[10]提出了利用双检数据自相关函数次极值与最大值比值确定海底反射系数的双检数据加权叠加+预测反褶积处理技术;贺兆全等[11]提出了基于虚反射是一次波的时间延迟、微屈多次波与虚反射成正比、比例系数是海底反射系数的处理技术;童思友等[12]提出了基于维纳滤波的双检数据鸣震压制技术;龚旭东等[13]分析了海水深度误差对双检数据处理的影响;王兆旗等[14]介绍了线性拉东变换双检数据上下行波场分离处理流程;梁鸿贤等[15]通过正演模拟分析了双检数据中海水鸣震的波场特征;秦宁[16]提出了陆检数据微分合并技术。另外,中国多所大学的研究团队也开展了水、陆检数据压制海水鸣震和上下行波场分离技术研究,完成了多篇硕、博士学位论文[17-31],特别是中国海洋大学的童思友研究团队,进行了系统的海洋OBC水陆检数据压制海水鸣震技术研究,对中国海上水陆检数据处理技术进步具有积极的意义。
随着中国石油集团2006年全面进入海洋勘探领域,东方地球物理公司(BGP)的高少武等[32-49]也开展了双检数据处理方法和技术研究,形成了国产超大型油气地球物理勘探软件GeoEast海洋双检数据处理方法和技术,BGP具备了海洋双检数据处理能力,标志着GeoEast成为国际三大地震数据处理软件之一。
针对深水勘探,BGP引入海底节点(Ocean Bottom Node,OBN)[50]和双检拖缆[51-52]等地震数据采集系统。双检地震勘探采集和处理技术渐渐成为海洋地震勘探的主流。BGP作为全球OBN业务的重要引领者和主要参与者,至2019年运营海洋节点数量已占到全球总量的近60%,并成功为BP、壳牌、雪佛龙等超大型国际石油公司运作OBN项目二十余个,实现了海洋勘探业务的“变轨超车”。
随着海洋油气地震勘探的深入,其难度和深度越来越大,对地震资料信噪比和分辨率的要求也越来越高。BGP虽然在海洋OBN双检数据采集技术方面处于国际领先,但是在OBN双检数据处理方面,与国际主流软件仍存在着一定的差距。因此,必须加强OBN双检数据处理方法和技术研究。双检数据上下行波场分离技术是双检数据处理的基础,利用两类检波器对上下行波场响应的不同将上行波和下行波进行分离,一方面消除检波点端虚反射影响,分离出上行波;另一方面通过上下行波场联合反褶积和镜像偏移成像技术,有效增加浅层照明度,提高成像质量。
本文系统地介绍了双检数据处理和上下行波场分离理论基础,归纳和总结了OBC/OBN双检数据合并处理技术和7种双检数据上下行波场分离技术,希望能为中国双检数据处理技术进一步发展提供帮助。
1 理论基础 1.1 上、下行波场海洋地震勘探中,气枪震源激发在海水中产生膨胀,产生一个正的地震脉冲(震源子波)。这个地震脉冲对其附近海水介质产生压力,伴随着压力也产生位移、速度和加速度。压力向周围传播,形成压力波场。位移、速度和加速度向周围传播,形成位移波场、速度波场和加速度波场。
在海底观测到的波场包括:由接收点之下介质传播到达接收点处被检波器接收的波场,称为上行波场,上行波场是由一次反射和炮点端虚反射及多次波组成的波场;由接收点之上介质传播到达接收点处被检波器接收的波场,就是下行波场,下行波场是由接收端虚反射和炮点接收端虚反射及多次波组成的波场。
Loewenthal等[3, 53]根据Newton第二定律和Hooke定律,建立起一维介质压力波场和质点垂直速度波场之间关系
| $ \left\{\begin{array}{l} \frac{\partial P}{\partial z}=-\rho \frac{\partial v}{\partial t} \\ \frac{\partial P}{\partial t}=-K \frac{\partial v}{\partial z} \end{array}\right. $ | (1) |
式中:P=P(z,t)为压力波场;v=v(z,t)为质点垂直速度波场;ρ为介质密度;K=ρc2为介质的杨氏模量,c为介质速度。式(1)分别对z和t求导,并代入式(1),有
| $ \left\{\begin{array}{l} \frac{\partial^{2} P}{\partial z^{2}}=\frac{1}{c^{2}} \frac{\partial^{2} P}{\partial t^{2}} \\ \frac{\partial^{2} v}{\partial z^{2}}=\frac{1}{c^{2}} \frac{\partial^{2} v}{\partial t^{2}} \end{array}\right. $ | (2) |
式(2)的解为
| $ \left\{\begin{array}{l} P(z, t)=D(z-c t)+U(z+c t) \\ v(z, t)=d(z-c t)+u(z+c t) \end{array}\right. $ | (3) |
式中:U为向上以速度c传播的压力波,即上行压力波场;D为向下以速度c传播的压力波,称为下行压力波场;d为向下以速度c传播的质点垂直速度波场;u为向上以速度c传播的质点垂直速度波。U、D可表示为
| $ \left\{\begin{array}{l} U=U(z, t)=U(z+c t) \\ D=D(z, t)=D(z-c t) \end{array}\right. $ | (4) |
u、d可表示为
| $ \left\{\begin{array}{l} u=u(z, t)=u(z+c t) \\ d=d(z, t)=d(z-c t) \end{array}\right. $ | (5) |
式(3)表明:水检数据就是由压力检波器记录的同一时刻、同一位置的上行压力波场与下行压力波场之和;陆检数据就是由质点垂直速度检波器记录的同一时刻、同一位置的上行质点垂直速度波场与下行质点垂直速度波场之和。
式(3)分别对z和t求导,有
| $ \left\{\begin{array}{l} \frac{\partial P}{\partial z}=D^{\prime}+U^{\prime} \\ \frac{\partial P}{\partial t}=-c D^{\prime}+c U^{\prime} \end{array}\right. $ | (6) |
| $ \left\{\begin{array}{l} \frac{\partial v}{\partial z}=d^{\prime}+u^{\prime} \\ \frac{\partial v}{\partial t}=-c d^{\prime}+c u^{\prime} \end{array}\right. $ | (7) |
式中:U'和D'分别是上、下行压力波场U和D的偏导数;u'和d'分别是上、下行质点垂直速度波场u和d的偏导数。将式(6)、式(7)代入式(1),有
| $ \left\{\begin{array}{l} D=\rho c d \\ U=-\rho c u \end{array}\right. $ | (8) |
由式(8)可知,下行压力波场与下行质点垂直速度波场相位是同相的,振幅成正比,比例系数是介质的声波阻抗(ρc);上行压力波场与上行质点垂直速度波场相位是反相的,振幅成正比,比例系数也是ρc。
将式(8)代入式(3),有
| $ \left\{\begin{array}{l} P=D+U \\ v=\frac{1}{\rho c}(D-U) \end{array}\right. $ | (9) |
| $ \left\{\begin{array}{l} P=\rho c(d-u) \\ v=d+u \end{array}\right. $ | (10) |
式(9)表明,压力波场和质点垂直速度波场可由上行压力波场和下行压力波场导出;式(10)表明,压力波场和质点垂直速度波场也可由上行质点垂直速度波场和下行质点垂直速度波场导出。
由式(9)和式(10)可得
| $ \left\{\begin{array}{l} U=\frac{1}{2}(P-\rho c v) \\ D=\frac{1}{2}(P+\rho c v) \end{array}\right. $ | (11) |
| $ \left\{\begin{array}{l} u=\frac{1}{2}\left(v-\frac{1}{\rho c} P\right) \\ d=\frac{1}{2}\left(v+\frac{1}{\rho c} P\right) \end{array}\right. $ | (12) |
式(11)和式(12)表明,上行压力波场和下行压力波场可以由压力波场和质点垂直速度波场导出;上行质点垂直速度波场和下行质点垂直速度波场可以由压力波场和质点垂直速度场导出。
1.2 双检数据标定时间域双检三维地震数据根据逆傅里叶变换可表示为
| $ \left\{\begin{array}{l} P=\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} \tilde{P} \exp \left[\mathrm{i}\left(k_{x} x+k_{y} y+k_{z} z+\omega t\right)\right] \mathrm{d} k_{x} \mathrm{~d} k_{y} \mathrm{~d} k_{z} \mathrm{~d} \omega \\ v=\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} \tilde{v} \exp \left[\mathrm{i}\left(k_{x} x+k_{y} y+k_{z} z+\omega t\right)\right] \mathrm{d} k_{x} \mathrm{~d} k_{y} \mathrm{~d} k_{z} \mathrm{~d} \omega \end{array}\right. $ | (13) |
式中:
三维、二维和一维频散方程分别为
| $ k_{z}=\sqrt{\frac{\omega^{2}}{c^{2}}-k_{x}^{2}-k_{y}^{2}} $ | (14) |
| $ k_{z}=\sqrt{\frac{\omega^{2}}{c^{2}}-k_{x}^{2}} $ | (15) |
| $ k_{z}=\frac{\omega}{c} $ | (16) |
式(13)P对z和v对t求导,有
| $ \left\{\begin{array}{l} \frac{\partial P}{\partial z}=\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} \mathrm{i} k_{z} \tilde{P} \exp \left[\mathrm{i}\left(k_{x} x+k_{y} y+k_{z} z+\omega t\right)\right] \mathrm{d} k_{x} \mathrm{~d} k_{y} \mathrm{~d} k_{z} \mathrm{~d} \omega \\ \frac{\partial v}{\partial t}=\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} \mathrm{i} \omega \tilde{v} \exp \left[\mathrm{i}\left(k_{x} x+k_{y} y+k_{z} z+\omega t\right)\right] \mathrm{d} k_{x} \mathrm{~d} k_{y} \mathrm{~d} k_{z} \mathrm{~d} \omega \end{array}\right. $ | (17) |
将式(17)代入式(1),有
| $ \widetilde{P}=-\frac{\rho \omega}{k_{z}} \tilde{\tilde{v}} $ | (18) |
由式(18)可知,同一地震波场由质点垂直速度检波器和压力检波器记录得到水、陆检数据,在频率、相位、振幅和能量等方面存在差异,因此在进行水陆检数据上下行波场分离处理之前,必须对水、陆检数据进行标定处理。令
| $ \alpha\left(k_{z}, \omega\right)=-\frac{\rho \omega}{k_{z}} $ | (19) |
α(kz, ω)即为频率—波数域陆检数据标定因子。一维时,有
| $ \alpha\left(k_{z}, \omega\right)=-\rho c $ | (20) |
标定因子为常数,就是介质的声波阻抗。因此,一维情况下,可使用常数标定因子对陆检数据进行标定。对于二维和三维数据,也可使用近炮检距数据进行常数标定因子计算,实现水、陆检数据近似标定。要实现精确的水、陆检数据标定,必须计算三维标定因子。
将式(19)代入式(18),得到计算频率—波数域水、陆检数据标定因子的目标函数
| $ Q=\sum\limits_{k_{x}, k_{y}, k_{z}, \omega}\left\|\widetilde{P}-\alpha\left(k_{z}, \omega\right) \widetilde{v}\right\|_{l} $ | (21) |
式中范数阶次l一般取1或2。通过求解式(21),可以得到标定因子,实现对陆检数据的标定处理。
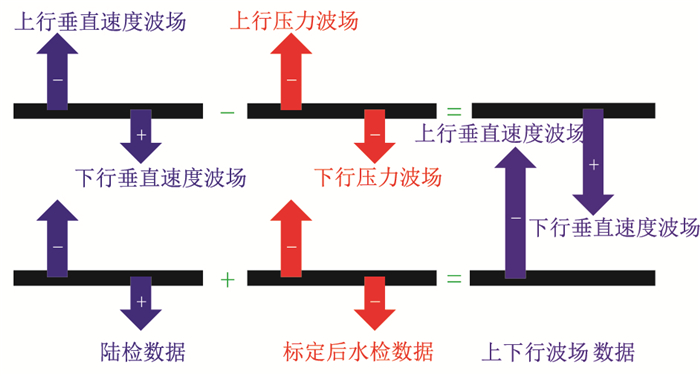
1.3 上下行波场分离双检数据上下行波场分离就是根据水检数据和标定后的陆检数据或者标定后的水检数据和陆检数据,求取上行波场和下行波场。根据式(11),水检数据和标定后陆检数据相减可得到下行压力波场,相加可得到上行压力波场(图 1)。

|
图 1 上下行压力波场分离示意图 |
根据式(12),陆检数据和标定后水检数据相加求和可得上行垂直速度波场,相减可得下行垂直速度波场(图 2)。
|
图 2 上下行垂直速度波场分离示意图 |
针对海洋OBC双检数据,高少武等[32-49]创建了一套完整的双检数据合并处理方法和技术,涉及到数据均方根振幅、标定因子、海底反射系数和海水深度等参数估算。高少武等[32]提出了消除海水鸣震的频率域水陆检数据合并(上行波场)方法,计算公式为
| $ S=\frac{A}{1+\alpha}\left(\frac{\widetilde{P}}{A_{\tilde{P}}}+\alpha \frac{\tilde{v}}{A_{\tilde{v}}}\right) \frac{\left(1-R_{\mathrm{s}} R Z\right)^{2}}{\left(1-R_{\mathrm{s}} R\right)^{2}} $ | (22) |
| $ Z=\exp \left(\mathrm{i} \omega t_{\mathrm{w}}\right) $ | (23) |
式中:S为水、陆检合并处理后数据;α为最佳标定因子;A为合并后数据期望均方根振幅;
式(22)可以实现水、陆检数据合并处理,即分离出的上行压力波场。式(22)中标定因子α前面符号“+”改为“-”,可以得到下行压力波场。
实际双检数据中包含噪声,为了提高抗噪性,高少武等[37]提出了频率域噪声加权的水、陆检数据合并(上行波场)方法,公式为
| $ S=\frac{A}{1+\alpha \beta}\left(\frac{\widetilde{P}}{A_{\tilde{P}}}+\alpha \beta \frac{\tilde{v}}{A_{\tilde{v}}}\right) \frac{\left(1-R_{\mathrm{s}} R Z\right)^{2}}{\left(1-R_{\mathrm{s}} R\right)^{2}} $ | (24) |
| $ \beta=\left(A_{1} A_{2}\right)^{\gamma} $ | (25) |
式中:β为抗噪因子;γ为幂指数;A1为当前地震道陆、水检道集数据平均均方根振幅比;A2为当前地震道水、陆检地震数据均方根振幅比。
高少武等[38]提出了基于镜像虚反射加权的频率域水、陆检数据合并(上行波场)方法,公式为
| $ S=\frac{A}{1+\alpha}\left(\frac{1-Z}{A_{\tilde{P}}} \widetilde{P}+\alpha \frac{1+Z}{A_{\tilde{v}}}{\tilde{v}}\right) \frac{\left(1-R_{\mathrm{s}} R Z\right)^{2}}{\left(1-R_{\mathrm{s}} R\right)^{2}} $ | (26) |
水、陆检数据合并或者上下行波场分离处理之前,必须进行水、陆检数据均方根振幅计算和准确的参数估算。高少武等[35-36]详细论述了水、陆检数据匹配方法和技术,实现了振幅和相位匹配;高少武等[37-38]详细论述了水、陆检数据标定因子估算方法和技术,实现了标定因子参数的准确估算;高少武等[39-40]详细论述了基于波场延迟特征的海底反射系数估算方法和技术,实现了海底反射系数参数准确估算;高少武等[41-44]详细论述了基于数据分段的海水深度估算方法和技术,实现了海水深度参数准确估算。以上研究成果构成了GeoEast系统海上低信噪比OBC/OBN双检地震数据配套和专有的合并处理技术,是该系统软件架构的基础技术和特色技术之一。
3 波场分离技术 3.1 常数标定因子分离技术地震数据大多包含噪声,因此常规处理方法使用能量匹配因子分离上下行波场时,分离出的上行波场中包含下行波场、下行波场中包含上行波场,即不能实现上下行波场完全分离。高少武等[45-48]详细论述了基于波场分离贡献因子的上下行波场分离技术,可以实现常数标定因子水、陆检数据的分离。纯上行波场、纯下行波场数据可表示为
| $ \left\{\begin{array}{l} \hat{U}_{i, j}=W_{P}^{U} P_{i, j}+W_{v}^{U} v_{i, j} \\ \hat{D}_{i, j}=W_{P}^{D} P_{i, j}+W_{v}^{D} v_{i, j} \end{array}\right. $ | (27) |
式中:
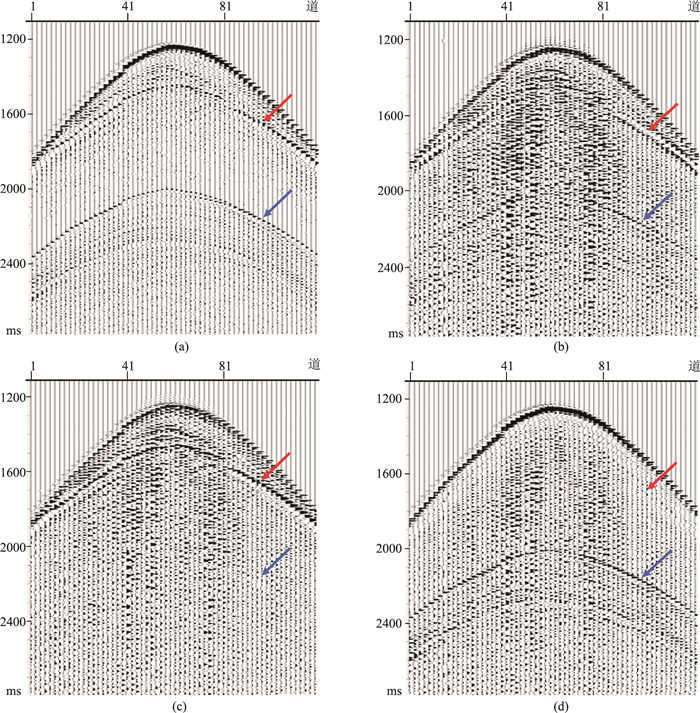
图 3是野外采集OBN共检波点道集数据处理结果对比,可见常数因子标定方法波场分离之后,上行波场(红色箭头)中没有下行波,下行波场(蓝色箭头)中未见上行波,实现了上、下行波场完全分离。
|
图 3 实际共接收点道集数据对比 (a)水检数据;(b)陆检数据;(c)常数因子标定法分离的上行波场数据;(d)常数因子标定法分离的下行波场数据 |
由式(16),有
| $ c=\frac{\omega}{k_{z}} $ | (28) |
将式(28)代入式(11),可得频率—波数域上、下行压力波场[54]
| $ \left\{\begin{array}{l} \hat{U}=\frac{1}{2}\left[\widetilde{P}+\alpha\left(k_{z}, \omega\right) \tilde{v}\right] \\ \hat{D}=\frac{1}{2}\left[\widetilde{P}-\alpha\left(k_{z}, \omega\right) \tilde{v}\right] \end{array}\right. $ | (29) |
将式(28)代入式(12),可得频率—波数域上、下行质点垂直速度波场
| $ \left\{\begin{array}{l} \hat{u}=\frac{1}{2}\left[\widetilde{v}+\frac{\widetilde{P}}{\alpha\left(k_{z}, \omega\right)}\right] \\ \hat{d}=\frac{1}{2}\left[\widetilde{v}-\frac{\widetilde{P}}{\alpha\left(k_{z}, \omega\right)}\right] \end{array}\right. $ | (30) |
Amundsen[54]提出了双检数据上、下行波场镜像分离方法,即
| $ \left\{\begin{array}{l} \hat{U}=\frac{1}{4}\left[G_{-}\left(k_{z}, z_{\mathrm{r}}\right) \widetilde{P}+G_{+}\left(k_{z}, z_{\mathrm{r}}\right) \alpha\left(k_{z}, \omega\right) \tilde{v}\right] \\ \hat{D}=\frac{1}{4}\left[G_{-}\left(k_{z}, z_{\mathrm{r}}\right) \widetilde{P}-G_{+}\left(k_{z}, z_{\mathrm{r}}\right) \alpha\left(k_{z}, \omega\right) \widetilde{v}\right] \end{array}\right. $ | (31) |
式中:zr是接收点深度;G-(kz, zr)是频率—波数域接收点处压力波场虚反射算子;G+(kz, zr)是频率—波数域接收点处质点垂直速度波场虚反射算子[54-56]。G-和G+可表示为
| $ \left\{\begin{array}{l} G_{-}\left(k_{z}, z_{\mathrm{r}}\right)=1-\exp \left(\mathrm{i} 2 k_{z} z_{\mathrm{r}}\right) \\ G_{+}\left(k_{z}, z_{\mathrm{r}}\right)=1+\exp \left(\mathrm{i} 2 k_{z} z_{\mathrm{r}}\right) \end{array}\right. $ | (32) |
式(31)是频率—波数域上、下行压力波场镜像分离公式,不但实现了上、下行波场分离,而且可有效去除接收点虚反射。同理,可以得到频率—波数域上下行质点垂直速度波场镜像分离公式。
3.4 去虚反射分离技术| $ \widetilde{v}=\frac{G_{+}\left(k_{z}, z_{\mathrm{r}}\right)}{G_{-}\left(k_{z}, z_{\mathrm{r}}\right) \alpha\left(k_{z}, \omega\right)} \widetilde{P} $ | (33) |
由于陆检数据包含严重的噪声干扰,因此通常可用式(33)由压力波场导出垂直速度波场,以提高上、下行波场数据信噪比。把式(33)代入式(29),有
| $ \left\{\begin{array}{l} \hat{U}=\frac{\widetilde{P}}{G_{-}\left(k_{z}, z_{\mathrm{r}}\right)} \\ \hat{D}=-\exp \left(\mathrm{i} 2 k_{z} z_{\mathrm{r}}\right) \hat{U} \end{array}\right. $ | (34) |
式(34)表明,对压力波场反褶积后,得到的是上行压力波场,且完全消除了接收点压力波场虚反射;上行压力波场经过波场延拓可得到下行压力波场。Amundsen[54]最早推导出式(34)。
3.5 最优去虚反射分离技术Caprioli等[57]提出了最优去虚反射上、下行波场分离方法,即
| $ \left\{\begin{array}{l} \hat{U}=W_{P} \frac{\widetilde{P}}{G_{-}\left(k_{z}, z_{\mathrm{r}}\right)}+W_{v} \frac{\alpha\left(k_{z}, \omega\right) \tilde{v}}{G_{+}\left(k_{z}, z_{\mathrm{r}}\right)} \\ \hat{D}=W_{P} \frac{\widetilde{P}}{G_{-}\left(k_{z}, z_{\mathrm{r}}\right)}-W_{v} \frac{\alpha\left(k_{z}, \omega\right) \tilde{v}}{G_{+}\left(k_{z}, z_{\mathrm{r}}\right)} \end{array}\right. $ | (35) |
| $ W_{P}=\frac{\frac{G_{-}^{*}}{\sigma_{P}^{2}}}{\frac{G_{-}^{*} G_{-}}{\sigma_{P}^{2}}+\frac{G_{+}^{*} G_{+}}{\alpha^{2}\left(k_{z}, \omega\right) \sigma_{v}^{2}}} $ | (36) |
| $ W_{v}=\frac{G_{+}^{*}}{\frac{G_{-}^{*} G_{-}}{\sigma_{P}^{2}}+\frac{G_{+}^{*} G_{+}}{\alpha^{2}\left(k_{z}, \omega\right) \sigma_{v}^{2}}} $ | (37) |
式中:上标“*”表示复共轭;σP2为水检数据方差;σv2表示陆检数据方差。水、陆检数据方差的引入进一步增加了上、下行波场分离方法的抗噪性,提高了数据的信噪比。
图 4是北海实际叠加数据对比,最优去虚反射分离方法取得了非常好的叠加结果,浅、中、深目的层细节非常清晰。

|
图 4 双检数据上下行波场分离前、后叠加剖面对比 (a)水检数据;(b)陆检数据;(c)常规上行波场数据;(d)最优去虚反射上行波场数据 |
Cambois等[58]提出了基于水、陆检波器脉冲响应的上、下行波场分离方法,即
| $ \left\{\begin{array}{l} \tilde{U}=\frac{1}{2}\left[\frac{\widetilde{P}}{h(\omega)}+\frac{\alpha\left(k_{z}, \omega\right) \tilde{v}}{g(\omega)}\right] \\ \hat{D}=\frac{1}{2}\left[\frac{\widetilde{P}}{h(\omega)}-\frac{\alpha\left(k_{z}, \omega\right) \tilde{v}}{g(\omega)}\right] \end{array}\right. $ | (38) |
式中:h(ω)表示接收点处压力检波器脉冲响应;g(ω)表示接收点处质点垂直速度检波器脉冲响应。式(38)表明,首先对水、陆检数据进行检波器脉冲响应校正,然后再进行标定及上、下行波场分离处理。
3.7 τ-p域分离技术τ-p域分离技术是利用了多次波的周期性。线性τ-p变换是平面波分解过程,在三维τ-p域,海水多次波具有周期性,其周期可表示为[59-60]
| $ T\left(p_{x}, p_{y}\right)=t_{\mathrm{w}} \sqrt{1-c^{2}\left(p_{x}^{2}+p_{y}^{2}\right)} $ | (39) |
式中px、py分别为x、y方向水平慢度。三维τ-p域延迟算子[4]可以表示为
| $ Z=\exp \left[\mathrm{i} \omega T\left(p_{x}, p_{y}\right)\right] $ | (40) |
在三维τ-p域,采用Soubaras[8]的一维近似,水、陆检数据处理包括三步:
(1) 估算一个依赖于频率的标定因子,对陆检数据进行标定处理;
(2) 对水检数据和标定的陆检数据进行求和,实现上、下行波场分离,以衰减虚反射多次波;
(3) 估算反射系数因子,在上、下行波场之间使用自适应相减法,消除剩余的微屈多次波。
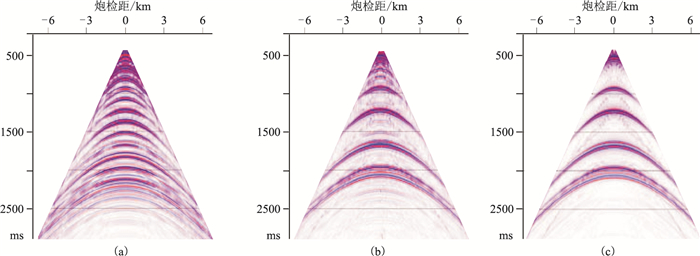
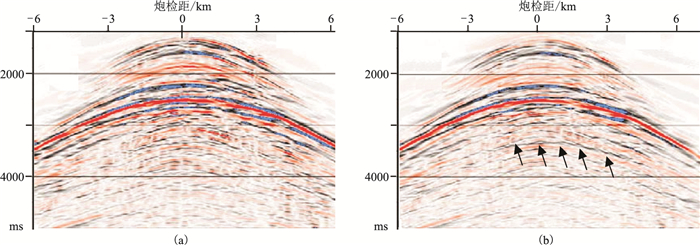
该方法为数据驱动,不需要任何海底参数的先验信息,可以有效压制海水多次波。图 5a是水检合成数据,包含非常严重的海水鸣震干扰;图 5b为三维τ-p域经上述三步处理去除虚反射后上行波场数据,有效去除了海水鸣震和微屈多次波,完全可以与没有海水鸣震的模型数据(图 5c)相匹配。图 6a是实际共接收点道集数据,τ-p域处理后,去除了剩余海水鸣震和微屈多次波干扰,有效信号得到明显增强(图 6b箭头所示)。
|
图 5 合成数据τ-p域波场分离结果 (a)合成水检数据;(b)三维τ-p域去除虚反射后上行波场数据;(c)没有海水鸣震的模型数据 |
|
图 6 实际数据τ-p域波场分离结果对比 (a)常规方法;(b)三维τ-p域去除虚反射分离 |
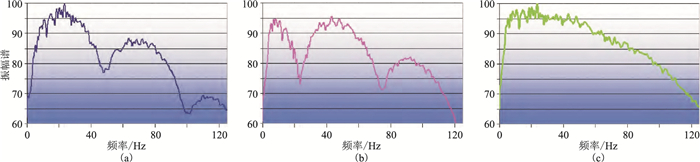
水、陆双检数据处理是一个系统工程,上下行波场分离之前,包括许多预处理环节和步骤。Carlson[61]提出的预处理还包括水、陆检数据检波器脉冲响应校正处理、利用水检数据低频分量计算陆检数据低频分量等技术。图 7为在北海由双检拖缆采集[4]的实际数据上下行波场分离前、后的叠加剖面对比,图 8为图 7数据的频谱,可见,去除虚反射后增强了低频成分和高频成分,提高了信噪比和分辨率。

|
图 7 实际双检数据上下行波场分离前、后叠加剖面对比 (a)水检数据;(b)陆检数据;(c)上行波场 |
|
图 8 双检数据上下行波场分离前、后叠加剖面的振幅谱对比 (a)水检数据;(b)陆检数据;(c)上行波场 |
双检数据上、下行波场分离之前的各种处理,包括匹配和标定等,目的都是实现压力波场(图 7a)与垂直速度波场(图 7b)完全匹配,且频率凹陷实现完全互补(图 8a左和图 8b),此时上、下行波场分离处理才能取得最佳效果(图 7c、图 8c)。
4 结束语(1) 地震波场包括压力波场和质点垂直速度波场;波场可以分解为上行波场和下行波场;上行波场包括上行压力波场和上行垂直速度波场,下行波场包括下行压力波场和下行垂直速度波场。
(2) 上下行波场分离是水、陆检数据处理技术的关键步骤,分离后的上行波场数据,既消除了检波点端虚反射多次波干扰,还提高了地震数据信噪比和分辨率,为后续联合反褶积和偏移成像等处理提供高保真的上行波场和下行波场数据。
(3) 双检数据上下行波场分离之前,必须进行匹配和标定等处理,以使水检数据中上、下行压力波场与陆检数据中上、下行垂直速度波场的振幅、频率和相位完全匹配,且频率陷波完全互补,实现最佳的上、下行波场分离处理。
(4) 水、陆检波器接收机理和制做工艺不同,造成水、陆检波器脉冲响应不同;必须先进行水、陆检波器脉冲响应校正处理,即采用基于检波器脉冲响应的上下行波场分离。
(5) 对于海洋OBC/OBN双检地震数据,要充分利用海洋OBC/OBN数据高密度、宽方位特征,建立一个真正的宽方位双检地震数据标定和上下行波场分离流程,实现高效的双检数据标定和上下行波场分离。
(6) 时间—空间域具有较低速度的线性同相轴,在三维τ-p域,变换成高p值,很容易切除。τ-p域双检数据标定与上下行波场分离方法,克服了时空域一维方法大炮检距数据振幅引入的偏差,有效衰减了炮点端虚反射和接收点端虚反射。
| [1] |
Loewenthal D, Jakubowicz H. Wave equation based source signature deconvolution[C]. SEG Technical Program Expanded Abstracts, 1983, 2: 430-431.
|
| [2] |
Barr F J, Sanders J I. Attenuation of water column reverberations using pressure and velocity detectors in a water-bottom cable[C]. SEG Technical Program Expanded Abstracts, 1989, 8: 653-656.
|
| [3] |
Loewenthal D. On dual field measurements using geohydrophones[C]. SEG Technical Program Expanded Abstracts, 1994, 13: 861-864.
|
| [4] |
Dragoset B, Barr F J. Ocean-bottom cable dual-sensor scaling[C]. SEG Technical Program Expanded Abstracts, 1994, 13: 857-860.
|
| [5] |
Barr F J. Dual-sensor OBC technology[J]. The Lea-ding Edge, 1997, 16(1): 45-51. DOI:10.1190/1.1437427 |
| [6] |
Max D, Ramesh N. OBC multiple suppression with the Texas two-step[C]. SEG Technical Program Expan-ded Abstracts, 2005, 24: 2123-2126.
|
| [7] |
Paffenholz J, Barr F J. An improved method for deriving water-bottom reflectivities for processing dual-sensor ocean-bottom cable data[C]. SEG Technical Program Expanded Abstracts, 1995, 14: 987-990.
|
| [8] |
Soubaras R. Ocean bottom hydrophone and geophone processing[C]. SEG Technical Program Expanded Abstracts, 1996, 15: 24-27.
|
| [9] |
全海燕, 韩立强. 海底电缆双检接收技术压制水柱混响[J]. 石油地球物理勘探, 2005, 40(1): 7-12. QUAN Haiyan, HAN Liqiang. Using OBC dual-receiver to suppress reverberation of water column[J]. Oil Geophysical Prospecting, 2005, 40(1): 7-12. DOI:10.3321/j.issn:1000-7210.2005.01.007 |
| [10] |
王振华, 夏庆龙, 田立新, 等. 消除海底电缆双检地震资料中的鸣震干扰[J]. 石油地球物理勘探, 2008, 43(6): 626-635. WANG Zhenhua, XIA Qinglong, TIAN Lixin, et al. Elimination of singing interference in OBC dual-geophone seismic data[J]. Oil Geophysical Prospecting, 2008, 43(6): 626-635. DOI:10.3321/j.issn:1000-7210.2008.06.003 |
| [11] |
贺兆全, 张保庆, 刘原英, 等. 双检理论研究及合成处理[J]. 石油地球物理勘探, 2011, 46(4): 522-528. HE Zhaoquan, ZHANG Baoqing, LIU Yuanying, et al. Response characteristics of dual-sensor and their applications in OBC data processing[J]. Oil Geophysical Prospecting, 2011, 46(4): 522-528. |
| [12] |
童思友, 向飞, 王东凯, 等. 基于维纳滤波的双检合成鸣震压制技术[J]. 海洋地质前沿, 2012, 28(10): 46-52. TONG Siyou, XIANG Fei, WANG Dongkai, et al. Suppression of reverberation by the technology of dual-sensor merger based on Wiener filtering[J]. Marine Geology Frontiers, 2012, 28(10): 46-52. |
| [13] |
龚旭东, 周滨, 高梦晗, 等. 检波点水深误差对OBC双检资料合并处理的影响与对策[J]. 石油物探, 2014, 53(3): 324-329. GONG Xudong, ZHOU Bin, GAO Menghan, et al. The influence and strategy of water depth error at receivers on dual-sensor summing processing[J]. Geophysical Prospecting of Petroleum, 2014, 53(3): 324-329. DOI:10.3969/j.issn.1000-1441.2014.03.010 |
| [14] |
王兆旗, 杨晓利, 张金陵. 上下行波场反褶积衰减OBC表面多次波方法研究[J]. 地球物理学进展, 2016, 31(6): 2415-2420. WANG Zhaoqi, YANG Xiaoli, ZHANG Jinling. Research on free-surface-related multiple attenuation of ocean-bottom cable data by up/down deconvolution[J]. Progress in Geophysics, 2016, 31(6): 2415-2420. |
| [15] |
梁鸿贤, 秦宁, 高丽. 海底电缆双检资料正演模拟及特征分析[J]. 地球物理学进展, 2017, 32(4): 1798-1802. LIANG Hongxian, QIN Ning, GAO Li. Numerical simulation and feature analysis of OBC dualsensor data[J]. Progress in Geophysics, 2017, 32(4): 1798-1802. |
| [16] |
秦宁. 海底电缆双检资料陆检微分合并技术[J]. 地球物理学进展, 2018, 33(3): 1269-1273. QIN Ning. Merging method using the derivative of geophone data in OBC dual-sensor seismic processing[J]. Progress in Geophysics, 2018, 33(3): 1269-1273. |
| [17] |
卢志君. 海底电缆双检鸣震压制技术研究[D]. 山东青岛: 中国海洋大学, 2012.
|
| [18] |
鲁统祥. OBS多分量地震资料成像处理技术研究[D]. 山东青岛: 中国海洋大学, 2013.
|
| [19] |
张省. OBS多分量地震数据成像关键技术研究[D]. 山东青岛: 中国海洋大学, 2014.
|
| [20] |
廖仪. 南黄海OBS地震资料应用研究[D]. 山东青岛: 中国海洋大学, 2014.
|
| [21] |
王东凯. 浅海OBC资料自由表面多次波压制方法研究[D]. 山东青岛: 中国海洋大学, 2014.
|
| [22] |
李洪建. 海洋宽频地震勘探方法与应用研究[D]. 吉林长春: 吉林大学, 2016.
|
| [23] |
张齐. 海洋地震勘探双检技术去鬼波方法研究[D]. 吉林长春: 吉林大学, 2017.
|
| [24] |
张保庆. 海底双检地震数据质量品质影响因素分析及关键处理技术研究[D]. 北京: 中国石油大学(北京), 2016.
|
| [25] |
薛维忠. OBC双检资料处理技术研究[D]. 山东青岛: 中国石油大学(华东), 2017.
|
| [26] |
王爽. 海底电缆资料合并处理方法研究[D]. 北京: 中国石油大学(北京), 2018.
|
| [27] |
张兴岩. 海底四分量地震资料处理方法研究[D]. 江苏徐州: 中国矿业大学, 2017.
|
| [28] |
陶建. 基于双检匹配的海底地震多次波压制方法研究[D]. 陕西西安: 长安大学, 2019.
|
| [29] |
周丽. OBC多分量的弹性介质时间域全波形反演研究[D]. 湖北武汉: 中国地质大学(武汉), 2017.
|
| [30] |
杨晓明. 海底电缆双检地震数据合并处理关键技术研究[D]. 北京: 中国地质大学(北京), 2019.
|
| [31] |
刘佳. 海洋地震数据鸣震压制及偏移成像研究[D]. 北京: 中国地质大学(北京), 2020.
|
| [32] |
高少武, 钱忠平, 马玉宁, 等. OBC水陆检数据合并处理技术[J]. 石油地球物理勘探, 2018, 53(4): 703-709. GAO Shaowu, QIAN Zhongping, MA Yuning, et al. OBC dual-sensor data combination processing[J]. Oil Geophysical Prospecting, 2018, 53(4): 703-709. |
| [33] |
高少武, 赵波, 罗国安, 等. 一种水陆检波器地震数据合并处理的方法及装置[P]. 中国, ZL201510556940.3, 2015-09-02.
|
| [34] |
高少武, 赵波, 钱忠平, 等. 一种水陆检波器地震数据合并处理的方法及装置[P]. 中国, ZL201710565184. X, 2017-07-12.
|
| [35] |
高少武, 祝宽海. 一种水陆检波器地震数据匹配的方法[P]. 中国, ZL201310531139.4, 2013-10-31.
|
| [36] |
高少武, 赵波, 高轩, 等. OBC水陆检数据匹配技术[J]. 石油地球物理勘探, 2015, 50(1): 29-32. GAO Shaowu, ZHAO Bo, GAO Xuan, et al. A me-thod for OBC dual-sensor data matching[J]. Oil Geophysical Prospecting, 2015, 50(1): 29-32. |
| [37] |
高少武, 黄燕. 一种水陆检波器地震数据标定因子反演的方法[P]. 中国, ZL201310736942.1, 2013-11-29.
|
| [38] |
高轩, 弓小平, 高少武, 等. OBC水陆检数据标定因子估算方法[J]. 石油地球物理勘探, 2016, 51(1): 49-53. GAO Xuan, GONG Xiaoping, GAO Shaowu, et al. Scale factor estimation for OBC dual-sensor seismic data[J]. Oil Geophysical Prospecting, 2016, 51(1): 49-53. |
| [39] |
高少武, 赵波, 罗国安, 等. 一种水陆检波器数据海底反射系数反演的方法[P]. 中国, ZL201410379202.1, 2014-08-04.
|
| [40] |
高少武, 钱忠平, 马玉宁, 等. 基于延迟波场特征法的海底反射系数估算技术[J]. 石油物探, 2018, 57(3): 389-394. GAO Shaowu, QIAN Zhongping, MA Yuning, et al. Estimating ocean bottom reflection coefficient using delayed wavefield charactistic method[J]. Geophysical Prospecting for Petroleum, 2018, 57(3): 389-394. DOI:10.3969/j.issn.1000-1441.2018.03.008 |
| [41] |
高少武, 赵波, 钱忠平, 等. 水陆检波器数据海水深度反演方法和装置[P]. 中国, ZL201410377324.7, 2014-08-01.
|
| [42] |
高少武, 赵波, 钱忠平, 等. 一种确定海水深度的方法及装置[P]. 中国, 201510963991.8, 2015-12-21.
|
| [43] |
高少武, 钱忠平, 孙鹏远, 等. 基于数据分段互双谱的海水深度计算方法[J]. 石油地球物理勘探, 2019, 54(4): 751-756. GAO Shaowu, QIAN Zhongping, SUN Pengyuan, et al. Seawater depth inversion based on segmented data cross-bispectrum[J]. Oil Geophysical Prospecting, 2019, 54(4): 751-756. |
| [44] |
高少武, 钱忠平, 黄少卿, 等. OBC水陆检数据海水深度估算方法[C]. 中国石油学会2017年物探技术研讨会论文集, 天津, 2017.
|
| [45] |
高少武, 钱忠平, 孙鹏远, 等. 水陆检数据上下行波场分离方法[J]. 石油地球物理勘探, 2020, 55(5): 991-996. GAO Shaowu, QIAN Zhongping, SUN Pengyuan, et al. A separation method of up-going and down-going wavefields for dual-sensor seismic data[J]. Oil Geophysical Prospecting, 2020, 55(5): 991-996. |
| [46] |
高少武, 钱忠平, 李建峰, 等. 水陆检数据上下行波场分离[C]. 中国石油学会2019年物探技术研讨会论文集, 四川成都, 2019.
|
| [47] |
高少武, 张少华, 钱忠平, 等. 一种水陆检波器地震数据上下行波场分离方法及装置[P]. 中国, 201810101188.7, 2018-02-01.
|
| [48] |
高少武, 张少华, 王成祥, 等. 海底节点地震数据上下行波场分离的方法及装置[P]. 中国, 201910144556.0, 2019-02-27.
|
| [49] |
高少武. 去除海洋拖缆数据接收点虚反射方法[C]. 勘探地球物理学进展学术研讨会论文集, 四川成都, 2018.
|
| [50] |
Ronen S, Anderson B. Seismic surveillance using redeployed ocean-bottom nodes[J]. The Leading Edge, 2008, 27(12): 1682-1687. DOI:10.1190/1.3036973 |
| [51] |
Tenghamn R, Vaage S, Borresen C. A dual-sensor towed marine streamer: Its viable implementation and initial results[C]. SEG Technical Program Expanded Abstracts, 2007, 26: 989-993.
|
| [52] |
Pharez S, Hendrick N, Tenghamn R. First look at seismic data from a towed dual-sensor streamer[J]. The Leading Edge, 2008, 27(7): 904-907. DOI:10.1190/1.2954031 |
| [53] |
Loewenthal D, Robinson E A. On unified dual fields and Einstein deconvolution[J]. Geophysics, 2000, 65(1): 293-303. DOI:10.1190/1.1444720 |
| [54] |
Amundsen L. Wavenumber-based filtering of marine point-source data[J]. Geophysics, 1993, 58(9): 1335-1348. DOI:10.1190/1.1443516 |
| [55] |
Day A, Klüver T, Söllner W, et al. Wavefield-separation methods for dual-sensor towed-streamer data[J]. Geophysics, 2013, 78(2): WA55-WA70. DOI:10.1190/geo2012-0302.1 |
| [56] |
Amundsen L, Secrest B G, Arntsen B. Extraction of the normal component of the particle velocity from marine pressure data[J]. Geophysics, 1995, 60(1): 212-222. DOI:10.1190/1.1443749 |
| [57] |
Caprioli P B A, Ozdemir A K, Ozbek A, et al. Combination of multi-component streamer pressure and vertical particle velocity: theory and application to data[C]. Extended Abstracts of 74th EAGE Conference and Exhibition, 2012, A033.
|
| [58] |
Cambois G, Carlson D, Jones C, et al. Dual-sensor streamer data: calibration, acquisition QC and attenuation of seismic interferences and other noises[C]. SEG Technical Program Expanded Abstracts, 2009, 28: 142-146.
|
| [59] |
Soudani M T A, Boelle J L, Hugonnet P, et al. 3D methodology for OBC pre-processing[C]. Extended Abstract of 68th EAGE Conference and Exhibition, 2006, B044.
|
| [60] |
Boelle J L, Hugonnet P, Navion S, et al. Wide-azimuth techniques for processing high density 3D OBC data[C]. SEG Technical Program Expanded Abstracts, 2008, 27: 973-977.
|
| [61] |
Carlson D, Söllner W, Tabti H, et al. Increased resolution of seismic data from a dual sensor streamer cable[C]. SEG Technical Program Expanded Abstracts, 2007, 26: 994-998.
|



 高少武, 河北省涿州市华阳东路东方地球物理公司科技园物探技术研究中心, 072751。Email:
高少武, 河北省涿州市华阳东路东方地球物理公司科技园物探技术研究中心, 072751。Email: 