② 中国石化胜利油田分公司石油开发中心, 山东东营 257000
② Petroleum Development Center of Shengli Oilfield, SINOPEC, Dongying, Shandong 257000, China
重力反演作为一种重要的定量解释手段,可以得到地下的密度分布特征,为地质解释提供支持。然而,重力反演的垂向分辨率低、多解性强,制约了其在高精度勘探领域中的应用。上述问题的根本原因在于重力反问题的不适定性。首先,重力资料采集密度低,数据量小,而高分辨率反演需要对地下半空间进行精细的网格剖分,使网格数量(即反演的未知参数数量)远大于数据数量,导致反演方程组严重欠定;其次,重力正演核函数随深度加大而迅速衰减,浅层网格的核函数与深层网格的核函数之间相差多个数量级,反演方程组稳定性差,当反演方程组欠定时,反演结果趋肤。因此,反演结果会被重力数据噪声、网格剖分误差和计算误差等严重污染,分辨率和可靠性均低。
目前,基于广义线性反演理论的重力反演方法已经取得了大量的研究成果,这些方法可大致分为三类。
第一类方法通过增加重力数据数量,改善反演方程组的欠定性。有学者提出了等维反演方法[1-2],综合利用不同高度上的位场数据联合反演,在一定程度上能解决重磁位场反演的“上漂”问题,提高重磁位场异常反演的垂向分辨率。近年来,随着航空重力梯度技术的发展,产生了利用重力梯度张量数据的反演方法[3-4]。另外,还有利用井中重力数据或者重力梯度数据联合地面重力数据反演的方法[5-7]。
第二类方法主要是通过核函数处理以改善反演方程组的适定性。目前,大部分反演方法都可归为该类方法。其中,用深度对核函数加权[8]是最具有代表性和影响力的方法,这种方法能够有效解决反演趋肤的问题。同时,多种与之类似的不同加权方法也被提出[9-10]。此外,各种约束类反演方法,如聚焦约束、平滑约束和先验模型约束等方法[2, 6, 11-13]也被归为第二类。因为约束方程的加入,可被看作是一种对正演核函数矩阵进行行扩展的处理方式。
第三类方法主要是利用某种函数作为密度函数代替离散化的密度模型矢量,减少反演参数数量,从而改善反演方程组的适定性。该类方法通常要求根据密度函数具体形式推导不同的正演公式。近年来,在重磁正演领域已经出现了大量研究成果,可以实现复杂形体的不同形式密度函数的变密度正演[14-16],但目前这些成果在反演领域的应用较少。刘洁等[17]利用高阶多项式作为密度函数实现了重力反演,但是多项式函数是连续平滑的,模型表达能力有限,而表达能力强的密度函数,其正演公式往往推导难度大,甚至无法推导解析公式。为了解决复杂函数形式正演公式推导难的问题,Tontini等[18]仍采用核函数矩阵,利用高斯函数生成模型矢量,提出了一种高斯包络磁力反演方法。该方法虽然没有对正演公式进行改进,但是与现在机器学习领域的压缩感知[19-20]和字典学习等技术[21-22]的核心思想有着异曲同工之处。
与广义线性反演不同,基于神经网络的重力反演方法是一种非线性反演方法[23-24]。此类方法的特点在于采用分层结构,网络结构清晰,神经元节点采用感知机模型,反向传播训练算法易于实现,鲁棒性强。神经网络反演方法分为训练和预测两个步骤,通过样本数据集(重力场—密度模型对)训练神经网络,建立重力场和对应模型的非线性映射关系;再在预测步骤里将实测重力场输入,神经网络输出预测密度模型,即反演结果。基于神经网络的重力反演方法存在以下几个方面的问题:第一,建立训练数据集困难,训练数据集中需要包含大量不同类型的模型和重力场,否则,实用效果大打折扣,而设计不同的模型并计算其重力场工作量巨大;第二,基于感知机模型的单隐层神经网络非线性映射能力弱,难以解决复杂非线性问题,使用深层网络则存在过拟合、梯度消失、梯度爆炸等问题,训练困难;第三,神经网络隐层可解释性差,尤其是深层神经网络,每层对应的物理意义不明确。针对神经网络存在的问题,有学者提出了拟神经网络的反演方法[25-26]。模拟神经网络的分层结构,但不需要样本数据集训练,且网络层具有较好的可解释性。但是,前人提出的拟神经网络各层定义不清晰,层间耦合严重,神经元多采用Sigmoid激活函数,模型表达能力弱。
本文在梳理了大量已有的重力反演方法基础上,提出了一种利用径向基函数(Radial Basis Function,RBF)的拟神经网络重力反演方法。该方法利用高斯径向基函数压缩模型空间,在保证复杂模型表达能力的前提下,实现反演参数的降维;提出一种拟神经网络结构,不需要训练样本标签,可以克服建立训练数据集的困难。理论模型试算和实际资料应用表明,基于该网络结构实现的重力反演提高了垂向分辨率,同时增强了可靠性,并且具有较强的抗噪能力。
1 方法原理 1.1 高斯径向基函数径向基函数是沿径向对称的标量函数,通常被定义为空间中任一点到某一中心点之间欧氏距离的单调函数。其作用往往是局部的,即当空间某点远离中心点时,函数取值很小,调整局部函数值大小和作用范围可以灵活地拟合复杂函数。本文采用最常用的高斯径向基函数,它在计算机视觉、人工智能、图像压缩和数据拟合等领域有着广泛的应用。其三维公式为
| $ \begin{aligned} \text {Gauss}_{3\mathrm{D}} &=\exp \left[-\frac{\left(x-\mu_{x}\right)^{2}}{2 \delta_{x}^{2}}-\right.\\ &\left.\frac{\left(y-\mu_{y}\right)^{2}}{2 \delta_{y}^{2}}-\frac{\left(z-\mu_{z}\right)^{2}}{2 \delta_{z}^{2}}\right] \end{aligned} $ | (1) |
式中:(x,y,z)是网格中心坐标;(μx,μy,μz)是径向基函数中心坐标;δx、δy、δz是径向基函数分布半径。二维公式则为
| $ \operatorname{Gauss}_{2 \mathrm{D}}=\exp \left[-\frac{\left(x-\mu_{x}\right)^{2}}{2 \delta_{x}^{2}}-\frac{\left(z-\mu_{z}\right)^{2}}{2 \delta_{z}^{2}}\right] $ | (2) |
根据高斯函数拟合原理[27],密度模型可以表示为多个不同振幅的高斯函数的叠加求和,即
| $ \rho = \sum\limits_{i = 1}^{{N_{\rm{G}}}} {{W_i}} {{\mathop{\rm Gauss}\nolimits} _i} $ | (3) |
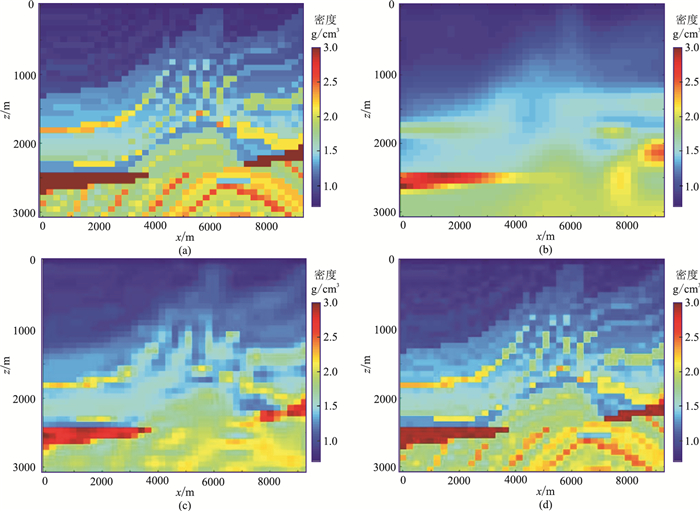
式中:NG是高斯径向基函数个数;Wi是第i个高斯径向基函数的振幅。高斯径向基函数具有很强的模型表达能力,使用远少于剖分网格个数的高斯径向基函数就可以对复杂模型进行较高精度地拟合。对于图 1a复杂模型,分别使用不同数量的高斯径向基函数拟合,效果如图 1b~图 1d所示。由图可见,当仅用25个高斯径向基函数拟合模型时,尽管分辨率较低,但已经能较好地恢复模型的背景;随着高斯径向基函数数量的增加,越来越多的模型细节被恢复。为保证反演方程组不欠定,用于表示密度模型的高斯径向基函数的数量理论上应该满足ND/NG≥5(二维反演)和ND/NG≥7(三维反演),其中ND是重力数据的数量。但是,后文中模型试验和实测资料反演结果表明,ND/NG低于上述比例时亦可获得较好效果。
|
图 1 复杂模型(a)及25(b)、100(c)、400(d)个高斯径向基函数的拟合结果 |
本文采用常密度立方体重力公式[28]作为正演公式,即
| $ \boldsymbol{g}=\boldsymbol{K}{\rho} $ | (4) |
式中K是核函数矩阵,即
| $ K = \sum\limits_{u = {u_1}}^{{u_2}} {\sum\limits_{v = {v_1}}^{{v_2}} {\sum\limits_{w = {w_1}}^{{w_2}} {\left[ {u\ln (v + R) + v\ln (u + R) + w\arctan \left( {\frac{{uv}}{{wR}}} \right)} \right]} } } $ | (5) |
式中:
| $ \boldsymbol{g} = \boldsymbol{K}\sum\limits_{i = 1}^{{N_G}} {{W_i}} {\rm{Gaus}}{{\rm{s}}_i} $ | (6) |
由于高斯径向基函数是径向基函数中心和分布半径的非线性函数,因此重力正演公式由线性变成了非线性,反演参数由网格密度变成了径向基函数的振幅W、中心(μx,μy,μz)和半径(δx,δy,δz)。式(6)仍然保留正演核函数矩阵,与采用g= f(m)形式的正演公式相比,具有以下优点。
正演核函数矩阵仅是观测点和网格坐标的函数,与密度解耦,在反演过程中只需计算一次,因而避免了计算量最大部分的重复计算。每次迭代只需计算高斯径向基函数生成密度矢量,增加的计算量很小,而不能将密度解耦的非线性正演公式在每次迭代时,都需要进行计算量巨大的正演和灵敏度矩阵计算。
式(6)的形式与压缩感知理论有着很好的对应关系。其中,核函数矩阵对应测量矩阵,高斯径向基函数生成稀疏基矩阵,高斯径向基函数的振幅对应稀疏系数。因此,可借鉴、应用压缩感知的相关理论和技术。当固定径向基函数的中心和半径而只是反演振幅时,可利用压缩感知的稀疏性原理实现稀疏约束反演,经典算法有OMP[29]和LASSO算法[30];当同时反演径向基函数的振幅、中心和半径时,可以利用字典学习技术中经典的MOD[31]和KSVD算法[21]快速实现。
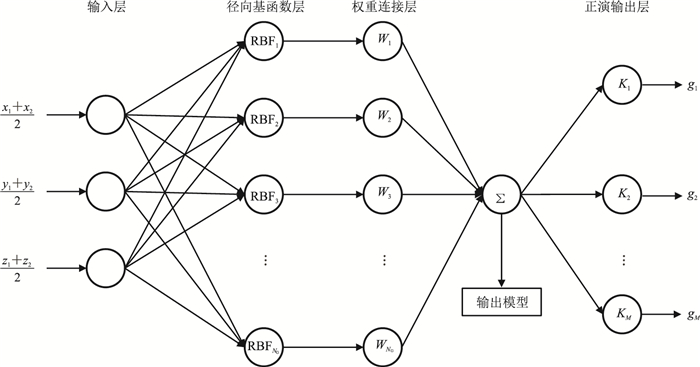
1.3 基于高斯径向基函数的拟神经网络在定义了基于高斯径向基函数的重力正演公式之后,本文提出了一种如图 2所示的拟神经网络结构。该网络由输入层、径向基函数层、权重连接层和正演输出层组成。其中,径向基函数层的节点为高斯径向基函数,权重连接层的节点为高斯径向基函数振幅,正演输出层的节点为重力正演核函数。与传统神经网络相比,本文提出的拟神经网络主要有以下几点不同。
|
图 2 径向基函数的拟神经网络结构图 M为观测点数量 |
(1) 本文方法的输入数据是模型网格中心的坐标,而传统神经网络重力反演方法中输入数据通常为重力样本数据集。
(2) 本文方法的输出数据是正演重力值,而传统神经网络重力反演方法中输出数据通常为密度模型数据集。
(3) 本文方法的损失函数是计算正演重力数据与实测重力数据之间的残差,而传统神经网络重力反演方法中损失函数是计算预测密度模型与密度模型样本之间的残差。损失函数的不同决定了神经网络各层的含义不同,本文拟神经网络各层可解释性清晰、明确,而传统神经网络中,若存在多个隐含层,则各层可解释性不明确,只能将整个网络解释为重力正演函数的反函数。
(4) 本文方法在训练结束后,径向基函数权重连接层的输出即为最终反演结果,即密度模型。而传统神经网络重力反演方法中,先使用样本数据集训练神经网络,再利用训练后的神经网络执行预测步骤,在网络输出层获得最终反演结果。
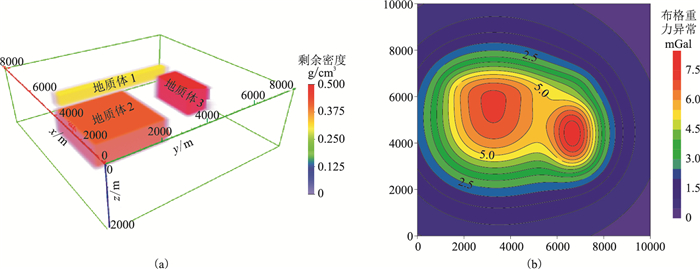
2 理论模型测试为了验证本文方法的有效性,在文献[32]中的实验模型基础上设计了三维组合模型。如图 3a所示,模型大小为9240m×9240m×3040m,模型网格剖分为15×15×10个小长方体。三个地质异常体(简称地质体)中,地质体1(黄色)的剩余密度为0.3g/cm3,尺寸为616m×6160m×608m,中心埋深为912m;地质体2(桔色)的剩余密度为0.4g/cm3,尺寸为3696m×3696m×1216m,中心埋深为2128m;地质体3(红色)的剩余密度为0.5g/cm3,尺寸为2464m×1232m×1216m,中心埋深为1216m。地质体1和地质体2为垂向叠置。观测系统范围x方向为0~10000m,y方向为0~10000m,观测点高度为0,每个方向均匀设置20个观测点。正演重力场如图 3b所示。
|
图 3 理论模型(a)及正演重力场(b) |
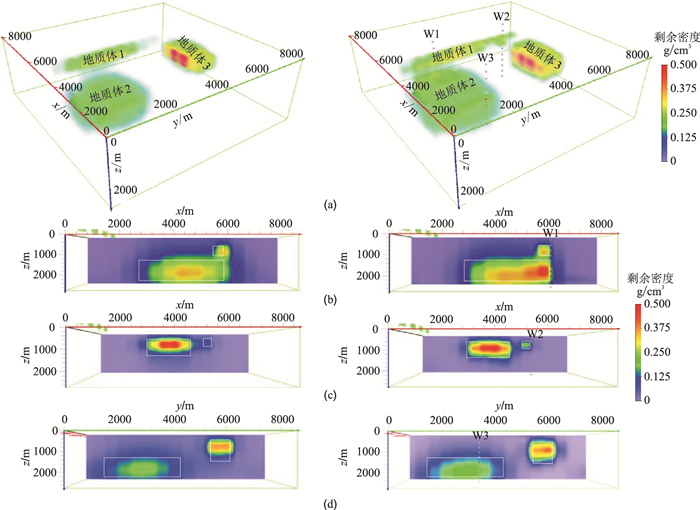
实验一采用与正演网格相同的剖分方案,即初始模型剖分为15×15×10个小长方体,径向基函数中心初始设置为在地下剖分空间均匀分布,x方向5个,y方向5个,z方向5个,径向基函数层共有5×5×5=125个节点,权重连接层初始权重均设为0,数据和径向基函数数量的比值为ND/NG=3.2,学习率为0.1,最大训练次数为2000,训练精度为1×10-6,训练算法为自适应距估计算法,反演结果如图 4所示。由图可见,无井约束反演可以恢复地质体的形态(图 4左),其中,地质体1的边界较为尖锐,与地质体2垂向叠加部分得到准确分离,但接近地质体3的部分较为模糊;地质体3的边界非常清晰,但下界面偏浅;地质体2的顶界面较准确,但因为埋深加大,边界较为模糊。有井约束反演可以使地质体1和2的边界更加清晰(图 4右),地质体3的下界面更接近真实深度。实验结果证明:由于反演参数的减少,在不施加任何约束的情况下,重力反演亦能获得较高的横向和垂向分辨率,垂向叠加的地质体能够准确恢复;在施加先验约束信息后,反演结果的横向和垂向分辨率得以提高,地质体的边界反演精度更高。
|
图 4 实验一无井(左)和有井(右)约束反演结果 (a)重力反演结果;(b)过W1井的x方向反演剖面;(c)过W2井的x方向反演剖面;(d)过W3井的y方向反演剖面。三口井坐标分别为(6450m,2770m)、(6450m,6450m)和(3380m,3380m),图 5同 |
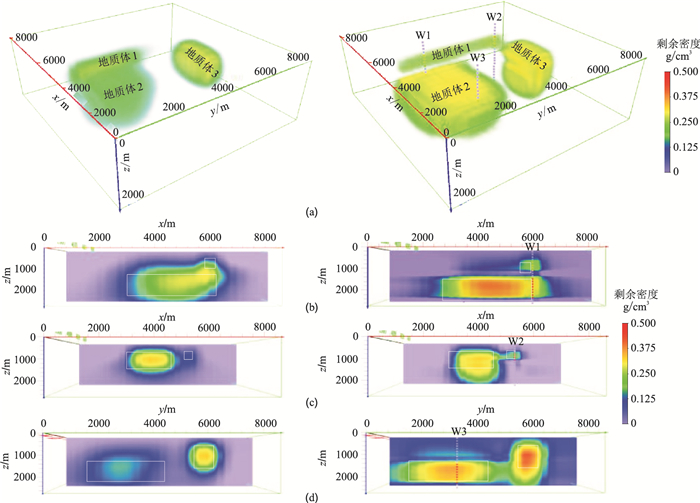
实验二的初始模型剖分为31×31×21个小长方体,对重力异常添加3%的白噪声,模拟在反演实测重力时存在网格剖分误差和数据噪声的情况,其他参数设置与实验一相同。反演结果如图 5所示。由图可见,无井约束反演结果横向和垂向分辨率远低于图 4(图 5左)。除网格剖分误差和数据噪声外,网格剖分数量是造成分辨率下降的主要原因。实验二的网格数量是实验一的8倍多,导致正演核函数矩阵的性状(条件数、列相关性)变差。尽管反演参数数量没有变化,但是在残差反向传播过程中,受到正演核函数矩阵性状变差的影响,反演分辨率下降。有井约束反演结果横向和垂向分辨率提高很大(图 5右),除了地质体1与地质体3相邻处和地质体3的下界面有些模糊外,整体反演效果甚至优于图 4中的约束反演,尤其是地质体2不仅与垂向叠加的地质体1准确分离,而且边界更接近真实模型。实验结果说明:在无约束信息时,模型网格剖分数量不宜过多;但是加入少量先验约束信息,即使在正演核函数矩阵性状很差时(即网格数量远大于重力数据数量时),仍可以得到较理想的反演结果。本文方法能够充分利用先验信息的约束作用,并具有良好的抗噪性能。
|
图 5 实验二无井(左)和有井(右)约束反演结果 (a)重力反演结果;(b)过W1井的x方向反演剖面;(c)过W2井的x方向反演剖面;(d)过W3井的y方向反演剖面 |
为检验方法的实用性,对车镇凹陷的重力资料进行反演,开展古潜山和洼陷的识别。
渤海湾盆地是叠置在华北克拉通基底之上的中、新生代断陷盆地,济阳坳陷是渤海湾盆地的坳陷之一,依据地层与潜山的关系大致可以将地层划分为两个构造层,即潜山内幕层和盖层。潜山内幕层由鲁西地块的基底、太古界泰山群、古生界和中生界组成;盖层由古近系孔店组、沙河街组、东营组和新近系馆陶组、明化镇组及第四系平原组组成。车镇凹陷是济阳坳陷最北部的一个凹陷,南北夹于义和庄凸起与埕子口凸起之间,西为庆云凸起,地表为第四系覆盖。该区地层密度特征如表 1所示。
|
|
表 1 车镇凹陷地层密度统计表 |
密度资料显示,馆陶组与东营组、沙一段与沙二段、上下古生界之间存在密度界面。由区域地质背景可知,东营组沉积后,构造运动导致的界面起伏不大,对重力异常形态的影响较小。下古生界起伏变化大,直接影响重力异常形态。下古生界与上覆地层构成的密度界面为主要密度界面,依据地层与潜山的关系,大致可以将该密度界面作为车镇凹陷的潜山顶界面。该区潜山表现为高密度、高阻抗的特征。相较于潜山,潜山之上地层呈现低密度特征。潜山与上覆地层的密度差最大可达0.18g/cm3,这为利用重力资料研究潜山构造提供了物性基础[17, 33]。
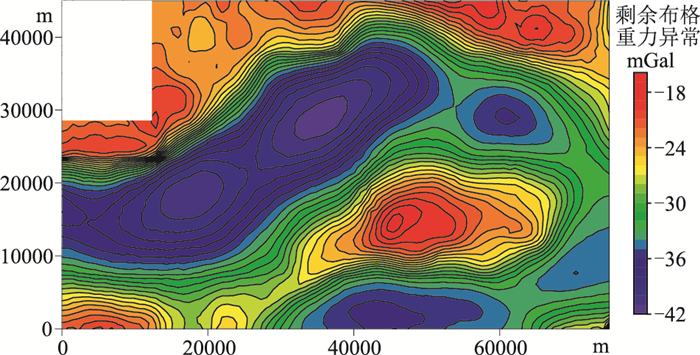
对研究区布格重力异常采用延拓分离法进行场分离,得到剩余布格重力异常(图 6)。由图可见,重力低值区对应断陷或凹陷,重力高值区对应基底隆起,相互之间吻合关系较好。重力高值区与低值区之间有较明显的梯度带出现,反映凹凸之间为断裂或者地层产状突变。
|
图 6 车镇凹陷剩余布格重力异常 |
将重力覆盖区域剖分成为500m×500m×250m的立方体网格,反演深度为8km,网格总数约为49.5万个。在x、y、z方向分别设置15、25、8个径向基函数,共计有3000个,在地下空间均匀分布。初始权重均设为0,重力观测点为20181个。数据量与径向基函数数量的比值为ND/NG=6.727。根据研究区地层密度资料,结合剩余布格重力异常的值域范围,通过多次实验、分析后确定了剩余密度的下限为-0.75g/cm3。反演得到的三维剩余密度模型如图 7所示,模型的剩余密度范围为-0.75~0.05g/cm3,与研究区地层密度最大值和最小值的差异范围基本一致。

|
图 7 车镇凹陷三维剩余密度模型 |
根据地层密度的统计结果,提取研究区下古生界的密度界面制作下古生界顶面构造图,如图 8所示。密度界面清晰地反映了车镇地区下古生界的分布情况,最深处位于大王北洼陷,最浅处位于埕子口凸起西部。研究区两凸一凹的格局非常清楚,埕子口凸起及义和庄凸起上的洼突分布比较明显,较低洼处反映为古冲沟。凹陷内不仅各级次洼清晰,凹陷深部的潜山也较清晰。另外,还清晰地显示了埕南大断层上的台阶状断块及义和庄凸起北部缓坡带上的近北东向断裂。

|
图 8 车镇凹陷下古生界顶面构造图黄线为图 9中剖面位置 |
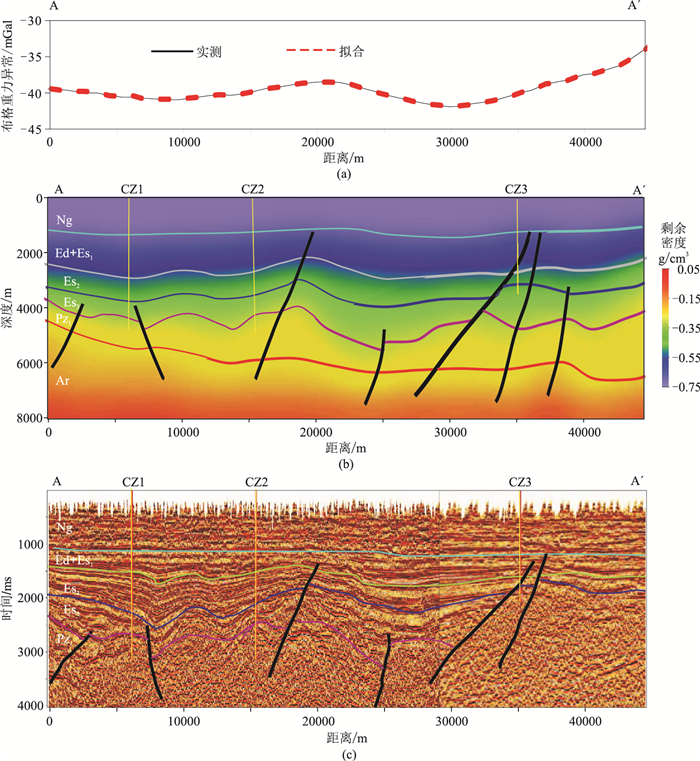
从三维剩余密度模型中提取剖面与相邻的地震剖面进行对比(图 9)。由图可见,实测重力异常与拟合重力异常的误差非常小,重力高、低值区与构造凸凹之间对应关系很好(图 9a)。地震剖面上(图 9c)新生界成像清晰,且与剩余密度剖面(图 9b)形态对应关系较好。参考地震层位解释方案,在密度剖面解释了新生界层位。因为地震剖面为时间域剖面,所以剩余密度剖面的解释方案与地震解释方案形态相似但不完全相同。地震剖面上新生界以下的地层成像较差,根据钻井资料在剖面左侧可以解释下古生界顶界面,而剖面右侧则难以解释。在剩余密度剖面上,可根据密度分布解释下古生界和太古界顶界面,下古生界顶界面左侧与地震解释方案基本一致,由此推断右侧的解释方案具有较高的可信度。太古界顶界面在地震剖面上无法识别,剩余密度剖面上所解释的太古界顶界面虽无法证实,但可作为研究深层目标的参考。
|
图 9 剩余密度剖面与地震剖面对比 (a)实测与拟合重力异常;(b)剩余密度剖面;(c)地震剖面 |
本文利用高斯径向基函数作为激活函数,定义了一种结构清晰明确的拟神经网络,在保证复杂模型表征能力的前提下,降低了重力反演参数的数量,改善了重力反演的不适定性,能够更充分的利用重力数据所包含的信息,反演结果更客观。模型实验表明在无约束或少量先验信息约束的情况下,本文方法可以获得较高横向和垂向分辨率的反演结果。将本文方法应用于车镇凹陷,得到的剩余密度模型与钻井、地震资料解释成果吻合度较高,较好地揭示了该地区下古生界的构造格局与潜山发育规律,检验了本文方法反演实测资料的有效性。车镇凹陷密度模型是在未施加层位和钻井等强约束信息的情况下反演得到的,证明该方法在低勘探程度区具有较大的实用价值和应用潜力。
| [1] |
张永明, 张贵宾. 二维重力"等维"反演研究[J]. 工程地球物理学报, 2009, 6(2): 137-142. ZHANG Yongming, ZHANG Guibin. Research on the equivalent dimensions of 2-D gravity[J]. Chinese Journal of Engineering Geophysics, 2009, 6(2): 137-142. DOI:10.3969/j.issn.1672-7940.2009.02.002 |
| [2] |
王逸宸. 重力等维聚焦反演研究[D]. 北京: 中国地质大学(北京), 2014. WANG Yichen. Study of Equidimension Focusing Inversion of Gravity Data[D]. China University of Geosciences(Beijing), Beijing, 2014. |
| [3] |
王浩然, 陈超, 杜劲松. 重力梯度张量数据的三维反演方法与应用[J]. 石油地球物理勘探, 2013, 48(3): 474-481. WANG Haoran, CHEN Chao, DU Jinsong. 3-D inversion of gravity gradient tensor data and its application[J]. Oil Geophysical Prospecting, 2013, 48(3): 474-481. |
| [4] |
耿美霞. 基于地质统计学的重力梯度全张量数据三维反演方法研究[D]. 吉林长春: 吉林大学, 2015. GENG Meixia. The Study of 3D Inversion of Full Tensor Gravity Gradiometry Data Based on Geostatistics Method[D]. Jilin University, Changchun, Jilin, 2015. |
| [5] |
Sun J J, Li Y G. Inversion of surface and borehole gra-vity with thresholding and density constraints[C]. SEG Technical Program Expanded Abstracts, 2010, 29: 1798-1803.
|
| [6] |
秦朋波, 黄大年. 重力和重力梯度数据联合聚焦反演方法研究[J]. 地球物理学报, 2016, 59(6): 2203-2224. QIN Pengbo, HUANG Danian. Integrated gravity and gravity gradient data focusing inversion[J]. Chinese Journal of Geophysics, 2016, 59(6): 2203-2224. |
| [7] |
王泰涵, 马国庆, 熊盛青, 等. 空-地-井重力异常正则化协同密度反演方法[J]. 地球物理学报, 2020, 63(7): 2737-2750. WANG Taihan, MA Guoqing, XIONG Shengqing, et al. Joint regularized density inversion method of airborne, surface and borehole gravity anomaly data[J]. Chinese Journal of Geophysics, 2020, 63(7): 2737-2750. |
| [8] |
Li Y G, Oldenburg D W. 3-D inversion of magnetic data[J]. Geophysics, 1996, 61(2): 394-408. DOI:10.1190/1.1443968 |
| [9] |
Portniaguine O, Zhdanov M S. 3-D magnetic inversion with data compression and image focusing[J]. Geophysics, 2002, 67(5): 1532-1541. DOI:10.1190/1.1512749 |
| [10] |
Zhdanov M S. Geophysical Inverse Theory and Regularization Problems[M]. Salt Lake City: Elsevier Science, 2002.
|
| [11] |
彭国民, 刘展, 于会臻, 等. 基于柯西分布约束和快速近端目标函数优化的三维重力反演方法[J]. 地球物理学报, 2018, 61(12): 4934-4941. PENG Guomin, LIU Zhan, YU Huizhen, et al. 3D gravity inversion based on Cauchy distribution constraint and fast proximal objective function optimization[J]. Chinese Journal of Geophysics, 2018, 61(12): 4934-4941. DOI:10.6038/cjg2018L0776 |
| [12] |
谷文彬, 陈清礼, 王余泉, 等. 饶阳凹陷虎8北潜山重力三维松约束反演[J]. 石油地球物理勘探, 2016, 51(6): 1219-1226. GU Wenbin, CHEN Qingli, WANG Yuquan, et al. Part-constrained 3D gravity inversion for the Hubabei buried hill in Raoyang Sag[J]. Oil Geophysical Prospecting, 2016, 51(6): 1219-1226. |
| [13] |
李海龙, 吴招才, 纪飞, 等. 南海北部地壳密度结构: 基于约束三维重力反演[J]. 地球物理学报, 2020, 63(5): 1894-1912. LI Hailong, WU Zhaocai, JI Fei, et al. Crustal density structure of the South China Sea from constrained 3-D gravity inversion[J]. Chinese Journal of Geophysics, 2020, 63(5): 1894-1912. |
| [14] |
Ren Z Y, Zhong Y Y, Chen C J, et al. Gravity anomalies of arbitrary 3D polyhedral bodies with horizontal and vertical mass contrasts up to cubic order[J]. Geophysics, 2018, 83(1). |
| [15] |
Wu L. Fourier-domain modeling of gravity effects caused by polyhedral bodies[J]. Journal of Geodesy, 2018, 93(6): 1-19. |
| [16] |
周印明, 戴世坤, 李昆, 等. 复杂形体重磁位场三维高效高精度数值模拟[J]. 石油地球物理勘探, 2020, 55(5): 1149-1159, 1168. ZHOU Yinming, DAI Shikun, LI Kun, et al. Three-dimensional high-efficiency and high-precision numerical simulation of gravity and magnetic potential fields of complex body[J]. Oil Geophysical Prospecting, 2020, 55(5): 1149-1159, 1168. |
| [17] |
刘洁, 张建中, 江丽, 等. 基于高阶多项式密度函数的重力反演[J]. 石油地球物理勘探, 2019, 54(3): 700-708. LIU Jie, ZHANG Jianzhong, JIANG Li, et al. Gravity inversion by high-order polynomial function of density contrast varying with depth[J]. Oil Geophysical Prospecting, 2019, 54(3): 700-708. |
| [18] |
Tontini F C, Faggioni O, Beverini N, et al. Gaussian envelope for 3D geomagnetic data inversion[J]. The Leading Edge, 2003, 68(13): 996-1007. |
| [19] |
Donoho D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306. DOI:10.1109/TIT.2006.871582 |
| [20] |
Candès E J. The restricted isometry property and its implications for compressed sensing[J]. Comptes Rendus Mathematique, 2008, 346(9-10): 589-592. DOI:10.1016/j.crma.2008.03.014 |
| [21] |
Aharon M, Elad M, Bruckstein A. K-SVD: An algorithm for designing overcomplete dictionaries for sparse re-presentation[J]. IEEE Transactions on Signal Proce-ssing, 2006, 54(11): 4311-4322. DOI:10.1109/TSP.2006.881199 |
| [22] |
Elad M, Aharon M. Image denoising via sparse and redundant representations over learned dictionaries[J]. IEEE Tip, 2006, 15: 3736-3745. |
| [23] |
郭文斌, 朱自强, 鲁光银. 重力异常的BP神经网络三维物性反演[J]. 地球物理学进展, 2012, 27(2): 409-416. GUO Wenbin, ZHU Ziqiang, LU Guangyin. 3-D gra-vity inversion for physical properties using BP network[J]. Progress in Geophysics, 2012, 27(2): 409-416. DOI:10.6038/j.issn.1004-2903.2012.02.004 |
| [24] |
耿美霞, 杨庆节. 应用RBF神经网络反演二维重力密度分布[J]. 石油地球物理勘探, 2013, 48(4): 651-657. GENG Meixia, YANG Qingjie. 2-D density inversion with RBF neural network method[J]. Oil Geophysical Prospecting, 2013, 48(4): 651-657. |
| [25] |
朱自强, 程方道, 黄国祥. 同时反演两个三维密度界面的拟神经网BP算法[J]. 石油物探, 1995, 34(1): 76-85. ZHU Ziqiang, CHENG Fangdao, HUANG Guoxiang. Quasi neural network BP algorithm for simultaneous inversion of two 3-D density interfaces[J]. Geophysical Prospecting for Petroleum, 1995, 34(1): 76-85. |
| [26] |
管志宁, 侯俊胜, 黄临平, 等. 重磁异常反演的拟BP神经网络方法及其应用[J]. 地球物理学报, 1998, 41(2): 242-251. GUAN Zhining, HOU Junsheng, HUANG Linping, et al. Inversion of gravity and magnetic anomalies using pseudo-BP neural network method and its application[J]. Chinese Journal of Geophysics, 1998, 41(2): 242-251. DOI:10.3321/j.issn:0001-5733.1998.02.013 |
| [27] |
唐冲, 惠辉辉. 基于Matlab的高斯曲线拟合求解[J]. 计算机与数字工程, 2013, 41(8): 1262-1263. TANG Chong, HUI Huihui. Gaussian curve fitting solution based on Matlab[J]. Computer & Digital Engineering, 2013, 41(8): 1262-1263. DOI:10.3969/j.issn.1672-9722.2013.08.016 |
| [28] |
Li X, Chouteau M. Three-dimensional gravity mode-ling in all space[J]. Surveys in Geophysics, 1998, 19(4): 339-368. DOI:10.1023/A:1006554408567 |
| [29] |
Tropp J A, Gilbert A C. Signal recovery from random measurements via orthogonal matching pursuit[J]. IEEE Transactions on Information Theory, 2007, 53(12): 4655-4666. DOI:10.1109/TIT.2007.909108 |
| [30] |
Lin J, Li S. Sparse recovery with coherent tight frames via analysis Dantzig selector and analysis LASSO[J]. Applied and Computational Harmonic Analysis, 2013, 37(1): 126-139. |
| [31] |
Engan K, Aase S O, Hakon Husoy J. Method of optimal directions for flame design[C]. Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing, Phoenix, USA, 1999, 2443-2446.
|
| [32] |
Fernando J S, Valéria C F, João B C. 3D gravity inversion through an adaptive-learning procedure[J]. Geophysics, 2009, 74(3): I9-I21. DOI:10.1190/1.3092775 |
| [33] |
胡加山, 胡贤根, 崔世凌. 东营凹陷典型剖面重磁电震综合解释方法研究[J]. 石油物探, 2009, 48(4): 401-406. HU Jiashan, HU Xian'gen, CUI Shiling. Gravity-magnetic-electric-seismic integrated interpretation method for typical profile of Dongying sag[J]. Geophysical Prospecting for Petroleum, 2009, 48(4): 401-406. DOI:10.3969/j.issn.1000-1441.2009.04.013 |



 相鹏, 山东省东营市北一路863号胜利油田分公司勘探开发研究院, 257000。Email:
相鹏, 山东省东营市北一路863号胜利油田分公司勘探开发研究院, 257000。Email: 