② 东华理工大学地球物理与测控技术学院, 江西南昌 330013;
③ 安徽省勘查技术院, 安徽合肥 230041
② School of Geophysics and Measurement-control Technology, East China University of Technology, Nanchang Jiangxi 330013, China;
③ Geological Exploration Technology Institute of Anhui Province, Hefei, Anhui 230041, China
地球物理单一方法的局限性、反演的多解性以及地质条件的复杂性使得联合反演成为地球物理领域的必然发展趋势[1]。联合反演是一种定量的综合地球物理解释技术,可以减少解的非唯一性。随着地球物理勘探向地球深部发展,联合反演的优势也越加突显[2-4]。基于线性优化算法的联合反演收敛速度快,但容易陷入局部极小。基于非线性优化算法的联合反演具有全局寻优、无需求偏导数矩阵、便于先验信息融入等特点。目前,很多非线性优化算法在地球物理联合反演领域得到了广泛应用,如模拟退火算法[5-7]、遗传算法[8-9]、差分进化算法[10-11]、人工鱼群算法[12]等。可见基于非线性优化算法的联合反演是地球物理联合反演领域的一个重要发展方向。
人工蜂群(ABC)算法是Karaboga[13]于2005年提出的一种非线性优化算法。在该算法中,存在引领蜂、跟随蜂和侦察蜂,每种蜜蜂各司其职,并存在独特的角色转换机制。由于该算法是一种较新颖的优化算法,相比传统的非线性优化算法(如模拟退火、遗传算法等),该算法在地球物理反演领域的应用相对偏少。王猛等[14]将ABC算法应用于瞬变电磁测深资料反演,并指出ABC算法可以提高瞬变电磁资料的解释精度;候征等[15]将ABC算法用于一维瑞雷波多阶模式联合反演,研究结果表明该算法可提高反演精度;Wen等[16]将该算法应用于某煤矿2.5维CSAMT数据反演,揭示出疑似陷落柱的地电结构。需要指出的是,ABC算法虽然具有较好的探索能力,但局部搜索能力较弱,收敛相对较慢[17-18]。引领蜂在蜜源附近搜索时,只随机地对解的某一个分量进行更新,当待解参数较多时,这样搜索方式效率偏低。此外,优质蜜源对蜂群影响不足。
在非线性优化算法研究领域,双种群架构是增强算法寻优能力的重要思路。赵燕伟等[19]实现了基于双种群的遗传算法,指出改进算法可以提高算法的全局收敛性能;吴亮红等[20]提出一种双种群差分进化(DE)算法,不同的种群使用不同的变异策略,仿真实验表明该算法全局搜索能力强、收敛速度快;暴励等[21]采用双种群架构使ABC算法与DE算法并行进化,每隔一定进化次数就分别比较两个种群的最优解个体,用最优个体替代次优个体,以促进种群间的相互学习;何光杰等[22]提出了一种双种群的准粒子群算法,两个种群分别使用不同的粒子进化方式,增强了算法的寻优能力;陈亚峰等[23]借助双种群对萤火虫算法的种群进行了全局和局部种群划分,一定程度上解决了萤火虫算法全局搜索和局部搜索不能兼顾、快速收敛和过早停滞相矛盾的问题。
基于前人的研究成果,本文提出一种基于双种群架构的ABC算法,并以大地电磁测深(MT)和重力联合反演为例,验证该算法的适用性和实用性。
1 基于双种群架构的ABC算法 1.1 方法原理标准ABC算法的基本流程可以概括为以下四个方面:蜜源的生成、引领蜂寻找更优质蜜源、跟随蜂决定是否跟随及判断是否达到局部搜索限制次数[24]。在标准ABC算法的基础上,本文提出基于双种群架构的改进ABC算法:将种群一分为二,在种群1中,尝试引入交叉和变异策略以提高ABC算法的搜索效率;在种群2中,尝试引入最优解邻域搜索以提高ABC算法的局部寻优能力。两个种群每经历一定代数后就进行互相交流。
1.1.1 变异和交叉操作在标准ABC算法生成蜜源阶段,只对模型分量进行随机的一维搜索,即
| $ U_{i, d}^{1 \mathrm{a}}=X_{i, d}^{t}+\alpha\left(X_{i, d}^{t}-X_{j, d}^{t}\right) $ | (1) |
式中:
在标准ABC算法搜索策略更新的蜜源U1a劣于上代蜜源时,按照下式进行搜索以提高寻优效率
| $ U_{i, d}^{1 \mathrm{~b}}= \begin{cases}X_{i, d}^{t}+F\left(X_{j, d}^{t}-X_{i, d}^{t}\right) & \operatorname{rand}(0, 1)<\mathrm{CR} \\ X_{i, d}^{t} & \text { 其他 }\end{cases} $ | (2) |
式中:U1b是根据变异和交叉操作搜索出的新蜜源;F和CR分别表示变异因子和交叉因子,取值范围均为[0, 1];rand (·)表示取随机数。
1.1.2 最优解邻域搜索上节介绍的变异和交叉操作加快了对个体的开发,但是优质蜜源在蜂群中仍然无法传播。故此,本文在种群2中加入最优解邻域搜索策略,利用下式对优质蜜源进行充分开采
| $ U_{i, d}^{2}=X_{\text {best }}+\left(X_{\text {best }}-X_{i, d}\right) $ | (3) |
式中:U2是种群2更新的蜜源;Xbest表示种群2中的最优个体,该参数的引入旨在提高ABC算法局部寻优能力并加快收敛速度。具体而言,式(3)表示将上次迭代中的最优个体作为被继承的父代,在最优解邻域进行探索。
两个种群每隔一定的代数就分别随机选取若干个个体并交换其在种群中的位置,进而促进优良蜜源信息在种群间的传播。该操作可在平衡全局寻优和局部寻优能力的同时维护种群的多样性,进一步提高解的搜索效率。
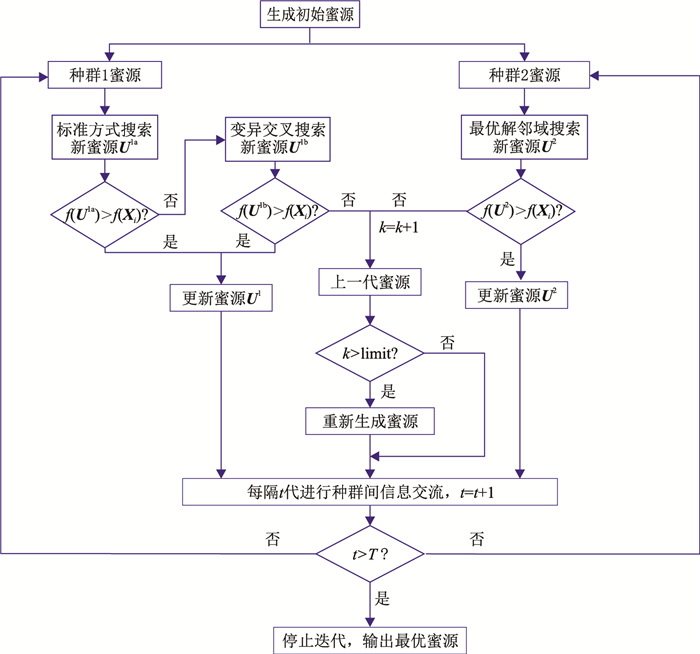
1.1.3 基本流程基于双种群架构的ABC算法流程见图 1,具体如下。
|
图 1 改进ABC算法流程图 |
(1) 生成初始蜜源:设置最大蜜源数、局部限制次数limit、最大迭代次数T。将蜜源平均分为两部分,即种群1和种群2。
(2) 种群1中的引领蜂搜寻蜜源:在种群1中,引领峰按照标准ABC算法搜索策略(式(1))搜索新蜜源,对比新蜜源适应度f(U1a)与上一次迭代发现蜜源的适应度f(Xi)并择优选择,若发现新蜜源的适应度优于上次迭代发现蜜源,则保留新蜜源,直接进入步骤(3);反之,按照式(2)借鉴交叉和变异的思想搜索新蜜源,再对比新蜜源的适应度f(U1b)与上一次迭代发现蜜源的适应度,择优选择新蜜源。
(3) 种群2中的引领峰搜索蜜源:在种群2中,按照式(3)在最优解附近搜索蜜源,同样对比新蜜源适应度f(U2)与上一次迭代发现蜜源的适应度,择优选择新蜜源。每迭代一定次数,两个种群随机交换种群中若干个蜜源的位置, 生成新蜜源。
(4) 跟随蜂的局部寻优:完成上述过程后,引领蜂飞回,与跟随蜂交流,与标准ABC算法一样,利用轮盘赌的方式计算跟随概率,然后选择是否更新。
(5) 判断蜜源Xi经历的局部搜索次数k是否大于限制次数limit:若是,则该引领蜂转变为侦察蜂,同时按照初始蜜源的生成方式产生新蜜源; 若否,保留该蜜源。
(6) 转到步骤(2)进行下一次循环, 直到满足最大迭代次数。
1.2 算法测试本文选择三种典型的测试函数[25]检验改进ABC算法的性能。
Griewank函数是典型的非线性多模态函数,其全局最小值0在(x1, x2, …, xn)=(0, 0, …, 0)处取得。此函数存在许多局部极小值点,并随着问题维数的增加而增加。此函数在优化过程中,具有广阔的搜索空间,通常被认为是优化算法很难处理的复杂多模态问题。其函数形式为
| $ \begin{aligned} f_{1}\left(x_{n}\right) &=\sum\limits_{n=1}^{N} \frac{x_{n}^{2}}{4000}-\prod\limits_{n=1}^{N} \cos \frac{x_{n}}{\sqrt{n}}+1 \\ &-600 \leqslant x_{n} \leqslant 600 \end{aligned} $ | (4) |
式中N表示函数的维度。
Resenbrock函数是一个测试最优化算法性能的非凸函数,全局最小值0在(x1, x2, …, xn)=(1, 1, …, 1)处取得,可用来检测算法的精度。其函数形式为
| $ \begin{gathered} f_{2}\left(x_{n}\right)=\sum\limits_{n=1}^{N-1}\left[100\left(x_{n+1}-x_{n}^{2}\right)^{2}+\left(x_{n}-1\right)^{2}\right] \\ -15 \leqslant x_{n} \leqslant 15 \end{gathered} $ | (5) |
Rastrigin函数存在多个波峰与波谷,易陷入局部极小,全局最小值0在(x1, x2, …xn)=(0, 0, …, 0)处取得,可用来检测算法跳出局部极小的能力。其函数形式为
| $ \begin{array}{c} {f_3}\left( {{x_n}} \right) = \sum\limits_{n = 1}^N {\left[ {x_n^2 - 10\cos \left( {2{\rm{ \mathsf{ π} }}{x_n}} \right) + 10} \right]} \\ - 15 \le {x_n} \le 15 \end{array} $ | (6) |
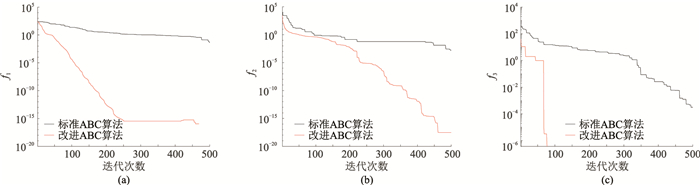
分别利用标准和改进的ABC算法对上述三种函数进行寻优测试,迭代次数设为500,每种算法独立重复试验30次,试验结果见表 1和图 2。可看出,与标准ABC算法相比,改进后的ABC算法不仅有较快的收敛速度,收敛精度也有较大提高,具有较强的全局寻优能力。
|
|
表 1 两种算法寻优结果对比 |
|
图 2 基于标准的和改进的ABC算法的不同函数进化曲线 (a)Griewank函数;(b)Resenbrock函数;(c)Rastrigin函数 |
根据正则化反演理论[26],MT数据和重力数据正则化联合反演的目标函数为
| $ \begin{gathered} P^{\beta}(\boldsymbol{m})=w^{\mathrm{MT}}\left(\left\|\boldsymbol{d}_{\mathrm{obs}}^{\mathrm{MT}}-\boldsymbol{d}_{\mathrm{cal}}^{\mathrm{MT}}\right\|^{2}+\beta^{\mathrm{MT}}\left\|\nabla \boldsymbol{m}^{\mathrm{MT}}\right\|^{2}\right)+ \\ w^{\mathrm{G}}\left(\left\|\boldsymbol{d}_{\mathrm{obs}}^{\mathrm{G}}-\boldsymbol{d}_{\mathrm{cal}}^{\mathrm{G}}\right\|^{2}+\beta^{\mathrm{G}}\left\|\nabla \boldsymbol{m}^{\mathrm{G}}\right\|^{2}\right) \end{gathered} $ | (7) |
式中:Pβ(m)表示联合反演目标函数,m表示模型向量,β是正则化因子;
本文采取双正则化因子自适应调整方案[27-28]。MT数据正演采用有限差分法,重力数据正演采用网格累加法。联合反演建模采用于鹏等[29]提出的物性参数随机分布的共网格模型建模技术,该技术已被应用于多种地球物理方法的二维联合反演[5-6, 30-33]。
3 模型测试 3.1 模型试验一为了验证ABC算法在二维MT和重力数据联合反演中的应用效果,设计了图 3所示的电阻率和密度模型。模型的背景电阻率为1000Ω·m,密度为2.68g/cm3。模型中包含四个异常体。MT数据的模拟频率范围为0.001~320Hz,按对数等间距取38个频点,测点间距为1km。

|
图 3 模型一电阻率(a)和密度(b)模型 |
设计了三种反演方案:方案一为基于标准ABC算法的联合反演;方案二为基于双种群架构的ABC算法单独反演;方案三为基于双种群架构的ABC算法联合反演。这三种方案的蜜源数量最大值均设为300,最大迭代次数为50。种群中初始蜜源位置按照真实模型上下扰动一定范围随机生成:异常体的上下界面深度扰动范围为真实值±30%,电阻率扰动范围为真实值±30%,密度扰动范围为真实值±0.02g/cm3。
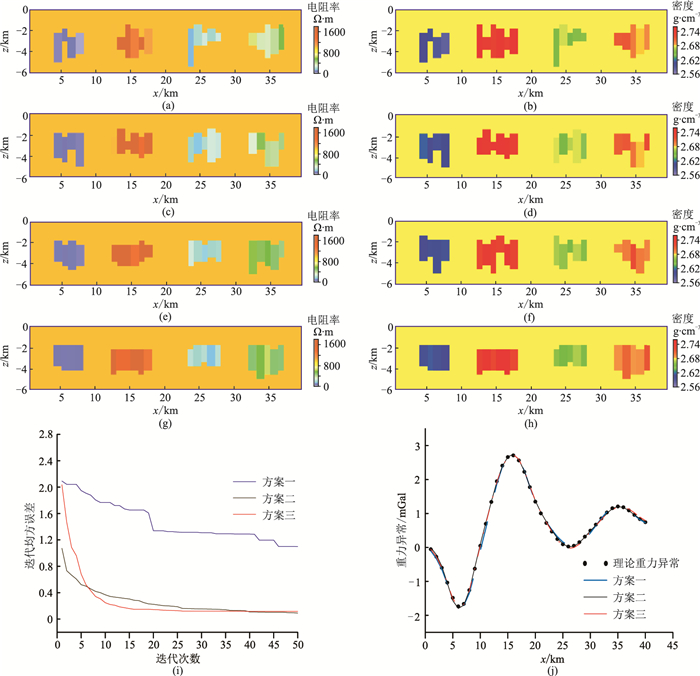
初始模型及反演结果见图 4。图 4a、图 4b是随机生成的电阻率和密度的初始扰动模型。首先,对比基于改进ABC算法的联合反演(方案三)和单独反演(方案二)结果,可以看到,虽然重力异常曲线(图 4j)的拟合效果都较好,但是单独反演结果(图 4f)的物性及界面还原效果较差。不同方案的反演结果与真实模型的残差(图 5)也表明,联合反演优于单独反演。
|
图 4 模型一及不同方案反演结果 (a)初始电阻率扰动模型;(b)初始密度扰动模型;(c)方案一电阻率联合反演结果;(d)方案一密度联合反演结果;(e)方案二电阻率单独反演结果;(f)方案二密度单独反演结果;(g)方案三电阻率联合反演结果;(h)方案三密度联合反演结果;(i)反演目标函数迭代误差曲线;(j)重力异常拟合曲线 |
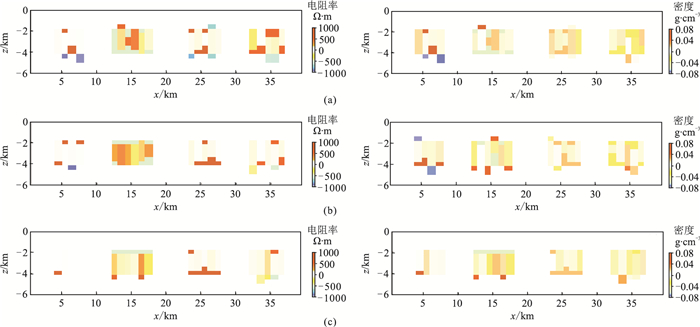
|
图 5 不同方案电阻率(左)和密度(右)反演结果与理论模型的残差 (a)方案一;(b)方案二;(c)方案三 |
对比基于标准ABC算法的联合反演(方案一)与基于改进ABC算法的联合反演(方案三)结果可见,在标准ABC算法的反演结果(图 4c、图 4d)中,界面起伏严重,物性差异大;而采用基于双种群架构的联合反演(图 4g、图 4h),物性界面起伏小且物性分布连续。由图 5的残差图也可以看出,标准ABC算法的反演结果偏离真实模型较大。此外,从迭代误差曲线(图 4i)也可以看出,改进ABC算法收敛快、寻优精度高。
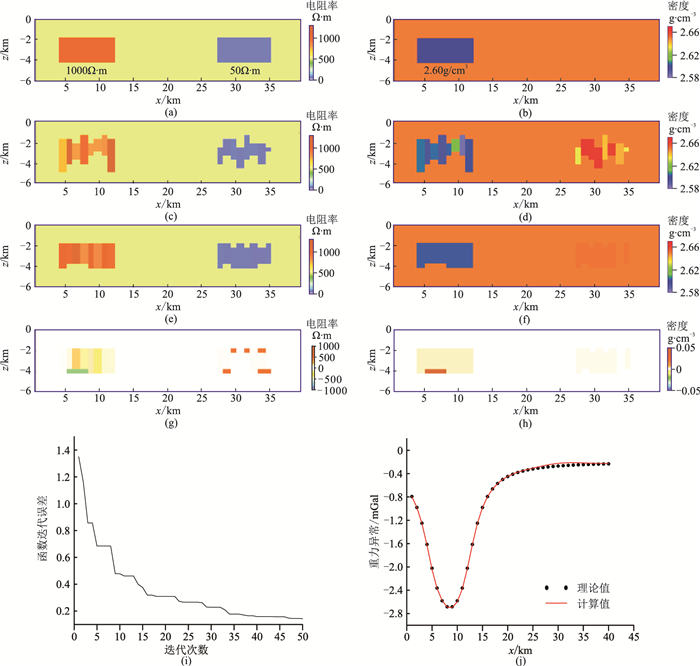
3.2 模型试验二为了检验本文反演算法对复杂模型的适应性,本文设计了图 6所示的电阻率界面与密度界面不完全一致的地球物理模型。该模型的背景电阻率为500Ω·m,背景密度为2.65g/cm3。反演过程中,假设电阻率和密度都是完全共界面进行扰动,其余参数设置与前述模型试验相同。初始扰动模型见图 6c和图 6d,基于改进ABC算法的联合反演结果见图 6e和图 6f。可以看出,反演的电阻率和密度异常分布与理论模型基本相符。从图 6i所示的迭代误差曲线及图 6j所示的重力异常拟合曲线也可以看出,反演得到的异常体电阻率和密度分布基本可靠。
|
图 6 模型二及联合反演结果 (a)电阻率模型;(b)密度模型;(c)初始电阻率扰动模型;(d)初始密度扰动模型;(e)电阻率联合反演结果;(f)密度联合反演结果;(g)电阻率残差;(h)密度残差;(i)目标函数迭代误差曲线;(j)重力异常拟合曲线 |
为进一步验证改进ABC算法的实用性,选择中国下扬子地区某测线MT和重磁实测数据进行联合反演。
依据测线实测数据的OCCAM反演结果、物性统计及文献[33]所揭示的构造格架建立初始模型,并对待解参数进行随机扰动(图 7)。反演过程对Tg印支面以上的界面不做反演,对其以下界面进行开放反演。物性约束范围根据该测区的岩石物性资料统计给定,见表 2。

|
图 7 实际测线电阻率(a)和密度(b)初始扰动模型 |
|
|
表 2 工区物性统计结果 |
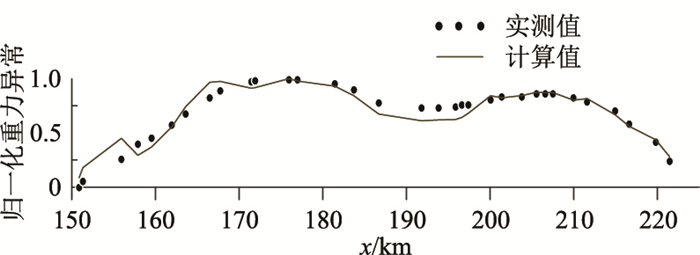
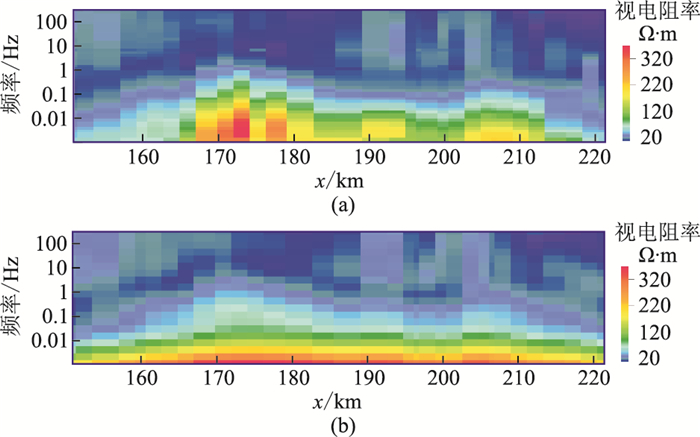
对比电阻率和密度的初始扰动结果,可见电阻率和密度的联合反演剖面(图 8)具有明显的成层性。此外,在反演剖面横向185~200km、纵向-5~-8km范围内,存在物性分布变化剧烈的地层,结合两侧的物性分布特征,推测此处可能存在断裂。反演的密度和电阻率模型的正演响应与实测数据的对比分别见图 9和图 10。上述认识与文献[33]基于模拟退火算法的联合反演结果也基本相符,验证了本文提出的双种群ABC算法的实用性。

|
图 8 基于双种群ABC算法的实测数据联合反演的电阻率(a)和密度(b)剖面 |
|
图 9 重力异常拟合曲线 |
|
图 10 实测视电阻率剖面(a)及反演结果对应的视电阻率剖面(b) |
(1) 本文通过双种群架构将蜂群一分为二。种群1结合标准ABC算法和变异交叉操作策略,保证了算法的全局寻优能力,又提高了解的搜索效率;种群2则利用最优解邻域的搜索,增强了算法的局部寻优能力。算法测试和模型试验结果证明双种群架构可以提高ABC算法的寻优能力。
(2) MT和重力数据联合反演模型试验及实际数据处理结果表明,MT与重力数据的联合反演优于单独MT或重力数据反演,改进ABC算法可以应用于实际数据处理,具有一定的实用性。
需要指出的是,ABC算法具有很强的开发潜力,多种群的设置方案也是不唯一的,如何进一步提升该算法的寻优能力值得进一步研究。
| [1] |
刘光鼎. 地球物理引论[M]. 上海: 上海科学技术出版社, 2005.
|
| [2] |
于鹏, 王家林, 吴健生, 等. 地球物理联合反演的研究现状和分析[J]. 勘探地球物理进展, 2006, 29(2): 87-92. YU Peng, WANG Jialin, WU Jiansheng, et al. Review and discussions on geophysical joint inversion[J]. Progress in Exploration Geophysics, 2006, 29(2): 87-92. |
| [3] |
相鹏, 王金铎, 谭绍泉, 等. 一种变密度-速度关系的重力与地震同步联合反演方法[J]. 石油地球物理勘探, 2020, 55(3): 686-693. XIANG Peng, WANG Jinduo, TAN Shaoquan, et al. A combined inversion method of gravity and seismic synchronization with variable density-velocity relationship[J]. Oil Geophysical Prospecting, 2020, 55(3): 686-693. |
| [4] |
彭国民, 刘展. 电磁和地震联合反演研究现状及发展趋势[J]. 石油地球物理勘探, 2020, 55(2): 465-474. PENG Guomin, LIU Zhan. The current status and development trend of joint inversion of electromagne-tic and seismic[J]. Oil Geophysical Prospecting, 2020, 55(2): 465-474. |
| [5] |
陈晓, 于鹏, 邓居智, 等. 基于宽范围岩石物性约束的大地电磁和地震联合反演[J]. 地球物理学报, 2016, 59(12): 4690-4700. CHEN Xiao, YU Peng, DENG Juzhi, et al. Joint inversion of MT and seismic data based on wide-range petrophysical constraints[J]. Chinese Journal of Geophysics, 2016, 59(12): 4690-4700. DOI:10.6038/cjg20161228 |
| [6] |
陈晓, 于鹏, 张罗磊, 等. 地震与大地电磁测深数据的自适应正则化同步联合反演[J]. 地球物理学报, 2011, 54(10): 2673-2681. CHEN Xiao, YU Peng, ZHANG Luolei, et al. Adaptive regularized synchronous joint inversion of MT and seismic data[J]. Chinese Journal of Geophysics, 2011, 54(10): 2673-2681. DOI:10.3969/j.issn.0001-5733.2011.10.024 |
| [7] |
于鹏, 王家林, 吴健生, 等. 重力与地震资料的模拟退火约束联合反演[J]. 地球物理学报, 2007, 50(2): 529-538. YU Peng, WANG Jialin, WU Jiansheng, et al. Constrained joint inversion of gravity and seismic data using the simulated annealing algorithm[J]. Chinese Journal of Geophysics, 2007, 50(2): 529-538. DOI:10.3321/j.issn:0001-5733.2007.02.026 |
| [8] |
过仲阳, 王家林, 吴健生. 应用遗传算法联合反演地震-大地电磁测深数据[J]. 石油物探, 1999, 38(1): 3-5. GUO Zhongyang, WANG Jialin, WU Jiansheng. Joint inversion of seismic and magnetotelluric sounding data using genetic algorithm[J]. Geophysical Prospecting for Petroleum, 1999, 38(1): 3-5. |
| [9] |
万玲, 林婷婷, 林君, 等. 基于自适应遗传算法的MRS-TEM联合反演方法研究[J]. 地球物理学报, 2013, 56(11): 3728-3740. WAN Ling, LIN Tingting, LIN Jun, et al. Joint inversion of MRS and TEM data based on adaptive genetic algorithm[J]. Chinese Journal of Geophysics, 2013, 56(11): 3728-3740. DOI:10.6038/cjg20131114 |
| [10] |
扈本娜. 浅层电震非线性反演理论的研究[D]. 河北石家庄: 石家庄经济学院, 2013.
|
| [11] |
Zeng Z W, Chen X, Liu X, et al. Joint inversion of MT and gravity based on differential evolution algorithm[C]. China International Geoelectromagnetic Workshop, 2019.
|
| [12] |
胡祖志, 石艳玲, 刘云祥, 等. 电磁与重力数据非线性约束联合反演[J]. 石油地球物理勘探, 2020, 55(1): 226-232. HU Zuzhi, SHI Yanling, LIU Yunxiang, et al. Nonlinear constrained joint inversion of MT and gravity data[J]. Oil Geophysical Prospecting, 2020, 55(1): 226-232. |
| [13] |
Karaboga D. An Idea Based on Honey Bee Swarm for Numerical Optimization[R]. Erciyes University, Kayseri, 2005.
|
| [14] |
王猛, 刘国辉, 王大勇, 等. 瞬变电磁测深资料的ABC算法反演研究[J]. 地球物理学进展, 2015, 30(1): 133-139. WANG Meng, LIU Guohui, WANG Dayong, et al. Application of ABC algorithm inversion of transient electromagnetic sounding files[J]. Progress in Geophysics, 2015, 30(1): 133-139. |
| [15] |
侯征, 熊盛青, 杨进, 等. 基于人工蜂群算法的瑞雷波多阶模式非线性联合反演研究[J]. 地球物理学进展, 2018, 33(1): 362-371. HOU Zheng, XIONG Shengqing, YANG Jin, et al. Research on nonlinear joint inversion of multimode Rayleigh wave based on artificial bee colony algorithm[J]. Progress in Geophysics, 2018, 33(1): 362-371. |
| [16] |
Wen L F, Cheng J L, Li F, et al. Global optimization of controlled source audio-frequency magnetotelluric data with an improved artificial bee colony algorithm[J]. Journal of Applied Geophysics, 2019, 170: 103845. DOI:10.1016/j.jappgeo.2019.103845 |
| [17] |
Zhu G, Kwong S. Best-guided artificial bee colony algorithm for numerical function optimization[J]. Applied Mathematics and Computation, 2010, 217(7): 3166-3173. DOI:10.1016/j.amc.2010.08.049 |
| [18] |
Banharnsakun A, Achalakul T, Sirinaovakul B. The Best-So-Far selection in artificial bee colony algorithm[J]. Applied Soft Computing, 2011, 11(2): 2888-2901. |
| [19] |
赵燕伟, 吴斌, 蒋丽, 等. 车辆路径问题的双种群遗传算法求解方法[J]. 计算机集成制造系统, 2004, 10(3): 303-306. ZHAO Yanwei, WU Bin, JIANG Li, et al. Double populations genetic algorithm for vehicle routing problem[J]. Computer Integrated Manufacturing System, 2004, 10(3): 303-306. |
| [20] |
吴亮红, 王耀南, 周少武, 等. 双群体伪并行差分进化算法研究及应用[J]. 控制理论与应用, 2007, 24(3): 453-458. WU Lianghong, WANG Yaonan, ZHOU Shaowu, et al. Research and application of pseudo parallel diffe-rential evolution algorithm with dual subpopulation[J]. Control Theory and Application, 2007, 24(3): 453-458. |
| [21] |
暴励, 曾建潮. 一种双种群差分蜂群算法[J]. 控制理论与应用, 2011, 28(2): 266-272. BAO Li, ZENG Jianchao. A dual-population differe-ntial bee colony algorithm[J]. Control Theory and Application, 2011, 28(2): 266-272. |
| [22] |
何杰光, 陈新度, 陈新, 等. 求解资源受限项目调度的双种群准粒子群算法[J]. 计算机集成制造系统, 2015, 21(9): 2446-2457. HE Jieguang, CHEN Xindu, CHEN Xin, et al. Double-population quasi particle swarm optimization for solving resource-constrained scheduling problem[J]. Computer Integrated Manufacturing System, 2015, 21(9): 2446-2457. |
| [23] |
陈亚峰, 张晓明, 曹国清, 等. 双种群协同下带混沌闪烁机制的萤火虫算法研究[J]. 西安交通大学学报, 2018, 52(3): 153-159. CHEN Yafeng, ZHANG Xiaoming, CAO Guoqing, et al. Research on firefly algorithm with chaotic blinking mechanism under dual-population cooperation[J]. Journal of Xi'an Jiaotong University, 2018, 52(3): 153-159. |
| [24] |
曾志文, 郭一豪. 基于人工蜂群算法的大地电磁测深二维反演[J]. 江西科学, 2020, 38(5): 701-704. ZENG Zhiwen, GUO Yihao. Two-dimensional magnetotelluric inversion based on artificial bee colony algorithm[J]. Jiangxi Science, 2020, 38(5): 701-704. |
| [25] |
Srinivasan D, Seow T H. Particle Swarm Inspired Evo-lutionary Algorithm(PS-EA) for Multi-Objective Optimization Problems[M]. London: Springer, 2003.
|
| [26] |
Zhdanov M S. Geophysical Inverse Theory and Regularization Problems[M]. Netherlands: Elsevier Science, 2002.
|
| [27] |
向阳, 于鹏, 陈晓, 等. 大地电磁反演中改进的自适应正则化因子选取[J]. 同济大学学报(自然科学版), 2013, 41(9): 1429-1434. XIANG Yang, YU Peng, CHEN Xiao, et al. An improved adaptive regularized parameter selection in magnetotelluric inversion[J]. Journal of Tongji University (Natural Science Edition), 2013, 41(9): 1429-1434. |
| [28] |
陈晓, 张磊, 郭曼, 等. 大地电磁测深和重力数据同步正则化联合反演[J]. 科学技术与工程, 2016, 16(8): 54-58. CHEN Xiao, ZHANG Lei, GUO Man, et al. Regula-rized synchronous joint inversion of magnetotelluric and gravity data[J]. Science Technology and Engineering, 2016, 16(8): 54-58. |
| [29] |
于鹏, 王家林, 吴健生. 二度半长方体组合模型的重力模拟退火反演[J]. 地球物理学报, 2007, 50(3): 882-889. YU Peng, WANG Jialin, WU Jiansheng. An inversion of gravity anomalies by using a 2.5 dimensional rectangle gridded model and the simulated annealing algorithm[J]. Chinese Journal of Geophysics, 2007, 50(3): 882-889. |
| [30] |
陈晓, 于鹏, 邓居智, 等. 地球物理联合反演新框架研究[J]. 石油地球物理勘探, 2017, 52(4): 851-858, 883. CEHN Xiao, YU Peng, DENG Juzhi, et al. Research on new framework of geophysical joint inversion[J]. Oil Geophysical Prospecting, 2017, 52(4): 851-858, 883. |
| [31] |
郭曼, 邓居智, 陈晓, 等. 基于岩石物性约束的大地电磁与重力贝叶斯联合反演[J]. 地球物理学进展, 2018, 33(5): 1897-1902. GUO Man, DENG Juzhi, CHEN Xiao, et al. Bayesian joint inversion of magnetotelluric and gravity based on rock property constraints[J]. Progress in Geophy-sics, 2018, 33(5): 1897-1902. |
| [32] |
曾志文, 陈晓, 杨海燕, 等. 基于改进差分进化算法的大地电磁测深和重力宽范围物性约束联合反演[J]. 地球物理学报, 2020, 63(12): 4565-4577. ZENG Zhiwen, CHEN Xiao, YANG Haiyan, et al. Joint inversion of magnetotelluric and gravity based on improved differential evolution algorithm and wide-range petrophysical constraints[J]. Chinese Journal of Geophysics, 2020, 63(12): 4565-4577. |
| [33] |
李华东, 于鹏, 刘振友. 基于随机分布共网格模型的重磁电震联合反演技术及应用[J]. 石油地球物理勘探, 2015, 50(4): 742-748. LI Huadong, YU Peng, LIU Zhenyou. Joint inversion technology and application of gravity, magnetotelluric and seismic data based on random distributed common grid model[J]. Oil Geophysical Prospecting, 2015, 50(4): 742-748. |



 陈晓, 江西省南昌市广兰大道418号东华理工大学地球物理与测控技术学院, 330013。Email:
陈晓, 江西省南昌市广兰大道418号东华理工大学地球物理与测控技术学院, 330013。Email: 